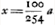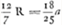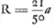Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 408]
| |||||||||||||||||||||||||||||||||||
Appendice VIGa naar voetnoot1)
| |||||||||||||||||||||||||||||||||||
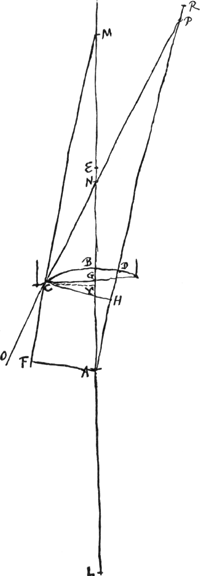
§ 1Ga naar voetnoot3).Aberratio superficiei cavae CBD, radio veniente ex M qui in Crefractus tendit per CO, retroque productus, occurrere axi ponitur in N. A est centr. superficiei CBD. AL ∞ 2AB. CG perpend. in BA. Sit AB ∞ a, BG ∞ b, MB ∞ d. ML (d+3a) ad MA (a+d) ut MB (d) ad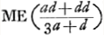 . E erit punctum dispersus radiorum ex M venientiumGa naar voetnoot4).
Sit AR parall. CM. Et DR ∞ 2 DA ∞ 2a. Item . E erit punctum dispersus radiorum ex M venientiumGa naar voetnoot4).
Sit AR parall. CM. Et DR ∞ 2 DA ∞ 2a. Item 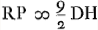 Ga naar voetnoot5), positâ CH perpend. in DA. Erit recta PCO refractio radij MC, secundum examinata in dioptricis nostrisGa naar voetnoot6). Sit AF parall. CH. Et centro M descriptus arcus CY.
MC (d+minimo) ad AB (a) ut BG (b) Ga naar voetnoot5), positâ CH perpend. in DA. Erit recta PCO refractio radij MC, secundum examinata in dioptricis nostrisGa naar voetnoot6). Sit AF parall. CH. Et centro M descriptus arcus CY.
MC (d+minimo) ad AB (a) ut BG (b)
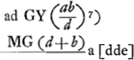 Ga naar voetnoot7) | |||||||||||||||||||||||||||||||||||
[pagina 409]
| |||||||||||||||||||||||||||||||||||
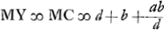 ut qu. MC (dd+minimo) ad qu. MA (dd+2ad+aa) sive ut qu. CG ad qu. AF vel CH ita BG (b) ad 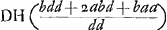 Ga naar voetnoot8). Ga naar voetnoot8).
| |||||||||||||||||||||||||||||||||||
[pagina 410]
| |||||||||||||||||||||||||||||||||||
 [Fig. 1.]
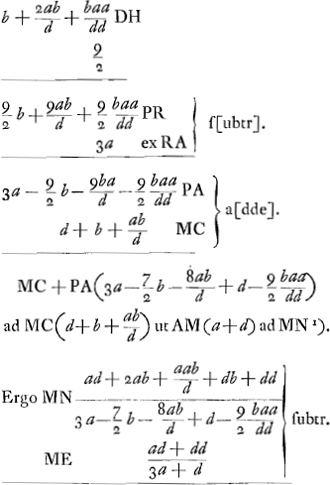 Ga naar voetnoot1) Ut auferatur ME ab MN, ducantur alternis denominatores in numeratores et productorum differentiae subscribetur denominator communis hoc est productum duorum denominatorum, quod neglectis minimis est qu. 3a+dGa naar voetnoot2). 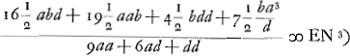 Ga naar voetnoot3) Si d infinite magna ponatur patet EN fore 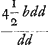 , hoc est 9/2 b, ut oportet. , hoc est 9/2 b, ut oportet.
| |||||||||||||||||||||||||||||||||||
[pagina 411]
| |||||||||||||||||||||||||||||||||||
§ 2Ga naar voetnoot4).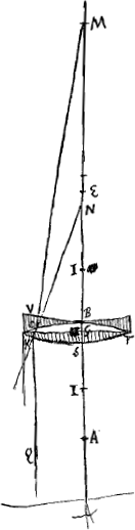 [Fig. 2.]
Cum radij MC refractio pertineat ad punctum N, aberrans à puncto dispersus E spatio EN; erunt eaedem aberrationes lentis cavae VBC [Fig. 2] si intelligatur superficies altera BV habere centrum M, quia hanc sine refractione radius MC penetrabit. Quod si jam lentem KST convexam ejusmodi invenire possim et cum cava componere, quae radium axi parallelum QK ipsi MC respondentem, hoc est, distantiam ab axe KS ipsi CB aequalem habentemGa naar voetnoot5), refringat versus N, focumque habeat et ipsa E punctum; Idem radius penetrata deinde lente cava CBV tendet ad punctum M. Eodemque dirigentur omnes radij paralleli axi AS, quoniam unâ aberratione respondentium radiorum aequali utrimque existente, omnes etiam reliquae inter se aequales sunt ut patet ex demonstratis in dioptr.Ga naar voetnoot6). Ponatur factum et sit lens KST quae id efficiat. Oportet igitur foci distantiam ejus esse aequalem GE, sive BE, nam hae aequales censendae sunt, quoniam lentes magnae spherae consideramus ubi crassitudinem pro nulla habemus. Sit ergo haec foci distantia lentis KSTG, nempe BE ∞ ∞ 2x. quia ergo posita BM ∞ d, erat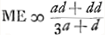 Ga naar voetnoot7), auferendoque eam ab MB ∞ d fiebat distantia puncti dispersus Ga naar voetnoot7), auferendoque eam ab MB ∞ d fiebat distantia puncti dispersus 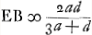 . Erunt aequalia . Erunt aequalia 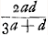 et 2x. Unde et 2x. Unde 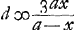 . .
| |||||||||||||||||||||||||||||||||||
[pagina 412]
| |||||||||||||||||||||||||||||||||||
 [Fig. 2.]
Porro quia foci distantia lentis convexae KST eâdem manente, itemque lentis latitudine, eadem quoque semper est crassitudo (quid vocetur crassitudo, in dioptr.)Ga naar voetnoot1) intelligatur primum lens KST planoconvexa; quia igitur proportio refractionis ponitur 3 ad 2, erit ut 2 ad 3 ita foci distantia EB ∞ 2x ad ipsam EB + radio convexi KSTGa naar margenoot*, hoc est ad 3x; unde ablata EB ∞ 2x, erit radius convexi KST ∞ x; diameter vero 2x. Quia autem arcuum CBT, KST eadem subtensa CT, erunt sinus versi BG ad GS reciproce ut diametriGa naar voetnoot3) itaque ut 2x ad 2a ita BG ∞ b ad GS ∞ ab/x; Itaque etiamsi non planoconvexa sed alia statuatur lens KST, tamen ejus crassitudo erit eadem ab/xGa naar voetnoot4). Quia vero aberratio EN erat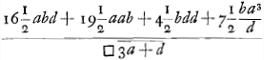 substituto ubique in locum d valore ejus substituto ubique in locum d valore ejus 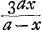 , fit , fit
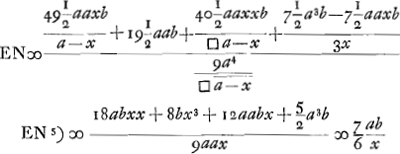 Ga naar voetnoot5) Ponatur jam KST lens convexa cujus aberratio aequatur 7/6 suae crassitudinis ab/xGa naar voetnoot6). Ergo 7/6 ab/x aequari debet aberrationi EN. | |||||||||||||||||||||||||||||||||||
[pagina 413]
| |||||||||||||||||||||||||||||||||||
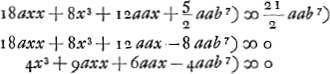 Ga naar voetnoot7)Ga naar voetnoot7)Ga naar voetnoot7)Ga naar voetnoot7) fit x proximè ∞ ⅖ a, sive accuratius 100/254 a. Diximus autem x esse radium convexi KST. Ergo is est ad radium cavi CBT ut 2 ad 5 proximè. Altera vero superficies lentis KST debet esse plana. Lentis vero cavae superficies altera VB radium habere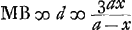 , quod aequabitur hic 2aGa naar voetnoot8), eademque erit foci distantia lentis compositae ex duabus VBC, KST, quae Hyperbolicae aut Ellipticae perfectionem aemulabitur. , quod aequabitur hic 2aGa naar voetnoot8), eademque erit foci distantia lentis compositae ex duabus VBC, KST, quae Hyperbolicae aut Ellipticae perfectionem aemulabitur.
Rad. cavae 1; alterius cavae 300/154; convexae 100/254; plano. vel 5133 Rad. cavae; 10000 alter. cavae; 2021 conv.; plana; 4042 foci dist. lentis convexae. Rad. alterius cavae semper aequalis est foci distantiae lentis ex duabus compositaeGa naar voetnoot9). | |||||||||||||||||||||||||||||||||||
§ 3Ga naar voetnoot10).Ponamus rursus lentem KST esse optimam illam cujus superficies utraque convexa, sed KST descripta sit radio qui sit ⅙ radij superficiei alterius KGTGa naar voetnoot11). Cujus lentis aberratio est 15/14 suae crassitudinis ergo ponendum 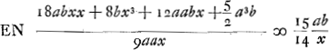 | |||||||||||||||||||||||||||||||||||
[pagina 414]
| |||||||||||||||||||||||||||||||||||
vel ad faciliorem calculum, ponendo x ∞ z-¾a, erit aequatio resolvenda hujusmodi 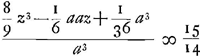 quae ad quamlibet lentem accommodata est, ita ut tantum proportionem aberrationis, ut hîc, ab una parte aequationis ponere opus sit, ab altera vero semper eaedem quantitates quae hic habeantur. 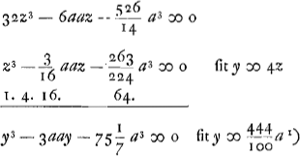 Ga naar voetnoot1). 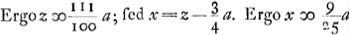 et 2 x foci dist. et 2 x foci dist. 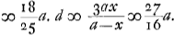
Radij convexae lentis sunt 21/50 aGa naar voetnoot2), et hujus sexcuplus. Radius cavi VB, eademque foci distantia compositae. Rad. superf. cavae 1; alterius cavae 27/16; convexae min. 21/50; conv. maj. 126/50. vel 593 Rad. cavae superfi.; 1000 alterius cavae et longitudo telesc.; 249 conv. minoris; 1493 conv. majoris; 427 foci dist. convexae lentis. | |||||||||||||||||||||||||||||||||||
[pagina 415]
| |||||||||||||||||||||||||||||||||||
§ 4Ga naar voetnoot3). [Fig. 3.]
Sit jam lens KST [Fig. 3] aequaliter utrimque convexa, cujus aberratio est 5/3 crassitudinisGa naar voetnoot4). 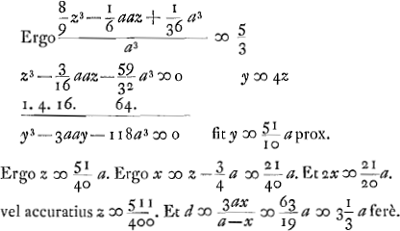 Quum 2x sit foci distantia lentis convexae, sitque aequaliter utrimque convexa, erit radius utriusque superficiei KST, KBT 2x hoc est 21/20a. At radius cavi interioris CB est a. Ergo proportio eorum ut 21 ad 20, ideoque cavum convexo fere convenit. at in totum convenire non posset, quia sic duae superficies istae inter se conjunctae nihil plane efficerent, eoque aberratio convexi KST non corrigeretur. Haec vero parva superficierum diversitas eam corrigit, nam calculus recte se habet. Superficies VB cava habebit radium MB ∞ d ∞ 3⅓a sere. | |||||||||||||||||||||||||||||||||||
§ 5Ga naar voetnoot5).Si KST ponatur lens planoconvexa, sed ita ut plana superficies radios parallelos excipiat, cujus aberratio est 9/2 crassitudinis. Ponendo | |||||||||||||||||||||||||||||||||||
[pagina 416]
| |||||||||||||||||||||||||||||||||||
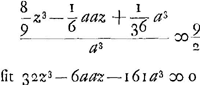 quod dividi potest per 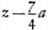 , fit enim 92aa+56az+32zz. Unde liquet tunc z esse 7/4a. Et , fit enim 92aa+56az+32zz. Unde liquet tunc z esse 7/4a. Et 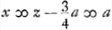 .
Tunc autem x est radius convexi, adeo ut tunc cavum exacte aptetur convexo. sed foci distantia lentis ita compositae d quae est .
Tunc autem x est radius convexi, adeo ut tunc cavum exacte aptetur convexo. sed foci distantia lentis ita compositae d quae est 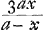 fit fit 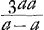 , hoc est infinitae extensionis, adeo ut plane inutilis sit lens ejusmodi, et revera vitro plano aequipollet. , hoc est infinitae extensionis, adeo ut plane inutilis sit lens ejusmodi, et revera vitro plano aequipollet.
Optima autem est compositio lentis proportionis sexcuplae de qua paulo ante, quia minus longe abscedit focus compositae. nam cum foci distantia lentis hujus convexae sit 18/25a, fit foci distantia compositae ex illa et cava 27/16, adeo ut illa sit ad hanc ut 1 ad 2⅓ fere. Parum autem huic cedit compositio planoconvexae, convexo ad radios parallelos converso. nam cum foci distantia ejus sit prox. ⅘a, fit foci distantia MB ∞ 2a, inter quae proportio est quae 1 ad 2½. Huic planoconvexae aequipollentem invenimusGa naar voetnoot1) in dioptr. aliam inaequaliter convexam cujus superficierum radij ut 5 ad 2, cujus nempe aberratio erit 7/6 crassitudinis, convexo minore ad radios obverso. quae itaque lens cum eadem cava componi poterit, eruntque radij 70/127 et 175/127 qualium cavi est 1, et altera 300/154. 5133 Rad. cavae superf. 10000 alter. cavae. 2829 conv. min. 7073 conv. maj. 4042 foci dist. convexae lentis. | |||||||||||||||||||||||||||||||||||
[pagina 417]
| |||||||||||||||||||||||||||||||||||
Lens e duabus composita hyperbolicam aemulaturGa naar voetnoot2).
6 febr. 1669 missum anagr. ad. Soc. Reg. Angl.Ga naar voetnoot3) |
|