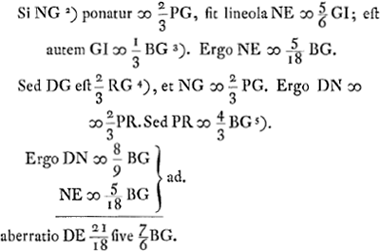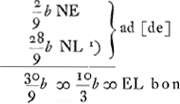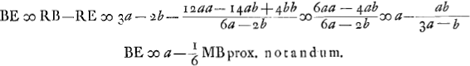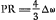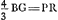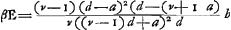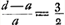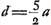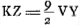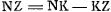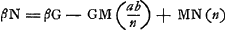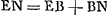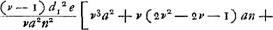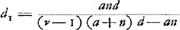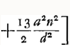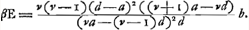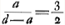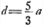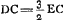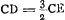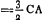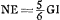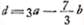|
-
voetnoot1)
- La pièce est empruntée aux p. 28-33 du manuscrit mentionné dans la note 1 de l'Appendice I, p. 355. Nous l'avons divisée en paragraphes.
-
voetnoot2)
- On trouvera d'autres recherches sur le même sujet au § 1 (p. 408) de l'Appendice VI et aux §§ 1 (p. 418), 4 (p. 420) et 6 (p. 424) de l'Appendice VII, de 1669.
-
voetnoot3)
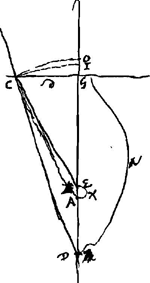
- A et N sont les centres des surfaces convexes de la lentille CΔBYM.
-
voetnoot4)
- À cause de la Prop. II, p. 275. On a πY = πC et on remplace dans le premier rapport πC par πB.
-
voetnoot5)
- Voir la Prop. I, p. 273. ΔωAPR est parallèle à Cπ; Aϕ et Cω sont perpendiculaires à cette ligne.
-
voetnoot6)
-
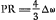 représente l'aberration sphérique du rayon CP qui provient du rayon tendant vers π, après sa réfraction à la surface CΔB, R étant le foyer, par rapport à cette surface, des rayons parallèles à Cπ. Comparez la formule représente l'aberration sphérique du rayon CP qui provient du rayon tendant vers π, après sa réfraction à la surface CΔB, R étant le foyer, par rapport à cette surface, des rayons parallèles à Cπ. Comparez la formule 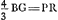 du § 1 de l'Appendice I, p. 357. du § 1 de l'Appendice I, p. 357.
-
voetnoot7)
- Voir la Prop. VIII, Part. I, Liv. I, p. 33.
-
voetnoot8)
- À cause de la similitude des triangles PAβ et Cπβ.
-
voetnoot10)
- Détermination, à l'aide de la Prop. XII, Part. I, Liv. I, p. 41, du point de concours E après la réfraction à la surface CΔB des rayons qui correspondent à π. Naturellement la même expression pour πE peut être obtenue en substituant b = o dans l'expression pour πβ.
-
voetnoot1)
- Plus généralement, en représentant par v l'indice de réfraction, on trouve:
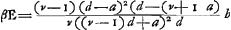 . .
-
voetnoot2)
- Consultez la p. 49 du Tome présent d'après laquelle le ‘casus perfectus’ se présente lorsque l'on a: πA/AB = v, c'est-à-dire, dans le cas du verre,
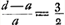 . Ce résultat est utilisé dans ce qui suit pour vérifier la justesse de l'expression pour βE qui doit, par conséquent, s'annuler pour . Ce résultat est utilisé dans ce qui suit pour vérifier la justesse de l'expression pour βE qui doit, par conséquent, s'annuler pour 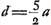 . .
-
voetnoot3)
- Danscette deuxième partie Huygens se propose de calculer l'aberration sphérique de la lentille entière BCMY. À cet effet il tire la droite NK parallèle à CP et calcule la valeur de VY à l'aide de la Prop. I, p. 273 pour en déduire celle de
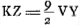 , qui représente l'aberration sphérique du rayon CP par rapport à la surface convexe CMY et qui aurait permis de calculer la valeur de , qui représente l'aberration sphérique du rayon CP par rapport à la surface convexe CMY et qui aurait permis de calculer la valeur de 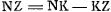 , puisqu'on a, d'après la Prop IX, Part. I, Liv. I, p. 37, NK = 3n, Kétant le foyer des rayons parallèles à CP par rapport à la même surface CMY. Comme il avait trouvé de plus Cβ et βG il lui était facile de déduire de cette dernière valeur celle de , puisqu'on a, d'après la Prop IX, Part. I, Liv. I, p. 37, NK = 3n, Kétant le foyer des rayons parallèles à CP par rapport à la même surface CMY. Comme il avait trouvé de plus Cβ et βG il lui était facile de déduire de cette dernière valeur celle de 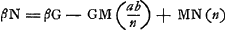 et de calculer ensuite par la similitude des triangles NDZ et CDβ la valeur de ND dont la différence d'avec la distance du point N au foyer de la lentille BΔCMY (à calculer à l'aide de la Prop. XVI, Part. I, Liv. I, p. 87) ferait enfin connaître l'aberration cherchée. Mais, comme on l'aperçoit, Huygens n'a pas conduit ce calcul par les dernières étapes, probablement à cause de la complication des formules. Voir à ce propos les dernières formules de la note 2 de la p. 396, dans lesquelles il suffit de remplacer d par - d pour trouver le résultat auquel Huygens aurait dû parvenir s'il avait poursuivi les calculs. et de calculer ensuite par la similitude des triangles NDZ et CDβ la valeur de ND dont la différence d'avec la distance du point N au foyer de la lentille BΔCMY (à calculer à l'aide de la Prop. XVI, Part. I, Liv. I, p. 87) ferait enfin connaître l'aberration cherchée. Mais, comme on l'aperçoit, Huygens n'a pas conduit ce calcul par les dernières étapes, probablement à cause de la complication des formules. Voir à ce propos les dernières formules de la note 2 de la p. 396, dans lesquelles il suffit de remplacer d par - d pour trouver le résultat auquel Huygens aurait dû parvenir s'il avait poursuivi les calculs.
-
voetnoot3)
-
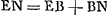 , mais on peut remplacer BN par MN = n, puisque les termes qui contiennent b sont supposés négligeables. , mais on peut remplacer BN par MN = n, puisque les termes qui contiennent b sont supposés négligeables.
-
voetnoot5)
- On a βC2:βN2 = CG2:FN2, à cause des triangles semblables βCG et βNF; mais FN = CV et CG2:CV2 = MG:VY, d'après la Prop. I, p. 273; donc βC2:βN2 = MG:VY, où l'on peut remplacer βC par EB et βN par EN avec une approximation suffisante.
-
voetnoot6)
- Toujours à cause de la Prop. II, p. 275. On a βC = βO; mais approximativement βC = EB. La valeur de GO va servir plus bas quand il s'agit de calculer βC plus exactement.
-
voetnoot7)
- Valeur trouvée plus haut vers la fin de la première partie.
-
voetnoot1)
- Huygens n'a pas poussé plus loin les calculs. Comparez la note 3 de la p. 395.
-
voetnoot2)
- Nous supprimons les calculs qui ont amené cette formule parce qu'ils sont analogues à ceux de la première partie de § 1 de cet Appendice. Inutile de dire que les résultats de cette première partie et du paragraphe présent peuvent se déduire l'un de l'autre par un simple changement de signe de la grandeur d.
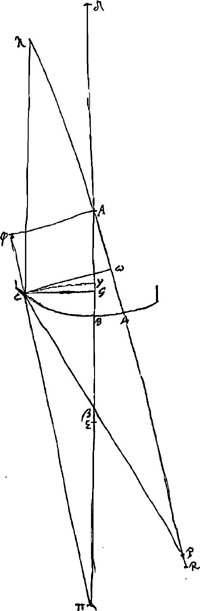
Quoique la figure indique qu'ici encore c'était l'intention de Huygens de déterminer l'aberration sphérique de la lentille entière, les calculs n'ont pas été poursuivis dans cette direction.
Toutefois, afin de nous en servir dans la suite, nous indiquerons ici le résultat sinal auquel les calculs auraient dû conduire dans le cas présent. Nous l'empruntons à la formule (293) du § 268, Chapitre XII, p. 388, de l'ouvrage de James P.C. Southall: ‘The principles and methods of geometrical optics’, New-York, Macmillan, 1910.
À cet effet nous remplaçons les notations de Southall par celles employées ici dans le texte, en représentant de plus par e l'épaisseur de la lentille entière, par dI la distance à la lentille du point qui correspond, par rapport à elle, au point π, et enfin par v l'indice de réfraction. Alors la formule mentionnée nous donne, après une légère réduction, pour l'aberration sphérique de la lentille entière l'expression suivante:
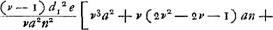 , où , où
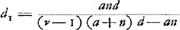
.
Posant ensuite, avec Huygens, v = 3/2, on trouve pour cette même aberration: 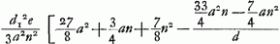 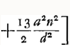 , où , où 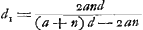 . .
-
voetnoot1)
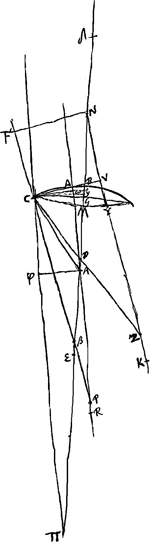
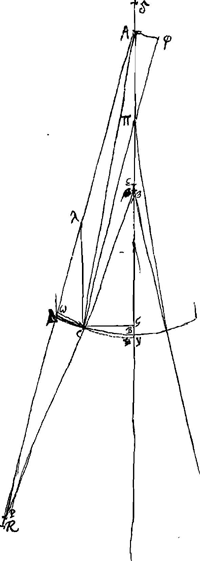
- A est le centre de la surface ΔCB; πC le rayon extrême; Cβ sa direction après la réfraction à la surface ΔCB; AλωΔPR est parallèle à πC; Cω et Aϕ lui sont perpendiculaires; Cλ est parallèle à l'axe AGY; de plus on a πY = πC. E est le point correspondant de π, par rapport à la surface réfringente ΔCB.
-
voetnoot4)
- On a
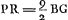 ; comparez la première partie du § 2 de l'Appendice I, p. 359. ; comparez la première partie du § 2 de l'Appendice I, p. 359.
-
voetnoot5)
- Voir la Prop. IX, Part. I, Liv. I, p. 37.
-
voetnoot6)
- Voir la Prop. XII, Part. I, Liv. I, p. 41; mais il aurait suffi de poser b = o dans l'expression pour πβ.
-
voetnoot7)
- Plus généralement on trouve, en remplaçant dans la formule de la note 1, p. 394, d par - d, a par-a et v par 1/v:
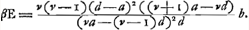
-
voetnoot8)
- Consultez la p. 69 d'après laquelle le ‘casus perfectus’ se présentera quand on aura BA/πA = v et qe la surface que le pointu'en même temps le point π se trouve plus éloigné de la surface que le point A. On aura donc ici:
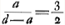 ; c'est-à-dire, ; c'est-à-dire, 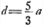 . .
-
voetnoot1)
- Aberration du rayon extrême ϕC d'un faisceau dirigé vers π avant sa réfraction à la surface CB, où le verre se trouve du côté du centre A. CβP est le rayon réfracté, R le foyer d'un faisceau de rayons parallèles à ϕC, E le point de concours des rayons réfractés du faisceau dirigé vers π.
Sur une autre feuille du manuscrit Huygens traite le cas, qu'on retrouvera encore dans le § 1 de l'Appendice VI, p. 408, où le verre se trouve du côté du point π, qui est, cette fois, l'origine du faisceau; ce qui amène la même formule. En effet, les positions des points E et β restent les mêmes dans les deux cas, le rayon πC suivant maintenant, après sa réfraction, le prolongement de βC.
-
voetnoot2)
- Nous avons supprimé les calculs à cause de leur ressemblance avec ceux du § 3, qui précède. Il est vrai que la signification de la lettre d s'écarte un peu de celle qu'elle a dans ce § 3. Cela entraîne, en effet, quelques changements dans les expressions pendant le calcul mais n'a pas d'influence sur le résultat qui se déduit d'ailleurs de celui du § 3 en substituant - d à d, et en changeant le signe de l'expression finale.
-
voetnoot3)
- Comparez la première partie du § 2 de l'Appendice I, p. 359.
-
voetnoot6)
- Voir le § 7, p. 405, où la formule pour βE est employée à calculer d'une nouvelle façon l'aberration sphérique d'une lentille biconvexe à courbure égale des deux faces pour un faisceau de rayons parallèles. La conformité du résultat obtenu de cette façon avec celui que nous avons indiqué dans la note 4 de la p. 365 est, en effet, une autre preuve de la justesse de cette formule.
-
voetnoot7)
- Voir la Prop. VII du Liv. I, p. 27 du Tome présent.
-
voetnoot8)
-
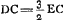 d'après la Prop. III, Part. I, Liv. I, p. 17. d'après la Prop. III, Part. I, Liv. I, p. 17.
-
voetnoot9)
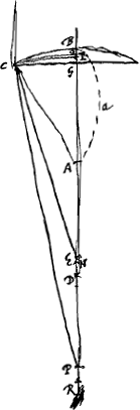
- GI = ⅔ GO d'après la Prop. II, p. 275, puisque
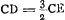 ou, par approximation, ou, par approximation, 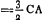 . .
-
voetnoot1)
- Inutile de dire que cette formule ne représente qu'un cas spécial de la formule du § 4; on l'obtient en remplaçant dans le premier terme du numérateur ab par ½CG2, en posant ensuite a = ∞, et en remplaçant enfin la d du § 4 par la lettre a, qui dans le paragraphe présent représente la même distance. Un autre cas, où un point lumineux se trouve au dehors du milieu réfringent limité par une surface plane sera traité au § 1 de l'Appendlce VII, p. 418, d'une manière entièrement différente.
-
voetnoot2)
- La troisième et principale partie du paragraphe présent contient une application des résultats obtenus dans les §§ 1, première partie, et 5, qui précèdent. À l'aide de ces résultats l'aberration d'une lentille planconvexe exposée par sa surface convexe à un faisceau de rayons parallèles à l'axe est calculée d'une saçon nouvelle. La première et la deuxième partie contiennent une déduction de cette même aberration d'après les principes déjà appliqués auparavant au § 1 de l'Appendice I, p. 355-357, mais cette fois d'une manière plus algébrique.
-
voetnoot3)
- Cette première partie donne la déduction de l'aberration PR causée par la seule surface convexe.
-
voetnoot4)
- A est le centre de la surface CB; R le foyer de cette surface.
-
voetnoot5)
- D'après la Prop. VIII, Part. I, Liv. I, p. 33.
-
voetnoot7)
- D'après la Prop. II, Part. I, Liv. I, p. 15, CP représentant le rayon parallèle à l'axe après sa première réfraction à la sursace convexe CB.
-
voetnoot8)
- Comparez la Prop. XIV, Part. I, Liv. I, à la p. 83.
-
voetnoot10)
- D'après la Prop. III, Part. I, Liv. I, p. 17.
-
voetnoot2)
- N est le point de concours après sa sortie de la lentille d'un faisceau qui, dans l'intérieur de la lentille, converge vers P. Or, puisque E est le point où le rayon extrême d'un tel faisceau coupe l'axe après sa réfraction à la surface plane, NE égale l'aberration calculée au § 5 qui précède. On a donc
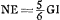 , en supposant PI = PC, et NG = ⅔ PG. , en supposant PI = PC, et NG = ⅔ PG.
-
voetnoot3)
- D'après la Prop. II, p. 275, puisqu'on a avec une approximation suffisante PC = 3AB.
-
voetnoot4)
- Puisque D, le foyer de la lentille planconvexe, est le point de concours d'un faisceau qui, dans l'intérieur de la lentille, se dirige vers R.
-
voetnoot6)
- Ce paragraphe contient une déduction nouvelle de l'aberration sphérique d'une lentille biconvexe à courbures égales. Elle est fondée sur l'emploi de la formule du § 4 et doit servir principalement à vérifier la justesse de cette formule. Comparez la p. 400 et surtout la note 6 qu'on y trouve.
-
voetnoot7)
- Voir la première partie, p. 402-403, du § 6, et comparez la troisième partie, p. 404, où le même principe, qui va servir ici, est appliqué à un cas plus simple.
-
voetnoot10)
- A et δ sont le centre et le foyer de la surface CB, R est le foyer de la surface CM.
-
voetnoot11)
- Voir le § 8, p. 406-407, où un autre problème, dont la solution dépend du même principe, est traité plus explicitement.
-
voetnoot12)
- Détermination du foyer de la lentille biconvexe par la règle de la p. 87.
-
voetnoot13)
- Valeur approximative qu'on obtient en exécutant la division de 12aa-14ab+4bb par 6a-2b.
-
voetnoot14)
- Voir la première partie du § 6, à la p. 402.
-
voetnoot15)
- N est le point de concours après sa sortie de la lentille d'un faisceau de rayons dirigés à l'intérieur de la lentille vers le point P. PN est donc déterminée par la règle de la Prop. XX, Part. I, Liv. I, p. 98.
-
voetnoot1)
- C'est cette valeur qui est calculée par la formule du § 4 (p. 400) en y substituant
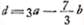 (la GP de la figure présente), ou plutôt d = 3a, ce qui revient au même puisqu'on peut négliger le carré de b. De cette manière on trouve l'aberration sphérique LN du rayon extrême CL, relative au point de concours N du faisceau dont il est question dans la note précédente. (la GP de la figure présente), ou plutôt d = 3a, ce qui revient au même puisqu'on peut négliger le carré de b. De cette manière on trouve l'aberration sphérique LN du rayon extrême CL, relative au point de concours N du faisceau dont il est question dans la note précédente.
-
voetnoot2)
- Ce paragraphe, qui probablement est d'une date postérieure mais que nous donnons ici parce qu'il traite un sujet analogue à celui des autres, contient le calcul de l'aberration sphérique d'un faisceau dirigé vers un point de l'axe d'une lentille planconvexe, la distance de ce point à la surface convexe antérieure étant égale à quatre fois le rayon de courbure de cette surface.
Ajoutons que ce qui suit sert d'introduction à la pièce que nous mentionnerons plus loin dans la dernière note de la p. 467. On le trouve avec cette pièce sur une même feuille, marquée 31.3, du manuscrit cité dans les notes 1 des pp. 355 et 392.
-
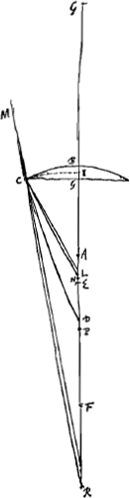
voetnoot3)
- Il y a dans la figure un double emploi de la lettre G. Nous indiquerons par G' le point G qui se trouve vers le haut de la figure et qui représente le foyer de la surface CB pour un faisceau de rayons parallèles à l'axe venant de l'intérieur de la lentille.
-
voetnoot4)
- Voir la Prop. XII, Part. I, Liv. I, p. 41. On a donc RP = 2a et, par conséquent, BP = 2a.
-
voetnoot5)
- Voir la première partie du § 1, p. 394, où l'on lit: ‘sit d ∞ 4a; βE ∞ ⅛b’.
-
voetnoot6)
- Par la Prop. VII, Part. I, Liv. I, p. 27.
-
voetnoot8)
- Il s'agit du § 5 de l'Appendice présent; voir les p. 401-402.
-
voetnoot9)
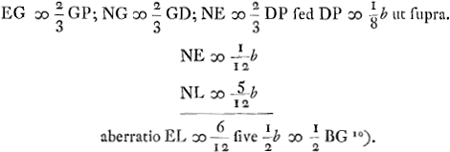
- CD représente le rayon MC après sa première réfraction à la surface convexe; CL le même rayon après les deux réfractions.
-
voetnoot10)
- On arrive au même résultat en substituant d = - 4a, n = ∞, e = b, dans les dernières formules de la note 2, p. 396.
|
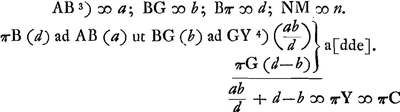
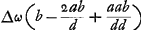
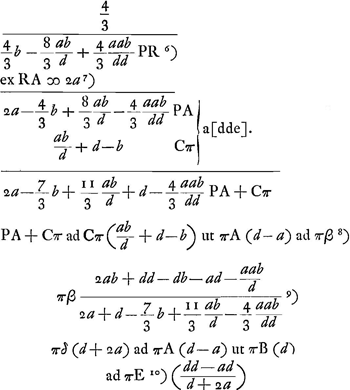
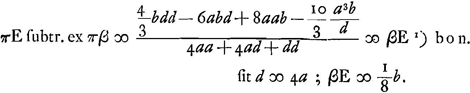

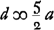 casus perfectus ubi nulla aberratio, qui est in Comm. SchotenijGa naar voetnoot2).
casus perfectus ubi nulla aberratio, qui est in Comm. SchotenijGa naar voetnoot2).
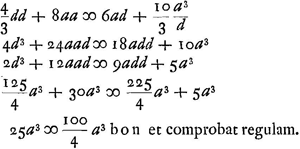

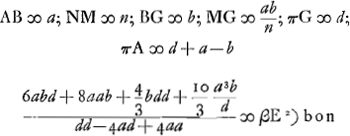
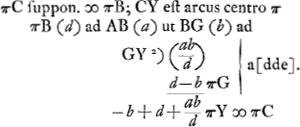
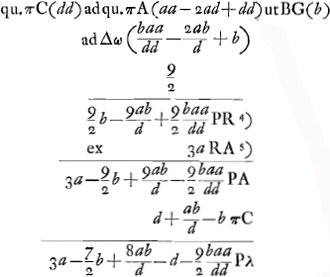
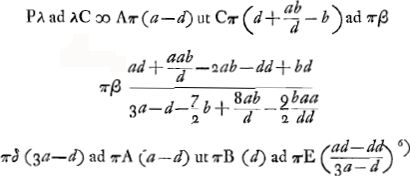
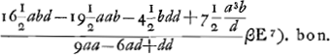
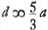 , casus perfectus, hoc est aberratio nullaGa naar voetnoot8).
, casus perfectus, hoc est aberratio nullaGa naar voetnoot8).
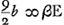 , ut oportetGa naar voetnoot3).
, ut oportetGa naar voetnoot3).
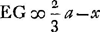

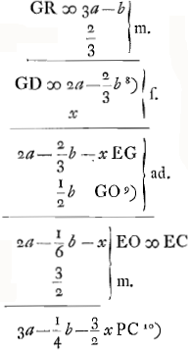

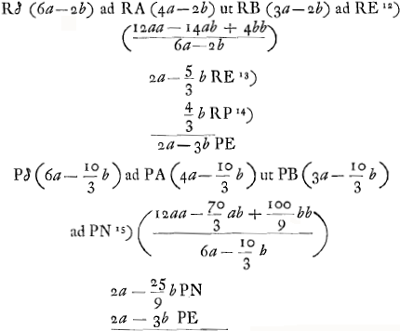
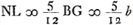 .
.


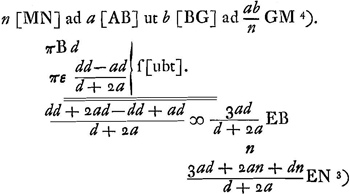
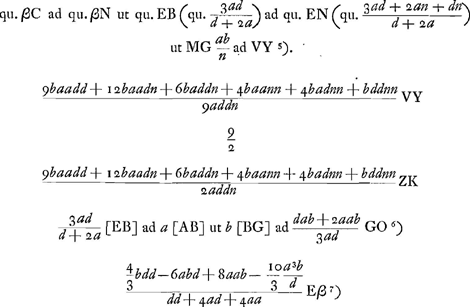
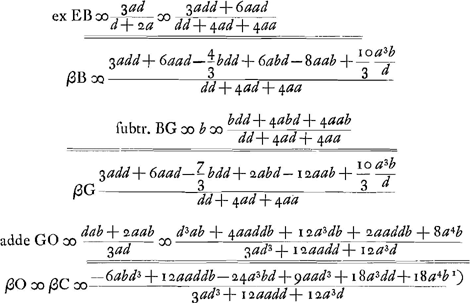
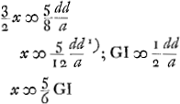
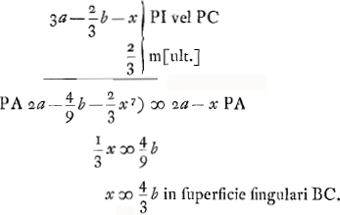
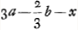 erat PC
erat PC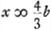 ,
, 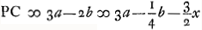
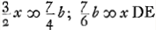 in lente planoconvexa convexo
in lente planoconvexa convexo