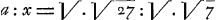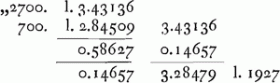Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 379]
| |||||||
Appendice IIIGa naar voetnoot1)
| |||||||
[pagina 380]
| |||||||
Primo itaque ostendendum aberrationem ED ad ML rationem habere compositam ex ratione qu. AB ad qu. GH et ex ratione KL ad CD. Sit CD ∞ a, CB ∞ b, KL ∞ c, KH ∞ d. Et ponatur lens alia OP [Fig. 3] ejusdem generis cum duabus alijs, cujus foci distantia QR sit aequalis CD sive a, aperturae vero semidiam. QP ad foci distantiam QR, se habeat ut HK ad KL. refractio autem radij extremi in hac lente sit PST faciens aberrationem SR, et semidiam. circelli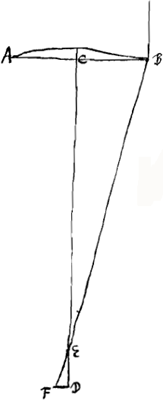 [Fig. 1.]
 [Fig. 2.]
 [Fig. 3.]
aberrationis RT. Quia ergo ut LK ad KH, hoc est, ut c ad d ita ponitur RQ sive a ad QP erit haecad/c. Sicut autem qu.CB ad qu.QP hoc est, sicut bb ad ddaa/cc, ita est aberratio ED ad aberrationem SRGa naar margenoot*. Itaque si ED ponatur ∞ e, fiet SR ∞ eddaa/bbcc. Atqui aberratio SR est ad ML sicut QR ad KL hoc est, sicut a ad c, quoniam arcus superficierum lentium OP et GH sunt partes similes cirumferentiae. Itaque fit aberratio ML ∞ edda/bbc ad quam ED, sive e, ita se habere apparet sicut bbc ad | |||||||
[pagina 381]
| |||||||
dda; quae ratio composita est ex ratione qu.ibb ad qu.dd hoc est qu.CB ad qu. KH, et ex ratione c ad a, hoc est KL ad CD, quod erat primo loco ostendendum. Nunc porro demonstrabimus circelli aberrationis semidiametros DF ad LN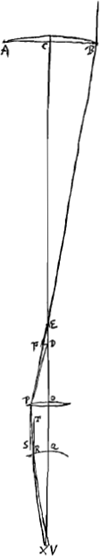 [Fig. 4.]
 [Fig. 5.]
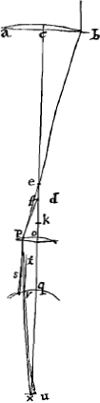
eam habere rationem quae componitur ex ratione cubi CB ad cubum KH, et ex ratione qu.iKL ad qu.CD. Quia ut EC ad CB, sive, ob minimam differentiam, ut DC ad CB, hoc est, ut a ad b ita ED, sive e, ad DF; erit proinde DF ∞ be/a. Similiter quia ut MK ad KH, sive, ob minimam differentiam, ut LK ad KH, hoc est, ut c ad d, ita ML, sive edda/bbc, ad LN; erit proinde LN ∞ ed3a/bbcc. Erat autem DF ∞ be/a. Cujus itaque ratio ad LN sive ed3a/bbcc, est ut apparet ea quae b3cc ad d3aa, hoc est, composita ex ratione cubi ex b sive CB ad cubum ex d sive KH, et ex ratione qu.iex c sive KL ad qu. ex a sive CD, quod supererat demonstrandum. His praemissis jam rationem aperturarum in telescopijs diversae longitudinis inquiremus, ostendemusque quod ad aeque clara atque aeque distincta efficienda telescopia, ratio foci distantiarum lentium exteriorum ejusdem generis debet esse sesquitertia rationisGa naar voetnoot2) quae in diametris aperturarum earundem lentium. Sive cubos dictarum foci distantiarum debere esse inter se sicut quadratoquadrata diametrorum aperturaeGa naar voetnoot3). Suntoenim [Fig. 4 et 5] duo diversae longitudinis telescopia, lentes exteriores ejusdem generis habentia, quorum alterius lens | |||||||
[pagina 382]
| |||||||
exterior quatenus adaperta sit AB [Fig. 4], lens ocularis OP, focis utriusque in idem punctum D compositis. ita enim disponi
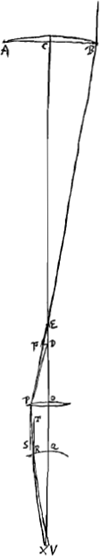 [Fig. 4.]
 [Fig. 5.]
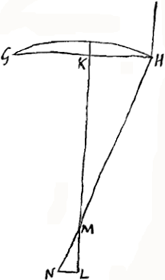
necesse est, ut radij paralleli ad oculum perveniant qui à punctis longinquis ad telescopium feruntur, axi proximi. Sit autem pupilla QR, fundum oculi ad X, centraque omnium C, O, Q, X in eandem rectam quae axis est telescopij. Intelligatur porro refractio radij extremi in lentem AB incidentis esse BEP, quae occurrat lenti oculari in P, cujusque aberratio sit ED, circelli vero aberrationis semidiameter DF. et jungatur DP. sitque PS axi parallela. Quoniam igitur si in lentem ocularem OP radius incidat DP ex foco ejus veniens, is axi parallelus efficitur, ita ut incedat secundum rectam PS (quia nempe, ut supra fieri licere ostendimusGa naar voetnoot1), lentem OP quasi aberrationis expertem hic consideramus), feretur proinde radius EP secundum PR, ut ang. SPR fiat aequalis ang.o DPEGa naar voetnoot2). Occurratergo pupillae in R, et agatur RT axi parallela. Quia ergo oculi ea est dispositio ut radios axi parallelos cogat ad punctum X, ideoque radium TR intro recepturus sit secundum rectam RX, sequitur radium PR intraturum secundum rectam RV, ita ut ang. XRV fiat aequalis TRPGa naar voetnoot3). Occurrat autem fundo oculi in V, ut nempe circelli aberrationis semidiam. fiat XV. Porro in telescopio altero [Fig. 5] eadem omnia effecta intelligantur, literis minoribus ejusdem nominis ad puncta adscriptis. Requiritur itaque ad aeque distinctam visionem faciendam ut XV sit aequalis xu, quod quidem | |||||||
[pagina 383]
| |||||||
fieri necesse est si fuerit angulus XRV aequalis xru, quandoquidem profunditas oculi XQ aequalis est xq. Angulo autem XRV aequalis est TRPGa naar voetnoot3) sive RPS et huic aequalis est DPF. Eademque ratione angulo xru aequalis est dpf. Ergo requiretur ut aequales sint anguli DPF, dpf. In priore figurâ omnia data sint, ut foci distantia CD ∞ a; semidiam. aperturae BC ∞ b. foci distantia DO ∞ d. In altera autem data duntaxat lentis exterioris foci distantia cd ∞ c; semidiameter autem aperturae quaesita cb ponatur ∞ x. Et do, foci distantia lentis ocularis quae similiter ignota est, ∞ y. Erit ex propos. praecedenti circelli aberrationis semid. FD ad fd ut b3cc ad x3aa; at quoniam aequalis utriusque telescopij claritas postulatur; hoc est, ut multiplicatio telescopij CDO sit ad multiplicationem telescopij cdo, ut semidiam. aperturae CB ad cb, quumque multiplicatio telescopij CDO sit a/d, quoniam res visas auget secundum ratione a ad d, hoc est CD ad DO. multiplicatio vero telescopij cdo similiter sit c/y. Oportet itaque esse a/d ad c/y sicut CB ad cb, hoc est ut b ad x; unde ax/d ∞ cb/y, ac proinde y sive do ∞ cbd/ax. At vero ut aequales sint anguli DPF, dpf, necesse est PD ad DF esse sicut pd ad df; et permutando, PD ad pd, sive, quae ratio eadem hic censenda est, OD ad od, ut DF ad df. Sed ratio DF ad df eadem ostensa est quam b3cc ad x3aa; et ratio OD ad od, ea quae d ad cbd/ax, ergo quum hae rationes aequales esse debeant, hoc est quantitas b3cc ad x3aa ut d ad cbd/ax, fiet b4c3d/ax ∞ x3aad, ideoque b4c3 ∞ x4a3, et b4c3/a3 ∞ x4, ac tandem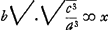 , quare patet, ut a3 ad c3, hoc est, ut cubus CD ad cubum cd ita esse b4 ad x4, hoc est, ita quadratoquadrati CB ad qu.qu.cb. Atque ex his jam poterimus, datâ telescopij unius foci distantiâ lentis exterioris, et maximâ quam ferre valet aperturâ, etiam alij ejusdem generis exteriori lenti cujus data sit foci distantia, debitam aperturam invenire, nec tantum si ejusdem generis fuerit, sed et si alterius, ut pluribus de hinc docebiturGa naar voetnoot4). Velut si lens quaedam data cujus foci distantia pedum 12, ferat aperturam duorum pollicum, sit autem proposita lens
alia cujus foci distantia sexdecuplo major, sive pedum 192. Et si quidem fuerit foci distantia lentis unius sexdecupla foci distantiae alterius lentis, debebit ratio aperturarum esse octupla, numerorum ratio usus. utendo et in his logarithmorum compendio; si enim in telescopio quodam dentur foci distantia a et aperturae semidiameter b numeris expressae, itemque foci distantia lentis exterioris alterius faciendi telescopij ∞ c, oportet logarithmi numeri b addere tres quartas , quare patet, ut a3 ad c3, hoc est, ut cubus CD ad cubum cd ita esse b4 ad x4, hoc est, ita quadratoquadrati CB ad qu.qu.cb. Atque ex his jam poterimus, datâ telescopij unius foci distantiâ lentis exterioris, et maximâ quam ferre valet aperturâ, etiam alij ejusdem generis exteriori lenti cujus data sit foci distantia, debitam aperturam invenire, nec tantum si ejusdem generis fuerit, sed et si alterius, ut pluribus de hinc docebiturGa naar voetnoot4). Velut si lens quaedam data cujus foci distantia pedum 12, ferat aperturam duorum pollicum, sit autem proposita lens
alia cujus foci distantia sexdecuplo major, sive pedum 192. Et si quidem fuerit foci distantia lentis unius sexdecupla foci distantiae alterius lentis, debebit ratio aperturarum esse octupla, numerorum ratio usus. utendo et in his logarithmorum compendio; si enim in telescopio quodam dentur foci distantia a et aperturae semidiameter b numeris expressae, itemque foci distantia lentis exterioris alterius faciendi telescopij ∞ c, oportet logarithmi numeri b addere tres quartas
| |||||||
[pagina 384]
| |||||||
logarithmi c et auferre à summa tres quartas logarithmi a. fietque logarithmus numeri quaesiti x qui semidiametrum aperturae alterius telescopij designat. Ut si lens cujus foci distantia est pedum 12 ferat aperturam, in telescopio suo, pollicum duorum, quam docet experientia lentem bonam perferre posseGa naar voetnoot1), quaeriturque apertura lentis aliûs, cujus foci distantia pedum 100. hic numerus a est 12; b, 1; c, 100. Logarithmus autem numeri 1, qui est o, additus ad ¾ logarithmi numeri c, hoc est, ad 1,50000 facit 1,50000; unde si auferantur ¾ logar. 12, quae sunt 0,80938, relinquitur 0,69062, logarithmus numeri 4 905/1000. qui itaque est ∞ x, designatque numerum pollicum qui deberentur semidiam.o aperturae quaesitae; adeo ut diameter fiat fere 10 poll. Et hoc modo composita est sequens tabella, nisi quod diametros totas aperturarum non numero pollicum sed centesimarum unius pollicis expressimus. Posuimus autem hic rursus ad lentem pedum 12 sive pollicum 144, aperturae diametrum duorum pollicum sive 20 decimarum, quoniam bonam lentem hanc facile perferre invenimus et fortasse si ad summam perfectionem daretur, majorem ferre posset. Sane quum utrimque convexa illa fuerit non tantam debuit aperturam pati potuisse quantam vel planoconvexa vel illa proportionis sexcuplae, quam in superioribus omnium praestantissimam esse docuimusGa naar voetnoot2). Quod si quae hujusmodi daretur quamque constaret exactissime formatam, posset ab hac omnium aliarum maxima apertura certo definiri; nunc autem quid jam nunc consequi possimus exponimus. Sciendum vero et multiplicationis rationem in telescopio illo lentis 12 pedum fuisse quae 72 ad 1, cum lens ocularis haberet foci distantiam poll. 2. Cumque rationem aperturae lentium exteriorum sequatur telescopiorum multiplicatio poterimus hinc suam cuique assignare diversae longitudinis lentibus quas tabella continetGa naar voetnoot3).
| |||||||
[pagina 385]
| |||||||
Data aberratione duarum diversi generis lentium quarum foci distantiae aequales, datâque apertura maxima unius, lenteque oculari quae cum illa telescopium efficiat, invenire alterius aperturam maximam, simulque lentem ocularem illi conjungendam ut fiat telescopium aeque clarum et aeque distinctum prioriGa naar voetnoot5).
Diversi generis intelliguntur hic etiam illae quae licet utramque superficiem utrique eandem habeant, non tamen easdem exterius conversas habent. Sunto lentes telescopiorum exteriores dissimilis generis AB [Fig. 6], CD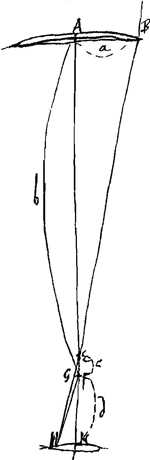 [Fig. 6.]
 [Fig. 7.]
[Fig. 7], quarum foci distantiae aequales AF, CM; aberrationes autem radiorum extremorum inaequales datae sint FE, ML, positis nempe aperturis aequalibus, quarum semidiametri AB, CD. Sitque AB semid. aperturae maximae quando lentis ocularis foci distantia est FK. Oporteat autem invenire CQ semid. aperturae lentis CD, itemque lentem ocularem OP, hoc est foci distantiam ejus OM, ut fiat ex his telescopium quo aeque lucidae ac distinctae appareant res visae atque eo quod ex lentibus AB, KH componitur. Sit semid. aperturae AB vel CD ∞ a, foci dist. AF vel CM ∞ b; aberratio FE ∞ c: foci distantia FK ∞ d. aberratio MV ∞ e quae omnia data sunt. Apertura autem quaesita CQ sit x. foci distantia MO ∞ y. Quoniam ergo multiplicatio telescopij AK ad multiplicationem telescopij CO debet esse ut semid. AB ad semid. CQ, ut nempe aeque lucida sint telescopia; multip.o autem telescopij AK designatur fractione b/a: et multip.o telescopij CO | |||||||
[pagina 386]
| |||||||
 [Fig. 6.]
 [Fig. 7.]
fractione b/y. Erit ergo b/d ad b/y ut AB ad CQ, hoc est, ut a ad x; unde bx/d ∞ ba/y. Et y ∞ da/x. Porro quia posita semidiam.o aperturae CD, aberratio est MV sive e, si fiat ut qu. CD ad qu. CQ hoc est ut aa ad xx ita VM sive e ad aliam; fiet exx/aa aequalis ML aberrationi radij extremi cum semid. aperturae est CQGa naar voetnoot1). Quod si porro fiat ut LC ad CQ, sive (quod idem hic censendum est ob exiguam differentiam), ut MC ad CQ, hoc est ut b ad x ita LM sive exx/aa ad aliam, fiet ex3/aab aequalis MN, semidiametro circelli aberrationis. at in telescopio AK, si fiat ut EA sive ut FA ad AB hoc est ut b ad a ita EF sive c ad aliam, oritur ac/b aequalis FG semidiam. circelli aberrationis. Quod si radij extremi refractio BEG continuetur donec occurrat lenti oculari in H, itemque radijextremi refractio QLN continuetur donec occurrat lenti oculari in P, et jungantur FH, MP. Constat angulos FHG, MPN aequales esse debere ut aeque distincte utrumque telescopium res visas referat, ut ex dictis in prop. [XI]Ga naar voetnoot2) manifestum est. itaque ratio PM ad MN, sive, quae hic pro eadem habenda est, OM ad MN, eadem debet esse quae HF sive KF ad FG. Itaque ut KF ad FG, hoc est ut d ad ac/b ita OM ad MN, hoc est ita da/x ad ex3/baa; ac proinde dex3/baa ∞ daac/bx. Unde invenit. x4 ∞ ca4/e; sive 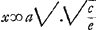 . Hoc est siGa naar voetnoot3). . Hoc est siGa naar voetnoot3).
| |||||||
[pagina 387]
| |||||||
Manente in telescopio lentis exterioris apertura, si lens ocularis convexiore mutetur, minus distincta fiet visioGa naar voetnoot4). 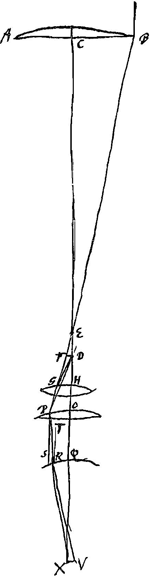 [Fig. 8.]
Repetatur adhoc fig. propos. [XI]Ga naar voetnoot5) ubi lens exterior telescopij AB, ocularis PO, sintque omnia similiter ut illic ordinata. Deinde vero pro lente OP substitui intelligatur alia convexior HG, quae proinde propius accedere debebit ad D focum lentis AB, quoniam in idem punctum D etiam focus ipsius lentis HG convenire debet; et occurrat radij extremi refractio BP lenti HG in G: et jungatur DG. Sicut igitur dum aderat lens OP, magni- | |||||||
[pagina 388]
| |||||||
tudo circelli aberrationis in fundo oculi, unde confusa visio nascitur, pendebat à magnitudine anguli DPFGa naar voetnoot1); ita nunc admota lente HG eam pendere constat a magn.e ang.i DGF; qui cum major sit quam DPF, etiam circulus aberrationis in fundo oculi major nunc erit, ac proinde major radiorum confusio quod erat ost. Et haec altera ratio est de qua superius dictumGa naar voetnoot2) cur non pro lubitu intendi possit telescopij multiplicatio, patet enim hinc si lentem ocularem brevioris foci in locum prioris adhibere velimus, arctandam esse lentis exterioris aperturam ut aeque distincta ac prius fiat visio. adeo ut ob hanc causam et ob majus incrementum dupliciter crescat obscuritas. |
|