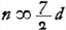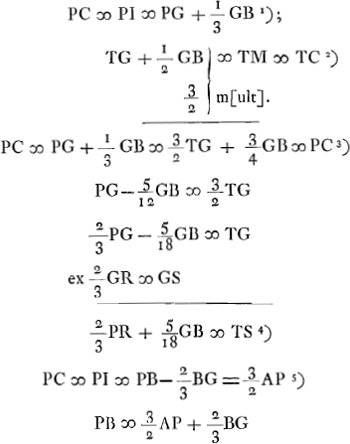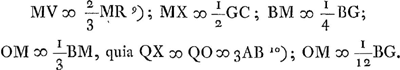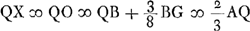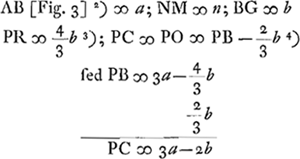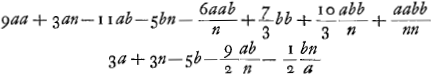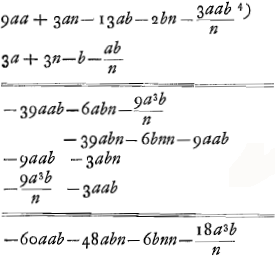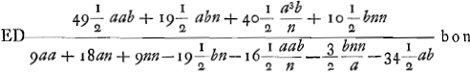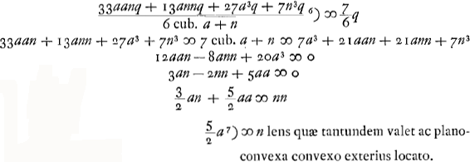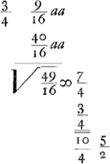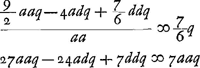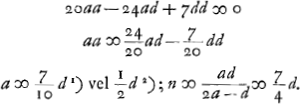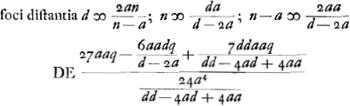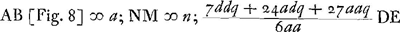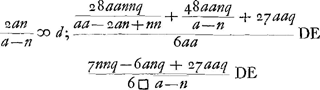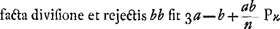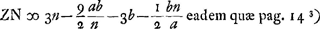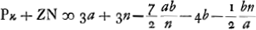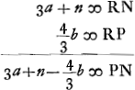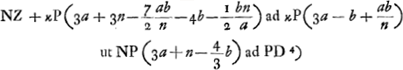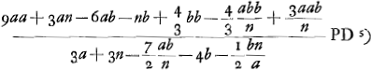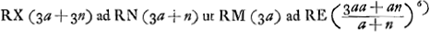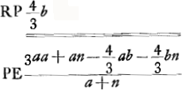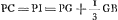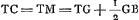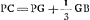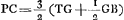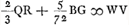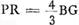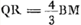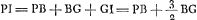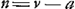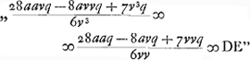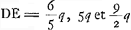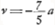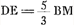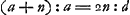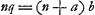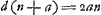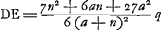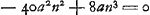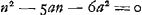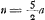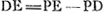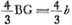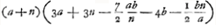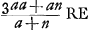 Ga naar voetnoot6) Ga naar voetnoot6); ex 3 a; 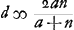 ; 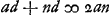 et hic etiam 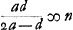 ergo ut illic 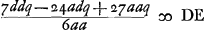 unde per reg. de max. et minim. 14 dd ∞ 24 ad; 7 d ∞ 12 a; 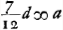 ergo 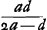 sive 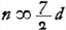
a ad n ut 7/12 ad 7/2 ut 1 ad 6.
Ergo lens cava optimè radios parallelos dispergit in usum myopum cujus semidiam. cavitatis quae radios excipit est ad semidiam. alterius cavitatis ut 1 ad 6. |
-
voetnoot1)
- Cet Appendice est emprunté aux p. 11-27 d'un manuscrit contenant 11 feuilles séparées de quatre ou deux pages chacune. Ces pages sont numérotées de 11 à 40 avec intercalation des pp. 19.1, 31.1, 31.2 et 31.3. Le contenu des pages 1-10, qui manquent, nous est inconnu.
-
voetnoot2)
- Ces ‘Adversaria’ donnent la déduction des règles pour le calcul de l'aberration sphérique, communiquées, sans démonstration, aux p. 285-307 du Tome présent. Nous avons ajouté une division en paragraphes.
-
voetnoot3)
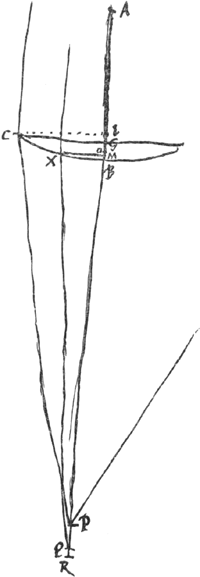
- Ce paragraphe se rapporte au cas d'une lentille planconvexe sur laquelle tombe du côté convexe un faisceau de rayons parallèles à son axe. Dans la première partie l'aberration sphérique des rayons extrêmes est déterminée par un calcul assez embarrassé qui porte les traces d'un premier essai. Aussi Huygens est-il revenu plus d'une fois sur cette détermination; voir le § 6 de l'Appendice V, p. 402-404 et surtout les §§ 2 et 3 de l'Appendice VII, p. 419-420, où la même aberration est calculée d'une façon beaucoup plus concise et plus élégante
-
voetnoot4)
- Dans la figure A représente le centre de courbure de la surface convexe, R le point de concours des rayons parallèles après une première réfraction à cette surface, S le foyer de la lentille. Si donc l'indice de réfraction égale 3/2, comme Huygens le suppose pour le verre, on a d'après le second alinéa de la p. 83 du Tome présent: BR = 3 BA, GS = ⅔ GR.
-
voetnoot1)
- Ici CP représente la direction du rayon qui, ayant passé par le point C, a subi une première réfraction à la surface convexe, CI et CM des arcs de cercle dont les centres sont respectivement P et W. La relation
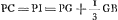 se déduit alors facilement de la Prop. II (p. 275 du Tome présent); puisque, d'après elle, les hauteurs des demi-segments CIG et CBG doivent être inversement proportionelles aux rayons de courbure PC et AB, où PC est à peu près égal à RB, c'est-à-dire à 3AB. se déduit alors facilement de la Prop. II (p. 275 du Tome présent); puisque, d'après elle, les hauteurs des demi-segments CIG et CBG doivent être inversement proportionelles aux rayons de courbure PC et AB, où PC est à peu près égal à RB, c'est-à-dire à 3AB.
-
voetnoot2)
- TC représente le rayon qui, après avoir passé par C, a subi les deux réfractions: à la surface convexe et à la surface plane. On a donc
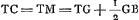 ; puisque le rayon de courbure du demi-segment MGC est à peu près le double de celui de demi-segment BGC. ; puisque le rayon de courbure du demi-segment MGC est à peu près le double de celui de demi-segment BGC.
-
voetnoot3)
- On a trouvé
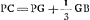 ; mais on a de même, d'après la Prop. III, Part. I, Liv. I, p. 17, PC = v. TC, c'est-à-dire, dans le cas présent: ; mais on a de même, d'après la Prop. III, Part. I, Liv. I, p. 17, PC = v. TC, c'est-à-dire, dans le cas présent: 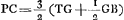 . .
-
voetnoot4)
- D'après cette formule l'aberration TS, qui est la conséquence des réfractions aux deux surfaces de la lentille, sera connue si on connaît l'aberration PR causée parla première réfraction à la surface convexe. Il ne s'agit donc plus maintenant que de calculer PR.
-
voetnoot5)
- Voir la Prop. II, Part. I, Liv. I, p. 15, d'après laquelle PC = v.AP.
-
voetnoot6)
- Comparez la règle énoncée à la p. 287 du Tome présent.
-
voetnoot7)
- Voir l'Appendice V aux p. 402-404, citées déjà dans la note 3 de la p. 355.
-
voetnoot8)
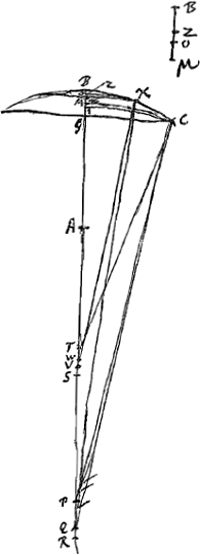
- Dans cette deuxième partie Huygens se propose de comparer les aberrations sphériques de deux lentilles planconvexes CBG et XBM qui possèdent des surfaces sphériques de même courbure, mais dont les largeurs GC et MX sont différentes, c'est-à-dire GC = 2MX.
-
voetnoot9)
- Quoique dans les deux parties Huygens se serve de la même figure il attache une signification différente au point M. Ainsi dans cette deuxième partie M est le point d'intersection de la surface plane de rayon MX = ½GC d'une lentille BXM avec l'axe de cette lentille dont le point V indique le foyer. De cette manière la relation MV = ⅔MR est analogue à celle GS = ⅔GR, qu'on trouve au début de la première partie.
-
voetnoot10)
- C'est-à-dire: par approximation; notons que Q remplace pour la petite lentille le point P de la plus grande, comme M le point G, V le point S et O le point I. De même, dans ce qui suit, W remplace le point T et Z le point M dans sa première signification. Voir d'ailleurs, pour la situation réciproque des points M, O, Z, B la petite figure en haut et à droite de la Fig. 1
-
voetnoot1)
- Dans les formules qui suivent Huygens applique à la petite lentille BXM les mêmes raisonnements qui l'ont guidé dans le paragraphe précédent, jusqu'au moment où il est arrivé à la relation;
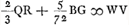 . .
-
voetnoot2)
- Dans l'ordre logique des choses Huygens devrait calculer QR de la même manière dont il a calculé PR dans la première partie, mais il aperçoit que la relation
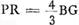 implique, dans le cas de la petite lentille, la relation implique, dans le cas de la petite lentille, la relation 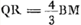 , dont on déduit QR = ¼PR, puisque BM = ¼BG. En comparant ensuite terme pour terme l'expression qu'il vient de trouver pour WV avec celle pour TS trouvée en premier lieu (p. 356) dans la partie précédente, il lui est facile d'en conclure WV = ¼TS; mais il ne manque pas d'observer que ce résultat n'avait pas besoin d'une démonstration élaborée, puisqu'il se déduit immédiatement en appliquant à la petite lentille le résultat obtenu (p. 357) pour la plus grande ainsi qu'il le montre dans la dernière phrase de ce § 1. En même temps il aura entrevu probablement la verité de la Prop. VI (p. 307 du Tome présent), dont il a prouvé ainsi un cas particulier. , dont on déduit QR = ¼PR, puisque BM = ¼BG. En comparant ensuite terme pour terme l'expression qu'il vient de trouver pour WV avec celle pour TS trouvée en premier lieu (p. 356) dans la partie précédente, il lui est facile d'en conclure WV = ¼TS; mais il ne manque pas d'observer que ce résultat n'avait pas besoin d'une démonstration élaborée, puisqu'il se déduit immédiatement en appliquant à la petite lentille le résultat obtenu (p. 357) pour la plus grande ainsi qu'il le montre dans la dernière phrase de ce § 1. En même temps il aura entrevu probablement la verité de la Prop. VI (p. 307 du Tome présent), dont il a prouvé ainsi un cas particulier.
-
voetnoot3)
- Ce paragraphe se rapporte au cas d'une lentille planconvexe sur le côté plan de laquelle tombe un faisceau de rayons parallèles à son axe. L'arrangement de la page dont nous avons emprunté le § 1 et ce § 2 ne laisse aucun doute que la première partie du § 1 a précédé celle du § 2; mais il en est autrement des deuxièmes parties. Il est probable que celle du § 2 a été rédigée avant celle du § 1 et il est certain qu'elle le fut avant que la dernière phrase du § 1: ‘hoc nihil’, etc. fut écrite.
-
voetnoot4)
- R représente le foyer de la lentille, A le centre de courbure, donc BR = 2AB; comparez Prop. XIV, Part. I, Liv. I, p. 81 du Tome présent.
-
voetnoot5)
- CP représente le rayon qui a subi la réfraction en C, CI un arc de cerclè dont P est le centre; on a donc
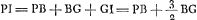 , d'après la Prop. II p. 275, et PC = ⅔ AP, d'après la Prop. III, Part. I, Liv. I, p. 17. , d'après la Prop. II p. 275, et PC = ⅔ AP, d'après la Prop. III, Part. I, Liv. I, p. 17.
-
voetnoot6)
- Comparez la règle de la p. 285 du Tome présent.
-
voetnoot7)
- Influence sur l'aberration sphérique d'une diminution de la surface réfringente.
-
voetnoot1)
- Ce paragraphe s'occupe du cas d'une lentille à deux surfaces convexes. Dans la première partie l'aberration sphérique d'une telle lentille est exprimée en fonction des rayons de courbure a et n et de l'épaisseur q.
-
voetnoot2)
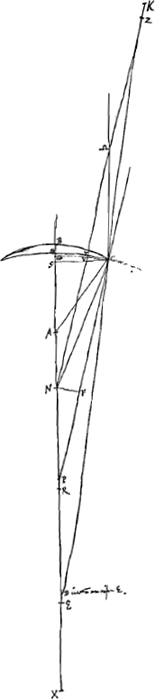
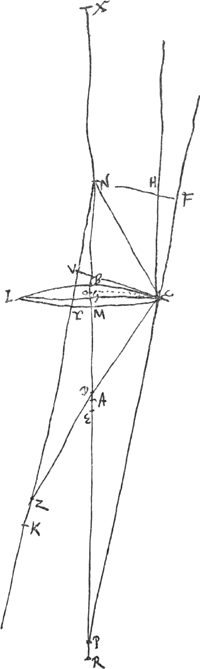
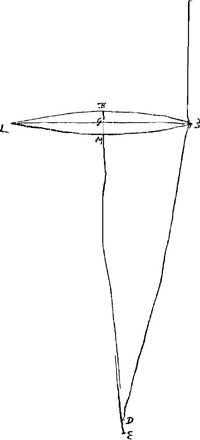
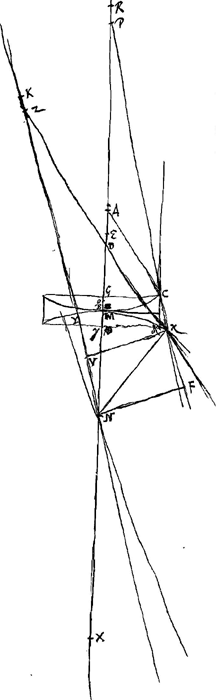
- Les notations de la figure sont conformes à celles de la Fig. 15, p. 289 du Tome présent, lesquelles sont expliquées dans le texte qui appartient à cette dernière figure. En voici le résumé: N et A sont les centres de courbure des surfaces de la lentille, E est son foyer, R le point de concours des rayons parallèles à l'axe venant du côté N après leur première réfraction à la surface IBC, X celui des rayons parallèles à l'axe venant de l'autre côté après la réfraction à la surface IMC, HC est un des rayons extrêmes parallèles à l'axe, CP la direction qu'il prend après la première réfraction à la surface IBC, CZ celle après les deux réfractions; NK est parallèle à FCP, NF et VC y sont perpendiculaires; enfin K est le point de concours, après leur réfraction à la surface IMC, des rayons qui se meuvent dans l'intérieur de la lentille dans la direction CP.
-
voetnoot3)
- Voir, p. 357, la première partie du § 1, vers la fin.
-
voetnoot4)
- D'après la Prop. II, p. 275, on a OG = ⅓BG; donc BO = ⅔b.
-
voetnoot6)
- Par suite de la similitude des triangles PGC et PFN et puísque FN = VC.
-
voetnoot8)
- La première approximation est ici suffisante.
-
voetnoot9)
- Voir, p. 359, la première partie du § 2, vers la fin.
-
voetnoot11)
- Il s'agit de trouver le foyer E de la lentille d'après la règle donnée dans la Prop. XVI, Part. I, Liv. 1, p. 87 du Tome présent.
-
voetnoot2)
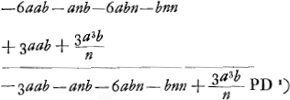
- Voir les trois multiplications qui suivent. Dans la première le produit des denominateurs es déterminé; mais dans le résultat les termes sont omis qui contiennent la seconde puissance de b. Huygens aurait pu aller plus loin et omettre tous les termes qui ont b pour facteur, comme il le fera dans la suite. Dans la deuxième multiplication le numérateur de PE est multiplié par le dénominateur de PD; dans la troisième le numérateur de PD par le dénominateur de PE.
-
voetnoot3)
- Les termes qui ne contiennent pas b devront disparaître dans l'expression pour DE, puisque cette grandeur doit s'annuler pour b = o, et ceux qui contiennent bb seront négligeables.
-
voetnoot4)
- C'est le numérateur de l'expression pour PD après que les termes qui contiennent bb ont été écartés.
-
voetnoot1)
- Huygens annota plus tard: ‘hoc jam dividitur per an+nn’; ce qu'il a découvert peut-être à propos de la réduction mentionnée dans la note suivante.
-
voetnoot2)
- Plus tard, posant
 et substituant et substituant 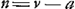 dans la formule présente, Huygens a trouvé encore dans la formule présente, Huygens a trouvé encore
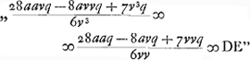
et il applique cette formule aux suppositions 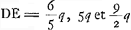 , trouvant respectivement dans ces cas: ‘3,23a ∞ v’ ‘1,261a ∞ v’ et ‘a ∞ v’. , trouvant respectivement dans ces cas: ‘3,23a ∞ v’ ‘1,261a ∞ v’ et ‘a ∞ v’.
Le premier résultat est exact; la seconde solution qui appartient au même cas représente une lentille concavo-convexe. Le second résultat, 1,261 a = v, repose sur une erreur de calcul. On trouve v < a, ce qui amène une lentille convexo-concave; l'autre solution indiquant une concavo-convexe. À propos du dernier résultat Huygens remarque: ‘imposs. nisi a ∞ o. rectè’; ce qui prouve qu'il ne s'est pas aperçu de la véritable solution a=∞, qui convient au cas de la lentille planconvexe, la seconde solution 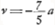 appartenant à une concavo-convexe. appartenant à une concavo-convexe.
-
voetnoot4)
- À la page du manuscrit qui suit on trouve encore un calcul indépendant du cas a = n. Huygens y trouve
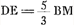 et fait suivre: ‘hoc idem ex regula pag. 17’ [la ‘Regula optima’] ‘poterat haberi’. et fait suivre: ‘hoc idem ex regula pag. 17’ [la ‘Regula optima’] ‘poterat haberi’.
-
voetnoot5)
- Dans cette deuxième partie Huygens calcule le rapport qui doit exister entre les deux rayons de courbure afin que l'aberration sphérique d'une lentille qui est convexe des deux côtés, soit égale à celle d'une lentille planconvexe équivalente, c'est-à-dire d'égale épaisseur, largeur et distance focale, tournant vers les rayons son côté convexe.
-
voetnoot6)
- La réduction de cette fraction par la suppression du facteur (a+n) n'avait donc pas encore été accomplie par Huygens, lorsqu'il composa cette partie du § 3.
-
voetnoot1)
- Dans cette partie Huygens détermine quel doit être le rapport des deux rayons de courbure, afin que l'aberration sphérique devienne un minimum en comparaison avec celle de toute autre lentille possédant la même distance focale, la même largeur et, par conséquent (voir la Prop. III, p. 277), la même épaisseur. À cet effet il commence par introduire la distance focale d dans l'expression pour DE, qu'il a trouvée dans la première partie et dont il n'a pas encore reconnu la réductibilité par le facteur (a+n).
-
voetnoot2)
- Voir le dernier alinéa de la Prop. XVI, Part. I, Liv. I, p. 89, d'après lequel pour une lentille en verre
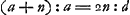 . .
-
voetnoot4)
- On a
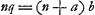 (voir la p. 364) et (voir la p. 364) et 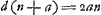 (voir la note 2). (voir la note 2).
-
voetnoot5)
- Il s'agit de la règle de Hudde. Consultez la note 11, p. 166 du Tome présent.
-
voetnoot7)
- Il s'agit de la ‘Regula optima’, p. 364, d'après laquelle
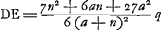 . Or, le minimum de cette expression pouvait s'obtenir par la règle mentionnée dans la note 5, qui, dans le cas présent, en omettant les constantes 6 et q, conduit à l'équation: -48a3n- . Or, le minimum de cette expression pouvait s'obtenir par la règle mentionnée dans la note 5, qui, dans le cas présent, en omettant les constantes 6 et q, conduit à l'équation: -48a3n- 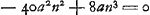 , ou , ou 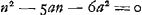 ; d'où l'on pouvait conclure n = 6a. ; d'où l'on pouvait conclure n = 6a.
-
voetnoot8)
- Le problème résolu dans la deuxième partie de ce même paragraphe est repris avec la formule nouvelle qui contient la distance focale au lieu du rayon de courbure n.
-
voetnoot1)
- Cette première solution amènera
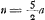 , comme dans la deuxième partie du paragraphe présent. , comme dans la deuxième partie du paragraphe présent.
-
voetnoot2)
- Inutile de dire que cette seconde solution correspond à la lentille planconvexe, où n = ∞.
-
voetnoot3)
- Ce paragraphe traite le cas d'une lentille concavo-convexe tournant vers les rayons sa surface convexe. Dans la première partie il s'agit du calcul de l'aberration sphérique en fonction des rayons de courbure AB = a et NM = n et de l'épaisseur BM de la lentille.
-
voetnoot4)
- Nou, supprimons les calculs qui ont amené ce résultat. Ils ressemblent tellement à ceux de la première partie du § 3 qu'il nous a paru inutile de les reproduire.
-
voetnoot5)
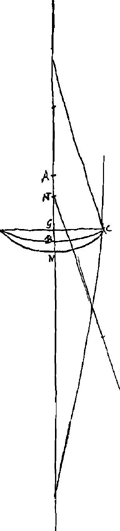
- Comme on le voit par l'annotation ‘incertum an infra E’ qu'on trouve dans la figure 6 près du point D, Huygens a été incertain au début de quel côté du point E, foyer de la lentille, se trouverait le point D, où le rayon ΩC, après les deux réfractions, coupe l'axe BA de la lentille. Toutefois dans ses calculs il a supposé la situation relative de ces deux points telle qu'elle est dans la figure. Il a donc posé
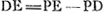 et c'est de cette manière qu'il a trouvé la valeur de DE. Si, par contre, la supposition contraire était la véritable on devrait changer les signes dans le numérateur. et c'est de cette manière qu'il a trouvé la valeur de DE. Si, par contre, la supposition contraire était la véritable on devrait changer les signes dans le numérateur.
-
voetnoot6)
- Cette remarque fut ajoutée plus tard. Dans ce qui suit Huygens va partir de la formule plus compliquée qui précède.
-
voetnoot7)
- Dans les calculs que nous avons supprimés Huygens avait trouvé MG = ba/n.
-
voetnoot9)
- Dans cette partie Huygens s'efforce à déterminer quel doit être le rapport de n à a pour que l'aberration sphérique devienne un minimum pour une lentille concavo-convexe dont la distance focale et la largeur (et par suite aussi l'épaisseur) sont données. À cet esset il commence par introduire dans la formule la distance focale d au lieu du rayon n.
-
voetnoot1)
- Application de la règle de Hudde pour les maxima et minima. Comparez la note 5, p. 366.
-
voetnoot3)
- Calcul, pour quelques cas spéciaux, de la distance focale pour une aberration de valeur donnée.
-
voetnoot5)
- Huygens recherche ici si l'aberration sphérique pourrait s'annuler pour un certain rapport entre les deux rayons de courbure.
-
voetnoot6)
- Calcul de la forme (Fig. 7) d'une lentille concavo-convexe équivalente sous le rapport de l'aberration à une lentille planconvexe de même épaisseur, largeur et distance focale, tournant le côté plan aux rayons.
-
voetnoot7)
- Dans ce paragraphe il s'agit du cas d'une lentille concavo-convexe qui tourne sa concavité du côté d'où viennent les rayons de lumière. Ce cas ne se trouve pas traité par Huygens indépendamment des autres, et il semble avoir estimé que pour l'examiner il suffirait de changer a en - a dans la formule qui, dans le cas du § 4, p. 370, donne l'aberration sphérique d'une lentille concavo-convexe en fonction de la distance focale d, de l'épaisseur q et du rayon de courbure a de la surface extérieure convexe. C'est, du moins, d'une formule qu'on peut obtenir de cette manière à l'aide de celle qu'on trouve en haut de la p. 370 qu'il va partir pour en déduire ensuite la formule qui donne l'aberration en fonction des deux rayons de courbure, a et n, et de l'épaisseur q.
-
voetnoot8)
- Ce paragraphe traite le cas d'une lentille biconcave.
-
voetnoot9)
- Les points M et B coïncident; comparez le troisième alinéa des ‘Definitiones’, p. 277.
-
voetnoot10)
- R est le point de dispersion des rayons parallèles après leur réfraction à la surface BC; PCF représente la direction du rayon extrême, parallèle à l'axe, après sa réfraction à cette surface. PR se trouverait égale à
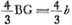 par un calcul tout semblable à celui qu'on rencontre vers la fin de la première partie du § 1 de cet Appendice (p. 357); mais ce calcul manque dans le manuscrit. par un calcul tout semblable à celui qu'on rencontre vers la fin de la première partie du § 1 de cet Appendice (p. 357); mais ce calcul manque dans le manuscrit.
-
voetnoot12)
- D'après la Prop. I, p. 273. NYZ est parallèle à FCP. YV, à laquelle Vκ et NF sont perpendiculaires, est considérée comme la hauteur du demi-segment YδκVY.
-
voetnoot2)
- Voir la première partie du § 3 de l'Appendice I, p. 360.
-
voetnoot3)
- Il s'agit de la première partie du § 3, p. 361, où la même formule est déduite pour le cas analogue d'une lentille biconvexe. Ajoutons, que ZDκ représente le rayon extrême, passant par C et parallèle à l'axe, après sa seconde réfraction par la surface Mδ, qui est supposée prolongée jusqu' en κ.
-
voetnoot4)
- À cause du parallélisme de NZ et de Pκ.
-
voetnoot6)
- Détermination du foyer E de la lentille d'après la règle de la Prop. XVII, Part. I, Liv. I, p. 91 du Tome présent.
-
voetnoot1)
- C'est le numérateur de la fraction qui représente PD après que cette fraction a été réduite au dénominateur
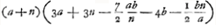 et que les termes sans b et ceux qui contiennent b2 ont été omis; comparez la note 3 de la p. 363. et que les termes sans b et ceux qui contiennent b2 ont été omis; comparez la note 3 de la p. 363.
-
voetnoot2)
- Il s'agit du numérateur de PE mis sous le dénominateur mentionné dans la note précédente. Nous avons supprimé le calcul.
-
voetnoot3)
- Comparez la première partie du § 3 de cet Appendice, en haut de la p. 362.
-
voetnoot5)
- Comparez, dans la troisième partie du § 3, p. 367, la phrase qui commence par les mots ‘Poterat methodus’. Ici, comme au lieu cité, la remarque en question fut ajoutée apres coup, c'est-à-dire, lorsque la déduction qui va suivre avait été écrite.
-
voetnoot6)
- Comparez, pour ce qui suit, la troisième partie du § 3, p. 366 et 367.
|
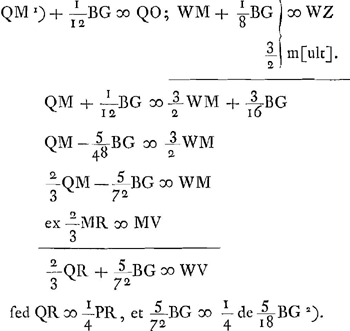
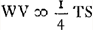 . hoc nihil opus demonstrare postquam ostensum quod aberratio
. hoc nihil opus demonstrare postquam ostensum quod aberratio 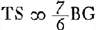 , et aberratio
, et aberratio 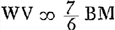 .
.

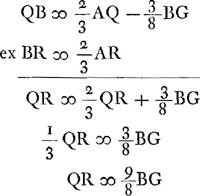
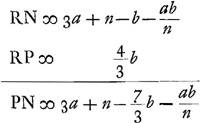
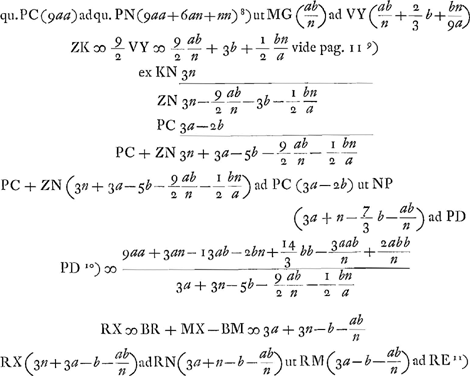
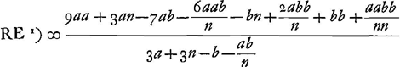
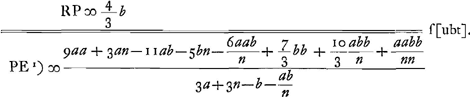
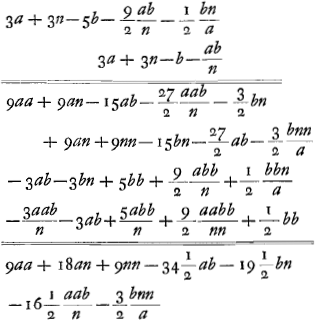
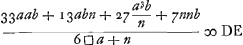 Ga naar voetnoot1) bon in divisore hoc rursus omisi in quibus b.
sit
Ga naar voetnoot1) bon in divisore hoc rursus omisi in quibus b.
sit 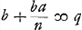 crassitudo totius lentis BM
crassitudo totius lentis BM
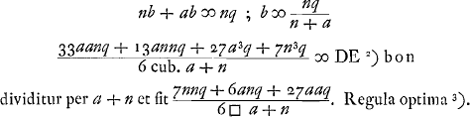
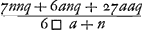 . Regula optimaGa naar voetnoot3)
. Regula optimaGa naar voetnoot3)
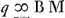 [Fig. 4].
[Fig. 4].
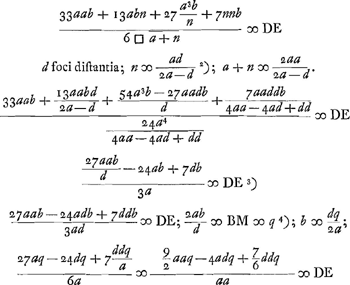
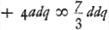 ;
; 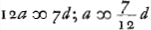 ; determinatio lentis optimae ad colligendos radios parallelos.
; determinatio lentis optimae ad colligendos radios parallelos.
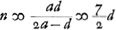
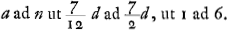

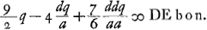
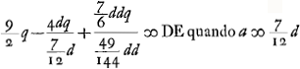
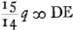
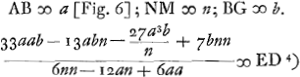
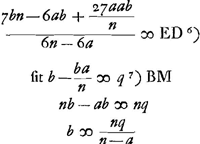
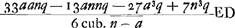
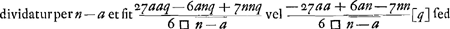
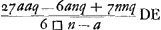 . Regula ad inveniendam DE ex datis semidiametris convexae et concavae superficiei in menisco.
. Regula ad inveniendam DE ex datis semidiametris convexae et concavae superficiei in menisco.
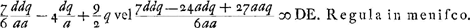
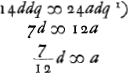
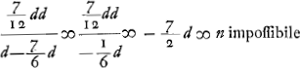
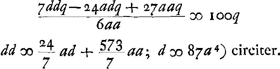
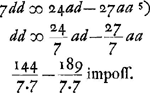

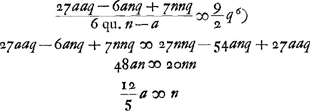
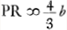 Ga naar voetnoot10)
Ga naar voetnoot10)
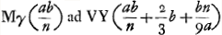 Ga naar voetnoot1)
si sumatur loco 9aa verum quadr. Pκ quae inventa est
Ga naar voetnoot1)
si sumatur loco 9aa verum quadr. Pκ quae inventa est 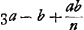 ut infra patet, fiet tamen, rejectis bb,
ut infra patet, fiet tamen, rejectis bb, 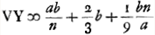 ut hic.
ut hic.
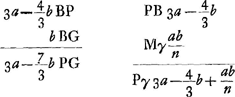
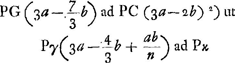
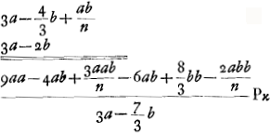
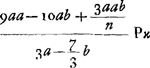
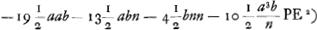
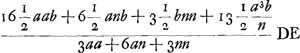

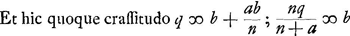
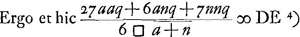
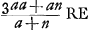 Ga naar voetnoot6); ex 3a;
Ga naar voetnoot6); ex 3a; 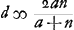 ;
; 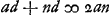 et hic etiam
et hic etiam 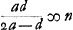 ergo ut illic
ergo ut illic 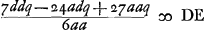 unde per reg. de max. et minim. 14dd ∞ 24ad; 7d ∞ 12 a;
unde per reg. de max. et minim. 14dd ∞ 24ad; 7d ∞ 12 a; 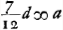 ergo
ergo 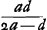 sive
sive