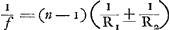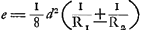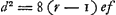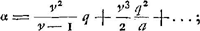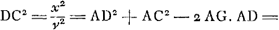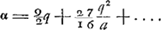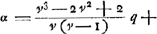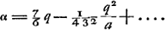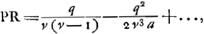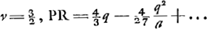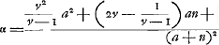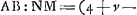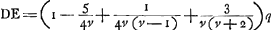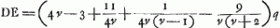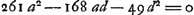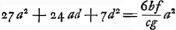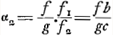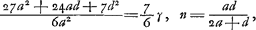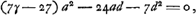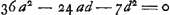Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 272]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
La Dioptrique.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 273]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dioptrica.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 274]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
acquiert une longueur de 871557 parties, et si nous supposons que FH soit égale à la moitié de cette droite, FH aura 435778 parties. Mais AG a une longueur 38053, et le quart de ce nombre est 9513. Si AH avait la longueur exprimée par ce dernier nombre, le rapport AG:AH serait égal à celui du carré de CD au carré de EF. On trouve cependant que AH a une longueur de 9500 parties, de sorte que la différence n'est que de 13/9500 ou de 1/731 AH et seulement de 13/20000000 du diamètre AB. Or, les surfaces convexes ou concaves des lentilles que nous considérerons dans ce qui suit n'embrassent en général que la centième ou la deux-centième partie d'une circonférence de cercle, comme nous le dirons plus loinGa naar voetnoot1). L'erreur qu'on commet en admettant la relation mentionnée plus haut entre le rapport des bases et celui des hauteurs est donc beaucoup moindre. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition II.Dans des segments extrêmement petits appartenant à des cercles différents et qui possèdent la même base ou des bases égales, le rapport des hauteurs des segments peut être estimé égal à l'inverse de celui des diamètresGa naar voetnoot2). Considérons deux petits segments ABC et ADC [Fig. 2] appartenant à des cercles différents et possédant la même base AC; puissent-ils être divisés en deux parties égales par la droite DE sur laquelle coïncident des diamètres des deux cercles, savoir BF, diamètre du cercle auquel appartient le segment ABC, et DG, diamètre du cercle plus petit dont le segment ADC fait partie. Je dis que le rapport des hauteurs DE et BE est à peu près égal à celui de BF à DG. En effet, comme les rectangles FEB et GED sont égaux entre eux, vu qu'ils sont l'un et l'autre égal au carré de EC, on aura FE:GE = DE:EB. Mais le rapport des diamètres FB et GD est à peu près égal à celui de FE et de GE, attendu que les parties EB et ED sont supposées fort petites par rapport aux diamètres entiers. On en conclut que DE est à la hauteur BE à peu près comme le diamètre FB est au diamètre GD. Supposons de nouveau que l'arc ADC soit égal à 1/36 de la circonférence ou à 10 degrés et le diamètre DG à 20000000 parties. La droite ED comprendra donc 38053 parties. Et si nous admettons que le diamètre BF est égal au double du diamètre DG, donc à 40000000 parties, on trouvera que la droite EB com- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 275]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
At AG est 38053; cujus quarta pars 9513, cui si aequalis esset AH, jam esset eadem ratio AG ad AH quae quadrati CD ad qu. EF. Nunc autem invenitur AH partium 9500, adeo ut differentia tantum sit 13/9500 sive 1/731 ipsius AH, ac tantum 13/20000000 diametri AB. Superficies vero convexae aut concavae lentium quas in sequentibus considerabimus plerumque tantum 1/100 vel 1/200 partem circumferentiae complectuntur ut postea diceturGa naar voetnoot1), in quibus proinde multo minus fallit dicta basium altitudinumque proportio. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Propos [itio II].In minimis circulorum inaequalium segmentis, aequales vel easdem bases habentibus, altitudines segmentorum, diametris ipsorum circulorum, contraria ratione respondere censendae suntGa naar voetnoot2). 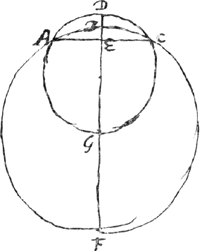 [Fig. 2.]
Sint segmenta exigua inaequalium circulorum, ABC, ADC, eandem basin AC habentia, ac bifariam divisa recta DE; in qua diametri circulorum, BF quidem ejus ex quo segmentum ABC, DG vero minoris ex quo segmentum ADC. Dico sicut BF ad DG ita proxime esse altitudinem DE ad BE. Cum enim rectangula FEB, GED inter se aequalia sint, quippe quae singula aequentur quadrato EC, Erit proinde ut FE ad GE ita DE ad EB. Sed ut FE ad GE, ita est proximè diameter FB ad diametrum GD, cum partes EB, ED minimae ponantur totarum diametrorum respectu. Ergo etiam ut diameter FB ad diam. GD ita est proxime DE ad altitudinem BE. Sit arcus ADC rursus 1/36 circumferentiae sive 10 gr. et diameter DG partium 20000000; Erit ED partium 38053. Jam si diameter BF diametri DG dupla statuatur, hoc est, partium 40000000, invenietur EB | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 276]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
prend 19000 parties, tandis qu'elle devait être égale à la moitié de ED, c'est-à-dire à 19026 parties. Par conséquent, il n'y a qu' une différence de 26/19000 ou 1/731 EB ou de 26/40000000 du diamètre BF. Et si nous prenons un arc ADC plus petit, le rapport des hauteurs et le rapport inverse des diamètres seront encore moins éloignés de l'égalité. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
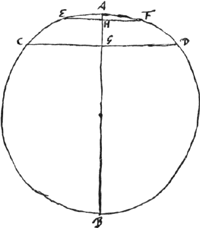
Définitions.Appelons ‘épaisseur d'une lentille convexe’ la distance qui sépare les points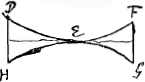 [Fig. 5.]
milieux des deux surfaces lorsque les bords des deux surfaces coïncident. Ainsi l'épaisseur de la lentille ABCD [Fig. 3 et 4] dont les bords coïncident avec la même circonférence de cercle AC, est BD:en effet, c'est là la distance des points milieux des deux surfaces. 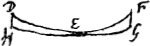 [Fig. 6.]
Par ‘épaisseur d'une lentille concave’ nous entendrons au contraire la distance [Fig. 5 et 6] entre les bords circulaires des deux surfaces lorsque leurs points milieux coïncident. Ainsi l'épaisseur de la lentille DEFGH, dont les points milieux coïncident en E, est DH ou FG: en effet, c'est là la génératrice d'un cylindre qui renferme les deux surfaces. Dans la suite nous considérerons donc toujours les lentilles de cette façon: et quoique les lentilles convexes aient le plus souvent une certaine épaisseur près des bords et que les lentilles concaves en aient toujours une au milieu, nous ne tiendrons compte que de cette épaisseur-là seulement qui resterait si les deux surfaces coïncidaient aux bords ou se touchaient au milieu. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition III.Les lentilles convexes possédant la même distance focale et les lentilles concaves ayant la même distance du point de dispersion, auront la même épaisseur si leurs largeurs sont égalesGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 277]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
partium 19074Ga naar voetnoot1), quae debebat esse dimidia ED, hoc est partium 19026. Itaque differentia tantum est 48/19074 five 1/397Ga naar voetnoot2), ipsius EB, nec nisi 48/40000000Ga naar voetnoot3), diametri BF. Et sumto minore arcu ADC tanto exactius quadrabit dicta altitudinum ac diametrorum contraria proportio. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Definitiones.]Crassitudo lentis convexae dicatur intervallum quo inter se distant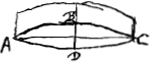 [Fig. 3.]
puncta media utriusque superficiei, lateribus coeuntibus. Ita lentis ABCD [Fig. 3 et 4] cujus latera in unum circulum AC conveniunt, crassitudo est BD, distantia nempe punctorum mediorum utriusque superficiei. Crassitudo autem lentis cavae dicatur distantia [Fig. 5 et 6] circumferentiarum utriusque superficiei, 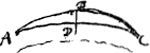 [Fig. 4.]
coeuntibus earum punctis medijs. Ita lentis DEFGH, cujus puncta media in E sese contingunt, crassitudo est DH vel FG, latus nimirum cylindri utramque supersiciem comprehendentis. Hoc modo enim in sequentibus lentes considerabimus. Et quamvis convexae lentes plerumque crassitudinem aliquam in ambitu habeant, cavae vero aliquam semper in medio. Eam tamen censebimus tantum omnium esse crassitudinem, quae superesset superficiebus se mutuo vel in ambitu vel in medio contingentibus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Propos[itio III].Lentes convexae eandem foci distantiam habentes, cavae vero eandem distantiam puncti dispersus si et latitudinem aequalem habuerint, etiam aequali erunt crassitudineGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 278]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
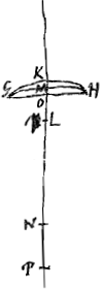
Supposons en premier lieu que AB, l'une des deux lentilles, soit planconvexe; et soit DC le rayon de courbure de la surface ACB, CE l'épaisseur de la lentille, CF la distance focale qui sera le double de CDGa naar voetnoot1). Prenons pour l'autre lentille la lentille biconvexe GH [Fig. 8], dont la largeur est par hypothèse égale à celle de la lentille AB et dont la distance focale MP est égale à CF. Je dis donc que l'épaisseur KM de la lentille GH est égale à EC, l'épaisseur de la lentille AB. En effet, soit LK le rayon de courbure de la surface GKH de la lentille GH, et MN celui de la surface GMH de la même lentille; et puisse la droite GH couper l'épaisseur KM de la lentille en O. On a alors: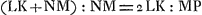 Ga naar margenoot*; MP étant Ga naar margenoot*; MP étant
 [Fig. 9.]
la distance focale qui est supposée égale à CF. Par conséquent, 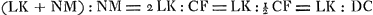 . Mais comme on a LK:NM = MO:OKGa naar margenoot*, on aura, par composition, . Mais comme on a LK:NM = MO:OKGa naar margenoot*, on aura, par composition, 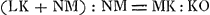 . Donc aussi MK:KO = LK:DC. Mais LK:DC = CE:KOGa naar margenoot*, parce que la corde GH est égale à la corde AB. Il s'ensuit que MK:KO = CE:KO. Par conséquent, MK = CE; ce qu'il fallait démontrer.
Remplaçons maintenant la lentille GH par une lentille concavo-convexe [Fig. 9], dont GMH soit la surface concave. La différence KM de KO et MO constituera son épaisseur. Faisons d'ailleurs les mêmes suppositions qu' auparavant. Comme . Donc aussi MK:KO = LK:DC. Mais LK:DC = CE:KOGa naar margenoot*, parce que la corde GH est égale à la corde AB. Il s'ensuit que MK:KO = CE:KO. Par conséquent, MK = CE; ce qu'il fallait démontrer.
Remplaçons maintenant la lentille GH par une lentille concavo-convexe [Fig. 9], dont GMH soit la surface concave. La différence KM de KO et MO constituera son épaisseur. Faisons d'ailleurs les mêmes suppositions qu' auparavant. Comme 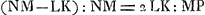 Ga naar margenoot*, distance focale qui est supposée égale à CF, on aura aussi Ga naar margenoot*, distance focale qui est supposée égale à CF, on aura aussi 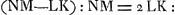 : CF = LK:½ CF = LK:DC. Mais comme NM:LK == OK:OM, il s'ensuit qu'on a également : CF = LK:½ CF = LK:DC. Mais comme NM:LK == OK:OM, il s'ensuit qu'on a également 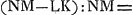 = KM:KO. Donc aussi KM:KO = LK:DC. En partant de là on démontrera de la même manière que dans le cas de la lentille biconvexe que MK = CE. = KM:KO. Donc aussi KM:KO = LK:DC. En partant de là on démontrera de la même manière que dans le cas de la lentille biconvexe que MK = CE.
Comme donc toute lentille biconvexe ou concavo-convexe qui possède la même distance focale et la même largeur que la lentille planconvexe AB a aussi la même épaisseur que cette dernière, il s'ensuit que toutes les lentilles biconvexes ainsi que toutes les lentilles concavo-convexes qui ont la même distance focale et la même largeur auront également la même épaisseur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 279]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
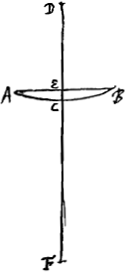
Sit primò lentium altera AB [Fig. 7] planoconvexa, sitque supersiciei
 [Fig. 7.]
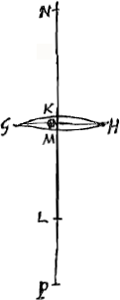 [Fig. 8.]
ACB semidiam. convexitatis DC. crassitudo lentis CE, foci distantia CF, quae erit dupla CDGa naar voetnoot1). Lens autem altera utrimque convexa sit GH [Fig. 8], cujus latitudo eadem quae lentis AB, et foci distantia MP aequalis CF. Dico igitur et crassitudinem KM lentis GH aequalem esse EC crassitudini lentis AB. Sit enim in lente GH superficiei GKH semidiameter convexitatis LK; superficiei vero GMH semidiam. convexitatis MN. rectaque GH secet crassitudinem lentis KM in O. Quia igitur ut duae simul LK, NM ad NM ita dupla LK ad foci distantiam MPGa naar margenoot*. quae aequalis ponitur CF. Erit proinde ut duae simul LK, NM ad NM ita dupla LK ad CF, sive ita LK ad dimidiam CF hoc est ad DC. Quia autem ut LK ad NM ita MO ad OKGa naar margenoot*. erit et componendo ut duae simul LK, NM ad NM ita MK ad KO. Itaque et MK ad KO ut LK ad DC. Sed ut LK ad DC ita quoque est CE ad KOGa naar margenoot[*], quia scilicet subtensa GH aequalis AB; Ergo MK ad KO ut CE ad KO; ac proinde MK aequalis CE: quod erat ostendendum. Sit jam pro lente GH meniscus [Fig. 9], cujus superficies cava GMH; crassitudo autem menisci KM erit id quo KO superat MO. Positis itaque caeteris ut prius; quia ut excessus NM supra LK ad NM ita dupla LK ad foci distantiam MPGa naar margenoot*, quae aequalis ponitur CF, Erit proinde ut dictus excessus duarum NM, LK ad NM ita dupla LK ad CF, sive ita LK ad dimidiam CF, hoc est, ad DC. Quia autem ut NM ad LK ita OK ad OM erit etiam ut excessus NM supra LK ad NM ita KM ad KO. Itaque et KM ad KO, ut LK ad DC. Unde porro sicut prius in lente utrinque convexa ostendetur quod MK aequalis CE. Cum igitur quaevis lens utrimque convexa vel meniscus, aequalem foci distantiam eandemque latitudinem habens atque lens planoconvexa AB, etiam crassitudinem ei aequalem habeat, sequitur et omnes utrimque convexas atque omnes meniscos qui foci distantiam latitudinemque inter se aequalem habuerint, etiam pari crassitudine futuros. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 280]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 12.]
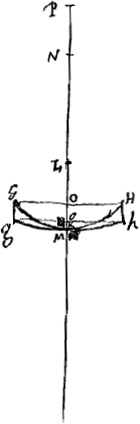
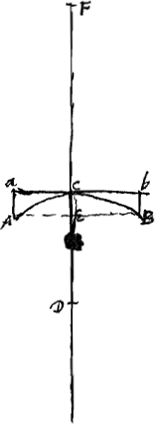
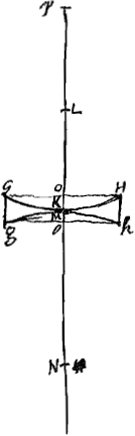
Considérons maintenant une lentille planconcave ACBba [Fig. 10], dont les deux surfaces se touchent au point C; et supposons de nouveau que D soit le centre de la surface ACB et CF la distance du point de dispersion, distance qui est égale à 2 CDGa naar voetnoot1). Soit Aa ou CE l'épaisseur de cette lentille. Soit GKHhMg l'autre lentille; elle est biconcave [Fig. 11] ou convexo-concave [Fig. 12] et a une largeur égale à AB et une distance PM du point de dispersion égale à FC. Les deux surfaces de ces lentilles se touchent par hypothèse au milieu, de sorte que les points K et M coïncident et que l'épaisseur de la lentille est égale soit à la somme des longueurs KO et Mo qui représentent les hauteurs des deux surfaces sphériques, soit à leur différence. Pour démontrer que cette épaisseur est égale à l'épaisseur CE de la lentille ACBba, il suffit de répéter les deux démonstrations précédentes; la première s'applique à la lentille biconcave, la seconde à la lentille convexo-concave. Il faut observer cependant qu'au lieu de la distance focale on doit toujours lire la distance du point de dispersion et il faut avoir égard à ce que la somme ou la différence des deux grandeurs KO et Mo est maintenant Oo, tandis qu' auparavant elle était égale à KM. Ces démonstrations nous permettent de conclure que la proposition est vraie aussi pour les lentilles biconcaves ou convexo-concaves. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition IV.Indiquer comment on peut trouver rapidement pour les lentilles les aberrations des rayons provenant de la forme sphérique des surfacesGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 281]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 10.]
 [Fig. 11.]
Sit jam etiam lens planocava ACBba [Fig. 10] supersicie utraque contigua in C; sitque rursus supersiciei ACB centrum D, et CF distantia puncti dispersus, quae est dupla CDGa naar voetnoot1); crassitudo autem sit Aa vel CE. Lens autem altera, vel utrimque cava [Fig. 11] vel cavoconvexaGa naar voetnoot2) [Fig. 12] sit GKHhMg aequalem ipsi AB latitudinem habens, punctique dispersus distantiam PM aequalem FC. Harum autem lentium superficies utraeque sese in puncto medio contingere ponuntur, ita ut puncta K et M in unum conveniant, ac crassitudo lentis sit, vel summa duarum KO, Mo, quae altitudines utriusque sphaericae superficiei referunt, vel earum differentia. Quae crassitudo ut aequalis ostendatur crassitudini CE lentis ACBba, repetenda tantum est utraque praecedens demonstratio, quarum prior convenit lenti utrimque cavae, posterior cavoconvexaeGa naar voetnoot2), ubi observandum tamen ut pro foci distantia semper legatur distantia puncti dispersus, et animadvertendum summam aut differentiam duarum KO, Mo, hic esse Oo, cum illic fuerit KM. Ex his vero rursus sequitur, veram quoque esse propositionem in quibusvis lentibus utrimque cavis vel cavoconvexisGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio IV.]Quomodo in lentibus aberrationes radiorum quae ex figura superficierum sphaerica oriuntur compendio inveniunturGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 282]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nous entendons par lentilles convexes toutes celles qui font concourir les rayons parallèles, soit qu'elles possèdent deux surfaces convexes, soit qu'elles aient une surface convexe et une surface plane ou une surface convexe et une surface concave. Parmi celles de ces lentilles qui possèdent la même distance focale, les unes font concourir les rayons parallèles mieux que les autres vers ce point qu'on appelle le foyer; c'est-à-dire en prenant égales entre elles les largeurs ou ouvertures des lentilles. Quoique cela ne soit pas de grande importance dans la construction des télescopes à cause d'une autre aberration bien plus considérable et d'une autre nature, dont nous parlerons lorsque nous serons arrivés à ce sujetGa naar voetnoot1), ces considérations ont cependant leur utilité ailleurs dans la théorie des microscopes; nous ne devons donc pas les passer sous silenceGa naar voetnoot2). Nous prendrons partout dans ces considérations la valeur 3/2 pour l'indice de réfraction du verre: en effet, on trouve à fort peu près cette valeur-là, comme nous l'avons expliqué plus hautGa naar voetnoot3). Commençons doncGa naar voetnoot4) par le cas d'une lentille planconvexe placée de telle manière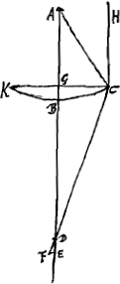 [Fig. 13.]
que sa surface plane est exposée aux rayons parallèles; c'est dans ce cas-là que le calcul est le plus facile. Je suppose que le segment de cercle KBC [Fig. 13] représente la section faite dans une lentille de ce genre par un plan passant par l'axe. Le point A est le centre de ce cercle, donc aussi celui de la surface convexe. La droite ABD représente l'axe de la lentille; elle divise l'arc KC en deux parties égales au point B et la corde KC au point G. La surface convexe KBC coupe la surface plane KC suivant une circonférence qui constitue le bord de la lentille. On demande d'examiner la réfraction du rayon HC parallèle à l'axe de la lentille et éloigné de cet axe à une distance aussi grande que possible. Le rayon réfracté est représenté par la droite CD: il est évident que dans cette lentille il n'y a qu'une seule réfraction qui a lieu à la surface convexe CBK. Quant au foyer E de la lentille, il sera situé au-delà du point D, comme cela a été démontré à la prop. IX du livre I de la première PartieGa naar voetnoot5); on le trouvera en prenant AE = 3 AB; en effet, de cette façon on aura AE:EB = 3:2, valeur que nous avons adoptée ici pour celle de l'indice de réfraction. Nous devons donc trouver la grandeur du segment DE, où tous les rayons réfractés provenant de rayons incidents parallèles rencontrent l'axe de la lentille: on sait que plus un rayon est proche de l'axe AB plus aussi il rencontre l'axe à petite distance du foyer, comme nous l'avons démontré à la proposition IX citée. Tirons la droite AC et soit celle-ci, ou AB, égale à a, et CG à b: ce sont là deux grandeurs données. Soit en outre AD = x. Comme le rapport AD:DC est égal à l'indice de réfractionGa naar voetnoot6), on aura DC = ⅔ x Et si nous retranchons le carré GC du carré DC nous trouvons que le carré GD est égal à 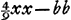 , et GD à , et GD à 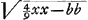 . D'autre part en retranchant le . D'autre part en retranchant le
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 283]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lentis sphaericae convexae nomine omnes eas intelligimus quae radios parallelos concurrere faciunt, sive duabus convexis superficiebus constent, sive convexa et plana, sive convexa et concava, harum vero aequales foci distantias habentium aliae alijs perfectius radios parallelos versus punctum illud quod focus dicitur inclinant, sumptis nimirum latitudinibus seu aperturis lentium aequalibus. quod licet in telescopiorum rationibus parum referat, propter aliam aberrationem longe majorem atque alterius naturae, de qua, ubi eo ventum erit, dicemusGa naar voetnoot1), habet tamen in microscopiorum examine alibi utilitatem haec cognitio, eoque non est praetereundaGa naar voetnoot2). Proportionem refractionis vitri sesquialteram in his ubique usurpabimus, quae quam proxime ejusmodi invenitur ut in praecedentibus dictum fuitGa naar voetnoot3). IncipiendoGa naar voetnoot4) itaque a planoconvexa lente atque ea illius positione qua supersicies plana radijs parallelis exposita est, ubi calculi ratio omnium facillima est; Sit lens ejusmodi [Fig. 13], cujus sectio per axem segmentum circuli KBC, cujus circuli atque item superficiei convexae centrum sit A, axis vero lentis ABD, secans bifarium arcum KC in B et subtensam KC in G, conveniatque superficies convexa KBC cum plana KC in lentis margine, et propositum sit examinare refractionem radij HC axi lentis paralleli atque ab eo remotissimi, quae refractio ponatur esse CD, et constat quidem in hac lente tantum unam fieri in superficie convexa CBK. Focus autem lentis E erit ultra punctum D ut ostensum est prop. [IX, Part. I, Lib. I]Ga naar voetnoot5) invenieturque sumendo AE triplam AB ita enim AE ad EB habebit rationem sesquialteram, quae hic est proportio refractionis. Inveniendum itaque est spatium DE, intra quod radiorum omnium parallelorum refractiones cum axe lentis conveniunt; etenim tanto quaeque propius convenit quanto vicinior radius fuerit axi AB, ut ostensum propos. [IX, Part. I, Lib. I]Ga naar voetnoot5). Jungatur AC, sitque haec five AB ∞ a, CG ∞ b, quarum utraque data est. AD vero sit ∞ x. Quia itaque AD ad DC habet rationem quae refractiones metiturGa naar voetnoot6), erit DC ∞ ⅔x. Et ablato quadrato GC à quadrato CD, fiet quadratum GD ∞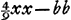 , et GD
∞ , et GD
∞ 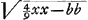 . Rursus ablato eodem . Rursus ablato eodem
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 284]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
même carré CG du carré AC, nous trouverons que le carré GA est égal à aa-bb et AG à 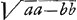 ; et en ajoutant cette expression à GD, c'est-à-dire à ; et en ajoutant cette expression à GD, c'est-à-dire à 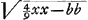 , nous obtiendrons pour la longueur entière AD ou x la valeur , nous obtiendrons pour la longueur entière AD ou x la valeur 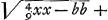 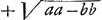 . D'où l'on tire . D'où l'on tire 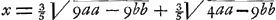 . Cette formule fait voir que si l'on prend la longueur AB égale à 6 pieds ou à 72 pouces et la longueur GC égale à 1 pouce, on trouve que x ou AD est un peu plus grande que 215 968747/1000000; et si l'on retranche cette longueur de AE = 216, le reste DE devient un peu plus petit que 31253/1000000 pouce. Par conséquent, dans une lentille de ce genre dont la distance focale BE est de 12 pieds et l'ouverture KC de deux pouces, tous les rayons coupent l'axe dans l'espace DE. . Cette formule fait voir que si l'on prend la longueur AB égale à 6 pieds ou à 72 pouces et la longueur GC égale à 1 pouce, on trouve que x ou AD est un peu plus grande que 215 968747/1000000; et si l'on retranche cette longueur de AE = 216, le reste DE devient un peu plus petit que 31253/1000000 pouce. Par conséquent, dans une lentille de ce genre dont la distance focale BE est de 12 pieds et l'ouverture KC de deux pouces, tous les rayons coupent l'axe dans l'espace DE.
Nous appellerons cet intervalle DE, c'est-à-dire la distance qui pour une lentille quelconque sépare le foyer du point où les rayons extrêmes coupent l'axe, l'aberration du rayon extrême. 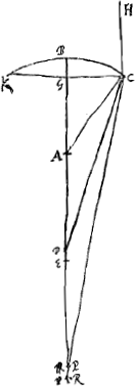 [Fig. 14.]
Il faut favoir en outre que pour une lentille donnée on peut aussi trouver cette aberration d'une autre manière plus facileGa naar voetnoot1), attendu que pour toute lentille planconvexe dont la surface plane est à l'extérieur l'aberration du rayon extrême est égale à 9/2 fois l'épaisseur de la lentilleGa naar voetnoot2). Il est vrai qu'il y a une différence minimale, mais elle est si petite que pour des lentilles d'une largeur telle qu'elle convient aux télescopes elle n'est d'aucune importance. Dans la lentille considérée par exemple nous trouverons, en prenant DE = 9/2GB, une distance de 31252/1000000 pouce environ, tandis que le calcul antérieur nous donnait 31253/1000000. Si nous retournons cette même lentille de telle manière que les rayons sont réfractés d'abord par la surface convexe, nous obtiendrons un rassemblement des rayons bien plus parfaitGa naar voetnoot3). Or, le calcul se fait de la manière suivante. On prend d'abord BR [Fig. 14] égale au triple du rayon BA, de sorte que R devient le foyer de la surfaceconvexe KBC. On pose ensuite GE égale aux deux tiers de GR et alors E sera le foyer de la lentille KBC, comme on le voit par la proposition XIV du Liv. I de la première PartieGa naar voetnoot4); la même proposition fait voir que la distance focale GE est à-peu-près la même que celle qui correspondait à la position | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 285]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 13.]
quadrato CG à quadrato AC, fiet quadratum GA ∞ aa-bb et AG ∞ 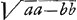 . qua addita ad GD ∞ . qua addita ad GD ∞ 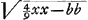 fiet tota AD sive x ∞ fiet tota AD sive x ∞ 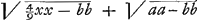 . Unde invenitur x ∞ . Unde invenitur x ∞ 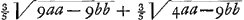 . Secundum quae si AB ponatur pedum 6 sive pollicum 72 et GC pollicis 1, invenitur x sive AD paulo major quam 215 968747/1000000, qua ablata ab AE ∞ 216, reliqua fit DE paulo minor quam 31253/1000000 unius pollicis. Itaque in lente hujusmodi cujus foci distantia BE est 12 pedum, apertura vero KC duorum pollicum, radij omnes intra spatium DE cum axe conveniunt. . Secundum quae si AB ponatur pedum 6 sive pollicum 72 et GC pollicis 1, invenitur x sive AD paulo major quam 215 968747/1000000, qua ablata ab AE ∞ 216, reliqua fit DE paulo minor quam 31253/1000000 unius pollicis. Itaque in lente hujusmodi cujus foci distantia BE est 12 pedum, apertura vero KC duorum pollicum, radij omnes intra spatium DE cum axe conveniunt.
Dicatur autem intervallum istud DE, quo nempe radij extremi, in quavis lente, concursus distat a foco lentis: Aberratio radij extremi. Hanc porro, in proposita lente, alia quoque faciliori ratione reperiri sciendum estGa naar voetnoot1); quandoquidem: In omni lente planoconvexa cujus plana superficies exterior est, aberratio radij extremi est quadrupla sesquialtera sive 9/2 crassitudinis lentisGa naar voetnoot2); Exigua quidem differentiola, sed quae in illa lentium latitudine quae telescopiorum usibus idonea est, nullius sit momenti. Ita, in proposita lente, si sumatur DE ∞ 9/2 GB, inveniemus eam 31252/1000000 unius pollicis proximè, cum ex priori calculo habuerimus 31253/1000000. In lente eadem inversa, ut superficies convexa primum radios inflectat, multo melior radiorum collectio invenieturGa naar voetnoot3). Est autem calculi ratio hujusmodi. Primo sumitur BR [Fig. 14] tripla semidiametri BA, ut fiat R focus superficiei convexae KBC, deinde ponitur GE aequalis duabus tertijs GR; tumque erit E focus lentis KBC, ut constat ex [Propos. XIV, Part. I, Lib. I.]Ga naar voetnoot4) ex qua apparet insuper foci distantiam GE proxime eandem esse quae fuit superiori lentis positu. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 286]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
précédente de la lentille. Or, le rayon extrême HC parallèle à l'axe est d'abord réfracté par la surface convexe KBC de manière à se diriger vers le point P, de telle façon que le rapport CP:PA devient égal à l'indice de réfraction, c'est-à-dire à-dire à 3:2Ga naar margenoot*; quittant ensuite la lentille par la surface plane KC le rayon est réfracté de manière à se diriger vers le point D, de telle façon que de nouveau le rapport PC:CD devient égal à l'indice de réfractionGa naar margenoot* et CD, par conséquent, égale à AP. Pour trouver AP il faut poser AB = a, CG = b, comme plus haut, et AP = x. Nous aurons donc 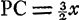 , et si du carré 9/4 xx de cette expression nous retranchons les carrés PA = xx et CA = aa, le reste , et si du carré 9/4 xx de cette expression nous retranchons les carrés PA = xx et CA = aa, le reste 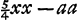 sera égal au double du rectangle PAG, c'est-à-dire à sera égal au double du rectangle PAG, c'est-à-dire à 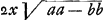 . De cette égalité on tire . De cette égalité on tire 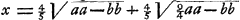 . Ayant trouvé ainsi la distance AP, à laquelle CD est égale comme nous l'avons dit, on retranche le carré CG du carré CD. Reste le carré GD, et si l'on retranche GD de GE, il reste DE comme aberration du rayon extrême. . Ayant trouvé ainsi la distance AP, à laquelle CD est égale comme nous l'avons dit, on retranche le carré CG du carré CD. Reste le carré GD, et si l'on retranche GD de GE, il reste DE comme aberration du rayon extrême.
Mais la même longueur DE peut être trouvée sans un si laborieux calcul, attendu que pour une lentille planconvexe dont la surface convexe reçoit les rayons, l'aberration du rayon extrême est égale a 7/6 fois l'épaisseur de la lentilleGa naar voetnoot3); et si nous indiquons les méthodes de calcul, c'est seulement dans le but de donner à tout-le-monde l'occasion de se convaincre par des exemples numériques de la justesse de nos règles. Pour la lentille considérée on trouve par le calcul indiqué plus haut, en posant comme précédemment AB égal à 72 pouces et CG à 1 pouce, DE = = 81021/10000000 pouce à peu près. Mais suivant la règle, c'est-à-dire en prenant pour DE les 7/6 de l'épaisseur BG, on obtient pour cette longueur la valeur 81022/10000000 à peu près. Il apparaît par là combien l'aberration est plus petite pour la même lentille planconvexe lorsqu'on la place dans cette position que lorsque sa surface plane reçoit les rayons parallèles. En effet, les fractions 7/6 et 9/2 sont entre elles comme 7 est à 27, de sorte que l'aberration est à peu près quatre fois plus petite dans le premier cas. On peut aussi considérer l'aberration due seulement à la surface convexe KBC, laquelle est représentée ici par PR, R étant le foyer de cette surface; cette longueur PR est toujours égale à 4/3 BGGa naar voetnoot4), où BG représente la hauteur de la surface convexe. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 287]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 14.]
Radius autem extremus HC axi parallelus a superficie convexa KBC primum flectitur versus P, ita ut CP ad PA habeat rationem quae est refractionis, nempe 3 ad 2Ga naar margenoot*; deinde ex superficie plana KC egrediens refringitur versus D, ut PC ad CD rursus habeat rationem quae est refractionisGa naar margenoot*, ita ut CD proinde aequalis sit AP. Ad inveniendam vero AP, positis ut ante AB ∞ a; CG ∞ b, AP vero ∞ x; erit PC ∞ ∞ 3/2 x. àcujus quadrato 9/4 xx, si auferantur quadrata PA ∞ ∞ xx et CA ∞ aa, quod restat 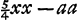 aequabitur duplo rectangulo PAG hoc est aequabitur duplo rectangulo PAG hoc est 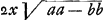 . Ex qua aequatione fit x ∞ . Ex qua aequatione fit x ∞ 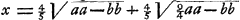 . Itaque investigatâ secundum haec AP, cui aequalem diximus CD, aufertur deinde ab hujus quadrato quadratum CG; unde relinquitur quadr. GD. ablata autem GD à GE, restat DE aberratio radij extremi. . Itaque investigatâ secundum haec AP, cui aequalem diximus CD, aufertur deinde ab hujus quadrato quadratum CG; unde relinquitur quadr. GD. ablata autem GD à GE, restat DE aberratio radij extremi.
Eadem vero DE absque tanto calculi labore haberi potest, quia In lente planoconvexa cujus convexa superficies radios parallelos excipit, aberratio radij extremi est 7/6 crassitudinis lentisGa naar voetnoot3). Atque eo tantum supputandi methodos describimus ut has regulas veras esse quivis per numeros examinare possit. Et in hac quidem lente posita AB ut ante pollicum 72; CG pollicis 1, invenitur praedicto calculo DE ∞∞ 81021/10000000 unius pollicis proximè. Secundum regulam vero, hoc est, sumtâ DE ∞ 7/6 crassitudinis BG, fit ipsa proxime 81022/10000000. Patet autem hinc quanto minor aberratio sit in eadem lente planoconvexa hoc modo collocata, quam si plana ejus superficies radios parallelos excipiat. sicut enim 7/6 ad 9/2 ita 7 ad 27, adeo ut aberratio fere quadruplo minor sit. Potest etiam solius superficiei convexae KBC aberratio considerari, ut hic PR, cum R sit focus illius superficiei: Estque PR semper aequalis 4/3 BGGa naar voetnoot4) sive altitudinis convexi. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 288]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
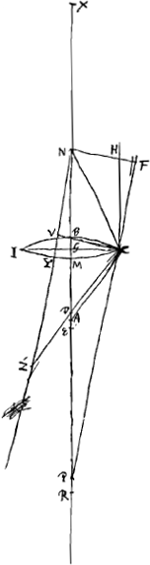
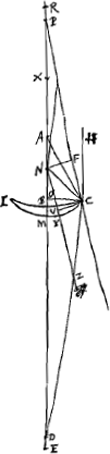
Supposons maintenant que la lentille considérée IC [Fig. 15] soit biconvexe et que le point A représente le centre de la surface IBC qui reçoit les rayons parallèles, tandis que N est le centre de la surface IMC, par lesquels passe la droite NA qui soit prolongée des deux côtés. Nous considérons comme donnés les rayons AB et NM, et le rayon GC de la lentille. Si nous appelons E le foyer de la lentille IC et que nous prenons BR = 3 BA et MX = 3 MN, nous devrons avoir RX:RN = RM:REGa naar voetnoot1). Or, les trois premières longueurs, RX, RN et RM, sont connues, car comme AB ou AC est donnée et CG aussi, AG sera également connue. Et de même NG sera connue vu que NC et CG le sont. Mais la longueur AR elle aussi est donnée, vu qu'elle est égale à 2 AB, et de même NX = 2 NM. Par conséquent la longueur entière RX sera donnée, ainsi que RN et RM. Il en résulte que la quatrième proportionelle RE sera également connue. Supposons ensuite que le rayon extrême parallèle à l'axe, HC, acquière après la première réfraction à la surface IBC une direction telle que, s'il conservait cette direction, il rencontrerait l'axe au point P, et que par la deuxième réfraction à la surface CMI ce rayon acquière la direction de la droite CD rencontrant l'axe au point D. L'aberration du rayon HC est donc DE, qu'on trouvera de la façon suivante. Supposons la droite NZ parallèle à CP et puisse le prolongement de CD la couper au point Z. Soit en outre CV une perpendiculaire à NZ et NF une perpendiculaire au prolongement de PC. On trouve donc premièrement AP, puisque AB et CG sont données, de la même manière qu' auparavant dans le cas de la lentille planconvexeGa naar voetnoot2). Or, AP est à PC comme 2 est à 3Ga naar voetnoot3); par conséquent, la grandeur PC elle aussi sera donnée. Mais AP et AR étant données, PR l'est également; et si nous retranchons PR de RN qui est connue d'après ce que nous avons démontré, il reste PN. On a ensuite PC:CG = PN:NF (ou CV); par conséquent, cette dernière grandeur sera également connue. Nousdevons maintenant considérer NZ comme l'axe de la surface convexe CYI qui dirige le rayon FC parallèle à l'axe vers le point Z situé de telle manière que le rapport NZ:ZC est égal à l'indice de réfraction, c'est-à-dire à 3:2Ga naar voetnoot4); NC et CV étant données on pourra donc trouver NZ de la même manière qu' auparavant dans le cas où la lentille planconvexe se trouvait dans sa première positionGa naar voetnoot5). Mais les triangles semblables ZND et CPD font voir que ZN:CP == ND:DP; et, par composition, que la somme de ZN et de CP est à CP comme NP est à PD. Or, nous avons fait voir que les longueurs ZN, CP et NP sont données; il en résulte que la longueur PD elle aussi est connue. Mais PR est également connue. DR l'est donc aussi, et si de cette dernière l'on retranche la longueur RE antérieurement trouvée, on obtiendra l'aberration cherchée DE du | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 289]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Esto jam proposita lens utrinque convexa IC [Fig. 15], sitque superficiei IBC, quae radios parallelos excipit, centrum A; superficiei vero IMC centrum N, per
 [Fig. 15.]
quae transiens axis lentis NA utrimque productus sit. datas autem ponimus semidiametros AB, NM, et semidiametrum lentis GC. Jam si E ponatur focus esse lentis IC et sumatur BR tripla BA et MX tripla MN, debebit esse ut RX ad RN ita RM ad REGa naar voetnoot1). Dantur autem tres istae priores RX, RN, RM, nam quia AB seu AC data est itemque CG, dabitur et AG. similiterque propter datas NC, CG dabitur NG. sed et AR datur, quippe dupla AB, et NX dupla NM. Ergo tota RX data erit nec non RN et RM. Quare et quarta proportionalis RE data erit. Ponamus jam porro radium extremum, axi parallelum, HC, post refractionem primam in superficie IBC ita ferri, ut cum axe concursurus sit in P, altera deinde refractione in superficie CMI flecti secundum rectam CD quae axi occurrat in D. Aberratio itaque radij HC est DE, quae hoc modo invenietur. Sit NZ parallela CP, atque ei occurrat producta CD in Z. Sit etiam CV perpendicularis ad NZ, et NF perpendicularis in PC productam. Primum itaque ex datis AB, CG invenitur AP sicut paulo ante in lente planoconvexaGa naar voetnoot2). Est autem AP ad PC ut 2 ad 3Ga naar voetnoot3) ergo et PC data erit. Ex datis autem AP et AR, datur PR; qua ablata ab RN, quam datam ostendimus, relinquitur PN. sicut porro PC ad CG ita PN ad NF sive CV, itaque et haec dabitur. Jam consideranda est NZ tanquam axis supersiciei convexae CYI, quae radium axi parallelum FC ita flectit versus Z, ut NZ ad ZC habeat rationem quae est refractionis, hoc est, 3 ad 2Ga naar voetnoot4); unde ex datis NC et CV invenietur NZ, eodem modo atque superius in prima positione lentis planoconvexaeGa naar voetnoot5). Jam vero propter triangula similia ZND, CPD, erit ZN ad CP ut ND ad DP; et componendo, ZN una cum CP ad CP ut NP ad PD. datas autem ostendimus ZN, CP, NP: ergo et PD hinc data erit. datur autem et PR. Ergo et DR. à qua si auferatur RE jam | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 290]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
rayon HC. Et c'est cette méthode qu'on devrait suivre pour calculer exactement cette aberration. Mais nous avons trouvéGa naar voetnoot1) pour ce cas aussi une règle abrégée qui nous permet de déterminer la ligne DE d'une manière semblable à celle dont nous nous sommes servis dans le cas précédent de la lentille planconvexe et avec le même degré de précision, en évitant le travail du calcul rigoureux. En effet, après avoir trouvé seulement BG et GM à l'aide des longueurs données AB, NM et CG, nous aurons, en posant la longueur totale BM, c'est-à-dire l'épaisseur de la lentille, égale à q, le rayon AB égal à a, et NM à n,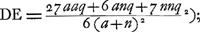 Ga naar voetnoot2); en d'autres termes: l'épaisseur BM de la lentille sera à l'aberration DE du rayon extrême comme 6 fois le carré d'une ligne égale à la somme de AB et de NM est à la somme de 27 fois le carré AB, de 6 fois le rectangle AB, NM et de 7 fois le carré NM. Cette règle, de même que celles que nous donnerons dans la suite, a été trouvée en négligeant des quantités fort petites; ce que nous avons fait pourtant avec le discernement qui était nécessaire. Si donc, par exemple, la lentille IC est une lentille biconvexe symétrique, c'est-à-dire si a = n, la longueur DE deviendra égale à 5/3 de l'épaisseur BM. Il s'ensuit qu'une lentille symétrique de ce genre et qui possède une largeur et une distance focale égales aux grandeurs correspondantes d'une lentille planconvexe, dont la surface convexe est située a l'extérieur, rassemble les rayons parallèles moins bien que cette dernière. En effet, puisque l'épaisseur de ces lentilles est la même d'après la prop. IIIGa naar voetnoot3), les rayons qui tombent sur la lentille planconvexe atteindront l'axe dans un espace égal à 7/6 fois l'épaisseur, tandis que pour la lentille symétrique l'espace correspondant sera égal à 5/3 fois l'épaisseur (qui est la même): ces deux intervalles seront donc entre eux comme les nombres 7 et 10. Si nous supposons que les rayons AB et NM soient entre eux comme 2 est à 5, c'est-à-dire que a soit composé de 2 et n de 5 parties, la distance DE deviendra égale d'après cette règle à 7/6 q, où q représente l'épaisseur de la lentille. Une lentille de cette espèce est donc équivalente sous ce rapport à la lentille planconvexe considéréeGa naar voetnoot2). De cette façon on peut aisément examiner la valeur relative de diverses lentilles quelconques possédant des surfaces convexes de courbure inégale. Mais si l'on demande de déterminer le minimum, c'est-à-dire de chercher la forme de la lentille qui donne une aberration DE moindre que celle due à toute autre lentille, je trouveGa naar voetnoot5) qu'on doit avoir AB:NM = 1:6Ga naar voetnoot6) et qu' alors la | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 291]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ante inventa, relinquetur DE aberratio radij HC quaesita. Et haec quidem methodus ad exactam supputationem adhibenda esset. InvenimusGa naar voetnoot1) autem et hic Regulam compendiosam qua, absque labore illo, lineam DE, sicut in praecedenti lente planoconvexa, atque aeque accuratè definire licet. Repertis enim tantummodo BG, GM, ex datis AB, NM, CG; ponendoque totam BM, hoc est, lentis crassitudinem ∞ q. semidiametrum AB ∞ a; NM ∞ n. Erit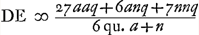 Ga naar voetnoot2), hoc est, sicut sexcuplum quadratum lineae aequalis duabus AB, NM, ad vigintiseptuplum quadratum AB, plus sexcuplo rectangulo AB, NM, plus septuplo quadrato NM, ita erit crassitudo lentis BM ad aberrationem radij extremi DE. Quae regula ut et sequentes quas dabimus inventa est neglectis minimis, sed necessario cum delectu. Ga naar voetnoot2), hoc est, sicut sexcuplum quadratum lineae aequalis duabus AB, NM, ad vigintiseptuplum quadratum AB, plus sexcuplo rectangulo AB, NM, plus septuplo quadrato NM, ita erit crassitudo lentis BM ad aberrationem radij extremi DE. Quae regula ut et sequentes quas dabimus inventa est neglectis minimis, sed necessario cum delectu.
Si itaque, exempli gratia, lens IC fuerit aequaliter utrinque convexa, hoc est, si a ∞ n, fiet DE ∞ 5/3 crassitudinis BM. Unde patet lentem utrimque aequaliter convexam, latitudine et foci distantia ijsdem, cum lente planoconvexa, cujus convexum exterius situm sit, non aeque bene atque illam radios parallelos colligere: talium enim lentium aequalis cum sit crassitudo, ut ostensum propos. [III]Ga naar voetnoot3), convenient radij in planoconvexa intra 7/6 suae crassitudinis; at in hac aequaliter convexa intra 5/3 suae, hoc est, ejusdem crassitudinis. quorum intervallorum proportio est ea quae 7 ad 10. Quod si semidiameter AB ad NM ponatur ut 2 ad 5; hoc est, a partium 2, et n partium 5; fiet ex hac regula DE aequalis 7/6 q sive crassitudinis lentis. adeo ut hujusmodi lens aequiparanda sit dictae planoconvexaeGa naar voetnoot4). atque ita facile in quibuslibet inaequalium convexorum lentibus investigari potest quanto quaeque melior sit. Quaesita vero minimi determinatione, hoc est, quaenam forma lentis faciat aberrationem DE reliquis minorem, invenioGa naar voetnoot5) debere esse AB ad NM ut 1 ad 6Ga naar voetnoot6); ac | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 292]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 17].
distance DE devient égale à 15/14 de l'épaisseurGa naar voetnoot1). Cette lentille-là doit donc être considérée comme la meilleure de toutes; quoique la lentille planconvexe ne lui soit pas beaucoup inférieure. Il faut remarquer toutefois que le rayon AB doit toujours être considéré comme appartenant à la surface qui est exposée aux rayons. Car cette même lentille la plus excellente de toutes devient beaucoup moins bonne, lorsqu'on la retourne: elle donne alors une aberration DE égale à 145/42 fois son épaisseurGa naar voetnoot2). Si l'on demande ensuite de déterminer l'aberration DE du rayon extrême, lorsque la distance focale de la lentille et le rayon de courbure de la surface extérieure sont donnés, on peut de la saçon suivante déduire une nouvelle règle de celle qui précède. Soit d la distance focale, et soit comme plus haut AB = a, NM == n et l'épaisseur de la lentille = q. Attendu que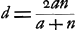 , comme cela ressort de la propos. XVI, Part. I, Liv. IGa naar voetnoot3), on aura , comme cela ressort de la propos. XVI, Part. I, Liv. IGa naar voetnoot3), on aura 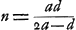 . En substituant partout cette valeur de n dans la formule précédente . En substituant partout cette valeur de n dans la formule précédente 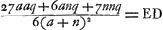 , on trouvera , on trouvera 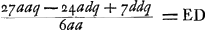 Ga naar voetnoot4). Ga naar voetnoot4).
Pour une lentille concavo-convexe la méthode du calcul est la même que pour une lentille biconvexe, soit que la surface convexe reçoive les rayons parallèles, soit qu'ils tombent sur la surface concave. Nous avons ajouté ici deux figures [Fig. 16 et 17] correspondant à ces deux cas. Il faut observer cependant qu'ici ce n'est pas la somme des longueurs NZ et CP mais leur différence qui est à CP comme NP est à PD. Si nous attribuons aux lettres les mêmes significations qu' auparavant, c'est-à-dire que le rayon AB de la surface extérieure IBC est représenté par a, le rayon NM de la surface IMC par n, et BM, l'épaisseur de la lentille, par q, la règle qui sert à trouver ED, sera exprimée par la formule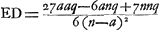 Ga naar voetnoot5). Mais dans le deuxième cas, où a > n, on trouvera Ga naar voetnoot5). Mais dans le deuxième cas, où a > n, on trouvera 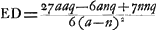 Ga naar voetnoot6). Ga naar voetnoot6).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 293]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tum quidem fit DE aequalis 15/14Ga naar voetnoot1) crassitudinis. adeo ut haec lens optima omnium censenda sit. quanquam planoconvexa non multum ei cedat. 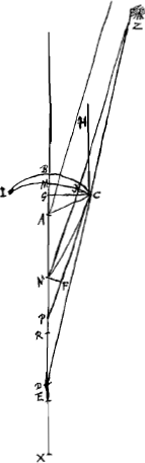 [Fig. 16.]
Notandum autem semidiametrum AB semper sumi ad eam superficiem pertinere quae radios parallelos primum excipit. Nam haec eadem lens optima, si invertatur, multo deterior fit, facitque aberrationem DE aequalem 145/42 crassitudinis suaeGa naar voetnoot2). Porro si ex data lentis foci distantia, ac semidiametro convexi exterioris invenienda sit aberratio DE radij extremi; ex praecedente regula habebitur alia hoc modo. Nempe si foci distantia sit ∞ d, et sicut prius AB ∞ a, NM ∞ n, crassitudo lentis ∞ q. quoniam d est ∞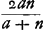 ut patet ex propos. [XVI, Part. I, Lib. I]Ga naar voetnoot3), erit n ∞ ut patet ex propos. [XVI, Part. I, Lib. I]Ga naar voetnoot3), erit n ∞ 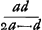 . quo ubique subrogato in locum n in Regula priori . quo ubique subrogato in locum n in Regula priori 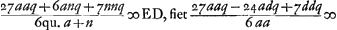 ∞ EDGa naar voetnoot4). ∞ EDGa naar voetnoot4).
In menisco eadem ratio est supputandi, quae in lente utrimque convexa, sive convexa superficies radios parallelos excipiat, sive cava; cujus utriusque casus figuram hic adscripsimus [Fig. 16 et 17]; illud tamen observandum non summam sed differentiam duarum NZ, CP esse hic ad CP ut NP ad PD. Positis vero literarum significationibus ijsdem, quae prius, ut nempe semidiam. AB superficiei exterioris IBC sit a, superficiei IMC semidiam. NM ∞ n, et BM crassitudo lentis ∞ q. Regula ad inveniendam ED ∞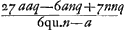 Ga naar voetnoot5). Posteriori vero [Fig. 17], ubi a major quam n, fit ED ∞ Ga naar voetnoot5). Posteriori vero [Fig. 17], ubi a major quam n, fit ED ∞ 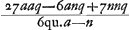 Ga naar voetnoot6). Ga naar voetnoot6).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 294]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
À l'aide de ce résultat les lentilles concavo-convexes quelconques peuvent, elles aussi, être comparées entre elles et avec les lentilles biconvexes. Si, par exemple, dans le premier cas [Fig. 16] nous prenons le rayon NM de la surface concave égal à trois fois le rayon AB, c'est-à-dire si a = 1 et n = 3, la distance ED deviendra égale à 3q, c'est-à-dire à trois fois l'épaisseur BM. Mais dans la meilleure lentille, définie plus haut, l'aberration DE ne serait égale qu'à 15/14 de son épaisseur, la distance focale et la largeur, donc aussi l'épaisseurGa naar margenoot*, étant les mêmes que pour la lentille concavo-convexe IBCM. Il apparaît ainsi qu'une lentille concavo-convexe de ce genre concentre les rayons environ trois fois plus mal que cette lentille la meilleure de toutes. Mais non seulement qu'aucune lentille concavo-convexe n'est aussi bonne qu'une lentille planconvexe, dont la surface sphérique est placée à l'extérieur: on peut même dire qu'elle est d'autant plus mauvaise que l'une de ses deux surfaces est plus concave, la distance focale et la largeur gardant les mêmes valeurs. Dans le premier cas cela peut être démontré comme suit. Désignons de nouveau par la lettre d la distance focale. Vu qu'elle est égale à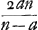 , comme cela ressort de la propos. XVI, Part. I, Liv. IGa naar voetnoot2), on aura , comme cela ressort de la propos. XVI, Part. I, Liv. IGa naar voetnoot2), on aura 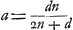 . Substituant partout cette valeur de a dans la première règle, on trouvera . Substituant partout cette valeur de a dans la première règle, on trouvera 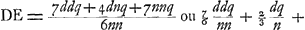 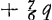 . On en conclut aisément que plus n, c'est-à-dire le rayon NM, est petit, plus la distance DE sera grandeGa naar voetnoot3); et que, quelque grande que soit la valeur qu'on donne
à n, DE sera toujours supérieure à 7/6 q.
Dans le second cas, celui où la surface concave de la lentille concavo-convexe est tournée à l'extérieur, on aura . On en conclut aisément que plus n, c'est-à-dire le rayon NM, est petit, plus la distance DE sera grandeGa naar voetnoot3); et que, quelque grande que soit la valeur qu'on donne
à n, DE sera toujours supérieure à 7/6 q.
Dans le second cas, celui où la surface concave de la lentille concavo-convexe est tournée à l'extérieur, on aura 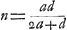 , parce que d, la distance focale, est égale à , parce que d, la distance focale, est égale à 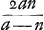 . En substituant partout cette valeur de n dans la deuxième règle on trouve . En substituant partout cette valeur de n dans la deuxième règle on trouve 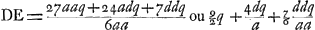 . Cette formule montre que plus a, le rayon de la surface concave, est petit, plus la distance DE devient grande; et que, quelque grande que soit la valeur qu'on donne à a, DE sera toujours supérieure à 27/6 q ou 9/2 q. Il en résulte qu'une lentille planconvexe, même lorsque sa surface plane est placée à l'extérieur, est toujours meilleure qu'une lentille concavo-convexe, dont la surface concave est également tournée vers l'extérieur. En effet, il a été démontré qu'une lentille de ce genre donne une aberration DE égale à 9/2 fois son épaisseurGa naar voetnoot4). . Cette formule montre que plus a, le rayon de la surface concave, est petit, plus la distance DE devient grande; et que, quelque grande que soit la valeur qu'on donne à a, DE sera toujours supérieure à 27/6 q ou 9/2 q. Il en résulte qu'une lentille planconvexe, même lorsque sa surface plane est placée à l'extérieur, est toujours meilleure qu'une lentille concavo-convexe, dont la surface concave est également tournée vers l'extérieur. En effet, il a été démontré qu'une lentille de ce genre donne une aberration DE égale à 9/2 fois son épaisseurGa naar voetnoot4).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 295]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Secundum quae et menisci quilibet inter se et cum lentibus utrimque convexis comparari possunt. Ut si, exempli gratia, in priore casu [Fig. 16], ponatur superficiei cavae semidiameter NM tripla semidiametri AB, hoc est, a ∞ 1, n ∞ 3. fiet ED ∞ 3q, hoc est, tripla crassitudinis BM. At in lente optima supra definita, cujus foci distantia ac latitudo eadem esset quae menisci IBCM, ac proinde eadem quoque crassitudoGa naar margenoot*, aberratio DE tantum 15/14 haberet crassitudinis suae, itaque apparet meniscum hujusmodi fere triplo deterius radios parallelos colligere quam lens illa omnium optima. Sed nec ullus meniscus tantum praestat quantum lens planoconvexa, cujus sphaerica superficies extrorsum collocatur. et tanto quisque pejor est quanto magis cavam superficiem alteram habuerit, eâdem scilicet manente foci distantia ac latitudine. quod in priore quidem casu sic fiet manifestum. Sit rursus foci distantia ∞ d. Ergo quia haec aequalis est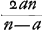 ut patet ex propos. [XVI, Part. I, Lib. I]Ga naar voetnoot2) erit a ∞ ut patet ex propos. [XVI, Part. I, Lib. I]Ga naar voetnoot2) erit a ∞ 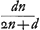 , quo substituto ubique in locum a in Regula harum priori, fiet DE ∞ , quo substituto ubique in locum a in Regula harum priori, fiet DE ∞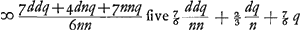 . Ubi facile perspicitur quo minor sumetur n hoc est semidiameter NM, eo majorem fore DEGa naar voetnoot3). Et quantumlibet magna sumetur n, semper DE majorem fore quam 7/6 q.
Secundo casu, cum nempe cava superficies menisci extrorsum conversa est, quia foci distantia . Ubi facile perspicitur quo minor sumetur n hoc est semidiameter NM, eo majorem fore DEGa naar voetnoot3). Et quantumlibet magna sumetur n, semper DE majorem fore quam 7/6 q.
Secundo casu, cum nempe cava superficies menisci extrorsum conversa est, quia foci distantia  ; quo ubique substituto in locum n in posteriori regula fit ; quo ubique substituto in locum n in posteriori regula fit 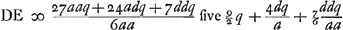 Ubi manifestum est, quo minor sumetur a, hoc est semidiameter superficiei cavae, eo majorem fieri DE. Et quantumvis magna sumetur a, semper DE majorem fore quam 27/6q sive 9/2q. adeo ut lens planoconvexa, licet plana superficies extrorsum collocetur, semper tamen melior sit menisco cujus cavitas itidem extrorsum conversa sit, ostensum enim est eam lentem facere aberrationem DE ∞ 9/2 crassitudinis suaeGa naar voetnoot4). Ubi manifestum est, quo minor sumetur a, hoc est semidiameter superficiei cavae, eo majorem fieri DE. Et quantumvis magna sumetur a, semper DE majorem fore quam 27/6q sive 9/2q. adeo ut lens planoconvexa, licet plana superficies extrorsum collocetur, semper tamen melior sit menisco cujus cavitas itidem extrorsum conversa sit, ostensum enim est eam lentem facere aberrationem DE ∞ 9/2 crassitudinis suaeGa naar voetnoot4).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 296]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition V.Chercher quelles sont parmi toutes les lentilles concaves celles qui dispersent le mieux les rayons parallèles. Nous entendons par ‘lentilles concaves’ toutes les lentilles capables de disperser les rayons parallèles, même lorsqu'elles ont une de leurs surfaces plane ou même convexeGa naar voetnoot1). Parmi elles il faut dire qu'une lentille quelconque disperse d'autant mieux les rayons qu'elle leur donne à moins de chose près des directions telles qu'ils semblent provenir d'un point unique, en d'autres termes, que les rayons réfractés prolongés en sens inverse interceptent sur l'axe une plus petite distance. Considérons d'abord la lentille planconcave KBCOI [Fig. 18] dans le cas où la surface plane OI reçoit les rayons parallèles; soit A le centre de la surface concave, ABE l'axe de la lentille et HO le rayon parallèle extrême qui traversera la surface plane sans être réfracté. Supposons qu'en quittant la surface concave ce rayon soit réfracté de manière à acquérir la direction de la droite CL laquelle prolongée en sens inverse coupe l'axe au point D. Le point de dispersion de la lentille soit désigné par E; on trouve ce point en prenant BE = 2BA, comme cela ressort de la proposition XI, Part. I, Liv. IGa naar voetnoot2). Cette proposition fait voir aussiGa naar voetnoot3) que tous les rayons parallèles moins distants de l'axe que HO, rencontrent l'axe en un point plus voisin de E que celui où LCD coupe l'axe; c'est-à-dire lorsqu'on proionge tous ces rayons réfractés en sens inverse. L'aberration due à cette lentille est donc la distance DE. Pour la trouver il faut suivre la même méthode de calcul que pour la lentille planconvexe. En effet, prolongeons HC vers Q, prenons la droite CG perpendiculaire à AB et tirons la droite CA; si nous supposons alors que KBCG désigne une lentille planconvexe, sur laquelle tombe le rayon QC parallèle à l'axe, il est nécessaire que ce rayon soit réfracté de telle manière au point C situé sur la surface KBC qu'il tombe ensuite dans le prolongement de CL, rayon réfracté provenant du rayon HCGa naar margenoot*. Il suivra donc la voie CD, et l'on calculera de la même manière que plus haut pour la lentille planconvexeGa naar voetnoot5) le point où cette droite CD coupe l'axe AE. Comme dans ce cas-là l'aberration ED sera donc dans celui-ci égale à 9/2 fois l'épaisseur OC ou BG de la lentille, épaisseur qui est trouvée ici, comme auparavant, à l'aide des grandeurs données AB et CG. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 297]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio V.]Concavarum lentium quaenam melius radios parallelos dispergant investigare. Concavarum nomine omnes eas lentes intelligimus quae radios parallelos dispergere aptae sunt, etsi alteram superficierum planam, aut etiam convexam habeantGa naar voetnoot1). Earum vero tanto melius quaeque dispergere radios dicenda est, quanto propius ita eos inclinat ut tanquam ab uno puncto manare videantur, sive ut refractiones eorum retro productae intra minimum spatium cum axe lentis conveniant. 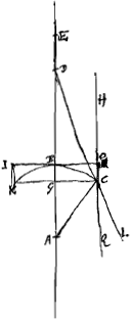 [Fig. 18.]
Sit primum lens planoconcava KBCOI [Fig. 18], superficie plana OI radios parallelos excipiente, centrum vero superficiei concavae sit A, axis lentis ABE; radius autem axi parallelus extremus sit HO, qui planam quidem superficiem irrefractus transibit. ex cava autem egrediens ita frangatur ut pergat secundum CL, quae retro producta conveniat cum axe in D. Punctum autem dispersus lentis sit E, quod invenitur ponendo BE duplam BA, ut constat ex propos. [XI, part. I, lib. I]Ga naar voetnoot2). Ex qua etiam apparetGa naar voetnoot3), radios omnes parallelos qui minus ab axe distant quam HO, propius concurrere ad punctum E quam LCD, si nempe similiter refractiones eorum retro producantur. Est itaque lentis hujus aberratio DE, quae ut inveniatur eadem est calculi ratio atque in lente planoconvexa. Producta enim HC versus Q, factaque CG perpendiculari ad AB, junctaque CA, si putemus lentem planoconvexam esse KBCG, in quam cadat radius axi parallelus QC, necesse est eum ita refringi in C, puncto superficiei KBC, ut refractio ejus sit in directum refractioni CL radij HCGa naar margenoot*. itaque incedet secundum CD. cujus proinde concursus cum axe AE, eodem calculo quo supra in lente planoconvexa investigabiturGa naar voetnoot5). Quemadmodum igitur illic ita et hic erit aberratio ED aequalis 9/2 crassitudinis lentis OC, sive BG. quae crassitudo invenitur ut illic ex datis AB, CG. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 298]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
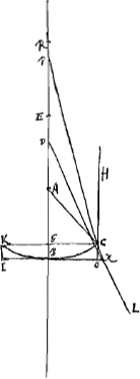
Mais dans la même lentille placée dans la position inverse [Fig. 19], celle où la surface concave KBC est exposée aux rayons parallèles, deux réfractions des rayons se produisent. En effet, le rayon HC est réfracté d'abord au point C et se meut ensuite selon Cκ qui, prolongée en sens inverse, doit couper l'axe en un point P; quittant ensuite la lentille au point κ par la surface plane ce rayon se dirige suivant une droite κL qui, prolongée en sens inverse, rencontre l'axe en-deçà du point P, supposons en D. Or, la distance BE du point de dispersion de la lentille ainsi placée est de nouveau égale au double de BAGa naar voetnoot1); et l'on trouve l'aberration ED du rayon extrême de la façon qui suit. D'abord le rayon Cκ, provenant de la réfraction du rayon HC à la surface concave KBC, tombe sur la même droite que le rayon réfracté qui proviendrait du rayon OC parallèle à l'axe de la lentille si la surface CBK était convexe. Par conséquent, la distance AP du point de concours de la droite Cκ prolongée au centre A sera trouvée de la même manière que plus haut dans le cas de la lentille planconvexeGa naar voetnoot2). Et on a de nouveau ici AP:PC = 2:3. La distance PC sera donc également donnée. Mais GP:PC = BP:Pκ. Cette dernière sera donc aussi connue, et l'on tirera Bκ de la considération des mêmes triangles semblables. Mais comme le rayon Cκ acquiert par la deuxième réfraction une direction κL telle que, si κL rencontre l'axe au point D, le rapport Pκ:κD devient égal à l'indice de réfraction du verre, c'est-à-dire à 3:2, et que Pκ est donnée, il en résulte que κD sera également connue. Et si du carré de cette dernière distance nous retranchons le carré de Bκ, nous obtiendrons le carré de BD, donc aussi BD ellemême, et ensuite aussi la longueur DE. Or, de même que pour la lentille planconvexe dont la surface sphérique est placée à l'extérieur, de même aussi pour la lentille planconcave ainsi placée l'aberration ED est à peu près égale à 7/6 fois l'épaisseur CO ou GB. Il faut donc dire que de cette façon une lentille concave disperse beaucoup mieux les rayons parallèles que lorsqu'elle les reçoit d'abord sur sa surface plane. Considérons maintenant une lentille biconcave IBCKBι [Fig. 20]. Soit A le centre de la surface IBC exposée aux rayons parallèles et N celui de l'autre surface ιBK. L'axe NA de la lentille qui traverse ces deux centres doit être supposé prolongé dans les deux sens. Étant donc donnés les rayons AB et NM, la distance BE du point de dispersion des rayons parallèles sera également donnée. En effet, si l'on prend BR égale à 3BA et MXGa naar voetnoot3) égale à 3MN, il est certain qu'on aura RX:RN = RB:REGa naar margenoot*; d'où il apparaît que RE, et, par conséquent, aussi EB, sont connues. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 299]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
At in eadem lente contrario modo collocata, ut nempe superficies cava KBC [Fig. 19] radios parallelos excipiat, duae fiunt radiorum refractiones. radius enim HC primum in C frangitur, ferturque inde secundum Cκ,
 [Fig. 19].
quae retro producta cum axe convenit in P, ac rursus ex plana superficie egrediens in κ pergit secundum κL, quae retro producta convenit cum axe citra punctum P, puta in D. Est autem distantia BE puncti dispersus lentis sic positae dupla rursus BAGa naar voetnoot1): Inveniturque aberratio radij extremi ED hoc pacto. Primum refractio radij HC facta in superficie cava KBC nempe Cκ in eandem rectam convenit cum refractione radij OC axi lentis paralleli si superficies CBK convexa foret, adeoque invenietur AP intervallum quo distat concursus productae Cκ, à centro A, eodem modo atque supra in lente planoconvexaGa naar voetnoot2); estque hic rursus AP ad PC ut 2 ad 3. Ergo et PC dabitur. Sicut autem GP ad PC ita BP ad Pκ. Ergo et haec data erit, et ex eadem triangulorum similitudine dabitur et Bκ. Jam vero cum secunda refractione radius Cκ ita inflectatur in κL, ut, concurrente ea cum axe in D, ratio Pκ ad κD sit eadem quae refractiones vitri metitur, nempe quae 3 ad 2; dataque sit Pκ. etiam κD dabitur, a cujus quadrato auferendo quadr. Bκ, habebitur quadr. BD, unde et ipsa BD, ac proinde et DE. Est autem sicut in lente planoconvexa, cujus sphaerica superficies exterior ponitur, ita et in hac lentis concavoplanae positione, aberratio ED proximè 7/6 crassitudinis CO sive GB. Adeo ut hoc modo longe melius radios parallelos haec lens cava dispergere dicenda sit quam cum superficie plana illos primum excipit. Esto autem jam lens utrinque cava IBCKBι [Fig. 20]. Sitque superficiei IBC, quae parallelos radios excipit, centrum A alterius vero superficiei ιBK centrum N. per quae transiens axis lentis NA utrimque productus intelligatur. datis igitur semidiametris AB, NM, dabitur et BE distantia puncti dispersus radiorum parallelorum. factis enim BR tripla BA, et MXGa naar voetnoot3) tripla MN, constat esse ut RX ad RN ita RB ad REGa naar margenoot*; unde RE, ac proinde et EB, datam esse liquet. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 300]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
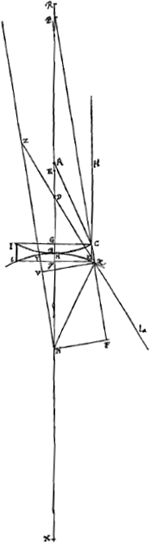
Supposons ensuite que le rayon extrême parallèle à l'axe HC suive après la première réfraction à la surface IBC la voie Cκ, de telle manière que ce rayon prolongé en sens inverse rencontre l'axe au point P; et que par la deuxième réfraction à la surface ιMK ce rayon acquière la direction de la droite κL qui, prolongée en sens inverse, coupe l'axe au point D. L'aberration du rayon extrême HC est donc DE, laquelle, comme nous le montrerons, doit être trouvée ici un peu autrement que pour la lentille biconvexeGa naar voetnoot1). Mais il faut remarquer d'abord que, quoique la surface ιMK soit supposée prolongée jusqu'à κ et qu'elle ait donc une étendue un peu plus grande que la surface IBC, nous considérons cependant ici comme épaisseur de la lentille la longueur Gγ égale à CK, c'est-à-dire à la partie de la droite HC qui est interceptée par les deux surfaces. De même il faut considérer comme ouverture de la lentille le double de CG, et non pas le double de la distance du point κ à l'axe. Supposons maintenant que NZ soit parallèle à CP et que le prolongement de κD la coupe en Z. Menons ensuite une perpendiculaire κV à NZ et une autre NF au prolongement de Pκ. D'abord on trouve donc AP et PC, d'après les longueurs données AB et CG, comme plus haut dans le cas de la lentille planconcave. Mais AP et AR étant données, on connaît aussi PR et si l'on retranche cette longueur de RN, qui est donnée, il reste PN. On sait ensuite que le rapport des longueurs données PC et CG est égal au rapport PN:NF; et en retranchant le carré de cette dernière longueur du carré de Nκ, on obtient comme reste le carré de κF. Mais comme PC est à PG (qui est connue, vu que AP et AG sont connues), ainsi est PN à PF, et si l'on en retranche la longueur trouvée κF, il restera Pκ. En considérant de nouveau NZ comme axe de la surface concave κYι qui réfracte le rayon Cκ de telle manière que, si l'on prolonge κL jusqu'au point Z, on a NZ:Zκ = 3:2, on trouvera la distance NZ au moyen du rayon donné NY et de Vκ, qui est égal à la longueur trouvée NF, de la même façon qu'antérieurement dans le cas de la lentille planconvexe dans sa première positionGa naar voetnoot2). Mais la similitude des triangles DPκ et DNZ nous conduit à la relation NZ:Pκ = ND:DP; d'où l'on tire, par composition, que la somme de NZ et Pκ est à Pκ comme NP est à PD. Si l'on ajoute cette longueur PD à la longueur donnée PR et qu'on retranche RE de leur somme, il restera ED qui était demandée. Voilà la méthode exacte de ce calcul. Mais la même distance ED peut être trouvée sans qu'on prenne la peine de faire ce calcul, d'après une règle entièrement identique à celle qui nous a servi pour la lentille biconvexeGa naar voetnoot3). En effet, en posant comme dans le cas de cette lentille AB = a, NM = n, et l'épaisseur de la lentille qui est ici CK ou Gγ = q, on | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 301]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 20.]
Ponamus porro radium extremum HC, axi parallelum, post refractionem primam in superficie IBC, ita ferri secundum Cκ, ut, retro productus, conveniat cum axe in P. Altera vero refractione, in superficie ιMK, flecti eum secundum κL, quae retro producta conveniat cum axe in D. Aberratio itaque radij extremi HC est DE, quam paulo alia ratione hic inveniri ostendemus quam in lente utrinque convexaGa naar voetnoot1). Sed prius animadvertendum est, licet superficies ιMK ad κ producta intelligatur, atque ita paulo amplius pateat quam superficies IBC, crassitudinem tamen lentis eam hic statui Gγ quae est aequalis CK parti nimirum rectae HC inter superficiem utramque interceptae. sicut et apertura lentis dupla CG censenda est, non vero distantia dupla ab axe puncti κ. Sit jam NZ parallela CP; atque ei occurrat producta κD in Z. ducatur deinde κV perpendicularis ad NZ, et NF ad Pκ productam. Primum itaque ex datis AB, CG, inveniuntur AP, PC, ut modo in lente planoconcava. Ex datis autem AP, AR datur PR, qua ablata ab RN quae data est, relinquitur PN. Porro sicut PC ad CG quae datae sunt ita PN ad NF, cujus quadrato subtracto a quadr. Nκ, reliquum erit quadratum κF. Sicut autem PC ad PG, (quae data est, propter datas AP, AG) ita PN ad PF, à qua si auferatur inventa κF, supererit Pκ. Consideratâ jam rursus NZ tanquam axe superficiei cavae κYι, quae radium Cκ ita flectit, ut producta κL ad Z, sit NZ ad Zκ ut 3 ad 2, invenietur ex data semidiametro NY et Vκ, quae aequalis est inventae NF, distantia NZ, eodem modo atque supra in lente planoconvexa ac positione ejus primaGa naar voetnoot2). Propter triangula autem similia DPκ, DNZ, erit ut NZ ad Pκ ita ND ad DP, et componendo ut utraque simul NZ, Pκ ad Pκ ita NP ad PD. qua addita ad datam PR, et ablata ab utrisque RE, supererit ED quae requirebatur. Et haec quidem calculi ratio exacta. Verum eadem ED, regulâ prorsus simili atque in lente utrinque convexaGa naar voetnoot3), invenitur absque illo calculi labore. Nam posita ut illic AB ∞ a; NM ∞ n, et crassitudine lentis quae hic est CK sive Gγ, ∞ q, fit semper ED ∞ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 302]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 22.]
aura toujours 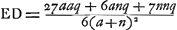 Ga naar voetnoot1) avec une approximation telle que la différence est négligeable par rapport à la distance ED elle même. Ga naar voetnoot1) avec une approximation telle que la différence est négligeable par rapport à la distance ED elle même.
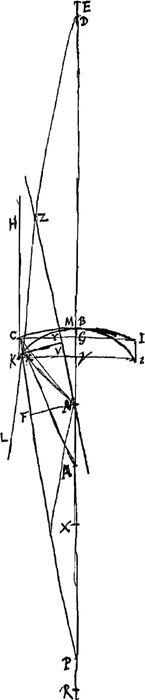
Au moyen de cette formule toutes les lentilles biconcaves peuvent être comparées entre elles et l'on peut trouver combien chacune d'elles disperse les rayons mieux qu'une autre. La meilleure sera trouvée par la détermination du minimum, laquelle sera nécessairement identique à celle qui se présentait dans létude de la lentille biconvexeGa naar voetnoot2). On trouve donc que a et n, c'est-à-dire les rayons AB et NM, doivent être entre eux comme 1 est à 6Ga naar voetnoot3). Il en résulte qu'une lentille de ce genre doit être considérée comme meilleure que toutes les autres pour corriger la vue des myopes et aussi pour rendre parallèles les rayons qui se dirigent vers un point unique quelconque. Mais comme dans les télescopes la lentille convexe antérieure ne concentre pas parfaitement tous les rayons en un point unique, il s'ensuit que si l'on cherche la lentille concave la plus apte à les rendre parallèles et à les transmettre à l'oeil dans cette condition, il ne faut aucunement choisir la lentille à rapport sextuple dont nous avons parlé, mais d'autres lentilles moins parfaites, telles que par leurs défauts ceux de la lentille convexe soient compensés et corrigésGa naar voetnoot4); de sorte qu'on peut obtenir par cet artisice des effets presque aussi excellents que ceux qu'on espère des lentilles de forme elliptique ou hyperbolique. Mais nous en dirons plus un peu plus loinGa naar voetnoot5). Ces lentilles moins parfaites mais plus utiles possèdent une surface convexe et une surface concave faisant partie d'une plus petite sphère. Or, le calcul relatif à ces lentilles est à peu près le même que pour une lentille biconcave. Mais il y a deux cas: la surface concave peut être tournée du côté des rayons parallèles incidents, ou bien c'est la surface convexe qui leur est opposée, comme on peut le voir dans les figures ci-jointes [Fig. 21 et 22]. Il faut remarquer à leur propos que ce n'est pas la somme mais la différence des deux longueurs ZN et κP qui est à κP comme NP est à PD. Attribuons aux lettres les mêmes significations que dans le cas de la lentille biconcave, c'est-à-dire représentons par a le rayon AB de la surface qui reçoit d'abord les rayons, par n le rayon NM de la deuxième surface | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 303]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 21.]
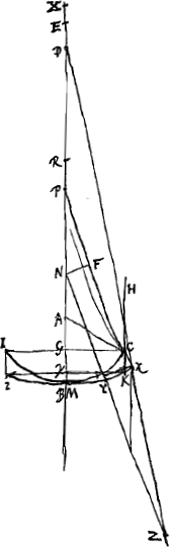
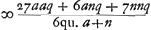 Ga naar voetnoot1): tam prope nimirum ut nullius momenti sit differentia respectu ipsius ED. Ga naar voetnoot1): tam prope nimirum ut nullius momenti sit differentia respectu ipsius ED.
Secundum haec omnes lentes utrimque cavae inter se comparari possunt, ac quanto quaeque melius radios dispergat reperiri. Optima autem ex minimi determinatione invenietur, quae hic necessario eadem est atque in lente utrimque convexaGa naar voetnoot2); ut nempe ratio a ad n, hoc est semidiametri AB ad NM sit ea quae 1 ad 6Ga naar voetnoot3). Adeo ut hujusmodi lens ad corrigendam myopum visionem omnium optima censeri debeat. nec non ad radios, qui ad unum aliquod punctum feruntur parallelos efficiendos. Sed quoniam in telescopijs lens anterior convexa non perfecte ad punctum unum radios inflectit, hinc fit ut si cava quaeratur quae optime ad parallelismum eos reducat, atque ita ad oculum transmittat, nequaquam illa quam diximus rationis sexcuplae deligenda sit, sed aliae minus perfectae, quarum nempe vitijs compensantur ac corriguntur vitia lentis convexaeGa naar voetnoot4), ut idem pene, quod de Ellipticae ac hyperbolicae figurae vitris speratur, hac arte consequi liceat. Qua de re paulo post pluribus ageturGa naar voetnoot5). Sunt autem ista imperfectiora sed usu meliora quibus superficies altera convexa, altera ex minori sphaera concava, in quibus calculi methodus eadem plane quae in lente utrimque cava. duplex autem casus, quia vel cava superficies radijs parallelis obvertitur, vel convexa, ut in adjectis schematis [Fig. 21 et 22] videre est. In quibus observandum, non summam sed differentiam duarum ZN, κP esse ad κP sicut NP ad PD. Positis vero literarum significationibus ijsdem quae in lente utrimque cava, ut nempe semidiameter AB, superficiei quae primum radios accipit, sit a, semidia- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 304]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
et par q l'épaisseur CK, ou Gγ, de la lentille. La règle qui sert à trouver l'aberration ED du rayon extrême sera exprimée dans le premier cas par la formule 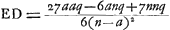 , et dans le deuxième cas, où a>n, par la formule , et dans le deuxième cas, où a>n, par la formule 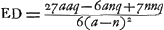 Ga naar voetnoot1). Or, il apparaît que ces formules sont absolument les mêmes que celles que nous avons données plus haut dans le cas des lentilles concavo-convexesGa naar voetnoot2). Elles nous permettront de comparer entre elles les lentilles concaves considérées et de déterminer les grandeurs relatives des aberrations propres à chacune d'elles. On peut démontrer en général que la même lentille convexo-concave placée comme dans le second cas, c'est-à-dire de telle façon que sa surface convexe reçoit les rayons, disperse moins bien ces rayons que lorsqu'elle est retournée. En effet, si les deux figures [Fig. 21 et 22] représentent la même lentille mais dans des positions différentes et que, par conséquent,
NM dans le deuxième cas est égale à AB dans le premier cas, desquelles l'une et l'autre s'appelle a, et que, de même, AB dans la deuxième figure est égale à NM dans la première desquelles l'une et l'autre s'appelle n, il est évident que dans le deuxième cas on aura Ga naar voetnoot1). Or, il apparaît que ces formules sont absolument les mêmes que celles que nous avons données plus haut dans le cas des lentilles concavo-convexesGa naar voetnoot2). Elles nous permettront de comparer entre elles les lentilles concaves considérées et de déterminer les grandeurs relatives des aberrations propres à chacune d'elles. On peut démontrer en général que la même lentille convexo-concave placée comme dans le second cas, c'est-à-dire de telle façon que sa surface convexe reçoit les rayons, disperse moins bien ces rayons que lorsqu'elle est retournée. En effet, si les deux figures [Fig. 21 et 22] représentent la même lentille mais dans des positions différentes et que, par conséquent,
NM dans le deuxième cas est égale à AB dans le premier cas, desquelles l'une et l'autre s'appelle a, et que, de même, AB dans la deuxième figure est égale à NM dans la première desquelles l'une et l'autre s'appelle n, il est évident que dans le deuxième cas on aura 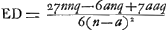 . Mais dans le premier nous avions . Mais dans le premier nous avions 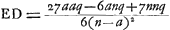 . Comme n est plus grand que a et que, par conséquent, . Comme n est plus grand que a et que, par conséquent, 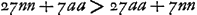 , il apparaît donc que la distance ED sera toujours plus grande dans le deuxième cas que dans le premier. Et il est aisé de voir que la même chose est vraie pour une lentille concavo-convexe placée dans les deux positions considérees.
De même que nous avons démontréGa naar voetnoot3) que toute lentille concavo-convexe concentre les rayons d'autant plus mal que l'une de ses deux surfaces est plus concave, lorsque la distance focale et la largeur de la lentille restent invariables, de même aussi nous pourrons faire voir ici qu'une lentille convexo-concave disperse les rayons parallèles d'autant plus mal que l'une de ses deux surfaces est plus convexe. En effet, comme ME, ou d, distance du point de dispersion, est égale ici, dans le premier cas, à , il apparaît donc que la distance ED sera toujours plus grande dans le deuxième cas que dans le premier. Et il est aisé de voir que la même chose est vraie pour une lentille concavo-convexe placée dans les deux positions considérees.
De même que nous avons démontréGa naar voetnoot3) que toute lentille concavo-convexe concentre les rayons d'autant plus mal que l'une de ses deux surfaces est plus concave, lorsque la distance focale et la largeur de la lentille restent invariables, de même aussi nous pourrons faire voir ici qu'une lentille convexo-concave disperse les rayons parallèles d'autant plus mal que l'une de ses deux surfaces est plus convexe. En effet, comme ME, ou d, distance du point de dispersion, est égale ici, dans le premier cas, à 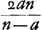 Ga naar voetnoot4) et que, par conséquent, Ga naar voetnoot4) et que, par conséquent, 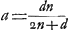 , on trouvera d'après la première règle, en substituant partout pour a l'expression , on trouvera d'après la première règle, en substituant partout pour a l'expression 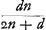 , , 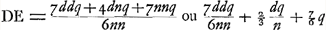 . Cette formule fait voir que plus la valeur qu'on prend pour n est petite, plus la distance DE sera grande, et qu'elle sera toujours supérieure à 7/6q.
Dans le second cas on aura . Cette formule fait voir que plus la valeur qu'on prend pour n est petite, plus la distance DE sera grande, et qu'elle sera toujours supérieure à 7/6q.
Dans le second cas on aura 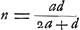 , attendu que , attendu que 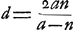 . En substi- . En substi-
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 305]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
meter superficiei alterius NM sit n; crassitudo lentis CK sive Gγ dicatur q; Regula ad inveniendam aberrationem radij extremi ED, priori casu erit ista, 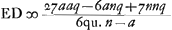 . Posteriori vero, ubi a major quam n, erit haec, . Posteriori vero, ubi a major quam n, erit haec, 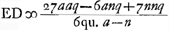 Ga naar voetnoot1). Quas apparet plane easdem esse quas ante in meniscis dedimusGa naar voetnoot2). Poterimus autem secundum has comparationem instituere lentium hujusmodi cavarum, et quanto quaeque majorem aberrationem faciat definire. In universum vero ostendi potest lentem eandem convexoconcavam, ita collocatam ut in casu horum posteriore, ut nempe superficies convexa radios parallelos accipiat, minus bene eos dispergere, quam si aliter inversa sit. Si enim in schemate horum utroque [Fig. 21 et 22] lens eadem sed diverso positu intelligatur, sitque proinde NM casu posteriore aequalis AB in priore, ac utraque dicatur a: item AB in posteriore aequalis NM in priori, atque utraque dicatur n: manifestum est, posteriore casu fore jam Ga naar voetnoot1). Quas apparet plane easdem esse quas ante in meniscis dedimusGa naar voetnoot2). Poterimus autem secundum has comparationem instituere lentium hujusmodi cavarum, et quanto quaeque majorem aberrationem faciat definire. In universum vero ostendi potest lentem eandem convexoconcavam, ita collocatam ut in casu horum posteriore, ut nempe superficies convexa radios parallelos accipiat, minus bene eos dispergere, quam si aliter inversa sit. Si enim in schemate horum utroque [Fig. 21 et 22] lens eadem sed diverso positu intelligatur, sitque proinde NM casu posteriore aequalis AB in priore, ac utraque dicatur a: item AB in posteriore aequalis NM in priori, atque utraque dicatur n: manifestum est, posteriore casu fore jam 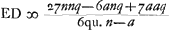 . At
priore erat . At
priore erat 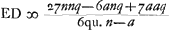 . Ergo cum n sit major quam a ideoque 27nn+7aa major quam 27aa+7nn, apparet ED posteriore casu semper majorem fore quam priori. Atque idem in menisco diversimode collocato obtinere perspicuum est.
Qua porro ratione meniscus quisque tanto pejus radios colligere ostensus fuitGa naar voetnoot3), quanto magis cavam superficiem alteram habuerit, manente eadem foci distantia ac latitudine lentis, eâdem poterit et hic de lente convexoconcava ostendi, tanto pejus eam radios parallelos dispergere, quanto magis convexam alteram superficiem habuerit. Etenim cum hic, priore casu, sit puncti dispersus distantia ME, quae dicitur d, aequalis . Ergo cum n sit major quam a ideoque 27nn+7aa major quam 27aa+7nn, apparet ED posteriore casu semper majorem fore quam priori. Atque idem in menisco diversimode collocato obtinere perspicuum est.
Qua porro ratione meniscus quisque tanto pejus radios colligere ostensus fuitGa naar voetnoot3), quanto magis cavam superficiem alteram habuerit, manente eadem foci distantia ac latitudine lentis, eâdem poterit et hic de lente convexoconcava ostendi, tanto pejus eam radios parallelos dispergere, quanto magis convexam alteram superficiem habuerit. Etenim cum hic, priore casu, sit puncti dispersus distantia ME, quae dicitur d, aequalis 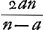 Ga naar voetnoot4): ideoque Ga naar voetnoot4): ideoque 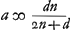 , siet ex priore regula, substituto ubique , siet ex priore regula, substituto ubique 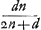 in locum a, in locum a, 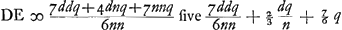 . ubi patet, quanto minor sumetur n tanto majorem fore DE, ac semper majorem fore quam 7/6 q.
Rursus secundo casu, cum sit . ubi patet, quanto minor sumetur n tanto majorem fore DE, ac semper majorem fore quam 7/6 q.
Rursus secundo casu, cum sit 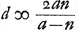 , erit , erit 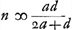 , quo ubique reposito , quo ubique reposito
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 306]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tuant partout cette expression à n dans la seconde règle, on trouve 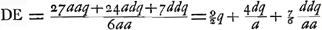 . Cette formule fait voir que plus la valeur de a est petite, plus la distance DE, ici aussi, devient grande, et qu'elle doit toujours être supérieure à 9/2q. Voilà donc les formules qui permettent d'examiner le degré dans lequel chaque lentille convexe ou concave a le pouvoir de concentrer ou de disperser les rayons; mais avant de montrer leur utilité, nous devons commencer par établir les deux théorèmes suivants. . Cette formule fait voir que plus la valeur de a est petite, plus la distance DE, ici aussi, devient grande, et qu'elle doit toujours être supérieure à 9/2q. Voilà donc les formules qui permettent d'examiner le degré dans lequel chaque lentille convexe ou concave a le pouvoir de concentrer ou de disperser les rayons; mais avant de montrer leur utilité, nous devons commencer par établir les deux théorèmes suivants.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VI.Dans des lentilles de largeurs diverses, convexes ou concaves, dont les surfaces exposées aux rayons ont la même courbure, et dont les surfaces opposeés ont également la même courbure quoique différente de la première, ou qui possèdent chacune une surface plane, les aberrations des rayons extrêmes parallèles à l'axe sont entre elles comme les épaisseurs des lentilles, ou bien comme les carrés des largeurs.On démontre facilement à l'aide de ce qui a été établi à la propos. IGa naar voetnoot2) que les épaisseurs de différentes lentilles de ce genre sont entre elles comme les carrés de leurs largeurs. En effet, si elles sont biconvexes comme le premier couple des lentilles ici représentées, ACBD et FHGK [Fig. 23], dont les épaisseurs ou les axes sont CD et HK, et qu'on considère donc dans ce cas les droites AB et FG comme définiant la largeur des lentilles, lesquelles droites coupent CD et HK en E et en L; il est certain, attendu que ACBE et FHGL sont des segments de cercles égaux, que leurs hauteurs CE et HL 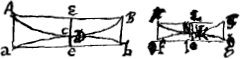 [Fig. 25.]
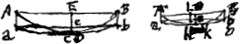 [Fig. 26.]
seront l'une à l'autre comme le carré AB est au carré FGGa naar margenoot*, bien entendu à si peu de chose près pour les petites parties des cercles considérées ici que la différence n'est d'aucune importance. Pour la même raison DE sera aussi à KL comme le carré AB est au carré FG, et, par conséquent, l'épaisseur CD toute entière sera à HK comme le carré AB est au carré FG. Mais dans le cas des lentilles concavo-convexes [Fig. 24] qui sont considérées ici en second lieu, nous conclurons aussi que la différence des deux longueurs CE et DE est à celle des deux longueurs HL et KL, c'est-à-dire, que l'épaisseur CD est à HK comme le carré AB est au carré FG. Dans le cas des lentilles biconcaves [Fig. 25], dont nous supposons que les sur- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 307]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
in locum n in posteriore regula, fit 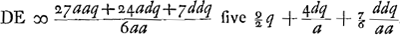 . Ubi apparet, quo minor sumetur a, eo majorem iterum sieri DE: Eamque semper majorem fore quam 9/2 q. Et haec quidem ad examinandam cujusque convexae aut cavae lentis in colligendis aut dispergendis radijs facultatem ac praestantiam, quorum antequam utilitatem ostendamus, theoremata duo sequentia praemittenda sunt. . Ubi apparet, quo minor sumetur a, eo majorem iterum sieri DE: Eamque semper majorem fore quam 9/2 q. Et haec quidem ad examinandam cujusque convexae aut cavae lentis in colligendis aut dispergendis radijs facultatem ac praestantiam, quorum antequam utilitatem ostendamus, theoremata duo sequentia praemittenda sunt.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Propo [sitio VI].In lentibus diversarum latitudinum, convexis aut concavis, quae superficies radijs expositas ex eadem sphaera habuerint, itemque adversas superficies ex eadem sphaera licet a priori diversa, vel quae alteram harum superficierum planam habuerintGa naar voetnoot1), aberrationes radiorum extremorum axi parallelorum sunt inter se sicut lentium crassitudines, sive etiam ut latitudinum quadrata. 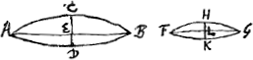 [Fig. 23.]
 [Fig. 24.]
Crassitudines lentium hujusmodi esse inter se sicut quadrata latitudinum, facile ostenditur ex demonstratis propos. [I]Ga naar voetnoot2). Si namque sint utrimque convexae, ut primum par hic depictarum, ACBD, FHGK [Fig. 23], quarum crassitudines seu axes CD, HK. hic ergo ductis AB, FG rectis quae latitudines lentium definiant, secentque CD, HK in E et L; constat, quia segmenta ACBE, FHGL sunt aequalium circulorum, fore eorum altitudines CE ad HL ut quadr. AB ad quadr. FGGa naar margenoot*; tam prope nimirum in exiguis hujusmodi circulorum portionibus ut nullius momenti sit differentia. Eadem ratione et DE erit ad KL ut quadr. AB ad FG. ac proinde ettota CD ad HK ut quadr. AB ad qu. FG. In meniscis autem, qui secundo loco hic ponuntur [Fig. 24], concludemus et differentiam duarum CE, DE, esse ad differentiam duarum HL, KL, hoc est, crassitudinem CD ad HK, ut quadr. AB ad FG. In lentibus utrimque cavis [Fig. 25], quarum superficies ACB, aDb sese | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 308]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
faces ACB et aDb, comme aussi FKG et fKg, se touchent, et dont les épaisseurs sont Ee et Ll, la démonstration est la même que dans le cas des lentilles biconvexes. Et dans le cas des lentilles convexo-concaves elle est identique à celle qui a servi dans le cas des lentilles concavo-convexes. Enfin, dans le cas ou l'une des deux surfaces, soit des lentilles convexes, soit des lentilles concaves, est plane, la démonstration est manifeste d'après ce qui a été dit. Il nous reste à démontrer que pour chaque couple de lentilles les aberrations des rayons extrêmes sont entre elles comme les épaisseurs. Pour les lentilles planconvexes et planconcaves il est manifeste qu'il doit en être ainsi, attendu que pour ces lentilles-là l'aberration du rayon extrême est égale, d'après ce qui a été dit plus hautGa naar voetnoot3), à 9/2 fois l'épaisseur des lentilles lorsque la surface plane reçoit les rayons parallèles, ou à 7/6 fois la même épaisseur lorsque la surface sphérique est exposée à ces rayons. Mais dans le cas des autres lentilles composées, attendu qu'il ressort des règles énoncées plus haut que, lorsque les rayons des deux surfaces restent les mêmesGa naar voetnoot4), le rapport de l'épaisseur de la lentille à l'aberration ED [Fig. 15-22] du rayon extrême reste également le même, il s'ensuit que cette aberration diminue dans le même rapport que l'épaisseur de la lentille, en d'autres termes dans le rapport des carrés des largeurs. Par exemple, comme nous avons ditGa naar voetnoot6) que dans le cas de la lentille biconvexe l'épaisseur de la lentille est à l'aberration ED comme 6 fois le carré de la somme des deux rayons de courbure est à 27 fois le carré AB+7 fois le carré NM+6 fois le rectangle AB, NM, il en résulte que le rapport de ces deux grandeurs reste le même lorsque les rayons AB et NM ne varient pasGa naar voetnoot7) et, par conséquent, que les aberrations propres aux lentilles possédant de telles surfaces convexes sont entre elles comme leurs épaisseurs. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VII.Dans le cas d'une lentille quelconque, convexe ou concave, les aberrations des rayons parallèles à l'axe sont entre elles comme les carrés des distances de ces rayons à l'axe. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 309]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
contingere ponuntur, itemque FKG, fKg; quarumque crassitudines Ee et Ll, eadem est demonstratio, quae in utrinque convexis. Et in cavoconvexisGa naar voetnoot1), eadem quae in meniscis. Quod si vero vel convexarum vel cavarum lentium altera superficies plana fuerit, manifesta ex his quae dicta sunt est demonstratio. SuperestGa naar voetnoot2) ut ostendamus aberrationes radiorum extremorum in unoquoque pari esse inter se ut lentium crassitudines. quod in planoconvexis et planoconcavis quidem ita se habere manifestum est, cum in his aberratio radij extremi ex supra scriptisGa naar voetnoot3) sit vel 9/2 crassitudinis lentium, si nempe plana superficies radios parallelos excipiat, vel 7/6 ejusdem crassitudinis, si sphaerica superficies radijs dictis exponatur. At in lentibus reliquis mixtis, quum ex Regulis supra traditis appareat manentibus ijsdem semidiametris utriusque superficieiGa naar voetnoot4) eandem etiam manere rationem crassitudinis lentis ad aberrationem radij extremi, ED [Fig. 15-22]; sequitur eadem proportione aberrationem hanc imminui qua decrescit lentis crassitudo; hoc est, secundum rationem quam habent latitudinum quadrataGa naar voetnoot5). Exempli gratia, cum in lente utrimque convexa dixerimusGa naar voetnoot6) esse sicut sexcuplum quadratum compositae ex semidiametris utriusque convexitatis ad vingintiseptuplum quadratum AB, plus septuplo quadrato NM, plus sexcuplo rectangulo AB, NM, ita crassitudinem lentis ad aberrationem ED. apparet rationem quae est inter has eandem manere, manentibus semidiametris AB, NM ijsdemGa naar voetnoot7), ac proinde sicut crassitudines lentium talibus convexis praeditarum, ita esse inter se earum aberrationes. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Propos [itio VII].In lente quavis convexa aut cava aberrationes radiorum axi parallelorum sunt inter se sicut quadrata distantiarum eorundem radiorum ab axe. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 310]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dans le cas des lentilles concaves la démonstration de cette proposition est la plus facile: elle dépend de la démonstration précédente. En effet, soit ACBDCF [Fig. 27] la lentille concave, CE son axe et E son point de dispersion. Supposons en outre que le rayon parallèle à l'axe qui frappe le point B soit dispersé de telle manière que prolongé en sens contraire il rencontre l'axe au point G, tandis qu'un autre rayon parallèle à l'axe mais plus près de ce dernier et frappant le point H soit dispersé de telle manière que prolongé en sens inverse il coupe l'axe au point K. Pour qu'il apparaisse que l'aberration EG est à l'aberration EK comme le carré de la distance du point B à l'axe est au carré de la distance correspondante du point H, il faut considérer que le cas est le même que s'il y avait deux lentilles différentes DBA et NHF dont les demies largeurs seraient égales aux distances respectives des points B et H à l'axe. Et comme les surfaces sphériques des deux lentilles sont les mêmes, il résulte de la proposition précédente que leurs épaisseurs BD et HN sont entre elles comme les carrés de ces demies largeurs. Mais comme les épaisseurs BD et HN, ainsi sont entre elles les aberrations EG et EK. Par conséquent le rapport de ces dernières est de même égal à celui des carrés des distances des points B et H à l'axe. 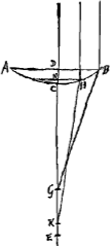 [Fig. 28.]
La démonstration est semblable dans le cas de la lentille planconvexe, lorsque la surface plane reçoit les rayons parallèles. En effet, soit ACB [Fig. 28] une lentille de ce genre, ayant l'axe DE et le foyer E, laquelle réfracte les rayons parallèles qui tombent sur la surface convexe aux points B et H après qu'ils ont traversé la surface plane AB sans changer de direction; supposons que ces rayons rencontrent l'axe aux points G et K. On peut donc, après avoir mené à l'axe DC la perpendiculaire HN, procéder de nouveau comme s'il y avait deux lentilles planconvexes, dont les épaisseurs sont DC et NC. Mais DC est à NC, comme le carré BD est au carré HN; et l'aberration EG est à l'aberration EK comme DC est à NC, attendu que EG = 9/2 DCGa naar voetnoot1) et EK = 9/2 NC. Par conséquent aussi l'aberration EG est à l'aberration EK comme le carré BD est au carré NH. Supposons maintenant la même lentille inversement placée [Fig. 29], c'est-à-dire de telle manière que les rayons parallèles tombent d'abord sur la surface convexe ACB, dont IC soit le rayon. Le foyer E peut donc être trouvé en prenant d'abord CR = 3 CI et ensuite DE = ⅔ DRGa naar voetnoot2). Supposons que le rayon | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 311]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In cavis lentibus facilior hujus rei est demonstratio pendetque à proximè praecedenti. Sit enim lens cava ACBDCF [Fig. 27] cujus axis CE: punctum dispersus E. Radiusque axi parallelus in B punctum incidens ita dispergatur ut retro productus conveniat cum axe in G. alius vero radius parallelus axi, sed propinquior incidens in H punctum dispergatur,
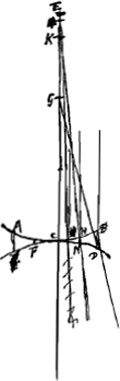 [Fig. 27.]
ita ut productus retro conveniat cum axe in K. Ut igitur appareat aberrationem EG esse ad EK sicut quadr. distantiae puncti B ab axe, ad quadr. distantiae puncti H, considerandum est ita se rem habere ac si sint lentes duae diversae DBA, NHF, quarum dimidiae latitudines sint dictae distantiae punctorum B et H ab axe. Cumque sphaericae superficies utrique lenti sint eaedem, patet ex prop. praecedenti crassitudines earum BD, HN, ita esse inter se sicut quadrata illarum dimidiarum latitudinum. Sicut autem crassitudines BD, HN, ita sunt inter se et aberrationes EG, EK. Ergo et harum ratio eadem est quae quadratorum à distantijs punctorum B et H ab axe. Non absimilis quoque demonstratio est in lente planoconvexa, cum plana superficies radijs parallelis opposita est. Si enim sit lens hujusmodi ACB [Fig. 28], axem habens DE, focum E, in qua refringantur radij paralleli qui incidunt in puncta B et H, superficiei convexae, postquam planam AB irrefracti transierint: occurrant autem axi in G et K. Hîc igitur ductâ HN perpendiculari ad axem DC, rursus tanquam duae lentes planoconvexae considerandae sunt, quarum crassitudines DC et NC. sicut autem quadratum BD ad quadratum HN ita est DC ad NC; et sicut DC ad NC ita aberratio EG ad EK, cum EG aequetur 9/2 DCGa naar voetnoot1), et EK 9/2 NC. Ergo sicut quadr. BD ad quadr. NH ita quoque aberratio EG ad EK. Sit autem nunc eadem lens contraria ratione disposita [Fig. 29], ut nempe radij paralleli incidant primùm in superficiem convexam ACB, cujus semidiameter sit IC. Focus ergo E invenitur sumta primum CR tripla CI, ac deinde posita DE aequali 2/3 DRGa naar voetnoot2). Ponatur radius extremus axi parallelus incidens in B, convenire cum axe in G, adeo ut aberratio ejus sit EG, radius vero parallelus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 312]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
extrême parallèle à l'axe qui tombe sur la lentille au point B rencontre l'axe au point G, de sorte que son aberration soit EG, et que le rayon parallèle qui rencontre la lentille au point H se meuve ensuite selon la droite HP qui coupe la surface AB en S, où il est réfracté de nouveau, rencontrant ensuite l'axe au point K, de sorte que l'aberration de ce rayon soit EK. Il faut donc démontrer que l'aberration EG est à l'aberration EK comme le carré BD est au carré HN. Menons la droite HQ parallèle à SK; puisse-t-elle rencontrer l'axe en Q. Soit également HT une parallèle à l'axe CD qui coupe la surface AB au point T; et supposons enfin que la droite KS prolongée rencontre la droite HT au point V. Si nous considérons maintenant la partie HCFN comme une autre lentille planconvexe, son foyer O pourra être trouvé en prenant NO = 2/3 NRGa naar voetnoot1). Or, le rayon extrême parallèle à l'axe qui tombe sur cette lentille au point H et qui est réfracté d'abord à la surface BCA de manière à se diriger vers le point P, se mouvra nécessairement selon la droite HQ après la deuxième réfraction à la surface plane HN; cette droite HQ étant parallèle à la droite SK suivant laquelle le rayon se meut après avoir été réfracté à la surface BD. Par conséquent, QO serait l'aberration du rayon extrême de la lentille HCFN; et il est connu que cette aberration est à l'aberration GE du rayon extrême de la lentille ACB comme le carré HN est au carré BDGa naar margenoot*. Si donc on démontre que l'aberration EK du rayon HH, après que celui-ci a traversé la lentille ACB, est égale à l'aberration OQ, il s'ensuivra aussi que l'aberration EG est à l'aberration EK comme le carré BD est au carré HN. Mais c'est ce qu'on démontre comme suit: Comme le rapport PS:SK est à peu près égal au rapport PD:DKGa naar voetnoot2), et que le rapport PS:SK égale 3:2Ga naar margenoot*, on aura aussi approximativement PD:DK = 3:2. Mais comme PD est à DK ainsi HT est à TV, à cause de la similitude des triangles SPD, SHT et SKD, SVT. Par conséquent, on a aussi à peu de chose près HT:TV = 3:2; et par suite HV est à peu près égale au tiers de HT. Mais HV = QK. La longueur QK est donc égale elle aussi au tiers de HT ou de ND. Mais comme d'après notre construction RE est égale au tiers de RD et RO au tiers de RN, la différence OE des longueurs RE et RO sera égale au tiers de la différence DN des longueurs RD et RN. Il apparaît donc que OE = QK. C'est pourquoi, en ajoutant ou en retranchant (car ce cas-là peut aussi se présenter) des deux côtés la longueur OK, on aura KE = QO. C'est ce qu'il restait à démontrer. Il faut entendre cette démonstration en ce sens qu'elle est valable si l'on néglige de fort petites différences qui par rapport à KE et à QO ne sont d'aucune importance. En ce même sens le théorème sera vrai aussi pour toutes les autres lentilles convexes ou concaves, comme nous l'avons trouvé par un calcul analytiqueGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 313]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
incidens in punctum H, feratur inde secundum rectam HP quae secet superficiem AB in S, ubi facta altera refractione, conveniat cum axe in K, adeo ut aberratio radij hujus sit EK. Ostendendum est igitur, quod sicut quadr. BD ad quadr. HN ita aberratio EG ad EK. Ducatur HQ parallela SK; atque occurrat axi in Q. Sit etiam HT parallela axi CD, quae superficiei AB occurrat in T; ac denique producta KS occurrat ipsi HT in V. Quod si jam consideretur tanquam lens alia planoconvexa HCFN, ejus focus O invenietur sumendo NO aequalem ⅔ NRGa naar voetnoot1). Radius autem ejus extremus axi parallelus qui incidit in H, primaque refractione in superficie BCA flectitur versus punctum P, is necessario post secundam refractionem in superficie plana HN feretur secundum HQ, quia haec parallela est SK,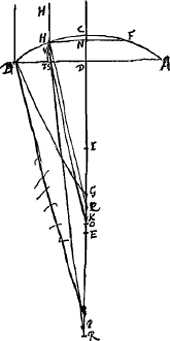 [Fig. 29.]
secundum quam incedit refractus a superficie BD. Esset itaque QO aberratio radij extremi lentis HCFN; quam constat esse ad aberrationem GE radij extremi lentis ACB, sicut quadr. HN ad quadr. BDGa naar margenoot*. Quare si ostendatur aberrationem EK radij HH, trans lentem ACB missi, aequalem esse aberrationi OQ; patebit etiam esse quemadmodum quadr. BD ad qu. HN ita aberrationem EG ad EK. Illud vero sic ostenditur. quum PS ad SK habeat eandem proxime rationem quam PD ad DKGa naar voetnoot2); ratio autem PS ad SK sit ut 3 ad 2Ga naar margenoot*, erit et PD ad DK ut 3 ad 2 proximè. Sicut autem PD ad DK ita est HT ad TV, propter similitudinem triangulorum SPD, SHT, et SKD, SVT. Ergo et HT ad TV proxime ut 3 ad 2; ac proinde HV proxime pars tertia HT. Sed HV aequalis est QK. Ergo et QK similiter pars tertia HT vel ND. Cum vero ex constructione sit RE pars tertia RD; et RO pars tertia RN; erit et differentia duarum RE, RO, nempe OE, pars tertia differentiae duarum RD, RN, quae est DN. Itaque apparet OE aequalem esse QK. quare si utrique addatur OK, vel utrinque auferatur (nam et hoc contingere potest) erit et KE aequalis QO; quod ostendendum supererat. Haec autem intelligenda sunt ita se habere neglectis minimis differentijs quae respectu ipsarum KE, QO nullius momenti sunt. Qua ratione theorema in caeteris quoque omnibus convexis cavisque lentibus verum erit, ut calculo analytico comperimusGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 314]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Propositions écartées de notre DioptriqueGa naar voetnoot1)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 315]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Rejecta ex Dioptricis nostrisGa naar voetnoot1).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 316]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dent extrême, y donne lieu à l'aberration ML, et LN représente le rayon du cercle d'aberration. Il faut donc démontrer en premier lieu que le rapport des aberrations ED:ML est composé du rapport AB2:GH2 ou CB2:KH2 et du rapport KL:CD. Prenons une troisième lentille OP [Fig. 32], également de même espèce, dont la distance focale QR soit égale à CD, tandis que le rayon QP de l'ouverture est à la distance focale QR comme HK est à KL. Soit PST pour cette lentille le rayon réfracté provenant du rayon incident extrême, SR l'aberration correspondante et RT le rayon du cercle d'aberration. Le rapport ED:ML est composé des rapports ED:SR et SR:ML, dont le premier ED:SR est égal à CB2:QP2Ga naar voetnoot1), et le second SR:ML à QR (ou CD):KLGa naar voetnoot2). Il en résulte que le rapport ED:ML est composé des rapports CB2::QP2 et CD:KL. Or, le rapport CB2:QP2 est composé à son tour des rapports CB2:KH2 et KH2:QP2, ou KL2:QP2, ou KL2:CD2. Mais le rapport CD:KL est égal à celui du carré CD au rectangle CD, KL. Le rapport ED:ML sera donc composé des rapports CB2:KH2, KL2:CD2 et CD. KL, mais le rapport composé des deux derniers rapports est égal au rapport du carré KL au rectangle CD, KL, ou à KL:CD. Le rapport ED:ML est donc composé du rapport CB2:KH2 et du rapport KL:CD, ce qui constitue le premier théorème qu'il fallait demontrer. Nous démontrerons maintenant le second théorème, suivant lequel le rapport DF:LN est composé du rapport CB3:KH3 et du rapport KL2:CD2. En effet, le rapport DF:LN est composé des rapports DF:DE, DE:ML et ML:LN, dont le premier DF:DE est égal à CB:CE ou CB:'CD (car ici la petite différence ED est négligeable) et le dernier ML:LN à MK (ou LK):KH. Le rapport DF:NL est donc composé des rapports CB:CD, KL:KH et ED:ML. Mais le rapport composé des deux premiers rapports est égal au rapport des rectangles BC, KL et CD, KH, c'est-à-dire au rapport composé des rapports CB:KH et KL:CD. Le rapport FD:NL est donc composé des rapports CB:KH, ED:ML et KL:CD. Mais il a été démontré que le rapport ED:ML est composé des rapports CB2:KH2 et KL:CD. Par conséquent, le rapport FD:NL sera composé des rapports CB:KH et CB2:KH2, qui ensemble produisent le rapport CB3:KH3, et de deux fois le rapport KL:CD. Il apparaît donc que le rapport FD:NL est composé des rapports CB3:KH3 et KL3:CD2. C'est là le second théorème que nous nous proposions de démontrer. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 317]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
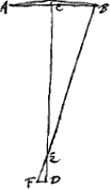 [Fig. 30].
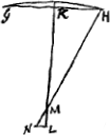 [Fig. 31].
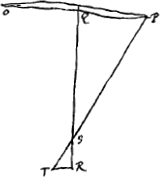 [Fig. 32].
ML, semidiametrum vero circelli aberrationis LN. Primo itaque ostendendum est aberrationem ED ad ML rationem habere compositam ex ratione quadrati AB ad qu. GH, sive qu. CB ad qu. KH, et ex ratione KL ad CD. Esto lens tertia OP [Fig. 32] ejusdem quoque generis, cujus foci distantia QR sit aequalis CD, aperturae vero semidiameter QP ad foci distantiam QR se habeat ut HK ad KL. Refractio autem radij extremi in hac lente sit PST, faciens aberrationem SR, et semidiametrum circelli aberrationis RT. Quia ergo ratio ED ad ML componitur ex rationibus ED ad SR et SR ad ML; quarum ED ad SR eadem quae quadrati CB ad qu. QPGa naar voetnoot1); altera SR ad ML eadem quae QR sive CD ad KLGa naar voetnoot2); apparet rationem ED ad ML componi ex rationibus quadrati CB ad qu. QP et rectae CD ad KL. Ratio autem quadrati CB ad qu. QP rursus composita est ex rationibus quadrati CB ad qu. KH, et quadrati KH ad qu. QP, sive quadrati KL ad qu. QR, hoc est, ad qu. CD. At ratio CD ad KL est eadem quae quadrati CD ad rectangulum CD, KL. Itaque ratio ED ad ML jam composita erit ex rationibus quadrati CB ad qu. KH, et quadrati KL ad qu. CD et quadrati CD ad rectangulum CD, KL: quae duae posteriores rationes aequantur rationi quadrati KL ad rectang. CD, KL, sive rationi KL ad CD. Ergo ratio ED ad ML componitur ex ratione quadrati CB ad qu. KH et ex ea quam habet KL ad CD, quod erat primum. Nunc alterum quoque ostendemus nimirum rationem DF ad LN componi ex ratione cubi CB ad cubum KH et ex ratione quadrati KL ad qu. CD. Quia enim DF ad LN rationem habet compositam ex rationibus DF ad DE et DE ad ML et ML ad LN, quarum prior DF ad DE eadem est quae CB ad CE sive CD, (nam exigua differentia ED hîc nullius momenti est,) posterior vero ML ad LN eadem quae MK seu LK ad KH. Componitur igitur ratio DF ad NL ex rationibus CB ad CD, et KL ad KH et ED ad ML. Harum vero priores duae constituunt rationem rectanguli BC, KL ad rectang. CD, KH, hoc est eandem compositae ex rationibus CB ad KH, et KL ad CD. Itaque ratio FD ad NL composita est ex rationibus CB ad KH, et ED ad ML et KL ad CD. Demonstratum vero fuit rationem ED ad ML componi ex rationibus quadrati CB ad qu. KH et ex ratione KL ad CD. Ergo FD ad NL componetur jam ex rationibus CB ad KH et quadrati CB ad qu. KH; quae simul efficiunt rationem cubi CB ad cubum KH; et ex ratione KL ad CD duplicata. Patet itaque rationem FD ad NL componi ex ratione cubi CB ad cubum KH et quadrati KL ad qu. CD. quod erat alterum eorum quae demonstrando proponebantur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 318]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition IX.Composer à l'aide de lentilles sphériques concaves et convexes des télescopes plus parfaits que les télescopes ainsi construits qu'on connaît jusqu' à ce jour et qui puissent égaler en perfection ceux qui sont composés de lentilles elliptiques ou hyperboliquesGa naar voetnoot1). Dans les télescopes composés d'une lentille convexe et d'une lentille concave, il est nécessaire que les rayons parallèles, c'est-à-dire, ceux qui proviennent d'un point fort éloigné de l'objet, et qui sont réunis en un point unique par la lentille convexe, redeviennent parallèles par la réfraction de la lentille concave et parviennent ainsi à l'oeil. Mais ni la lentille sphérique convexe ne peut rassembler exactement en un point unique les rayons parallèles; ni la lentille concave, en supposant qu'ils tendent réellement vers un point unique, ne peut les rendre de nouveau exactement parallèles. On a donc cru jusqu'ici que les surfaces sphériques sont, pour ces deux raisons, moins propres à cet usage: personne ne soupçonnait que le défaut des lentilles convexes pût être corrigé à l'aide des lentilles concaves. Mais nous démontrerons ici que cette correction est possible et que, par conséquent, les télescopes de ce genre peuvent être rendus plus parfaits que ceux qu'on construit ordinairement. Si l'on pouvait également corriger à l'aide d'une lentille oculaire convexe l'aberration de la lentille extérieure (en effet, pour observer les étoiles il faut nécessairement se servir de télescopes composés de lentilles convexes parce que ceux-ci embrassent un champ plus large), rien ne serait plus désirable dans cet artGa naar voetnoot2). Mais il est certain que cette correction mutuelle n'a pas lieu dans le cas d'une combinaison de deux lentilles convexes. Au contraire, le défaut de la lentille extérieure est toujours quelque peu augmenté par la lentille oculaireGa naar voetnoot3) et il n'y a aucun moyen d'y rémédier. Mais lorsque la lentille convexe est combinée avec une lentille concave, la méthode à suivre sera la suivante. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 319]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Propos [itio IX].Ex lentibus sphaericis cavis et convexis telescopia componere hactenus cognitis ejus generis meliora, perfectionemque eorum quae ellipticis hyperbolicisve lentibus constant aemulantiaGa naar voetnoot1). Cum in telescopijs, ex convexa et concava lente compositis, requiratur ut radij paralleli, hoc est, à puncto longinquo rei visae venientes, atque opera convexae lentis versus punctum unum contracti, lentis cavae refractione rursus paralleli fiant, atque ita ad oculum perveniant; cumque nec lens sphaerica convexa exacte ad punctum unum radios parallelos flectere possit; neque cava ut jam ad punctum unum tendant, exactè denuo parallelos efficere, creditum est hactenus utraque de causa fieri ut sphaericae superficies minus aptae essent his usibus, nemine suspicante vitium convexarum lentium lentibus cavis tolli posse. Hoc autem fieri licere, eoque telescopia hujus generis praestantiora quam solita fint construi, hic ostendere pergemus. Quod si perinde convexa lente oculo admota aberratio lentis exterioris corrigi posset (ad sidera enim spectanda ex convexis lentibus telescopia componi necesse est quo amplius spatium intercipiant), nihil in hac arte foret optabiliusGa naar voetnoot2). Sed certum est in convexis inter se compositis emendationem illam mutuam non reperiri. Imo contra, vitium exterioris lentis a lente oculari augetur semper nonnihilGa naar voetnoot3) neque id ulla ratione impediri potest. In compositione autem convexae lentis cum cava haec erit methodus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 320]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Supposons donnée la grande lentille, c'est-à-dire la lentille extérieure ABCD [Fig. 33] du télescope, laquelle a une distance focale DE. Nous supposons également donné le grossissement, c'est-à-dire le rapport suivant lequel le télescope à construire doit agrandir les diamètres des objets; soit b:c, par exemple 10:1, ce rapport. Divisons la droite DE en F de telle manière que DE soit à EF comme b est à c, ou dans le cas considéré comme 10 est à 1. Il est connu que la lentille concave doit être placée au point F pour que le grossissement requis ait lieuGa naar margenoot*; il faut bien entendu que le point de dispersion de cette lentille pour des rayons parallèles venant du côté E soit le point E. Mais comme les surfaces de la lentille ABCD sont données, l'aberration propre à cette lentille sera également donnée, c'est-à-dire, le rapport de l'aberration du rayon extrême à l'épaisseur de la lentille; soit f:g ce rapport. Par exemple si la lentille ABCD est de la meilleure forme telle que nous l'avons définie précédemmentGa naar voetnoot2), le rapport f:g sera égal à 15:14, vu que l'aberration due à une lentille de ce genre est égale à 15/14 fois son épaisseur. Prenons un nombre tel que c soit à b (ici 1:10) comme f/g (ici 15/14) est à ce nombre; ce nombre sera bf/cg (ici 150/14 ou 75/7). Il faut alors trouver une lentille concave à placer au point F, ayant FE comme distance du point de dispersion et dont l'aberration du rayon parallèle à l'axe venant du côté E soit égale au produit de son épaisseur par le nombre bf/cg, c'est-à-dire dans le cas considéré, à 75/7 fois son épaisseur. Cette lentille pourra être biconcave si la fraction bf/cg est inférieure à 9/2Ga naar voetnoot3); mais si cette fraction est plus grande, comme dans le cas considéré, il faut prendre une lentille convexo-concave et la meilleure sera celle dont la surface convexe doit être tournée du côté de l'oeilGa naar voetnoot4), vu qu' alors elle | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 321]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Data sit lens telescopij magna sive exterior ABCD [Fig. 33], foci distantiam habens DE. ac data praeterea ratio multiplicationis, hoc est, secundum quam res visas telescopio construendo augeri cupimus secundum diametrum; quae sit ea quae b ad c, exempli gratia 10 ad 1. Divisa igitur DE in F, ut sit sicut b ad c,
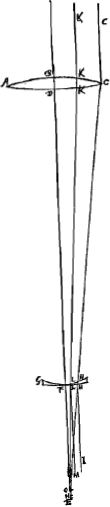 [Fig. 33.]
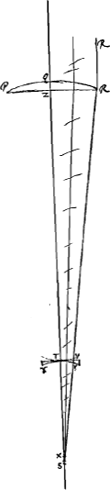 [Fig. 34.]
vel hîc, 10 ad 1, ita DE ad EF; constat lentem cavam ad F constituendam fore, ut fiat dicta multiplicatioGa naar margenoot*. cujus nimirum lentis punctum dispersus radiorum parallelorum a parte E venientium sit in E. Quoniam vero et superficies lentis ABCD datae sunt, dabitur et Aberratio ejus, hoc est, ratio quam habet aberratio radij extremi ad lentis crassitudinem, quae sit ea quae f ad g. Ex. gr. si lens ABCD ponatur omnium optima, quam in praecedentibus definivimusGa naar voetnoot2), erit ratio f ad g ea quae 15 ad 14, quia aberratio lentis ejusmodi est 15/14 suae crassitudinis. Jam sicut c ad b, (hîc 1 ad 10) ita sit f/g (hic 15/14) ad alium numerum qui erit bf/cg (hic 150/14 sive 75/7). Inveniaturque lens cava ad F constituenda, ac puncti dispersus distantiam habens FE, cujus aberratio radij axi paralleli à parte E venientis aequetur crassitudini suae ductae in numerum bf/cg; hoc est, in hoc exemplo, cujus aberratio sit 75/7 suae crassitudinis. Quae quidem lens poterit utrinque cava esse, si bf/cg sit minus quam 9/2Ga naar voetnoot3); si vero majus, ut hic, quaerenda est cavoconvexa, meliorque erit cujus superficies convexa ad oculum convertenda eritGa naar voetnoot4), quia minus cavam superficiem quam altera requi- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 322]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
exige une surface moins concave que dans l'autre casGa naar voetnoot1). Si donc nous appelons a le rayon de courbure de la surface convexe de la lentille cherchée, d la distance EF du point de dispersion, et q l'épaisseur de la lentille, l'aberration du rayon extrême est donnée d'après la règle énoncée plus hautGa naar voetnoot2) par l'expression 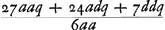 . Il faut donc que cette expression soit égale à bf/cg q, et dans le cas considéré à 75/7 q. Cette équation permet de trouver a, le rayon de la surface convexe, lequel aura ici à-peu-près la valeur 86/100 dGa naar voetnoot3). Mais lorsque le rayon a est connu, on trouvera aussi n, le rayon de la surface concave, attendu que, comme nous l'avons dit plus hautGa naar voetnoot4), . Il faut donc que cette expression soit égale à bf/cg q, et dans le cas considéré à 75/7 q. Cette équation permet de trouver a, le rayon de la surface convexe, lequel aura ici à-peu-près la valeur 86/100 dGa naar voetnoot3). Mais lorsque le rayon a est connu, on trouvera aussi n, le rayon de la surface concave, attendu que, comme nous l'avons dit plus hautGa naar voetnoot4), 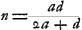 . Ici l'on aura . Ici l'on aura 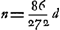 ou 32/100 d. Supposons donc la lentille GH [Fig. 33] construite avec les rayons trouvés de la surface convexe et de la surface concave. Je dis qu'un rayon quelconque parallèle à l'axe, tel que CC et KK, qui tombe sur la lentille AC, sortira de nouveau parallèlement à l'axe après avoir traversé cette lentille-là et ensuite la lentille GH. En effetGa naar voetnoot5), pour démontrer ce théorème d'abord pour le rayon extrême CC, supposons que celui-ci après avoir traversé la lentille AC se meuve suivant la droite CO, qui coupe la lentille GH au point H, par lequel nous tirons la droite HI parallèle à l'axe. Considérons ensuite une autre lentille PQR [Fig. 34], qui soit planconvexe et dont la distance focale ZS et la largeur soient les mêmes que pour la lentille AC. Prenons ST = EF et plaçons au point T une lentille planconcave YTV, ayant le point de disperfion en S. Soit, pour la lentille PQR, RR le rayon extrême parallèle à l'axe, lequel après avoir été réfracté par la lentille se meuve suivant la droite RX qui coupe la lentille YTV au point V. ou 32/100 d. Supposons donc la lentille GH [Fig. 33] construite avec les rayons trouvés de la surface convexe et de la surface concave. Je dis qu'un rayon quelconque parallèle à l'axe, tel que CC et KK, qui tombe sur la lentille AC, sortira de nouveau parallèlement à l'axe après avoir traversé cette lentille-là et ensuite la lentille GH. En effetGa naar voetnoot5), pour démontrer ce théorème d'abord pour le rayon extrême CC, supposons que celui-ci après avoir traversé la lentille AC se meuve suivant la droite CO, qui coupe la lentille GH au point H, par lequel nous tirons la droite HI parallèle à l'axe. Considérons ensuite une autre lentille PQR [Fig. 34], qui soit planconvexe et dont la distance focale ZS et la largeur soient les mêmes que pour la lentille AC. Prenons ST = EF et plaçons au point T une lentille planconcave YTV, ayant le point de disperfion en S. Soit, pour la lentille PQR, RR le rayon extrême parallèle à l'axe, lequel après avoir été réfracté par la lentille se meuve suivant la droite RX qui coupe la lentille YTV au point V.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 323]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 33.]
 [Fig. 34.]
ritGa naar voetnoot1). Quia igitur, positâ semidiametro convexae supersiciei lentis quaesitae ∞ a et puncti dispersus distantia EF ∞ d; crassitudine vero lentis ∞ q; fit secundum regulam supra traditamGa naar voetnoot2) aberratio radij extremi 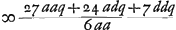 , oportet proinde hanc aequari bf/cg q, et in hoc exemplo 75/7 q. Ex qua aequatione invenietur a semidiameter superficiei convexae; quae hic erit proximè 86/100 dGa naar voetnoot3). data autem a invenietur et n semidiameter superficiei cavae; quia, ut superius dictum estGa naar voetnoot4), , oportet proinde hanc aequari bf/cg q, et in hoc exemplo 75/7 q. Ex qua aequatione invenietur a semidiameter superficiei convexae; quae hic erit proximè 86/100 dGa naar voetnoot3). data autem a invenietur et n semidiameter superficiei cavae; quia, ut superius dictum estGa naar voetnoot4), 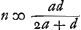 . fietque hic . fietque hic
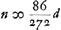 , sive 32/100 d. His itaque semidiametris superficiei convexae et concavae formata sit lens GH. Dico radium quemvis axi parallelum atque in lentem AC incidentem ut CC et KK, penetrata illa, ac postea lente GH, rursus axi parallelum evadere. Ut enimGa naar voetnoot5) de radio CC extremo primùm hoc demonstremus, ponamus eum ex lente AC egressum pergere secundum rectam CO, quae secet lentem GH in H, unde agatur HI axi parallela. Sit deinde lens alia planoconvexa PQR [Fig. 34], cujus foci distantia, ZS, atque etiam latitudo, eadem sit quae lentis AC. Et sumta ST aequali EF, ponatur in T lens planoconcava YTV, punctum dispersus habens S. Sitque in lente PQR radius extremus axi parallelus RR, qui ab ea fractus incedat secundum rectam RX secantem lentem YTV in V. , sive 32/100 d. His itaque semidiametris superficiei convexae et concavae formata sit lens GH. Dico radium quemvis axi parallelum atque in lentem AC incidentem ut CC et KK, penetrata illa, ac postea lente GH, rursus axi parallelum evadere. Ut enimGa naar voetnoot5) de radio CC extremo primùm hoc demonstremus, ponamus eum ex lente AC egressum pergere secundum rectam CO, quae secet lentem GH in H, unde agatur HI axi parallela. Sit deinde lens alia planoconvexa PQR [Fig. 34], cujus foci distantia, ZS, atque etiam latitudo, eadem sit quae lentis AC. Et sumta ST aequali EF, ponatur in T lens planoconcava YTV, punctum dispersus habens S. Sitque in lente PQR radius extremus axi parallelus RR, qui ab ea fractus incedat secundum rectam RX secantem lentem YTV in V.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 324]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 33.]
 [Fig. 34.]
Comme donc la distance focale ZS est égale au diamètre de la surface PQRGa naar voetnoot1), et la distance TS du point de dispersion au diamètre de la surface concave YTVGa naar voetnoot2); comme en outre ZS:ST = RZ:VT (car les points X et S sont si peu éloignés l'un de l'autre que le rapport ZS:ST peut ici être estimé égal au rapport ZX:XT), les arcs de cercle QR et TV seront semblables; et, par conséquent, le rapport de l'épaisseur QZ à celle de la lentille concave au point V sera égal à ZS::ST. Or, l'épaisseur BD de la lentille AC est égale à l'épaisseur QZ de la lentille PR, à cause de l'égalité des distances focales et des largeurs des deux lentillesGa naar margenoot*, et pour la même raison l'épaisseur de la lentille concave GH au point H sera égale à celle de la lentille YV au point V. Par conséquent, l'épaisseur BD sera aussi à l'épaisseur de la lentille GH au point H comme ZS est à ST, ou comme DE est à EF, c'est-à-dire comme b est à c. Si l'on pose DB = e, l'épaisseur de la lentille GH au point H sera donc égale à ce/b; mais l'aberration du rayon IH, réfracté par la lentille GH et prolongé en sens inverse, est égale, d'après la construction, à l'épaisseur de la lentille au point H multipliée par l'expression bf/cg. Cette aberration sera donc égale au produit de ce/b par bf/cg, c'est-à-dire, à ef/g. Mais comme l'épaisseur DB est e et que cette épaisseur est à l'aberration du rayon extrême due à la lentille AC comme g est à f, on voit que cette aberration-là est également exprimée par fe/g. Attendu que l'aberration du rayon IH est donc égale à celle de ce rayon extrême et que par conséquent le rayon réfracté provenant du rayon considéré correspond au point O, lorsqu' on le prolonge en sens inverse, il s'ensuit que le | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 325]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Quia ergo foci distantia ZS est diameter convexitatis PQRGa naar voetnoot1), et distantia puncti dispersus TS diameter cavitatis YTVGa naar voetnoot2); sicut autem ZS ad ST ita RZ ad VT; (nam puncta X, S, tam parum distant ut ratio ZS ad ST eadem hic quae ZX ad XT censeri possit) erunt arcus similes QR, TV; ideoque et crassitudo QZ ad crassitudinem lentis cavae in V sicut ZS ad ST. Est autem crassitudo lentis AC, nempe BD, aequalis crassitudini QZ lentis PR, propter focorum distantias latitudinesque utriusque aequalesGa naar margenoot*; eandemque ob rationem lentis cavae GH crassitudo in H aequalis crassitudini lentis YV in V. Erit ergo et crassitudo BD ad crassitudinem lentis GH in H sicut ZS ad ST, sive ut DE ad EF, hoc est ut b ad c. Unde si DB dicatur e, erit crassitudo lentis GH in H aequalis ce/b, atqui aberratio radij IH, refracti in lente GH, retroque producti, aequalis est, ex constructione, crassitudini ejus quam habet in H, ductae in bf/cg. Ergo haec aberratio erit id quod fit ducto ce/b in bf/cg, nempe ef/g. Sed cum crassitudo DB sit e, cumque ipsa sit ad aberrationem radij extremi in lente AC ut g ad f, patet etiam hanc aberrationem esse fe/g. Cum igitur huic aequalis sit aberratio radij IH, ac proinde refractio ejus retro producta pertineat ad punctum O; sequitur et radium CH ad O tendentem ita | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 326]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
rayon CH qui se dirigeait vers le point O est réfracté de telle manière par la lentille concave au point H qu'il se meut ensuite suivant la droite HI parallèle à l'axe. Or, la même chose peut maintenant aisément être démontrée pour un rayon quelconque plus rapproché de l'axe, tel que KK. Supposons que ce rayon, après avoir été réfracté par la lentille AC, se meuve suivant la droite KN qui coupe la lentille GH au point L et rencontre l'axe au point N, et soit LM une droite parallèle à l'axe. Comme la distance du point H à l'axe est alors à la distance de L comme la distance de C est à la distance de K, les carrés des distances nommées seront aussi dans les mêmes rapports. Or, comme le carré de la distance de C est au carré de la distance de K, ainsi est l'aberration OE du rayon CC à l'aberration NE du rayon KKGa naar margenoot*. Et comme le carré de la distance de H est au carré de la distance de L, ainsi est l'aberration du rayon IH, réfracté par la lentille GH, aberration égale à OE d'après ce qui a été démontré, à l'aberration du rayon ML. Par conséquent, l'aberration du rayon ML, elle aussi, sera égale à l'aberration NE. Il en résulte que comme le rayon réfracté provenant du rayon ML correspond au point N lorsqu'on le prolonge en sens inverse, le rayon KL qui se dirige vers le point N doit réciproquement être réfracté selon LM; en d'autres termes, ce rayon réfracté se mouvra parallèlement à l'axe, ce qu'il fallait démontrer.
Nous avons trouvé par le calcul, d'après la méthode décrite, les rayons des surfaces contenus dans le tableau suivant; ce sont ces valeurs qu'il faut donner aux rayons de courbure des deux surfaces de la lentille convexo-concave pour obtenir quelques télescopes parfaits de cette espèce. La plus grande des deux lentilles y est supposée planconvexe, avec la surface sphérique tournée vers l'extérieur, parce qu'une lentille de ce genre est plus facile à construire que la lentille de la meilleure forme décrite plus haut possédant un rayon 6 fois plus grand que l'autreGa naar voetnoot2), et que son aberration peut être corrigée par une lentille concave tout aussi bien que celle de la lentille de la meilleure formeGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 327]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
frangi à lente cava in H ut inde feratur secundum rectam HI axi parallelam. Idem vero et de radio quolibet axi propiore ut KK facile nunc ostendetur. Pergat enim hic, post refractionem in lente AC, secundum rectam KN quae secet lentem GH in L, et conveniat cum axe in N, et sit LM axi parallela. Cum ergo distantia puncti H ab axe sit ad distantiam L ut distantia C ad distantiam K erunt et quadrata earum distantiarum in eadem ratione. Sicut autem quadr. distantiae C ad quadr. distantiae K ita est aberratio radij CC quae est OE ad aberrationem radij KK, quae est NEGa naar margenoot*. Et sicut quadr. distantiae H ad quadr. distantiae L ita est aberratio radij IH, fracti in lente GH, quae aberratio ipsi OE aequalis ostensa est, ad aberrationem radij ML. Itaque aberratio radij ML aequalis quoque erit ipsi NE. Quare cum refractio radij ML retro producta pertineat ad punctum N, etiam radius KL tendens ad N flectetur secundum LM, hoc est, axi parallelus feretur, quod erat ostendendum.
Secundum haec instituto calculo invenimus semidiametros superficierum, sequenti tabella comprehensas, quibus utrumque latus lentis cavoconvexae formari debeat, ad perfecta aliquot hujusmodi telescopia. Ponitur autem in his lens major planoconvexa, superficie sphaerica extrorsum versa, quod parabilior sit haec lens quam optima illa superius descripta rationis sexcuplaeGa naar voetnoot2), aberratioque ejus lente cava aeque ut in altera corrigaturGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 328]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L'usage du tableau est manifeste. Si j'ai par exemple une lentille planconvexe possédant une distance focale de 3 pieds et que je désire construire avec cette lentille un télescope qui grossit les diamètres des objets dans le rapport de 1 à 27, le tableau m'apprend qu'il faut prendre le rayon de la surface convexe de la lentille oculaire égal à 393/1000 ou ⅖ pouce à peu près et le rayon de la surface concave de cette même lentille à 247/1000 ou ¼ pouce environ. Mais si avec cette même lentille convexe de 3 pieds je désire construire un télescope qui grossit 40 fois le diamètre des objets et trouver la lentille concave nécessaire à ce but, il faut, puisque le tableau indique ce grossissement pour un télescope de 5 pieds dont les rayons de la lentille concave sont 331/1000 et 230/1000, prendre un | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 329]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Usus tabellae manifestus est; ut si habeam lentem planoconvexam cujus foci distantia 3 pedum, cupiamque ex ea telescopium adaptare quod 27ties res visas secundum diametrum multiplicet; docet tabella semidiametrum superficiei convexae lentis ocularis debere sumi 393/1000 sive ⅖ proxime unius pollicis; semidiametrum vero superficiei cavae ejusdem lentis, 247/1000 sive proxime ¼ pollicis. Quod si vero eadem lente convexa 3 pedum telescopium parare velim cujus multiplicatio sit quadragecupla, lentemque cavam reperire quae ad hoc requiritur, quoniam tabella hanc multiplicationem dat telescopio pedum 5, cujus cavae lentis semidiametri sunt 331/1000, 230/1000, oportet facere ut longitudo pedum 5 ad longit. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 330]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nombre tel que la longueur de 5 pieds soit à la longueur de 3 pieds comme la fraction 331/1000 est à ce nombre. On trouve ainsi le nombre 199/1000 qui représente le rayon de la surface convexe de la lentille oculaire cherchée. En prenant de nouveau un nombre tel que 5 est à 3 comme 230/1000 est à ce nombre-là, on trouve le nombre 138/1000. Il représente le rayon de la surface concave. Il est suffisamment clair d'après ce qui a été dit plus haut qu'il faut tourner du côté de l'oeil la surface convexe de la lentille oculaire. Il faut avoir soin de placer les axes des deux lentilles exactement sur la même droite et d'amener la pupille de l'oeil au centre de la lentille concave. Pour pouvoir le faire plus facilement, on doit couvrir le reste de la lentille et laisser au centre une ouverture de la grandeur de la pupille ou même un peu plus petite. Car quoique le champ visuel du télescope devienne moins étendu de cette façon, sa clarté ne sera diminuée en aucune façon, attendu que le cône des rayons à l'endroit où se trouve la lentille oculaire est réduit déjà à un si petit diamètre que souvent il ne remplit ni la moitié, ni même le tiers, de la largeur de la pupille, comme on le voit aisément par le calcul. Si, par exemple, dans le télescope de 12 pieds qui donne un grossissement centuple, l'ouverture de la plus grande des deux lentilles est de 3 pouces, ce qui suffit amplement, comme nous l'expliquerons plus loinGa naar voetnoot1), la largeur du cône lumineux là où il coupe la lentille oculaire sera seulement la centième partie de 3 pouces, c'est-à-dire, les 3/100 d'un seul pouce, largeur inférieure au tiers d'une pupille médiocrement ouverte. L'utilité des lunettes de ce genre, l'avantage qu'elles ont sur celles qu'on a construit ordinairement jusqu' à ce jour à l'aide de lentilles convexes et concaves sera d'abord celui-ci qu'ils rendront la vision plus nette, attendu qu'ils envoient parallèlement à l'oeil les rayons issus des différents points de l'objet, à-peu-près comme le feraient des verres de forme elliptique ou hyperboliqueGa naar voetnoot2); mais surtout que, sans être plus longs que les télescopes ordinaires, ils pourront grossir beaucoup plus les objets, vu que leurs lentilles extérieures souffriront une ouverture plus grande que celles des télescopes ordinaires parce que l'aberration de cette lentille due à la propriété de la figure sphérique est corrigée par la lentille oculaire. Mais il faut savoir surtout que, pour atteindre ce but, il est indispensable que les surfaces de la plus grande lentille, aussi bien que celles de la lentille oculaire, soient parfaitement sphériques. Or, il y a raison de croire que même les surfaces qu'on pense être travaillées avec la plus grande persection, en sont en réalité bien éloignées, comme nous le ferons voir après plus explicitementGa naar voetnoot3); de sorte qu' à mon avis il faut avec un nouveau zèle et en se servant de nouveaux instruments, s'appliquer à la construction des lentilles, si nous désirons obtenir des résultats supérieurs à ceux de nos prédécesseurs et faire en sorte que les effets s'accordent avec les démonstrationsGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 331]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pedum 3, ita 331/1000 ad aliud, nempe 199/1000, quae erit semidiameter superficiei convexae lentis ocularis quaesitae, ac rursus ut 5 ad 3 ita 230/1000 ad aliud, nempe 138/1000, quae erit semid. superficiei cavae. Porro convexam lentis ocularis superficiem ad oculum obvertendam ex jam dictis satis patet. cura autem adhibenda est ut axes utriusque lentis in eandem exacte lineam disponantur, atque oculi pupilla ad punctum medium cavae admoveatur, quod quo facilius fiat, tegendae sunt reliquae partes lentis, ac foramen in medio relinquendum ad pupillae magnitudinem, vel etiam minus aliquanto. Nam licet hoc modo angustius fiat spatium quod conspectu telescopij comprehenditur, claritati tamen nihil decedet, quoniam conus radiorum, eo loco ubi lens ocularis consistit, adeo jam in arctum contrahitur ut nec dimidiam nec saepe tertiam partem pupillae latitudinis aequet, ut calculo facile deprehenditur. Si enim ex. gr. in telescopio 12 pedum, cujus multiplicatio centupla, apertura lentis majoris sit 3 pollicum, quae abunde sufficit, ut insequentibus diceturGa naar voetnoot1), hic jam latitudo coni radiosi, quo loco lenti oculari occurrit, centesima tantum pars est pollicum trium, id est, 3/100 pollicis unius, quae latitudo minor est parte tertia pupillae mediocriter apertae. Utilitas autem ac praestantia hujusmodi perspicillorum, prae ijs quae huc usque ex convexis et cavis lentibus fieri consuerunt, haec primum erit, quod distinctiorem visionem efficient, quoniam radios à singulis rei visae punctis manantes parallelos ad oculum mittunt, sicuti fere figurae ellipticae aut hyperbolicae vitraGa naar voetnoot2); praecipua vero quod, longitudine vulgaribus aequalia, longe magis res visas multiplicare poterunt, eo quod in lente exteriori solito majorem aperturam ferent, quum aberratio ejus lentis a figurae sphaericae proprietate profecta, lente oculari corrigatur. Sed ad haec requiri omnino sciendum ut tam majoris quam ocularis lentis superficies perfectam sphaericae convexitatis figuram accipiant, a qua multum abesse, etiam illas quae exquisitissime elaboratae creduntur, putandum est, ut postea pluribus docebiturGa naar voetnoot3). adeo ut nova industria novisque machinationibus hac in re incumbendum existimem, si quid praeteritis majus consequi cupimus, atque efficere ut cum demonstrationibus effectus consentiantGa naar voetnoot4). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 332]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition X.Examiner le degré de clarté qu'on peut obtenir avec des télescopes quelconques. Le grossissement qu'on obtient avec des télescopes composés de deux lentilles convexes est égal au rapport de la distance focale de la lentille extérieure à celle de la lentille intérieure. Il est donc évident qu'on peut donner à cette lentille intérieure ou oculaire des rayons de courbure si petits que les objets considérés, même avec un télescope de petite longueur, paraissent grossis dans un rapport arbitrairement grand. Il en est de même pour les télescopes composés d'une lentille convexe et d'une lentille concave, attendu que le grossissement est égal au rapport de la distance focale de la lentille extérieure à la distance du point de dispersion de la lentille concave. Il y a pourtant deux raisons pour lesquelles il faut dans l'un et l'autre cas observer une certaine mesure. La première, c'est que, lorsque l'ouverture de la lentille extérieure reste la même, le télescope rend les objets d'autant plus obscurs qu'il les grossit davantage. La seconde, c'est qu'il donne aussi des images de moins en moins distinctes; nous traiterons plus loin de ce sujetGa naar voetnoot1). Mais pour comprendre comment il faut évaluer le degré de l'obscurité, il faut faire attention à l'image qui, comme nous l'avons dit souventGa naar voetnoot2), se forme au fond de l'oeil et observer qu'elle est d'autant plus lumineuse qu'un plus grand nombre et d'autant plus obscure qu'un plus petit nombre de rayons, issus de l'objet, arrivent à l'oeil pour la former. Par exemple, si je regarde d'abord un objet à l'oeil nu et que je considère ensuite le même objet à travers une ouverture placée fort près de l'oeil et dont le diamètre n'est que la moitié de celui de la pupille et la surface donc quatre fois moindre, l'image formée au fond de l'oeil de l'objet regardé à travers l'ouverture, deviendra aussi quatre fois plus obscure | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 333]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio X.]Rationem lucis et obscuritatis in perspicillis quibuslibet examinare. Quandoquidem ratio incrementi secundum quam species rerum augentur in telescopijs, quae duabus convexis lentibus constant, est ea quae foci distantiae lentis exterioris ad foci distantiam interioris, manifestum est adeo exigui convexi assumi posse lentem hanc interiorem sive ocularem, ut res visae, etiam brevi telescopio, quantumlibet auctae appareant. Eodemque modo se res habet in his quae ex convexa et cava lente componuntur, quum ratio incrementi sit ea quae foci distantiae lentis exterioris ad distantiam puncti dispersus lentis cavae. Cur tamen modus utrobique adhibendus sit duplex causa est: una, quod manente eadem apertura lentis exterioris, quanto magis telescopium res visas dilatat tanto quoque obscuriores videri facit. altera quod et minus distinctas exhibet, cujus consideratio ad sequentiaGa naar voetnoot1) pertinet. Obscuritatis autem ratio quomodo estimanda sit ut intelligatur ad picturam illam attendendum est quae in fundo oculi saepe fieri diximusGa naar voetnoot2), ac tenendum eam tanto lucidiorem aut obscuriorem contingere quanto plures paucioresque radij ad eam formandam ex re visa affluunt. Ut si ex. gr. oculo libero primum rem aliquam intuear, deinde vero trans foramen eandem aspiciam oculo proxime admotum cujus diameter tantum dimidia sit diametri pupillae, ac proinde capacitas quadruplo minor. fiet in fundo oculi imago rei trans foramen spectatae | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 334]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
que lorsque je le regardais à l'oeil nu; parce que la quatrième partie seulement des rayons issus de l'objet traversent l'ouverture et que ceux-ci doivent illuminer sur la rétine le même espace qu' auparavant. Par suite, si l'on doit construire un télescope qui grossit dix fois le diamètre des objets et qu'on exige que ce télescope forme de tous les objets des images aussi lumineuses que celles qu'on obtient sans lui, je dis que le diamètre de l'ouverture de la lentille extérieure devra, lui aussi, être dix fois plus grand que celui de la pupille, même dans le cas où pas la moindre partie des rayons ne serait détruite par la réflexion due aux lentilles ou par l'opacité du verre. En effet, de même que la surface de l'image formée sur la rétine à l'aide d'un télescope de ce genre est cent fois plus grande que celle qui s'y forme lorsqu'on regarde à l'oeil nu, de même aussi l'ouverture de la lentille extérieure devra embrasser cent fois plus de rayons que la pupille de l'oeil, pour que cette grande image ait le même degré de clarté dans toutes ses parties que la petite image avait dans les parties correspondantes. Mais il faut savoir qu'une clarté bien plus faible suffit pour les télescopes de sorte qu'on regarde comme satisfaisant ceux dont nous nous servons le jour, si les images qu'ils donnent n'ont qu'une dixième partie, ou même moins, de la clarté de celles qu'on obtient en regardant à l'oeil nu; tandis que les télescopes de plus grandes dimensions que nous n'employons que pour regarder les étoiles, n'exigent qu'une soixantième ou soixante-dixième partie de cette clarté. Je trouve, par exemple, que dans un télescope de 22 piedsGa naar voetnoot1) qui grossit cent vingt cinq fois les diamètres des objets, l'ouverture de la lentille extérieure est de deux pouces et d'un tiers, c'est-à-dire quinze fois plus grande environ que la largeur moyenne d'une pupille, tandis qu'elle devrait être cent vingt cinq fois plus grande que cette dernière si la clarté d'une image produite par ce télescope devait être égale à celle qu'on obtient en regardant à l'oeil nu. Il s'ensuit que le télescope considéré ne reçoit que la soixante-dixième partie de la lumière qui serait nécessaire pour cela, attendu que les surfaces des cercles dont les diamètres sont entre eux comme les nombres 15 et 125, ou 3 et 25, sont entre elles à-peu-près dans le rapport 1:70. La cause qui fait que nous nous contentons ici d'une si petite fraction de la lumière doit être cherchée dans l'éclat extraordinaire des corps célestes, c'est-à-dire de la Lune et des autres planètes. Eclairés par les rayons du soleil, ils émettent tant de lumière qu'il en faut beaucoup moins pour les contempler aisément et distinctement. De la même manière nous voyons qu' aux jours nuageux il reste assez de lumière pour nous faire apercevoir facilement tous les objets, quoique cette quantité de lumière soit fort petite comparée avec celle que nous envoient les rayons du soleil. Il faut savoir d'ailleurs que l'effet obtenu s'explique aussi en partie par cette circonstance que les yeux réagissent sur une bien plus petite quantité de lumière dans les ténèbres qu'en plein jour et que dans l'obscurité ils peuvent apercevoir des objets pour lesquels ils sont absolument aveuglés lorsqu'ils viennent d'avoir vu la lumière du jour. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 335]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
quadruplo etiam obscurior quam dum libero oculo spectabatur; quoniam tantum pars quarta radiorum ab re visa manantium foramen ingreditur, quibus spatium idem quod prius in retina collustrari debeat. Quod si jam telescopium parandum sit, decuplo augens visibilia secundum diametrum, ac postuletur ut aeque clare omnia referat atque cum citra telescopium spectantur, dico et diametrum aperturae lentis exterioris decuplam esse debere ad pupillae diametrum, idque etiamsi neque ex reflexione lentium, neque ex vitri opacitate pars ulla radiorum interciperetur. Sicut enim superficies picturae in retina ejusmodi telescopio centupla existit ejus quae fit nudo oculo spectanti, ita quoque centuplo plus radiorum apertura lentis exterioris quam pupilla oculi comprehendere debebit ut magna haec pictura aeque illustris sit omnibus sui partibus ac prius minor illa fuerat. Sed enim multo minorem claritatem in telescopijs sufficere sciendum est, adeo ut satis habere existimentur, quibus interdiu utimur, si modo decimam partem aut etiam minorem habeant lucis ejus quam nudus oculus percipit. Majora autem, quibus tantum sidera spectamus, non nisi sexagesimam aut septuagesimam requirant. Ita namque experior in telescopio 22 pedumGa naar voetnoot1), quod res visas centies vicesies quinquies ampliores secundum diametrum reddit, aperturam lentis exterioris esse duorum pollicum cum triente, hoc est, circiter quindecuplo majorem quam sit mediocris pupillae latitudo; cum tamen centies vicecies quinquies eam continere debuerit si lux eadem telescopio atque oculo non armato percipienda fit. Unde sequitur tantum septuagesimam circiter partem ejus quae ad hoc requiritur luminis dicto telescopio adesse: quia areae circulorum, quorum diametri ut 15 ad 125, sive ut 3 ad 25, sunt fere ut 1 ad 70. Causa autem cur tantilla lucis pàrtiuncula hic contenti simus, insignis ille corporum caelestium est splendor, Lunae nimirum ac reliquorum planetarum. qui cum solis radijs illustrentur, tam intensum lumen vibrant ut longe minori opus sit ad ipsa commode ac distinctè contemplanda. quemadmodum et diebus nubilis abunde lucis superesse videmus ad rerum omnium facilem perceptionem, etsi lux haec perexigua sit ad eam comparata quam solis radij inferunt. Caeterum aliquid hic etiam conferre sciendum est quod per tenebras multo minori luce oculi quam interdiu moveantur, atque illa conspicere valeant ad quae a diei luce recentes prorsus caecutiunt. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 336]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ensuite il est évident, d'après ce que nous avons dit jusqu'ici, que dans deux télescopes qui doivent donner des images également lumineuses, le diamètre de l'ouverture de l'un d'eux surpassera nécessairement celui de l'autre dans un rapport égal au rapport du grossissement linéaire du premier télescope à celui du second. Si nous voulons, tandis que l'ouverture du télescope reste la même, substituer à la lentille oculaire une autre qui grossit deux fois plus, il est évident que tous les objets seront vus quatre fois plus obscurs, parce que la même quantité de rayons doit éclairer sur la rétine un espace quatre fois plus grand qu' auparavant. Et de la même manière, l'image sera toujours obscurcie dans un rapport égal au carré de celui qui exprime l'augmentation du grossissement. Il ne faut donc pas à la légère remplacer la lentille oculaire par une lentille plus convexe ou plus concave, mais calculer exactement quel agrandissement l'ouverture de la lentille extérieure peut supporter de manière que le télescope ne donne pas en même temps des images moins lumineuses qu'on ne doive les exiger. Et, en vérité, toute la puissance et l'effet d'un télescope quelconque dépendent à ce point de la grandeur de son ouverture qu'après avoir considéré cette dernière on peut, si elle est petite, dire avec certitude que le télescope a peu de puissance, quel que soit le nombre des autres lentilles et de quelque façon qu'elles soient placées à l'intérieur du tube. En effet, pour qu'un grossissement important soit obtenu avec une clarté suffisante il est nécessaire que beaucoup de rayons soient rassemblés, ce qui est absolument impossible si la lentille extérieure n'a pas une grande ouverture. Toutefois il en est autrement pour les microscopes: ils peuvent grossir les diamètres soixante ou cent fois ou même davantage, sans que l'image soit obscure, tandis que l'ouverture de la lentille extérieure est petite, même beaucoup plus petite que la pupille. Il en faut chercher la cause uniquement dans la faibledistance qui sépare l'objet de la petite lentille. Pour expliquer cela par une figure, soit C [Fig. 35] l'objet placé sous le microscope et K sa lentille la plus basse ou extérieure, AB le diamètre de l'ouverture de cette lentille. Supposons que D et L représentent les autres lentilles; qu'il y en ait une ou plusieurs, c'est une chose sans importance. EF représente la pupille de l'oeil. Tirons à partir d'un point quelconque de l'objet, tel que C, les droites CA et CB qui interceptent le diamètre AB de l'ouverture; prolongeons-les jusqu'aux points G et H où elles coupent une droite tirée par la pupille et faisant des angles droits avec l'axe des lentilles; il apparaît alors que l'ouverture circulaire AB embrasse une quantité de rayons provenant du point C égale à celle qu'embrasserait la pupille de l'oeil si elle avait un diamètre égal à la ligne GH. Par conséquent, si le grossissement de ce microscope serait exprimé par le rapport de GH à EF, diamètre de la pupille, l'objet C paraîtrait aussi lumineux que lorsqu'on le contemple à l'oeil nu et sans lentillesGa naar voetnoot1). Mais comme nous pouvons, dans ce cas aussi bien que dans celui des télescopes, nous passer d'une grande partie de la lumière, le grossissement peut même être rendu beaucoup supérieur à celui qu'exprime le rapport GH:EF. Par | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 337]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ex his porro quae diximus hactenus manifesto liquet necesse esse ut in telescopijs duobus quorum aequalis futura sit claritas, diametri aperturarum tanto una aliam superet quanto magis telescopium illud altero res visas secundum diametrum amplificat. Manente vero eadem apertura telescopij, si in locum lentis ocularis aliam substituere velimus, quae duplo majus priori incrementum efficiat; patet quadruplo obscuriora omnia visum iri, eo quod eadem radiorum multitudo spatium in retina prioris quadruplum illustrare jam debeat. atque eadem ratione semper haec obscuritatis proportio dupla erit proportionis aucti incrementi. Quare non temere lens ocularis convexiore vel magis cava mutanda est, sed diligenter expendendum quale incrementum exterioris lentis apertura perferre valeat, ita ut simul non minori luce quam quae requiritur praeditum sit telescopium. Ac sane in tantum vis omnis atque effectus telescopij cujuslibet ex aperturae illius magnitudine pendet, ut hac inspecta, si parva est, etiam exiguae virtutis telescopium esse, certam ferre sententiam possimus, quotcunque etiam lentes aliae et quocunque modo intra tubum aptatae sint. Ut enim insignis habeatur multiplicatio cum sufficienti lumine multos radios colligi necesse est, quod sine magna lentis exterioris apertura nequaquam fieri potest. Attamen in microscopijs alia ratio est, cum in his exiguo licet lenticulae exterioris foramine, imo pupillâ longe minori, multiplicatio sexagecupla vel centupla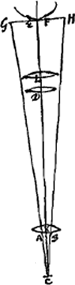 [Fig. 35.]
aut major etiam secundum diametrum praestari possit, non deficiente luminis claritate. cujus rei causa non alia est quam rei visae a lenticula exigua distantia. quod ut figurâ explicemus, esto visibile microscopio subjectum C, lens ejus infima sive exterior K; cujus aperturae diameter AB. Reliquae vero lentes una vel plures, hoc enim nihil refert, sunto D, L. Oculi autem pupilla EF. ductis jam à visibilis puncto aliquo, ut C, rectis CA, CB, diametrum aperturae AB intercipientibus, ijsdem continuatis usque in G et H, ubi occurrant rectae per pupillam ductae, rectosque angulos cum axe lentium facienti: constat jam aeque magnam radiorum copiam à puncto C venientium apertura circulari AB comprehendi atque oculi pupilla comprehenderet si diametrum lineae GH aequalem haberet. Quamobrem si multiplicatio perspicilli hujus fuerit ea quae GH ad EF pupillae diametrum, aeque illustre apparebit visibile C, atque cum simplici visione absque perspicillo cerniturGa naar voetnoot1). Sed cum et hic, ut in telescopijs, parte magna luminis carere possimus, etiam major | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 338]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
exemple, si GH:EF = 20, le microscope supportera aisément un grossissement linéaire centuple. On peut même remédier à la trop grande obscurité des images en éclairant l'objet plus vivement, ce qui peut être fait de diverses manières. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XI.Chercher les diamètres des ouvertures qui conviennent aux lentilles extérieures d'un télescope. Comme la grandeur de l'ouverture des télescopes est d'une si grande importance que le jugement qu'on porte sur leur puissance et leur qualité est principalement basé là-dessus, et comme cette ouverture ne peut pas être choisie arbitrairement, attendu que si on la prend trop grande la vision distincte est diminuée par la confusion des rayons, tandis qu'une ouverture trop petite donne des images obscures; il faut examiner généralement quelle règle on peut donner pour la grandeur des ouvertures. Mais pourtant il n'est pas précisément notre intention de rechercher à l'aide de ces considérations la plus grande ouverture pour une lentille donnée: en effet, c'est ce que l'expérience peut indiquer le mieux; mais nous nous proposons de faire connaître, étant données l'ouverture et la longueur d'un seul télescope excellent et d'ailleurs quelconque, les ouvertures qui conviennent à d'autres télescopes plus longs ou plus courts. La règle doit nous apprendre la grandeur de l'ouverture pour chaque télescope séparément, de manière que sa puissance ne soit pas inférieure à ce qu'elle doit être eu égard à sa longueur; et cela non seulement pour ceux de 20, de 30 ou de 40 pieds qui ont déjà été construits effectivement, mais aussi pour des télescopes beaucoup plus grands, par exemple de 100 pieds, de 200 pieds ou davantage. Il apparaîtra en même temps de cette façon quels plus grands avantages nous pouvons nous promettre de ces grands télescopes dans la considération des corps célestes; et l'on se sentira encouragé à faire de nouveaux efforts pour pousser les essais plus loin. Or, comme il y a deux sortes de télescopes, dont les premiers sont composés d'une lentille convexe et d'une lentille concave, et les seconds de lentilles convexes seulement, il faut savoir que ce que nous irons ici à-propos des rapports des ouvertures ne s'applique qu'aux télescopes de la deuxième espèce. En effet, nous avons fait voir plus hautGa naar voetnoot1) comment dans les lunettes composées d'une lentille concave et d'une lentille convexe, la lentille concave peut corriger l'aberration de la lentille convexe, et comment l'ouverture de la lentille convexe peut, par conséquent, être considérablement agrandie de manière à surpasser de beaucoup les limites que nous lui assignons ici. Mais comme une lentille oculaire concave ne peut être tolérée dans les tubes de fort grande longueur, parce qu'un espace trop étroit est embrassé par un télescope de ce genre, nous ne devons attendre un effet considérable dans la considération des corps célestes que des lunettes pourvues de lentilles convexes seulement. C'est donc de l'ouverture extérieure de ce | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 339]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
multo quam pro ratione GH ad EF multiplicatio induci potest. Ut si GH ad EF vigecupla est, facile centuplam multiplicationem secundum diametrum perferet microscopium. Quin imo et obscuritate nimia laboranti remedium adferre licet, validiori luce in rem visam derivata, quod pluribus modis fieri potest. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio XI].Aperturarum amplitudines quae lentibus telescopij exterioribus conveniant investigare. Cum aperturae magnitudo in telescopijs tanti sit momenti, ut efficacia ac bonitas eorum inde praecipue judicetur, cumque apertura illa non pro lubitu constitui possit, quod nimiam faciendo distincta visio radiorum confusione diminuatur; exigua autem obscuritatem pariat. omnino videndum est quaenam in his mensura praescribi possit. quod tamen non tam eo pertinet, ut datae lentis alicujus aperturam maximam hac ratione inquiramus; cum hoc experientia optime docere possit; verum ut unius telescopij cujusdam optimi apertura ac longitudine data, etiam aliarum longiorum aut breviorum aperturae cognoscantur; quantae videlicet in singulis esse debeant; ut pro ratione longitudinis effectus telescopij non minor debito sequatur; idque non tantum in his quae jam arte effecta habemus pedum 20, 30 vel 40, sed et in majoribus multo, puta quae ad 100 vel 200 pedes, aut amplius extendantur: quo simul manifestum fiat quanto plus opis in his ad caelestium contemplationem nobis polliceri possimus, animique addantur ad ulteriora conandum. Cum autem duo sint telescopiorum genera, alterum convexa et cava lente constans, alterum solis convexis, tantum ad ea quae posterioris generis sunt pertinere sciendum quae de aperturarum rationibus hic dicentur. In illis enim, quae cava et convexa lente componuntur, ostendimus supraGa naar voetnoot1), qua arte lens cava aberrationem convexae emendare possit; eoque apertura convexae insigniter deduci, adeo ut limites quos hic ponimus multum excedat. Sed cum lens ocularis cava in praelongis tubis tolerari nequeat, quod nimis angustum spatium telescopio tali comprehendatur, nihil eximium ad sidera spectanda nisi ab illis sperare debemus quae solis convexis instructa sunt. Itaque de horum telescopiorum exteriori apertura acturi, inprimis picturam illam considerabimus quae lente convexaGa naar voetnoot2) in loco tenebroso, vulgata jam arte, exhiberi solet, quoniam persimilis est ei quae in fundo oculi effingitur. Sit igitur convexae ejusmodi lentis apertura AB [Fig. 36], axis CD, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 340]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dernier genre de lunettes que nous parlerons. Nous considérons d'abord l'image qu'une lentille convexe, par un artifice fort connu, forme dans un endroit obscur attendu qu'elle est fort semblable à l'image formée au fond de l'oeil. Supposons donc que AB [Fig. 36] représente l'ouverture d'une lentille convexe de ce genre, CD son axe et D son foyer, c'est-à-dire, le point où se réunissent les rayons parallèles à l'axe. Soit DG l'aberration du rayon extrême. Prolongeons BG, rayon
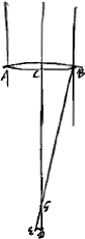 [Fig. 36.]
réfracté correspondant au rayon extrême, jusqu' à ce qu'il rencontre en E un plan parallèle à la lentille AB et passant par le foyer D. Les rayons réfractés provenant des autres rayons parallèles à l'axe s'approchent d'autant plus du foyer D que ceux-ci se trouvent à une plus petite distance de l'axe; il s'ensuit que les extrémités de toute la série de rayons parallèles, c'est-à-dire, de rayons issus d'un seul point de l'objet, occupent sur le plan un petit cercle de rayon DE; plus ce cercle est petit, plus aussi l'image de l'objet formé sur le plan sera nette. Or, comme les images formées par deux lentilles différentes seront également brillantes et également distinctes lorsque les cercles d'aberration que celles-ci produisent seront égaux entre eux; de même aussi des télescopes différents donneront lieu à une vision également distincte, lorsqu'ils produiront sur le fond de l'oeil des images également bien définies, je veux dire des images dans lesquelles les cercles d'aberration ont le même diamètre. Je pense qu'il n'existe pas de proposition plus certaine ou plus évidente qui puisse ici servir de base à nos raisonnements. Or, pour qu'on puisse examiner plus facilement la largeur de ces petits cercles formés sur le fond de l'oeil, nous démontrerons d'abord, vu que la lentille oculaire pourrait sembler donner lieu à quelque difficulté: Que les petits cercles d'aberration, formés au fond d'un oeil qui regarde à travers un télescope, sont produits presque exclusivement par l'aberration de la lentille extérieure, tandis que la lentille oculaire augmente à peine leur diamètre, de sorte que cette dernière lentille peut dans le télescope être considérée comme parfaite, c'est-à-dire, comme si elle rendait exactement parallèles les rayons issus d'un seul pointGa naar voetnoot1). En effet, soit AB [Fig. 37] la lentille extérieure du télescope, et GF la lentille oculaire; les foyers des deux lentilles coïncident au point C. Supposons que MB, le rayon extrême parallèle à l'axe, coupe l'axe au point D, faisant ainsi l'aberration DC, et la lentille GF au point G. Joignons les points C et G. Si nous supposons maintenant qu'un rayon HG parallèle à l'axe tombe sur la lentille FG, ce rayon rencontrera l'axe non pas au point C, foyer de la lentille GF, mais au point E, situé en-deçà du point C, de telle manière que l'aberration CE sera à l'aberration CD comme CF est à AC. En effet, comme AB et FG sont | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 341]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
focus, seu punctum quo colliguntur radij ad axem paralleli, D. Aberratio autem radij extremi sit DG. et producatur BG refractio ejusdem radij quousque occurrat tabulae, quae per focum D lenti AB parallela intelligenda est, in E. Cum itaque radiorum caeterorum axi parallelorum refractiones, quanto quisque axi propinquior fertur, tanto propius concurrant ad focum D, sequitur extremitates totius seriei parallelorum, sive ab uno aliquo rei visae puncto manantium occupare in tabula circellum cujus semidiam. DE; qui circellus quo minori fuerit magnitudine tanto perfectior erit in tabula rei visae repraesentatio. Sicut autem aeque nitidae ac distinctae a duabus diversis lentibus picturae futurae sunt quando istos aberrationum circulos aequales facient; ita quoque aeque distincta visio diversis continget telescopijs,
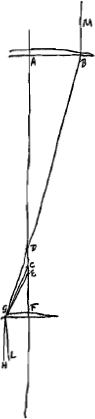 [Fig. 37.]
cum et ab illis in fundo oculi picturae aeque terminatae, hoc est in quibus aberrationum circuli aequali latitudine sint, describentur. Neque enim certius aut evidentius quicquam fundamenti vice hic statui posse existimo. Ut autem minori negotio circellorum istorum in fundo oculi latitudo inquiratur, quoniam lens ocularis difficultatem aliquam adferre videri possit, ostendemus primo, Circellos aberrationis, in fundo oculi per telescopium spectantis, fere tantum ab aberratione lentis exterioris oriri, lente oculari vix quicquam eorum latitudinem augente, adeo ut lens haec in telescopio tanquam perfecta censeri possit, hoc est, ac si radios à puncto venientes exacte parallelos redderetGa naar voetnoot2). Sit enim lens telescopij exterior AB [Fig. 37], ocularis GF, quarum utriusque foci sunt in puncto C. Radius autem extremus axi parallelus MB secet axem in D, faciens aberrationem DC, atque occurrat lenti GF in G; et jungatur CG. Si jam fingamus radium HG axi parallelum incidere in lentem FG, is non conveniet cum axe in C, foco lentis GF, sed citra punctum C in E, ita ut aberratio CE sit ad aberrationem CD sicut AC ad CFGa naar voetnoot3). Nam cum AB et FG sint portiones similes lentium ejusdem generis, constat utriusque aberrationes radiorum paralle- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 342]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
des parties semblables de deux lentilles de la même espèce, il est établi que les aberrations des deux rayons parallèles qui passent par les points B et G respectivement, sont entre elles comme les distances focales de ces lentilles. C'est pourquoi,
 [Fig. 37.]
réciproquement, le rayon issu du point E et qui suit la route EG sera réfracté de manière à se mouvoir selon GH parallèle à l'axe. Mais le rayon DG sera réfracté de telle manière en GL, que l'angle HGL deviendra égal à l'angle DGEGa naar margenoot*. Les deux lentilles ensemble donneront donc au rayon qui devait être parallèle à l'axe, une aberration représentée par l'angle HGL qui est égal à cet angle DGE; tandis que l'aberration de ce rayon n'excéderait pas l'angle DGC, si la lentille FG était telle qu'elle rendait parallèles à l'axe les rayons issus du foyer C. En effet, le rayon CG étant réfracté en GH et le rayon DG, comme auparavant, en GL, l'angle LGH serait alors égal à l'angle DGC. Il apparaît donc que la lentille GF augmente l'aberration du rayon BD d'un angle égal à CGE, lequel est à l'angle DGC à-peu-près comme EC est à CD, ou comme FC est à CA. Ceci fait voir combien cette augmentation due à la lentille oculaire est petite et négligeable, surtout dans les télescopes fort longs qui grossissent les objets cinquante ou cent fois et davantage. Nous parlerons maintenant des rapports des ouvertures et nous démontrerons la proposition suivanteGa naar voetnoot2): Dans des télescopes de différentes longueurs il faut, pour qu'ils donnent des objets des images également lumineuses et nettes, que le rapport des distances focales des lentilles extérieures de la même espèceGa naar voetnoot3) soit égal à la ¾ième puissance du rapport des diamètres des ouvertures de ces mêmes lentilles; en d'autres termes, il faut que les cubes de ces distances focales soient entre eux comme les quatrièmes puissances des diamètresGa naar voetnoot4). En effet, considérons deux télescopes de longueurs différentes ayant des lentilles extérieures de la même espèce: soit AB [Fig. 38] le diamètre de la lentille extérieure de l'un des deux, ou plutôt de la partie de cette lentille qui n'est pas recouverte, et OP la lentille oculaire; les foyers des deux lentilles coïncident au point D; en effet, cette disposition est nécessaire pour que les rayons issus d'un point lointain arrivent parallèlement à l'oeil après avoir traversé le télescope. Supposons que QR soit la pupille, que le fond de l'oeil se trouve en X et que tous les centres C, O, Q, X se trouvent sur la même droite qui est l'axe du télescope. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 343]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lorum in B et G incidentium esse inter se sicut ipsae lentium foci distantiae Quamobrem itaque et vice versa radius, ex E incidens secundum EG, flectetur secundum GH axi parallelam. At radius DG ita refringetur in GL, ut angulus HGL fiat aequalis DGEGa naar margenoot*. Itaque lens utraque simul nunc aberrare faciet radium. qui axe parallelus esse debuerat hoc angulo HGL ipsi DGE aequali, qui radius tantum aberraret angulo aequali ipsi DGC si lens FG ejusmodi esset ut radios ex foco C egredientes axi parallelos redderet. Tunc enim radio CG refracto in GH, et radio DG, ut ante, in GL, aequaretur angulus LGH angulo DGC. Patet igitur lentem GF augere aberrationem radij BD angulo aequali CGE, qui est ad angulum DGC proximè ut EC ad CD, sive ut FC ad CA. Unde apparet quam exigua sit haec additiuncula ab oculari lente profecta, quamque nullius momenti, praesertim
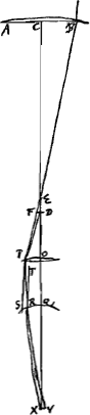 [Fig. 38.]
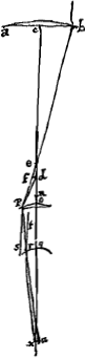 [Fig. 39.]
in praelongistelescopijs quae quinquagies vel centies et amplius res visas multiplicant. Nunc ad rationes aperturarum pergemus ostendemusqueGa naar voetnoot2): In telescopijs diversae longitudinis ut aeque lucidas ac distinctas rerum imagines referant, rationem foci distantiarum lentium exteriorum, ejusdem generisGa naar voetnoot3), sesquitertiam esse debere ejus quae in diametris aperturarum earundem lentium; sive, cubos dictarum foci distantiarum, eandem habituros rationem quadratoquadrata diametrorum aperturaeGa naar voetnoot4). Sunto enim duo diversae longitudinis telescopia lentes exteriores ejusdem generis habentia, quorum alterius lens exterior, quatenus adaperta, sit AB [Fig. 38], lens ocularis OP, focis utriusque in idem punctum D compositis; ita enim collocari necesse est ut radij ad oculum paralleli perveniant qui à puncto longinquo ad telescopium feruntur. Sit autem pupilla QR, fundus oculi ad X, centraque omnium C, O, Q, X in eadem recta quae est axis telescopij. Intelligatur | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 344]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Représentons en outre par BEP le rayon réfracté provenant du rayon extrême qui tombe sur la lentille AB; nous supposons que ce rayon réfracté coupe la lentille oculaire en P et que son aberration soit ED, de sorte que le rayon du petit cercle d'aberration est DF. Joignons les points D et P par une droite, et soit PS une parallèle à l'axe. Si un rayon DP, provenant du foyer de la lentille oculaire OP, tombe sur cette lentille, il devient parallèle à l'axe de manière à se mouvoir suivant la droite PS; en effet, nous considérons ici la lentille OP comme dénuée d'aberration, comme cela est permis d'après ce que nous avons démontré plus haut. Il en résulte que le rayon EP se mouvra suivant PR de telle sorte que l'angle SPR devient égal à l'angle DPE. Supposons que ce rayon réfracté coupe la pupille en R et tirons la droite RT parallèle à l'axe. Comme la disposition de l'oeil est telle qu'il réunit les rayons parallèles à l'axe, tels que TR, au point X, il s'ensuit qu'il réfractera le rayon PR vers l'intérieur, par exemple vers un point V de la rétine, de sorte que XV y sera le rayon du petit cercle d'aberration. Il apparaît que la grandeur de ce rayon dépend de la grandeur de l'angle que font entre eux au point R à l'intérieur de la pupille les rayons réfractés provenant des rayons PR et TR. Or, cet angle a à l'angle PRT un certain rapportGa naar margenoot* qui aurait la valeur ¾Ga naar voetnoot2) si le pouvoir réfringent de la cornée pouvait être considéré comme égal a celui de l'eau; mais cette valeur est ici sans importance. Il faut se figurer ensuite que dans le second télescope [Fig. 39] toutes les mêmes choses soient supposées et les mêmes constructions faites, les points qui correspondent à ceux de la première figure étant indiqués par les mêmes lettres, minuscules cette fois, que dans la première figure. Il est évident que tout ce qui a été dit jusqu' ici à propos du premier télescope, s'applique de même au second. Pour que la vision soit également distincte dans tous les deux, il faut donc que XV soit égal à xu, et, par conséquent, que l'angle TRP soit égal à l'angle trp. Mais l'angle DPF est égal à l'angle TRP ou RPS, et de même l'angle dpf est égal à l'angle trp. Il faut donc que les angles DPF et dpf soient égaux entre eux. Pour qu'il en soit ainsi, il faudra qu'on ait PD:DF = pd:df, et, par permutation, PD:pd, ou OD:od (rapport qui doit ici être censé avoir la même valeur) = DF:df. Prenons un point n tel qu'on ait CD:DO = cd:dn. Si donc, après avoir enlevé la lentille op, on plaçait une autre lentille oculaire au point n, possédant une distance focale dn, les grossislements des deux télescopes seraient les mêmesGa naar margenoot*, mais celui que donnerait alors le télescope abopGa naar voetnoot4) est au grossissement de ce même | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 345]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
porro refractio radij extremi in lentem AB incidentis esse BEP, quae occurrat lenti oculari in P, cujusque aberratio sit ED, circelli vero aberrationis semidiameter DF. Et jungatur DP, sitque PS axi parallela.  [Fig. 38.]
 [Fig. 39.]
Quoniam igitur, si in lentem ocularem OP radius incidat DP, ex foco ejus adveniens, is axi parallelus efficitur, ita ut incedat secundum rectam PS; (nam, ut supra fieri licere ostendimus, lentem OP quasi aberrationis expertem hîc consideramus;) feretur proinde radius EP secundum PR, ut angulus SPR fiat aequalis DPE. Occurrat ergo pupillae in R et agatur RT axi parallela. Quia ergo oculi ea est dispositio ut radios axi parallelos, qualis TR, cogat ad punctum X, sequitur radium PR interius deflexurum puta ad punctum retinae V, ita XV illic futura sit semidiameter circelli aberrationis; cujus quidem magnitudinem pendere apparet à magnitudine anguli quem refractiones radiorum PR, TR intra pupillam ad punctum R efficiunt. Hic vero angulus certam proportionem habet ad angulum PRTGa naar margenoot*, quae subsesquitertia essetGa naar voetnoot2), si corneae refractio eadem quae aquae ponatur; sed quaecunque sit, nihil hic refert. Porro in telescopio altero [Fig. 39] eadem omnia posita atque effecta intelligantur, literis minoribus ejusdem nominis atque in priore ad puncta correspondentia adscriptis; Et constat eadem omnia, quae hactenus dicta sunt, etiam illi telescopio convenire. Requiritur itaque, quo aeque distincta utrobique contingat visio, ut XV sit aequalis xu, ac proinde ut angulus TRP sit aequalis trp. Angulo autem TRP sive RPS aequalis est DPF, similiterque angulo trp aequalis dpf. Ergo requiritur ut aequales sint anguli DPF, dpf. Quod ut fiat, debebit esse ut PD ad DF ita pd ad df; et permutando, ut PD ad pd, sive, quae eadem ratio hic censenda est, OD ad od, ita DF ad df. Sit ut CD ad DO ita cd ad dn. Quod si igitur, ablata lente op, lens alia ocularis ad n poneretur, foci distantiam habens dn, jam eadem esset utriusque telescopij multiplicatioGa naar margenoot*; sed ea quam tunc haberet telescopium abopGa naar voetnoot4) est ad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 346]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
télescope dans le cas où la lentille op y est placée, comme od est à dnGa naar margenoot*. Il paraît donc que le grossissement dû au télescope ABOP est lui aussi au grossissement dû au télescope abop muni de la lentille op comme od est à dn. Mais comme on exige que les objets soient vus par les deux télescopes avec le même degré de clarté, il faut que le rapport od:dn, c'est-à-dire le rapport des grossissements, soit égal à CB:cb, c'est-à-dire au rapport des ouvertures. Puis, en partant de là, nous raisonnerons comme il suit. Le rapport OD:od est composé des rapports OD:dn et dn:do, dont le premier OD:dn est égal à CD:cd, puisque nous avons choisi le point n de telle manière que CD:DO = cd:dn; tandis que le second dn:do est égal à cb:CB, comme nous venons de le faire voir. Le rapport OD:od se compose donc des rapports CD:cd et cb:CB. Or, nous avons montré plus haut que ce même rapport OD:od est égal au rapport DF:df, dont il est établi qu'il se compose des rapports CB3:cb3 et cd2:CD2Ga naar margenoot*. Le rapport composé des rapports CD:cd et cb:CB sera donc égal à celui que composent les rapports CB3:cb3 et cd2:CD2. Multiplions des deux côtés par le rapport CD2:cd2. Les deux rapports suivants deviendront donc égaux entre eux: un premier composé des rapports CD3:cd3 et cb:CB, un second des rapports CB3:cb3, cd2:CD2 et CD2:cd2; le second est donc simplement égal à CB3:cb3, vu que les deux derniers rapports se détruisent mutuellement. Multiplions de nouveau des deux côtés par le rapport CB:cb. Alors deviendront égaux, un premier rapport composé des rapports CD3:cd3, cb:CB et CB:cb étant donc simplement égal au rapport CD3:cd3, et un second qui se compose des rapports CB3:cb3 et CB:cb, et qui est donc égal au rapport BC4:bc4. Comme le cube de CD est au cube de cd, ainsi est donc la quatrième puissance de CB à la quatrième puissance de cb. Ce qu'il fallait démontrer. Il s'ensuit que si le rapport des distances focales CD et cd est égal à 16:1, celui des diamètres des ouvertures BA et ba sera 8:1. Généralement, étant donnés dans un seul télescope quelconque la distance focale de la lentille extérieure et la plus grande ouverture que ce télescope peut supporter, nous trouverons d'après cette règle l'ouverture qui convient à un autre télescope quelconque ayant une lentille extérieure de la même espèce; le plus facile sera de se servir de logarithmes. En effet, si l'on donne numériquement la distance focale CD du télescope donné, le diamètre AB de son ouverture et la distance focale cd du second télescope qu'il s'agit de construire, il faut ajouter au logarithme du nombre AB les trois quarts du logarithme de cd et retrancher de la somme les trois quarts du logarithme de CD:on obtiendra ainsi le logarithme de l'ouverture ab. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 347]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
eam quam praestat posita lente op, sicut od ad dnGa naar margenoot*, Ergo patet et multiplicationem telescopij ABOP ad eam quae est telescopij abop instructi lente op, se habere ut
 [Fig. 38.]
 [Fig. 39.]
od ad dn. Cum autem aequalis claritas utrinque rebus visis postuletur, oportet ut sit od ad dn hoc est multiplicatio ad multiplicationem sicut CB ad cb, apertura ad aperturam, unde jam porro sic argumentabimur. Ratio OD ad od, componitur ex rationibus OD ad dn et dn ad do; quarum OD ad dn est eadem quae CD ad cd; cum fecerimus CD ad DO ut cd ad dn; altera vero dn ad do eadem quae cb ad CB, ut modo ostendimus; itaque ratio OD ad od componitur ex rationibus CD ad cd et cb ad CB. Atque eadem ratio OD ad od aequalis antea ostensa est rationi DF ad df, quam componi constat ex rationibus cubi CB ad cubum cb et quadrati cd ad qu. CDGa naar margenoot*. Ergo ratio composita ex CD ad cd et cb ad CB aequabitur compositae ex rationibus cubi CB ad cubum cb et quadrati cd ad qu. CD. Addatur utrinque ratio quadrati CD ad qu. cd. fient igitur aequales inter se, illinc composita ex rationibus cubi CD ad cubum cd et rectae cb ad CB, hinc composita ex rationibus cubi CB ad cubum cb et quadrati cd ad qu. CD et quadrati CD ad qu. cd; hoc est, sola ratio cubi CB ad cubum cb; quia duae posteriores sese mutuo tollunt. Addatur rursus utrinque ratio CB ad cb; fientque rationes aequales, illinc, composita ex rationibus cubi CD ad cubum cd, et rectae cb ad CB et CB ad cb, hoc est sola ratio cubi CD ad cubum cd. Hinc vero composita ex rationibus cubi CB ad cubum cb, et rectae CB ad cb, quae duae rationes constituunt rationem quadratoquadrati BC ad qu. qu. bc. Sicut igitur cubus CD ad cubum cd ita est qu. qu. CB ad qu. qu. cb. quod erat dem. Hinc sequitur, si ratio foci distantiarum CD ad cd sit ea quae 16 ad 1, rationem diametrorum aperturae BA ad ba futuram quae 8 ad 1. In universum vero, data in uno aliquo telescopio foci distantia lentis exterioris, et maxima quam ferre valet apertura, etiam alij cuivis, ejusdem generis lentem exteriorem habenti, debitam aperturam secundum haec invenimus, et facillime quidem per logarithmos. Si enim dentur numero foci distantia dati telescopij, CD, et diameter aperturae AB, itemque foci distantia alterius construendi telescopij cd, oportet logarithmo numeri AB addere tres quartas logarithmi cd et à summa auferre tres quartas logarithmi CD; fietque logarithmus aperturae ab. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 348]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Supposons, par exemple, qu'une lentille ayant une distance focale de 12 pieds, supporte dans son télescope une ouverture de deux poucesGa naar voetnoot1) et qu'on demande l'ouverture d'une autre lentille ayant une distance focale de 100 pieds. Le logarithme de 100 est 2,00000; en ajoutant les trois quarts de ce logarithme, c'est-à-dire 1,50000, au logarithme de 2, qui est 0,30103, on obtiendra 1,80103. Si l'on en retranche les trois quarts du logarithme de 12, c'est-à-dire 0,80938, il reste 0,99165, logarithme du nombre 981/100, qui désigne le nombre des pouces du diamètre cherché de l'ouverture, lequel est un peu inférieur à dix, ainsi qu'on voit. Nous avons construit de cette façon le tableau suivantGa naar voetnoot2) en prenant, comme nous l'avons dit, une ouverture de 2 pouces pour une lentille de 12 pieds, attendu que l'expérience nous a enseigné qu'une bonne lentille, quoique également convexe des deux côtés, peut avoir une ouverture de cetté grandeurGa naar voetnoot3); d'où il résulte qu'une lentille planconvexe ou une lentille à rapport sextuple des rayons de courbure laquelle est supérieure à toutes les autres comme nous l'avons démontré plus hautGa naar voetnoot4), supporte encore plus facilement une pareille ouverture. Si une lentille de cette dernière espèce était donnée et qu'on pouvait être assuré qu'elle était façonnée fort exactement, on pourrait se baser sur elle pour trouver la plus grande ouverture de toutes les autres lentilles de cette espèce. Mais nous avons préféré tenir compte de ce qu'on peut espérer déjà maintenant des efforts des artisans. Dans le même tableau nous avons indiqué quelles sont les lentilles oculaires qui conviennent à chaque grande lentille; pour trouver leurs distances focales, nous admettons qu'une lentille qui a une distance focale de deux pouces peut être combinée proprement avec une grande lentille de 12 pieds, comme l'expérience l'a enseignéGa naar voetnoot5). En se basant là-dessus, on peut calculer la mesure de chacune des autres lentilles oculaires; en effet: Dans des télescopes de longueurs différentes dont les lentilles extérieures sont de la même espèce, les distances focales des lentilles oculaires doivent être entre elles comme les racines bicarrées des distances focales des grandes lentillesGa naar voetnoot6). Cela se tire de la manière suivante de ce que nous avons démontré plus haut. Nous y avons montré que les distances focales, OD et od, des lentilles oculaires [Fig. 38 et 39] dans les télescopes considérés qui forment à l'intérieur de l'oeil des images également lumineuses et également distinctes quoique non pas également grandes, sont entre elles dans un rapport composé des rapports CD:cd et cb:CBGa naar voetnoot7). Par conséquent, la quatrième puissance du rapport OD:od sera aussi | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 349]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ut si lens, cujus foci distantia pedum 12, ferat aperturam in telescopio suo quae sit pollicum duorumGa naar voetnoot1), et quaeratur apertura lentis alius cujus foci distantia pedum 100. Logarithmus 100 est 2,00000 cujus tres quartae 1,50000 additae ad logarithmum 2, qui est 0,30103, faciunt 1,80103. Unde si auferantur ¾ logarithmi 12, hoc est, 0,80938, reliquum est, 0,99165, logarithmus numeri 981/100, qui designat numerum pollicum diametri aperturae quaesitae; paulo minorem, ut apparet, denario. Et hoc modo composita est sequens tabellaGa naar voetnoot2), sumtâ, ut jam diximus, aperturâ 2 pollicum in lente pedum 12: quandoquidem bonam lentem eousque
 [Fig. 38.]
 [Fig. 39.]
aperiri posse re ipsa invenimus, etsi utrimque aequaliter convexamGa naar voetnoot3); ut tanto proinde facilius id latura sit planoconvexa, vel illa proportionis sexcuplae, quae praestare caeteris omnibus supra ostensa fuitGa naar voetnoot4). Quodsi quae hujusmodi daretur, quamque constaret exactissime formatam, posset ab hac omnium aliarum maxima apertura certo definiri. Nos vero, quid jam nunc ab artificum industria sperare liceat, attendimus. In eadem porro tabella et lentes oculares definivimus quae cuique majori lenti conveniunt; ad quarum foci distantias inveniendas, ponimus eam quae duos pollices habeat recte aptari cum lente magna pedum 12, sicut experientia comprobatum estGa naar voetnoot5). Hinc vero et reliquae omnes mensuram suam accipiunt; quandoquidem: In diversae longitudinis telescopijs, quibus lentes exteriores ejusdem sunt generis, lentium ocularium foci distantiae subquadruplam rationem habere debent ejus quam foci distantiae lentium magnarumGa naar voetnoot6). Quod ex ante demonstratis hoc modo conficitur. Foci distantiae lentium ocularium, OD ad od [Fig. 38 et 39], in telescopijs ibi propositis, quae res visas aeque clare ac distincte, etsi non aeque amplas, intra oculum depingunt, rationem compositam habere ostensae sunt ex rationibus CD ad cd, et cb ad CBGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 350]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
composée des quatrièmes puissances des rapports CD:cd et cb:CB. De ces deux dernières la quatrième puissance de CD:cd est composée du rapport CD:cd et de la troisième puissance de ce même rapport CD:cd. Et l'autre, la quatrième puissance de cb:CB, est égale, d'après ce que nous avons démontréGa naar voetnoot1), au rapport du cube cd au cube CD. Par conséquent, la quatrième puissance du rapport OD::od sera composée des rapports CD:cd, (CD:cd)3 et (cd:CD)3. Les deux derniers rapports se détruisent mutuellement, et il ne reste donc que le rapport CD:cd égal à la quatrième puissance de OD:od; c'est pourquoi le rapport OD:od sera réciproquement égal à la racine bicarrée du rapport CD:cd. Ce qu'il fallait démontrer. D'ailleurs les mesures des lentilles oculaires convexes peuvent se tirer de ce qui précède encore d'une autre façon. En effet, de l'ouverture adoptée pour une lentille de 12 pieds on déduit les ouvertures de toutes les autres lentilles semblables; mais comme les ouvertures, ainsi sont entre eux les grossissements des télescopes donnant des images également lumineuses; il en résulte que lorsque les ouvertures sont données et de même aussi le grossissement propre à un télescope de 12 pieds, lequel est de 72 à 1 lorsque la lentille oculaire de ce télescope a une distance focale de 2 pouces, on connaîtra aussi le grossissement d'un autre télescope quelconque. Mais lorsque le grossissement et la distance focale de la grande lentille sont connus, on connaîtra aussi la distance focale de la lentille oculaire, attendu que le rapport des distances focales est égal au grossissement du télescope composé de ces lentillesGa naar voetnoot3).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 351]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
 [Fig. 39.]
Itaque et ratio quadruplicata OD ad od, componetur ex quadruplicatis rationibus CD ad cd, et cb ad CB. Harum vero CD ad cd quadruplicata componitur ex simplici ratione CD ad cd et ex eadem CD ad cd triplicata. altera vero cb ad CB quadruplicata, eadem ostensa estGa naar voetnoot1) quae cubi cd ad cubum CBGa naar voetnoot2); Ergo ratio quadruplicata OD ad od jam componetur ex rationibus CD ad cd et ex eadem CD ad cd triplicata et ex triplicata cd ad CD. quae duae posteriores se mutuo tollunt, adeoque superest ratio sola CD ad cd aequalis quadruplicatae OD ad od, quare et contra, ratio OD ad od subquadrupla erit rationis CD ad cd; quod erat ostendendum. Caeterum alia quoque ratione convexorum ocularium mensurae ex supra dictis haberi possunt. Cum enim ex constituta apertura in lente 12 pedum, aliarum omnium similium aperturae deducantur: Sicuti autem aperturae inter se ita et multiplicationes telescopiorum aequali luce gaudentium: datis proinde aperturis, itemque multiplicatione telescopij 12 pedum, quae est 72 ad 1, cum lens ocularis habeat 2 pollicum foci distantiam, dabitur et multiplicatio alîus cujuslibet. Sed cognita multiplicatione et foci distantia lentis majoris, noscetur etiam foci distantia lentis ocularis, cum harum sit ratio eadem inter se quae est multiplicationis telescopij compositiGa naar voetnoot3).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 352]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
FIN DE LA DEUXIÈME PARTIE. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 353]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[FINIS PARTIS SECUNDAE.] |
|