Oeuvres complètes. Tome XIII. Dioptrique

[p. 271]

Appendice¹⁾
Au troisième livre du ‘Tractatus de refractione et telescopiis’.
[1691.]

OF ad OΔ ut OΔ ad OZ

oftendendum ∠QZΔ ad QOΔ seu RKH²⁾ ut OE seu FH ad FΔ

hoc est OΔ ad ΔZ ut FH ad FΔ

demonstration OF ad OΔ ut OΔ ad OZ

OF ad FΔ ut OΔ ad AZ

HF³⁾ ad FΔ ut OΔ ad ΔZ.

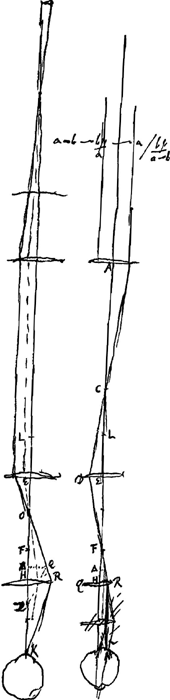
1) La pièce est empruntée à la p. 129 du ‘Manuscrit G’. Elle sert à démontrer l'assertion, faite à la p. 263 du Tome présent, que si dans la lunette représentée par les figures 10 et 11, p. 262 on remplace la lentille H, dont la distance focale FH est égale à celle de la lentille E (EL ou OE), par une autre, dont la distance focale FΔ soit plus petite, le grossissement sera mesuré par le rapport AC:FΔ, où AC égale la distance focale de l'objectif. À cet effet, après avoir supposé que la nouvelle lentille soit placé en Δ, Huygens commence par déterminer le point Z correspondant au point O, par rapport à la lentille en Δ, pour y placer l'oeil.
Or, comme il a démontré dans la Prop. IV (voir la p. 261) que dans le cas où la lentille de distance focale HF fût placée en H le grossissement se mesure par le rapport AC:EL, où EL = HF, il suffira de prouver que l'ancien et le nouveau grossissement sont dans le rapport inverse des distances focales des lentilles employées, c'est-à-dire, que le nouveau grossissement se rapporte à l'ancien comme FH à FΔ. Or, il est clair que ces grossissements sont dans le rapport des angles QZΔ et RKH, puisque l'angle qui correspond à l'angle SΛX de la figure 11 de la p. 262, (voir la note 2, p. 263) et qu'on retrouve ici (également sans lettre) dans la figure de gauche, est le même dans les deux cas. Il reste donc à démontrer qu'on a ∠QZΔ:∠RKH = FH:FΔ. C'est là la deuxième proportion du texte, où nous renvoyons pour le reste de la démonstration.

2) L'égalité des angles QOΔ et RKH résulte de celle des segments HK et HO; laquelle est expliquée dans la note 1, p. 262.

3) OF = HF puisque les points O et F divisent la distance EH en trois parties égales. Comparez la note 1, p. 262, déjà citée.