Oeuvres complètes. Tome XIII. Dioptrique

[p. 244]

La Dioptrique.
Première partie. Traité de la Réfraction et des Télescopes.
1653.
Livre troisième. Des télescopes.

Proposition I¹⁾.

Accommoder à un oeil quelconque une lunette composée de deux lentilles données.

Il est certain que de chaque point d'un objet partent des rayons qui atteignent toutes les parties de la pupille; et ces rayons sont estimés parallèles lorsqu'ils émanent d'un point fort éloigné. Or, comme ceux qui jouissent d'une bonne vue ont naturellement les yeux disposés de telle manière que sans effort ils aperçoivent distinctement les objets éloignés, c'est-à-dire que leurs yeux rassemblent en un point unique de la rétine un faisceau de rayons incidents parallèles, il s'ensuit que pour eux il faut placer les lentilles de telle manière que les rayons émanant de chaque point de l'objet redeviennent parallèles après avoir traversé les deux lentilles. Par conséquent, si AB représente une lentille convexe [Fig. 1 et 2], ayant pour axe la droite BE et que les rayons émanant d'un point de l'objet sont réfractés par cette lentille de telle façon qu'ils vont se réunir au point E, foyer de la lentille A, lorsque l'objet est à grande distance, et en un autre point qu'on trouve d'après la proposition XX du premier livre⁵⁾ lorsqu'il est à petite distance, et si GE est la distance focale de la seconde lentille DD supposée convexe [Fig. 1]

1) Huygens annota en marge ‘Omittetur, et docebitur hoc obiter in Explicatione peculiari telescopiorum’. Il s'agit bien des Prop. I et III de la troisième Partie de la Dioptrique; toutefois on ne trouvera que dans la première de ces propositions quelques lignes qui se rapportent à l'accommodation d'une lunette à la vue des myopes.

5) Voir la p. 99 du Tome présent.

[p. 245]

Dioptrica.
[Pars prima. Tractatus de Refractione et Telescopiis.]
[1653.]
[Liber III. De telescopiis.]
[Propositio I.]¹⁾

Perspicillum ex datis duabus lentibus compositum cuilibet visui accommodare.

A²⁾ punctis singulis rei visae ad totam oculi pupillam radios manare constat³⁾: qui quidem pro parallelis habentur cum procedunt a procul remotis. Itaque cum recta oculi constitutione gaudentibus ita sponte sua disponantur ut longinqua distincte cernant, hoc est, ut radios parallelos sibi incidentes colligant in unum retinae punctum; sequitur ijs ita lentes collocari debere, ut radij a punctis singulis rei visae venientes⁴⁾, postquam utramque lentem penetrarint denuo fiant paralleli. Quamobrem si lens convexa ponatur AB [Fig. 1 et 2], axem habens BE, et radij a rei visae puncto exeuntes ejus refractione cogantur ad punctum E, quod erit in foco lentis A, si visibile longinquum fuerit; si vero propinquum invenietur per propos. [XX. Lib. I]⁵⁾, fuerit autem lentis alterius DD foci

1) Huygens annota en marge ‘Omittetur, et docebitur hoc obiter in Explicatione peculiari telescopiorum’. Il s'agit bien des Prop. I et III de la troisième Partie de la Dioptrique; toutefois on ne trouvera que dans la première de ces propositions quelques lignes qui se rapportent à l'accommodation d'une lunette à la vue des myopes.

2) Dans la copie de Niquet et dans la leçon primitive ce mot était précédé par ‘Notum est’.

3) Aux lieux cités: ‘advehi’.

4) ‘manantes’, l.c.

5) Voir la p. 99 du Tome présent.

[p. 246]

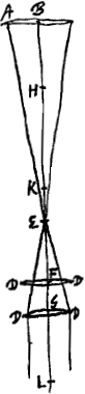
ou la distance du point de dispersion de cette lentille supposée concave [Fig. 2]; tout ceci étant posé, il faut porter la dite distance EG à partir du point E du côté de la lentille A et placer la lentille concave au point G, ou bien il faut porter la même distance dans le sens opposé à partir du point E et placer la lentille convexe en son extrémité G. En effet, de cette façon il arrivera dans l'un et l'autre cas que les rayons, après avoir traversé la lentille DD, atteignent l'oeil parallèlement, ainsi que cela résulte des prop. XVI et XVII du Livre Premier¹⁾, et ainsi une image distincte sera aperçue par celui dont la vue est bonne.

Mais lorsqu'il s'agit d'accommoder cette même lunette à un myope qui commence seulement à voir distinctement un objet lorsque celui-ci se trouve à la distance FH, il faut prendre FL²⁾ égale à GE, distance du foyer ou du point de dispersion à la lentille DD, car cette dernière distance est donnée. Il faut retrancher FL de FH lorsque la lentille DD est concave, et ajouter ces deux longueurs lorsqu'elle est convexe. Cherchons, de plus, une longueur qui soit à LF, comme LF est à HL. Je dis que cette longueur est égale à l'intervalle GF qui représente dans l'un et l'autre cas la grandeur dont il faut diminuer, pour qu'elle convienne au myope, la longueur de la lunette qui était auparavant GB³⁾.

En effet, plaçons la lentille DD en F et prenons FK égale à FL. Comme HL::LF = LF:FG ou = FK:KE, on aura aussi HF:FL (ou FK) = FE:EK. Et, par permutation, HF:FE = FK:KE; donc aussi HE:EF = FE:EK. Comme le point E est celui où se dirigent ou dont proviennent les rayons qui rencontrent la lentille DD et le point K celui auquel correspondent les rayons réfractés provenant des rayons parallèles venant du côté opposé, il s'ensuit que les rayons qui se dirigent vers le point E ou qui en émanent sont réfractés de telle manière par la lentille DD qu'après cette réfraction ils semblent provenir du point H⁴⁾. Par conséquent, la lunette sera dans l'état propre à donner des images distinctes pour l'oeil du myope.

1) Voir les pp. 85 et 89.

2) Plus tard Huygens ajouta en marge: ‘non definivisti punctum F.’ En effet, pour exécuter la construction indiquée on doit faire une figure à part.

3) Soit donc d la distance de la vue distincte, f la distance focale de l'oculaire; on trouve alors dans le cas de l'oculaire convexe et dans celui de l'oculaire concave .

4) D'après la Prop. XX du Livre Premier, p. 99 du Tome présent.

Proposition II⁵⁾.

Indiquer la construction d'un télescope servant à observer les éclipses ou les taches du Soleil et faire voir quelle sera la grandeur de son image.

5) Plus tard Huygens annota en marge ‘hoc ubi de usu telesc.’ Dans le manuscrit la Proposition présente précédait celles du Livre Deuxième, qui débute à la p. 173 du Tome présent.

[p. 247]

[Fig. 1.]

[Fig. 2.]

distantia GE, si convexa sit [Fig. 1]; si vero cava [Fig. 2], distantia puncti dispersus. His inquam positis, accipienda est dicta distantia EG à puncto E versus lentem A ponendaque lens cava in puncto G; vel eadem distantia accipienda versus alteram partem a puncto E, atque in termino G ponenda lens convexa. Sic enim utroque casu fiet ut penetrata lente DD radij paralleli ad oculum perveniant, ut constat ex prop. [XVI et XVII. Lib. I]¹⁾ atque ita distincta continget visio ei qui bona est oculi formatione.

Si vero myopi aptandum sit idem perspicillum qui visibile ad distantiam FH demum distinctè cernere possit, sumatur FL²⁾ aequalis distantiae GE, qua focus suus aut punctum dispersus abest a lente DD, haec enim data est; Et auferatur quidem FL ab FH si lens DD cava sit, addatur vero si convexa. Et ut HL ad LF ita sit LF ad aliam. dico huic aequale sumendum esse intervallum GF secundum quod minuenda est utroque casu longitudo perspicilli, quae prius erat GB, ut myopi conveniat³⁾.

Posita enim lente DD in F et sumtâ FK aequali FL. quia HL ad LF ut LF ad FG, sive ut FK ad KE; erit et HF ad FL sive FK ut FE ad EK:Et permutando HF ad FE ut FK ad KE, quare et HE ad EF ut FE ad EK. Cum itaque punctum E sit ad quod vel a quo tendentes radij occurrunt lenti DD; punctum vero K sit illud, quo pertinent refractiones parallelorum a parte opposita venientium; sequitur radios ad E vel ab E venientes ita flecti a lente DD, ut inde ferantur tanquam egressi a puncto H⁴⁾. Unde recte se habebit perspicillum ad distinctam visionem myopi praestandam.

1) Voir les pp. 85 et 89.

2) Plus tard Huygens ajouta en marge: ‘non definivisti punctum F.’ En effet, pour exécuter la construction indiquée on doit faire une figure à part.

3) Soit donc d la distance de la vue distincte, f la distance focale de l'oculaire; on trouve alors dans le cas de l'oculaire convexe et dans celui de l'oculaire concave .

4) D'après la Prop. XX du Livre Premier, p. 99 du Tome présent.

[Propositio II.]⁵⁾

Constitutionem telescopij ad observandas Solis Eclipses maculasve demonstrare et quanta futura sit ejus imago.

5) Plus tard Huygens annota en marge ‘hoc ubi de usu telesc.’ Dans le manuscrit la Proposition présente précédait celles du Livre Deuxième, qui débute à la p. 173 du Tome présent.

[p. 248]

[Fig. 5.]

[Fig. 6.]

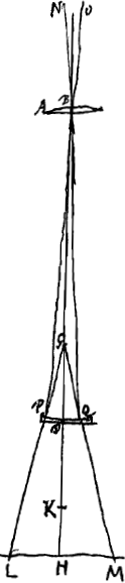
On a trouvé que pour observer les éclipses du soleil et les taches qui circulent à sa surface, il est utile de se servir du télescope, pourvu qu'on fasse tomber l'image du soleil, obtenue par le passage de ses rayons à travers les deux lentilles, sur une table blanche qui ne reçoit d'ailleurs aucune lumière. Pour comprendre cette invention, il faut d'abord connaître la disposition des lentilles: c'est-à-dire savoir comment elles doivent être placées pour donner l'image la plus brillante du soleil.

Soit donc AB la lentille convexe opposée au soleil et E son foyer [Fig. 3 et 5]. Supposons la seconde lentille, concave ou convexe, située en D. L'une et l'autre forme de télescope peut servir ici; mais la meilleure est celle qui est composée de deux lentilles convexes, parce qu'elle donne des images droites, tandis que l'autre les renverse. Soit K le point de concours ou de dispersion de la lentille D pour des rayons parallèles venant du côté H, et supposons placée en H une table blanche servant à recevoir l'image du soleil. Pour que cette image paraisse distincte et que son contour soit net, il est nécessaire que les rayons, provenant d'un point du soleil et qui tombent donc parallèlement sur la lentille AB, se réunissent de nouveau en un seul point de la table. Il faut donc que la distance des lentilles AB et D soit un peu plus grande que dans la condition moyenne du télescope, c'est-à-dire dans celle qui convient à une personne ayant la vue bonne: la position de la lentille D doit être telle que les grandeurs EK, ED et EH forment une proportion continue. En effet, de cette façon il arrivera que les rayons qui se dirigeaient vers E, foyer de la lentille AB, sont réfractés de telle manière qu'ils se dirigent vers le point H après cette réfraction²⁾. Mais dans la condition moyenne du télescope le point K doit coïncider avec le point E, comme nous l'avons démontré plus haut³⁾. Il en résulte qu'ici la distance des lentilles doit être augmentée de l'intervalle EK, lequel doit nécessairement être d'autant plus petit que la distance EH est plus grande; car la longueur DK qui est donnée, vu que c'est la distance focale ou la distance du point de dispersion de la lentille D, doit être divisée par le point E de manière qu'on ait HE:ED = ED:EK.

2) Voir la Prop. XX, Lib. I, p. 99 du Tome présent.

3) Voir les pp. 245 et 247 du Tome présent.

[p. 249]

[Fig. 3.]

[Fig. 4.]

Observandis solis eclipsibus nec non maculis quae in superficie ejus circumferuntur telescopium utiliter adhiberi inventum est, si nimirum solis imago per utramque lentem trajecta tabulâ alba excipiatur, in quam nullum aliunde lumen adveniat. Cujus inventi ratio ut intelligatur primum dispositio lentium cognoscenda est, quomodo nempe aptatae picturam solis quam nitidissimam efficiant.

Sit igitur lens convexa AB soli obversa [Fig. 3 et 5], cujus focus E punctum. Altera vero in D concava vel convexa, nam utraque telescopij forma huic rei idonea est, et magis quidem quae duorum est convexorum, quoniam picturas erectas exhibet, cum altera invertat. Lentis autem D sit K punctum concursus vel dispersus radiorum parallelorum à parte qua est¹⁾ H venientium. sitque in H constituta tabula alba ad excipiendam solis imaginem. Quae igitur ut distincta ac terminata appareat, oportet radios qui ab uno solis puncto procedunt, hoc est, qui paralleli inter se deferuntur in lentem AB, in uno rursus tabulae puncto colligi. Quapropter paulo major debet esse distantia lentium AB et D quam in constitutione telescopij media, sive quae bene videnti fuerit accommodata; ac talis requiritur positio lentis D, ut in continua sint proportione EK, ED, EH. Sic enim fiet ut radij tendentes ad E, focum lentis AB, deducantur ad punctum H²⁾. at in telescopij constitutione media congruere debet punctum K foco E, ut superius est ostensum³⁾. adeo ut hic distantia lentium augenda sit intervallo EK, quod quidem tanto minus esse necesse est quanto distantia EH fuerit major; nam longitudo DK quae data est, quippe distantia foci vel puncti dispersus lentis D, ea sic dividitur in E ut sicut HE ad ED ita sit haec ad EK.

1) Les mots en italiques manquent dans la leçon primitive et dans la copie de Niquet.

2) Voir la Prop. XX, Lib. I, p. 99 du Tome présent.

3) Voir les pp. 245 et 247 du Tome présent.

[p. 250]

[Fig. 5.]

[Fig. 6.]

Nous apprendrons à connaître le diamètre de l'image du soleil sur la table H de la manière suivante. Tirons les droites BP et BQ [Fig. 4 et 6] du centre de la lentille AB à la lentille D, l'angle de ces deux droites étant égal à celui sous lequel on voit en regardant sans télescope le diamètre du soleil. Soit BG une troisième proportionnelle à BK et à BD. Tirons les droites GP et GQ et prolongeons-les jusqu' à ce qu'elles rencontrent la table placée en H aux points L et M. Je dis que LM sera le diamètre du soleil sur la table LHM. En effet, prolongeons PB et QB du côté de O et de N. Comme les rayons issus d'un point situé à droite du disque solaire tombent sur toute la surface de la lentille AB et que tous ces rayons sont estimés parallèles entre eux et à la droite OB, l'un d'eux se mouvra suivant la droite OB, et ce même rayon, après avoir traversé la lentille AB, suivra ensuite la route BP^*, parce que B est le centre de la lentille, dont nous négligeons l'épaisseur. De la même manière un des rayons parallèles issus du bord gauche du soleil se mouvra suivant la droite NBQ. Plus tard les deux rayons nommés seront réfractés par la lentille D de manière à se mouvoir suivant les droites PL et QM, prolongements de GP et de GQ, d'après la proposition XX²⁾ ou...³⁾ du Premier Livre. En effet, BK, BD et BG forment une proportion continue. Il est donc évident que l'image d'un point situé à droite sur le contour du soleil tombe en L, et celui d'un point situé à gauche en M. Car en tant qu'il se forme une image distincte du soleil entier, il est nécessaire que là où un des rayons issus d'un point quelconque du soleil est arrêté par la table, les autres rayons partis du même point s'y réunissent également. Par conséquent le diamètre de l'image sera LM, comme nous l'avons dit.

Or il faut savoir que plus l'image LM du soleil sera grande, lorsque les lentilles AB et D restent les mêmes, moins elle sera lumineuse. Si tous les rayons partis du soleil et parvenant à la lentille AB occupent de nouveau sur la table LHM un espace aussi large que la lentille AB, c'est-à-dire s'ils forment une image du soleil égale à la partie découverte de cette lentille, cette image sera aussi lumineuse que si le soleil éclairait la table, aucune lentille n'étant interposée;

* vid. Propos. [XXIII. Lib. I]¹⁾

1) Voir la p. 119 du Tome Présent

2) Voir la p. 99 du Tome présent.

3) Nous ne savons pas quelle autre proposition Huygens aurait pu citer encore.

[p. 251]

[Fig. 3.]

[Fig. 4.]

Quanta porro futura sit diameter picturae solis in tabula H sic definiemus: ducantur ex centro lentis AB [Fig. 4 et 6] ad lentem D rectae BP, BQ comprehendentes angulum aequalem ei quo solis diameter comprehenditur absque telescopio spectantibus; Et sit duabus BK, BD tertia proportionalis BG, et jungantur GP, GQ, et producantur usque dum tabulae ad H collocatae occurrant in punctis L, M. Dico LM fore diametrum solis in tabula LHM. Producantur enim PB, QB versus O et N. Itaque cum a puncto circumferentiae solis dextro radij ferantur ad superficiem totam lentis AB, qui omnes inter se et rectae OB paralleli censentur, incedet unus istorum radiorum secundum lineam OB, idemque, penetrata lente AB, perget secundum lineam BP^*, quoniam B centrum est lentis cujus crassitudinem pro nulla ducimus. Eadem ratione unus radiorum parallelorum è sinistro solis margine venientium incedet secundum rectam NBQ. Porro autem uterque a lente D inflectetur ut pergant secundum rectas PL, QM, in quas productae sunt GP, GQ per [prop. XX]²⁾ vel...³⁾ hujus [Libri]⁴⁾ quia scilicet in continua proportione sunt BK, BD, BG. Itaque manifestum est punctum in dextro solis latere pingi in L, punctum vero oppositum in sinistro in M. Quatenus enim distincta totius solis pictura existit, necesse est ubi unus radiorum a quolibet ejus puncto venientium in tabula sistitur, ibi quoque caeteros colligi ab eodem puncto egressos. Ergo diameter picturae uti diximus erit LM.

Sciendum vero, quo major erit imago solis LM, lentibus AB et D ijsdem manentibus, eo minus lucidam fore. Etenim si radij omnes a sole in lentem AB descendentes, occupent rursus in tabula LHM spatium aeque latum atque est lens AB, hoc est, si solem depingant lenti AB quatenus adaperta est aequalem, erit haec imago aeque clara ac si nullis interpositis lentibus sol tabulam illustraret; non

* vid. Propos. [XXIII, Lib. I]¹⁾

1) Voir la p. 119 du Tome présent.

2) Voir la p. 99 du Tome présent.

3) Nous ne savons pas quelle autre proposition Huygens aurait pu citer encore.

4) C'est-à-dire du Livre I, auquel la Proposition appartenait primitivement; voir la note 5 de de la p. 247.

[p. 252]

bien entendu, si nous ne tenons pas compte des rayons réfléchis par les lentilles ou absorbés par elles à cause du manque de transparence de la matière dont elles sont formées, la réflexion et l'absorption pouvant parfois faire perdre la moitié de tous les rayons ou davantage. Mais si l'image est plus grande, comme cela est nécessaire dans les observations de ce genre, elle sera aussi d'autant plus obscure. L'expérience fera voir quelle est l'amplitude la plus propre aux observations: pour la trouver, il faut essayer toutes sortes de distances de la table au télescope. Il faut observer à ce sujet que, lorsque cette distance augmente, on doit diminuer un peu en même temps celle qui sépare les lentilles AB et D pour obtenir une image nette: la raison en est facile à découvrir d'après ce qui précède.

Proposition III¹⁾.

Faire voir que les télescopes précédents peuvent être rendus meilleurs lorsqu'on remplace les deux lentilles convexes par trois lentilles; ce qui est vrai aussi pour ceux dont nous nous servons la nuit pour observer les étoiles.

Quoique les lentilles ne doivent pas être multipliées sans necessité, parce que beaucoup de lumière est perdue à cause de l'épaisseur du verre et par les réflexions répétées, l'expérience a cependant montré qu'ici il y a avantage à le faire. Car si nous ajoutons à la grande lentille deux oculaires ayant entre eux un certain rapport et une distance déterminée, non seulement le champ du télescope est admirablement élargi, de sorte qu'on embrasse d'un seul regard beaucoup plus que lorsque l'instrument est construit avec une seule lentille oculaire, mais aussi les images paraissent moins déformées. Enfin toute impureté due aux irrégularités des oculaires est soustraite au regard d'une façon si complète que, quoiqu' il y ait deux lentilles, on ne l'aperçoit aucunement tandis que dans le cas d'une seule lentille elle nuit beaucoup à la netteté des images²⁾. Nous décrivons ici sinon la meilleure combinaison des lentilles parmi toutes celles qui sont possibles, ce qui serait d'ailleurs difficile et peut-être impossible, du moins celle que l'expérience nous a montré être utile.

Supposons donc que AB [Fig. 7] soit la grande lentille ou l'objectif, et LG sa distance focale qui peut être de deux ou de trois pieds seulement, ou bien de 6, de 10 ou de 20 pieds, car nous pouvons employer les mêmes oculaires en combinaison avec chacun de ces objectifs. Soient EF et CD les oculaires, et supposons la distance focale KT du dernier quatre fois plus grande, ou un peu

1) La Proposition présente, où Huygens décrit l'oculaire qui porte son nom, fut presqu' entièrement refondue à une époque inconnue, mais après 1666 et probablement beaucoup plus récente. Pour cette raison, nous croyons utile de donner ici, par exception, le texte tel qu'il était en 1666, lorsque la copie de Niquet fut prise; sauf à faire connaître dans les notes quelques variantes d'après une leçon encore plus primitive, qu'on retrouve, biffée, dans le manuscrit écrit par Huygens lui-même. Quant à la leçon définitive on la trouvera plus loin dans la Prop. IV de la troisième Partie de cette ‘Dioptrique’.
Ajoutons, qu'il y a lieu de supposer que même la première leçon doit dater de 1662 ou de plus tard, puisqu'en juin 1662 (voir la p. 152 du T. IV) Huygens parle de l'emploi de deux oculaires au lieu d'un seul, pour augmenter le champ de vision, comme d'une ‘maniere nouvelle’. En effet, dans la lunette de 23 pieds, dont il se servit en 1656 dans les observations de Saturne, les deux lentilles oculaires étaient contigues; comme cela résulte indubitablement de ce qu'on lit aux pp. 358 et 362 du T. II et à la p. 58 du T. III.

2) La leçon primitive fait suivre encore: ‘sunt enim in ipsa vitri materia semper bullae quaedam minutissimae quibus transitus radiorum impeditur, quae veluti puncta nigra rebus ipsis quas telescopio aspicimus in [haere]re videntur. Hac autem quam describimus lentium compositione omnia evanescunt’.

[p. 253]

habita videlicet ratione eorum quos lentes reflectunt vel propter obscuritatem materiae non transmittunt, quo fortè dimidia pars omnium vel amplius intervertitur. Quod si vero major imago fuerit, ut in hujusmodi observationibus exigitur, jam tanto quoque erit obscurior. Experientia vero ostendet quaenam amplitudo ad observationem utilissimè adhibeatur, tentata alia atque alia tabulae a telescopio distantia. Ubi illud observandum ut aucta hac distantia simul tantillum minuatur ea quae est inter lentes AB et D, ut distincta pictura efficiatur: cujus ratio ex ante dictis intelligitur.

Propos [itio III]¹⁾.

Quomodo pro duobus convexis tria adhibendo meliora fiant praecedentia telescopia ostendere, ut et illa quibus noctu ad sidera spectanda utimur.

Quanquam lentes non frustra sint mutiplicandae, quod et vitri crassitudine et iteratis reflexionibus non parum lucis depereat; hic tamen utiliter id fieri experientia docuit. Adsumtis enim praeter magnam lentem ocularibus duobus certam inter se rationem distantiamque habentibus, cum mirum in modum dilatatur telescopij conspectus ut plura longe unico intuitu comprehendat quam si simplici lente oculari instruatur; tum distortae minus rerum species apparent; ac denique naevi impuritas omnis lentium ocularium ita visui subducatur, ut licet binae sint nulla prorsus animadvertatur cum alioqui ex una lente non parum adferat incommodi²⁾. Dabimus autem in his, etsi non omnium optimam lentium compositionem, quam investigare longum esset ac forsan impossibile, at ejusmodi quam nobis experientia utilem esse ostendit.

Esto igitur [Fig. 7] lens magna sive exterior AB, quae foci distantiam habeat LG, sive ea sit duorum aut trium pedum tantum, aut etiam 6 vel 10 vel 20, possumus enim ad omnes has ijsdem ocularibus uti, hae vero sint EF, CD, quarum posterioris foci distantia KT quadrupla sit, vel paulo minus,

1) La Proposition présente, où Huygens décrit l'oculaire qui porte son nom, fut presqu' entièrement refondue à une époque inconnue, mais après 1666 et probablement beaucoup plus récente. Pour cette raison, nous croyons utile de donner ici, par exception, le texte tel qu'il était en 1666, lorsque la copie de Niquet fut prise; sauf à faire connaître dans les notes quelques variantes d'après une leçon encore plus primitive, qu'on retrouve, biffée, dans le manuscrit écrit par Huygens lui-même. Quant à la leçon définitive on la trouvera plus loin dans la Prop. IV de la troisième Partie de cette ‘Dioptrique’.
Ajoutons, qu'il y a lieu de supposer que même la première leçon doit dater de 1662 ou de plus tard, puisqu'en juin 1662 (voir la p. 152 du T. IV) Huygens parle de l'emploi de deux oculaires au lieu d'un seul, pour augmenter le champ de vision, comme d'une ‘maniere nouvelle’. En effet, dans la lunette de 23 pieds, dont il se servit en 1656 dans les observations de Saturne, les deux lentilles oculaires étaient contigues; comme cela résulte indubitablement de ce qu'on lit aux pp. 358 et 362 du T. II et à la p. 58 du T. III.

2) La leçon primitive fait suivre encore: ‘sunt enim in ipsa vitri materia semper bullae quaedam minutissimae quibus transitus radiorum impeditur, quae veluti puncta nigra rebus ipsis quas telescopio aspicimus in [haere]re videntur. Hac autem quam describimus lentium compositione omnia evanescunt’.

[p. 254]

[Fig. 8.]

moins, que la distance focale SH de la lentille EF¹⁾, laquelle ne dépasse pas deux pouces. La largeur CD soit de 3½ pouces et la largeur EF la moitié²⁾. Supposons la distance SK des deux lentilles égale au double environ de la distance SH. Elles doivent être combinées avec la lentille extérieure AB de telle manière que le foyer G de cette dernière tombe entre la lentille EF et son foyer H, et que GT, GK et GH forment une proportion. En effet, on obtiendra ainsi que les rayons issus d'un point lointain, tel que Q, qui, après avoir traversé la lentille AB, viendraient se diriger vers son foyer G, se réunissent maintenant en H³⁾, s'y croisent et arrivent à l'oeil M parallèlement après avoir passé par la lentille EF et y avoir été réfractés. La meilleure place qu'on puisse donner à l'oeil est une place telle que les longueurs VH, VS et VM forment une proportion, où V représente le point dans lequel la lentille CD réunit les rayons issus du centre L de la lentille AB⁵⁾. Par cet artifice l'oculaire EF sera vu rempli d'images, quelle que petite que soit l'ouverture de la lentille AB; attendu que tous les rayons qui passent par L se réunissent au point M après avoir traversé les lentilles CD et EF. Et le rapport dans lequel seront agrandis les objets lointains sera égal au produit des rapports LG:GK et KH:HS, ce qui se démontre de la façon suivante. Supposons que les rayons QA et QB, allant du point lointain Q à l'extremité de la lentille AB, soient séparés par la distance XY, lorsqu'ils sont arrivés, après les réfractions par les trois lentilles, près de l'endroit M où est situé l'oeil. Par conséquent, si nous faisons changer de place l'oeil et l'objet, transportant l'oeil en Q et l'objet en M, nous verrons la ligne XY occuper toute la largeur de la lentille AB. Elle paraîtra

1) La leçon primitive donnait au lieu du passage qui précède: ‘Sit igitur lens magna sive exterior AB, oculares CD et EF, quarum CD habeat foci distantiam KT quadruplam circiter vel quintuplam foci distantiae HS, quae est lentis EF. Ut enim exacte quadrupla sit nihil refert, sed hanc proportionem experientia utile esse demonstravit. Distantia lentium KS sit dupla HS.’ Ajoutons qu'il y a encore une leçon intermédiaire qui débutait comme dans le texte mais qui, après les mots ‘hae vero sint EF, CD’, faisait suivre: ‘quarum posterioris foci distantiae lentis KT tripla sit, vel paulo amplius’.

2) Les phrases précédentes à commencer par ‘Et haec quidem’ furent intercalées à une époque inconnue avant 1666. Ajoutons qu'on trouve en marge du texte une figure que nous reproduisons, à côté de la fig. 7, comme fig. 8. Comme on le voit, les dimensions des diverses parties y diffèrent notablement de celles de la fig. 7, à laquelle se rapporte évidemment la description donnée dans le texte. Puisque cette figure 7 fut attachée par Huygens avec de la cire à la feuille en question du manuscrit, couvrant la fig. 8, il est clair que celle-ci est la plus primitive et qu'elle fut même dessinée avant que le texte fut écrit.

3) Comparez la Prop. XX, p. 99 du Tome présent. H et G sont des points correspondants par rapport à la lentille CD.

5) De cette manière l'oeil est placé au point qui correspond à V par rapport à la lentille EF; c'est-à-dire au point qui correspond au centre L de l'objectif après les deux réfractions par les lentilles oculaires CD et EF. Consultez encore la note 1, p. 196 du Tome présent et le texte auquel elle se rapporte.

[p. 255]

[Fig. 7.]

foci distantiae lentis EF quae sit SH¹⁾. Et haec quidem duos pollices non excedat. latitudo CD sit 3½ poll. EF duplo minor²⁾. Intervallum SK inter utramque lentem sit circiter duplum SH. Ita vero cum lente exteriori AB componantur ut hujus focus G cadat inter lentem EF et focum ejus H, atque sint proportionales GT, GK, GH. Sic enim fiet ut radij a puncto longinquo, puto Q, advenientes, qui trajecta lente AB tenderent ad focum ejus G, nunc concurrant ad H³⁾, atque ibi facta intersectione pergentes ad lentem EF, ejus refractione paralleli ferantur ad oculum M. Hic autem ita optime collocatur⁴⁾, ut si punctum V sit illud quo lens CD cogit radios ab L puncto medio lentis AB venientes, fiant proportionales VH, VS, VM⁵⁾. quandoquidem⁶⁾ hoc pacto, quantulocunque⁷⁾ foramine pateat lens AB, tamen ocularis EF tota imaginibus plena spectabitur, quoniam radij omnes per L transeuntes colliguntur ad punctum M, postquam lentes CD, EF penetrarint. Proportio autem incrementi rerum procul dissitarum erit ea quae componitur ex rationibus LG ad GK et KH ad HS. quod sic ostenditur. Putemus radios QA, QB a puncto remoto Q ad extremam utrimque lentem AB manantes, post trium lentium refractiones, comprehendere latitudinem XY quo loco ponitur oculus M. Quod si itaque facta permutatione transferatur oculus in Q et res visa in M, videbitur

1) La leçon primitive donnait au lieu du passage qui précède: ‘Sit igitur lens magna sive exterior AB, oculares CD et EF, quarum CD habeat foci distantiam KT quadruplam circiter vel quintuplam foci distantiae HS, quae est lentis EF. Ut enim exacte quadrupla sit nihil refert, sed hanc proportionem experientia utile esse demonstravit. Distantia lentium KS sit dupla HS.’ Ajoutons qu'il y a encore une leçon intermédiaire qui débutait comme dans le texte mais qui, après les mots ‘hae vero sint EF, CD’, faisait suivre: ‘quarum posterioris foci distantiae lentis KT tripla sit, vel paulo amplius’.

2) Les phrases précédentes à commencer par ‘Et haec quidem’ furent intercalées à une époque inconnue avant 1666. Ajoutons qu'on trouve en marge du texte une figure que nous reproduisons, à côté de la fig. 7, comme fig. 8. Comme on le voit, les dimensions des diverses parties y diffèrent notablement de celles de la fig. 7, à laquelle se rapporte évidemment la description donnée dans le texte. Puisque cette figure 7 fut attachée par Huygens avec de la cire à la feuille en question du manuscrit, couvrant la fig. 8, il est clair que celle-ci est la plus primitive et qu'elle fut même dessinée avant que le texte fut écrit.

3) Comparez la Prop. XX, p. 99 du Tome présent. H et G sont des points correspondants par rapport à la lentille CD.

4) Dans la leçon primitive on trouve ‘constituendus’.

5) De cette manière l'oeil est placé au point qui correspond à V par rapport à la lentille EF; c'est-à-dire au point qui correspond au centre L de l'objectif après les deux réfractions par les lentilles oculaires CD et EF. Consultez encore la note 1, p. 196 du Tome présent et le texte auquel elle se rapporte.

6) ‘quoniam’, d'après la leçon primitive.

7) ‘licet exiguo tantum’, d'après la leçon primitive.

[p. 256]

donc agrandie dans le rapport AB:XY, puisque, en effet, le point Q est situé à grande distance tant par rapport à la lentille AB que par rapport à la ligne XY et que, par conséquent, les angles AQB et XQY ont entre eux le même rapport que les largeurs AB et XY¹⁾. Mais le rapport AB:XY ou AB:ZΔ est composé des rapports AB:ΛΦ et ΛΦ:ZΔ, dont le premier est égal à LG:GK et le second à KH::HS. Il apparaît ainsi que, lorsque l'oeil est placé en Q et l'objet en M, le rapport qui exprime l'agrandissement est composé des rapports LG:GK et KH:HS. C'est pourquoi lorsque l'oeil est placé en M et l'objet en Q, où se trouve PR, l'agrandissement sera indiqué par ce même rapport^*. C'est ce qu'il fallait démontrer.

Or, si nous supposons la distance focale KT exactement quatre fois plus grande que la distance focale SH, et l'intervalle KS égal au double de SH, le rapport qui exprime l'agrandissement sera simplement égal à LG:GK. Et l'intervalle HG devra être le tiers de HS ou de HK³⁾. Or la diftance entre l'oeil et la lentille EF dépend dans une certaine mesure de la grandeur de la distance focale LG de l'objectif. Mais elle sera toujours plus petite que SH, attendu que VH, VS et VM forment une proportion, comme nous l'avons dit plus haut. Il résulte de cette petitesse de la distance de l'oeil à la lentille que les taches ou bulles d'air très petites dont la matière du verre n'est jamais exempte ne peuvent pas être aperçues dans la lentille EF. Mais on ne les voit pas non plus dans la lentille CD, attendu que l'oeil aperçoit confusément les objets placés là et distinctement ceux qui se trouvent auprès de H⁴⁾.

Nous avons tracé de plus dans la figure ci-jointe [Fig. 7], pour que la nature et l'effet de ce télescope puissent être mieux compris, les rayons qui proviennent de quelques autres points de l'objet non situés sur l'axe, tels que P et R. Car de même que les rayons issus du point Q, après avoir traversé les lentilles AB et CD, se réunissent au point H; de même aussi les rayons partis du point P sont assemblés en O, et ceux qui viennent de R, au point N. Mais ensuite, après avoir atteint la lentille EF, ils se dirigent tous parallèlement vers l'oeil M; c'est-à-dire ces rayons ne sont pas tous parallèles entre eux, mais ceux qui viennent du point O sont parallèles à la droite FM et ceux qui viennent de N parallèles à la droite EM, de même que ceux qui proviennent du point H deviennent parallèles à l'axe des lentilles. Il s'ensuit que l'oeil aperçoit clairement et séparément les points P, Q et R. Et si nous

1) De ce raisonnement il résulte que dans chaque lunette où un anneau oculaire existe, le grossissement sera égal au rapport du diamètre de l'objectif à celui de cet anneau, quel que soit l'arrangement des lentilles. C'est, comme on sait, le principe sur lequel Ramsden a fondé l'emploi de son dynamètre.

* Prop. VI, Liv. II²⁾.

2) Voir la p. 199 du Tome présent.

3) En effet, puisque H et G sont des points correspondants par rapport à la lentille CD dont KT est la distance focale, on doit avoir, d'après la Prop. XX, Liv. I, p. 99, HT′:HK = = HK:HG, où T′ représente l'autre foyer de la lentille CD et HT′ = KT-HK = 3 HK; donc HK:HG = 3:1.

4) À une autre occasion, vers 1661, à la p. 23 du Manuscrit B, Huygens a formulé la condition de l'invisibilité des défauts des lentilles comme il suit: ‘efficiendum ne ullius coni radiorum vertex in vitrum aliquod incedat ut hic,’ (il s'agit du dessein d'un système de lentilles où l'un des sommets des cônes, formés par les rayons qui entrent dans l'objectif parallèles à l'axe, tombe dans l'intérieur d'une lentille) ‘quia omnes naevi ejus vitri apparebunt’.

[p. 257]

[Fig. 7.]

linea XY occupare latitudinem omnem lentis AB: ideoque aucta apparebit secundum rationem ipsius AB ad XY; quia videlicet punctum Q in longinqua distantia est tam respectu lentis AB quam lineae XY, ac proinde anguli AQB, XQY eandem inter se rationem servant quam latitudines AB, XY¹⁾. Ratio autem AB ad XY sive ad ZΔ, componitur ex rationibus AB ad ΛΦ et ΛΦ ad ZΔ; quarum AB ad ΛΦ eadem quae LG ad GK et ΛΦ ad ZΔ eadem quae KH ad HS. Itaque apparet, posito oculo in Q, visibili vero in M, rationem incrementi esse eam quae ex rationibus LG ad GK et KH ad HS componitur. Quamobrem et oculo ad M collocato visibili vero ad Q, uti est PR, eadem quoque erit incrementi ratio^*. Quod erat ostendendum.

Quod si ponatur foci distantia KT exactè quadrupla foci distantiae SH, et intervallum KS duplum SH; erit ratio incrementi simpliciter ea quae LG ad GK, ac debebit intervallum HG esse pars tertia HS vel HK³⁾. Distantia autem inter oculum ac lentem EF pendet aliquatenus ab amplitudine foci distantiae lentis exterioris, LG. Sed minor semper erit quam SH, quoniam proportionales sunt VH, VS, VM ut antea diximus. Atque ex hac oculi propinquitate fit primum ut naevi, seu bullulae minutissimae, quibus vitri materia nunquam caret, in lente EF percipi non possint. Sed neque in lente CD; quoniam oculus confuse cernit quae hic objiciuntur, distincte vero quae ad H⁴⁾.

Caeterum expressimus in schemate hoc, quo penitius perspici queat telescopij hujus natura atque effectus, etiam radios illos qui ab alijs punctis rei visae, praeter id quod in axe lentium positum est, procedunt: uti à P et R. Nam sicut qui a puncto Q exeunt, penetratis lentibus AB et CD, conveniunt ad punctum H; ita, qui à P, colliguntur ad O, et, qui ab R, ad N. Deinde vero ad lentem EF delati omnes paralleli ad oculum M pergunt; non quidem paralleli inter se omnes, sed qui ab O, paralleli rectae FM; qui ab N, rectae EM, quemadmodum qui ab H lentium axi paralleli efficiuntur. Atque ita singula puncta P, Q, R distincta

1) De ce raisonnement il résulte que dans chaque lunette où un anneau oculaire existe, le grossissement sera égal au rapport du diamètre de l'objectif à celui de cet anneau, quel que soit l'arrangement des lentilles. C'est, comme on sait, le principe sur lequel Ramsden a fondé l'emploi de son dynamètre.

* [Prop. VI, Lib. II.]²⁾

2) Voir la p. 199 du Tome présent.

3) En effet, puisque H et G sont des points correspondants par rapport à la lentille CD dont KT est la distance focale, on doit avoir, d'après la Prop. XX, Liv. I, p. 99, HT′:HK = = HK:HG, où T′ représente l'autre foyer de la lentille CD et HT′ = KT-HK = 3 HK; donc HK:HG = 3:1.

4) À une autre occasion, vers 1661, à la p. 23 du Manuscrit B, Huygens a formulé la condition de l'invisibilité des défauts des lentilles comme il suit: ‘efficiendum ne ullius coni radiorum vertex in vitrum aliquod incedat ut hic,’ (il s'agit du dessein d'un système de lentilles où l'un des sommets des cônes, formés par les rayons qui entrent dans l'objectif parallèles à l'axe, tombe dans l'intérieur d'une lentille) ‘quia omnes naevi ejus vitri apparebunt’.

[p. 258]

[Fig. 9.]

approchons de la lentille EF le miroir dont nous parlerons plus loin¹⁾, de telle manière que ce miroir touche à-peu-près la lentille EF, l'oeil verra les objets debout. Ce redressement est indispensable dans l'emploi pendant le jour; mais lorsqu'on veut contempler les étoiles pendant la nuit il vaut mieux omettre le miroir.

1) Voir la Prop. V, p. 265 du Tome présent.

Proposition IV²⁾.

Voir distinctement et debout les objets lointains à l'aide de trois lentilles convexes, le grossissement étant donné.

Prenons une grande lentille AB, dont AC est la distance focale; et ensuite deux plus petites DT et QR, dont les distances focales EL et HF sont égales entre elles et telles que AC est à l'une d'elles dans un rapport égal à celui qui exprime l'agrandissement. Plaçons ces deux lentilles de telle manière que la distance CE qui sépare l'une d'elles du foyer de la lentille A, soit égale à 2 EL, et l'intervalle EH qui les sépare l'une de l'autre à 3 EL. Ensuite plaçons l'oeil au point K, la distance HK étant prise égale au double³⁾ de la longueur nommée, EL ou FH. Je dis que cet arrangement satisfait au problème.

En effet, supposons l'objet situé à grande distance et soit S le point où l'axe commun des lentilles passe par cet objet. Les rayons, tels que SB et SY, qui viennent du point S à la lentille AB, doivent donc être estimés parallèles et se réuniront donc au foyer C où ils se croiseront. Or, L est le foyer de la lentille DE, CL est égale à la moitié de CE et EF à CE elle-même, attendu que EH est égale à trois fois FH ou LC. Les longueurs CL, CE et CF formeront donc une proportion continue. Il en résulte que les dits rayons réfractés par la lentille DT aux points M et Z se réuniront de nouveau au point F^* et qu' ensuite, rencontrant la lentille QR en I et en G, ils deviendront parallèles par la réfraction due à cette lentille, vu que F est le foyer de la lentille HG. Ils arrivent donc à la pupille de l'oeil, placée en K, selon les droites parallèles IP et GN, et de cette façon une vision distincte sera obtenue. Et nous avons placé l'oeil en ce point pour qu'il puisse embrasser d'un seul regard un plus grand nombre d'objets: il en sera ainsi parce que, si nous considérons des rayons tels que AT et AD allant du centre de la lentille AB aux bords de la lentille E, ces rayons se réuniront au-

2) Beaucoup plus tard Huygens ajouta en marge: ‘Sufficiet dicere hoc fieri posse’ [Comparez le dernier alinéa de la Prop. III de la troisième Partie de cette ‘Dioptrique’] ‘sed melius adhibitis 4 lentibus’ [Voir la Prop. V de cette troisième Partie] ‘quia majorem campum aperiunt. Varias conjugationes lentium quaesitas fuisse ante has. deinde invento diaphragmate nostro quaternas optimè junctas fuisse nescio à quo. an Campano?’

3) La copie de Niquet et la leçon primitive ajoutaient: ‘vel paulo amplius’. Comparez les notes 1 et 2 des p. 260 et 261.

* Prop. XX. Liv. I.⁴⁾

4) Voir la p. 99 du Tome présent.

[p. 259]

visione oculus percipit. ac admoto quidem speculo de quo inferius dicetur¹⁾ sed ita ut pene lentem EF contingat, erecta cernet visibilia. Quod interdiu plane necesse est; noctu vero ad sidera satius est omitti.

1) Voir la Prop. V, p. 265 du Tome présent.

[Propositio IV.]²⁾

Tribus convexis lentibus distincta et erecta spectare visibilia longinqua et majora secundum datam rationem.

Accipiatur lens major AB [Fig. 9], cujus foci distantia sit AC. Deinde vero aliae duae minores DT et QR, quarum foci distantiae EL, HF sint inter se aequales et ad quarum utramvis habeat AC rationem eam secundum quam facienda est multiplicatio. Collocentur autem hoc pacto ut distantia CE, qua altera earum abest à foco lentis A, sit dupla EL:Et EH intervallum inter utramque ejusdem EL triplum. Denique ad K punctum constituatur oculus, sumtâ HK distantia dictae EL vel FH dupla³⁾. Quibus sic comparatis propositum dico absolvi.

Sit enim visibile longinquum cui axis lentium communis occurrat in puncto S. Radij itaque ex puncto S ad lentem AB delati ut SB, SY habendi sunt pro parallelis, ideoque convenient in foco C, ibique erit eorum intersectio. Est autem L focus lentis DE, et CL subdupla CE, et EF aequalis EC, quoniam EH est tripla FH seu LC; ergo erunt in continuà proportione CL, CE, CF. Quare radij ijdem refracti in lente DT ad M et Z denuo convenient in puncto F^*, atque inde occurrentes lenti QR in I et G, refractione ejus efficientur paralleli, quia F est focus lentis HG. Paralleli itaque secundum rectas IP, GN perveniunt ad pupillam oculi quae est in K⁵⁾, eoque visio fiet distincta. Posuimus autem oculum hoc loco ut unico intuitu plura simul conspiceret: cujus ratio est, quod si à centro lentis AB intelligantur radij pervenire ad extremas margines lentis E, veluti AT, AD, hi cum axe convenient post lentem in puncto O, quod erit in foco lentis E,

2) Beaucoup plus tard Huygens ajouta en marge: ‘Sufficiet dicere hoc fieri posse’ [Comparez le dernier alinéa de la Prop. III de la troisième Partie de cette ‘Dioptrique’] ‘sed melius adhibitis 4 lentibus’ [Voir la Prop. V de cette troisième Partie] ‘quia majorem campum aperiunt. Varias conjugationes lentium quaesitas fuisse ante has. deinde invento diaphragmate nostro quaternas optimè junctas fuisse nescio à quo. an Campano?’

3) La copie de Niquet et la leçon primitive ajoutaient: ‘vel paulo amplius’. Comparez les notes 1 et 2 des p. 260 et 261.

* [Prop. XX, Lib. I.]⁴⁾

4) Voir la p. 99 du Tome présent.

5) ‘in K constituti’ (l.c.).

[p. 260]

[Fig. 9.]

-delà de la lentille au point O, foyer de la lentille E, vu qu'ils sont parallèles à l'axe¹⁾. Par conséquent OF sera égale à FH et HK au double de FH²⁾, comme nous avons dit qu'il faut la prendre, et le point K sera celui où se réuniront les rayons DO et TO après avoir traversé la lentille QR et la lentille H dont la largeur est égale au double de celle de la lentille E paraîtra toute entière illuminée d'images: elle nous fera voir tout ce qui est compris dans l'angle DAT ou VAX.

Ensuite on voit aisément, en considérant les changements de direction éprouvés par les rayons, que l'objet placé en S donne une image droite. En effet, si nous considérons l'oeil, placé en K, comme un seul point, les droites brisées qui représentent les rayons sont KQTAV et KRDAX. Il apparaît par là que le point V de l'objet est aperçu en Q, et le point X en R: chaque point est donc vu du côté de l'axe où il se trouve réellement.

Nous démontrerons enfin de la manière suivante que le grossissement doit être égal à AC:CL, ou LE, ou FH. Supposons⁶⁾ l'objet placé en K sur lequel nous notons les points N et P; et que l'oeil se trouve au point S. Comme le rayon issu du point N parviendra ainsi à l'oeil S suivant la droite BS et celui qui vient de P suivant la droite YS et que l'oeil est placé à grande distance, il s'ensuit que l'oeil apercevra l'objet PN grossi dans le rapport YB:PN, attendu que l'angle YSB sera à l'angle formé par les droites SP et SN comme YB est à PN. Or, on a YB::MZ = AC:CE et MZ:IG (ou PN) = EF (ou EC):FH. On aura donc, en combinant ces deux proportions, YB:PN == AC:FH, ou EL. Il en résulte que, l'oeil étant placé en S, l'objet PN paraîtra grossi dans le rapport AC:EL; c'est pourquoi aussi le grossissement de l'objet, lorsqu'il est placé à grande distance au point S, et que l'oeil est transféré en PN ou au point K, sera le même⁷⁾. Il est évident aussi que le grossissement ne change pas lorsque la distance de l'oeil à la lentille QR est augmentée ou diminuée, attendu que YB et PN conservent leurs valeurs. C'est ce qu'il fallait démontrer.

Ceci⁸⁾ peut être démontré autrement, sans qu'il soit nécessaire de se servir du théorème sur la transposition de l'oeil et de

1) Au lieu des mots en italiques on lit aux lieux cités: ‘tantillo plus abest a lente E quam sit ejus foci distantia; quia videlicet in continua erunt proportione AL, AE, AO.’ Remarquons, que la leçon du texte est embrouillée. En effet, si l'adjectif ‘parallelae’ se rapporte aux lignes AT et AD, il est évident que les lignes indiquées ne sont parallèles que par approximation. Ainsi, ici et dans le passage qui suit, l'ancienne leçon est préférable à la nouvelle, qui doit provenir de quelque inadvertance.

2) ‘paulo tantum minor erit quam FH; ideoque si fiat ut OF ad OH ita haec ad OK, siet HK paulo major quam dupla FH’ (l.c.).

6) Huygens ajouta en marge: ‘hoc aliter demonstrari potest, ut non opus sit theoremate de transpositione oculi et objecti.’ Comparez l'alinéa en italique qui va suivre.

7) Voir la Prop. VI du Liv. II, p. 199 du Tome présent.

8) L'alinéa qui suit manque dans la copie de Niquet et nous ne l'avons trouvé nulle part dans les manuscrits de Huygens. Il ne nous semble pas improbable qu'il ait été intercalé par de Volder et Fullenius lors de la préparation de l'édition de la ‘Dioptrique’ de 1703, d'où nous l'avons emprunté.

[p. 261]

quia axi parallelae sunt¹⁾. Itaque OF aequalis erit FH, et HK dupla ad FH²⁾, sicut sumendam diximus, punctumque K erit illud quo convenient radij DO, TO, postquam transierint lentem QR. ac³⁾ lens tota H duplam habens latitudinem lentis E, imaginibus lucida apparebit, omniaque spectanda praebebit⁴⁾ quae angulo DAT sive VAX comprehenduntur.

Porro erectum spectari visibile ad S positum facile apparet ex ipsis radiorum flexionibus; si enim oculus ad K puncti instar consideretur, flexiones istae sunt KQTAV, KRDAX, ex quibus manifestum fit punctum visibile V spectari in Q, et X in R, singula nimirum ad eandem quam obtinent axis partem.

Denique quod ratio incrementi continget ea quae est AC ad CL, vel LE vel FH⁵⁾, ostendetur hoc modo. Putemus⁶⁾ visibile collocari in K, inque eo notari puncta N et P: oculus autem intelligatur in puncto S. Quia itaque radius ab N puncto fluens perveniet ad oculum S per rectam BS, et qui à puncto P, per rectam YS; oculus autem in longinqua positus est distantia; sequitur ipsi visibile PN auctum videri secundum rationem YB ad PN, quia angulus YSB ad angulum quem facerent SP, SN, eandem rationem habebit quam YB ad PN. Quia autem YB ad MZ ut AC ad CE; MZ vero ad IG sive PN sicut EF, sive ipsa EC, ad FH. Erit igitur ex aequo YB ad PN ut AC ad FH sive EL. Itaque patet oculo in S constituto visibile PN auctum videri secundum rationem AC ad EL. ac proinde et visibile longinquum in S positum, oculo in PN sive ad K translato secundum eandem rationem auctum spectabitur⁷⁾. Quam etiam nihil mutari liquet etsi oculus a lente QR plus minusve removeatur, quod eaedem maneant YB et PN. Atque haec quidem erant demonstranda.

Hoc⁸⁾ aliter demonstrari potest, ut non opus sit theoremate de transpositione

1) Au lieu des mots en italiques on lit aux lieux cités: ‘tantillo plus abest a lente E quam sit ejus foci distantia; quia videlicet in continua erunt proportione AL, AE, AO.’ Remarquons, que la leçon du texte est embrouillée. En effet, si l'adjectif ‘parallelae’ se rapporte aux lignes AT et AD, il est évident que les lignes indiquées ne sont parallèles que par approximation. Ainsi, ici et dans le passage qui suit, l'ancienne leçon est préférable à la nouvelle, qui doit provenir de quelque inadvertance.

2) ‘paulo tantum minor erit quam FH; ideoque si fiat ut OF ad OH ita haec ad OK, fiet HK paulo major quam dupla FH’ (l.c.).

3) ‘Unde etiamsi exiguo tantum foramine pateret lens AB, nihilo minus’ (l.c.)

4) ‘praeberet’ (l.c.).

5) ‘sive ad HF’ (l.c.).

6) Huygens ajouta en marge: ‘hoc aliter demonstrari potest, ut non opus sit theoremate de transpositione oculi et objecti.’ Comparez l'alinéa en italique qui va suivre.

7) Voir la Prop. VI du Liv. II, p. 199 du Tome présent.

8) L'alinéa qui suit manque dans la copie de Niquet et nous ne l'avons trouvé nulle part dans les manuscrits de Huygens. Il ne nous semble pas improbable qu'il ait été intercalé par de Volder et Fullenius lors de la préparation de l'édition de la ‘Dioptrique’ de 1703, d'où nous l'avons emprunté.

[p. 262]

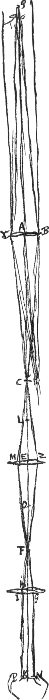[Fig. 10.]

[Fig. 11.]

l'objet. En effet, le rapport HKR [Fig. 11]¹⁾:SΛX²⁾, ou AΛΔ, est composé des rapports HKR:HOR, ou HO:HK, et HOR (ou EOD):AΛΔ, c'est-à-dire, AΛ (ou AC):EO (ou EL). Mais comme HO = HK, on aura HKR:SΛX = AC::EL; ce qu'il fallait démontrer.

Il n'est d'ailleurs nullement nécessaire de choisir les lentilles DT et QR également convexes. En effet, si au lieu d'une des petites lentilles convexes on en prend une autre, par exemple au lieu de la lentille QR une dont la distance focale est FΔ [Fig. 9], il sussira de placer cette dernière en Δ, tandis que les autres restent aux endroits qu'ils occupaient; le grossissement sera alors plus considérable que dans le premier cas; en effet il sera exprimé par le rapport AC:ΔF³⁾. Mais si au lieu de la lentille DT nous en prenons une autre de convexité quelconque et que nous la plaçons de telle manière que les cônes de rayons MCZ et MFZ sont égaux, c'est-à-dire que CE = 2 EL, EL étant la distance focale de la lentille DT, le grossissement ne sera pas changé du tout⁴⁾. Quant à la lentille QR, elle doit toujours être placée de telle manière que son foyer tombe au point F⁵⁾.

Il⁶⁾ faut savoir toutefois que les télescopes de ce genre sont composés de plus de deux lentilles dans le seul but d'agrandir le champ qu'on embrasse d'un seul regard; mais qu'il est certain d'autre part que les lunettes composées d'une lentille convexe et d'une lentille concave grossissent davantage les objets (eu égard à leur longueur) et donnent des images plus nettes et dépourvues des bandes colorées qu'on ne peut guère éviter lorsqu'on se sert de la combinaison décrite de trois lentilles. Cependant ces couleurs étrangères disparaissent plus ou moins si du côté de l'oeil on ajoute encore une ou deux lentilles, et les images des objets apparaissent alors moins défor-

1) On remarquera auprès de la figure 9 l'annotation de Huygens: ‘Faire deux figures de celle-cy.’ Or, deux pages du manuscrit plus loin ce dédoublement a été accompli et les deux fig. 10 et 11 en sont le résultat. Seulement il y a un petit changement, en comparaison avec la fig. 9, dans le placement des points O et K. En effet, le point O n'est pas seulement comme dans la figure 9 (d'après la leçon primitive de la note 1, p. 260) très-près du foyer de la lentille E, mais il se confond avec ce foyer de manière que les points O et F divisent la distance des lentilles E et H en trois parties égales. Ensuite K est le point correspondant de O par rapport à la lentille H, d'où il suit HK = OH, puisqu' alors OF:OH = OH:OK (voir la Prop. XX, Liv. I, p. 99). L'oeil K n'est donc pas, comme dans la fig. 9 (d'après la leçon primitive), placé là où se trouve l'anneau oculaire, mais un peu plus près de la lentille (comparez la note 2, p. 261), ce qui ne change pas le grossissement, suivant la Prop. XIII du Liv. II, p. 233.

2) Le point Λ, qui manque dans la figure, est le foyer de la lentille A, par lequel passent les lignes Vθ et XΔ.

3) À propos de cette remarque Huygens ajouta en marge: ‘hoc ostende, ut est in lib. G pag. 129.’ Voir l'Appendice au Livre présent, p. 271.

4) C'est-à-dire le grossissement sera toujours mesuré par le rapport AC:FH.

5) Dans la copie de Niquet et dans la leçon primitive, où elles furent biffées depuis, on trouve encore les phrases suivantes: ‘Sed et retenta lente utraque DT, QR [Fig. 9], ac tantum situ earum mutato, amplius augere licebit visibilia. Si enim DT propior fiat foco C, erit quidem CE quam fuerat minor, at EF, distantia puncti correspondentis, major, et FH eadem quae prius. unde major quam antea erit ratio AC ad CE, itemque ratio EF ad FH, ex quibus componitur ratio YB ad PN, secundum quam res visas augeri diximus.’ Plus tard Huygens annota en marge: ‘omittatur’.

6) A côté de l'alinéa qui va suivre on trouve en marge les annotations suivantes: 1 ‘Haec mutanda dicendumque de telescopio ex 4 lentibus cum diaphragmate’ [Comparez la note 2, p. 264 qui suit] ‘quod est optimum ad usus diurnos diaphragma a nobis inventum’; 2. ‘An non de telescopijs singulis parvulis ex convexa et cava’ [Voir les Prop. I et II de la troisième Partie] ‘nocturnis ex 2 convexis’ [Prop. III de la Troisième Partie] ‘diurnis ex 4 convexis de aperturis’; 3. ‘de inventore’ [telescopij]. ‘de nostra mechanica’ [probablement les machines à fabriquer les lentilles]. Toutes ces annotations sont de dates probablement différentes et de beaucoup postérieures à celle du texte.

[p. 263]

oculi et objecti. Scilicet HKR [Fig. 11]¹⁾ ad SΛX²⁾ sive AΛΔ rationem habet compositam ex HKR ad HOR, id est, ex HO ad HK, et ex HOR sive EOD ad AΛΔ, id est, ex AΛ sive AC ad EO sive EL; quia vero HO aequalis HK, erit HKR ad SΛX ita AC ad EL. q.e.d.

Caeterum haudquaquam necesse est aequaliter convexas sumi lentes DT, QR. Etenim si e minori convexo adhibeatur alia pro lente QR, puta quae foci distantiam habeat aequalem FΔ [Fig. 9], ea tantum in Δ collocanda erit, manentibus reliquis ut prius, eritque ratio incrementi major priori, videlicet ea quae AC ad ΔF³⁾. Quod si vero pro lente DT aliam quamvis convexam accipiamus, eamque sic collocemus, ut coni radiorum MCZ, MFZ aequales sint; hoc est, ut CE sit dupla intervalli EL, quo distat à lente DT focus suus; nihil prorsus ratio incrementi inde immutabitur⁴⁾. Debet autem ita semper disponi lens QR ut focus ejus incidat in punctum F⁵⁾.

Sciendum⁶⁾ vero ea tantum gratia ex pluribus quam duabus lentibus telescopia hujusmodi componi, ut latior fiat uno intuitu prospectus, cum alioqui certum sit ea quae ex convexa et cava lente componuntur magis augere, pro sua longitudine, res visas, atque etiam distinctiores efficere, nullisque colorum pigmentis infectas quod in hac lentium trium compositione aegre vitari potest. Veruntamen si a parte oculi alia adhuc lens vel duae insuper addantur evanescunt aliquatenus adventitij colores isti, minusque distortae apparent rerum imagines, ac plures etiam uno obtutu

1) On remarquera auprès de la figure 9 l'annotation de Huygens: ‘Faire deux figures de celle-cy.’ Or, deux pages du manuscrit plus loin ce dédoublement a été accompli et les deux fig. 10 et 11 en sont le résultat. Seulement il y a un petit changement, en comparaison avec la fig. 9, dans le placement des points O et K. En effet, le point O n'est pas seulement comme dans la figure 9 (d'après la leçon primitive de la note 1, p. 260) très-près du foyer de la lentille E, mais il se confond avec ce foyer de manière que les points O et F divisent la distance des lentilles E et H en trois parties égales. Ensuite K est le point correspondant de O par rapport à la lentille H, d'où il suit HK = OH, puisqu' alors OF:OH = OH:OK (voir la Prop. XX, Liv. I, p. 99). L'oeil K n'est donc pas, comme dans la fig. 9 (d'après la leçon primitive), placé là où se trouve l'anneau oculaire, mais un peu plus près de la lentille (comparez la note 2, p. 261), ce qui ne change pas le grossissement, suivant la Prop. XIII du Liv. II, p. 233.

2) Le point Λ, qui manque dans la figure, est le foyer de la lentille A, par lequel passent les lignes Vθ et XΔ.

3) À propos de cette remarque Huygens ajouta en marge: ‘hoc ostende, ut est in lib. G pag. 129.’ Voir l'Appendice au Livre présent, p. 271.

4) C'est-à-dire le grossissement sera toujours mesuré par le rapport AC:FH.

5) Dans la copie de Niquet et dans la leçon primitive, où elles furent biffées depuis, on trouve encore les phrases suivantes: ‘Sed et retenta lente utraque DT, QR [Fig. 9], ac tantum situ earum mutato, amplius augere licebit visibilia. Si enim DT propior fiat foco C, erit quidem CE quam fuerat minor, at EF, distantia puncti correspondentis, major, et FH eadem quae prius. unde major quam antea erit ratio AC ad CE, itemque ratio EF ad FH, ex quibus componitur ratio YB ad PN, secundum quam res visas augeri diximus.’ Plus tard Huygens annota en marge: ‘omittatur’.

6) A côté de l'alinéa qui va suivre on trouve en marge les annotations suivantes: 1 ‘Haec mutanda dicendumque de telescopio ex 4 lentibus cum diaphragmate’ [Comparez la note 2, p. 264 qui suit] ‘quod est optimum ad usus diurnos diaphragma a nobis inventum’; 2. ‘An non de telescopijs singulis parvulis ex convexa et cava’ [Voir les Prop. I et II de la troisième Partie] ‘nocturnis ex 2 convexis’ [Prop. III de la Troisième Partie] ‘diurnis ex 4 convexis de aperturis’; 3. ‘de inventore’ [telescopij]. ‘de nostra mechanica’ [probablement les machines à fabriquer les lentilles]. Toutes ces annotations sont de dates probablement différentes et de beaucoup postérieures à celle du texte.

[p. 264]

mées et le champ visuel s'agrandit. Or, la longueur du télescope n'augmente pas par l'addition de ces lentilles, attendu qu'elles sont placées de telle manière que les rayons ne se croisent que deux fois, comme dans le cas de trois lentilles. Cependant les différentes personnes combinent différemment entre elles les lentilles oculaires de ces télescopes, cherchant le meilleur système par la seule expérience. Et certes, il serait malaisé de donner à ce sujet des préceptes théoriques, parce que la considération des couleurs ne peut être réduite à des lois géométriques, et qu'il est fort difficile de calculer d'une manière satisfaisante cette courbure des lignes droites qu'on voit souvent près des bords des lentilles. Je pourrais en vérité, en reproduisant les résultats des investigations laborieuses d'autres auteurs, faire connaître quelques constructions de télescopes de ce genre; mais comme je pense que celle que je décrirai dans ce qui suit¹⁾, dans laquelle les images ne sont pas redressées par la multiplication des lentilles mais par la réflexion d'un miroir, est beaucoup meilleure, il me semble que je ne dois pas m'attarder plus longtemps sur ce sujet.

1) Voir la Prop. V qui suit.

Proposition V²⁾.

Construire à l'aide de deux lentilles convexes un télescope donnant des images droites et qui nous permette d'embrasser d'un seul regard un champ étendu³⁾.

Nous avons indiqué à la Prop. V, Liv. II⁴⁾ comment on peut construire avec deux lentilles convexes convenablement placées, l'une par rapport à l'autre et par rapport à l'oeil, un télescope permettant d'embrasser d'un seul regard un champ étendu. Ce télescope est le plus utile de tous pour contempler les étoiles; en effet, quoiqu'il donne des images renversées, il n'en résulte qu'un inconvénient faible ou nul. Mais lorsqu'on veut observer du jour des hommes, des tours ou des navires se trouvant à grande distance, l'inversion des images ne permet

2) Plus tard, après 1666, Huygens ajouta en marge: ‘Omittenda ac potius telescopium 4 lentium convexarum explicandum,’ [voir la Prop. V de la troisième Partie de cette ‘Dioptrique’] ‘cui diaphragma ex nostro invento additum perfectionem attulit.’ Le diaphragme en question est, en effet, mentionné dans la proposition citée.

3) Huygens a longtemps attaché beaucoup d'importance aux lunettes à miroir, dont il s'agit ici. On les trouve mentionnées pour la première fois dans sa lettre à van Schooten du 20 sept. 1653 (p. 242 du T. I), dans laquelle il invite celui-ci à venir voir sa nouvelle forme de lunette. Ensuite le 24 août 1654 (p. 295 du T. I) le frère Constantyn avertit Christiaan qu'il a parlé à un visiteur, qui s'intéressait aux lunettes, ‘de vostre invention des petits miroirs d'acier sans la luy enseigner pourtant quoy qu'il l'eust voulu scauoir de tout son coeur.’ Et plus tard il est encore souvent question de ces sortes de lunettes; à propos de quoi on peut consulter les pp. 277 (22 nov. 1658) du T. II; 14 (25 janv. 1662), 100, 112, 118, 133, 136, 210, 215, 236, 241, 250, 303 (1 févr. 1663) du T. IV; 145 (nov. 1664) du T. V et 87 (5 nov. 1666) du T. VI.

4) Voir l'alinéa qui commence au pied de la p. 195. Toutefois cette citation et la suivante de la même portée ne se rapportent pas précisément à la Prop. V, Liv. II dans la rédaction de 1653 que nous avons donnée p. 187-197 du Tome présent, mais à une nouvelle rédaction projetée, esquissée par Huygens dans l'annotation reproduite dans la note 3 de la p. 186, où on lit ‘casus telescopij et microscopij rursus hic annotentur’; ce qui veut dire que Huygens se proposa de faire débuter la partie de la ‘Dioptrique’ qui traite les téléscopes et les microscopes par une discussion du télescope et du microscope à deux lentilles. En effet, cette intention a été réalisée, quant au télescope, dans les Prop. I, II et III de la troisième Partie de la ‘Dioptrique’, lesquelles on trouvera plus loin; mais ces propositions ne furent rédigées que bien plus tard, au moins après 1665, puisqu'on ne les trouve pas dans la copie de Niquet. Toutefois il sera utile de prendre connaissance à l'occasion présente de la troisième de ces propositions qui traite le cas de deux lentilles convexes.

[p. 265]

comprehenduntur; nec longitudo telescopij propterea augetur, quoniam ita lentes collocantur, ut non plures quam duae fiant radiorum intersectiones, sicuti in compositione trium. Alij vero aliter lentes oculares in his inter se consociant, sola experientia duce quid optimum sit quaerentes. nec sane facile foret certa ratione aliquid circa haec praecipere, quum colorum consideratio ad geometriae leges revocari nequeat, nec nisi difficile admodum illa quae circa latera lentium saepe cernitur rectarum linearum incurvatio. Possem equidem, quae ab alijs magno labore hic investigata sunt, proponendo, aliquot ejusmodi perspicillorum constructiones docere, sed cum longè potiora existimem quae in sequentibus proferam¹⁾, ubi non multiplicatione lentium sed speculi reflexione visibilia eriguntur, non videtur diutius in his immorandum.

1) Voir la Prop. V qui suit.

[Propositio V.]²⁾

E duabus convexis lentibus telescopium construere quo visibilia erecta spectentur ac magna copia simul uno intuitu comprehendatur³⁾.

Convexis duobus recte inter se atque ad oculum comparatis telescopium componi quo insignis visibilium amplitudo uno intuitu apparet propos. [V, Libr. II]⁴⁾ indicavimus quod ad sidera contemplanda omnium est utilissimum, quia licet inversas rerum imagines referat, exiguum inde aut nullum incommodum nascitur. Sed interdiu ad conspiciendos homines turresve aut naves procul dissitas, situs

2) Plus tard, après 1666, Huygens ajouta en marge: ‘Omittenda ac potius telescopium 4 lentium convexarum explicandum,’ [voir la Prop. V de la troisième Partie de cette ‘Dioptrique’] ‘cui diaphragma ex nostro invento additum perfectionem attulit.’ Le diaphragme en question est, en effet, mentionné dans la proposition citée.

3) Huygens a longtemps attaché beaucoup d'importance aux lunettes à miroir, dont il s'agit ici. On les trouve mentionnées pour la première fois dans sa lettre à van Schooten du 20 sept. 1653 (p. 242 du T. I), dans laquelle il invite celui-ci à venir voir sa nouvelle forme de lunette. Ensuite le 24 août 1654 (p. 295 du T. I) le frère Constantyn avertit Christiaan qu'il a parlé à un visiteur, qui s'intéressait aux lunettes, ‘de vostre invention des petits miroirs d'acier sans la luy enseigner pourtant quoy qu'il l'eust voulu scauoir de tout son coeur.’ Et plus tard il est encore souvent question de ces sortes de lunettes; à propos de quoi on peut consulter les pp. 277 (22 nov. 1658) du T. II; 14 (25 janv. 1662), 100, 112, 118, 133, 136, 210, 215, 236, 241, 250, 303 (1 févr. 1663) du T. IV; 145 (nov. 1664) du T. V et 87 (5 nov. 1666) du T. VI.

4) Voir l'alinéa qui commence au pied de la p. 195. Toutefois cette citation et la suivante de la même portée ne se rapportent pas précisément à la Prop. V, Liv. II dans la rédaction de 1653 que nous avons donnée p. 187-197 du Tome présent, mais à une nouvelle rédaction projetée, esquissée par Huygens dans l'annotation reproduite dans la note 3 de la p. 186, où on lit ‘casus telescopij et microscopij rursus hic annotentur’; ce qui veut dire que Huygens se proposa de faire débuter la partie de la ‘Dioptrique’ qui traite les téléscopes et les microscopes par une discussion du télescope et du microscope à deux lentilles. En effet, cette intention a été réalisée, quant au télescope, dans les Prop. I, II et III de la troisième Partie de la ‘Dioptrique’, lesquelles on trouvera plus loin; mais ces propositions ne furent rédigées que bien plus tard, au moins après 1665, puisqu'on ne les trouve pas dans la copie de Niquet. Toutefois il sera utile de prendre connaissance à l'occasion présente de la troisième de ces propositions qui traite le cas de deux lentilles convexes.

[p. 266]

[Fig. 12.]

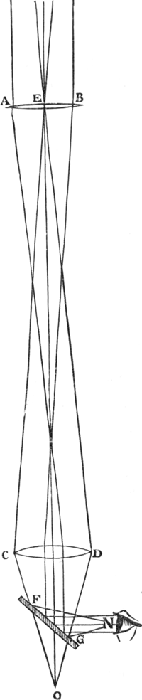
pas de reconnaître les objets; c'est pourquoi on a coutume de se servir alors de plusieurs lentilles convexes, dont quelques-unes doivent redresser l'image renversée produite par deux d'entre elles. Nous avons parlé de ces choses dans la proposition précédente. Mais comme ce résultat ne peut être atteint sans qu'on augmente beaucoup la longueur du tube et que le champ visuel se rétrécisse considérablement, nous avons inventé la méthode suivante d'après laquelle les images renversées produites par un télescope de deux lentilles convexes sont renversées en plaçant près de l'oeil un petit miroir, dont nous expliquons la position dans la figure suivante.

Soit AB [Fig. 12]²⁾ la lentille extérieure, CD la lentille oculaire, lesquelles composent le télescope tel que nous l'avons décrit plus haut à la Prop. V, Liv. II³⁾, où nous avons dit que le point O où il faut mettre l'oeil doit être choisi de telle manière que sa distance à la lentille CD soit à peu près égale à la distance focale⁴⁾. Nous plaçons donc un miroir plan FG entre cette lentille et le point O où l'oeil devrait se trouver si le miroir était absent. Ce miroir est de forme elliptique et a la longueur d'un pouce; il a été fondu en métal et soigneusement poli (les miroirs de verre ne peuvent servir en aucune façon à cause de leur surface double). Nous l'inclinons sous un angle de 45^o ou un peu moins sur l'axe de la lentille et nous l'enfermons dans le tube de telle manière que l'oeil N puisse en être approché jusqu' à une fort petite distance. On regarde vers le miroir d'en haut à travers une ouverture pratiquée dans la paroi du tube, en inclinant la tête vers la terre; l'oeil voit ainsi debout les objets vers lesquels le télescope est dirigé et le champ visuel est aussi étendu que si l'oeil se trouvait en O et que le miroir était absent. La raison en est évidente pour celui qui sait que les rayons incidents et les rayons réfléchis forment avec un miroir plan des angles égaux. On peut voir la marche de ces rayons dans la figure ci-jointe où nous avons tracé tant ceux qui, issus du centre de l'objet, tombent parallèlement

2) La figure du manuscrit étant endommagée nous empruntons la figure présente à l'édition de de Volder et Fullenius de 1703. De plus nous reproduisons ici deux petites figures se rapportant à la partie oculaire d'une lunette à miroir. La première, qu'on trouve à la p. 62 du Manuscrit A, doit dater de 1659; l'autre, empruntée



à la p. 75 du Manuscrit B, de 1662.

3) Voir la note 4 de la p. 265.

4) Plus précisément au lieu où se trouve l'image de l'objectif, formée par l'oculaire, comme, d'ailleurs, le cours des rayons ECFN et EDGN l'indique; mais ce lieu se trouve à peu de distance du foyer en question puisque, si H représente le foyer de l'oculaire, lequel est situé du côté de l'objectif, et K le point milieu de l'oculaire, on doit avoir (d'après la Prop. XX, Liv. I, p. 99) EH:EK = EK:EO, ou bien, EH:HK = EK:KO. Or. le rapport EH:EK ne diffère pas beaucoup de l'unité, il en est donc de même pour le rapport HK:KO. Voir encore la ‘Prop. III’ de la troisième Partie de cette ‘Dioptrique’.

[p. 267]

eversio res agnosci non patitur, atque ideo plures convexae lentes adhiberi solent, ut imaginem quam duae invertunt aliae denuo erigant, de quibus propos. praecedenti egimus. Quia vero hoc fieri nequit quin simul insigniter augeatur tubi longitudo atque amittatur multum de picturae amplitudine; excogitavimus rationem hanc qua eversae species in telescopio duorum convexorum erigantur adjecto ad oculum speculo exiguo, cujus positum locumque sequenti schemate explicamus¹⁾.

Esto lens AB [Fig. 12]²⁾ exterior, CD vero quae oculo propinquior est, è quibus compositum sit telescopium quale supra exhibitum fuit prop. [V, Libr. II]³⁾ ubi diximus recte sic collocari oculum in O, ut a lente CD distet circiter quantum focus ejus⁴⁾. Itaque inter lentem hanc punctumque O, ubi alioqui oculus statuendus foret, speculum planum FG interponimus, elliptica forma, longitudine pollicari, e metallo fusum atque accurate expolitum, (nam vitrea ob duplicem superficiem omnino ad hunc usum inepta sunt) anguloque inclinamus semirecto ad axem lentium, aut paulo etiam minore, atque ita tubo includimus, ut quam proxime illi admoveri possit oculus N; qui desuper per foramen, in tubi lamina excavatum, in speculum aciem dirigit, inclinato capite terram versus, atque ita visibilia ad quae tubus dirigitur et erecta conspicit et eadem copia, ac si, nullo interposito speculo, in O constitutus esset. Neque causa ignota esse potest ei qui in speculo plano radios incidendo ac resiliendo aequales angulos facere noverit, quos radios uti hic feruntur in schemate delineatos cernere licet; tum hos qui a medio rei visae puncto venientes, paralleli incidunt in lentem AB ac denique

1) La copie de Niquet et la leçon primitive donnent ‘explicabimus’.

2) La figure du manuscrit étant endommagée nous empruntons la figure présente à l'édition de de Volder et Fullenius de 1703. De plus nous reproduisons ici deux petites figures se rapportant à la partie oculaire d'une lunette à miroir. La première, qu'on trouve à la p. 62 du Manuscrit A, doit dater de 1659; l'autre, empruntée



à la p. 75 du Manuscrit B, de 1662.

3) Voir la note 4 de la p. 265.

4) Plus précisément au lieu où se trouve l'image de l'objectif, formée par l'oculaire, comme, d'ailleurs, le cours des rayons ECFN et EDGN l'indique; mais ce lieu se trouve à peu de distance du foyer en question puisque, si H représente le foyer de l'oculaire, lequel est situé du côté de l'objectif, et K le point milieu de l'oculaire, on doit avoir (d'après la Prop. XX, Liv. I, p. 99) EH:EK = EK:EO, ou bien, EH:HK = EK:KO. Or. le rapport EH:EK ne diffère pas beaucoup de l'unité, il en est donc de même pour le rapport HK:KO. Voir encore la ‘Prop. III’ de la troisième Partie de cette ‘Dioptrique’.

[p. 268]

sur la lentille AB et à la fin arrivent parallèlement à l'oeil N, que ceux qui partent des points extrêmes de l'objet et qui, après s'être croisés au centre de la lentille AB, atteignent l'oeil en se mouvant selon les lignes ECFN et EDGN.

Le télescope ainsi construit, et qui sous d'autres rapports est le mieux approprié à nous donner une image des objets qu'on voit sur la terre et sur la mer, a cependant un seul défaut, celui de nous faire voir à notre gauche ce qui se trouve à notre droite; mais c'est là un faible inconvénient, pourvu qu'on en soit averti.

FIN DU TROISIÈME ET DERNIER LIVRE.

[p. 269]

etiam paralleli ad oculum N deferuntur; tum eos qui ab extremis punctis mittuntur, atque in media lente AB sese intersecantes, inde ad oculum pergunt secundum lineas ECFN, EDGN.

Haec vero telescopij ratio alioqui praestantissima ad ea quae terra marique spectanda occurrunt, hoc unum habet incommodum quod quae dextra sunt sinistra videri faciat; sed hoc admonitis exiguum est.

[FINIS TERTII ET ULTIMI LIBRI.]

1) Voir la p. 119 du Tome Présent

1) Voir la p. 119 du Tome présent.

2) Voir la p. 199 du Tome présent.

2) Voir la p. 199 du Tome présent.

4) Voir la p. 99 du Tome présent.

4) Voir la p. 99 du Tome présent.