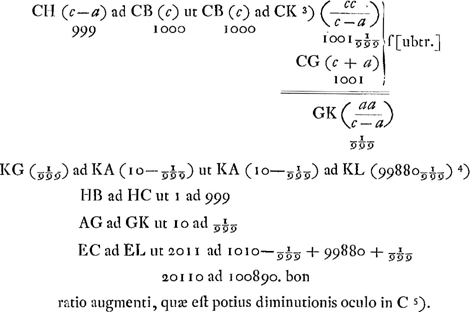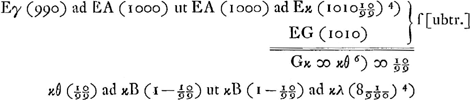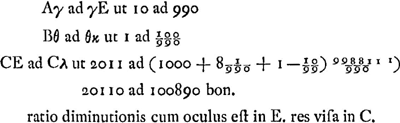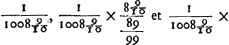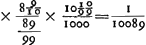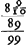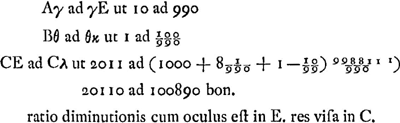Oeuvres complètes. Tome XIII. Dioptrique

[p. 240]

Appendice IV¹⁾
Au deuxième livre du ‘Tractatus de refractione et telescopiis’.
[1692.]

Theorema ex dioptricis nostris a dubio liberatum, ac numeris comprobatum, de permutatione oculi et rei visae mutua ac

1) La pièce est empruntée à la p. 24 verso du Manuscrit II. D'après le lieu où elle se trouve elle doit dater des premiers mois de l'année 1692. On y trouve une vérification numérique de la Prop. VI, Liv. II (p. 199), qui énonce que l'oeil et l'objet peuvent être échangés sans altération du grossissement. Toutefois cette vérification se borne au cas de deux lentilles A et B qui ont un foyer commun au point G.
Remarquons que les notations de la figure correspondent en général avec celles de la fig. 27 de la p. 205. Ainsi γ et G, G et H représentent les foyers des lentilles A et B, dont les distances focales sont supposées égales respectivement à 10 et à 1; E est l'objet se trouvant à la distance 1000 de la lentille A; C l'oeil qui se trouve à cette même distance de la lentille B. Ensuite K est le point correspondant à l'oeil C par rapport à la lentille B de manière que le calcul donne CK = 1001 1/999, GK 1/999; enfin L est le point correspondant à K par rapport à la lentille A, et on trouve KL = 99880 1/999.
Ces données permettent de calculer, par la règle énoncée dans la Prop. V, Liv. II (p. 195 du Tome présent), le grossissement de l'objet placé en E et vu par l'oeil en C.
Pour obtenir ce grossissement dans le cas réciproque, où l'oeil est en E et l'objet en C, Huygens détermine successivement la position du point κ correspondant à E par rapport à la lentille A et celle du point λ correspondant à κ par rapport à la lentille B. De cette manière il retrouve la même proportion 20110 à 100890 représentant le grossissement, ou plutôt l'amoindrissement, dans les deux cas.

[p. 241]

manente eadem ratione magnitudinis apparentis ad veram. Vide ibi pag. 92²⁾.

<sup>3)4)5)



4)6)4)</sup>

2) C'est la page, dans la numération en noir du manuscrit de la ‘Dioptrica’, qui contient le commencement de la démonstration pour le cas de deux lentilles de la règle de la Prop. VI, citée dans la note précédente.

3) Voir la Prop. XX du Livre Premier, p. 99 du Tome présent.

4) Nous supprimons quelques calculs.

5) Voir la règle de la p. 189 du Tome présent, confirmée pour le cas de deux lentilles convexes à la p. 195.

4) Nous supprimons quelques calculs.

6) Ici θ représente l'un des foyers de la lentille B, lequel coïncide avec G dans le cas considéré.

4) Nous supprimons quelques calculs.

[p. 242]

¹⁾

radij qui ab M ad λ tendunt, flectuntur in lente B ut pergant ad κ. hinc diminutio ingens²⁾.

1) Nous supprimons quelques calculs.

2) Évidemment Huygens a en vue la construction suivante, qui peut conduire à une détermination, indépendante de la formule employée, du grossissement: Tirons la droite Mλ et soit β le point où elle traverse la lentille B; tirons de même la droite βκ et soit α le point où le prolongement de cette droite rencontre la lentille A; tirons enfin αE; alors la ligne brisée MβαE représentera le parcours du rayon de lumière qui, partant du point M, atteindra l'oeil placé en E. 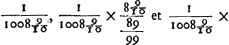Soit donc CM = 1; alors on trouvera successivement pour les angles CλM, Cκβ et CEα, supposés très-petits, les valeurs 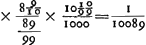et enfin 1/2011 pour l'angle CEM, sous lequel l'objet CM serait vu sans l'intervention des lentilles. Le rapport de la grandeur apparente à la grandeur véritable, c'est-à-dire le rapport des angles CEα et CEM, est donc de 2011 à 10089, conformément à la valeur déduite dans le texte.
Mais cela n'explique pas la remarque de Huygens qui semble manquer de justesse, puisque la réfraction en B amène le facteur 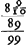et qu'elle a donc plutôt la tendance de diminuer l'amoindrissement.