Oeuvres complètes. Tome XIII. Dioptrique

[p. 172]

La Dioptrique.
Première partie. Traité de la Réfraction et des Télescopes.
1653.
Livre deuxième. De la grandeur apparente des objets vus par réfraction.

Proposition I¹⁾.

[Fig. 1.]

[Fig. 2.]

Les objets qu' on aperçoit confusément soit à cause des lentilles placées entre eux et le spectateur soit à cause de la distance, peuvent être rendus nettement visibles soit à l'aide d'une lentille unique placée devant l'oeil soit à l'aide d'un écran placé au même endroit et pourvu d'une très petite ouverture, si du moins l'oeil ne se trouve pas précisément au point de confusion maximum²⁾. L'image aperçue sera la même en grandeur et en position quelle que soit celle des deux méthodes dont on se serve pour corriger le défaut de netteté.

En effet, si les rayons partis d'un point quelconque d'un objet se dirigent vers l'oeil et qu'ils ont un point de concours placé derrière l'oeil, on comprend aisément, d'après ce qui a été démontré plus haut, par quelle espèce de lentille concave on peut les rendre parallèles³⁾. Et de même s'ils atteignent l'oeil en divergeant de

1) La rédaction de cette proposition et de sa démonstration, telle que nous la faisons suivre ici, doit dater d'une époque inconnue, mais postérieure à l'année 1666. On trouvera la rédaction primitive, qui nous a été conservée par la copie de Niquet, dans l'Appendice I au Livre II, p. 235 du Tome présent. Elle diffère de celle que nous donnons ici surtout parce que l'idée, d'obtenir des images distinctes à l'aide d'une lentille placée devant l'oeil, n'y est mentionnée qu'en passant, vers la fin de la démonstration.

2) Le ‘point de confusion maximum’, ou simplement ‘point de confusion’, comme Huygens l'a appelé plus tard (Voir l'Appendice X du Livre I, p. 170 du Tome présent), est le point où il faut placer l'oeil pour que l'agrandissement, tel qu'il est défini par Huygens dans les propositions qui suivent, devienne infiniment grand. Ainsi, dans le cas d'une seule lentille, ce point se confond pour un objet très éloigné, dans la direction de l'axe, avec le foyer de la lentille, pour d'autres objets, placés dans l'axe de la lentille, avec le point de l'axe où se forme leur image.
Si l'objet est une source lumineuse étroite on voit donc, en approchant l'oeil du point de confusion, l'image de la source s'agrandir démesurément et devenir de plus en plus confuse, jusqu' à ce qu'elle est remplacée, lorsque l'oeil se trouve précisement dans le point en question, par une clarté uniforme s'étendant sur toute la surface de la lentille. Ensuite, en passant avec l'oeil à l'autre côté du point de confusion, on voit l'image directe changée dans une image renversée ou vice versa.
Ajoutons que dans la ‘Correspondance’ de Huygens le point de confusion n'est mentionné qu'une seule fois. C'est dans une lettre au frère Constantyn du 7 octobre 1686 que l'on lit (p. 104 du T. IX) à propos d'une lentille d'environ 90 pieds de distance focale: ‘Cependant je l'ay exposè à la reflexion de la chandelle, dont il renverse la flamme assez bien mais tenant l'oeuil au foier et dans le point de confusion il me semble que j'y vois des choses qui marquent quelque défaut et beaucoup de drabbigheyt[trouble]’. Il est clair qu'il s'agit ici d'un point de confusion dans le genre de ceux traités dans l'Appendice X mentionné plus haut.

3) Voir la Prop. XV, Liv. I, p. 83 du Tome présent.

[p. 173]

Dioptrica.
[Pars prima. Tractatus de refractione et telescopiis.]
[1653.]
[Liber II. De apparenti augmento vel decremento eorum, quae per refractionem conspiciuntur.]
[Propositio I.]¹⁾

Quae vel ob interpositas lentes, vel ratione distantiae, confusè spectantur, distincta reddi possunt, vel addita lente una juxta oculum, vel opposita ibidem lamina cum foramine minimo; dummodo non in ipso maximae confusionis puncto²⁾ oculus positus fuerit. Utracunque vero correctio adhibeatur, eadem magnitudine et positu visibile spectabitur.

Si enim ab unoquoque rei visae puncto egressi radij ad oculum ferantur tendantque velut ad punctum post oculum, facile ex supra demonstratis intelligitur cujusmodi cava lente reddantur paralleli³⁾. Item si divergentes, ac tanquam ex puncto

1) La rédaction de cette proposition et de sa démonstration, telle que nous la faisons suivre ici, doit dater d'une époque inconnue, mais postérieure à l'année 1666. On trouvera la rédaction primitive, qui nous a été conservée par la copie de Niquet, dans l'Appendice I au Livre II, p. 235 du Tome présent. Elle diffère de celle que nous donnons ici surtout parce que l'idée, d'obtenir des images distinctes à l'aide d'une lentille placée devant l'oeil, n'y est mentionnée qu'en passant, vers la fin de la démonstration.

2) Le ‘point de confusion maximum’, ou simplement ‘point de confusion’, comme Huygens l'a appelé plus tard (Voir l'Appendice X du Livre I, p. 170 du Tome présent), est le point où il faut placer l'oeil pour que l'agrandissement, tel qu'il est défini par Huygens dans les propositions qui suivent, devienne infiniment grand. Ainsi, dans le cas d'une seule lentille, ce point se confond pour un objet très éloigné, dans la direction de l'axe, avec le foyer de la lentille, pour d'autres objets, placés dans l'axe de la lentille, avec le point de l'axe où se forme leur image.
Si l'objet est une source lumineuse étroite on voit donc, en approchant l'oeil du point de confusion, l'image de la source s'agrandir démesurément et devenir de plus en plus confuse, jusqu' à ce qu'elle est remplacée, lorsque l'oeil se trouve précisement dans le point en question, par une clarté uniforme s'étendant sur toute la surface de la lentille. Ensuite, en passant avec l'oeil à l'autre côté du point de confusion, on voit l'image directe changée dans une image renversée ou vice versa.
Ajoutons que dans la ‘Correspondance’ de Huygens le point de confusion n'est mentionné qu'une seule fois. C'est dans une lettre au frère Constantyn du 7 octobre 1686 que l'on lit (p. 104 du T. IX) à propos d'une lentille d'environ 90 pieds de distance focale: ‘Cependant je l'ay exposè à la reflexion de la chandelle, dont il renverse la flamme assez bien mais tenant l'oeuil au foier et dans le point de confusion il me semble que j'y vois des choses qui marquent quelque défaut et beaucoup de drabbigheyt[trouble]’. Il est clair qu'il s'agit ici d'un point de confusion dans le genre de ceux traités dans l'Appendice X mentionné plus haut.

3) Voir la Prop. XV, Liv. I, p. 83 du Tome présent.

[p. 174]

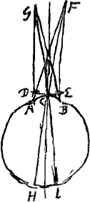
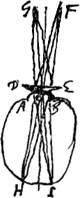
telle façon qu'ils semblent provenir d'un point placé devant l'oeil, on comprend aisément comment ils peuvent être rendus parallèles à l'aide d'une lentille convexe¹⁾. Dans l'un et l'autre cas la vision est rendue nette par ce moyen. Mais nous obtiendrons le même résultat en plaçant une très petite ouverture devant l'oeil. Car dans ce cas l'on peut dire que parmi les innombrables rayons qui sont autrement envoyés à la pupille par chaque point de l'objet un seul est transmis par l'ouverture. En effet, supposons que les rayons partis des points extrêmes de l'objet atteignent la pupille AB [Fig. 1 et 2] de l'oeil comme s'ils provenaient des points F et G. Et plaçons devant l'oeil une petite ouverture C [Fig. 1] percée dans un écran et ne laissant passer, pour ainsi dire, que les rayons uniques FC, GC qui atteignent le fond de l'oeil aux points H et I. Là se formeront donc les images des différents points de l'objet vu, d'où sont partis les rayons FA, FC, FB et GA, GC, GB. Et à cause de l'exclusion des rayons autres que FC, GC, l'image sera nette et la vision donc également.

Faisons de nouveau les mêmes suppositions, mais enlevons l'écran perforé et soit placée en son lieu, fort près de l'oeil, la lentille DE [Fig. 2] par laquelle la vision est rendue nette. Je dis que l'image aperçue sera la même qu' auparavant en grandeur et en position. En effet, comme les rayons FC, GC passent sans changer de direction par le milieu de la lentille DE^*, dont nous négligeons l'épaisseur, il est évident qu' à l'intérieur de l'oeil ils suivent la même route qu'auparavant, lorsqu'ils traversaient l'ouverture C, et qu'ils atteindront donc le fond de l'oeil aux mêmes points H, I. Et comme, par hypothèse, la vision devient nette lorsque nous plaçons la lentille DE devant l'oeil, il est nécessaire que tous les rayons qui proviennent de G se réunissent en un seul point au fond de l'oeil, et ceux qui proviennent de F pareillement. Par conséquent, tous les rayons qui sont partis du point G se réuniront en I et tous ceux qui sont partis de F en H: les images des points extrêmes de l'objet se formeront donc nécessairement en H et en I. Il s'ensuit que les dimensions latérales de l'objet seront en apparence les mêmes, que se soit une lentille DE ou une très-petite ouverture que l'on place devant l'oeil. Et la position de l'image sera aussi la même. Ce qu'il fallait démontrer.

Ainsi, lorsque dans la suite nous définirons la grandeur apparente même dans les cas où la vision est confuse, nous entendrons par là la grandeur que l'on voit après que la confusion a été corrigée, soit à l'aide d'une lentille soit à l'aide d'une très-petite ouverture, comme nous l'avons déjà dit.

1) Voir la Prop. XIV, Liv. I, p. 81.

* Prop. XXIII, Liv. I²⁾.

2) Voir la p. 119 du Tome présent.

Proposition II.

Lorsque l'oeil est placé entre une lentille convexe et son foyer, un objet quelconque est vu droit et agrandi à travers la lentille. Si alors l'objet est fort éloigné la grandeur appa-

[p. 175]

[Fig. 1].

[Fig. 2].

ante oculum egressi adveniant, quomodo convexa lente ad parallelismum redigantur¹⁾; utroque vero casu visio efficitur distincta. Sed hoc idem quoque consequemur opposito ad oculum minimo foramine, quia tunc velut uni tantum radiorum qui a singulis rei visae punctis innumeri alioqui ad pupillam feruntur, transitus datur. Ponantur enim radij ab extremis rei visae punctis profecti, ad oculi pupillam AB [Fig. 1 et 2] accidere tanquam ex punctis F, G, venientes. Et objiciatur ante oculum foramen in lamina exiguum C [Fig. 1]; nonnisi singulos veluti radios FC, GC admittens, qui occurrant oculi fundo in punctis H et I. Itaque hic pingentur puncta rei visae singula, unde manarunt radij FA, FC, FB; et GA, GC, GB. Et propter exclusos ceteros radios praeter FC, GC, distincta erit pictura eoque et visio.

Rursus ijsdem positis, sed ablatâ lamellâ perforatâ, sit hujus loco lens oculo proxima DE [Fig. 2] quae distinctam visionem efficiat. Dico eadem qua prius magnitudine eodemque positu spectatum iri visibile. Quia enim per mediam lentem DE, cujus crassitudo tanquam nulla censetur, radij FC, GC, rectis lineis penetrant^*. manifestum est eos eodem modo intra oculum ferri, atque ante per foramen C transcuntes, atque idcirco oculi fundo in ijsdem punctis H, I occursuros. Cum autem ob interpositam lentem DE distincta visio fieri ponatur, necesse est omnes radios ex G venientes ad unum punctum in fundo oculi convenire, atque ita quoque omnes ex F venientes. Igitur omnes a puncto G egressi convenient in I, et omnes ex F egressi convenient in H. atque idcirco pingentur necessario extrema illa rei visae puncta in H et I. eoque non alia apparebit ejus latitudo objectu lentis DE, ac foraminis minimi; nec non positus quoque idem; quae fuere demonstranda.

Itaque cum in sequentibus apparentem magnitudinem definiemus etiam ijs casibus quibus confusa visio contingit, intelligenda erit ea magnitudo quae cernitur correcta confusione, seu lente seu minimo foramine, ut jam diximus.

1) Voir la Prop. XIV, Liv. I, p. 81.

* ex propos. [XXIII, Lib. I.]²⁾

2) Voir la p. 119 du Tome présent.

Propositio [II].

Oculo constituto inter lentem convexam et focum ejus, visibile quodvis per lentem spectatur situ recto, et auctum magnitudine; habetque magnitudo apparens ad veram, si visibile

[p. 176]

rente est à la grandeur vraie comme la distance focale de la lentille est à la distance du foyer à l'oeil; mais si l'objet se trouve à une plus petite distance, le rapport de la grandeur apparente

[Fig. 3.]

à la grandeur vraie se compose du rapport que nous venons de nommer et du rapport de la distance entre l'oeil et l'objet à la distance entre l'objet et le ‘point dirigeant’¹⁾. Mais lorsque l'oeil est placé dans le foyer de la lentille, les objets éloignés paraissent infiniment grands, et les objets rapprochés paraissent agrandis dans un rapport égal à celui de la distance de l'objet à l'oeil à la distance de l'oeil à la lentille²⁾.

Soit donnée la lentille convexe AB, dont A est le centre et O le foyer. L'oeil D soit placé sur l'axe AO de la lentille. L'objet soit la ligne NM parallèle à la lentille et dont le point milieu E se trouve sur le même axe. Il est évident qu'un objet quelconque, placé au même endroit, sera nécessairement agrandi dans une direction latérale dans la même proportion que cette ligne ou qu'une partie EN de cette ligne vue à travers la lentille. Soit ensuite DP une troisième proportionnelle à DO et DA. P sera alors le point qui correspond à l'oeil D. En effet, comme d'après la prop. XX, Liv. I⁴⁾ les rayons qui proviennent du point D sont réfractés par la lentille AB de telle manière qu'ils continuent leur chemin comme s'ils provenaient du point P, il est clair que, réciproquement, les rayons qui se dirigent vers P, au moment où ils rencontrent la lentille AB, auront le point D où se trouve l'oeil comme point de concours. Tirons la droite NP qui coupe la lentille en B (elle la coupera puisque nous supposons que le point N est vu à travers la lentille), et joignons les points B et D. Ainsi le point N sera aperçu à travers le point B de la lentille, vu que le rayon NB est réfracté de telle manière qu'il se dirige ensuite vers D, le point où se trouve l'oeil, ce qui n'est vrai pour aucun autre rayon provenant du point N. Quant au point E, il est clair qu'il doit être vu à travers le centre A de la lentille, parce que, ce point étant situé sur l'axe de la lentille, le rayon ED atteint l'oeil sans avoir été réfracté.

Nous voyons donc en premier lieu que l'image de l'objet NM est droite, puisque le point B est situé du même côté de l'axe EAO que le point N qui lui corres-

1) La leçon primitive et la copie de Niquet donnent ‘correspondens’. Il s'agit du point où la lentille fait apparaître l'image de l'oeil, c'est-à-dire d'un point tel que, réciproquement, les rayons émanant de ce point correspondraient, après la réfraction, avec le point où se trouve l'oeil. Consultez encore sur cette nomenclature les notes 1, p. 180 et 2, p. 185.

2) Soient o et v les distances de l'oeil et de l'objet à la lentille, f sa distance focale, g le grossissement; alors la proposition présente équivaut, dans le cas le plus général, à la relation:



laquelle dans le cas v = ∞ se réduit à et dans celui où .
De plus, puisque le numérateur excède le dénominateur par la valeur de ov, il est clair qu'on aura toujours g > 1.

4) Voir la p. 99 du Tome présent.

[p. 177]

longinquum est, rationem eam quam distantia inter lentem et focum ad distantiam inter focum et oculum; si vero propinquum, rationem compositam ex eadem quae dicta est, et ex ratione distantiae inter oculum et visibile, ad distantiam inter visibile et punctum dirigens¹⁾; Si vero in foco lentis oculus statuatur, visibilia longinqua in infinitum augentur; propinqua vero secundum rationem quam habet distantia eorum ab oculo ad distantiam oculi a lente²⁾.

Esto lens convexa AB [Fig. 3], cujus medium punctum seu umbilicus A. focus O. Oculus vero D, in axe lentis AO positus. Visibile vero linea NM, lenti parallela, cujusque medium E sit in eodem axe. Quantum enim linea haec vel ejus pars EN augebitur, trans lentem spectata, tantum quoque aliud quodvis visibile, eo loci positum, secundum diametrum augeri necesse est³⁾. Porro duabus DO, DA sit tertia proportionalis DP, eritque P punctum oculo D correspondens. Quia enim radij ex puncto D prodeuntes a lente AB ita inflectuntur ut pergant inde tanquam venientes ex P, per prop. [XX, Lib. I]⁴⁾ vicissim quoque qui ad P tendentes incidunt in lentem AB concurrent ad punctum oculi D. Ducatur NP recta secans lentem in B, (secabit enim quia punctum N per eam conspici ponimus) et jungatur BD. Itaque per punctum lentis B cernetur punctum N, quum radius NB refringatur versus punctum oculi D, neque alius quisquam eorum qui ex N promanant. Punctum autem E per medium lentis A apparere manifestum est, quia cum in axe lentis situm sit radius ED irrefractus ad oculum pervenit.

Patet itaque primùm, visibile NM conspici situ erecto, quum punctum B sit ad eandem partem axis EAO ac punctum N quod ibi refertur. Liquet etiam

1) La leçon primitive et la copie de Niquet donnent ‘correspondens’. Il s'agit du point où la lentille fait apparaître l'image de l'oeil, c'est-à-dire d'un point tel que, réciproquement, les rayons émanant de ce point correspondraient, après la réfraction, avec le point où se trouve l'oeil. Consultez encore sur cette nomenclature les notes 1, p. 180 et 2, p. 185.

2) Soient o et v les distances de l'oeil et de l'objet à la lentille, f sa distance focale, g le grossissement; alors la proposition présente équivaut, dans le cas le plus général, à la relation:



laquelle dans le cas v = ∞ se réduit à et dans celui où .
De plus, puisque le numérateur excède le dénominateur par la valeur de ov, il est clair qu'on aura toujours g > 1.

3) La leçon primitive et la copie de Niquet donnent ‘sciemus’.

4) Voir la p. 99 du Tome présent.

[p. 178]

pond. Il est également évident que BA est l'étendue occupée dans la lentille par l'image de la ligne NE. Or, si nous tirons une droite ND qui coupe la lentille en C, il est clair que AC sera l'étendue occupée par le même objet EN dans un plan où n'aurait lieu aucune réfraction. Le rapport BA:CA définit donc le rapport de la grandeur apparente à la grandeur véritable, et il est évident que BA est plus grande que CA, vu que BA:NE = PA:PE, tandis que CA est à la même longueur NE comme DA:DE. Or PA:PE > DA:DE, parce que PA:AE >> DA:AE. En effet PA > DA, attendu que D tombe ici nécessairement entre A et P. Il est donc déjà établi par ce raisonnement que l'image de l'objet est droite et plus grande que l'objet.

Il s'agit maintenant de faire voir que lorsque l'objet NM est fort éloigné BA::CA = AO:OD, mais que lorsqu'il est situé à plus petite distance BA:CA est composé des rapports AO:OD et DE:EP. Le premier théorème découle du second; c'est pourquoi nous démontrerons celui-ci d'abord. Le rapport BA:CA se compose des rapports BA:NE et NE:CA. De ces deux derniers rapports BA:NE est égal à PA:PE. Quant au rapport NE:CA il est égal à ED:AD. Par conséquent, le rapport BA:CA se compose de PA:PE et de ED:AD, c'est-à-dire,

[Fig. 4.]

il est égal à celui des rectangles PA, ED et PE, AD. Mais ce dernier rapport se compose des rapports ED:EP et PA:AD, ou AO:OD, car comme on a, par construction, PD:DA = AD:DO, on aura aussi, par composition, PA:AD = AO:OD. Le rapport BA:CA se compose donc des rapports AO:OD et ED:EP.

Si, ensuite, nous supposons l'objet placé à grande distance, le rapport ED:EP est égal à l'unité; ce rapport, composé avec le rapport AO:OD, ne l'augmente donc ni ne le diminue. Le rapport BA:CA sera donc alors égal au rapport AO:OD. Et c'est cela qu'il fallait démontrer pour le cas où l'oeil est placé entre la lentille et son foyer.

Supposons maintenant que l'oeil se trouve précisément dans le foyer O [Fig. 4] et que NM soit un objet rapproché. Menons NB parallèle à l'axe EA et soit B le point où cette droite rencontre la lentille. Tirons aussi BO et NO qui coupe la lentille au point C. Comme le rayon NB est donc parallèle à l'axe de la lentille AB, il est nécessaire que ce rayon soit réfracté de manière à se diriger vers le foyer O où nous plaçons l'oeil. C'est pourquoi le point N sera vu seulement à travers le point B de la lentille. Mais le point E, qui se trouve au milieu de NM, est aperçu comme auparavant au centre A de la lentille. L'image de l'objet NM est donc droite, et le rapport de la grandeur apparente à la grandeur vraie est de nouveau égal à BA:CA. Mais comme BA, c'est-à-dire NE, est à CA, ainsi est EO à AO. L'image est donc plus grande que l'objet dans le rapport EO:AO.

[p. 179]

BA spatium esse quod in lente occupat imago lineae NE. At vero ducta ND rectâ quae secet lentem in C, apparet AC fore spatium quod occuparet idem visibile

[Fig. 3.]

EN in superficie quae refractionis expers esset. Itaque ratio BA ad CA definit proportionem magnitudinis apparentis ad veram. atque apparet quidem BA ipsa CA majorem esse, cum BA ad NE sit ut PA ad PE; CA vero ad eandem NE sicut DA ad DE; ratio autem PA ad PE major quam DA ad DE, quia PA ad AE major quam DA ad AE; est enim PA major quam DA quia D cadit hic necessario inter A et P. Ergo jam et recto situ et auctum magnitudine visibile cerni per haec constat.

Nunc porro ostendendum, cum visibile NM longinquum est, habere BA ad CA rationem eam quam AO ad OD; cum vero propinquum, rationem compositam ex AO ad OD et ex DE ad EP. Prius autem ex posteriori sequitur ac proinde hoc primum demonstrabimus. Ratio BA ad CA componitur ex ratione BA ad NE et NE ad CA; quarum ratio BA ad NE est eadem quae PA ad PE: ratio vero NE ad CA eadem quae ED ad AD. Habet igitur BA ad CA rationem eandem compositae ex rationibus PA ad PE et ED ad AD, hoc est, rationem quam rectangulum PA, ED ad rectangulum PE, AD. Haec autem componitur ex ratione ED ad EP et PA ad AD sive AO ad OD, nam ex constructione cum sit PD ad DA ut AD ad DO, etiam componendo erit PA ad AD ut AO ad OD. Ergo ratio BA ad CA componitur ex ratione AO ad OD et ED ad EP.

Porro cum longinquum intelligitur visibile, ratio ED ad EP est ratio aequalitatis, quae proinde composita cum ratione AO ad OD, eam nec auget nec diminuit. Itaque tum ratio BA ad CA erit eadem quae AO ad OD. Atque haec quidem demonstranda erant oculo inter lentem focumque ejus constituto.

Ponatur autem nunc oculus in ipso foco O [Fig. 4], et sit propinquum visibile NM. Ducatur NB parallela axi EA quae occurrat lenti in puncto B, et jungatur BO, itemque NO secans lentem in puncto C. Quia igitur radius NB parallelus est axi lentis AB, eum necesse est refringi versus focum O, ubi oculus ponitur. Quamobrem punctum N spectabitur per solum lentis punctum B. Sed punctum E medium NM spectatur, uti prius, in centro lentis A. Igitur erectum apparet visibile NM; et magnitudo apparens ad veram rursus eam rationem habet quam BA ad CA. Verum ut BA, hoc est, NE ad CA, ita EO ad AO; ergo auctum cernitur secundum rationem EO ad AO.

Quod si vero longinquum fuerit visibile, jam ratio EO ad AO erit tanquam infinitae inaequalitatis majoris, ac proinde infinita continget ampliatio.

[p. 180]

[Fig. 4.]

Mais si l'objet est placé à grande distance, le rapport EO:AO sera celui de deux longueurs dont la première est infiniment plus grande que la seconde. L'agrandissement sera, par conséquent, infini.

Et il mérite d'être remarqué que lorsque l'oeil occupe cette position l'image de l'objet NM paraît toujours de même grandeur, quelle que devienne la distance de l'objet à la lentille. En effet, le point N sera toujours aperçu au même endroit B.

Proposition III.

Si nous plaçons l'oeil sur l'axe d'une lentille convexe, mais de telle manière que sa distance à la lentille soit plus grande que la distance focale, l'objet, placé de l'autre côté de la lentille, mais en-deçà du point correspondant¹⁾, est aperçu droit et agrandi. Mais s'il est plus éloigné de la lentille que le point correspondant, il sera vu renversé et plus grand ou plus petit selon la diversité de sa distance et de celle de l'oeil à la lentille. Le rapport de la grandeur apparente à la grandeur vraie se trouvera de la même manière que dans le théorème précédent²⁾.

Supposons comme plus haut que la lentille soit AB [Fig. 5 et 6] et O son foyer. Quant à l'oeil, il est placé au point D de l'axe, lequel est plus éloigné de la lentille que le foyer. Et soit DP une troisième proportionnelle aux deux longueurs DO et DA; d'après la prop. XX, Liv. I³⁾ P sera alors le point qui correspond à l'oeil, vu que, de même que les rayons issus de D se dirigent vers le point P après avoir traversé la lentille, de même aussi ceux qui viennent de P se dirigent vers l'oeil D.

Supposons que, comme auparavant, l'objet soit représenté par la droite MN, divisée en E par l'axe de la lentille en deux parties égales, et supposons en premier lieu que l'objet soit situé entre la lentille AB et le point corre spondant P [Fig. 5]. Tirons du point P par l'extrémité N la droite PNB qui rencontre la lentille en B et joignons les points B et D. Tirons aussi la droite ND qui coupe la lentille au point C. Il est évident par cette construction que l'extrémité N de l'objet sera aperçue à travers le point B de la lentille, tandis qu'elle serait vue en C si le

1) C'est le ‘punctum dirigens’ de la proposition précédente. Comparez la note 1, p. 176.

2) En employant les notations de la note 2, p. 177 la proposition amène, dans le cas de la fig. 5, la relation:



c'est-à-dire, la même formule que celle de la note citée. Et il est clair qu'on peut retenir encore cette formule dans le cas de la fig. 6, pourvu qu'on attribue à une image renversée un grossissement négatif.

3) Voir la p. 99 du Tome présent.

[p. 181]

Est autem animadversione dignum, hoc oculi positu, eadem semper magnitudine cerni visibile NM, quantumcunque a lente recesserit; semper enim punctum

[Fig. 5.]

N in eodem puncto B percipietur.

Propositio [III].

Posito oculo in axe lentis convexae, sed ita ut ultra focum ab ea distet, visibile ad alteram partem lentis situm, sed citra punctum correspondens¹⁾, erectum et majus spectatur. Ulterius vero quam punctum correspondens a lente remotum, videbitur inversum, et majus vel minus pro diversa ipsius atque oculi a lente distantia. Ratio autem magnitudinis apparentis ad veram se habebit eodem modo atque in Theoremate praecedenti²⁾.

Ponatur ut supra lens AB [Fig. 5 et 6], et focus ejus O. Oculus autem in puncto axis D, distans a lente ultra focum. Et duabus DO, DA ponatur tertia proportionalis DP, secundum prop. [XX, Lib. I]³⁾. Erit igitur P punctum oculo correspondens, quum sicuti radij ex D procedentes diriguntur à lente versus punctum P, ita vicissim qui ex P veniunt dirigantur ad oculum D.

Sit jam visibile, ut antea, recta MN, quam mediam dividat axis lentis in E, sitque primo situm inter lentem AB punctumque correspondens P [Fig. 5]. et ducatur ex P per terminum N recta PNB, lenti occurrens in B, et jungatur BD. Ducatur autem et recta ND secans lentem in puncto C. Manifestum itaque est per punctum lentis B appariturum visibilis terminum N, quod conspiceretur in C si radius ND sine refractione transmitteretur; punctum vero

1) C'est le ‘punctum dirigens’ de la proposition précédente. Comparez la note 1, p. 176.

2) En employant les notations de la note 2, p. 177 la proposition amène, dans le cas de la fig. 5, la relation:



c'est-à-dire, la même formule que celle de la note citée. Et il est clair qu'on peut retenir encore cette formule dans le cas de la fig. 6, pourvu qu'on attribue à une image renversée un grossissement négatif.

3) Voir la p. 99 du Tome présent.

[p. 182]

[Fig. 5.]

rayon ND était transmis sans réfraction. Mais le point E doit être aperçu dans l'un et l'autre cas à travers A, vu qu'aucun rayon issu de E ne parvient à D si ce n'est EA qui coupe à angles droits les deux surfaces de la lentille et qui continue donc sa route sans être réfracté.

Il est donc établi que dans ce cas l'image de l'objet apparaît droite, vu que les points N et B se trouvent du même côté de l'axe PAD. Et de nouveau le rapport de la grandeur apparente à la grandeur vraie sera égal au rapport BA:CA. C'est pourquoi, BA étant plus grande que CA (car BA > NE > CA), l'image de l'objet NE sera agrandie.

Supposons ensuite que, dans l'autre cas, l'objet MN [Fig. 6] soit placé au-delà du point correspondant P et faisons la même construction qu'auparavant. Par conséquent, le point N sera de nouveau aperçu à travers le point B de la lentille et le point E à travers le point A. Mais si le point N se trouve en vérité au-dessus du point E, il sera maintenant vu en-dessous, parce que les points E¹⁾ et B sont situés de différents côtés de l'axe EAD. L'image de l'objet MN sera donc maintenant renversée. Or, le rapport de l'agrandissement apparent sera de nouveau, comme dans le cas précédent, égal à celui des longueurs BA et CA. Il faut donc démontrer que ce rapport, lorsque l'objet est rapproché, est composé des rapports AO:OD et ED:EP; et qu'il est égal à AO:OD, lorsque l'objet est situé à fort grande distance, ce qui ne peut avoir lieu que dans le second cas. Et la démonstration de ce théorème est la même que celle du théorème précédent. Il est donc manifeste que dans le deuxième cas les objets éloignés sont vus agrandis lorsque AO >> OD, et réduits, lorsque AO < OD, et en vraie grandeur lorsque AO = OD. Mais lorsqu'il s'agit d'un objet rapproché, et qu'on veut savoir quand cet objet doit être vu agrandi ou réduit, il faut examiner si le rapport AO:OD est plus grand ou plus petit que le rapport EP:ED, ou si les deux rapports sont égaux, car suivant que cela se trouve, le rapport qui est composé des rapports AO:OD et ED:EP, c'est-à-dire le rapport BA:CA, sera celui d'une quantité plus grande à une quantité plus petite, d'une plus petite à une plus grande ou enfin celui de deux quantités égales.

Il est d'ailleurs évident dans les deux cas, que le rapport de la grandeur apparente à la grandeur vraie augmente d'autant plus que l'objet se rapproche davantage du point correspondant P, l'oeil et la lentille demeurant fixes; cela résulte de ce que le rapport DE:EP augmente, tandisque le rapport AO:OD demeure invariable. On en conclut aussi qu'un objet placé précisément au point P doit être vu infiniment agrandi.

1) Lisez N.

[p. 183]

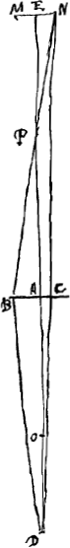[Fig. 6.]

E utroque modo per A cerni necesse est, quia radius ex E ad D nullus pervenit praeter EA qui utramque lentis superficiem secat ad rectos angulos, ideoque irrefractus permeat.

Constat itaque hic visibile cerni situ erecto quum puncta N et B sint ad easdem partes axis PAD. Rursusque ratio apparentis magnitudinis ad veram erit ea, quae BA ad CA. Quare, cum BA sit major quam CA (nam BA major est quam NE, et NE major quam CA) auctum magnitudine conspicietur visibile NE.

Porro in casu altero [Fig. 6] sit visibile MN positum ultra punctum correspondens P, et eadem construantur quae prius. Igitur per punctum lentis B rursus aspicietur punctum N, et E per A. Sed si N fuerit reipsa superius puncto E, nunc cernetur inferius, quia ad contrarias partes axis EAD sita sunt puncta E¹⁾ et B. Itaque inversum jam apparebit visibile MN. Ratio autem apparentis incrementi rursus ut in casu priore, erit ea quae BA ad CA; ideoque demonstrandum est rationem hanc, cum visibile propinquum est, componi ex rationibus AO ad OD et ED ad EP. Cum vero longinquum, quod tantum posteriore casu locum habet, eandem esse quae AO ad OD. Quae quidem demonstratio eadem est quae in Theoremate praecedenti. Itaque manifestum est posteriore casu majora cerni visibilia longinqua quando AO major fuerit quam OD, et minora cum minor, cumque aequalis, aequalia. Sed visibili propinquo, ut sciatur quando auctum vel diminutum spectari debeat, videndum utrum major ratio AO ad OD quam EP ad ED, an minor an aequalis. nam prout haec se habuerint, ratio quoque composita ex ratione AO ad OD et ED ad EP, hoc est, ratio BA ad CA erit majoris vel minoris inaequalitatis, vel denique aequalitas ipsa.

Manifestum autem utroque casu, quod quanto propius accedet visibile ad punctum correspondens, manente oculo et lente, tanto major erit ratio apparentis ad veram magnitudinem; crescente nimirum ratione DE ad EP, at ratione AO ad OD eadem manente; adeo ut positum in puncto ipso P, augeri debeat in infinitum.

1) Lisez N.

[p. 184]

Proposition IV.

Lorsque l'oeil est placé derrière une lentille concave, les images de tous les objets sont vues droites et plus petites que les objets eux-mêmes, et la grandeur apparente est à la grandeur vraie, lorsque l'objet est placé à grande distance, comme la distance entre la lentille et le point de dispersion est à la distance de ce point à l'oeil. Mais si l'objet est rapproché, le rapport de la grandeur apparente à la grandeur vraie se composera du rapport dont nous venons de parler, et du rapport de la distance entre l'oeil et l'objet d'une part et la distance de l'objet au point dirigeant²⁾ d'autre part.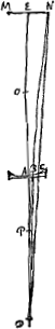

[Fig. 7.]

Soit AC la lentille concave, et AO son axe; soit O le point de dispersion, et D l'oeil placé sur l'axe. Supposons de plus que l'objet MEN se trouve de l'autre côté de la lentille, étant donc placé de la même manière que dans le théorème précédent. Prenons DP comme troisième proportionnelle aux deux longueurs DO et DA et dans le même sens que celles-là. P sera le point vers lequel tendent les rayons qui sont réfractés par la lentille AC de manière à se diriger vers l'oeil D, parceque les rayons qui proviennent de D et qui tombent sur cette même lentille sont réfractés de telle manière qu'ils semblent provenir du point P^*. Tirons la droite NP qui coupe la lentille en B et joignons les points B et D; tirons aussi la droite ND qui coupe la lentille en C. Le point N sera donc aperçu au point B, et la ligne NE correspondra à l'intervalle BA de la lentille, tandis qu'elle correspondrait à l'intervalle CA si au lieu de la lentille il y avait une surface plane où n'aurait lieu aucune réfraction.

On voit donc en premier lieu que l'image de l'objet MN est droite, vu que le point N de l'objet est aperçu à travers la lentille AC du même côté de l'axe où ce point se trouve en réalité; il en est nécessairement ainsi, parce que le point P est plus éloigné de NE que le point A.

Quant à notre thèse d'après laquelle l'image est plus petite que l'objet, la vérité en peut être démontrée de la façon suivante. EA:AP > EA:AD. D'où l'on tire par composition EP:PA > ED:DA. Mais EP:PA = NE:BA. Et ED:DA = EN:CA. Par conséquent, NE:BA > NE:CA; partant BA < CA. Or, le rapport de la grandeur apparente à la grandeur vraie est égal à BA:CA. Il est donc établi que la grandeur apparente est plus petite que la grandeur véritable.

On peut démontrer ensuite que le rapport BA:CA, lorsque l'objet est situé à grande distance, est égal au rapport de la distance de la lentille au point de

2) Dans la leçon primitive et la copie de Niquet le dernier mot manquait, étant indiqué toutefois par des points. Huygens semble donc avoir beaucoup hésité sur le nom à donner au point correspondant à l'oeil, c'est-à-dire au point dont l'image coïncide avec l'oeil et qui joue un rôle si important dans la formulation des propositions du Livre présent.
Quant à la proposition présente, elle conduit à la formule:



qui se déduit de celle de la note 2, p. 177 en remplaçant f par - f.

* Prop. XX, Liv. I.³⁾

3) Voir la p. 99 du Tome présent.

[p. 185]

Propositio [IV].

Posito oculo post lentem cavam, visibilia omnia erecta videntur et vero minora; habetque magnitudo apparens ad veram, si visibile fuerit longinquum, rationem eam quam distantia inter lentem et punctum dispergens¹⁾ ad distantiam hujus ab oculo. Si vero propinquum, rationem compositam ex illa quae dicta est, et ex ratione distantiae inter oculum et visibile ad distantiam visibilis a puncto directionis²⁾.

Esto lens cava AC, cujus axis AO; punctum dispergens O; oculus vero in axe positus sit D. Visibile vero ad alteram partem lentis MEN, ita situm uti in Theor. praecedenti. Et fiat duabus DO, DA tertia proportionalis DP, sumenda in partem eandem ac duae reliquae. Eritque P punctum quo tendentes radij flectuntur a lente AC versus oculum D, quoniam qui veniunt ab D in eandem lentem, ita flectuntur quasi procedant a puncto P^*. Ducatur recta NP secans lentem in B, et jungatur BD; ac denique recta ND secet lentem in C. Percipietur ergo punctum N in puncto B, lineaque NE occupabit in lente intervallum BA, quae occuparet intervallum CA, si loco lentis esset superficies refractionis expers.

Ac primum quidem apparet erectum spectari debere visibile MN, cum punctum ejus N spectetur in lente AC ad eandem partem axis ubi revera situm est; quod quidem necessario fieri liquet eo quod punctum P ulterius quam A distet ab NE.

Quod autem magnitudine diminutum spectabitur sic constabit. Ratio EAad AP major est quam EA ad AD. Unde et componendo, ratio EP ad PA major ratione ED ad DA. Sicut autem EP ad PA ita est NE ad BA. at sicut ED ad DA ita EN ad CA. Ergo major ratio NE ad BA quam NE ad CA; ideoque BA minor quam CA. Ratio autem apparentis ad veram magnitudinem est ea quae BA ad CA, itaque illam magnitudinem hac minorem esse constat.

Porro quod ratio BA ad CA, cum visibile longinquum est, eadem fiat, quae distantiae lentis a puncto dispersus ad distantiam hujus ab oculo, hoc est, quae AO

1) La leçon primitive et la copie de Niquet donnent ‘lentis a puncto dispergente’ Il s'agit du foyer virtuel des rayons parallèles ayant la direction EA.

2) Dans la leçon primitive et la copie de Niquet le dernier mot manquait, étant indiqué toutefois par des points. Huygens semble donc avoir beaucoup hésité sur le nom à donner au point correspondant à l'oeil, c'est-à-dire au point dont l'image coïncide avec l'oeil et qui joue un rôle si important dans la formulation des propositions du Livre présent.
Quant à la proposition présente, elle conduit à la formule:



qui se déduit de celle de la note 2, p. 177 en remplaçant f par - f.

* [Prop. XX, Lib. I.]³⁾

3) Voir la p. 99 du Tome présent.

[p. 186]

dispersion d'une part et de la distance de ce dernier point à l'oeil d'autre part, c. à. d. au rapport AO:OD; mais que, lorsque l'objet est situé plus près, il se compose du rapport dont nous venons de parler et du rapport DE:EP. Cette double démonstration est identique mot à mot à celle de la proposition II de ce Livre¹⁾.

Or, il résulte clairement de tout ceci que, lorsque l'oeil et la lentille concave demeurent fixes, le rapport de la grandeur apparente à la grandeur véritable devient d'autant plus petit que l'objet s'éloigne davantage de la lentille. En effet, le rapport DE:EP se rapproche alors de plus en plus de l'égalité.

Il est évident en outre que si l'oeil D se trouve très-près de la lentille C le point P lui aussi s'en rapproche indéfiniment, de sorte que les rapports AO:OD et DE:EP doivent alors l'un et l'autre être estimés égaux à l'unité. C'est pourquoi en ce cas ni les objets éloignés ni les objets situés à petite distance ne seront alors aperçus plus petits que lorsque la lentille est absente²⁾.

1) Voir la p. 179 du Tome présent.

2) Huygens a annoté ici, à une date beaucoup plus récente, probablement en 1684 ou plus tard: ‘Hinc perge ad Propositionem quae in fine pag. 76 a: Si sit angulus etc.’ Nous donnerons cette proposition comme Appendice III au Livre présent (voir la p. 238).
L'annotation, comme aussi celles que nous faisons suivre, prouve une fois de plus que Huygens avait alors en vue une révision assez étendue de toute sa ‘Dioptrique’.

Proposition V³⁾.

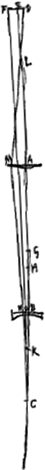[Fig. 8.]

Étant données deux lentilles et leurs positions tant celle de l'une par rapport à l'autre que celles par rapport à l'oeil et à l'objet, trouver dans quel rapport elles augmentent ou diminuent la grandeur de l'objetet si l'image qu'elles en donnent est droite ou renversée⁴⁾.

Il y a quatre combinaisons de deux lentilles, car elles peuvent être convexes l'une et l'autre, ou toutes les deux concaves; ou bien celle qui est le plus près de l'oeil peut être concave et l'autre convexe; ou inversement⁶⁾.

Supposons donc d'abord que les deux lentilles données soient la lentille convexe A et la lentille concave B, et que cette dernière soit placée le plus près de l'oeil [Fig. 8-12]. Supposons en outre l'oeil situé en C sur l'axe commun aux deux lentilles, et soit l'objet la ligne droite DF perpendiculaire à ce même axe et divisée par elle en E en deux parties égales.

3) Huygens a annoté plus tard: ‘Haec necessaria ad sequentem’ et ensuite ‘Haec universalis prop.^o ponenda non hic sed ante illam quae pag. 91’ [voir la Prop. VI, p. 199] ‘cui probandae praecipue conducit, tamen casus telescopij et microscopij rursus hic annotentur.’
Ajoutons que dans la leçon primitive et la copie Niquet la proposition présente était suivie de la Prop. III du Livre III (p. 253 du Tome présent), dont on trouvera une autre leçon plus récente et profondément altérée dans la Prop. IV de la troisième Partie de cette ‘Dioptrique’.
Quant aux cas ‘du télescope et du microscope,’ on les trouvera traités de même dans cette troisième Partie, là où il s'agit des lunettes à deux verres convexes et du microscope composé.

4) Plus tard, à une époque inconnue, Huygens ajouta: ‘Et ostendere in Telescopijs ex convexa et cava lente compositis res visas longe remotas augeri secundum rationem foci distantiae lentis convexae ad distantiam puncti dispersus lentis cavae. In telescopijs verò quae gemina convexa lente componuntur amplificationem istam fieri secundum rationem foci distantiae lentis convexae exterioris ad foci distantiam interioris sive ocularis.’ Toutefois ces phrases furent biffées depuis.

6) Aux lieux cités on lit encore: quarum secunda differentia minuendo visibile tantum idonea est: posterior et augere potest et minuere, sed nullo egregio effectu. Reliquae vero duae in augendis rerum speciebus, seu remotarum seu propinquarum, multo maximi sunt usus, ut pridem experientia cognitum est. Ratio autem omnium hic manifesta fiet. Nam quamvis positiones utiles tantum persequi propositum sit; tamen et reliquas quivis cum his comparare poterit, quia eodem modo in quavis differentia magnitudo apparens definitur.’

[p. 187]

ad OD; cum vero propinquum, eadem compositae ex jam dicta ratione et ex ratione DE ad EP: haec utraque ijsdem verbis demonstrantur ac in propositione [II hujus Libri]¹⁾.

Manifestum vero hinc est, manente oculo et lente cava, quo magis removebitur ab ea visibile, eo magis diminui rationem apparentis ad veram magnitudinem, quippe ratione DE ad EP magis ac magis accedente ad aequalitatem.

Manifestum quoque si oculus D sit lenti C proximus etiam punctum P proximum fieri, adeo ut aeque ratio AO ad OD, ac DE ad EP, tunc habendae sint pro ratione aequalitatis. Quamobrem nec longinqua nec propinqua tunc minora conspicientur quam lente remota²⁾.

1) Voir la p. 179 du Tome présent.

2) Huygens a annoté ici, à une date beaucoup plus récente, probablement en 1684 ou plus tard: ‘Hinc perge ad Propositionem quae in fine pag. 76 a: Si sit angulus etc.’ Nous donnerons cette proposition comme Appendice III au Livre présent (voir la p. 238).
L'annotation, comme aussi celles que nous faisons suivre, prouve une fois de plus que Huygens avait alors en vue une révision assez étendue de toute sa ‘Dioptrique’.

Propositio [V]³⁾.

Datis duabus lentibus, et positione earum, tam inter se, quam inter oculum et visibile, invenire qua proportione illud augeant vel imminuant, et utrum situ erecto an everso referant⁴⁾.

Duarum lentium quatuor sunt conjugationes⁵⁾, nam vel convexa est utraque, vel utraque cava; vel cava quae propior est oculo, altera convexa; vel contra⁶⁾.

Sint igitur primum propositae lentes duae, convexa A et concava B, ita ut haec oculo propior consistat [Fig. 8-12]. Sit autem oculus ad C, in communi duarum lentium axe constitutus; visibile vero DF sit linea recta eidem axi ad angulos

3) Huygens a annoté plus tard: ‘Haec necessaria ad sequentem’ et ensuite ‘Haec universalis prop.^o ponenda non hic sed ante illam quae pag. 91’ [voir la Prop. VI, p. 199] ‘cui probandae praecipue conducit, tamen casus telescopij et microscopij rursus hic annotentur.’
Ajoutons que dans la leçon primitive et la copie Niquet la proposition présente était suivie de la Prop. III du Livre III (p. 253 du Tome présent), dont on trouvera une autre leçon plus récente et profondément altérée dans la Prop. IV de la troisième Partie de cette ‘Dioptrique’.
Quant aux cas ‘du télescope et du microscope,’ on les trouvera traités de même dans cette troisième Partie, là où il s'agit des lunettes à deux verres convexes et du microscope composé.

4) Plus tard, à une époque inconnue, Huygens ajouta: ‘Et ostendere in Telescopijs ex convexa et cava lente compositis res visas longe remotas augeri secundum rationem foci distantiae lentis convexae ad distantiam puncti dispersus lentis cavae. In telescopijs verò quae gemina convexa lente componuntur amplificationem istam fieri secundum rationem foci distantiae lentis convexae exterioris ad foci distantiam interioris sive ocularis.’ Toutefois ces phrases furent biffées depuis.

5) La leçon primitive et la copie de Niquet donnent ‘esse variationes seu differentias constat.’

6) Aux lieux cités on lit encore: quarum secunda differentia minuendo visibile tantum idonea est: posterior et augere potest et minuere, sed nullo egregio effectu. Reliquae vero duae in augendis rerum speciebus, seu remotarum seu propinquarum, multo maximi sunt usus, ut pridem experientia cognitum est. Ratio autem omnium hic manifesta fiet. Nam quamvis positiones utiles tantum persequi propositum sit; tamen et reliquas quivis cum his comparare poterit, quia eodem modo in quavis differentia magnitudo apparens definitur.’

[p. 188]

On demande de trouver le rapport de la grandeur vue à travers les deux lentilles à la grandeur qu'on apercevrait sans lentilles.

Or, comme les lentilles sont données, on connaît aussi le foyer G de la lentille convexe correspondant aux rayons parallèles venant du côté de l'objet, et le point de dispersion H de la lentille concave. On doit donc construire d'abord une troisième proportionnelle CK aux deux longueurs CH et CB, laquelle doit être portée vers le point H; et ensuite une troisième proportionnelle KL aux deux longueurs KG et KA qui sera portée du côté de G, à moins que le point K ne coïncide avec le point G [Fig. 12]. Dans ce dernier cas on doit omettre la troisième proportionnelle KL¹⁾. Je dis maintenant que le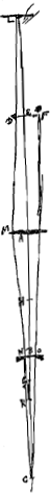

[Fig. 11.]

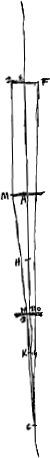[Fig. 12.]

rapport de la grandeur apparente vue à travers les lentilles à celle qu'on apercevrait à l'oeil nu est composé des rapports HB:HC, AG:GK et EC:EL ou bien dans le cas que nous avons excepté, celui où EL n'existe pas, des rapports HB:HC et EC:AK.

En effet, menons une droite par les points L et D qui coupe la lentille A en M, ou bien, dans le cas où L n'existe pas [Fig. 12], menons la droite DM parallèle à l'axe des lentilles. Tirons ensuite MK qui coupe la lentille B en N, et joignons les points N et C. Menons enfin du point F à l'oeil C la droite FC qui coupe la même lentille B en O. Vu que G est le foyer de la lentille convexe A, et que KG est à KA comme KA est à KL, il s'ensuit que les rayons qui issus du point K rencontrent la lentille A, sont réfractés de telle manière qu'ils correspondent ensuite au point L⁴⁾. D'où l'on conclut que réciproquement les rayons qui partent du point L, ou qui se dirigent vers lui en venant de l'autre côté de la lentille, se réuniront au point K. Et comme les longueurs CH, CB et CK forment une proportion et que H est le point de dispersion de la lentille B pour les rayons venant du côté A, il est établi que les rayons qui proviennent du point C sont réfractés par la lentille B de manière à correspondre ensuite au point K⁴⁾. D'où l'on conclut que réciproquement les rayons qui rencontrent la lentille B en venant de l'autre côté et qui se dirigent vers le point K seront réfractés de telle manière qu'ils se réuniront au point C. Il apparaît donc que le rayon DM qui va d'un point D de l'objet à la lentille A et qui correspond au point L est celui qui atteint l'oeil C après avoir été réfracté par la première lentille en M et par la seconde en N. L'oeil verra donc le point D au point N de la lentille B et la droite DE occupera dans la lentille B la partie BN. Or, la droite EF qui est égale à ED, occuperait dans cette même lentille B la partie OB si elle était aperçue sans aucune réfraction par les lentilles,

1) Puisque KG = o amène KL = ∞ d'après la proportion KG:KA = KA:KL.

4) D'après la Prop. XX du Liv. I, p. 99 du Tome présent.

4) D'après la Prop. XX du Liv. I, p. 99 du Tome présent.

[p. 189]

rectos, ab eoque in E bifariam divisa. Et oporteat invenire rationem magnitudinis per utramque lentem conspectae ad eam quae sine lentibus perciperetur.

Quia autem datae sunt lentes, datur et convexae focus G, radiorum a parte visibilis advenientium, et concavae punctum dispersus H. Igitur primum inveniatur duabus CH, CB tertia proportionalis CK, versus H sumenda. Deinde duabus KG, KA tertia proportionalis KL, sumenda versus G, nisi contingat punctum K incidere in G [Fig. 12], quo casu proportionalis KL omittenda¹⁾. Dico jam rationem apparentis magnitudinis trans lentes ad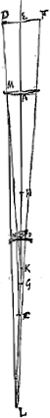

[Fig. 9]

[Fig. 10.]

eam quae nudo oculo spectaretur, habere rationem compositam ex rationibus HB ad HC, et AG ad GK, et EC ad EL, vel, in casu excepto, ubi deest EL, ex rationibus HB ad HC et EC ad AK.

Ducatur enim recta per L, D, secans lentem A in M, vel in casu quo deest L [Fig. 12], agatur DM axi lentium parallela. Deinde²⁾ ducatur MK secans lentem B in N, et jungatur NC. Et tandem ex F ad oculum C protendatur recta FC, secans eandem³⁾ lentem B in O. Quoniam igitur lentis convexae A focus est G, estque KG ad KA ut haec ad KL; sequitur radios qui à puncto K venientes occurrunt lenti A, ita flecti ut pertineant inde ad punctum L⁴⁾. Unde vicissim qui a puncto L exeunt vel ad ipsum feruntur, occurrentes lenti ab altera parte, concurrent ad punctum K. Rursus quia proportionales sunt CH, CB, CK, estque H punctum dispersus lentis B radiorum a parte A venientium; constat radios a C puncto venientes, flecti à lente B ut inde pertineant ad punctum K⁴⁾. Unde vicissim qui ab altera parte occurrunt lenti B tenduntque ad punctum K, ita inflectentur ut concurrant ad punctum C. Patet itaque radium DM, qui per punctum rei visibilis D ducitur ad lentem A, pertinetque ad punctum L, eum esse qui post refractionem in lente utraque primum in M, deinde in N, pervenit ad oculum C; a quo itaque cernetur punctum D in puncto N lentis B, occupabitque recta DE in lente B partem BN. recta autem EF ipsi ED aequalis, si nulla in lentibus refractione cerneretur, occuparet in eadem lente B partem OB, quoniam FOC recta est linea. Itaque ratio magnitudinis apparentis per lentes ad veram est ea quae rectae BN ad BO.

1) Puisque KG = o amène KL = ∞ d'après la proportion KG:KA = KA:KL.

2) La leçon primitive et la copie de Niquet donnent ‘Porro’.

3) Ce mot manque aux lieux cités.

4) D'après la Prop. XX du Liv. I, p. 99 du Tome présent.

4) D'après la Prop. XX du Liv. I, p. 99 du Tome présent.

[p. 190]

vu que FOC est une ligne droite. Le rapport de la grandeur apparente vue à travers les lentilles à la grandeur véritable est donc égale à BN:BO.

Or, le rapport BN:BO est composé des rapports BN:AM, AM:ED et ED:BO. Le premier, BN:AM, est égal à BK:AK. Et le deuxième AM:ED, est égal à AL:EL; ou bien, dans le cas [Fig. 12] où DM est parallèle à EA, au rapport de deux longueurs égales. Enfin, le troisième rapport ED ou FE:BO est égal à EC:BC. Le rapport BN:BO sera donc composé des rapports BK:AK, AL:EL (qui se réduit à celui de l'égalité dans le cas excepté) et EC:BC. Or, le rapport qui est composé des rapports BK:AK et EC:BC est égal au rapport qui se compose des rapports BK:BC et EC:AK. Par conséquent, le rapport BN:BO sera composé des rapports BK:BC, EC:AK et AL:EL, et, dans le cas excepté, des deux premiers seulement, vu que le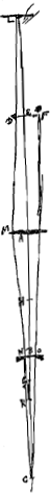

[Fig. 11.]

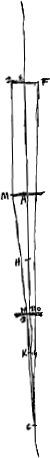[Fig. 12.]

rapport de deux longueurs égales n'augmente ni ne diminue les rapports avec lesquels on le compose. D'autre part le rapport qui est composé des rapports EC:AK et AL:EL est égal à celui qui se compose des rapports EC:EL et AL:AK. Par conséquent, le rapport BN:BO sera composé des rapports BK:BC, AL:AK et EC:EL; mais comme CH:CB = CB:CK, on aura aussi CH:HB = CB:BK, et, par inversion, HB:CH = BK:BC. De même, comme KG:KA = KA:KL, on aura aussi KG:AG = KA:LA, et, par inversion, AG:GK == AL:AK. Par conséquent, le rapport BN:BO, celui de la grandeur apparente à la grandeur vraie, sera composé des rapports HB:HC, AG:GK et EC:EL, et dans le cas excepté des rapports HB:HC et EC:AK.; ce qu' il fallait démontrer.

Il faut remarquer cependant que si la lentille concave B est placée de telle manière entre la lentille A et son foyer G que la distance BG est égale à la distance BH [Fig. 9 et 10] de la lentille B à son point de dispersion, ce qui est la position ordinaire dans un télescope de ce genre, parce que les rayons venant d'un point quelconque de l'objet parviennent alors parallèlement à l'oeil, la grandeur apparente d'un objet fort éloigné sera toujours la même en quelque endroit que l'oeil C soit placé derrière la lentille B: et que le rapport de la grandeur apparente à la grandeur vraie sera égal à AG:GB ou BH. En effet, il a été démontré que le rapport de la grandeur apparente à la grandeur vraie se compose des rapports HB:HC, AG:GK et EC:EL; de plus, le rapport EC:EL est ici celui de deux longueurs égales parce que l'objet est par hypothèse à grande distance et que, par conséquent, le point E est supposé infiniment éloigné tant de C que de L, dont la distance est ici finie. Il en résulte que le rapport de la grandeur apparente à la grandeur vraie est composé des rapports

[p. 191]

Ratio autem BN ad BO componitur ex rationibus BN ad AM et AM ad ED, et ED ad BO. quarum ratio prima BN ad AM est eadem quae BK ad AK. Secunda vero AM ad ED eadem quae AL ad EL; aut, in casu [Fig. 12], quo DM est parallela EA, eadem cum ratione aequalitatis. Et denique tertia ratio ED vel FE¹⁾ ad BO, eadem quae EC ad BC. Igitur ratio BN ad BO componetur ex rationibus BK ad AK, et AL ad EL, (cujus loco in casu excepto est

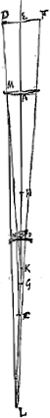[Fig. 9.]

[Fig. 10.]

ratio aequalitatis) et ex ratione EC ad BC. Ratio autem composita ex ratione BK ad AK, et EC ad BC est eadem compositae ex BK ad BC et EC ad AK. Igitur ratio BN ad BO componetur ex rationibus BK ad BC et EC ad AK et AL ad EL; et in casu excepto ex duabus prioribus tantum, cum ratio aequalitatis rationes quibuscum composita est non augeat nec imminuat. Rursus vero ratio composita ex EC ad AK et AL ad EL eadem est compositae ex EC ad EL et AL ad AK. Igitur ratio BN ad BO composita erit ex rationibus BK ad BC et AL ad AK et EC ad EL. quia autem CH ad CB ut CB ad CK, erit quoque CH ad HB ut CB ad BK: et invertendo, ratio HB ad CH eadem quae BK ad BC. Item quia KG ad KA ut KA ad KL, erit et KG ad AG ut KA ad LA; et invertendo, ratio AG ad GK eadem quae AL ad AK. Itaque ratio BN ad BO, apparentis nempe magnitudinis ad veram, componetur ex rationibus HB ad HC et AG ad GK et EC ad EL; et in casu excepto ex rationibus HB ad HC et EC ad AK. quod erat demonstr.

Notandum vero, si lens cava B ita posita sit inter lentem A focumque ejus G, ut distantia BG sit aequalis BH [Fig. 9 et 10] quae est inter lentem B et punctum suum dispersus, quae positio ordinaria est telescopij hujusmodi, qua nempe paralleli ad oculum feruntur radij a singulis rei visae punctis manantes²⁾, quod eadem tunc semper erit magnitudo apparens rei longinquae, quocunque loco oculus C post lentem B statuatur: ac ratio ejus ad veram magnitudinem ea quae AG ad GB vel BH³⁾. Cum enim ostensum sit rationem apparentis magnitudinis ad veram componi ex rationibus HB ad HC, et AG ad GK, et EC ad EL; cumque hic ratio EC ad EL sit aequalitatis, eo quod visibile longinquum ponatur; eoque punctum E censeatur

1) Ces deux mots manquaient dans la leçon primitive, où ils ont été ajoutés depuis. Ils manquent de même dans la copie de Niquet.

2) La leçon primitive et la copie de Niquet donnent: ‘ut postea dicetur’.

3) Les mots en italique manquaient dans la leçon primitive, où ils ont été ajoutés depuis. Ils manquent de même dans la copie de Niquet.

[p. 192]

HB:HC et AG:GK. Mais comme CH:CB = CB:CK, on aura aussi CH::CB = HB:BK, c.à.d. = GB:BK, vu que GB = HB. Donc aussi CH:HB == BG:GK et, par conversion, BH:HC = KG:GB. Par conséquent, le rapport de la grandeur apparente à la grandeur véritable est composé des rapports AG::GK et GK:GB; ce rapport sera donc égal au rapport AG:GB ou BH.

Il est done étali³⁾ que dans un télescope pourvud'une lentille convexe et d'une lentille concave la grandeur apparente des objets fort éloignés est à celle qu'on aperçoit à l'oeil nu, comme la distance focale de la lentille convexe est à la distance du point de dispersion à la lentille concave. Cela sera démontré de nouveau plus loin⁵⁾.

La considération des figures suffit pour faire voir si dans chaque cas particulier l'image doit apparaître droite ou renversée. On remarquera que l'image sera droite dans tous les cas excepté celui où le foyer G de la lentille A tombe entre la lentille et le point K, et où l'objet est en même temps situé au-delà du point L [Fig. 8]; car alors le point D est aperçu à travers le point N de la lentille B qui est situé de l'autre côté de l'axe EB, et l'image paraîtra donc nécessairement renversée.

Supposons maintenant que les deux lentilles soient convexes, et soit G [Fig. 13-21] de nouveau le foyer de la lentille A, et H le foyer de la lentille B;

3) La leçon primitive et la copie de Niquet donnent ‘Itaque’. De plus, on y trouve intercalé entre cet alinéa et celui qui précède le passage suivant, biffé depuis: ‘Porro quoque ex ante demonstratis colligitur, si punctum C incidat in B, hoc est si oculus lenti cavae prope admoveatur, quod lens cava tunc effectu carebit quantum ad apparentem visibilis magnitudinem, sive longinquum sive vicinum, quae tanta erit quanta foret si lente B amota per solam lentem A oculus intueretur. Cadat enim C in B [voir la figure de cette note]. Ergo et K in B incidet, quia continuè debent esse proportionales CH, CB, CK. Itaque jam ratio HB ad HC erit aequalitatis, quae cum in compositione pro nulla sit habenda, dicemus jam rationem apparentis magnitudinis ad veram componi ex rationibus, AG ad GK et EC ad EL, hoc est ex rationibus AG ad GB, et EB ad EL. Est autem duabus BG, BA tertia proportionalis BL, quia hae tres jam eaedem sunt quam KG, KA, KL. Ergo cum per ea quae supra demonstrata sunt, ratio apparentis magnitudinis ad veram, rei per solam lentem A spectatae posito oculo in C, similiter componatur ex rationibus AG ad GB et EB ad EL [d'après la Prop. II, p. 175; le point L étant ici conforme au “point dirigeant” P de la figure 3], apparet eam nunc plane eandem esse licet duae lentes inter oculum et visibile interjiciantur dummodo altera earum oculo contigua sit.
Apparet praeterea, etiam hic rationem EB ad EL, si visibile longinquum ponatur, fieri rationem aequalitatis; ideoque tunc rationem magnitudinis apparentis ad veram esse eam quae AG ad GB.’
Remarquons que, en effet, ce passage biffé était devenu superflu depuis la nouvelle rédaction donnée à la Prop. I, p. 174, laquelle conduit bien plus simplement à la même conclusion, c'est-à-dire à celle que dans le cas considéré la lentille B n'a aucun effet surle grossissement.

5) Aux lieux cités on trouve ‘distantia lentis convexae à foco suo, seu puncto concursus parallelorum a parte rei visae venientium, ad distantiam ejusdem foci a lente cava cui oculus admovetur; quod hucusque a nemine fuit demonstratum.’ On doit remarquer à ce propos que, vu aussi la manière dont cette règle a été déduite dans la leçon primitive et la copie de Niquet, elle est plus générale que celle dont Huygens s'est servi dans la leçon actuelle, puisqu' elle s'étend au cas où BG ≠ BH, c'est-à-dire, à celui où il n'y a pas de coïncidence des foyers.
Quant à la dernière phrase de cette leçon elle se rapporte à la Prop. I de la troisième Partie. Voir le dernier alinéa de la note 3, p. 187.

[p. 193]

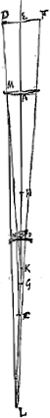[Fig. 9.]

[Fig. 10.]

infinitè remotum tam à C quam ab L, cujus hic definita est distantia¹⁾, componetur ergo ratio apparentis magnitudinis ad veram ex rationibus HB ad HC et AG ad GK. Quia autem ut CH ad CB ita CB ad CK, Erit etiam ut CH ad CB ita HB ad BK, hoc est, ita GB ad BK, quia GB aequalis HB. Itaque et CH ad HB, ut BG ad GK, et convertendo, BH ad HC ut KG ad GB. Proinde²⁾ ratio apparentis ad veram magnitudinem componitur ex rationibus AG ad GK et GK ad GB, hoc est, erit eadem ac ratio AG ad GB vel BH¹⁾.

Constat igitur³⁾ in telescopio, quod convexo et cavo vitro instructum sit, esse magnitudinum apparentem⁴⁾ rerum procul dissitarum ad eam quae nudo oculo percipitur, sicut foci distantia lentis convexae ad distantiam puncti dispersus a lente cava. Quod etiam in sequentibus ostendetur⁵⁾.

Porro ex sola inspectione schematum ad casus singulos, apparet utrum erectum cerni debeat visibile an eversum. Nempe omnibus casibus erectum appariturum praeterquam in [illo casu] ubi nimirum focus G lentis A cadit inter ipsam et punctum K, simulque visibile remotum est ultra punctum L [Fig. 8]. hic enim punctum D spectatur per punctum N lentis B quod ad alteram partem axis EB situm est, ideoque visibile eversum spectari necesse est.

Proponatur nunc convexa lens utraque, et rursus lentis A [Fig. 13-21] sit focus G; lentis vero B focus H, uterque a

1)




Les mots en italique manquaient dans la leçon primitive, où ils ont été ajoutés depuis. Ils manquent de même dans la copie de Niquet.

2) La leçon primitive et la copie de Niquet donnent ‘Itaque’.

1)




Les mots en italique manquaient dans la leçon primitive, où ils ont été ajoutés depuis. Ils manquent de même dans la copie de Niquet.

3) La leçon primitive et la copie de Niquet donnent ‘Itaque’. De plus, on y trouve intercalé entre cet alinéa et celui qui précède le passage suivant, biffé depuis: ‘Porro quoque ex ante demonstratis colligitur, si punctum C incidat in B, hoc est si oculus lenti cavae prope admoveatur, quod lens cava tunc effectu carebit quantum ad apparentem visibilis magnitudinem, sive longinquum sive vicinum, quae tanta erit quanta foret si lente B amota per solam lentem A oculus intueretur. Cadat enim C in B [voir la figure de cette note]. Ergo et K in B incidet, quia continuè debent esse proportionales CH, CB, CK. Itaque jam ratio HB ad HC erit aequalitatis, quae cum in compositione pro nulla sit habenda, dicemus jam rationem apparentis magnitudinis ad veram componi ex rationibus, AG ad GK et EC ad EL, hoc est ex rationibus AG ad GB, et EB ad EL. Est autem duabus BG, BA tertia proportionalis BL, quia hae tres jam eaedem sunt quam KG, KA, KL. Ergo cum per ea quae supra demonstrata sunt, ratio apparentis magnitudinis ad veram, rei per solam lentem A spectatae posito oculo in C, similiter componatur ex rationibus AG ad GB et EB ad EL [d'après la Prop. II, p. 175; le point L étant ici conforme au “point dirigeant” P de la figure 3], apparet eam nunc plane eandem esse licet duae lentes inter oculum et visibile interjiciantur dummodo altera earum oculo contigua sit.
Apparet praeterea, etiam hic rationem EB ad EL, si visibile longinquum ponatur, fieri rationem aequalitatis; ideoque tunc rationem magnitudinis apparentis ad veram esse eam quae AG ad GB.’
Remarquons que, en effet, ce passage biffé était devenu superflu depuis la nouvelle rédaction donnée à la Prop. I, p. 174, laquelle conduit bien plus simplement à la même conclusion, c'est-à-dire à celle que dans le cas considéré la lentille B n'a aucun effet surle grossissement.

4) La leçon primitive et la copie de Niquet donnent ‘erit magnitudo apparens.’

5) Aux lieux cités on trouve ‘distantia lentis convexae à foco suo, seu puncto concursus parallelorum a parte rei visae venientium, ad distantiam ejusdem foci a lente cava cui oculus admovetur; quod hucusque a nemine fuit demonstratum.’ On doit remarquer à ce propos que, vu aussi la manière dont cette règle a été déduite dans la leçon primitive et la copie de Niquet, elle est plus générale que celle dont Huygens s'est servi dans la leçon actuelle, puisqu' elle s'étend au cas où BG ≠ BH, c'est-à-dire, à celui où il n'y a pas de coïncidence des foyers.
Quant à la dernière phrase de cette leçon elle se rapporte à la Prop. I de la troisième Partie. Voir le dernier alinéa de la note 3, p. 187.

[p. 194]

l'un et l'autre se trouvant du côté opposé à celui où est placé l'objet FED. L'oeil est en C. Soient CH, CB, CK trois grandeurs qui forment une proportion continue,

[Fig. 17.]

[Fig. 18.]

et KG, KA, KL de même. Supposons le reste construit comme auparavant. Tout ce qui a été dit plus haut à propos de la grandeur apparente de l'image formée par la lentille convexe combinée avec la lentille concave, sera applicable également aux deux lentilles que nous considérons maintenant, et la démonstration sera la même. Seulement l'oeil C peut ici être placé au point H [Fig. 17], auquel cas on ne peut pas trouver le point K, mais où l'on doit prendre AL = AG et tirer du point D la droite DLM qui rencontre la lentille A en M, d'où l'on doit mener la droite MN parallèle à l'axe AB, laquelle rencontre la lentille B en N. Il faut ensuite joindre les points N et C. La démonstration est la suivante. Le rapport BN:BO [Fig. 17], celui de la grandeur apparente à la grandeur vraie, est composé des rapports BN:DE ou AM:DE et DE:BO. De ces rapports le premier AM:DE est égal à AL:LE, et le second DE:BO à EC:BC. Le rapport BN:BO se compose donc des rapports AL:LE et EC:BC, c'est-à-dire des rapports AL:BC et EC:EL²⁾. D'où l'on conclut que si l'objet est placé à grande distance, vu qu'alors le rapport EC:EL est égal à l'unité, le rapport AL:BC sera le seul qui reste et qui représentera celui de la grandeur apparente à la grandeur vraie. Or, AL est la distance focale de la lentille A, vu que AL = AG, et BC est la distance focale de la lentille B³⁾.

Lorsque le point K coïncide avec le centre de la lentille A [Fig. 18], ce qui arrive lorsque l'oeil C est placé de telle manière qu'une troisième proportionnelle CK prise par rapport aux deux longueurs CH et CB se trouve être égale à la distance CA, le point L coïncidera également avec le centre de la lentille A, et le rapport de la grandeur apparente à la grandeur vraie sera composé des seuls rapports HB:HC

2) Dans le cas traité le rapport AL:BC remplace donc le rapport composé de HB:HC et de AG:GK, lequel a servi (voir la p. 189) dans le cas général, mais qui perd ici toute signification puisqu'on a HC = o et que GK est devenu infini.

3) Huygens annota ici en marge: ‘vide ad dioptr. spectantia ubi haec mutavi’. Quoique nous possédions une feuille séparée qui porte la suscription ‘Ad Dioptricen spectantia’, écrite de la main de Huygens, nous n'avons pu trouver la nouvelle leçon mentionnée.

[p. 195]

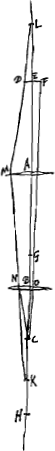[Fig. 13.]

[Fig. 14.]

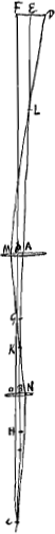[Fig. 15.]

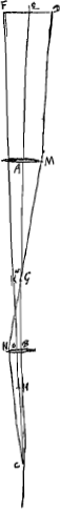[Fig. 16.]

visibili FED aversus. Oculus vero¹⁾ in C. Et continuè proportionales CH, CB, CK, itemque KG, KA, KL; et reliqua similiter uti prius construantur. Et omnia quae modo de convexa et cava lente dicta fuere ad apparentem magnitudinem attinentia, etiam his lentibus convenient, eademque erit demonstratio. Nisi quod hic potest poni oculus C in puncto H [Fig. 17], quo casu punctum K non invenitur, sed sumenda est AL aequalis AG, et ex puncto D ducenda recta DLM occurrens lenti A in M, unde parallela facienda MN axi AB, quae occurrat lenti B in N, et jungenda NC. Demonstratioque erit hujusmodi: Ratio BN ad BO [Fig. 17], nempe apparentis magnitudinis ad veram, componitur ex rationibus BN seu AM ad DE et DE ad BO. Quarum AM ad DE eadem est quae AL ad LE: et DE ad BO eadem quae EC ad BC. Ergo ratio BN ad BO componetur ex rationibus AL ad LE et EC ad BC, hoc est, ex rationibus LA ad BC et EC ad EL²⁾. Unde si visibile longinquum fuerit, quia tunc ratio EC ad EL est aequalitatis, supererit sola ratio AL ad BC, quae erit apparentis magnitudinis ad veram. Est autem AL foci distantia lentis A, quippe aequalis AG; et BC foci distantia lentis B³⁾.

Quando autem punctum K incidit in centrum lentis A [Fig. 18], quod contingit quando oculus C ita positus est, ut, sumta duabus CH, CB tertia proportionali CK, ea aequetur distantiae CA; etiam punctum L eodem incidet, ratioque magni-

1) On trouve aux lieux cités: ‘lentis vero focus H et oculus in C.’

2) Dans le cas traité le rapport AL:BC remplace donc le rapport composé de HB:HC et de AG:GK, lequel a servi (voir la p. 189) dans le cas général, mais qui perd ici toute signification puisqu'on a HC = o et que GK est devenu infini.

3) Huygens annota ici en marge: ‘vide ad dioptr. spectantia ubi haec mutavi’. Quoique nous possédions une feuille séparée qui porte la suscription ‘Ad Dioptricen spectantia’, écrite de la main de Huygens, nous n'avons pu trouver la nouvelle leçon mentionnée.

[p. 196]

et EC:EL, parce que le troisième rapport AG:GK est alors égal à l'unité. Et cette disposition de l'oeil est utile dans le cas des télescopes et des microscopes¹⁾, attendu qu' une grande partie de l'objet est alors aperçue d'un seul regard, puisque l'image remplit toute la lentille B, même si l'ouverture de la lentille A est fort petite.

Mais quand il arrivera que le foyer G [Fig. 20] de la lentille A tombe entre cette lentille et la lentille B et que la distance GB est égale à la distance BH, c'est-à-dire à la distance focale de la lentille B, le rapport de la grandeur apparente à la grandeur vraie d'un objet placé à grande distance sera égal à AG:GB, en quelque point de l'axe des lentilles que l'on place l'oeil C. Il sera donc égal au rapport des distances focales de la lentille extérieure et de la lentille intérieure, c'est-à-dire de la lentille placée près de l'oeil, comme cela a été démontré plus haut dans le cas de la lentille convexe combinée avec la lentille concave⁷⁾. En effet, la démonstration donnée dans ce cas est applicable également au cas que nous considérons maintenant. Or, c'est là la disposition ordinaire dans les télescopes à deux lentilles convexes par laquelle il se fait que ceux qui ont la vue sans défaut voient clairement les objets situés à grande distance⁹⁾.

D'ailleurs, comme auparavant, il ressort clairement de la considération des figures dans chaque cas particulier si l'image est aperçue droite ou renversée. Car là où les points N et D se trouvent du même côté de l'axe AB, l'image apparaîtra droite, mais là où ces points se trouvent de différents côtés de l'axe, elle sera renversée, et il appert que l'un aussi bien que l'autre peut avoir lieu dans différents cas qu'il ne vaut pas la peine d'examiner à part.

1) C'est-à-dire, la disposition où l'oeil est placé à l'endroit où l'image de l'objectif est formée par l'oculaire. Consultez encore à ce propos les Prop. III et IV du Liv. III (pp. 255 et 259 du Tome présent) et de même les propositions de la troisième Partie de cette ‘Dioptrique’, lesquelles traitent le télescope à deux verres convexes et le microscope composé.

7) Voir la p. 191 du Tome présent, à commencer par les mots: ‘Notandum vero’.

9) Huygens annota encore en marge à propos des figures 13-22: ‘an addendus casus cum ocularis ponitur in foco anterioris lentis?’ (phrase qu'on retrouve dans la copie de Niquet). Mais il ajouta plus tard ‘nil opus’. En effet, la figure qu'il ne manqua pas de dessiner, tout en la biffant ensuite, ne diffère de la fig. 14 que par la seule circonstance que le point G s'y trouve marqué dans l'intérieur de la lentille B.

[p. 197]

tudinis apparentis ad veram componetur tantum ex rationibus HB ad HC et EC ad EL, quia ratio tertia AG ad GK jam est aequalitatis. Et haec quidem oculi dispositio utilis est in telescopijs ac microscopijs¹⁾, quia magna rei visae pars uno intuitu sic percipitur, totam lentem B complente imagine, etiam si lentis A minima fuerit apertura²⁾

Quandocunque autem³⁾ foco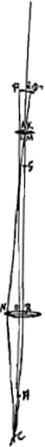

[Fig. 19.]

[Fig. 20.]

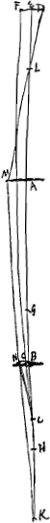[Fig. 21.]

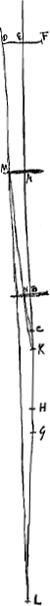[Fig. 22.]

G [Fig. 20] lentis A cadente inter ipsam lentemque B, distantia GB aequalis erit⁴⁾ BH, qua distat a lente B focus suus H: erit ratio⁵⁾ apparentis ad veram magnitudinem rei longinquae, ubicunque oculus C in axe lentium⁶⁾ ponatur ea quae AG ad GB, hoc est ea quae foci distantiarum lentis exterioris atque interioris sive oculo proximae⁶⁾, sicut ante in compositione lentis convexae cum cava ostensum est⁷⁾. Demonstratio enim eadem quae illic habetur etiam huic casui accomodata est⁶⁾. Haec vero⁸⁾ ordinaria est telescopij ex duabus convexis dispositio, qua nempe fit ut, qui nullo visus vitio laborant, res remotas distincte contueantur⁹⁾.

De caetero utrum erecto situ an everso visibile spectetur¹⁰⁾, ex figuris cujusque casus hic quoque manifestum est. Nempe ubi puncta N et D reperiuntur ad eandem partem axis AB, erectum spectabitur visibile; ubi vero ad contrarias axis partes, inversum erit, atque apparet utrumque horum varijs casibus contingere posse, de quibus singillatim inquirere operae pretium non est.

1) C'est-à-dire, la disposition où l'oeil est placé à l'endroit où l'image de l'objectif est formée par l'oculaire. Consultez encore à ce propos les Prop. III et IV du Liv. III (pp. 255 et 259 du Tome présent) et de même les propositions de la troisième Partie de cette ‘Dioptrique’, lesquelles traitent le télescope à deux verres convexes et le microscope composé.

2) Ces mots en italique furent ajoutés à une époque postérieure à celle où la copie de Niquet fut prise.

3) La leçon primitive et la copie de Niquet donnent ‘At cum’.

4) Aux lieux cités: ‘est’.

5) Aux lieux cités le mot ‘rursus’ se trouve intercalé.

6) Mots qui manquent aux lieux cités.

6) Mots qui manquent aux lieux cités.

7) Voir la p. 191 du Tome présent, à commencer par les mots: ‘Notandum vero’.

6) Mots qui manquent aux lieux cités.

8) Aux lieux cités: ‘Et haec’.

9) Huygens annota encore en marge à propos des figures 13-22: ‘an addendus casus cum ocularis ponitur in foco anterioris lentis?’ (phrase qu'on retrouve dans la copie de Niquet). Mais il ajouta plus tard ‘nil opus’. En effet, la figure qu'il ne manqua pas de dessiner, tout en la biffant ensuite, ne diffère de la fig. 14 que par la seule circonstance que le point G s'y trouve marqué dans l'intérieur de la lentille B.

10) Aux lieux cités ‘representetur’.

[p. 198]

Proposition VI. Théorème¹⁾.

Lorsqu' un objet est vu à travers un nombre quelconque de lentilles, et qu'on intervertit les positions de l'oeil et de l'objet tandis que les lentilles demeurent en place, la grandeur apparente de l'objet sera la même et l'image aura la même position, droite ou renversée²⁾.

1) Ce théorème fut mentionné pour la première fois dans une lettre à Kinner à Löwenthurn du 16 déc. 1653 (p. 261 du T. I). Comme Bosscha l'a remarqué (Arch. Néerl. 1^e Sér. T. XXIX (1896), p. 394) il constitue bien certainement le premier théorème trouvé et publié (en 1703) qui s'applique à un système centré quelconque de lentilles et de plus il contient en germe toute la théorie d'un tel système. Pour le reconnaître il suffira de considérer (avec Bosscha) sur l'axe d'un système C...D, six points successiss A, B, C, D, E, F, dont C et D représentent les lentilles extrêmes, E l'image de A, F celui de B. Posons alors AC = x, BC = x′, DE = y, DF = y′. Si donc un objet de hauteur h est placé en A, l'oeil, que nous supposons se trouver en F, verra l'image formée en E sous un angle Gh::(y′-y), lorsque G est l'agrandissement. Si, au contraire, le même objet se trouve en F, l'oeil en A, il se formera une image en B qui se montrera à l'oeil sous un angle h:G'(x-x′), lorsque G' est l'agrandissement de l'image en F d'un objet qui se trouverait en B. Or, d'après le théorème de Huygens, ces deux angles sont égaux. On a donc .
Pour introduire ensuite dans cette équation les constantes du système, on pourra supposer que l'objet se trouve placé en C, contre l'objectif, que l'image se forme alors à une distance o₂ en arrière de D et que son agrandissement soit G₂. En introduisant ces deux constantes de l'appareil dans la formule au lieu de y′ et de G′, on aura . De même, si nous supposons que l'image se sorme en D, la distance de l'objet à C sera une autre constante du système que nous désignons par o₁. Il en sera de même de l'agrandissement G₁ de l'image en D. On aura donc encore . De ces deux dernières équations on peut éliminer soit G, soit x, et arriver de cette manière à des formules de la forme r+sx+ qui suffisent pour résoudre tous les problèmes relatifs au lieu et à la grandeur des images, ou plus généralement à la marche d'un rayon à travers le système. Quant à la signification optique des constantes o₁, o₂, G₁ et G₂ et quelques autres considérations qui se rapportent à ce qui précède nous renvoyons à la note originale de Bosscha.
Voici, d'ailleurs, une démonstration du théorème de Huygens pour le cas général où l'indice de réfraction n et le rayon de courbure R des surfaces de densité égale varient continûment le long de l'axe.
Soient x et y les coordonnées cartésiennes des points d'un rayon, x étant compté le long de l'axe et y perpendiculairement sur lui. Soient , y₊₁) trois points consécutifs du même rayon, où les indices sont n_-1, n, n₊₁. Remplaçons d'abord la distribution continue de la matière transparente par une autre où l'indice change subitement à la surface de densité égale qui passe par P de la valeur ½(n_-1+n) à la valeur ½(n+n₊₁); on aura alors, négligeant les infiniments petits de second ordre:







On en déduit ensuite par les substitutions:















l'équation différentielle:




Soient maintenant P₁ et P₂ deux points de l'axe, x₁ et x₂ leurs coordonnées, y = u et y = v les équations de rayons passant respectivement par P₁ et par P₂; soit, de plus, u₂ la valeur de u pour x = x₂, c'est-à-dire, dans le voisinage du point P₂, v₁ celle de v dans le voisinage du point P₁.
Alors les grossissements g₁, d'un objet placé en P₂ et vu de P₁, et g₂, d'un objet en P₁ vu de P₂, seront:



et on aura:




Or, puisque u et v satisfont à l'équation différentielle déduite plus haut, on trouve aisément:



ou bien, en intégrant:



où C est une constante.
Aux voisinages des points P₁ et P₂ cette dernière formule se réduit respectivement à:



donc g₁:g₂ = n₂:n₁; d'où résulte, pour n₂ = n₁, le théorème en question.
Voir encore sur ce théorème (en outre de la partie de l'Avertissement laquelle traite le Livre présent) l'Appendice IV (p. 240), qui en contient une vérification numérique par Huygens, datant de 1692. Ajoutons qu'on en rencontrera des applications remarquables aux Prop. III et IV du Liv. III, pp. 257 et 261; voir surtout la note 1 de la p. 256.

2) Plus tard Huygens souligna les deux mots ‘similique situ’ et il ajouta en marge: ‘omittatur forsan de situ quia in binis vitris longa est demonstr.’ On remarquera que, en effet, cette démonstration manque dans le texte; probablement elle n'a jamais été rédigée.

[p. 199]

[Propositio VI.] Theorema¹⁾.

Si per lentes quotlibet visibile conspiciatur, ijsque manentibus oculus et visibile vicissim loca permutent. Eâdem hoc quâ prius magnitudine apparebit, similique situ²⁾.

1) Ce théorème fut mentionné pour la première fois dans une lettre à Kinner à Löwenthurn du 16 déc. 1653 (p. 261 du T.I). Comme Bosscha l'a remarqué (Arch. Néerl. 1^e Sér. T. XXIX (1896), p. 394) il constitue bien certainement le premier théorème trouvé et publié (en 1703) qui s'applique à un système centré quelconque de lentilles et de plus il contient en germe toute la théorie d'un tel système. Pour le reconnaître il suffira de considérer (avec Bosscha) sur l'axe d'un système C...D, six points successiss A, B, C, D, E, F, dont C et D représentent les lentilles extrêmes, E l'image de A, F celui de B. Posons alors AC = x, BC = x′, DE = y, DF = y′. Si donc un objet de hauteur h est placé en A, l'oeil, que nous supposons se trouver en F, verra l'image formée en E sous un angle Gh::(y′-y), lorsque G est l'agrandissement. Si, au contraire, le même objet se trouve en F, l'oeil en A, il se formera une image en B qui se montrera à l'oeil sous un angle h:G'(x-x′), lorsque G' est l'agrandissement de l'image en F d'un objet qui se trouverait en B. Or, d'après le théorème de Huygens, ces deux angles sont égaux. On a donc .
Pour introduire ensuite dans cette équation les constantes du système, on pourra supposer que l'objet se trouve placé en C, contre l'objectif, que l'image se forme alors à une distance o₂ en arrière de D et que son agrandissement soit G₂. En introduisant ces deux constantes de l'appareil dans la formule au lieu de y′ et de G′, on aura . De même, si nous supposons que l'image se sorme en D, la distance de l'objet à C sera une autre constante du système que nous désignons par o₁. Il en sera de même de l'agrandissement G₁ de l'image en D. On aura donc encore . De ces deux dernières équations on peut éliminer soit G, soit x, et arriver de cette manière à des formules de la forme r+sx+ qui suffisent pour résoudre tous les problèmes relatifs au lieu et à la grandeur des images, ou plus généralement à la marche d'un rayon à travers le système. Quant à la signification optique des constantes o₁, o₂, G₁ et G₂ et quelques autres considérations qui se rapportent à ce qui précède nous renvoyons à la note originale de Bosscha.
Voici, d'ailleurs, une démonstration du théorème de Huygens pour le cas général où l'indice de réfraction n et le rayon de courbure R des surfaces de densité égale varient continûment le long de l'axe.
Soient x et y les coordonnées cartésiennes des points d'un rayon, x étant compté le long de l'axe et y perpendiculairement sur lui. Soient , y₊₁) rois points consécutifs du même rayon, où les indices sont n_-1, n, n₊₁. Remplaçons d'abord la distribution continue de la matière transparente par une autre où l'indice change subitement à la surface de densité égale qui passe par P de la valeur ½(n_-1+n) à la valeur ½(n+n₊₁); on aura alors, négligeant les infiniments petits de second ordre:




On en déduit ensuite par les substitutions:



l'équation différentielle:




Soient maintenant P₁ et P₂ deux points de l'axe, x₁ et x₂ leurs coordonnées, y = u et y = v les équations de rayons passant respectivement par P₁ et par P₂; soit, de plus, u₂ la valeur de u pour x = x₂, c'est-à-dire, dans le voisinage du point P₂, v₁ celle de v dans le voisinage du point P₁.
Alors les grossissements g₁, d'un objet placé en P₂ et vu de P₁, et g₂, d'un objet en P₁ vu de P₂, seront:



et on aura:




Or, puisque u et v satisfont à l'équation différentielle déduite plus haut, on trouve aisément:



ou bien, en intégrant:



où C est une constante.
Aux voisinages des points P₁ et P₂ cette dernière formule se réduit respectivement à:



donc g₁:g₂ = n₂:n₁; d'où résulte, pour n₂ = n₁, le théorème en question.
Voir encore sur ce théorème (en outre de la partie de l'Avertissement laquelle traite le Livre présent) l'Appendice IV (p. 240), qui en contient une vérification numérique par Huygens, datant de 1692. Ajoutons qu'on en rencontrera des applications remarquables aux Prop. III et IV du Liv. III, pp. 257 et 261; voir surtout la note 1 de la p. 256.

2) Plus tard Huygens souligna les deux mots ‘similique situ’ et il ajouta en marge: ‘omittatur forsan de situ quia in binis vitris longa est demonstr.’ On remarquera que, en effet, cette démonstration manque dans le texte; probablement elle n'a jamais été rédigée.

[p. 200]

Considérons d'abord le cas où une lentille unique A [Fig. 23-26]¹⁾ est placée entre l'oeil situé au point D et l'objet situé au point E. Je dis que si l'oeil est transporté en E et l'objet en D, tandisque la lentille demeure en place, la grandeur

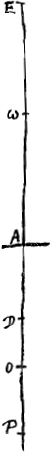[Fig. 25.]

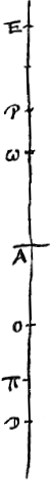[Fig. 26.]

apparente de l'objet sera la même que lorsque l'oeil se trouvait au point D et l'objet au point E.

En effet, soit O le foyer de la lentille A, c'est-à-dire le point qui correspond aux rayons parallèles venant du côté de E. Prenons DP comme troisième proportionelle aux deux grandeurs DO et DA, et portons DP du côté de O. Le point P est donc conjugué avec l'oeil qui se trouve au point D. C'est pourquoi, d'après la prop. II²⁾, ou III³⁾, ou IV⁴⁾, lorsque l'oeil est placé en D, le rapport de la grandeur apparente de l'objet placé en E à sa grandeur véritable sera composé des rapports AO:OD et DE:EP. Pour ces mêmes raisons, lorsque l'oeil sera placé en E et l'objet en D, qu'on aura pris Aω = AO et Eπ comme troisième proportionelle aux deux grandeurs Eω et EA, le rapport de la grandeur apparente de l'objet placé en D à sa grandeur véritable sera composé des rapports Aω:ωE et ED:Dπ.

Par conséquent, comme dans les deux positions la grandeur véritable de l'objet est évidemment la même, il s'agit de démontrer que le rapport de la grandeur apparente à la grandeur véritable est le même dans les deux cas. En d'autres termes, il faut démontrer que le rapport composé des rapports AO::OD et DE:EP, c'est-à-dire le rapport des rectangles AO, DE et OD, EP est égal au rapport composé des rapports Aω::ωE et ED:Dπ, c'est-à-dire au rapport des rectangles Aω, ED et ωE, Dπ. Or, les premiers termes des deux rapports sont égaux entre eux, c'est-à-dire le rectangle AO, DE est égal au rectangle Aω, DE, vu que AO = Aω; il suffit donc de faire voir que le rectangle OD, EP est égal au rectangle ωE, Dπ. Cela peut se faire comme suit. Comme DO:DA == DA:DP, on aura aussi DO:OA = DA:AP, et, par permutation, OD:DA == OA (ou ωA):AP. Donc aussi OD:OA = ωA:ωP. D'autre part, comme Eω::EA = EA:Eπ, nous aurons Eω:ωA = EA:Aπ et, par permutation, Eω:EA = ωA (ou OA):Aπ, d'où résulte Eω:ωA = OA:Oπ. Mais nous avions trouvé ωA:ωP = OD:OA. Nous avons donc, par la règle de la proportion dérangée⁵⁾, Eω:ωP = OD:Oπ, et par conséquent aussi Eω:EP = OD:Dπ. C'est pourquoi le rectangle Eω, Dπ est égal au rectangle EP, OD. Ce qu'il fallait démontrer.

1) À propos de la fig. 23, Huygens annota en marge: ‘Cadat potius P intra E ut inversum spectetur. nam eadem est demonstr.’ C'est le cas de la fig. 26, qui fut dessinée plus bas sur la même feuille du manuscrit.

2) Voir la p. 175 du Tome présent.

3) Voir la p. 181.

4) Voir la p. 185.

5) Voir la note 1, p. 103.

[p. 201]

Primùm esto lens unica A [Fig. 23-26]¹⁾, posita inter oculum in D et visibile in E. dico si oculus transeat in E et visibile in D, lente A non mota, quod eadem sic magnitudine spectabitur, atque cum oculus erat in D et visibile in E.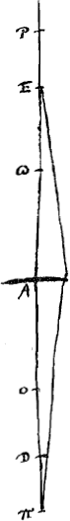

[Fig. 23.]

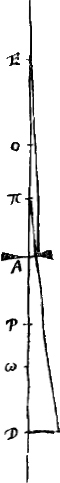[Fig. 24.]

Sit enim O focus lentis A seu punctum quo pertinent radij paralleli venientes a partibus E. Et duabus DO, DA sit tertia proportionalis DP sumpta versus O. Est igitur punctum P oculo in D conjugatum. Quapropter per propos. [II]²) aut [III]³⁾ aut [IV]⁴⁾, oculo in D constituto ratio magnitudinis apparentis ad veram visibilis in E erit ea quae componitur ex rationibus AO ad OD et DE ad EP. Per haec eadem, cum oculus ponetur in E et visibile in D, sumptâ Aω aequali AO, et duabus Eω, EA tertia proportionali Eπ, erit ratio magnitudinis apparentis ad veram visibilis in D, composita ex rationibus Aω ad ωE et ED ad Dπ.

Itaque cum utraque positione vera magnitudo sit prorsus eadem, oportet ostendere rationem magnitudinis apparentis ad veram utrobique eandem esse. Hoc est rationem compositam ex rationibus AO ad OD et DE ad EP, quae est ratio rectang.ⁱ AO, DE ad rectang.^m OD, EP, esse eandem rationi compositae ex rationibus Aω ad ωE et ED ad Dπ, hoc est rationi rectang.ⁱ Aω, ED ad rectang. ωE, Dπ. Atqui priores termini rationum sunt aequales, hoc est, rectang. AO, DE aequale rectang. Aω, DE, quoniam AO aequalis Aω, ergo opus tantum est ostendere, quod rectang. OD, EP aequale rectang. ωE, Dπ. Quia ergo DO ad DA ut DA ad DP, erit et DO ad OA ut DA ad AP, et permutando OD ad DA ut OA sive ωA ad AP; quare et OD ad OA ut ωA ad ωP. Rursus cum sit Eω ad EA ut EA ad Eπ erit Eω ad ωA ut EA ad Aπ, et permutando Eω ad EA ut ωA sive OA ad Aπ, quare et Eω ad ωA, ut OA ad Oπ. Erat autem ut ωA ad ωP ita OD ad OA. Ergo ex aequali in perturbata proportione⁵⁾ erit Eω ad ωP ut OD ad Oπ. ideoque et Eω ad EP ut OD ad Dπ. Quare rectang. Eω, Dπ aequale rectang.^o EP, OD, quod erat ostendendum.

1) À propos de la fig. 23, Huygens annota en marge: ‘Cadat potius P intra E ut inversum spectetur. nam eadem est demonstr.’ C'est le cas de la fig. 26, qui fut dessinée plus bas sur la même feuille du manuscrit.

2 Voir la p. 175 du Tome présent.

3) Voir la p. 181.

4) Voir la p. 185.

5) Voir la note 1, p. 103.

[p. 202]

Quant à la question de la position, c'est-à-dire, de savoir si l'image est droite ou renversée, il est manifeste si la lentille est concave [Fig. 24] que l'image sera dans la même position dans les deux cas, vu que pour celui qui regarde à travers une lentille de cette espèce toutes les images sont droites¹⁾. Mais

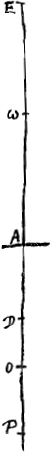[Fig. 25.]

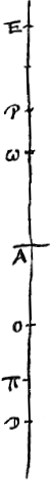[Fig. 26.]

si la lentille est convexe la démonstration sera la suivante.

D'abord, si l'oeil est situé en D entre A et O [Fig. 25], il voit, d'après la prop. II²⁾, d'un objet en E une image droite quelle que soit la distance AE. D'autre part, si l'oeil est transporté en E et l'objet en D, le point π³⁾ conjugué avec l'oeil tombera au-delà de D, vu que Eω, EA et Eπ forment une proportion continue et que par conséquent πA est plus grande que Aω ou que AO. C'est pourquoi l'image d'un objet en D sera vue droite l'oeil étant placé en E⁴⁾; de même que l'image d'un objet en E se trouvait être droite pour l'oeil placé en D.

Lorsqu' en second lieu l'oeil est placé au point D en-dehors de AO [Fig. 23 et 26], le point conjugué P tombera de l'autre côté de la lentille. Et si l'image de l'objet situé en E est renversée pour l'observateur dont l'oeil se trouve en D, la cause en est que E est situé au-delà de P [Fig. 26]⁵⁾. Mais alors, vu que D est conjugué avec le point P (en effet, la conjugaison est réciproque), et que le point E est plus éloigné de la lentille que le point P, le point π qui est conjugué avec le point E tombera en-deçà du point D. Par conséquent, du point E on verra une image renversée des objets placés en D, de même qu'au point D on voit une image renversée des objets placés en E. Mais si le point conjugué avec le point D est plus éloigné de la lentille que le point E [Fig. 23], c'est-à-dire si l'objet situé en E est aperçu droit par l'oeil placé en D, le point π, conjugué avec le point E, tombera pour la même raison au-delà de D. Par conséquent, l'oeil en E apercevra alors une image droite de l'objet placé en D, ce qui était également le cas lorsque l'objet se trouvait en E et l'oeil en D. C'est ce qu'il fallait démontrer.

Considérons maintenant le cas de deux lentilles A et B [Fig. 27 et 28]⁶⁾ et supposons que l'objet situé en E soit vu par l'oeil placé en C. Je dis qu'on apercevra une image de même grandeur si l'oeil est placé en E et l'objet en C. En effet, soit G le foyer de la lentille A et H celui de la lentille B, et K le point conjugué avec l'oeil placé en C par rapport à la lentille B, de sorte que CH, CB et CK forment une proportion continue. Soit de même L le point conjugué avec le point K par rapport à la lentille A, de sorte que KG, KA et KL forment une proportion continue. Par conséquent, lorsque l'objet placé en E est regardé

1) Voir la ‘Prop. IV,’ p. 185.

2) Voir la p. 175 du Tome présent.

3) Ce point manque dans la figure.

4) C'est-à-dire, d'après la Prop. III dont la première partie est applicable, puisque AD << AO < Aπ.

5) Comparez la seconde partie de la Prop. III, p. 181 du Tome présent.

6) De ces deux figures la première représente le cas de deux lentilles convexes, la seconde celui où l'une des lentilles est convexe et l'autre concave. Quant à l'annotation ‘sit potius E ultra γ’, qu'on lit sur la seconde figure, il est à remarquer qu'une troisième figure fut dessinée où la condition indiquée est remplie; mais elle fut biffée depuis.

[p. 203]

De situ vero, quod similis utrâque positione appareat, id quidem si lens cava sit [Fig. 24] manifestum est, quoniam omnia per hanc spectanti erecta apparent¹⁾. In convexa autem ostendetur in hoc modo.

Primùm si oculus in D inter A et O [Fig. 25] situs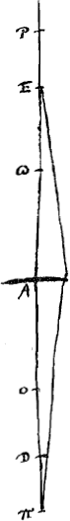

[Fig. 23.]

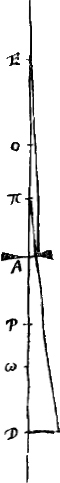[Fig. 24.]

fuerit, erectum conspicit visibile in E quaecunque fuerit AE distantia per prop. [II]²⁾. Et vicissim translato oculo in E, visibili in D, cadet punctum oculo conjugatum π³⁾ ultra D quoniam in continua sunt proportione Eω, EA, Eπ ideoque πA major quam Aω sive AO. Ergo visibile in D ex E spectabitur erectum⁴⁾, sicut in E ex D.

Rursus posito oculo in D extra AO [Fig. 23 et 26], cadet punctum conjugatum P ad alteram lentis partem. Et si quidem visibile in E inversum spectatur ex D, fit hoc quia E situm est ultra P [Fig. 26]⁵⁾. Tunc vero quia puncto P conjugatum est D, (est enim conjugatio reciproca) et distat punctum E ulterius à lente quam P, cadet punctum ipsi E conjugatum quod est π, citra D. Ideoque ex E videbuntur quae in D sunt situ everso, sicut ex D quae in E. Quod si punctum ipsi D conjugatum ulterius à lente absit quam E [Fig. 23], hoc est si visibile in E oculo in D spectatum fuerit erectum, cadet simili ratione punctum π ipsi E conjugatum ultra D, atque idcirco erectum tunc conspicietur visibile in D ex E, sicut et in E positum spectabatur ex D. Quae quidem erant ostendenda.

Proponantur nunc lentes duae A et B [Fig. 27 et 28]⁶⁾, sitque visibile in E spectatum oculo in C. Dico eâdem magnitudine spectatum iri si oculus in E ponatur et visibile in C. Sit enim lentis A focus G et H lentis B et oculo in C conjugatum punctum K, pertinens ad lentem B, ut sint videlicet in continua proportione CH, CB, CK. Item puncto K conjugatum punctum sit L pertinens ad lentem A, ut sint in continua proportione KG, KA, KL. Itaque

1) Voir la ‘Prop. IV,’ p. 185.

2) Voir la p. 175 du Tome présent.

3) Ce point manque dans la figure.

4) C'est-à-dire, d'après la Prop. III dont la première partie est applicable, puisque AD << AO < Aπ.

5) Comparez la seconde partie de la Prop. III, p. 181 du Tome présent.

6) De ces deux figures la première représente le cas de deux lentilles convexes, la seconde celui où l'une des lentilles est convexe et l'autre concave. Quant à l'annotation ‘sit potius E ultra γ’, qu'on lit sur la seconde figure, il est à remarquer qu'une troisième figure fut dessinée où la condition indiquée est remplie; mais elle fut biffée depuis.

[p. 204]

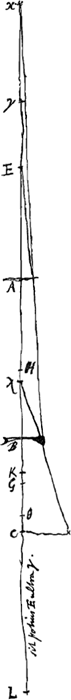[Fig. 28.]

par l'oeil placé en C, le rapport de la grandeur apparente à la grandeur véritable est composé des rapports HB:HC, AG:GK et EC:EL, comme nous l'avons démontré à la propos. V¹⁾. De même, lorsque l'oeil est placé en E et l'objet en C, appelons γ le foyer de la lentille A et θ celui de la lentille B, et κ le point conjugué avec le point E par rapport à la lentille A, de sorte que Eγ, EA et Eκ forment une proportion continue; appelons aussi λ le point conjugué avec ce point κ par rapport à la lentille B, de sorte que κθ, κB et κλ forment une proportion continue. Le rapport de la grandeur apparente à la grandeur véritable sera composé alors des rapports Aγ:γE, Bθ:θκ et CE:Cλ. Or, la vraie grandeur est la même dans les deux positions. Il s'agit donc de démontrer que le rapport composé des trois rapports que nous venons de nommer est égal à celui composé des trois rapports nommés plus haut. Or, le rapport composé des trois rapports nommés plus haut est égal à celui du solide HB, AG, EC au solide HC, GK, EL. Mais le rapport composé des trois rapports nommés en second lieu est égal à celui du solide Aγ, Bθ, CE au solide γE, θκ, Cλ. Et le solide HB, AG, EC est égal au solide Aγ, Bθ, CE, vu que les lignes sont égales deux à deux, savoir HB = Bθ et AG = Aγ, tandis que CE est la même dans les deux solides. Il suffira donc de faire voir que le solide HC, GK, EL est égal au solide γE, θκ, Cλ. C'est ce que nous démontrerons de la manière suivante. Vu que CH:CB = CB::CK, on aura aussi CH:CB = HB (ou Bθ):BK, et, par conséquent, CH:HB = Bθ:θK. De même, comme κθ:κB = κB::κγ, on aura aussi κθ:κB = θB (ou BH):Bλ, et, par conséquent, κθ:Bθ = BH:Hλ. Mais nous avions Bθ:θK = CH:BH. D'après la règle de la proportion dérangée²⁾, on aura donc κθ::θK = CH:Hλ. Donc aussi θκ:κK = CH:Cλ et, par permutation, θκ:CH = κK:Cλ. D'autre part, comme Eγ:EA == EA:Eκ, on aura Eγ:EA = γA (ou AG):Aκ, et, par conséquent, Eγ:γA = AG:Gκ. De même, comme KG:KA == = KA:KL, nous aurons KG:KA = GA (ou γA):AL, et, par conséquent, KG:AG = γA:γL. Or, nous avions AG::Gκ = Eγ:γA. Donc, d'après la règle de la proportion dérangée, nous aurons KG:Gκ = Eγ:γL. Donc aussi KG:Kκ = Eγ::EL et, par permutation et inversion, Eγ:KG = EL:Kκ. Mais le rapport EL:Cλ est composé des rapports EL:Kκ et Kκ:Cλ, dont le premier EL:Kκ est égal à Eγ:KG, et le second Kκ:Cλ, comme nous l'avons démontré, à θκ:CH. Le rapport

1) Voir les pp. 189 et 191 du Tome présent.

2) Voir la note 1, p. 103.

[p. 205]

[Fig. 27.]

cum ex C conspicitur visibile in E positum, ratio apparentis ad veram magnitudinem est ea quae componitur ex rationibus HB ad HC, AG ad GK et EC ad EL ut ostensum fuit propos. [V]¹⁾. Similiter posito oculo in E et visibili in C, et notato γ in foco lentis A, et θ in foco lentis B: et puncto κ ipsi E conjugato ad lentem A ut sint in contin. prop. Eγ, EA, Eκ. et puncto λ conjugato ipsi κ ad lentem B ut sint in contin. prop. κθ, κB, κλ. componetur magnitudinis apparentis ad veram ratio, ex rationibus Aγ ad γE, Bθ ad θκ et CE ad Cλ. Est autem vera magnitudo utraque positione eadem. Igitur ostendendum quod composita ex tribus hisce rationibus eadem est compositae ex tribus illis. Est autem ratio ex prioribus tribus composita quae solidi ex HB, AG, EC ad solidum ex HC, GK, EL. At ratio ex tribus posterioribus, ea quae solidi ex Aγ, Bθ, CE ad solidum ex γE, θκ, Cλ. Estque solidum ex HB, AG, EC aequale solido ex Aγ, Bθ, CE, quum lineae singulae fingulis sint aequalis, nempe HB ipsi Bθ, et AG ipsi Aγ et CE utrimque eadem. Igitur opus tantum erit ostendere quod solidum ex HC, GK, EL aequale solido ex γE, θκ, Cλ. Id vero sic ostendemus. Quoniam est CH ad CB ut CB ad CK, erit et CH ad CB ut HB sive Bθ ad BK. ideoque ut CH ad HB ita quoque Bθ ad θK. Similiter cum sit κθ ad κB ut κB ad κλ, erit et κθ ad κB ut θB sive BH ad Bλ, ideoque κθ ad Bθ ut BH ad Hλ. Erat autem Bθ ad θK ut CH ad BH. Igitur ex aequo in prop.^e perturbata²⁾, erit κθ ad θK ut CH ad Hλ. Quare et θκ ad κK ut CH ad Cλ et permutando θκ ad CH ut κK ad Cλ. Rursus quoniam Eγ ad EA ut EA ad Eκ, erit Eγ ad EA ut γA sive AG ad Aκ, ideoque ut Eγ ad γA ita AG ad Gκ. Similiter quia KG ad KA ut KA ad KL, erit KG ad KA ut GA sive γA ad AL, ideoque ut KG ad AG ita γA ad γL: et erat AG ad Gκ ut Eγ ad γA: Ergo ex aequo in perturb. prop. erit KG ad Gκ ut Eγ ad γL. Quare et KG ad Kκ ut Eγ ad EL, et permutando et invertendo Eγ ad KG ut EL ad Kκ. Ratio autem EL ad Cλ componitur ex rationibus EL ad Kκ, et Kκ ad Cλ, quarum EL ad Kκ eadem est quae Eγ ad KG; altera vero Kκ ad Cλ eadem quoque ostensa fuit quae θκ ad CH. Ergo ratio EL ad Cλ componetur ex rationibus Eγ ad KG et θκ ad CH, ac proinde eadem erit quae rectang.ⁱ sub Eγ, θκ ad rectang.^m sub KG, CH. Ideoque solidum

1) Voir les pp. 189 et 191 du Tome présent.

2) Voir la note 1, p. 103.

[p. 206]

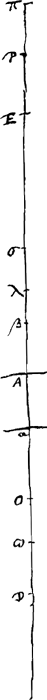[Fig. 29.]

EL:Cλ sera donc composé des rapports Eγ:KG et θκ à CH, c'est-à-dire il sera égal à celui du rectangle Eγ, θκ au rectangle KG, CH. Par conséquent, le solide EL, KG, CH sera égal au solide Cλ, Eγ, θκ; ce qu'il fallait démontrer.

Et lorsqu'on veut considérer trois ou plusieurs lentilles, on pourra en vérité donner une démonstration semblable à celle qui précède.

Ainsi donc, lorsque nous voudrons examiner quelles sont la grandeur et la position¹⁾ apparente des objets et déterminer si la vision sera distincte, on pourra obtenir des réponses à ces trois questions²⁾ en les posant pour le cas où l'objet occupe la place de l'oeil et l'oeil réciproquement celle de l'objet. En effet, on pourra aisément déduire toutes ces réponses en considérant la marche et la flexion des rayons. Supposons, par exemple, que dans les figures proposées [fig. 27 et 28] les rayons qui proviennent des différents points E de l'objet correspondent au point κ après la réfraction due à la lentille A, et ensuite au point λ, lorsqu' ils ont traversé la lentille B. On en conclura aisément si pour un oeil placé en C la vision est distincte ou non.

1) Comparez toutefois la note 2, p. 199.

2) Toutefois il est à remarquer que la réciprocité, indiquée dans la proposition quant au grossissement et à la position, n'existe nullement par rapport à la vision distincte. Ainsi p.e. dans le cas d'une seule lentille convexe l'objet placé au foyer sera vu distinctement partout à travers la lentille par un oeil accommodé pour l'infini; mais en plaçant l'oeil à ce même foyer on ne verra distinctement que les objets qui se trouvent près de l'autre foyer. En effet, comme Huygens l'indique à la fin de cet alinéa, il faut décider si la vision sera distincte ou non d'après la position de la dernière image.

Proposition VII³⁾.

Lorsque l'oeil et l'objet occupent des positions invariables, on apercevra une image droite, à quelque endroit qu'on place entre ces deux une lentille convexe dont la distance focale est plus grande que le quart de la distance de l''oeil à l'objet et l'image sera la plus grande, lorsque la lentille sera placée au milieu entre l'objet et l'oeil. Mais si la distance focale de la lentille sera plus petite que le quart de la distance de l'oeil à l'objet, l'image sera aussi quelquefois renversée, et cette image renversée sera la plus petite lorsque la lentille sera placée au milieu de la distance considérée⁴⁾.

Supposons l'oeil placé en D, l'objet en E et la lentille convexe en un point A quelconque entre ces deux. Soit O le foyer de la lentille et considérons d'abord [Fig. 29] une distance focale AO supérieure au quart de la distance DE. Il faut démontrer en premier lieu que l'image de l'objet placé en E sera droite. Or, il y a un cas où cela

3) Cette proposition et la suivante furent mentionnées par Huygens dans sa lettre à de Sluse du 12 octobre 1657 (p. 66 du T. II), comme faisant partie du traité sur la Dioptrique, rédigé par lui il y avait alors quatre ans.

4) Si nous posons , où d représente la distance entre l'oeil et l'objet, la formule de la note 2, p. 177 peut s'écrire




Il est donc clair que pour obtenir un grossissement minimum ou maximum, étant données, il faut qu'on aît v = o = ½d, et que l'image sera toujours droite quand on aura f > ¼d; mais qu' elle sera invertie dans la position du grossissement minimum pour f < ¼d.

[p. 207]

sub EL, KG, CH aequale erit ei quod sub Cλ, Eγ, θκ. quod erat ostendendum.

Propositis vero tribus pluribusve lentibus demonstratio ad praecedentium similitudinem conscribi poterit.

Per haec igitur quando de apparente visibilium magnitudine et situ¹⁾, inquirere volemus, itemque an distincta futura fit visio, haec tria²⁾ simul cognoscere poterimus, si eodem modo rationem ineamus ac si visibile in oculi loco fuerit constitutum et hic vicissim in illius locum successerit. Omnia enim ex progressu flexuque radiorum facile apparent. Ut ex. gr. in fig. proposit. [Fig. 27 et 28] quum radij ex singulis punctis E visibilis promanantes post refractionem in lente A pertineant ad punctum κ; deinde vero postquam lentem B transierint, ad punctum λ, facile hinc colligetur utrum oculo in C distincta sit futura visio an secus.

1) Comparez toutefois la note 2, p. 199.

2) Toutefois il est à remarquer que la réciprocité, indiquée dans la proposition quant au grossissement et à la position, n'existe nullement par rapport à la vision distincte. Ainsi p.e. dans le cas d'une seule lentille convexe l'objet placé au foyer sera vu distinctement partout à travers la lentille par un oeil accommodé pour l'infini; mais en plaçant l'oeil à ce même foyer on ne verra distinctement que les objets qui se trouvent près de l'autre foyer. En effet, comme Huygens l'indique à la fin de cet alinéa, il faut décider si la vision sera distincte ou non d'après la position de la dernière image.

[Propositio VII.]³⁾

Manente oculo et visibili quocunque loco inter utrumque lens convexa statuatur cujus foci distantia major sit quarta parte intervalli quod inter oculum et visibile, erectum hoc conspicietur; et maximum tunc apparebit, cum medio loco inter visibile et oculum lens statuetur. Si vero foci à lente distantia dicti intervalli quarta parte minor fuerit, etiam inversum quandoque visibile conspicietur; eritque inversarum specierum minima, cum lens medium intervalli locum tenebit⁴⁾.

Positus esto oculus in D, visibile in E, et lens convexa quovis loco inter utrumque ut in A, focus autem lentis sit O, et distantia AO primum [Fig. 29] major quarta parte intervalli DE. Ostendendum est imprimis quod visibile in E

3) Cette proposition et la suivante furent mentionnées par Huygens dans sa lettre à de Sluse du 12 octobre 1657 (p. 66 du T. II), comme faisant partie du traité sur la Dioptrique, rédigé par lui il y avait alors quatre ans.

4) Si nous posons , où d représente la distance entre l'oeil et l'objet, la formule de la note 2, p. 177 peut s'écrire




Il est donc clair que pour obtenir un grossissement minimum ou maximum, étant données, il faut qu'on aît v = o = ½d, et que l'image sera toujours droite quand on aura f > ¼d; mais qu' elle sera invertie dans la position du grossissement minimum pour f < ¼d.

[p. 208]

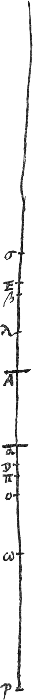[Fig. 32.]

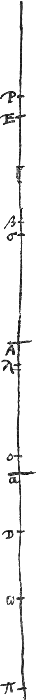[Fig. 33.]

est évident d'après la Prop. II¹⁾: c'est celui où la lentille est placée si près de l'oeil que ce dernier se trouve entre la lentille et son foyer [Fig. 31 et 32]. Mais lorsque la lentille sera placée à plus grande distance de l'oeil [Fig. 30 et 33], la démonstration sera la suivante. Soit P le point conjugué avec l'oeil placé en D: pour trouver ce point il faut prendre une troisième proportionnelle DP aux deux longueurs DO et DA. Prenons aussi Aσ = AO. Alors, comme DO:DA = DA:DP, on aura DO::DA = OA (ou Aσ):AP et, par conséquent, DO:OA = Aσ::σP. Il s'ensuit que la somme de DO et σP n'est pas plus petite que celle de OA et Aσ. Mais cette dernière somme est plus grande que la moitié de DE, vu que chacune de ses parties est supérieure au quart de DE. En y ajoutant encore OD et σP on voit donc que la distance totale DP doit être plus grande que DE. Par conséquent, le point P conjugué avec l'oeil tombe au-delà de l'objet situé en E et l'image sera donc nécessairement droite d'après la Prop. III²⁾.

Il faut démontrer ensuite que lorsque le point où est placé la lentille divise la distance DE en deux parties égales, l'objet situé en E donnera l'image la plus grande possible. Soit donc A, le point où la lentille est placée d'abord, situé au milieu entre D et E; et supposons ensuite que la lentille soit placée en un autre point α quelconque, plus près de l'oeil D, ou en un point β plus éloigné de l'oeil et à la même distance du point A. Ainsi, lorsque nous aurons fait voir que l'image est plus petite quand la lentille est placée en α que quand elle est placée en A, il s'ensuivra d'après la proposition précédente qu'elle sera également plus petite lorsque la lentille sera placée en β. En effet, transporter la lentille de α en β équivaut à laisser la lentille elle-même en sa place α, mais à faire changer de position l'oeil placé en D et l'objet placé en E. Or, dans le premier cas que nous avons supposé, la démonstration sera la suivante. Soit le point ω le foyer de la lentille placée en α; prenons αλ = αω et soit π le point conjugué avec l'oeil placé en D⁴⁾ par rapport à la lentille α, en d'autres termes soit Dπ la troisième proportionnelle à Dω et Dα. Par conséquent, pour un observateur qui regarde l'objet à travers la lentille placée en A, le rapport de la grandeur apparente à la grandeur véritable sera composé des rapports AO:OD et DE:EP, d'après les prop. II et III⁵⁾. Et pour un observateur qui regarde à travers la lentille placée en α, le rapport de la grandeur apparente à la grandeur véritable sera com-

1) Voir la p. 175 du Tome présent.

2) Voir la p. 181 du Tome présent.

4) Aux lieux cités on trouve: ‘atque tum focus sit ω punctum. Dico visibile in E majus conspici per lentem in A constitutam quam in α. Sumatur enim αλ aequalis αω. Et sit’.

5) Voir les pp. 175 et 181 du Tome présent.

[p. 209]

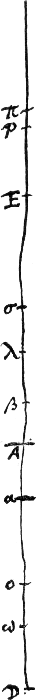[Fig. 30.]

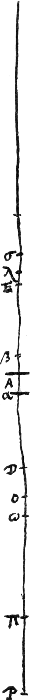[Fig. 31.]

erectum conspicietur. Hoc autem uno casu [Fig. 31 et 32] manifestum est, scilicet si tam propinqua oculo lens collocetur, ut is inter ipsam et focum consistat. per Theorem. [Prop. II]¹⁾. At cum ulterius [Fig. 30 et 33] ab oculo distabit sic demonstrabitur. Sit oculo in D punctum conjugatum P, faciendo nimirum ut duabus DO, DA sit tertia proportionalis DP. et sumatur ipsi AO aequalis Aσ. Ergo quoniam DO ad DA ut DA ad DP crit et DO ad DA ut OA sive Aσ ad AP, quare et DO ad OA ut Aσ ad σP; itaque DO et σP simul sunt non minores duabus simul OA, Aσ. Sed hae simul duae majores sunt dimidia DE, cum sint singulae quarta parte majores, ergo additis OD et σP, erit tota DP major quam DE. Ergo punctum oculo conjugatum P cadit ultra visibile in E, ideoque erectum hoc spectari necesse est per theor. [Prop. III]²⁾.

Porro demonstrandum quod cum locus lentis intervallum DE bifariam dividit maximum apparebit visibile in E. Sit igitur A medium inter D et E, ubi primo lens constituta sit, deinde et alio quovis loco in a posita intelligatur³⁾ oculo D propinquior; vel in β tantundem ab oculo remotior. Quod si igitur posita lente in a ostendatur minus apparere visibile quam eadem posita in A; etiam posita in β, minus apparebit ex prop. praec. quia nempe transponenda lente ex α in β idem fit ac si ipsa manente in α, oculus et visibile invicem loca D et E permutent. Horum vero prius istud sic ostendemus. Sit ω punctum focus lentis in α positae, et sumatur αλ aequalis αω, sitque,⁴⁾ oculo in D conjugatum punctum π ad lentem in α pertinens, posita nimirum duabus Dω, Dα tertia proportionali Dπ. Itaque spectando visibile per lentem in A, ratio apparentis ad veram magnitudinem erit ea quae componitur ex rationibus AO ad OD et DE ad EP, per prop. [II et III]⁵⁾ et inspiciendo per lentem in α ratio magnitudinis apparentis ad veram componetur ex rationibus αω ad ωD et DE ad

1) Voir la p. 175 du Tome présent.

2) Voir la p. 181 du Tome présent.

3) La leçon primitive et la copie de Niquet donnent: ‘alius intelligatur situs ejus in α’.

4) Aux lieux cités on trouve: ‘atque tum focus sit ω punctum. Dico visibile in E majus conspici per lentem in A constitutam quam in α. Sumatur enim αλ aequalis αω. Et sit’.

5) Voir les pp. 175 et 181 du Tome présent.

[p. 210]

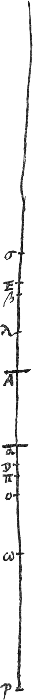[Fig. 32.]

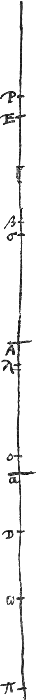[Fig. 33.]

posé des rapports αω:ωD et DE:Eπ. Or, la vraie grandeur est la même dans les deux positions, vu que nous avons admis que l'oeil et l'objet demeurent en place. Il s'agit donc de démontrer que le rapport composé des rapports AO:OD et DE:EP, qui est aussi celui du rectangle AO, DE au rectangle OD, EP est plus grand que le rapport composé des rapports αω:ωD et DE::Eπ, c'est-à-dire que le rapport du rectangle αω, DE au rectangle ωD, Eπ. Mais les premiers termes de ces rapports sont égaux entre eux, c'est-à-dire le rectangle AO, DE est égal au rectangle αω, DE, vu que αω = AO. Il faut donc démontrer que le rectangle OD, EP est plus petit que le rectangle ωD, Eπ. Or, comme on a AD = AE et AO = Aσ, on aura aussi OD = σE. De même, comme AO = αω, on aura, après avoir retranché [Fig. 30-32] ou ajouté [Fig. 33] des deux côtés la même grandeur αO, αA = Oω. De la même manière on verra que λσ est égale à Aα, partant aussi à Oω. Mais nous avons démontré un peu plus haut que DO:OA = Aσ:σP; il en résulte que le rectangle DO, σP est égal au rectangle OA, Aσ, c'est-à-dire au carré de OA. Et le rectangle DO, σE est égal au carré de OD, attendu que, comme nous l'avons démontré, σE est égale à DO. Par conséquent l'excès du rectangle DO, σP sur le rectangle DO, σE ou DO, EP est égal à l'excès du carré AO sur le carré OD. En effet, il est certain que AO est plus grande que OD, parce que AO est plus grande que la quatrième partie de la longueur totale ED et, par conséquent, plus grande aussi que la moitié de AD. Et il est certain aussi que le rectangle DO, σP est plus grand que le rectangle DO, σE; car, si O tombe entre A et D [Fig. 30 et 33], σ tombera entre A et E et P se trouvera devant la lentille et au-delà de l'objet placé en E, attendu que, comme nous l'avons démontré, l'image aperçue sera droite. D'autre part, lorsque D se trouve entre A et O [Fig. 31 et 32], E tombe aussi entre A et σ et P derrière la lentille. Par conséquent, dans ces cas E est toujours situé entre σ et P, d'où il résulte que σP est plus grande que σE et que le rectangle OD, σP surpasse donc le rectangle OD, σE. De plus, comme Dω:Dα = Dα:Dπ, on aura aussi Dω:Dα = ωα (ou αλ):απ, d'où l'on tire Dω::ωα = ωα:λπ. Par conséquent, le rectangle Dω, λπ est égal au carré ωα. Or, dans le premier cas [Fig. 30] aussi bien que dans le second cas [Fig. 31], le rectangle ωD, Eπ est égal à l'excès du rectangle ωD, λπ sur le rectangle ωD, λE³⁾. Le même rectangle ωD, Eπ est donc égal à l'excès du carré ωα ou OA sur

3) Puisque, dans ces deux cas, des trois points E, λ et π, les points extrémes sont λ et π.

[p. 211]

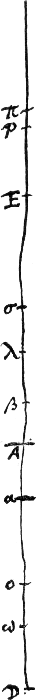[Fig. 30.]

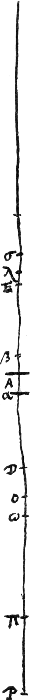[Fig. 31.]

Eπ. Est autem apparens¹⁾ magnitudo positione utrâque eadem, quoniam oculus et visibile manere dicuntur; Itaque ostendere oportet majorem esse rationem compositam ex rationibus AO ad OD et DE ad EP quae est rectang.ⁱ AO, DE ad rectang. OD, EP, quam compositam ex rationibus αω ad ωD et DE ad Eπ, hoc est, quam rationem rectang.ⁱ αω, DE ad rectang. ωD, Eπ. Priores autem rationum termini aequales sunt, rectang. scilicet AO, DE, rectang.^o αω, DE, quoniam Aω²⁾ aequalis AO. Ergo ostendendum quod rectang. OD, EP minus est rectang.^o ωD, Eπ. Quoniam igitur AD aequalis AE et AO aequalis Aσ, erit et OD aequalis σE. Item quia AO aequalis αω demtâ [Fig. 30-32] vel additâ [Fig. 33] communi αO erit αA aequalis Oω. Eadem ratione erit λσ ipsi Aα aequalis ac proinde quoque ipsi Oω. Quoniam ergo paulo ante ostensum fuit quod DO ad OA ut Aσ ad σP erit rectang. DO, σP aequale rectang.^o OA, Aσ hoc est quadr.^o OA. Et est rectang. DO, σE aequale quadr.^o OD, quia σE aequalis ostensa est ipsi DO. Itaque excessus rectang.ⁱ DO, σP supra rectang. DO, σE hoc est rectang. DO, EP aequale excessui quadr.ⁱ AO supra qu.^d OD. Etenim manifestum est quod AO excedit OD, quoniam AO major est quarta parte totius ED, ideoque major dimidiâ AD. et manifestum quoque quod rectang. DO, σP excedit rectang. DO, σE, nam si O cadit inter A, D [Fig. 30 et 33], cadet σ inter AE; et P ante lentem ultraque visibile in E, quoniam erectum conspici ostensum fuit. Rursus cum D inter A, O [Fig. 31 et 32], etiam E inter Aσ, et P cadit post lentem. Semper ergo his casibus E inter σ et P situm est, unde major σP quam σE, et proinde rectang. OD, σP excedit rectang. OD, σE. Porro quoniam Dω ad Dα ut Dα ad Dπ, etiam Dω ad Dα ut ωα sive αλ ad απ, unde et Dω ad ωα ut ωα ad λπ, Ergo rectang. Dω, λπ aequale qu. ωα. Est autem in primo et secundo casu [Fig. 30 et 31] rectang. ωD, Eπ aequale excessui rectang.^li ωD, λπ supra rectang. ωD, λE³⁾. Ergo idem rectang. ωD, Eπ aequale excessui quadrati ωα, hoc est qu.ⁱ OA supra rectang. ωD, λE. In tertio

1) Lisez: ‘vera’.

2) Lisez: ‘αω’.

3) Puisque, dans ces deux cas, des trois points E, λ et π, les points extrémes sont λ et π.

[p. 212]

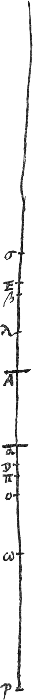[Fig. 32.]

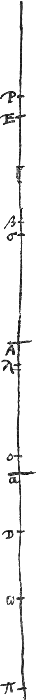[Fig. 33.]

le rectangle ωD, λE. Mais dans le troisième et le quatrième cas [Fig. 32 et 33] le rectangle ωD, Eπ est égal à la somme des deux rectangles ωD, λπ et ωD, λE¹⁾. Par conséquent, le même rectangle ωD, Eπ est ici égal à la somme du rectangle ωD, λE et du carré ωα ou OA. Or, il a été démontré que le rectangle DO, EP est égal à l'excès du carré OA sur le carré OD. Il en résulte que dans le troisième et le quatrième cas le rectangle DO, EP est plus petit que le rectangle ωD, Eπ, ce qu'il fallait démontrer. Mais dans le premier et le second cas la même chose peut séparément être démontrée de la manière suivante. Vu que dans le premier cas [Fig. 30] Dω < DO, on aura ωO:Dω > ωO:DO, ou σλ:σE. En effet, nous avons fait voir que DO = Eσ, et que Oω = σλ. On a donc, par composition, OD:Dω >> λE:Eσ. C'est pourquoi le rectangle OD, Eσ ou le carré OD sera plus grand que le rectangle Dω, λE. L'excès du carré AO sur le carré OD est donc plus petit que celui du même carré AO sur le rectangle Dω, λE. Mais le rectangle OD, EP était égal au premier de ces deux excès, et le rectangle ωD, Eπ au second. Le premier rectangle est donc inférieur au deuxième. Et dans le deuxième cas [Fig. 31], attendu que Dω > DO, on aura Dω:Oω > DO:Oω, ou σE:σλ. On obtient donc, par conversion de ces rapports, ωD:DO < σE:Eλ, et, par conséquent, rectang. DO, Eσ, ou carré DO > rectang. ωD, Eλ. Nous en conclurons, de la même maniére que dans le cas précédent, que le recangle OD, EP est inférieur au rectangle ωD, Eπ. Ce qu'il fallait démontrer.

Et dans le cinquième cas, celui où O tombe en D [Fig. 34]²⁾, le point σ coïncide aussi avec E. Pour un

1) Puisqu'ici E et π sont les extrêmes. Remarquons que le cas où les extrêmes sont E et λ ne peut pas se rencontrer dans la supposition, énoncée dans la première partie de la proposition, que la distance focale excède la quatrième partie de la distance entre l'objet et l'oeil.
Soit, pour le montrer, a la distance DA, a-f la distance DO (f la distance focale) et x la distance. αA. Nous tenons compte ici et dans ce qui suit de la direction positive ou négative des segments, comme nous l'avons indiqué dans la note 1, p. 98 du Tome présent. On trouve alors DE = 2a, , , d'où l'on déduit . Or, puisqu'on a f > ¼DE = ½a, les numérateurs des expressions pour λπ et πE auront toujours le même signe, tandis que les dénominateurs sont les mêmes; donc λπ et Eπ auront la même direction; ce qui exclut le cas où λ et E seraient les points extrêmes.

2) Il s'agit ici du cas intermédiaire entre ceux des figures 32 et 33. En effet, quand D et O se confondent, on trouve facilement que E et π sont les extrêmes des trois points E, λ, π. Ainsi la transition du cas de la fig. 30 à celui de la fig. 31 (où λ et π sont les extrêmes dans les deux figures, mais où la situation de D et O diffère) ne peut pas se faire directement d'une manière continue, mais seulement en passant successivement par les cas des figures 33 et 32. Consultez encore, sur la transition entre les cas des figures 30 et 33, 32 et 31, les notes 2, p. 214, et 5, p. 215.

[p. 213]

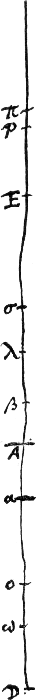[Fig:30.]

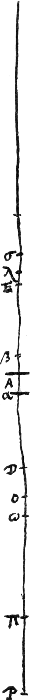[Fig:31.]

autem et quarto casu [Fig. 32 et 33] rectang. ωD, Eπ aequale duobus simul rectang.^o ωD, λπ et rectang. ωD, λE¹⁾; Ergo hic idem rectang. ωD, Eπ aequale est rectang. ωD, λE cum qu. ωα hoc est cum qu. OA. Ostensum autem quod rectang. DO, EP aequale excessui quadr.ⁱ OA supra qu. OD. Apparet itaque in tertio et quarto casu quod rectangulo ωD, Eπ minus est rectangulum DO, EP, quod erat demonstr. In primo autem et secundo casu separatim idem ostendetur hoc modo. Quoniam in primo [Fig. 30] est Dω minor quam DO, erit major ratio ωO ad Dω quam ωO ad DO, hoc est quam σλ ad σE. ostensum enim quod DO ∞ ∞ Eσ. quodque Oω ∞ σλ. Itaque componendo major ratio OD ad Dω quam λE ad Eσ. Quare majus erit rectang. OD, Eσ hoc est qu. OD quam rectang. Dω, λE. Unde minor est excessus quad.ⁱ AO supra quad. OD, quam ejusdem qu.ⁱ AO supra rectang. Dω, λE. Erat autem priori horum excessuum aequale rectang. OD, EP, alteri vero aequale rectang. ωD, Eπ. Ergo illud quàm hoc minus est. In secundo autem casu [Fig. 31] quoniam Dω major est quam DO, erit major ratio Dω ad Oω quam DO ad Oω. hoc est quam σE ad σλ. Proinde per conversionem rationis erit minor ratio ωD ad DO quam σE ad Eλ, ideoque rectang. DO, Eσ hoc est qu. DO majus rectang.^o ωD, Eλ: unde reliqua similiter concludemus ut in casu praecedente. nempe quod rectang. OD, EP minus est rectangulo ωD, Eπ. Quod demonstrare oportebat.

Quinto autem casu cum O incidit in D [Fig. 34]²⁾,

1) Puisqu'ici E et π sont les extrêmes. Remarquons que le cas où les extrêmes sont E et λ ne peut pas se rencontrer dans la supposition, énoncée dans la première partie de la proposition, que la distance focale excède la quatrième partie de la distance entre l'objet et l'oeil.
Soit, pour le montrer, a la distance DA, a-f la distance DO (f la distance focale) et x la distance. αA. Nous tenons compte ici et dans ce qui suit de la direction positive ou négative des segments, comme nous l'avons indiqué dans la note 1, p. 98 du Tome présent. On trouve alors DE = 2a, , , d'où l'on déduit . Or, puisqu'on a f > ¼DE = ½a, les numérateurs des expressions pour λπ et πE auront toujours le même signe, tandis que les dénominateurs sont les mêmes; donc λπ et Eπ auront la même direction; ce qui exclut le cas où λ et E seraient les points extrêmes.

2) Il s'agit ici du cas intermédiaire entre ceux des figures 32 et 33. En effet, quand D et O se confondent, on trouve facilement que E et π sont les extrêmes des trois points E, λ, π. Ainsi la transition du cas de la fig. 30 à celui de la fig. 31 (où λ et π sont les extrêmes dans les deux figures, mais où la situation de D et O diffère) ne peut pas se faire directement d'une manière continue, mais seulement en passant successivement par les cas des figures 33 et 32. Consultez encore, sur la transition entre les cas des figures 30 et 33, 32 et 31, les notes 2, p. 214, et 5, p. 215.

[p. 214]

[Fig. 35.]

observateur qui regarde à travers la lentille placée en A, le rapport de la grandeur apparente à la grandeur véritable est alors égal à ED:DA, c'est-à-dire à 2, d'après la prop. II¹⁾. Mais si l'on regarde à travers la même lentille transportée en α, le rapport en question est égal, comme plus haut, à celui du rectangle αω, DE au rectangle ωD, Eπ. Or, dans le cas présent le rectangle αω, DE est égal au double du carré αω, attendu que DE = 2 AO = 2 αω. Et le rectangle ωD, Eπ est égal à la somme du rectangle ωD, λπ et du rectangle ωD, λE, dont le premier (ωD, λπ) seul, d'après ce que nous avons démontré, est égal au carré αω. Par conséquent, le rectangle αω, DE est plus petit que le double du rectangle ωD, Eπ. Il en résulte que le rapport de la grandeur apparente à la grandeur véritable est inférieur à 2, la valeur qu'avait ce rapport lorsque la lentille se trouvait en A.

Ensin, si ω coïncide avec D [Fig. 35]²⁾, le rapport de la grandeur de l'image à celle de l'objet est composé, comme précédemment, des rapports AO:OD et DE (ou ωE):EP, lorsque la lentille est placée en A, mais lorsque la lentille est placée en α, ce rapport sera égal à Eω:ωα d'après la prop. II¹⁾. Or, le rapport Eω:ωα est composé des rapports Eω:EP et EP:ωα, dont le dernier (EP:ωα) est inférieur à AO:OD. En effet, nous avons démontré dans ce qui précède que Pσ:σA (ou ωα) = AO:OD³⁾. Et PE < Pσ, attendu que E tombe entre P et σ, comme nous l'avons également démontré plus haut⁴⁾. Le rapport composé des rapports Eω:EP et EP:ωα est donc plus petit que celui qui se compose des rapports ωE:EP et AO:OD. Le rapport de la grandeur de l'image à celle de l'objet, lorsque la lentille est placée au point α, est donc plus petit que lorsqu' elle se trouve en A⁵⁾.

Supposons maintenant que la distance AO [Fig. 36] qui sépare la lentille de son foyer soit moindre que la quatrième partie de l'intervalle DE qui est celui de l'objet à l'oeil. Il s'agit donc de démontrer en premier lieu que la lentille peut être placée en un point tel que l'image paraît renversée⁶⁾. Comme

1) Voir l'avant-dernier alinéa de la p. 179 du Tome présent.

2) Il s'agit du cas intermédiaire entre le cas de la figure 30 et celui de la figure 33. Dans ce cas le point π s'éloigne à l'insini et ne peut plus servir dans la démonstration.

1) Voir l'avant-dernier alinéa de la p. 179 du Tome présent.

3) Voir le premier alinéa de la p. 209.

4) Voir la p. 211.

5) Le cas intermédiaire entre ceux des figures 31 et 32 n'est pas traité. Dans ce cas les points E et λ se confondent; mais alors aucun des points entrant dans les démonstrations ne s'éloigne à l'infini et les démonstrations du deuxième et du troisième cas sont également applicables avec des modifications bien évidentes.

6) D'après la formule de la note 4, p. 207, il est clair que l'image sera invertie toutes les fois qu' on aura fd < vo. Posons donc , où s désigne la distance Aα de la lentille au point A qui se trouve au milieu du segment DE = d. La condition s'écrit alors:




conforme à celle, , du texte.

[p. 215]

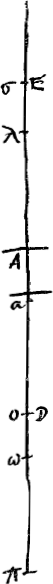[Fig. 34]

etiam σ cadit in E. Et tum quidem per lentem in A positam inspiciendo apparentis magnit.^is ad veram ratio est ea quae ED ad DA per prop. [II]¹⁾ hoc est, dupla. At inspiciendo per eandem transpositam in α, dicta ratio ut antè est ea quae rectang. αω, DE ad rectang. ωD, Eπ. Est autem hic rectang. αω, DE aequale duplo qu. αω, quia DE dupla AO, vel αω. Et est rectang. ωD, Eπ aequale rectang. ωD, λπ una cum rectang. ωD, λE quorum solum rectang. ωD, λπ ostensum fuit aequale qu. αω. Itaque rectangulum αω, DE, minus est quam duplum rectang. ωD, Eπ. Et minor proinde jam ratio apparentis ad veram magnitudinem quam dupla, qualis erat positâ lente in A.

Denique si ω incidat in D [Fig. 35]²⁾, erit ratio augmenti positâ lente in A, ut in praecedentibus ea quae componitur ex rationibus AO ad OD et DE sive ωE ad EP. at lente positâ in α ratio augmenti erit ea, quae Eω ad ωα per prop. [II]¹⁾. Componitur autem ratio Eω ad ωα ex rationibus Eω ad EP et EP ad ωα, quarum EP ad ωα minor est quam AO ad OD. Nam ostensum fuit in praecedentibus quod Pσ ad σA seu ωα sicut AO ad OD³⁾; et est PE minor quam Pσ quia E cadit inter P et σ, ut ostensum itidem est superius⁴⁾. Itaque composita ex rationibus Eω ad EP et EP ad ωα minor est compositâ ex rationibus ωE ad EP et AO ad OD. Hoc est ratio augmenti posita lente in α minor quam cum eadem ponitur in A⁵⁾.

Esto nunc distantia AO [Fig. 36] quae est inter lentem et focum, minor quarta parte intervalli DE quod inter visibile et oculum. Itaque primum ostendere oportet quod lens eo loco poni potest ut inversum conspiciatur visibile⁶⁾. Quoniam ergo AO minor est

1) Voir l'avant-dernier alinéa de la p. 179 du Tome présent.

2) Il s'agit du cas intermédiaire entre le cas de la figure 30 et celui de la figure 33. Dans ce cas le point π s'éloigne à l'insini et ne peut plus servir dans la démonstration.

1) Voir l'avant-dernier alinéa de la p. 179 du Tome présent.

3) Voir le premier alinéa de la p. 209.

4) Voir la p. 211.

5) Le cas intermédiaire entre ceux des figures 31 et 32 n'est pas traité. Dans ce cas les points E et λ se confondent; mais alors aucun des points entrant dans les démonstrations ne s'éloigne à l'infini et les démonstrations du deuxième et du troisième cas sont également applicables avec des modifications bien évidentes.

6) D'après la formule de la note 4, p. 207, il est clair que l'image sera invertie toutes les fois qu' on aura fd < vo. Posons donc , où s désigne la distance Aα de la lentille au point A qui se trouve au milieu du segment DE = d. La condition s'écrit alors:




conforme à celle, Aα² < ¼DE²-AO.DE, du texte.

[p. 216]

AO est inférieure au quart de DE, le rectangle AO, DE sera excédé d'une certaine quantité par le quart du carré DE, c'est-à-dire par le rectangle DAE. Prenons une longueur Aα dont le carré soit moindre que cette quantité, et plaçons la lentille en α. Je dis que l'image de l'objet placé en E sera renversée. En effet, supposons les autres constructions faites comme dans les cas précédents. Vu que DE est alors divisée en deux parties égales par le point A et en deux parties inégales par le point α, le carré Aα sera égal à l'excès du rectangle DAE sur le rectangle DαE. Mais le même carré Aα est plus petit que l'excès du rectangle DAE sur le rectangle DE, AO, d'après notre construction. Ce dernier excès est donc plus grand que le précédent, et, par conséquent, rectang. DE, AO < rectang. DαE. C'est pourquoi le rapport DE:Eα est plus petit que le rapport αD:AO (ou αω). Et, par conversion, ED:Dα > αD:Dω. Mais πD:Dα = αD:Dω. Par conséquent, πD < ED. Or, π est le point conjugué avec le point D, où se trouve l'oeil, par rapport à la lentille placée en α. L'image de l'objet sera donc nécessairement renversée d'après la prop. III¹⁾. C'est ce qu'il fallait démontrer. Par conséquent, la lentille, pour donner une image renversée, pourra également être placée au-delà du point milieu A dans un intervalle égal à celui où elle peut être placée en-deçà de ce point. C'est ce qui est évident d'après le théorême...²⁾.

Or, on peut faire voir de la manière suivante que la lentille, placée précisément au point milieu A, donne aussi des images renversées. Les longueurs DO, DA et DP forment une proportioncontinue, où DO > ½DA, attendu que AO < ½DA. Il en résulte que DA est plus grande que ½DP, et par conséquent DP < DE. Or, P est le point conjugué avec le point où se trouve l'oeil, par rapport à la lentille placée en A. Par conséquent, dans cette position la lentille donne une image renversée de l'objet placé en E.

Reste à faire voir que l'image aperçue à travers la lentille placée au point milieu A est plus petite que l'image aperçue à travers la lentille placée en α. Cela sera démontré lorsque, contrairement à ce qui a été prouvé antérieurement, nous aurons fait voir que le rectangle OD, EP est plus grand que le rectangle ωD, Eπ. Comme le point P tombe ici entre σ et E³⁾, le rectangle OD, EP sera égal à l'excès du rectangle OD, σE sur le rectangle OD, σP, c'est-à-dire à l'excès du carré OD sur le carré OA. En effet, nous avons démontré plus haut⁴⁾ que le rectangle OD, σE est égal au carré OD, et le rectangle OD, σP au carré AO. Mais le rectangle ωD, Eπ sera égal à l'excès du rectangle ωD, λE sur le rectangle ωD, λπ, c'est-à-dire à l'excès du rectangle ωD, λE sur le carré AO. En effet, nous avons démontré également⁴⁾ que le rectangle ωD, λπ est égal au carré αω ou AO. Or, le carré OD est plus grand que le rectangle ωD, λE: cela se démontre de la même manière que dans le premier des cas précé-

1) Voir la p. 181 du Tome présent.

2) Il s'agit d'un théorème que nous donnerons plus loin, p. 237, comme Appendice II au Livre présent. Ce théorème fait suite dans la leçon primitive à la Prop. VI (p. 199 du Tome présent); mais il fut biffé et on ne le rencontre pas à cette place dans la copie de Niquet; consultez toutefois la note 3, p. 222.

3) Employant les notations de la note 4, p. 207, on aura .

4) Voir la p. 211 du Tome présent.

4) Voir la p. 211 du Tome présent.

[p. 217]

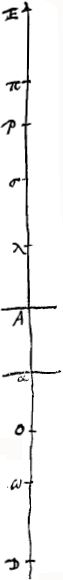[Fig. 36.]

quartâ parte DE, superabitur rectang. sub AO, DE à ¼ quadrati DE hoc est a rectang.^o DAE certo excessu. Ponatur autem Aα cujus quadr. isto excessu minus sit, et constituatur lens in α. dico inversam exhibitum iri visibilis in E speciem. Sint enim reliqua constructa ut in casibus prioribus. Quia igitur DE bifariam aequaliter secta est in A et inaequaliter in α, erit quadr. Aα aequale excessui rectang.ⁱ DAE supra rectang. DαE. Idem vero quadratum Aα minus est excessu rectang.ⁱ DAE supra rectang. sub DE, AO ex constr. Itaque hic excessus quam ille major est, ideoque rectang. sub DE, AO minus erit rectang.^o DαE. Quare minor ratio DE ad Eα quam αD ad AO seu αω. Et per conversionem rationis major ratio ED ad Dα quam αD ad Dω. Sed est πD ad Dα ut αD ad Dω. Ergo πD minor est quam ED. Est autem π punctum oculo in D conjugatum ad lentem in α. Itaque per prop. [III]¹⁾ inversum apparere necesse est visibile. quod erat ostendendum. Poterit ergo et ultra medium A lens constitui ut inversam speciem exhibeat, tanto quidem intervallo, quanto citerior esse potest; idque constat per [Theor...]²⁾.

At in ipso A medio constitutam inversa quoque visui offerre sic fiet manifestum. Quoniam scilicet in continua sunt proport.^e DO, DA, DP, estque DO major dimidiâ DA, quia AO est minor dimidia DA, erit et DA major dimidia DP, ideoque DP minor quam DE. Est autem P punctum oculo conjugatum ad lentem in A. Ergo et hìc inversum exhibet visibile in E positum.

Superest ut ostendatur minus spectari visibile per lentem in A medio positam, quam per eandem in α. De quo constabit si contra quam in praecedentibus ostensum fuerit quod rectang. OD, EP majus est rectang. ωD, Eπ. Quum igitur hic cadat P inter σ et E³⁾, erit rectang. OD, EP aequale excessui rectang. OD, σE supra rectang. OD, σP, hoc est excessui qu.ⁱ OD supra qu. OA; nam rectang. OD, σE superius⁴⁾ aequale ostensum fuit qu. OD, et rectang. OD, σP aequale qu. AO. Rectang. verò ωD, Eπ, aequale erit excessui rectang. ωD, λE supra rectang. ωD, λπ; hoc est, excessui rectang. ωD, λE supra qu. AO, nam ostensum quoque fuit⁴⁾, quod rectang. ωD, λπ aequale qu. αω sive AO. Est autem qu. OD majus rectang.^o ωD, λE, nam hoc eodem modo

1) Voir la p. 181 du Tome présent.

2) Il s'agit d'un théorème que nous donnerons plus loin, p. 237, comme Appendice II au Livre présent. Ce théorème fait suite dans la leçon primitive à la Prop. VI (p. 199 du Tome présent); mais il fut biffé et on ne le rencontre pas à cette place dans la copie de Niquet; consultez toutefois la note 3, p. 222.

3) Employant les notations de la note 4, p. 207, on aura .

4) Voir la p. 211 du Tome présent.

4) Voir la p. 211 du Tome présent.

[p. 218]

dents¹⁾. Par conséquent l'excès du carré OD sur le carré OA, c'est-à-dire le rectangle OD, EP, est plus grand que l'excès du rectangle ωD, λE sur le carré OA, c'est-à-dire que le rectangle ωD, Eπ. Ce qu'il fallait démontrer.

1) Voir la p. 213.

Proposition VIII.

Supposons l'oeil et l'objet situés en des points fixes et une lentille concave placée entre eux: plus cette lentille sera proche du point milieu entre l'oeil et l'objet, plus auffi l'image sera petite. Elle aura les plus petites dimensions, lorsque la lentille sera placée précisément au point milieu²⁾.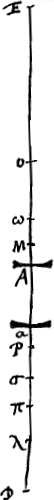

[Fig. 37.]

Supposons [Fig. 37] l'objet placé en E, l'oeil en D, et soit M le point milieu de l'intervalle DE. Plaçons d'abord la lentille concave en A entre M et D, et ensuite en α, entre A et D, de telle manière que la distance αM soit plus grande que AM. Il faut démontrer que l'image de l'objet situé en E sera plus petite lorsqu'on regarde par la lentille placée en A que lorsque celle-cise trouve en α. Soit O le point de dispersion de la lentille placée en A, et ω celui de la lentille placée en α. Et construisons la figure entière de la même manière que celle qui correspond au théorème précédent⁴⁾. Par conséquent la même manière de raisonner nous conduira à dire qu'il suffit de démontrer que le rectangle OD, EP est plus grand que le rectangle ωD, Eπ, tandis que dans le cas précédent il devait être plus petit⁵⁾. Comme DA < AE, et AO = Aσ, la somme de DA et de AO, c'est-à-dire DO, sera plus petite que celle de AE et de Aσ, c'est-à-dire que Eσ. Mais les trois longueurs Aα, Oω, σλ sont manifestement égales entre elles, comme auparavant. Et de même les rectangles DO, σP et ωD, λπ sont chacun égal, comme plus haut⁵⁾, au carré AO. Mais ici l'excès du rectangle OD, σE sur le rectangle OD, σP est égal au rectangle OD, EP; et l'excès du rectangle ωD, λE sur le rectangle ωD, λπ est égal au rectangle ωD, Eπ. Il faut donc démontrer que le premier excès est plus grand que le second, ce qui sera établi dès que nous aurons fait voir que le rectangle OD, σE est plus grand que le rectangle ωD, λE: en effet, nous avons dit que les rectangles OD, σP et ωD, λπ sont égaux entre eux. Comme Dω < DO, on aura Oω:ωD > Oω:OD. Mais ce dernier rapport est également plus grand que σλ:σE; en effet, nous avons dit que σλ = Oω, et σE > DO. Par conséquent, Oω:ωD > σλ:σE. Et, par composition, OD:Dω > λE:Eσ. C'est pourquoi le rectangle OD, Eσ est aussi plus grand que le rectangle Dω, λE, ce qui restait à démontrer.

2) Posant , on a d'après la formule de la note 2, p. 185:




Le grossissement sera donc minimum quand ov est maximum pour o+v donné, c'est-à-dire, quand on aura o = v; et si l'on pose , il est clair, qu'il diminue avec s.

4) Consultez les pp. 209 et 211 du Tome présent.

5) Voir la p. 211.

5) Voir la p. 211.

[p. 219]

ostenditur quo in casuum praecedentium primo¹⁾; Ergo excessus qu. OD supra qu. OA, hoc est rectang. OD, EP majus est excessu rectang. ωD, λE supra quadr. OA, hoc est rectangulo ωD, Eπ. quod erat ostendendum.

1) Voir la p. 213.

[Propositio VIII.]

Manente oculo et visibili, si lens cava inter utrumque constituatur, quò propinquior erit loco inter oculum et visibile medio, eo minorem hujus speciem efficiet, et minimam omnium cum medium tenebit ipsum²⁾.

Esto visibile in E positum [Fig. 37], oculus in D, sitque punctum³⁾ M intervalli DE medium; Et primum lens cava constituatur in A inter M et D, deinde autem in α, inter A, D, ita ut distantia αM major sit quam AM. Oportet ostendere quod minor erit species visibilis in E per lentem in A spectati quam per eandem in α. Sit O punctum dispersus lentis in A. Sed ω cum est in α. Et omnia similiter construantur ac in theorem. praecedenti⁴⁾. Itaque eâdem argumentandi ratione devenietur eo, ut ostendere oporteat rectang. OD, EP majus esse rectang.^o ωD, Eπ, cum illic ostensum fuerit minus⁵⁾. Quia ergo DA minor est quam AE, et AO aequalis Aσ; Erit utraque simul DA, AO hoc est DO minor utrâque AE, Aσ, hoc est Eσ. Tres autem hae Aα, Oω, σλ manifestò inter se sunt aequales, sicut et in praecedentibus. Itemque rectang.^m DO, σP et rectang. ωD, λπ ut illic⁵⁾ singula aequalia qu.^o AO. Est autem hic excessus rectang.ⁱ OD, σE supra rectang. OD, σP aequalis rectang. OD, EP: et excessus rectang.ⁱ ωD, λE supra rectang. ωD, λπ aequalis rectang. ωD, Eπ. Ergo ostendendum est quod excessus ille quam hic major est; quod erit manifestum si ostendatur rectang. OD, σE majus rectang.^o ωD, λE. cum rectang.^a OD, σP et ωD, λπ inter se aequalia dicta sint. Quia ergo Dω minor est quam DO erit major ratio Oω ad ωD quam Oω ad OD. Sed haec etiam major est quam σλ ad σE; nam dictum est quod σλ aequalis Oω: quodque σE major quam DO. Ergo major ratio Oω ad ωD quam σλ ad σE. Et componendo, major OD ad Dω quam λE ad Eσ. Quamobrem majus quoque rectang. OD, Eσ rectangulo Dω, λE, quod reliquum erat ostendere.

2) Posant , on a d'après la formule de la note 2, p. 185:




Le grossissement sera donc minimum quand ov est maximum pour o+v donné, c'est-à-dire, quand on aura o = v; et si l'on pose , il est clair, qu'il diminue avec s.

3) Les mots en italique manquent dans la leçon primitive et dans la copie de Niquet.

4) Consultez les pp. 209 et 211 du Tome présent.

5) Voir la p. 211.

5) Voir la p. 211.

[p. 220]

Mais si l'on prend un intervalle égal à MA et situé de l'autre côté du point milieu M, et qu'on place la lentille à l'extrémité de cet intervalle, l'image aura la même grandeur que lorsqu' on regarde à travers la lentille placée en A, comme nous l'avons sait voir à la prop...¹⁾ Il est evident en outre que l'image sera d'autant plus petite que la lentille est située à une plus petite distance du point milieu M. Il en résulte enfin que l'image est la plus petite lorsque la lentille est placée précisément au point milieu M. Ce qu'il fallait démontrer.

1) Voir le théorème mentionné dans la note 2, p. 217.

Proposition IX.
Théorème²⁾.

Si la distance de l'oeil à une lentille convexe demeure invariable et que l'oeil est situé entre la lentille et son foyer, l'image apparaîtra d'autant plus petite que l'objet sera placé à une plus grande distance. Mais si la distance de l'oeil à la lentille est plus grande que la distance focale, l'objet en s'éloignant paraîtra devenir plus grand, aussi longtemps que l'image est droite; mais dès que l'image sera devenuerenversée sa grandeur diminuera lorsqu'on continue à éloigner l'objet. Et si l'oeil est situé au foyer de la lentille, l'image aura toujours la même grandeur, quelle que soit la distance de l'objet à la lentille³⁾.

Prenons les mêmes notations que précédemment et servons nous des résultats obtenus là où il était question de l'agrandissement apparent produit par une seule lentille convexe⁴⁾. En premier lieu, comme le point conjugué P, lorsque l'oeil est placé derrière la lentille à une distance inférieure à la distance focale⁵⁾, tombe en-deçà de la lentille et de l'oeil, il est clair qu' alors plus on éloigne l'objet MN plus aussi la longueur AB diminuera: en effet, NBP est une ligne droite; mais DA, la distance de l'oeil à la lentille, demeure la même par hypothèse; l'angle ADB devient donc plus petit lorsque l'objet s'éloigne; c'est pourquoi l'image doit devenir plus petite.

Lorsque, au contraire, l'oeil est placé à une distance de la lentille supérieure à la distance focale⁷⁾, et que le point P tombe donc au delà de la lentille, il est évident que, aussi longtemps que l'image de l'objet MN est droite, c'est-à-dire aussi long-

2) On trouve encore en marge l'annotation suivante: ‘Ordo theorematum sit hic. Primum de augmento lentium singularum’ [Voir les Prop. II, p. 175, III, p. 181 et IV, p. 185] ‘Tum de duarum’ [Prop. V, p. 187] ‘et telescopio’ [Voir la note 3, p. 186, là où il s'agit du cas du télescope]. ‘Tum de lentibus quotcunque interpositis’ [Prop. VI, p. 199]. ‘Tum de aequali ab oculo vel visibili distantia et maximo minimoque in medio’ [Voir les Prop. VII, p. 207 et VIII, p. 219]. ‘Tum theorema quod hic juxta positum est’ [Voir la note 3, p. 222]. ‘Tum denique quod est in fine hujus pag.^ae’ [Prop. X, p. 223].
Ajoutons que cette annotation se retrouve dans le manuscrit de Niquet. Elle doit donc dater d'avant 1666.

3) Employons les notations des notes 2, p. 177 et 181; il est évident alors que la grandeur de l'image, étant proportionnelle au grossissement g et inversement proportionnelle àla distance o+v, dépendra dans les trois cas de la valeur du facteur:




où v doit être considérée comme la seule variable, et il est bien facile de déduire, à l'aide de cette expression, les résultats formulés dans la proposition présente; toutefois, ici, les considérations géométriques du texte mènent encore plus simplement au but désiré.

4) Il s'agit des Prop. II (p. 175) et III (p. 181) du Livre présent.

5) Voir la fig. 3, p. 176, où l'oeil se trouve en D, et où O est le foyer.

7) Voir la fig. 5, p. 182.

[p. 221]

Quod si verò ipsi MA intervallo ad alteram partem puncti medij M aequale sumatur, ac in eo lens constituatur. Eâdem magnitudine cernetur visibile atque per lentemin in A, ut ostensum est propos...¹⁾ Proinde constat tanto exilius conspici quanto propior erit lens puncto medio M. Ex quo denique manifestum est, minimum conspici visibile cum in ipso M puncto lens constituitur. Quae fuere demonstranda.

1) Voir le théorème mentionné dans la note 2, p. 217.

[Propositio IX.]
Theorema²⁾.

Manente distantia oculi à lente convexa, si inter lentem et focum oculus situs sit, quo magis visibile removebitur eo minori conspicietur magnitudine. Si vero ultra focum oculus à lente distet, abscedens visibile augebitur, quamdiu erectum apparet; inde vero si porro removeatur decrescet inversa imago. Quod si in foco lentis constitutus fuerit oculus, quacunque visibilis à lente distantiâ, eâdem semper magnitudine cernetur³⁾.

Ponantur quae in praecedenti; nempe in quo de augmento unius lentis convexae⁴⁾. Primum itaque quoniam oculo citra focum à lente distante, punctum conjugatum P cadit post lentem et oculum⁵⁾, manifestum est quo magis visibile NN⁶⁾ removebitur, eo minorem fore AB; recta enim ducta est NBP, verum DA distantia oculi à lente eadem manere ponitur; ergo minuitur angulus ADB recedente visibili, quapropter minui speciem ejus necesse est.

Oculo autem ultra focum remoto⁷⁾, quoniam punctum P cadit ante lentem, apparet quamdiu visibile NN⁶⁾ erectum spectatur, hoc est, quamdiu non ultra

2) On trouve encore en marge l'annotation suivante: ‘Ordo theorematum sit hic. Primum de augmento lentium singularum’ [Voir les Prop. II, p. 175, III, p. 181 et IV, p. 185] ‘Tum de duarum’ [Prop. V, p. 187] ‘et telescopio’ [Voir la note 3, p. 186, là où il s'agit du cas du télescope]. ‘Tum de lentibus quotcunque interpositis’ [Prop. VI, p. 199]. ‘Tum de aequali ab oculo vel visibili distantia et maximo minimoque in medio’ [Voir les Prop. VII, p. 207 et VIII, p. 219]. ‘Tum theorema quod hic juxta positum est’ [Voir la note 3, p. 222]. ‘Tum denique quod est in fine hujus pag.^ae’ [Prop. X, p. 223].
Ajoutons que cette annotation se retrouve dans le manuscrit de Niquet. Elle doit donc dater d'avant 1666.

3) Employons les notations des notes 2, p. 177 et 181; il est évident alors que la grandeur de l'image, étant proportionnelle au grossissement g et inversement proportionnelle àla distance o+v, dépendra dans les trois cas de la valeur du facteur:




où v doit être considérée comme la seule variable, et il est bien facile de déduire, à l'aide de cette expression, les résultats formulés dans la proposition présente; toutefois, ici, les considérations géométriques du texte mènent encore plus simplement au but désiré.

4) Il s'agit des Prop. II (p. 175) et III (p. 181) du Livre présent.

5) Voir la fig. 3, p. 176, où l'oeil se trouve en D, et où O est le foyer.

6) Lisez MN.

7) Voir la fig. 5, p. 182.

6) Lisez MN.

[p. 222]

temps que cet objet n'est pas plus éloigné de la lentille que le point P, AB sera d'autant plus grande que l'objet sera moins éloigné du point P. L'angle ADB augmentera donc en même temps, attendu que la distance AD est invariable. Mais dès que l'image sera devenue renversée¹⁾, ce qui aura lieu lorsque l'objet aura dépassé, en s'éloignant, le point P, AB deviendra d'autant plus petite que l'objet ira plus loin, et il en sera par conséquent de même de l'angle ADB.

Et lorsque l'oeil est placé au foyer même de la lentille²⁾, aucun point conjugué ne pourra être trouvé, ainsi que nous l'avons dit, mais la droite NB deviendra parallèle à l'axe EA. Quelle que soit la distance de l'objet, AB a donc la même grandeur, et l'angle ADB aussi. On apercevra donc toujours une image de même grandeur. Ce qu'il fallait démontrer.

1) Voir la fig. 6, p. 183.

2) Voir la fig. 4, p. 178.

Proposition X³⁾. Théorème.

Si la distance d'une lentille convexe à l'objet demeure invariable et que l'objet se trouve entre la lentille et un de ses foyers, l'image sera d'autant plus petite que l'oeil sera plus éloigné de la lentille. Mais si l'objet se trouve à une distance de la lentille supérieure à la distance focale, l'image grandira, tant qu'elle est droite, lorsque l'onéloigne l'oeil de la lentille. Mais dès que l'image sera devenue renversée, elle deviendra plus petite lorsqu'on continue à éloigner l'oeil. Et si l'objet se trouve au foyer de la lentille, l'image aura la même grandeur quelle que soit la distance de l'oeil à la lentille.

La démonstration de cette proposition est évidente: il suffit d'appliquer à notre théorème ce qui a été dit⁴⁾ de la permutation mutuelle des endroits où sont situés l'oeil et l'objet.

3) Entre cette proposition et celle qui précède le manuscrit que nous suivons, et de même la copie de Niquet, intercalent: ‘Intercedit Theorema. Manente distantia visibilis ab oculo, &c.’ Il n'est presque pas douteux qu'il s'agit du théorème mentionné dans la note 2, p. 217. Mais ce théorème ne serait pas bien placé au lieu indiqué ici par Huygens, puisqu' il s'en est déjà servi dans les propositions VII (voir la note citée) et VIII (voir la note 1, p. 220) qui précèdent. Ainsi il était mieux à sa place là où il se trouvait primitivement, c'est-à-dire, immédiatement après la Prop. VI; mais puisqu'il fut biffé et que, de plus, les phrases en italique de la p. 209 prouvent que Huygens se proposait de s'en passer, nous avons préféré le reléguer à un appendice (voir la p. 237).

4) Voir la Prop. VI, p. 199 du Tome présent.

[p. 223]

P distat; tanto majorem fore AB quanto propius ad P visibile accesserit. Ergo tanto major quoque fiet angulus ADB, quia distantia AD non mutatur. Sed postquam everso situ spectari ceperit¹⁾, remotum videlicet ultra punctum P, quanto ulterius ibit tanto minor fiet AB, ideoque et angulus ADB.

Posito autem oculo in foco lentis ipso²⁾, nullum inveniri punctum conjugatum diximus, sed rectam duci NB axi EA parallelam, igitur quacunque visibilis distantia aequè magna est AB ideoque et angulus ADB. Quare ejusdem ubique magnitudinis visibile conspicietur. Quae fuerant demonstranda.

1) Voir la fig. 6, p. 183.

2) Voir la fig. 4, p. 178.

[Propositio X.]³⁾ Theorema.

Manente distantia lentis [convexae] ab aspectabili, si fuerit hoc lenti propius quam focus suus; quo magis oculus à lente distabit, eo minori magnitudine conspicietur. Si vero ultra focum à lente dissitum fuerit aspectabile removendo oculum à lente, augebitur quandiu erectum apparebit. Inde vero si porro recesserit oculus, eversa species diminuetur. Quod si ad focum lentis situm sit, quacunque oculi à lente distantia aequali magnitudine conspicietur.

Cujus demonstratio evidens est, si id quod modo de permutatione loci mutua inter oculum et rem visam dictum fuit⁴⁾, applicetur Theoremati.

3) Entre cette proposition et celle qui précède le manuscrit que nous suivons, et de même la copie de Niquet, intercalent: ‘Intercedit Theorema. Manente distantia visibilis ab oculo, &c.’ Il n'est presque pas douteux qu'il s'agit du théorème mentionné dans la note 2, p. 217. Mais ce théorème ne serait pas bien placé au lieu indiqué ici par Huygens, puisqu' il s'en est déjà servi dans les propositions VII (voir la note citée) et VIII (voir la note 1, p. 220) qui précèdent. Ainsi il était mieux à sa place là où il se trouvait primitivement, c'est-à-dire, immédiatement après la Prop. VI; mais puisqu'il fut biffé et que, de plus, les phrases en italique de la p. 209 prouvent que Huygens se proposait de s'en passer, nous avons préféré le reléguer à un appendice (voir la p. 237).

4) Voir la Prop. VI, p. 199 du Tome présent.

[p. 224]

Proposition XI¹⁾. Théorème²⁾.

[Fig. 38.]

Si, au lieu de prendre une lunette composée de deux lentilles, l'une convexe et l'autre concave, on adapte à l'oeil un corps construit d'une matière solide et transparente et possédant une surface convexe et une surface concave, ce corps agrandira les objets lointains dans la même proportion que la lunette composée de deux lentilles. C'est-à-dire, le rapport de la grandeur apparente de l'image à celle de l'objet sera égal au rapport de la distance focale de la surface convexe à la distance du foyer de cette surface à la surface concave, contre laquelle se trouve l'oeil.

Soit AM [Fig. 38] la surface convexe d'une lunette de ce genre, construite d'une pièce, et N le centre de courbure de cette surface. Soit en outre BQ la surface concave, et P son centre de courbure. Supposons que G soit le foyer de la surface AM, c'est-à-dire le point de concours de rayons incidents parallèles, et R le point de dispersion de la surface BQ pour des rayons parallèles se mouvant à l'intérieur du corps solide. Soit de plus DED un objet visible situé à grande distance. Nous devons donc démontrer que lorsque l'oeil est appliqué à la surface B, l'objet DED est augmenté dans le rapport AG:GB⁴⁾.

Supposons d'abord que l'oeil, situé en C, ne soit pas encore proche de la surface BQ et construisons une quatrième proportionnelle CK à CR, CP et CB, d'après la prop. XII⁵⁾. Comme alors des rayons partis du point C correspondraient au point K après avoir été réfractés à la surface BQ, réciproquement les rayons qui, à l'intérieur du corps transparent solide, se dirigent vers le point K, correspondront au point C après avoir été réfractés à la surface B. De la même manière il arrivera, si l'on construit une quatrième proportionnelle KS aux trois lon-

1) Les considérations qui suivent, et qui ont amené la proposition présente, ont leur origine dans la théorie du grossissement des lunettes exposée par Descartes dans le ‘Discours septiesme’ de sa Dioptrique ‘Des moyens de perfectionner la vision’ (voir les p. 155-160 du T. VI de l'édition récente des Oeuvres de Descartes par Adam et Tannery).
Cette théorie, vague et erronée, se fonde en premier lieu sur l'examen du cas où le tuyau de la lunette serait rempli entièrement d'une matière réfringente homogène bornée par deux surfaces courbes, l'oeil étant placé devant l'une d'elles.
C'est dans une lettre du 2 avril 1654 à Grégoire de St. Vincent qu'on rencontre dans la Correspondance la première allusion à la proposition présente; on y lit (p. 281 du T. I) ‘In reliqua autem Cartesij explicatione et praesertim ubi ad telescopij venit demonstrationem plurima mihi quoque improbantur. Seposui ad tempus quae in hac materia conscripta habeo.’

2) Huygens annota plus tard en marge: ‘Omittatur haec vel paucioribus demonstretur. debebat dici BG esse distantiam puncti dispersus parallelorum a parte G venientium ad cavum BQ. estque BG ∞ 3/2 BR.’ Nous reviendrons sur cette annotation dans la note 3, p. 227.

4) C'est là, en effet, la valeur de l'agrandissement dans le cas de deux lentilles dont les distances focales coïncident avec celles des surfaces AM et BQ, quand l'oeil se trouve à l'intersection de l'axe et de la surface de la lentille concave. Pour s'en convaincre il suffit de consulter la note 3 de la page 192, ou bien de considérer que, d'après la Prop. I du Livre présent (p. 173), l'agrandissement ne dépend pas de la lentille concave contre laquelle l'oeil est appliqué, mais seulement de la lentille convexe. Il est donc égal, d'après la première partie de la Prop. II, p. 175, au rapport de la distance socale AG à la distance BG du foyer à l'oeil.

5) Voir la p. 41 du Tome présent.

[p. 225]

[Propositio XI.]¹⁾ Theorema²⁾.

Si loco conspicilli duarum lentium ejusmodi adaptetur ex solido materiae diaphanae frusto, cujus altera superficies convexa sit altera cava, eâdem proportione visibilia augebit longinqua, atque conspicillum duarum lentium. Scilicit augmenti ratio ea erit, quae distantiae superficiei convexae à foco suo ad distantiam foci à cava, cui oculus admotus est.

Esto talis specilli continui superficies convexa AM [Fig. 38], ex sphaera cujus N centrum. Superficies vero BQ cava centro P. Et focus superficiei AM seu concursus parallelorum sit G punctum. at R punctum dispersus superficiei BQ radiorum parallelorum qui intra solidum feruntur³⁾. Porro visibile longinquum sit DED. Itaque ostendendum cum oculus superficiei B applicabitur ea proportione visibile DED augeri, quam habet AG ad GB⁴⁾.

Ponatur prius oculus in C non adhuc superficiei BQ prope admotus, et tribus hisce CR, CP, CB, ponatur quarta proportionalis CK, secundum prop. [XII]⁵⁾. Ergo quoniam radij ex C puncto si egrederentur, refracti in superf. BQ pertinerent ad punctum K, ideo vicissim qui intra diaphani soliditatem ita feruntur ut tendant ad K, pertinebunt post refractionem in superf. B ad punctum C.

1) Les considérations qui suivent, et qui ont amené la proposition présente, ont leur origine dans la théorie du grossissement des lunettes exposée par Descartes dans le ‘Discours septiesme’ de sa Dioptrique ‘Des moyens de perfectionner la vision’ (voir les p. 155-160 du T. VI de l'édition récente des Oeuvres de Descartes par Adam et Tannery).
Cette théorie, vague et erronée, se fonde en premier lieu sur l'examen du cas où le tuyau de la lunette serait rempli entièrement d'une matière réfringente homogène bornée par deux surfaces courbes, l'oeil étant placé devant l'une d'elles.
C'est dans une lettre du 2 avril 1654 à Grégoire de St. Vincent qu'on rencontre dans la Correspondance la première allusion à la proposition présente; on y lit (p. 281 du T. I) ‘In reliqua autem Cartesij explicatione et praesertim ubi ad telescopij venit demonstrationem plurima mihi quoque improbantur. Seposui ad tempus quae in hac materia conscripta habeo.’

2) Huygens annota plus tard en marge: ‘Omittatur haec vel paucioribus demonstretur. debebat dici BG esse distantiam puncti dispersus parallelorum a parte G venientium ad cavum BQ. estque BG ∞ 3/2 BR.’ Nous reviendrons sur cette annotation dans la note 3, p. 227.

3) Les mots en italiques manquent dans la leçon primitive et dans la copie de Niquet.

4) C'est là, en effet, la valeur de l'agrandissement dans le cas de deux lentilles dont les distances focales coïncident avec celles des surfaces AM et BQ, quand l'oeil se trouve à l'intersection de l'axe et de la surface de la lentille concave. Pour s'en convaincre il suffit de consulter la note 3 de la page 192, ou bien de considérer que, d'après la Prop. I du Livre présent (p. 173), l'agrandissement ne dépend pas de la lentille concave contre laquelle l'oeil est appliqué, mais seulement de la lentille convexe. Il est donc égal, d'après la première partie de la Prop. II, p. 175, au rapport de la distance socale AG à la distance BG du foyer à l'oeil.

5) Voir la p. 41 du Tome présent.

[p. 226]

[Fig. 38.]

gueurs KG, KN et KA, que les rayons qui se dirigent vers le point S et qui sont réfractés à la surface AM, se dirigent vers le point K. Tirons la droite DS qui coupe la surface AM au point M, et ensuite la droite MK qui coupe la surface BQ en Q. Joignons aussi les points Q et C. Et que la droite DC coupe la surface BQ en O. Par conséquent, le rayon provenant du point D de l'objet et qui se meut selon la droite DM, sera réfracté au point M de manière à se diriger vers le point K, mais après avoir été réfracté une deuxième fois en Q, ce rayon parviendra à l'oeil situé en C. Il est donc établi que le point D est aperçu au point Q de la surface BQ:tandis que ce point serait vu en O si, au lieu de la lunette, il n'y avait qu'une seule surface B, où n'aurait lieu aucune réfraction. Le rapport de la grandeur apparente à la grandeur véritable, lorsque l'oeil est placé en C, est donc égal au rapport QB:OB. Mais le rapport QB:OB est composé des rapports QB:MA, MA:ED et ED::OB:OB qui sont respectivement égaux aux rapports KB:KA, SA::SE et EC:BC. Or, le rapport composé des rapports SA:SE et EC:BC est égal à celui que composent les rapports SA:BC et EC:SE. Le rapport QB:OB sera donc composé des rapports KB:KA, SA:BC et EC:ES. Mais le rapport composé des rapports KB:KA et SA:BC est égal au rapport composé des rapports KB:BC et SA:KA, et le rapport EC:ES est égal à l'unité, attendu que nous supposons l'objet DED situé à grande distance. Par conséquent le rapport QB:OB est composé des rapports KB:BC et SA:KA. Mais comme, par construction, CR:CP = CB:CK, on aura PR:RC = KB:BC. De même, comme KG:KN = KA:KS, il s'ensuit NG:GK = SA:AK. Le rapport QB:OB sera donc composé des rapports PR:RC et NG:GK, l'oeil étant toujours placé en C. Mais lorsque l'oeil est supposé très-voisin de la surface BQ, le point C tombera en B, et le point K également en B; en ce cas le rapport PR:RC (ou RB) sera donc égal à l'indice de réfraction¹⁾, et, par conséquent, aussi au rapport AG:NG²⁾. Mais le rapport NG:GK devriendra NG:GB. Le rapport QB:OB, qui est celui de la grandeur apparente à la grandeur véritable, sera donc alors composé des rapports AG:NG et NG::GB; il sera donc égal à AG:GB. Ce qu'il fallait démontrer.

Il est nécessaire toutefois que la courbure de la surface BQ ait une valeur déterminée pour que la vision soit distincte³⁾. Mettant cela de côté, l'agrandissement serait, en effet, absolument le même, soit qu'on suppose cette surface plus ou moins concave soit qu'on la suppose plane ou même convexe, si seulement

1) Voir la Prop. XI, p. 41 du Tome présent.

2) Voir la Prop. VIII, p. 33.

3) Cette condition exige, pour un oeil accommodé pour l'infini, que le foyer G de la surface convexe AM coïncide avec le point de dispersion des rayons parallèles venant du côté S et tombant sur la surface concave BQ. Or, posant n pour l'indice de réfraction, on aura alors, d'après la Prop X, p. 39, ; mais d'autre part , d'après la Prop. XI, p. 41. On aura donc dans ce cas BG = n. BR, c'est-à-dire, pour le verre: BG = 3/2 BR.
Si nous revenons maintenant à l'annotation citée dans la note 2, p. 225, il devient évident que Huygens se propose de simplifier la démonstration en se bornant au cas de la vision distincte dans lequel on aura, en effet, BG = 3/2 BR ou, plus généralement, BG = n. BR.

[p. 227]

eâdem ratione si tribus hisce KG, KN, KA collocetur quarta proportionalis KS, fiet ut radij ad punctum S tendentes refractique in superficie AM tendant ad punctum K. Jungatur DS secans superf. AM in M. deinde MK secans superficiem BQ in Q, et connectatur QC. Recta vero DC secet superficiem BQ in O. Itaque radiorum ex puncto visibilis D is qui fertur secundum rectam DM, flectetur ab M versus K, sed iterum refractus in Q perveniet ad oculum in C. Quare constat in puncto Q superficiei BQ spectari punctum D: quod spectaretur in O si loco specilli, una tantum superficies B poneretur refractionis expers. Est igitur ratio magnitudinis apparentis ad veram oculo in C constituto, ea quae QB ad OB. Ratio autem QB ad OB composita est ex rationibus QB ad MA; et MA ad ED; et ED ad OB. quae sunt eaedem rationibus KB ad KA; SA ad SE; et EC ad BC. Et est ratio composita ex rationibus SA ad SE, et EC ad BC, eadem compositae ex rationibus SA ad BC et EC ad SE. Itaque ratio QB ad OB componetur ex rationibus KB ad KA, SA ad BC, et EC ad ES; ratio autem composita ex rat.^s KB ad KA et SA ad BC est eadem compositae ex rat. KB ad BC et SA ad KA, reliqua vero EC ad ES est ratio aequalitatis, quoniam visibile DED longinquum ponitur. Ergo ratio QB ad OB composita ex ratione KB ad BC et SA ad KA. Quia verò ex constr. est CR ad CP ut CB ad CK, erit PR ad RC ut KB ad BC. Item quia KG ad KN ut KA ad KS erit NG ad GK ut SA ad AK. Igitur ratio QB ad OB componetur ex rat.^s PR ad RC et NG ad GK, oculo adhuc in C constituto. Cum vero superficiei BQ oculus contiguus ponetur cadet C in B, item K in B, quare tunc erit ratio PR ad RC seu RB eadem quae est refractionis¹⁾, ac proinde eadem rationi AG ad NG²⁾. Ratio vero NG ad GK erit NG ad GB. Ergo tunc ratio QB ad OB, quae est ratio magnitudinis apparentis ad veram erit composita ex rat.^s AG ad NG et NG ad GB hoc est, erit ea quae AG ad GB; quod erat demonstr.

Oportet autem superficiem BQ certa ratione cavam esse si distincta visio requiritur³⁾. Nam alioqui etsi magis minusve cava esset, aut plana aut convexa quoque, idem prorsus contingeret augmentum, si modo oculus prope admotus ponatur.

1) Voir la Prop. XI, p. 41 du Tome présent.

2) Voir la Prop. VIII, p. 33.

3) Cette condition exige, pour un oeil accommodé pour l'infini, que le foyer G de la surface convexe AM coïncide avec le point de dispersion des rayons parallèles venant du côté S et tombant sur la surface concave BQ. Or, posant n pour l'indice de réfraction, on aura alors, d'après la Prop X, p. 39, ; mais d'autre part , d'après la Prop. XI, p. 41. On aura donc dans ce cas BG = n. BR, c'est-à-dire, pour le verre: BG = 3/2 BR.
Si nous revenons maintenant à l'annotation citée dans la note 2, p. 225, il devient évident que Huygens se propose de simplifier la démonstration en se bornant au cas de la vision distincte dans lequel on aura, en effet, BG = 3/2 BR ou, plus généralement, BG = n. BR.

[p. 228]

l'oeil est supposé voisin de la surface. Car on pourra démontrer toujours de la même manière que le rapport de la grandeur apparente à la grandeur véritable est égal au rapport AG:GB.

Cependant ces conclusions ne sont nullement d'accord avec la théorie par laquelle Descartes essaie d'expliquer l'invention du télescope en nous amenant à considérer un corps tubulaire solide de cette conformation. Car il veut que la surface concave soit telle qu'elle fasse changer de direction les rayons provenant des divers points de l'objet, après qu'ils auront traversé la surface extérieure du corps tubulaire, et qu'elle les dirige vers l'oeil de façon qu'ils semblent provenir de points situés à plus petite distance. Et il affirme que le rapport de la distance de ces points plus proches à la distance de l'objet lui-même est égal au rapport¹⁾ de la grandeur apparente à celle qu'on apercevrait à l'oeil nu²⁾. Comment cela pourrait-il être vrai, attendu que pour les yeux des vieillards la construction des télescopes doit être telle que les rayons, en atteignant l'oeil, soient convergents ou au moins parallèles, mais non pas telle que ces rayons semblent provenir d'un point plus rapproché? Et l'on sait pourtant que les images s'agrandissent non moins pour les vieillards que pour ceux qui ont la vue bonne.

Il y a encore cela d'absurde dans l'explication de Descartes: il dit que tous les objets sont vus agrandis parce que les rayons provenant des divers points de ces objets se croisent à la surface extérieure convexe du corps tubulaire, tandisque, si ce corps était absent, ils se croiseraient dans la pupille de l'oeil³⁾. Or, s'il y avait une surface plane ou concave au lieu de la surface convexe, il y aurait là néanmoins un semblable croisement des rayons. Ainsi tous les objets devraient être également vus agrandis lorsque le tube est retourné. Mais cela est en contradiction avec ce qui a été démontré plus haut et de plus avec l'expérience.

1) Il s'agit en vérité du rapport réciproque.

2) Voir le passage, d'ailleurs difficile à comprendre, qu'on trouve à la p. 158 du lieu cité dans la note 1, p. 224 et qui débute comme il suit: ‘Puis de rechef, que ces mesmes rayons,’ [venant d'un même point de l'objet] ‘en sortant de ce tuyau se plient & se redressent en telle sorte qu'ils puissent entrer dans l'oeil tout de mesme que s'ils n'auoient point du tout esté pliés, mais seulement qu'ils vinssent de quelque lieu qui fust plus proche. Et ensuite, que ceux qui viendront de diuers points, s'estant croisés dés l'entrée de ce tuyau, ne se decroysent point à la sortie, mais qu'ils aillent vers l'oeil en mesme façon que s'ils venaient d'un obiet qui fust plus grand, ou plus proche.’

3) Allusion au passage suivant qui se trouve p. 155-157 du lieu cité dans la note que nous venons de mentionner: ‘Il ne reste plus qu' vn autre moyen pour augmenter la grandeur des images, qui est de faire que les rayons qui viennent de diuers points de l'obiet, se croisent plus loin qu'il se pourra du fonds de l'oeil; mais il est bien, sans comparaison, le plus important & le plus considerable de tous. Car c'est l'vnique qui puisse seruir pour les obietsinacces



sibles, aussy bien que pour les accessibles, & dont l'effet n'a pas de bornes: en sorte qu'on peut, en s'en seruant, augmenter les images de plus en plus jusques a vne grandeur indefinie. Comme, par exemple, d'autant que la premiere des trois liqueurs dont l'oeil est rempli, cause a peu près mesme refraction que l'eau commune, si on applique tout contre vn tuyau plein d'eau, comme EF, au bout duquel il y ait vn verre GHI, dont la figure soit toute semblable a celle de la peau BCD qui couure cete liqueur, & ait mesme rapport a la distance du sonds de l'oeil, il ne se fera plus aucune refraction a l'entrée de cet oeil; mais celle qui s'y faisoit auparauant, (& qui estoit cause que tous les rayons qui venoient d'vn mesme point de l'obiet commençoient a se courber dés cet endroit là, pour s'aller assembler en vn mesme point sur les extremités du nerf optique, & qu' ensuite tous ceux qui venoyent de diuers points s'y croisoient, pour s'aller rendre sur diuers points de ce nerf), se fera dés l'entrée du tuyan GI: si bien que ces rayons, se croisans dés là, formeront l'image RST beaucoup plus grande que s'ils ne se croisoient que sur la supersicie BCD; & ils la formeront de plus en plus grande selon que ce tuyau sera plus long. Et ainsi l'eau EF saisant l'office de l'humeur K; le verre GHI, celuy de la peau BCD; & l'entrée du tuyau GI, celuy de la prunelle; la vision se fera en mesme façon que si la Nature auoit fait l'oeil plus long qu'il n'est de toute la longueur de ce tuyau’.

[p. 229]

Nam semper eadem demonstratione ostendetur magnitudinis apparentis ad veram, esse rationem eandem, quae AG ad GB.

Hisce vero nequaquam consentiunt ea quibus Cartesius Telescopij inventum explicare contendit, similem huic tubum proponens solidum. Vult enim cavam superficiem ejusmodi esse ut radios à singulis visibilium punctis procedentes et per superficiem tubi exteriorem transmissos, ita inflectat ac ad oculum mittat tanquam si a propioribus punctis advenirent. Et quam rationem habuerit distantia horum punctorum propinquiorum ad distantiam ipsius visibilis, eandem¹⁾ magnitudinis apparentis ad eam quae solis oculis perciperetur definit²⁾. Hoc autem quomodo verum sit, quum senum oculis ea conveniat telescopij constitutio, ut radij convergentes aut certè paralleli ad oculum deferantur, non autem quasi ex puncto aliquo propiori manantes. Et notum est tamen non minus senibus quam qui visu pollent specierum magnitudines multiplicari.

Porro illud quoque in eâdem Cartesij explicatione absurdum, quod eam ob causam majora omnia videri ait, quoniam ex diversis rei visae punctis venientes radij decussentur in exteriori convexa tubi superficie, qui tubo non adhibito ad pupillam oculi decussarentur³⁾; quoniam enim si plana aut concava esset loco convexae superficiei nihilominus decussatio similis ibi contingeret. efficietur aeque etiam inverso tubo majora omnia conspici debere. Quod ijs quae superius demonstrata fuere atque ipsi adeo experientiae adversatur.

1) Il s'agit en vérité du rapport réciproque.

2) Voir le passage, d'ailleurs difficile à comprendre, qu'on trouve à la p. 158 du lieu cité dans la note 1, p. 224 et qui débute comme il suit: ‘Puis de rechef, que ces mesmes rayons,’ [venant d'un même point de l'objet] ‘en sortant de ce tuyau se plient & se redressent en telle sorte qu'ils puissent entrer dans l'oeil tout de mesme que s'ils n'auoient point du tout esté pliés, mais seulement qu'ils vinssent de quelque lieu qui fust plus proche. Et ensuite, que ceux qui viendront de diuers points, s'estant croisés dés l'entrée de ce tuyau, ne se decroysent point à la sortie, mais qu'ils aillent vers l'oeil en mesme façon que s'ils venaient d'un obiet qui fust plus grand, ou plus proche.’

3) Allusion au passage suivant qui se trouve p. 155-157 du lieu cité dans la note que nous venons de mentionner: ‘Il ne reste plus qu' vn autre moyen pour augmenter la grandeur des images, qui est de faire que les rayons qui viennent de diuers points de l'obiet, se croisent plus loin qu'il se pourra du fonds de l'oeil; mais il est bien, sans comparaison, le plus important & le plus considerable de tous. Car c'est l'vnique qui puisse seruir pour les obietsinacces



sibles, aussy bien que pour les accessibles, & dont l'effet n'a pas de bornes: en sorte qu'on peut, en s'en seruant, augmenter les images de plus en plus jusques a vne grandeur indefinie. Comme, par exemple, d'autant que la premiere des trois liqueurs dont l'oeil est rempli, cause a peu près mesme refraction que l'eau commune, si on applique tout contre vn tuyau plein d'eau, comme EF, au bout duquel il y ait vn verre GHI, dont la figure soit toute semblable a celle de la peau BCD qui couure cete liqueur, & ait mesme rapport a la distance du sonds de l'oeil, il ne se fera plus aucune refraction a l'entrée de cet oeil; mais celle qui s'y faisoit auparauant, (& qui estoit cause que tous les rayons qui venoient d'vn mesme point de l'obiet commençoient a se courber dés cet endroit là, pour s'aller assembler en vn mesme point sur les extremités du nerf optique, & qu' ensuite tous ceux qui venoyent de diuers points s'y croisoient, pour s'aller rendre sur diuers points de ce nerf), se fera dés l'entrée du tuyan GI: si bien que ces rayons, se croisans dés là, formeront l'image RST beaucoup plus grande que s'ils ne se croisoient que sur la supersicie BCD; & ils la formeront de plus en plus grande selon que ce tuyau sera plus long. Et ainsi l'eau EF saisant l'office de l'humeur K; le verre GHI, celuy de la peau BCD; & l'entrée du tuyau GI, celuy de la prunelle; la vision se fera en mesme façon que si la Nature auoit fait l'oeil plus long qu'il n'est de toute la longueur de ce tuyau’.

[p. 230]

Proposition XII¹⁾.

Lorsque sur la droite qui joint l'oeil et l'objet sont placées des lentilles ou des surfaces en nombre quelconque et de forme arbitraire, ayant cette même droite pour axe commun, l'oeil apercevra après toutes les réfractions une certaine partie de l'objet, même dans le cas où l'oeil est pour ainsi dire réduit à un point unique, pourvu que ce point ne soit pas celui où concourent après la réfraction les rayons issus du point de l'objet qui se trouve sur l'axe.

Soit FE l'axe commun sur lequel se trouve l'oeil au point A, et les lentilles en B et en C. Cherchons ensuite d'après le théorème...²⁾ le point F auquel correspondent des rayons tels que GF qui par la réfraction due à la lentille B doivent parvenir à l'oeil A en se mouvant selon HA. Cherchons de même le point D auquel correspondent des rayons tels que DG qui par la réfraction due à la lentille C doivent prendre la direction GF, de sorte qu'ils correspondent alors au point F; et ainsi de suite s'il y a un plus grand nombre de lentilles ou de surfaces. Or, le point F ou le point D peuvent être situés à une distance infinie et dans ces cas les rayons GF ou les rayons DG deviennent parallèles à l'axe. Alors si l'objet était placé au point D, il paraît que l'oeil serait situé au point de concours des rayons qui proviennent du point D, et que, par suite, ce point unique de l'objet donnerait alors une image quasi infinie. Mais supposons ici que l'oeil ne soit pas situé au point de concours nommé. Le point D tombe donc soit au-delà soit endeçà de l'endroit où est situé l'objet, lequel puisse se trouver en E ou en K.

Comme la droite FHG peut être tracée de telle manière que les angles GFC, GDC ou EDN deviennent chacun aussi petit qu'on le voudra, il paraît qu'on peut obtenir que les droites FHG et GDN ne tombent pas à l'extérieur des lentilles B et C. La dernière de ces droites, GDN, interceptera nécessairement une partie des droites EM ou KL perpendiculaires à l'axe, telle que NE ou KO, que l'oeil apercevra sous l'angle BAH. L'oeil verra donc une certaine partie de l'objet, ce qu'il fallait démontrer.

Mais si le point D est à une distance infinie, DG, parallèle à l'axe, interceptera de nouveau une partie des droites EM ou KL. Et si F est à une distance infinie, FH devient parallèle à l'axe; cela ne change rien dans la démonstration du théorème.

1) Cette proposition et la suivante manquent dans la copie de Niquet. Elles doivent donc dater en tout cas d'après 1666, et probablement de beaucoup plus tard.

2) Voir la Prop. XX, Lib. 1, p. 99 du Tome présent.

[p. 231]

[Propositio XII.]¹⁾

Dispositis in linea recta, oculum et visibile jungente lentibus aut superficiebus quotvis et quibuslibet, communem axem habentibus eandem lineam rectam, Percipiet oculus post omnium refractiones aliquam visibilis partem etiamsi veluti ad punctum reductus fuerit dummodo hoc punctum non sit quo post refractionem concurrunt radij a puncto visibilis quod in axe est egressi.

[Fig. 39.]

Sit recta FE axis communis in quo oculus ad A punctum, lentes ad B et C. Inveniatur porro ex Theor....²⁾ punctum F ad quod pertinentes radij ut GF flectantur refractione lentis B per HA ad punctum oculi A. Itemque inveniatur punctum D, ad quod pertinentes radij ut DG flectantur refractione lentis C in GF; ut pertineant ad punctum F atque ita porro si plures fuerint lentes superficiesve. Potest autem infinite distare puncta F vel D. quibus casibus axi paralleli fiunt radij GF vel DG. Quod si jam visibile ad punctum D positum esset, apparet oculum fore in puncto concursus radiorum e puncto D venientium, eoque unum hoc visibilis punctum tantummodo infinitè tuncexpansum cerni. Ponimus autem hic oculum esse extra hoc concursus punctum. Ergo punctum D cadit vel ultra vel citra locum rei visibilis, quae nempe sit in E vel K.

Quoniam igitur ita duci potest FHG ut quamlibet exigui fiant anguli singuli GFC, GDC, seu EDN, apparet effici posse ut rectoe FHG, GDN non extra lentes B, C aberrent. Harum vero postrema GDN, necessario partem aliquam rectarum EM vel KL axi per pendicularium intercipiet, velut NE vel KO, quas oculus comprehendet angulo BAH. Itaque aliquam visibilis partem cernet, quod erat dem.

Quod si infinite distet punctum D, tunc DG axi parallela intercipiet rursus partem rectarum EM vel KL. Si vero F infinite distat fit FH axi parallela, nec id quicquam in demonstratione mutat.

1) Cette proposition et la suivante manquent dans la copie de Niquet. Elles doivent donc dater en tout cas d'après 1666, et probablement de beaucoup plus tard.

2) Voir la Prop. XX, Lib. 1, p. 99 du Tome présent.

[p. 232]

Proposition XIII.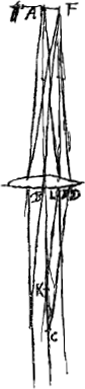

[Fig. 40.]

Si entre l'oeil et l'objet sont placées un nombre quelconque de lentilles ou de surfaces d'un corps transparent et que des rayons issus d'un point de l'objet situé sur l'axe commun de toutes ces lentilles et surfaces sortent parallèles après les avoir traversées, la grandeur et la position de l'image seront les mêmes à quelque distance derrière elles que se trouve l'oeil.

Soit ABC l'axe commun d'un nombre quelconque de lentilles ou de surfaces sphériques, et la ligne AF, perpendiculaire à l'axe ABC, l'objet. Le point F y soit situé à si petite distance du point A qu'il peut être aperçu par l'oeil, placé en K ou en C, deux points quelconques de l'axe, et réduit à un point: en effet, la proposition précédente fait voir que cela est possible. Je dis que pour les deux positions de l'oeil la ligne AF donnera une image de même grandeur. En effet, attendu que les rayons issus du point A, après avoir traversé les corps transparents interposés, deviennent parallèles entre eux, les rayons provenant du point F seront également parallèles entre eux en sortant^*. Supposons que de ces rayons DC parvienne à l'oeil situé en C, et LK à l'oeil situé en K. Attendu que les rayons DC et LK sont parallèles entre eux, les angles BKL et BCD seront égaux. Mais par un oeil situé en K la droite AF est vue sous un angle BKL, et par un oeil situé en C la même droite AF est vue sous l'angle BCD. Dans l'un et l'autre cas cette droite est donc vue sous le même angle et son image aura, par conséquent, la même grandeur. Mais il paraît aussi que les droites CD et KL tombent du même côté de l'axe, puisqu' elles émanent parallèlement des points C et K. On apercevra donc une même position de la ligne AF soit qu'on regarde du point C, soit qu'on se trouve placé en K. Ce qu'il fallait démontrer.

FIN DU DEUXIÈME LIVRE.

* Prop. XXII. Liv. I¹⁾.

1) Voir la p. 111 du Tome présent.

[p. 233]

[Propositio XIII.]

Si inter oculum et rem visam quotlibet lentes aut superficies diaphani interjaceant et a puncto rei visoe quod sit in omnium axe communi manantes radij, trajectis ijsdem lentibus aut superficiebus paralleli exeant; quocunque intervallo post ipsas oculus statuatur, eadem apparebit rei visoe magnitudo; idemque positus.

Sit axis communis [Fig. 40] quotlibet lentium vel superficierum sphoericarum ABC, res visa linea AF, axi ABC perpendicularis in qua punctum F tam propinquum sit ipsi A, ut oculo in K aut C, quibuslibet nempe duobus axis punctis, collocato et ad punctum redacto, in conspectum venire possit. hoc enim possibile esse ex prop. antecedente constat. Dico utroque oculi positu, eadem magnitudine apparituram lineam AF. Quum enim a puncto A manantes radij, trajectis interpositis diaphanis inter se fiant paralleli, etiam ab F puncto egressi inter se paralleli exibunt^*. Quorum DC ad oculum in C positum pergat, LK ad oculum positum in K. Quia igitur inter se paralleli sunt radij DC, LK, oequales erunt anguli BKL, BCD, atqui oculo in K spectatur recta AF angulo BKL, oculo vero in C spectatur eadem AF angulo BCD, Ergo utrobique oequali angulo, ideoque pari magnitudine. Sed et ad eandem axis partem cadere apparet rectas CD, KL, cum ex punctis C, K paralleloe exeant. Ergo sive ex C sive ex K idem positus percipietur lineoe AF. Quoe erant dem.

[FINIS SECUNDI LIBRI.]

* [Per Prop. XXII. Lib. I.]¹⁾

1) Voir la p. 111 du Tome présent.

2) Voir la p. 119 du Tome présent.

2) Voir la p. 119 du Tome présent.

3) Voir la p. 99 du Tome présent.

3) Voir la p. 99 du Tome présent.

1) Voir la p. 111 du Tome présent.

1) Voir la p. 111 du Tome présent.