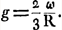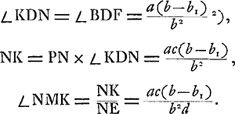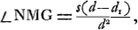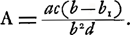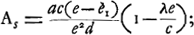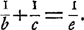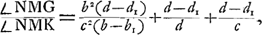Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–Troisième partie: Des Télescopes et des Microscopes. 1685-1692.Chap. I. Des Télescopes.Préface et considérations sur le grossissement et le champ de vision des lunettes à deux lentilles.Le traité ‘des télescopes’, que nous allons analyser maintenant, est précédé d'une préface qu'on peut dater avec certitudeGa naar voetnoot9) de 1685, et il est probable | |||||||||||||||||||
[pagina LXXXIV]
| |||||||||||||||||||
que le traité lui-même fut composé, ou du moins reçut sa forme definitive, en grande partie pendant cette même annéeGa naar voetnoot1). Dans cette préface Huygens s'occupe d'abord de l'invention du télescope dont il attribue la priorité à Lippersheim ou à Zacharias JanssenGa naar voetnoot2). À cette occasion il se réfère à un document, dont il a pu prendre connaissance et qui réfute définitivement les promoteurs de Jacob MetiusGa naar voetnoot3). Toutefois il insiste sur les droits de Porta à une invention préalable, qui n'était qu'un ‘rude commencement’ et qui ne portait pas de fruitsGa naar voetnoot4). Ensuite Huygens expose les services immenses rendus par le télescope à la science de l'astronomie, et il exprime l'espoir que son invention des lunettes sans tube, en permettant d'arriver à des grossissements beaucoup plus forts, nous révélera bientôt ‘d'autres spectacles nouveaux et nombreux’Ga naar voetnoot5). Passant alors à la considération ‘des causes et des propriétés de cet oeil factice’, il déduit dans la Prop. I (p. 443-451) pour le cas de la lunette hollandaise la formule bien connue du grossissement. Dans cette Proposition, et dans la Prop. III (p. 455-461) qui concerne la lunette keplérienne, Huygens ne donne pas moins de trois ou quatre démonstrations différentes de cette formule pour chacun des deux instruments. On pourrait s'étonner d'une telle profusion, mais elle s'explique facilement par le désir de Huygens de montrer, par cet exemple, la supériorité de ses méthodes sur celles de ses prédécesseurs. En effet, on peut lire dans sa préface: ‘on n'est pas parvenu jusqu'à ce jour à ce qui est le plus important en cette matière, c'est-à-dire à la connaissance de la nature et de la grandeur du grossissement de l'objet visé, étant données la forme et la position des lentilles. Kepler ne l'a pas enseigné, quoiqu'il soit digne de beaucoup de louanges à cause des explications de phénomènes dioptriques qu'il a données le premier. Descartes ne fut pas plus heureux que lui; en | |||||||||||||||||||
[pagina LXXXV]
| |||||||||||||||||||
vérité il s'écarta plutôt de la bonne route dans les démonstrations qu'il voulut donner de la nature et de l'effet du télescope’. Ces phrases nous font comprendre la satisfaction que Huygens éprouve évidemment en multipliant les démonstrations simples et élégantes d'un théorème si importantGa naar voetnoot6); après en avoir achevé la dernière, pour le cas de la lunette hollandaise, il ajoute: ‘De cette manière Descartes aurait pu établir la théorie du télescope mieux que par la considération de l'intersection des rayons qui a lieu à la surface de la lentille extérieure’, et il critique ensuite les idées par trop exagérées de ce philosophe au sujet de la puissance qu'on pourrait donner aux télescopesGa naar voetnoot7). Dans la première de ses démonstrations, p. 445, Huygens suppose que l'oeil se trouve immédiatement derrière la lentille oculaire. Alors, d'après une proposition prouvée dans la première Partie de la DioptriqueGa naar voetnoot8), l'objet est vu sous le même angle que dans le cas où, au lieu de l'oculaire, il y aurait simplement un petit trou; on peut dire que dans ces circonstances la lentille oculaire sert seulement à rendre la vision distincte sans avoir aucune influence sur la grandeur apparente. Cette remarque conduit facilement au théorème que le grossissement est déterminé par le rapport des distances de l'objectif et de l'oculaire au foyer de l'objectif; c'est-à-dire au point où se formerait l'image de l'objet éloignéGa naar voetnoot9) s'il n'y avait pas d'oculaireGa naar voetnoot10). Sous cette forme la règle s'applique à tous les cas, quel que soit l'état d'accommodation de l'oeilGa naar voetnoot11), pourvu seulement qu'il se trouve tout près de l'oculaire. Cette restriction n'est pas nécessaire quand on suppose que l'oeil est adapté à une distance insinie. Dans cette hypothèse, le point de dispersion de l'oculaire devra coïncider avec le foyer de l'objectif, de sorte que les rayons provenant d'un point de l'objet redeviennent parallèles entre eux après | |||||||||||||||||||
[pagina LXXXVI]
| |||||||||||||||||||
leur passage à travers l'instrument; mais alors, d'après un théorème démontré dans la première Partie de la DioptriqueGa naar voetnoot1), la grandeur apparente de l'objet sera indépendante de la position de l'oeil et la règle peut être donnée sous sa forme usuelle d'après laquelle le grossissement égale le quotient des distances focales. D'ailleurs, pour trouver cette règle, il suffira alors de considérer la marche d'un rayon incident quelconque, incliné sur l'axe. Pour ce rayon Huygens choisit successivement un de ceux qui atteignent le centre de l'oculaire (p. 447), un autre qui, après avoir passé par le premier foyer de l'objectif, parcourt la lunette parallèlement à l'axe (p. 449) et enfin un rayon qui passe par le centre de l'objectif. C'est ainsi qu'il obtient les trois autres démonstrations. Dans la Prop. II (p. 451-453) il s'agit du champ de la lunette hollandaise. Huygens suppose qu'on place l'oeil tout près de la lentille oculaire concave, ce qui est, en effet, la position dans laquelle l'oeil embrasse d'un seul regard le plus grand nombre d'objets. Dans les circonstances ordinaires, l'étendue du champ dépend alors en premier lieu de la grandeur de la pupille de l'oeil, étant déterminée par le cône qui a pour base cette pupille et pour sommet le centre de l'objectif. Cependant si la pupille se contracte de plus en plus, ou si l'on place devant elle un trou de plus en plus petit, le champ ne se rétrécira pas indéfiniment; en effet, lorsque la pupille sera réduite à un point, le champ aura toujours une certaine grandeur, déterminée par les rayons passant par le bord de l'objectif (p. 453). Il faut remarquer aussi que Huygens se rend compte de l'affaiblissement graduel de l'intensité lumineuse vers la périphérie du champ et qu'il sait donc distinguer entre la partie centrale uniformément éclairée et l'étendue totale. Signalons encore une jolie expérience que Huygens décrit ici (p. 453). Elle consiste à regarder au travers de la lunette après s'être trouvé quelque temps dans l'obscurité. On peut remarquer alors que dans les premiers moments l'étendue du champ est plus grande qu'à l'ordinaire, mais qu'elle diminue rapidement par suite de la contraction de la pupille, qui s'était dilatée dans l'obscurité. | |||||||||||||||||||
[pagina LXXXVII]
| |||||||||||||||||||
Dans la Prop. III (p. 455-461) Huygens passe aux lunettes keplériennes à deux verres convexes. Il y détermine le grossissement d'une manière entièrement analogue à celle qu'il suit dans la Prop. I pour le cas de la lunette hollandaise; mais il s'occupe aussi de l'endroit où se trouve la pupille de sortie et où il faut donc placer la pupille de l'oeil si l'on veut que le plus de rayons possibles contribuent à la vision; question à laquelle il s'était déjà beaucoup interessé en 1653 dans la première Partie de la DioptriqueGa naar voetnoot2). En effet, dans le cas où la pupille de sortie est plus petite que celle de l'oeil, comme il en était dans les télescopes construits par Huygens, on peut dire que lorsque l'oeil a la position indiquée, tous les rayons qui sont transmis par l'instrument atteignent la rétine. La pupille peut alors se contracter encore plus ou moins sans que la clarté de l'image en souffre (p. 459). Le champ de la lunette keplérienne est déterminé suivant Huygens, par le cône ayant pour base l'oculaire et pour sommet le centre de l'objectifGa naar voetnoot3); il est donc, en général, beaucoup plus étendu que celui de la lunette hollandaise; différence sur laquelle Huygens insiste dans sa comparaison des deux espèces de télescopes (p. 459-461). Il faut dire ici qu'on ne trouve nulle part chez Huygens une théorie de champ de vision aussi complète que celle de l'aberration sphérique, par exemple. Il est vrai que, dans sa généralité, le problème est assez compliqué, revenant à la détermination des lignes droites qu'on peut tirer par trois plans circulaires, à savoir celui de l'oculaire, celui de la pupille de l'oeil et celui de la pupille de sortie. La question se simplifie lorsque le centre du deuxième cercle coïncide avec celui du premier ou du troisième; ce sont là précisément les cas qui se présentent dans la lunette hollandaise et dans la lunette keplérienne, si l'oeil a la position que Huygens lui assigne. On obtient aussi une simplification en supposant qu'un des trois cercles est très petit. Dans une annotation de l'année 1686Ga naar voetnoot4) Huygens cherche la position que l'oeil, considéré comme un point, doit avoir dans le cas de la keplérienne pour obtenir la plus grande étendue du champ. Cette positionGa naar voetnoot5) est plus rapprochée de l'oculaire que la pupille de sortie et même que le second foyer. | |||||||||||||||||||
[pagina LXXXVIII]
| |||||||||||||||||||
Lunettes à plus de deux lentilles.Nous avons vuGa naar voetnoot1) que, vers 1653, dans le Traité de la réfraction et des télescopes, qui constitue la première Partie de la Dioptrique, Huygens avait recommandé deux différents systèmes de lunettes à plus de deux lentilles; l'un (Part. I, Liv. III, Prop. III, p. 253-259) pour les observations célestes, l'autre (Part. I, Liv. III. Prop. IV, p. 259-264) pour l'usage terrestre; en outre il avait fait grand cas d'un système où le redressement des images formées par une keplérienne était obtenu à l'aide d'un petit miroir (Part. I, Liv. III, Prop. V, p. 265-269). De ces trois systèmes il n'a jamais abandonné entièrement le premier dont l'oculaire est connu sous son nom. Jusqu'en 1692, il s'en occupeGa naar voetnoot2) et dans le projet relatif à l'arrangement des matières dans sa Dioptrique, conçu cette année, il lui réserve une place prédominanteGa naar voetnoot3). Au contraire les deux systèmes terrestres, celui à trois lentilles et images droites, et celui à miroir, sont considérés par lui comme inférieurs au système de Campani à quatre lentilles, dès que, vers 1666Ga naar voetnoot4), l'expérience lui a fait connaître les mérites de ce dernier. Guidé par ces considérations, Huygens a ajouté au manuscrit de sa Dioptrique une nouvelle proposition (la Prop. V, p. 469-473, de la troisième Partie), concernant les lunettes de Campani; il a conservé la Prop. III de la première Partie, mais il l'a soumise à une révision complète. C'est sous cette nouvelle forme que nous l'avons reproduite comme Prop. IV (p. 461-467) de la troisième Partie. Cependant, comme nous l'avons indiqué dans les notesGa naar voetnoot5), la nouvelle rédaction eft un peu fragmentaire et confuse. Déjà la seconde phrase pourrait donner lieu à un malentendu. On y lit que ‘l'aberration des rayons qui se dirigent vers l'oeil à partir des différents points de l'objet devient beaucoup moindre’ [dans l'oculaire à deux lentilles] ‘que lorsqu'on prend une lentille oculaire unique, donnant le même grossissement’. | |||||||||||||||||||
[pagina LXXXIX]
| |||||||||||||||||||
Or, il ne peut pas s'agir ici, comme on le croirait au premier abord, de l'effet nuisible de l'aberration sphérique ou chromatique sur la netteté des images, puisque Huygens savait trop bien que, dans les circonstances ordinaires, l'oculaire n'y contribue que très peuGa naar voetnoot6). Il faut donc que Huygens ait en vue un autre phénomène, dont il ne parle dans sa Dioptrique qu'en passant et qui consiste dans une distorsion des images causée par l'aberration sphérique de l'oculaire. Nous savons, en effet, que, vers 1692, Huygens s'est occupé de ce phénomène et nous reviendrons bientôt sur ce sujet. Ajoutons encore que, dans la nouvelle rédaction, Huygens a adopté pour les dimensions de son oculaire les relations f1 = 4f2, e = 2f2, où f2 représente la distance focale de la lentille qui se trouve du côté de l'oeil, f1 celle de l'autre lentille et e leur distance mutuelleGa naar voetnoot7). Partant de ces relations, il apprend à calculer quelles doivent être les valeurs de f1, f2 et e, si l'on veut obtenir avec une lunettte de longueur donnée un grossissement donné, et quel est le lieu précis où l'on doit placer l'oculaire pour que les rayons venant d'un point très éloigné redeviennent parallèles entre eux après leur sortie de la lunette. Quant aux lunettes ‘Campanines’ à quatre verres, l'inspection des figures 14 et 15 de la p. 469 en fera connaître immédiatement la disposition des lentilles. Huygens préfère ces Campanines à ses propres lunettes terrestres à trois lentillesGa naar voetnoot8), parce que dans celles-ci ‘les lentilles oculaires, ou tout au moins celle qui est la plus proche de l'oeil, doivent être composées de portions plus grandes de surfaces sphériques, par rapport à la distance focale, si l'angle visuel doit être le même dans les deux casGa naar voetnoot9), d'où il s'ensuit que les objets semblent colorés et que les lignes droites auprès des bords paraissent courbées’ (p. 469). Plus loin (p. 473) il ajoute que, toutefois, les Campanines doivent ‘une grande partie de leur supériorité à l'anneau ou diaphragme’, qu'on introduit entre les deux lentilles qui sont les plus proches de l'oeil et dont l'avantage consiste à ‘donner au champ une limite circulaire nette’, et à faire ‘disparaître en même temps les couleurs aux bords, couleurs qu'il était impossible d'éviter entièrement avant | |||||||||||||||||||
[pagina XC]
| |||||||||||||||||||
cette invention’. Or, l'usage d'un tel diaphragme, qui était auparavant inconnu, fut expliqué par lui dans son Systema SaturniumGa naar voetnoot1). D'ailleurs les frères Huygens, Constantyn et Christiaan, ont construit des ‘Campanines’ eux-mêmesGa naar voetnoot2). Une d'elles est conservée à l'Observatoire de Leiden. Nous en avons indiqué les mesures au § 7 de l'Appendice VI, p. 607Ga naar voetnoot3). | |||||||||||||||||||
Considérations et calculs de Huygens sur la distorsion des images.C'est ici la place de parler de la distorsion des images, causée par l'aberration sphérique de l'oculaire, puisque les calculs faits par Huygens à ce sujet se rapportent précisément aux deux systèmes d'oculaires que nous venons de décrire. Or, quoique Huygens ait eu, vers 1692, l'intention d'exposer dans sa Dioptrique ses idées sur la cause de cette distorsion et sur la manière de la déterminer pour un oculaire donné, il n'a pas exécuté ce projetGa naar voetnoot4). Aussi le seul moyen de connaître ces idées, c'est l'examen attentif des deux Pièces qui contiennent les calculs que nous venons de mentionner. Ces Pièces sont reproduites au § 14 de l'Appendice VI (p. 615-617) et dans l'Appendice VII (p. 618-620). Commençons par donner un aperçu des conceptions de Huygens qui ont dû servir de base à ses calculs. À cet effet nous suivrons, dans son parcours à l'intérieur d'une lunette, le faisceau de rayons qui émane d'un point éloigné, situé à côté de l'axe de la lunette. Ce faisceau, qui, à son entrée dans l'instrument, a la largeur de l'ouverture de l'objectif, se rétrécit ensuite pour se réduire presqu'à un point dans le plan focal. Après avoir passé ce plan il s'élargit un peu; mais | |||||||||||||||||||
[pagina XCI]
| |||||||||||||||||||
cela n'empêche pas qu'il ne frappe qu'une partie très restreinte de la première surface de l'oculaire. Par suite, les rayons qui le composent suivront dans l'oculaire des routes très voisines. L'aberration sphérique de cette lentille aura donc à peu près le même effet sur chacun de ces rayons; elle ne produira pas de diminution appréciable dans la netteté des images, mais une déviation dans la direction des rayons, qui sera à peu près la même pour tous. C'est cette déviation qui cause la distorsion des images. Afin de la calculer, il suffira de considérer un seul rayon du faisceau, pour lequel on peut choisir, comme Huygens le fait dans les deux cas traités par lui, le rayon qui, passant près du premier foyer de l'objectif, se meut parallèlement à l'axe à l'intérieur du tube entre l'objectif et l'oculaireGa naar voetnoot5). Pour ce rayon on peut déterminer en premier lieu l'angle qu'il ferait avec l'axe après sa sortie de l'oculaire, simple ou composé, dans l'hypothèse où il n'y aurait pas d'aberration sphérique, et ensuite l'angle qu'il fait, en réalité, avec l'axe après cette sortie, en tenant compte de l'aberration sphérique. La différence entre ces deux angles constituera ce que Huygens appelle l'angle d'aberration sphériqueGa naar voetnoot6). C'est cet angle qu'il emploie pour mesurer la distorsion de l'imageGa naar voetnoot7). Dans la première des deux Pièces que nous venons de citer (§ 14, p. 615), Huygens démontre que la distorsion causée par l'oculaire de Campani à trois lentilles, est égale à celle que produirait une seule de ces lentilles si l'on s'en servait comme lentille oculaire unique. En reproduisant cette Pièce, qui n'est qu'une ébauche, nous avons dû suppléer mainte fois dans les notes aux lacunes du raisonnement. La seconde Pièce (§ 15, p. 618) est encore moins achevée. Elle est si peu explicite que nous avons même hésité sur sa véritable portée lors de sa reproduction dans le texte du présent TomeGa naar voetnoot8). Toutefois un nouvel examen a fait disparaître cette hésitation. Il ne nous semble plus douteux que Huygens y compare, en effet, la distorsion causée par l'oculaire, qui porte son nom, à celle pro- | |||||||||||||||||||
[pagina XCII]
| |||||||||||||||||||
venant d'une lentille oculaire unique donnant le même grossissement et le même champ de vision. Nous croyons que, lorsque Huygens y prend pour angle d'aberration un angle qui ne lui est pas égal, il s'agit d'une inadvertanceGa naar voetnoot1). D'ailleurs cette erreur n'infirme pas sa conclusion que l'angle d'aberration (et par conséquent la distorsion) propre à son oculaire est beaucoup moindre que l'angle d'aberration qui appartient à la lentille unique; ce qui constitue l'un des principaux avantages de son oculaire. Disons encore que dans ses calculs Huygens se sert continuellement d'une proposition importante (Prop. VI, p. 475-479) sur l'égalité des petits angles entre deux rayons perpendiculaires à l'arête d'un prisme avant leur entrée dans le prisme et après qu'ils en sont sortis; proposition que nous avons déjà mentionnée à la p. XLV de cet Avertissement. | |||||||||||||||||||
Considérations générales sur la clarté et la nettété des images formées par les télescopes. Déduction des nouvelles règles pour la détermination de l'ouverture et du grossissement admissibles dans un télescope de longueur donnée.La partie de la théorie des lunettes qui occupe les p. 481-511 est sans doute la plus importante et celle qui montre le mieux le talent avec lequel Huygens a su approfondir les problèmes qu'il fallait résoudre pour bien comprendre les effets produits par ces instruments. Il y considère les limites qu'on doit s'imposer dans la construction des télescopes pour que l'image ne soit ni trop obscure, ni trop confuse et il reprend donc les questions qu'il avait traitées autrefois dans les ‘Rejecta’ et dont nous avons donné un résumé aux p. LXVI-LXXII de cet Avertissement. Seulement les nouvelles règles, qu'il va déduire maintenant, sont basées sur la considération de l'aberration chromatique, dont il avait appris à reconnaître la prépondérance sur l'aberration sphérique, quant à l'effet produit sur la netteté des images formées par les télescopesGa naar voetnoot2). | |||||||||||||||||||
[pagina XCIII]
| |||||||||||||||||||
Mais c'est d'abord la clarté des images qu'il étudieGa naar voetnoot3). Elle est déterminée par la quantité de lumière que la rétine reçoit par unité de surface. Huygens démontre que, dans l'observation à l'oeil nu, elle est indépendante de la distance à laquelle on place l'objet (p. 481) et que, si dans l'observation télescopique la clarté devait être la même qu'à la vue directe, il faudrait que le rapport entre le diamètre de l'objectif et celui de la pupille de l'oeil fût égal au grossissement. Cependant il ajoute qu'en réalité cette condition est trop rigoureuse, et qu'on peut se contenter d'une clarté bien moindre. L'expérience lui a appris que, dans les observations diurnes, il suffit d'avoir une clarté qui est la sixième ou la septième partie de celle qu'on observe à l'oeil nu, et que, dans les observations nocturnes de la lune et des planètes, elle peut être réduite encore sans inconvénient à la moitié de cette fraction. La relation dont il s'agit ici peut, comme on sait, être exprimée bien simplement quand on y introduit la grandeur de la pupille de sortie de l'instrument. Si cette pupille est plus grande que celle de l'oeil, qui se trouve au même point de l'axe, et si, par conséquent, la pupille de l'oeil est entièrement remplie de rayons, on a la même clarté que dans le cas de l'observation directe. Lorsque, au contraire, la pupille de sortie a un diamètre inférieur à celui de la pupille de l'oeil, la clarté diminue dans le rapport qu'il y a entre la surface de cette dernière et celle de la pupille de sortie. Or, dans les télescopes construits d'après le tableau de la p. 497, qui étaient destinés à l'observation de SaturneGa naar voetnoot4), le diamètre de la pupille de sortie était la quarantième partie d'un pouce, c'est-à-dire 0,65 mm. environ. Si l'on estime à 2,5 mm. celui de la pupille de l'oeilGa naar voetnoot5), on trouve (2,5/0,65)2 = 15 pour le rapport en questionGa naar voetnoot6). | |||||||||||||||||||
[pagina XCIV]
| |||||||||||||||||||
Il importe maintenant d'évaluer les effets de l'aberration chromatique. Il ne paraît nulle part que Huygens ait mesuré les indices de réfraction de ses verres pour les rayons de différentes couleurs. Il se base presque toujours sur le résultat, indiqué en 1672 par Newton, d'après lequel le diamètre du cercle d'aberration chromatique serait égal à la cinquantième partie du diamètre de la lentille employéeGa naar voetnoot1). Or ce résultat, il l'a mal interprété en confondant le cercle d'aberration visé par Newton, qui est situé dans un plan placé à mi-distance entre les foyers des rayons rouges et des rayons violets, avec le cercle d'aberration, tel qu'il le concevait lui-même, c'est-à-dire avec celui qui est situé dans le plan focal des rayons violetsGa naar voetnoot2); les diamètres de ces deux cercles étant dans le rapport de 1 à 2. Si donc, dans le calcul qu'il fait suivre, il pose l'aberration chromatique longitudinale égale à la cinquantième partie de la distance focale, il réduit, sans s'en douter, l'évaluation de Newton à la moitié. Pour comparer entre elles les deux aberrations, chromatique et sphérique, Huygens prend comme exemple (p. 485) un télescope dont l'objectif, qui est planconvexe, a une distance focale d'un pied, et une ouverture d'un demipouce ‘ce qui est environ l'ouverture qu'il faut donner à cette lentilleGa naar voetnoot3) dans un télescope d'un pied’. L'épaisseur mathématiqueGa naar voetnoot4) d'une telle lentille est égale à 1/192 pouce. Sa surface courbe étant tournée vers l'extérieur, on trouve | |||||||||||||||||||
[pagina XCV]
| |||||||||||||||||||
 pouce pour l'aberration sphérique longitudinaleGa naar voetnoot5). Or, l'aberration chromatique longitudinale étant évaluée à 12/50 pouce, elle est 39 fois plus forte que l'aberration sphérique. Elle l'emporte donc de beaucoup sur cette dernière, et Huygens remarque (p. 487) que dans les télescopes plus longs la différence des deux aberrations sera plus grande encore. pouce pour l'aberration sphérique longitudinaleGa naar voetnoot5). Or, l'aberration chromatique longitudinale étant évaluée à 12/50 pouce, elle est 39 fois plus forte que l'aberration sphérique. Elle l'emporte donc de beaucoup sur cette dernière, et Huygens remarque (p. 487) que dans les télescopes plus longs la différence des deux aberrations sera plus grande encore.
Il s'agit, par conséquent, de baser les nouvelles règles pour déterminer l'ouverture et le grossissement d'une lunette de longueur donnée, non plus, comme en 1666 dans les ‘Rejecta’, sur l'aberration sphériqueGa naar voetnoot6), mais sur l'aberration chromatique. Cette fois encore, Huygens suppose connues les dimensions d'une lunette qui donne des résultats satisfaisants et il se propose d'en déduire celles qu'on doit donner à une autre lunette de longueur différente, afin d'obtenir dans les deux instruments la même clarté et une netteté égale des images. Soient donc de nouveau f et f′ les distances focales des objectifs, ϕ et ϕ′ celles des oculaires, g et g′ les grossissements, d et d′ les diamètres des ouvertures des objectifs. La condition pour l'égalité de la clarté sera la même que celle que nous avons déduite à la p. LXVIII, c'est-à-dire:
De même, nous pouvons emprunter à la p. LXIX l'équation:
Au contraire, la formule (11) de la p. LXVIII subira une modification profonde. En effet, on aura cette fois, puisque les aberrations chromatiques longitudinales sont proportionnelles aux distances focales:
| |||||||||||||||||||
[pagina XCVI]
| |||||||||||||||||||
De ces trois équations, combinées avec la formule (15) de la p: LXIX, on déduit facilement les relations:
Partant d'une lunette étalon dans laquelle la distance focale de l'objectif est égale à 30 pieds, et le diamètre de l'ouverture à 3 pouces, Huygens a déduit de ces relations, la règle de la p. 495, et de même le tableau des p. 497-499. Seulement, en calculant ce tableau, il a supposé que la distance focale de l'oculaire égalait le diamètre de l'ouverture, tandis que, lorsqu'il établissait la règle de la p. 495, qui est postérieure au tableau, il a estimé qu'on obtiendrait de meilleurs résultats en employant avec l'objectif de 30 pieds un oculaire de 3,3 pouces de distance focaleGa naar voetnoot1).
Faisons remarquer encore que Huygens estime que l'évaluation de l'aberration chromatique longitudinale à un cinquantième de la distance focale est exagérée quand il s'agit de comparer entre elles les deux aberrations, chromatique et sphérique. Il en donne la raison (p. 487) que, dans la lumière blanche, les rayons jaunes présentent la plus grande intensité, et que les rayons extrêmes du spectre y sont relativement faiblesGa naar voetnoot2). Toutefois dans le texte de la Dioptrique, pour la théorie des microscopes comme pour celle des télescopes, Huygens emploie toujours cette fraction 1/50 pour représenter le rapport de l'aberration longitudinale à la distance focale, ou, ce qui revient au même, celui du diamètre du cercle d'aberration, placé au plan focal des rayons violets, au diamètre de l'ouverture de la lentille. Toutefois dans le dernier projet de rédaction de sa Dioptrique il | |||||||||||||||||||
[pagina XCVII]
| |||||||||||||||||||
avait remplacé la fraction 1/50 par 1/200Ga naar voetnoot3). Il le faisait évidemment à propos de quelques recherches qu'on trouve dans l'Appendice IX, et qui ont précédé la rédaction définitive de la partie de la Dioptrique, dont nous nous occupons à présent. En effet, aux §§ 4-14 (p. 633-654) de cet Appendice, Huygens calcule pour des microscopes et petits télescopes, dont les mérites lui sont connus, les angles d'aberration sphérique et d'aberration chromatique, en se servant pour le calcul de ces derniers de la fraction 1/50. Nous avons désini à la p. XCI celui de ces angles qui se rapporte à l'aberration sphérique; l'autre est formé par les rayons extrêmes, du côté rouge et du côté violet, sortant de l'oculaire et provenant du rayon blanc qui a passé par le bord de l'ouverture de l'objectifGa naar voetnoot4); c'est-à-dire, en prenant pour ces rayons extrêmes ceux qui embrassent la partie du spectre qui est supposée avoir une influence sensible sur la netteté des images. Ces deux angles sont évidemment proportionnels aux rayons des cercles d'aberration sur la rétine, pourvu qu'on néglige les aberrations sphérique et chromatique de l'oeil. Si la fraction 1/50 avait été bicn choisie, leurs valeurs respectives devaient donc pouvoir servir à comparer entre eux les effets de l'une et de l'autre aberration sur la netteté des images. Or, quoique les résultats des calculs prémentionnés ne fussent pas toujours concordants, on peut bien dire qu'ils ont dû donner à Huygens l'impression que les télescopes et microscopes examinés peuvent souffrir un angle d'aberration chromatique, calculé avec la fraction 1/50, beaucoup plus grand que l'angle d'aberration sphérique qui semblait être admissible d'après ces mêmes cal- | |||||||||||||||||||
[pagina XCVIII]
| |||||||||||||||||||
culsGa naar voetnoot1). Il en devait donc conclure que, lorsqu'on veut rendre comparables entre elles, quant à l'influence sur la netteté des images, les valeurs obtenues pour les deux angles en question, on
doit diminuer considérablement la fraction 1/50; c'est-à-dire rétrécir de beaucoup la partie du spectre qu'on suppose contribuer sensiblement à l'effet nuisible de l'aberration chromatiqueGa naar voetnoot2). Huygens peut d'ailleurs avoir été conduit à la même conclusion par les considérations qu'on trouve au § 2 (p. 629-631) du même Appendice. Il y calcule les aberrations latérales sphérique et chromatique d'une lentille planconvexe, tournant sa convexité vers les rayons incidents. Appellant R le rayon de la surface convexe, et r celui de l'ouverture de la lentille, on trouve  pour l'aberration sphérique latérale et ηr pour l'aberration chromatique, où η représente la fraction à laquelle Huygens donne successivement les valeurs 1/50 et 1/200. L'aberration sphérique l'emporte donc sur l'aberration chromatique quand on a pour l'aberration sphérique latérale et ηr pour l'aberration chromatique, où η représente la fraction à laquelle Huygens donne successivement les valeurs 1/50 et 1/200. L'aberration sphérique l'emporte donc sur l'aberration chromatique quand on a
 , c'est-à-dire quand on a , c'est-à-dire quand on a 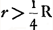 environ pour η = 1/50, et environ pour η = 1/50, et 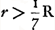 pour η = 1/200. Or, par une expérience ingénieuse, pour laquelle nous renvoyons au paragraphe en question, Huygens arrive à la conclusion que déjà pour pour η = 1/200. Or, par une expérience ingénieuse, pour laquelle nous renvoyons au paragraphe en question, Huygens arrive à la conclusion que déjà pour  l'effet de l'aberration sphérique surpasse celui de l'aberration chromatiqueGa naar voetnoot3). l'effet de l'aberration sphérique surpasse celui de l'aberration chromatiqueGa naar voetnoot3).
Les nouvelles règles pour les ouvertures et les grossissements, telles qu'on les trouve formulées à la p. 495, s'appliquent aux télescopes qui doivent servir pour | |||||||||||||||||||
[pagina XCIX]
| |||||||||||||||||||
les observations nocturnes. Comme il a déjà été ditGa naar voetnoot4), les observations qu'on fait pendant le jour exigent une clarté à peu près double; c'est pour cela que Huygens s'occupe aux p. 503-505 de la manière dont on pourra adapter les lunettes à ces dernières observations. S'il ne s'agissait ici que de la clarté, on pourrait porter au double la surface de l'objectif, ou bien changer dans le rapport de 1 à √2 la distance focale de l'oculaire, chacun de ces changements augmentant la clarté dans le rapport voulu. Mais évidemment le premier moyen nuirait à la netteté des images; c'est donc au second que Huygens s'arrête. Cependant il se demande s'il n'y aurait pas avantage à agrandir dans une certaine mesure le diamètre de l'objectif, en augmentant en même temps plus ou moins la distance focale de l'oculaire. En effet, si le diamètre de l'objectif est changé dans le rapport de 1 à α et la distance focale de l'oculaire dans celui de 1 à β, le grossissement, la clarté et le diamètre du cercle d'aberration sur la rétine changent respectivement dans les rapports de 1 à β-1, α2 β2 et α β-1Ga naar voetnoot5). On aura donc une clarté double et le même degré de netteté si l'on fait en sorte que
 . .
Par conséquent, en portant la surface de l'objectif à 1,41 fois sa grandeur - et non pas au double - et en augmentant la distance focale de l'oculaire dans le rapport de 1 à 1,19, on obtiendrait la même netteté des images qu'avec le télescope étalon, la clarté nécessaire, et en même temps un grossissement égal à 0,84 de ce qu'il était primitivement, tandis que, si on laissait à l'objectif son ouverture primitive, en augmentant seulement la distance focale de l'oculaire, le grossissement serait réduit dans le rapport de 1 à 0,71. La première solution semble donc se recommander, mais Huygens remarque | |||||||||||||||||||
[pagina C]
| |||||||||||||||||||
‘que le nuage provenant de l'aberration Newtonienne nuit d'autant plus à la netteté que l'image formée sur le fond de l'oeil est plus lumineuse’ et que l'expérience lui a appris qu'il ‘ne faut rien changer aux ouvertures’. On voit, par ce qui précède, avec combien de soin Huygens a toujours adapté ses instruments au but auquel ils devaient servir. Sous ce rapport il faut signaler encore ce qu'il dit (p. 511) de l'observation des corps célestes qui ne présentent pas de grandeur angulaire appréciable, tels que les étoiles faibles, ou les satellites de Jupiter et de Saturne. Dans leur cas on n'a pas à se préocuper du grossissement; l'intensité de la lumière, qui est proportionnelle à la surface de l'objectif, et la netteté de l'image importent seules. Pour ces objets on peut donc avec avantage agrandir considérablement l'ouverture du télescope en diminuant en même temps le grossissement de manière à conserver la même netteté des images. Enfin nous voulons avertir le lecteur que la question de l'emploi le plus avantageux de diaphragmes dans le tube d'un télescope, pouvant empêcher la lumière qui tombe sur la paroi de pénétrer dans l'oeil de l'observateur, n'a pas non plus échappé à l'attention de Huygens. Nous renvoyons à ce propos au § 6 de l'Appendice VI, p. 603-607, et surtout à la note 6 de la p. 603. | |||||||||||||||||||
Effets causés par la diffraction de la lumière dans les télescopes et les microscopes.Une autre question, discutée par Huygens, donne lieu à une de ses plus importantes découvertes en optique; celle de l'influence du diamètre du faisceau lumineux qui entre dans l'oeil de l'observateur sur la netteté des images. C'est à propos d'observations de la surface de la lune qu'il a fait cette découverte. Le télescope étalon, et tous ceux qui en sont dérivés d'après les nouvelles règles, étaient adaptés surtout à l'observation de corps célestes assez faiblement éclairés, tel que la planète SaturneGa naar voetnoot1). Or, si l'on veut observer la Lune, dont la distance au Soleil est environ dix fois moindre, et dont, par conséquent, l'éclat est environ cent fois plus fort, le télescope recevra une lumière trop abondanteGa naar voetnoot2). Il semble donc qu'il serait raisonnable dans ces circonstances de diminuer l'ouverture de l'objectif et en même temps la distance focale de l'oculaire, de manière à obtenir | |||||||||||||||||||
[pagina CI]
| |||||||||||||||||||
la même clarté que dans le cas de Saturne (c'est-à-dire une clarté 100 fois moindre qu'avec le télescope étalon), la netteté normale, et un grossissement plus fort. Les nombres α et β que nous avons introduits plus haut devraient alors être tels que α2β2 = 1/100, α/β = 1, d'où l'on tire α = β = 1/√10. Pour le télescope de 30 pieds, l'ouverture, qui est de 3 poucesGa naar voetnoot3), pourrait donc être réduite à √9/10 pouce et la distance focale de l'oculaire pourrait être prise √10 fois plus petite; le grossissement deviendrait ainsi √10 fois plus fort. Ce changement semble donc promettre beaucoup, mais l'expérience apprend à Huygens que cette promesse ne se réalise pas et c'est avec une sagacité admirable qu'il sait reconnaître, sinon la nature de l'obstacle qui s'oppose à cette réalisation, du moins les conditions dans lesquelles il se présente. ‘En effet’ dit-ilGa naar voetnoot4) ‘plus l'ouverture est diminuée plus minime aussi devient le diamètre du petit cylindre suivant lequel les rayons issus d'un point quelconque de l'objet parviennent à l'oeil..or, si ce diamètre..est plus petit que ⅕ à ⅙ ligne’ (0,44 à 0,36mm.) ‘..le contour net des images disparaît par une cause inconnue, inhérente à la constitution naturelle de l'oeil, soit qu'il faille chercher cette cause dans la choroïde ou dans la rétineGa naar voetnoot5), soit qu'elle provienne de la nature des humeurs de l'oeil. Car aussi, lorsqu'on place devant l'oeil nu une lamelle munie d'une ouverture large de moins de ⅕ ou ⅙ ligne, les bords des objets commencent à paraître moins nets, et la confusion devient plus grande plus on diminue la largeur de l'ouverture’Ga naar voetnoot6). Ensuite Huygens montre que, dans le cas de l'exemple choisi plus haut, le dia- | |||||||||||||||||||
[pagina CII]
| |||||||||||||||||||
mètre du faisceau qui entre dans la pupille serait, en effet, de beaucoup inférieur à 1/6 ligneGa naar voetnoot1). Comme on le sait aujourd'hui, il s'agit ici d'un phénomène de diffraction dont l'explication devait échapper à Huygens, puisqu'il n'avait pas les notions du temps de vibration et de la longueur d'onde; en effet, ce n'est que plus d'un siècle plus tard que Fresnel a créé la théorie de la diffraction. Toutefois les phénomènes qui se montrent quand la lumière a passé par une ouverture très étroite avaient été décrits en 1666 par GrimaldiGa naar voetnoot2), et Newton en avait fait mention dans ses ‘Principia’ de 1687Ga naar voetnoot3); mais il semble que Huygens n'ait jamais rapproché ses propres observations de celles de Grimaldi qu'il ne connaissait peut-être que par les indications données par NewtonGa naar voetnoot4). Quoi qu'il en soit, il n'en est pas moins remarquable que Huygens ait compris l'importance du rétrécissement des faisceaux lumineux, dont la considération est devenue une des bases principales de la théorie moderne des instruments optiques. Il est d'ailleurs intéressant de calculer l'influence que la diffraction doit avoir | |||||||||||||||||||
[pagina CIII]
| |||||||||||||||||||
eue dans les instruments de Huygens. Lorsqu'une lentille convergente reçoit un faisceau de rayons parallèles dont la section normale est un cercle de diamètre d, il se forme dans le plan focal une tache lumineuse centrale entourée d'un système d'anneaux circulaires. Nous pouvons faire abstraction de ces derniers dont la luminosité diminue rapidement et nous borner au cercle central qui s'étend jusqu' au premier minimum. Si la diffraction n'existait pas - et si de plus la lentille ne montrait aucune aberration - l'image se réduirait à un point mathématique. La distance du premier minimum au centre, c'est-à-dire le rayon de la tache lumineuse, pourra donc nous fournir une idée de la confusion des images qui est causée par la diffraction. La valeur angulaire du rayon en question est donnée par l'expression  dans laquelle λ représente la longueur d'onde, et on pourra comparer cet ‘angle de diffraction’ δ avec l'angle d'aberration, si l'on veut évaluer l'influence relative de la diffraction et de l'aberration sur la netteté des images.
En prenant 5,7×10-4 mm. pour la longueur d'onde de la lumière jaune, on trouve dans laquelle λ représente la longueur d'onde, et on pourra comparer cet ‘angle de diffraction’ δ avec l'angle d'aberration, si l'on veut évaluer l'influence relative de la diffraction et de l'aberration sur la netteté des images.
En prenant 5,7×10-4 mm. pour la longueur d'onde de la lumière jaune, on trouve  Ga naar voetnoot5), où d doit être exprimé en mm. Dans la lunette étalon de Huygens, et dans tous les instruments qui en dérivent d'après la règle de la p. 495, on a d = 0,72 mm. On en déduit pour l'angle de diffraction 3′20″Ga naar voetnoot6). C'est moins que la neuvième partie de l'angle d'aberration chromatique 31′15″ qu'on trouve dans ces mêmes lunettes, arrangées pour les observations nocturnesGa naar voetnoot7), Ga naar voetnoot5), où d doit être exprimé en mm. Dans la lunette étalon de Huygens, et dans tous les instruments qui en dérivent d'après la règle de la p. 495, on a d = 0,72 mm. On en déduit pour l'angle de diffraction 3′20″Ga naar voetnoot6). C'est moins que la neuvième partie de l'angle d'aberration chromatique 31′15″ qu'on trouve dans ces mêmes lunettes, arrangées pour les observations nocturnesGa naar voetnoot7),
| |||||||||||||||||||
[pagina CIV]
| |||||||||||||||||||
si l'on pose η = 1/50. Et même en posant η = 1/200Ga naar voetnoot1), ce qui réduit l'angle d'aberration à sa quatrième partie, cet angle est encore toujours plus du double de l'angle de diffraction. Il s'ensuit que dans les lunettes en question l'effet nuisible de la diffraction pouvait être négligé par rapport à celui de l'aberration chromatique; mais, en poussant plus loin le grossissement, la ténuité du faisceau qui entre dans la pupille diminuerait bientôt sensiblement la netteté de l'image. En effet, pour la valeur limite, assignée par Huygens, d = ⅕ à ⅙ ligne (0,44 à 0,36 mm.), on trouve δ = 5′30″ à 6′30″. Remarquons encore que le calcul dont nous venons de nous servir, et qui fait dépendre la diffraction du diamètre du faisceau émergent, c'est-à-dire de la largeur de la pupille de sortie, donne le même résultat que la théorie usuelle dans laquelle l'ouverture diffringente est censée être celle de l'objectis. Pour s'en assurer on peut employer le raisonnement suivant, également applicable aux lunettes et aux microscopes à faible ‘aperture numérique’ tels qu'étaient les instruments de Huygens. Soient q la distance de l'objectif à l'image réelle qui se forme dans le plan focal A de l'oculaire, f la distance focale de l'oculaire et D le diamètre de l'objectif. Le rayon du cercle de diffraction qui se forme dans le plan A a la grandeur et il sera vu sous l'angle et il sera vu sous l'angle  . Or cette expression est identique avec la valeur . Or cette expression est identique avec la valeur  parce que, entre le diamètre D de l'objectif et le diamètre d de la pupille de sortie, il y a la relation D:d = q:f. parce que, entre le diamètre D de l'objectif et le diamètre d de la pupille de sortie, il y a la relation D:d = q:f.
| |||||||||||||||||||
Chap. II. Des Microscopes.Origine et historique des recherches de Huygens sur la construction et la théorie des microscopes.Nous avons vu (p. XLVII), qu'environ au même temps où les frères Constantyn et Christiaan Huygens commencent à l'age de 25 et de 24 ans, à s'occuper de la fabrication des lunettes, ils s'appliquent aussi à la construction des microscopes. Si on peut en croire leur père, c'est même avec les microscopes qu'ils | |||||||||||||||||||
[pagina CV]
| |||||||||||||||||||
réussissent premièrement à faire des instruments qui les satissontGa naar voetnoot2). En mars 1655 ils font don à un des amis de leur père, le pasteur A. Colvius de Dordrecht, d'un microscope qui vient de sortir de leur atelierGa naar voetnoot3). Il trouvera, lui écrit Christiaan, l'explication du merveilleux grossissement qu'on peut obtenir avec des lentilles ainsi disposées dans un traité qu'il espère publier bientôt et qui contiendra aussi la théorie des télescopes. En décembre 1657 van Schooten demande à Christiaan de lui prêter un de ses microscopes, dont il a entendu louer les effetsGa naar voetnoot4); mais ce microscope se trouve déjà, à ce qu'il paraît, entre les mains de Isaac VossiusGa naar voetnoot5). Nous ne connaissons pas avec certitude la disposition des lentilles dans ces premiers microscopes fabriqués par les frères Huygens. D'après la description donnée à ColviusGa naar voetnoot6), c'étaient des microscopes composés de deux lentilles et il nous semble probable que l'instrument dessiné et décrit aux p. 674-675 du présent Tome en représente un exemplaireGa naar voetnoot7). Dans ce cas cette disposition différait beaucoup de celle adoptée dans les microscopes dont Huygens a exposé la théorie dans sa DioptriqueGa naar voetnoot8). En effet, dans ces derniers microscopes le faisceau de rayons émanant d'un point de l'objet est converti à la sortie de l'oculaire en un faisceau de rayons parallèles. Au contraire, | |||||||||||||||||||
[pagina CVI]
| |||||||||||||||||||
dans le microscope mentionné, qui doit dater d'environ 1654, une image réelle et agrandie de l'objet est formée dans le plan indiqué par les lettres PPP de la Fig. 2 de la p. 674Ga naar voetnoot1), c'est-à-dire entre la lentille oculaire et l'oeil qui regarde cette image à une certaine distance. La Correspondance nous montre que dans les années qui suivent, jusqu'en 1677, Huygens s'est occupé plusieurs fois encore de la microscopie. En 1663, pendant un séjour à Paris, où il accompagne son père, il cherche à y vendre des microscopes de sa façon, mais, écrit-il à son frère, ‘Jusqu'icy il ne s'est point encore presentè d'occasion pour debiter de nos Teles- et Microscopes, quoyque presque tous les jours il ne me manque des spectateurs’Ga naar voetnoot2). À plus d'un endroitGa naar voetnoot3) il motive la préférence qu'il donne à ses microscopes composés de deux lentilles, sur d'autres dont les objectifs sont plus petits et sur les boulettes sphériques que Hudde a commencé à fabriquer pour s'en servir à la manière d'une loupeGa naar voetnoot4). Il leur reproche, outre leur manque de clarté, que ‘la distance de l'objet est si fort determinee, qu'on ne peut voir le dessus et le dessous d'un cheveu én mesme temps, ce qui est fort incommodeGa naar voetnoot5), et me fait penser s'il ne seroit pas bon de prendre l'objectif encore moins convexe de beaucoup que celuy qui se fait dans le petit creux de fer que vous avez, et de faire en sorte que l'objectif et l'oculaire fussent a peu pres de la mesme force, chacun environ d'un pouce: car il est certain que tant que l'objectif est moins convexe d'autant la distance de l'objet souffre plus de variation. Je viens d'experimenter qu'avec deux oculaires de CampanineGa naar voetnoot6) eloignez l'un de l'autre de quelque 14 ou 15 pouces et avec ouverture de 3 lignes, l'on peut faire quelque chose de bon, et on n'a qu'a les eloigner d'avantage si on veut qu'ils grossissent d'avantage’Ga naar voetnoot7). Vers 1677 l'intérêt de Huygens pour la microscopie reçoit une nouvelle impulsion par les observations de Leeuwenhoek sur les infusoires, les spermatozoïdes et sur d'autres objets microscopiquesGa naar voetnoot8); observations qu'il avait considérées au | |||||||||||||||||||
[pagina CVII]
| |||||||||||||||||||
début avec méfianceGa naar voetnoot9). À peu près à la même époque il change d'opinion sur les avantages relatifs des microscopes composés par rapport aux boulettes sphériques. Dès le 26 mars 1678 il déclare préférer aux autres microscopes ceux ‘qui n'ont qu'une petite boule de verre, la quelle sorte, tout bien considerè, je crois estre la meilleure et qui fait le plus d'effect’Ga naar voetnoot10) et il persiste dans ce jugement, pour autant du moins qu'il s'agisse de l'observation d'objets transparentsGa naar voetnoot11). C'est dans ces circonstances que, pendant l'année 1678, il prend une part très active au perfectionnement de la fabrication et de l'emploi de ces petites boules de verreGa naar voetnoot12) et que, durant cette même année, il commence la première série de ses remarquables observations microscopiques dont nous parlerons plus loinGa naar voetnoot13). Mais auparavant nous analyserons les considérations théoriques et pratiques sur les microscopes simples et compofés que Huygens a exposées dans la partie de sa Dioptrique dont nous nous occupons à présentGa naar voetnoot14). | |||||||||||||||||||
Préface. Microscope simple.Après une préface très courteGa naar voetnoot15) où il soutient, avec une certaine réserve, les droits de Drebbel à la priorité de l'invention des microscopes composésGa naar voetnoot16), Huygens commence à exposer la construction et l'emploi des microscopes simples à lentille ou à boulette. | |||||||||||||||||||
[pagina CVIII]
| |||||||||||||||||||
Il parle d'abord (p. 515) de l'effet d'une lentille convexe à courte distance focale, en supposant, comme il l'avait fait aussi dans sa théorie de la lunette, que l'oeil soit adapté à une distance infinie. Alors l'objet devra être placé au foyer de la loupe et la grandeur apparente sous laquelle on le verra sera indépendante de la position de l'oeilGa naar voetnoot1). Dès qu'on connaît cette grandeur, on connaîtra aussi le grossissement g, que Huygens définit, exactement ainsi qu'on le fait de nos jours, comme le rapport entre la grandeur apparente sous laquelle on voit l'objet à l'aide du microscope, et la grandeur apparente sous laquelle il se présenterait à l'oeil nu, s'il se trouvait à une distance déterminéeGa naar voetnoot2) pour laquelle Huygens choisit 8 pouces (21 cm.) et que nous représenterons par ω. Cette ‘distance de vision distincte’ est une valeur moyenne de la distance à laquelle des personnes aux yeux normaux ont coutume de placer les objets qu'elles veulent examiner à l'oeil nuGa naar voetnoot3). Cela posé, le grossissement produit par la loupe est trouvé sans peine si l'on imagine que l'oeil se trouve tout près de la surface postérieure. Dans ce cas la lentille est sans influence sur la grandeur apparente et n'a d'autre effet que de rendre la vision distincteGa naar voetnoot4). La grandeur apparente est donc égale à celle qu'on observerait à l'oeil nu si l'objet se trouvait à une distance égale à la distance focale de la lentille, et on a la formule:
On peut obtenir le même résultat de différentes autres manières. Supposons que, dans une direction perpendiculaire à l'axe, l'objet ait la petite longueur h et que, par conséquent, sa grandeur apparente ait la valeur h:ω pour un oeil nu placé à la distance ω. D'autre part, la grandeur apparente sous laquelle l'objet est vu à travers le microscope est donnée par l'angle ϕ que font entre eux, après leur passage par la lentille, deux rayons quelconques partis des extrémités de l'objet. Nous aurons donc:
Si on choisit pour les rayons en question ceux qui sont parallèles à l'axe et qui, | |||||||||||||||||||
[pagina CIX]
| |||||||||||||||||||
par suite, se réunissent, après la réfraction, au second foyer de la lentille, on aura évidemment ϕ = h:f et l'on retrouve la formule (1). C'est là, comme il sembleGa naar voetnoot5), la méthode suivie primitivement par Huygens pour la déduction de la formule (1). Il s'en sert également pour calculer le grossissement produit par une sphère en verre. En effet, dans la figure 31 de la p. 517, CE représente l'objet placé au foyer C de la sphère et les rayons dont il s'agit sont CKD, passant par le centre K, et EGHD. Or, le point essentiel dans l'exposition de Huygens, c'est que le rayon HD est parallèle à la ligne EK; on le voit immédiatement si l'on considère que le point E est le foyer de la sphère sur l'axe KE, et que, par conséquent, tous les rayons sortant du point E finiront par devenir parallèles à cet axe KE. La valeur de ϕ est donc égale à l'angle CKE sous lequel l'objet serait vu du centre K. La distance BC étant égale à la moitié du rayon R de la sphèreGa naar voetnoot6) (si l'on prend 3/2 pour l'indice de réfraction), on aura et, par conséquent, d'après la formule (2): et, par conséquent, d'après la formule (2):
Cette formule s'applique aux petites sphères de verre dont Huygens s'est servi si fréquemment dans ses observations microscopiquesGa naar voetnoot7) et dont il parle dans la Prop. XI (p. 521) en indiquant la manière de les fabriquer et de les enchâsser entre deux lamelles d'airain, dans lesquelles on a pratiqué de petits trousGa naar voetnoot8). Seulement l'emploi de ces microscopes extrêmement simples est limité au cas où l'objet est regardé à la lumière transmiseGa naar voetnoot9); la petite distance CB (voir toujours la Fig. 31 de la p. 517) = ½R entre la sphère et le foyer ne permettant pas déclairer suffi- | |||||||||||||||||||
[pagina CX]
| |||||||||||||||||||
samment le côté de l'objet qui est tourné vers la boulette. Sous ce rapport les boulettes sont inférieures aux petites lentilles, auxquelles, pour avoir le même grossissement, on doit donner une distance focale égale à 3/2 fois le rayon de la bouletteGa naar voetnoot1). Dans le cas où l'épaisseur de ces lentilles pourrait être négligée, l'espace disponible pour l'éclairage, serait donc trois fois plus grand pour les petites lentilles ‘mais comme..il faut nécessairement leur laisser une certaine épaisseur, afin qu'elles ne deviennent pas incapables d'être maniées à cause de leur extrême petitesse et qu'elles ne prennent pas moins bien la forme sphérique’ (p. 519), cet espace s'amoindrit nécessairement. Toutefois, pour un cas extrême (représenté par la Fig. 33 de la p. 519), où l'épaisseur de la lentille est égale à 1¼ fois sa distance focale comptée depuis sa surface inférieure, il trouve que l'espace disponible sous la lentille est encore toujours le double de l'espace libre sous une boulette donnant le même grossissementGa naar voetnoot2). Huygens n'a pas négligé non plus de considérer l'étendue du champ et la netteté des images qu'on peut obtenir avec les microscopes simples. Quand on se sert d'une boulette il faut placer l'oeil tout près du verre pour avoir le champ le plus vaste (p. 523)Ga naar voetnoot3). La netteté des images exige en général que les faisceaux lumineux qui partent des points de l'objet et sont admis dans l'oeil soient suffisamment étroits par rapport aux rayons de courbure des lentilles ou boulettes. Quelquefois, quand on emploiera par exemple une loupe dont la distance focale n'est pas inférieure à un demi-pouce (1,3 cm.), la pupille de l'oeil elle-même exclura des faisceaux trop larges (p. 531). Mais il faudra souvent se servir à cet effet d'un diaphragme convenablement placéGa naar voetnoot4). Ainsi dans le cas des petites boulettes trouve-t-on grand avantage à placer un écran muni d'un petit trou à une certaine distance de l'objet, entre ce dernier et la source de lumièreGa naar voetnoot5). Dans la Prop. XIII (p. 531) Huygens démontre que pour de petites lentilles, dont il est nécessaire de limiter les ouvertures, les diamètres de ces dernières doivent être proportionnels aux distances focales afin que les images soient également nettes. Pour autant que le degré de netteté dépende de l'aberration | |||||||||||||||||||
[pagina CXI]
| |||||||||||||||||||
chromatique, cela se voit presque immédiatement à l'inspection des figures 36 et 37 de cette page 531. Elles représentent deux lentilles P et p ayant les foyers F et f pour les rayons rouges, B et b pour la lumière violette. L'objet se trouvant en F ou en f, et D ou d étant un point du bord l'ouverture, les angles EDK == FDBGa naar voetnoot6) et edk = fdb seront respectivement les angles d'aberration qui déterminent, si l'oeil est supposé sans aberration, les diamètres des cercles d'aberration sur la rétine et, par conséquent, le degré de netteté des images. Or, ces angles seront égaux si PD et pd sont proportionnels à PF et pf, car nous savons que PF:FB = pf:fb, et les figures DPBF et dpbf seront donc semblables. Dans le texte de la Dioptrique Huygens ne s'occupe à cette occasion que de l'aberration chromatique. Il en est de même dans une annotation de 1684 que nous avons reproduite au § 2 de l'Appendice VIII (p. 624-625), mais à une époque postérieure, probablement en 1692, Huygens a ajouté à cette annotation la remarque ‘tout cecy convient aussi à l'aberration ancienne’. En effet, les mêmes figures 36 et 37 (p. 531) peuvent servir quand on veut considérer l'aberration sphérique qui dans les lentilles fortement courbées prédomine sur l'autreGa naar voetnoot7). Soient alors F et f les foyers des lentilles, et B et b les points où des rayons parallèles à l'axe, venant du côté de l'oeil, rencontrent l'axe après leur passage par la loupe. Les rayons partant de F ou de f et passant par le centre de la lentille resteront parallèles à l'axe, c'est-à-dire qu'ils auront les directions des lignes DE et de; les rayons FD et fd, au contraire, qui passent par le bord de la lentille prendront les directions DK et dk qu'on obtient en prenant les angles EDK et edk égaux aux angles FDB et fdbGa naar voetnoot8). Les angles EDK = FDB et edk = fdb seront donc de nouveau les angles d'aberration, et, si les lentilles P et p ont des figures semblables, il est clair que l'égalité de ces angles résultera de la similitude complète des figures DPBF et dpbf. Huygens ne manque pas de parler aussi de la clarté qu'on obtient avec les deux lentilles représentées dans ces figures 36 et 37. Comme les angles DFP et dfp sont égaux, la quantité de lumière qu'un point de l'objet envoie vers la rétine sera la même dans les deux cas. La clarté de l'image sera donc inversement propor- | |||||||||||||||||||
[pagina CXII]
| |||||||||||||||||||
tionnelle au carré du grossissement, c'ést-à-dire proportionnelle au carré de la distance focale (p. 531). En employant une lentille qui grossit beaucoup, on risquera donc toujours de rendre l'image trop obscure; on devra y parer en éclairant fortement l'objet, en concentrant par exemple à l'aide d'une lentille convergente la lumière qu'il reçoit. À plusieurs reprises Huygens s'est occupé de la meilleure manière d'éclairer les objets; le lecteur qui voudra connaître ses idées sur ce sujet pourra consulter, quant à l'éclairage des objets transparents les références indiquées dans la note 6 de la p. 521, et pour l'éclairage des objets opaques le § 2 de l'Appendice VIII (p. 624-625) et le § 12 de l'Appendice X (p. 694-697). Il y verra, comme ailleurs, combien de peine Huygens s'est donnée pour faire ses observations microscopiques dans les conditions les plus favorables. Nous avons déjà vu que l'usage de petites sphères est limité aux corps diaphanes qu'on voit à la lumière transmise et que pour l'observation des objets plus ou moins opaques on doit préférer les petites lentilles. Or, Huygens distingue nettement entre la manière dont se comportent ces deux espèces de corps. Un corps transparent ‘intercepte de la lumière mais n'en émet pas’, tandis que les points d'un objet opaque ‘rayonnent eux mêmes’ (p. 522). Il veut dire que, lors même que les rayons qui éclairent un corps opaque sont contenus dans un faisceau peu divergent, la réflexion diffuse peut remplir un cône assez large, qu'il faudra limiter pour ne pas avoir une image trop confuse. Cependant, en rétrécissant convenablement l'ouverture de la lentille, ce qu'on pourrait faire, si l'on avait à sa disposition une source de lumière suffisamment intense, on serait libre de pousser le grossissement aussi loin qu'on le voudrait; ‘mais’ comme Huygens le fait remarquer à la p. 533 ‘même ainsi nous n'avançons guère, parce que la largeur auprès de la pupille, c'est-à-dire celle du petit cylindre lumineux émanant de chaque point de l'objet, duquel nous avons parlé dans l'explication des télescopes et qui possède ici une largeur précisément égale à celle de l'ouverture, ne peut être diminuée de manière à devenir inférieure à ⅕ ou ⅙ ligne; de sorte que de toutes façons un terme est posé | |||||||||||||||||||
[pagina CXIII]
| |||||||||||||||||||
à l'efficacité de ces petites lentilles’. Il s'agit donc du même effet nuisible (celui de la diffraction) dont nous avons parlé aux p. C-CIV. Huygens en a compris toute l'importance aussi bien pour le microscope que pour le télescope. Il le mentionne comme une des raisons qui doivent faire préférer le microscope composé si on désirerait des grossissements toujours plus fortsGa naar voetnoot1). Huygens en voit d'autres (p. 628) dans la ‘commodité de voir et d'esclairer à costè’. De plus ‘les tres petites lentilles malaisement sont si bien formées que les moins petites’. Toutefois, ce qui est bien curieux, il semble s'être servi du microscope composé seulement pour l'observation des corps opaques; les petites boulettes le satisfont pleinement pour celle des objets transparents. Il en donne les raisons dans un passage remarquable, annoté en marge dans le manuscrit de la DioptriqueGa naar voetnoot2): ‘On doit se demander’ dit-il ‘quelle est la raison pour laquelle on ne peut avoir avec les microscopes composés, qui montrent les couleurs des objets, un grossissement aussi fort que celui qu'on obtient avec les boulettes ou petites lentilles en observant les objet transparents. Pourquoi ne tournerait-on pas vers la lumiere un microscope composé prossissant beaucoup avec une ouverture plus grande? Serait-ce parce qu'on ne sait pas former les lentilles assez exactement? Mais pourquoi chercher dans cette direction? Ces microscopes seraient plus obscurs à cause de la matière de la seconde lentille et des réflexions de la lumière. Et de plus la lentille inférieure est beaucoup plus grossière qu'une boulette de verre’. Nous croyons pouvoir conclure de ce passage que c'étaient surtout les imperfections techniques de la fabrìcation des lentilles qui ont fait préférer à Huygens les microscopes simples à boulettes aux microscopes composés à lentilles. | |||||||||||||||||||
Théorie de Huygens du microscope composé.Nous avons vu aux p. CV-CVI quelle était probablement la disposition des lentilles dans les premiers microscopes composés des frères Huygens. Durant les années suivantes des microscopes composés de leur fabrique sont quelquefois mentionnés dans les lettres qu'ils échangentGa naar voetnoot3), mais avant l'année 1679 les rares renseignements qu'on y trouve sont insuffisants pour faire connaître la structure | |||||||||||||||||||
[pagina CXIV]
| |||||||||||||||||||
de ces instruments. Ensin, la Correspondance de l'année 1679 nous apporte le dessin d'un petit microscope qui doit servir à disséquer des insectes ou d'autres objets. Ce dessin est fait par Christiaan sur la marge d'une lettre de son frère Constantyn du 26 août 1679Ga naar voetnoot1) et répété à une échelle plus petite dans sa réponse du 8 septembre 1679Ga naar voetnoot2). Il y s'agit de perfectionner, au point de vue de l'éclairage et de la facilité du maniement, l'idée, émise par Constantyn dans la première lettre citée, de se servir d'un tel microscope ‘afin de.. separer de petites pieces ou de membres d'insectes, et autre choses que je veux observer et que l'on ne peut coupper avec l'oeil non armè’. Quoique ces dessins soient peu détaillés, il nous semble évident qu'ils représentent des microscopes à deux lentilles construits d'après les mêmes principes que ceux dont nous parlerons bientôt. De cette même année, ou d'un peu plus tôt, doit dater la description détaillée d'un microscope à trois lentilles, qu'on trouve au § 3 de l'Appendice X (p. 677). Dans ce microscope le faisceau de rayons partant d'un point donné de l'objet est converti à la sortie de l'oculaire en un faisceau de rayons parallèles et l'oeil y est placé au lieu où se forme l'image de l'objectif; c'est-à-dire là où se trouve la pupille de sortie. Il paraît qu'on a affaire ici à un des microscopes dont les verres furent polis par la veuve Le Bas et à la construction duquel Huygens avait probablement pris partGa naar voetnoot3). En 1684, Huygens découvre les nouvelles règles pour la construction des télescopes, basées sur la considération de l'aberration chromatiqueGa naar voetnoot4). Dès lors il était tout indiqué pour lui de tâcher d'établir une théorie analogue pour le microscope, c'est-à-dire de rechercher, en partant d'un microscope étalon, de quelle manière on devrait en changer les mesures pour obtenir, avec la même clarté et la même netteté des images, un grossissement plus fort. Mais ce nouveau problème était beaucoup plus difficile que l'autre, surtout parce que le faisceau de rayons émanant d'un point de l'objet ne pouvait pas, ainsi que dans le cas du télescope, être considéré comme un faisceau de rayons parallèles. Aussi Huygens ne s'est-il | |||||||||||||||||||
[pagina CXV]
| |||||||||||||||||||
pas mis à cette recherche avant l'année 1692 et même alors n'a-t-il pas complétement réussi à ce propos, comme nous le verrons dans la suiteGa naar voetnoot5). En attendant, il donne aux §§ 2 et 3 de l'Appendice VIII (p. 624-628) quelques calculs relatifs au microscope simple et au microscope composé qui datent de 1684. Ne se doutant pas encore que l'aberration sphérique joue un rôle tout autrement important dans le microscope que dans le télescope, Huygens n'y considère que l'aberration chromatique. Au § 3 il calcule l'aberration chromatique d'un microscope à 2 lentilles et la compare à celle d'un microscope simpleGa naar voetnoot6). Lorsqu'il eut reconnu plus tardGa naar voetnoot7) que l'aberration sphérique ne peut pas être négligée dans les microscopes, le problème devint encore beaucoup plus compliqué. Toutefois, en 1692, il en entreprit et en acheva la solution.
Les microscopes composés dont Huygens a donné alors la théorie consistent en deux verres planconvexes tournant l'un et l'autre leur surface plane vers l'objetGa naar voetnoot8). L'oeil étant supposé adapté à une distance infinie, l'objet doit avoir une position telle que l'image réelle formée par l'objectif se trouve au foyer de l'oculaire. La pupille de l'oeil coïncidera avec la pupille de sortie de l'instrument quand on voudra avoir un champ de vision aussi étendu que possible. Si l'on désigne avec Huygens par b la distance de l'objet à l'objectif, par c la distance de cette lentille à l'image réelle, par d la distance focale de l'oculaire, et enfin par ω la distance de la vision distincte, le grossissement g sera donné par l'équation:
Dans la déduction des règles pour la construction de ces microscopes Huygens | |||||||||||||||||||
[pagina CXVI]
| |||||||||||||||||||
compare continuellement deux instruments différents. Mais, pour en donner un résumé facilement intelligible, il nous semble préférable d'établir d'abord les formules générales, applicables à un instrument quelconque, pour les différentes grandeurs dont il s'agit. Ces grandeurs sont: le grossissement g, pour lequel nous avons déjà donné la formule (4), la clarté I, l'angle A de l'aberration, soit sphérique (As), soit chromatique (AC), et enfin le diamètre D du faisceau émergent, ou bien, ce qui revient au même, celui de la pupille de sortie. Si l'on désigne par a le rayon de l'ouverture de l'objectif, on a:
Pour évaluer la clarté I il faut remarquer que la quantité de lumière qui entre dans le microscope peut être considérée comme proportionnelle à la surface S de l'objet et à celle de l'ouverture de l'objectif, et comme inversement proportionnelle au carré de la distance b; elle peut donc être représentéeGa naar voetnoot3) par a2S/b2 multiplié par une constante. Si la pupille de l'oeil est plus grande que la pupille de sortie, toute cette quantité sera admise dans l'oeil et contribuera à la vision. D'autre part la partie de la rétine occupée par l'image est proportionnelle à S et à g2. On peut donc poser:
| |||||||||||||||||||
[pagina CXVII]
| |||||||||||||||||||
Il nous reste à calculer les angles d'aberration. À cet effet nous suivrons exactement le mode de raisonnement de Huygens, en nous servant de la figure 38 (p. 535) dans laquelle BPE est l'axe, PD l'objectif, PO = e sa distance focale, EZ l'oculaire, BX l'objet et N le foyer de l'oculaire. On aura donc d'après ce qui a été dit:
Lorsqu'il s'agira de l'aberration chromatique, nous nous figurerons que c'est pour les rayons rouges que N est en même temps l'image réelle du point B et le foyer de l'oculaire. Nous supposerons de plus que G est ce foyer pour les rayons violets et qu'un tel rayon, parti du point N et tombant sur la lentille PD, rencontre l'axe au point F. Nous poserons
Lorsque, au contraire, nous voudrons étudier l'aberration sphérique, nous supposerons que, N étant toujours le foyer de l'oculaire, B est conjugué avec ce point par rapport à la lentille PD pour des rayons infiniment voisins de l'axe, tandis que DF sera la ligne suivie par un rayon provenant de N et atteignant l'objectif au point D du bord. Ensin G sera le point de rencontre avec l'axe pour un rayon RM parallèle à cette ligne et entrant dans l'oculaire au point M que nous déterminerons bientôt. Et nous nous servirons de nouveau des notations (8) et (9). On voit que, dans les deux cas, représente l'aberration longitudinale de l'objectif pour des rayons venant du point N, et représente l'aberration longitudinale de l'objectif pour des rayons venant du point N, et 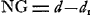 , celle de l'oculaire pour des rayons incidents parallèles à l'axe et venant du côté V. , celle de l'oculaire pour des rayons incidents parallèles à l'axe et venant du côté V.
| |||||||||||||||||||
[pagina CXVIII]
| |||||||||||||||||||
Voici maintenant comment on détermine l'angle de l'aberration chromatique. Comme la lumière violette peut suivre le chemin NDF, elle peut aussi se propager suivant FDN. Par conséquent, un rayon violet qui suit d'abord la ligne BD donnera lieu à un rayon réfractéDK d'une direction telle que l'angle NDK soit égal à l'angle BDF; cela résulte de la Prop. VI, p. 475. On aura donc un rayon rouge DN et un rayon violet DK provenant du même point B de l'objet. Le premier entre dans l'oculaire au point I et en sort dans la direction de l'axe. Le second passe par l'oculaire au point M et est réfracté suivant une certaine ligne MS, dont on détermine la direction en remarquant que le rayon réfracté serait MR, parallèle à l'axe, si le rayon venait du point G, et que, par suite, l'angle SMR est égal à l'angle GMKGa naar voetnoot1). C'est cet angle SMR = GMK qui détermine l'influence de l'aberration chromatique; en effet, la distance des points de la rétine où elle est frappée par les rayons rouges qui ont la direction de l'axe et par le rayon violet MS peut être considérée comme proportionnelle à l'angle SMR. On peut faire un raisonnement tout à fait analogue quand on veut déterminer l'aberration sphérique. Il faut alors distinguer les rayons centraux sortant du microscope parallèlement à l'axe et les rayons périphériques qui prennent une direction différente. Or, comme la lumière peut se propager suivant NDF, elle peut également suivre le chemin FDN, d'où l'on peut conclure que la direction du rayon DK, provenant du rayon périphérique BD, est déterminée exactement comme dans le cas précédent. On trouve ainsi le point M, ce qu'il importe de remarquer parce que dans le cas présent la position de G dépend de celle de M. Ensuite, d'après la manière dont le point G a été défini, on peut dire qu'un rayon incident GM serait réfracté suivant MR, parallèle à l'axe. Par conséquent, si de nouveau on prend l'angle SMR égal à GMK, c'est la ligne MS qui indique la direction finale du rayon extrême BD et l'influence de l'aberration est de nouveau déterminée par l'angle SMR ou GMK. C'est donc cet angle, pour lequel nous avons déja choisi la notation A, qu'il faut calculer pour chacune des deux aberrations. Or, on trouve facilement, en introduisant quelques simplifications qui sont permises tant que les rayons ne forment pas avec l'axe des angles trop grands, | |||||||||||||||||||
[pagina CXIX]
| |||||||||||||||||||
et en traitant comme infiniment petites les grandeurs qui proviennent des aberrations:
Reste à calculer l'angle NMG. On a d'abord, si la ligne DN prolongée rencontre la lentille oculaire au point I: EI = ad/c, 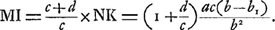 Si donc nous posons:
| |||||||||||||||||||
[pagina CXX]
| |||||||||||||||||||
Après ces calculs préparatoires il sera facile de comprendre la portée des théorèmes de Huygens. La Prop. XIV (p. 535-543) nous apprend que, lorsqu'un microscope quelconque est donné, on peut, en conservant la lentille oculaire, trouver un autre microscope plus court, dont le grossissement et la clarté de l'image sont les mêmes tandis que la vision est plus nette ou bien le grossissement et la netteté les mêmes et la clarté plus grande. Huygens démontre qu'il suffira pour obtenir le premier de ces avantages de diminuer dans le même rapport la distance focale e de l'objectif, le rayon a de l'ouverture et la distance b de l'objet à l'objectif. En effet, on constate facilement que, quelle que soit l'aberration qu'on a en vue, la proportionnalité des valeurs de e, a et b dans les deux instruments qu'il s'agit de comparer entraîne celle de ces grandeurs avec b1 et c. Les formules (4) et (7)Ga naar voetnoot1) montrent que le grossissement g et la clarté I ne changent pas. Il en est de même de la largeur DGa naar voetnoot2) du faisceau émergent, comme Huygens ne manque pas de le faire remarquerGa naar voetnoot3), mais l'angle NMK, qui est déterminé par l'équation (10) diminue dans le même rapport que les longueurs indiquées. Quant à l'angle NMG, déterminé par l'équation (13), on peut remarquer d'abord que la grandeur s, définie par la formule (12), se compose de trois parties dont la première et la dernière restent constantes, tandis que la seconde diminue. La somme s devient donc plus petite, et il en est de même de l'angle NMG, parce que la différence d-d1 reste constante dans le cas de l'aberration chromatique et diminue dans celui de l'aberration sphérique à cause de la diminution de ME = sGa naar voetnoot4). En somme on voit que
l'angle d'aberration dont la première et la dernière restent constantes, tandis que la seconde diminue. La somme s devient donc plus petite, et il en est de même de l'angle NMG, parce que la différence d-d1 reste constante dans le cas de l'aberration chromatique et diminue dans celui de l'aberration sphérique à cause de la diminution de ME = sGa naar voetnoot4). En somme on voit que
l'angle d'aberration 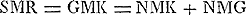 est devenu plus petit, en même temps que la longueur c+d du microscope; mais si l'on préfère une augmentation de clarté, on peut, en sacrifiant en partie ou entièrement l'avantage de la plus grande netteté, agrandir un peu l'ouverture 2a de l'objectif et obtenir en même temps une plus grande largeur D du faisceau émergentGa naar voetnoot3). est devenu plus petit, en même temps que la longueur c+d du microscope; mais si l'on préfère une augmentation de clarté, on peut, en sacrifiant en partie ou entièrement l'avantage de la plus grande netteté, agrandir un peu l'ouverture 2a de l'objectif et obtenir en même temps une plus grande largeur D du faisceau émergentGa naar voetnoot3).
| |||||||||||||||||||
[pagina CXXI]
| |||||||||||||||||||
Jusqu'ici nous avons maintenu dans l'expression (15) tous les termes qui représentent les grandeurs dont il est question dans la discussion de la Prop. XIV par Huygens, et nous avons pu démontrer l'exactitude de cette Proposition en suivant de très près son raisonnement. Or, dans les Propositions qui suivent, Huygens néglige les termes qui proviennent de l'angle NMG, ce qui veut dire qu'il considère l'aberration causée par l'oculaire comme négligeable par rapport à celle qui dérive de l'objectifGa naar voetnoot5). Nous commencerons par admettre cette simplification, sauf à examiner plus loin jusqu'à quel point elle peut être acceptée. Nous attribuons donc à l'angle d'aberration la valeur:
 l'aberration longitudinale pour des rayons parallèles à l'axe et l'aberration longitudinale pour des rayons parallèles à l'axe et  l'aberration des rayons partant du point N, on a: l'aberration des rayons partant du point N, on a:
 Dans le cas de l'aberration chromatique les angles FDB et ODH peuvent être considérés comme égaux d'après le Lemme 1 de la p. 551. On en déduit   , et l'on trouve donc: , et l'on trouve donc:
Au contraire, dans le cas de l'aberration sphérique, l'égalité des angles FDB et ODH ne peut pas être admise puisque le Lemme 3 de la p. 561, qui correspond pour l'aberration sphérique au Lemme 1 que nous venons de citer, a besoin d'une correction que nous avons indiquée dans la note 4 de cette p. 561. En | |||||||||||||||||||
[pagina CXXII]
| |||||||||||||||||||
tenant compte de la différence des notations, employées ici et dans cette note, on peut écrire:
Appliquant en outre la formule (6) de la p. LVIIIGa naar voetnoot2), en y posant n = 3/2, on trouve facilement:
Nous pouvons maintenant résumer le contenu des Prop. XV (p. 543) et XVIII (p. 569) où Huygens montre comment on peut faire en sorte qu'en diminuant la longueur du microscope on obtienne un grossissement plus fort, tout en conservant la même clarté et la même netteté, ainsi que la même largeur du faisceau | |||||||||||||||||||
[pagina CXXIII]
| |||||||||||||||||||
émergent, et la même valeur du rapport de b à c, c'est-à-dire de BP à PNGa naar voetnoot3). Il s'occupe d'abord (Prop. XV, p. 543-551) de l'aberration chromatique. Or, on voit facilement que si les distances b et c changent dans le même rapport il en sera de même de la distance focale e de la lentille DP, puisqu'on a:
Par conséquent, si l'angle d'aberration Ac ne change pas de valeur, cela exige, d'après la formule (17), qu'il en soit de même du rapport de a à d. De plus, comme la clarté doit demeurer la même, il faudra, d'après la formule (7) de la p. CXVI, que ad/c reste constant. Cela assure en même temps que le diamètre de la pupille de sortie ne variera pasGa naar voetnoot4). Mais si a/d et ad/c doivent rester constants, c doit varier proportionnellement au carré de a ou de d, et de même b et e. Quant au grossissement g = cω/bdGa naar voetnoot5), il variera dans le rapport inverse de d; c'est-à-dire dans le rapport inverse de la racine carrée de c. On voit donc qu'on peut en effet obtenir de cette manière un grossissement plus fort avec une longueur c+d plus petite, et que, si l'on distingue par un accent les valeurs qui se rapportent au microscope plus court, les relations qui existent entre les grandeurs appartenant aux deux microscopes peuvent être exprimées par les formules de transsormation:
Nous ajoutons que d'après la formule (21) on aura alors:
| |||||||||||||||||||
[pagina CXXIV]
| |||||||||||||||||||
mais cette formule nous montre qu'on ne peut pas poursuivre indéfiniment la ‘progression des microscopes’ de plus en plus puissants et de plus en plus courts, qu'on obtiendrait par l'application des formules (23). Huygens s'en est aperçu. En effet, après avoir trouvé (p. 565) que dans un microscope déduit du microscope étalon, en posant k = ½, l'angle de l'aberration sphérique est à peu près égal à 20′, il ajoute: ‘Par conséquent, cet angle sera lui aussi à peine assez grand pour nuire; de sorte que l'effet obtenu avec un microscope de ce genre sera excellent. Mais si nous construisons, d'après la formule de la règle trouvée plus haut, des microscopes encore plus courts et plus grossissants, cet angle d'aberration croîtra toujours; et cette cause empêche donc que, en nous basant sur cette règle, nous puissions augmenter indéfiniment la puissance des microscopes’. Pour contrôler cette assertion et pour trouver la valeur minimum de k qu'on puisse admettre, nous calculerons d'abord l'angle de l'aberration sphérique dans le microscope étalon de Huygens, dont nous avons indiqué les dimensions dans la note 4 de la p. CXVII. À cet effet nous observons que la lentille DPGa naar voetnoot1) était dans les microscopes de Huygens une lentille planconvexe tournant sa surface plane vers l'objetGa naar voetnoot2), qui se trouve en B. Dans ces circonstances on a ε1 = 7/6Ga naar voetnoot3); λ = -1Ga naar voetnoot4) et l'on trouve facilement As = 11/6720 = 5′38″; ce qui correspond assez bien avec la valeur 5′8″ trouvée par HuygensGa naar voetnoot5), si l'on prend en considération qu'il a negligé le facteur . .
Cet angle de 5′, ou d'un peu plus, est trop petit pour nuire d'une manière sensible à la netteté de l'image. Huygens s'en assure en retournant l'objectif de manière à tourner sa surface sphérique vers l'objetGa naar voetnoot6). L'aberration sphérique | |||||||||||||||||||
[pagina CXXV]
| |||||||||||||||||||
doit devenir alors, d'après le calcul de Huygens, à peu près quatre fois plus grandeGa naar voetnoot7) et l'angle As sera donc porté à 20′ environ; toutefois il peut à peine observer une diminution de la netteté. Il en conclut que non seulement un angle de 5′, mais même un angle de 20′, peut être toléré, et cela malgré la circonstance que l'angle de l'aberration chromatique s'y ajoute encore. Suivant notre calcul plus complet, on aurait après le retournement de l'objectif ε1 = 9/2, λ = 11/9; ce qui conduit à As = 79/15680 = 17′19″. On voit donc que, dans l'application des formules (23), on ne peut pas, en partant du microscope étalon, prendre k beaucoup plus petit que ½, et que ce fait est reconnu par Huygens. C'est pourquoi, pour obtenir des grossissements plus forts, il a recours dans la Prop. XVIII, p. 569-575, à d'autres règles, qu'il déduit cette fois de la considération de l'aberration sphérique. En effet, si l'on admet, comme plus hautGa naar voetnoot8), la proportionnalité des grandeurs b, c et e dans les deux microscopes, la condition que la clarté et l'angle d'aberration sphériqueGa naar voetnoot9) doivent rester constantes exige qu'il en soit de même des expressions ad/c et a3c/e3d et, par conséquent, aussi de leur produit a4/e3. On satisfait à cette dernière condition en posant a′ = k3a, e′ = k4e; ce qui entraîne b′ = k4b, c′ = k4c et enfin, à cause de la valeur constante de la clarté, d′ = kd, d'où l'on déduit les nouvelles formules de transformation:
Comme on le voit, la condition que le diamètre de la pupille de sortieGa naar voetnoot10) ne varie pas, condition d'ailleurs équivalente à celle de la conservation de la clarté, est réalisée elle aussi par la nouvelle transformation. Il semble donc qu'on pourrait | |||||||||||||||||||
[pagina CXXVI]
| |||||||||||||||||||
obtenir à l'aide de cette transformation, comme Huygens le ditGa naar voetnoot1) ‘une progression pour ainsi dire infinie du grossissement, si la petitesse des lentilles n'y faisait obstacle, laquelle devient bientôt telle que nous ne pouvons ni leur donner des formes sphériques parfaites ni nous en servir assez aisément, attendu qu'elles finissent par échapper même aux regards’. Mais il est clair que tout dépend de l'exactitude des expressions (17) et (21) pour Ac et As, dans lesquelles nous avons omis les termes qui proviennent de l'angle NMG; c'est-à-dire de l'aberration causée par l'oculaire. Examinons donc jusqu'à quel point cette omission est permise.
Nous commencerons par déterminer, pour le cas de l'aberration chromatique, le rapport des termes dans Ac, que nous avons omis, à celui que nous avons pris en considération, ou, ce qui revient au mêmeGa naar voetnoot2), le rapport des angles NMG et NMK. On trouve facilement pour ce rapportGa naar voetnoot3):
 On en déduit:
| |||||||||||||||||||
[pagina CXXVII]
| |||||||||||||||||||
Posant η = 1/50Ga naar voetnoot5), on trouve pour le microscope étalonGa naar voetnoot6):
 et pour ceux qu'on en déduit à l'aide de la première transformationGa naar voetnoot7):  Or, puisque Huygens n'a pas l'intention de pousser à l'aide de cette transformation la réduction des dimensions des microscopes beaucoup plus loin que jusqu'à celle qui correspond à la valeur k = ½Ga naar voetnoot8), on peut en conclure que l'omission des termes dépendant de l'angle NMG est justifiée dans ce cas. Quant à la seconde transformation (25), elle donne: mais on doit observer que par cette transformation l'angle NMK diminue dans le rapport de 1 à k2Ga naar voetnoot9). Il faut donc plutôt comparer la valeur de l'angle NMG dans le microscope plus court à celle de l'angle NMK dans le microscope étalon, valeur que l'expérience a fait connaître comme admissible. On a alors:  ce qui montre déjà qu'on ne peut pas diminuer indéfiniment la valeur de k; mais nous découvrirons dans l'aberration sphérique un obstacle beaucoup plus sérieux à la ‘progression indéfinie du grossissement’ que Huygens suppose possible avec cette seconde transformation. | |||||||||||||||||||
[pagina CXXVIII]
| |||||||||||||||||||
Dans le cas de l'aberration sphérique, dont nous allons traiter maintenant, on a:
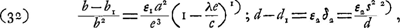 Ga naar voetnoot1)Ga naar voetnoot2) où δ2 représente l'épaisseur mathématiqueGa naar voetnoot3) de la lentille oculaire quand on lui attribue la demi-largeur ME = s. De plus, ε2 est un facteur qui depend de la forme de la dite lentille, et l'on a d'après la formule (12) de la p. CXIX:  λ étant déterminée, suivant la formule (19), p. CXXII, par les rayons de courbure des surfaces de l'objectif. On a donc, en substituant les valeurs de 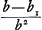 et d-d1 dans la formule (26): et d-d1 dans la formule (26):
 Si maintenant on calcule la valeur de s dans les microscopes qu'on déduit du microscope étalon par chacune des deux transformations, on trouve, en posant ε1 = ε2 = 7/6, λ = -1Ga naar voetnoot4), dans le cas de la première transformationGa naar voetnoot5):  et dans celui de la secondeGa naar voetnoot6): 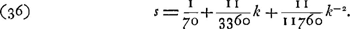 Or, pour les instruments dérivés du microscope étalon par la première transformation l'équation (34) peut s'écrire:  | |||||||||||||||||||
[pagina CXXIX]
| |||||||||||||||||||
En substituant dans cette formule k = ½, et à s la valeur correspondante 0,0246 qu'on obtient à l'aide de la formule (35), on trouve:
De la même manière ce quotient est trouvé égal à 0,00920 pour k = ⅓. Il est donc évident qu'il n'y a rien qui s'oppose à l'emploi de la première transformation jusqu'à la limite indiquée par HuygensGa naar voetnoot7), du moins lorsqu'on applique cette transformation à des microscopes qui ne sont pas trop différents du microscope étalon de Huygens. Dans le cas de la deuxième transformation la formule (37) doit être remplacée par l'équation: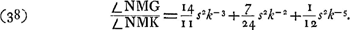 Or, si dans cette équation on substitue successivement ¼, ⅕ et ⅙ à k, et à s les valeurs correspondantes qu'on déduit de la formule (36), on trouve pour le quotient des angles NMG et NMK: dans le premier cas 0,155, dans le deuxième 0,627 et dans le troisième 2,196. Cela nous apprend que déjà pour k = ⅙ la somme des trois derniers termes de l'expression (15), p. CXIX, qui ont été négligés, dépasse considérablement le premier terme de cette expression, le seul qui ait été pris en considération par Huygens. Il en résulte qu'on ne pourrait guère obtenir par la seconde transformation qu'un grossissement un peu plus que cinq fois plus fort que celui du microscope étalon (qui grossit 36 fois) sans une diminution sensible de la netteté des images; ce qui est bien loin de la ‘progression pour ainsi dire infinie du grossissement’ supposéc par Huygens. Il est vrai d'ailleurs que déjà pour k = ⅓ la lentille objective devient d'une petitesse extraordinaire puisque sa distance focale est proportionnelle à la quatrième et le diamètre de son ouverture à la troisième puissance de k. | |||||||||||||||||||
[pagina CXXX]
| |||||||||||||||||||
Ajoutons enfin que nous n'avons trouvé aucune indication que Huygens ait jamais essayé de mettre en pratique les résultats des considérations théoriques qui précèdent; c'est-à-dire, qu'il ait jamais construit en réalité des microscopes dérivés de son microscope étalon d'après l'une ou l'autre des deux transformations. Il nous faut dire encore quelques mots à propos du facteur  qu'on rencontre dans la formule (20) de la p. CXXII, et qui a été négligé par Huygens. Comme celui-ci ne connaissait pas la formule générale de l'aberration longitudinale des rayons émanant d'un point quelconque de l'axeGa naar voetnoot1), il lui était impossible de déterminer avec exactitude la différence b-b1 dans le cas de l'aberration sphérique. Il s'est tiré d'affaire en admettant après quelque hésitationGa naar voetnoot2), la proportion: qu'on rencontre dans la formule (20) de la p. CXXII, et qui a été négligé par Huygens. Comme celui-ci ne connaissait pas la formule générale de l'aberration longitudinale des rayons émanant d'un point quelconque de l'axeGa naar voetnoot1), il lui était impossible de déterminer avec exactitude la différence b-b1 dans le cas de l'aberration sphérique. Il s'est tiré d'affaire en admettant après quelque hésitationGa naar voetnoot2), la proportion:
 qui est vraie pour l'aberration chromatiqueGa naar voetnoot3), et qu'il croyait pouvoir démontrer aussi pour l'aberration sphériqueGa naar voetnoot4), du moins dans le cas, qui se présente dans le microscope, où b est peu différent de eGa naar voetnoot5). Nous avons signalé dans la note 4, p. 559Ga naar voetnoot6), l'erreur qui s'est glissée dans cette démonstration et nous avons montré plus haut à la p. CXXII de cet Avertissement comment cette erreur est corrigée par l'introduction du facteur en question dans les formules (20) et (21). Il en résulte que, même dans le cas où l'objet se trouve tout près du foyer, le calcul de Huygens ne conduit pas à un résultat bien exact, puisque la présence de ce facteur augmente la valeur de As, calculée d'après la formule (21), dans le rapport de 10 à 11 lorsque la lentille | |||||||||||||||||||
[pagina CXXXI]
| |||||||||||||||||||
objective tourne sa surface plane vers l'objet, et qu'elle la réduit dans le rapport de 90 à 79 lorsque cette lentille est dans la position inverse. Or, il est curieux de constater que Huygens lui-même n'a pas manqué de découvrir la défectuosité de sa démonstration. Cela résulte du § 19 (p. 661-662) de l'Appendice IX. Huygens y montre d'une façon ingénieuse que le théorème de l'égalité des angles de deux rayons, avant et après la réfraction par un prisme très aigu, n'est pas suffisamment exact pour justifier l'application qu'il en a faite dans sa démonstration. Il prouve à cet effet, par un exemple particulier, que ce théorème peut induire en erreur, quand on l'emploie pour le calcul de l'aberration sphérique d'un faisceau de lumière partant d'un point de l'axe situé à distance finie, en supposant connue l'aberration près du foyer. C'est à cette occasion qu'il se résoud à ne pas admettre dans sa Dioptrique un théorème sur les effets de l'intervertissement des lentilles oculaire et objective dans un microscope composéGa naar voetnoot7); théorème dont la démonstration lui semble devoir | |||||||||||||||||||
[pagina CXXXII]
| |||||||||||||||||||
dépendre de la proportion (39) dont l'exactitude lui parait maintenant douteuse. Il maintient au contraire les Prop. XV et XVIII, concernant la construction de microscopes plus puissants, déduits du microscope étalonGa naar voetnoot1), parce que la démonstration de ces propositions peut être rendue indépendante de la proportion (39) en appliquant le ‘Theorema demonstrandum’ du § 15 de l'Appendice IX (p. 654) dont il ne semble pas mettre en doute la justesseGa naar voetnoot2). Et nous avons vu, en effet, que le facteur  n'a pas d'influence sur les formules de transformation (23) et (25) puisque sa valeur ne change pas par ces transformations. n'a pas d'influence sur les formules de transformation (23) et (25) puisque sa valeur ne change pas par ces transformations.
Dans la dernière des propositions de sa Dioptrique (la Prop. XIX, p. 577) Huygens s'affranchit d'une restriction qu'il s'est imposée dans les propositions précédentes, à savoir de la condition que le rapport b/c des distances PBGa naar voetnoot3) et PN de l'objectif à l'objet et à l'image réelle soit maintenu constant. En premier lieu il considère comme données les valeurs de la distance focale EN = d de la lentille oculaire, du grossissement g, de la clarté I et de l'angle Ac d'aberration chromatique et il se propose d'en déduire la distance focale e de l'objectif, la position de cette lentille, c'est-à-dire les distances b et c, et le rayon a de son ouverture. Pour déterminer ces inconnues, nous avons les quatre équations suivantesGa naar voetnoot4): Ga naar voetnoot5)Ga naar voetnoot6)Ga naar voetnoot7) De la première et de la deuxième on déduit facilement:  ; ensuite la quatrième donne a, la troisième c et la deuxième b; de cette manière on trouve: ; ensuite la quatrième donne a, la troisième c et la deuxième b; de cette manière on trouve:
| |||||||||||||||||||
[pagina CXXXIII]
| |||||||||||||||||||
 Ga naar voetnoot8) Ces formules montrent de nouveau que, pour autant qu'elles restent applicables, on peut augmenter le grossissement en diminuant les dimensions de l'objectif. Huygens en déduit encore (p. 579) qu'on ne peut pas gagner beaucoup sous ce rapport par un changement de la distance focale de l'oculaire. Il le démontre à l'aide d'une formule, qu'on obtient en éliminant le facteur (dg+ω) entre les deux premières formules (41). Dans nos notations cette formule s'écrit:  Elle fait voir qu'en augmentant le grossissement g sans que la distance focale e change de valeur, on obtiendrait bientôt des valeurs de b plus petites que e, surtout parce que dans le microscope étalon b n'est déjà pas plus grand que 10/9 e. Or, une valeur de b plus petite que e n'est pas admissible. | |||||||||||||||||||
[pagina CXXXIV]
| |||||||||||||||||||
Cette argumentation est irréfutable, mais elle ne montre pas d'une manière convaincante ce qui arrive lorsqu'on augmente le grossissement sans changer la distance focale de la lentille objective. Pour élucider ce point, nous partirons plutôt de la première formule (41), en l'écrivant:
 On voit alors que si l'on veut maintenir constante la valeur de e, le facteur  ne doit pas varier. Ainsi, pour obtenir un grossissement plus fort avec la même clarté et la même valeur de Ac, on doit nécessairement augmenter la distance focale de l'oculaire; mais si nous représentons par go et par do les valeurs de g et de d dans le microscope étalon, le grossissement ne pourra jamais surpasser, pour des valeurs positives de d, la valeur ne doit pas varier. Ainsi, pour obtenir un grossissement plus fort avec la même clarté et la même valeur de Ac, on doit nécessairement augmenter la distance focale de l'oculaire; mais si nous représentons par go et par do les valeurs de g et de d dans le microscope étalon, le grossissement ne pourra jamais surpasser, pour des valeurs positives de d, la valeur  Ga naar voetnoot1).
Voyons encore ce qui arrive, lorsqu'on approche indéfiniment de la limite Ga naar voetnoot1).
Voyons encore ce qui arrive, lorsqu'on approche indéfiniment de la limite  . Alors d devient infiniment grand (comme aussi PN = c), la valeur de PB = b devient égale à celle de PO = e, et DP = a prend la valeur limite finie: . Alors d devient infiniment grand (comme aussi PN = c), la valeur de PB = b devient égale à celle de PO = e, et DP = a prend la valeur limite finie:  . .
Or, dans le microscope étalon de HuygensGa naar voetnoot2), on a do = 2 pouces, go = 36, tandis qu'il suppose ω = 8 poucesGa naar voetnoot3). On ne pourrait donc, en partant de ces données, obtenir avec une lentille oculaire convexe un grossissement g plus grand qu'à peu près 40, et cela encore seulement en donnant au microscope des dimensions impraticables. Ajoutons encore que, pour pouvoir appliquer les formules (41) à des exemples numériques, on doit commencer par calculer pour un microscope étalon les valeurs | |||||||||||||||||||
[pagina CXXXV]
| |||||||||||||||||||
des grandeurs constantes qu'on rencontre dans ces formules. Si nous prenons, à l'exemple de Huygens, pour ce microscope celui dont les dimensions sont indiquées dans la note 4 de la p. CXVII, nous avons (en supposant toujours ω = 8, η = 1/50):
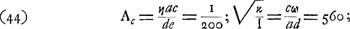 ce qui donne:  Pour g = 36, d = 2, on retrouve ainsi, en effet, les dimensions du microscope étalon, et pour g = 72, d = 1, celles de l'instrument qui en est dérivé à la p. 548.
Les formules trouvées (41) sont plus générales que la règle dont il est question dans la Prop. XV (p. 543) et que nous avons résumée dans les formules de transformation (23) de la p. CXXIII. Elles peuvent servir à leur tour pour la détermination des dimensions d'un nouveau microscope plus grossissant qu'un instrument donné et équivalent à ce dernier au point de vue de la netteté et de la clarté des images. Mais elles cessent d'être applicables dès que l'aberration sphérique devient trop sensible. Elles doivent alors être remplacées par d'autres qui peuventêtre considérées comme une extension des formules de transformation (25). Pour les déduire on doit remplacer la dernière des formules (40) par une autre qui se rapporte à l'aberration sphérique, c'est-à-dire, on doit résoudre les équations: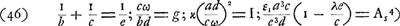 Ga naar voetnoot4) par rapport aux inconnues e, b, c et a. | |||||||||||||||||||
[pagina CXXXVI]
| |||||||||||||||||||
Cette résolution ne présente aucune difficulté; les trois premières équations nous font connaìtre les rapports de c, b et a à e, et la quatrième la valeur de e. De cette manière on trouve:
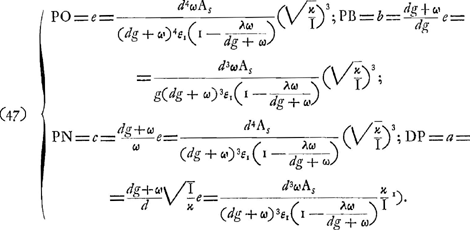 Ga naar voetnoot1) Pour arriver à des applications numériques Huygens suppose, cette fois encore, que la clarté et l'angle d'aberration sont les mêmes que dans le microscope étalon, mentionné plus haut. Dans ce cas on doit substituer dans les formules (47):  | |||||||||||||||||||
[pagina CXXXVII]
| |||||||||||||||||||
Il est évident que la théorie assez compliquée du microscope composé, que nous venons d'analyser, ne pouvait pas avoir d'avenir. Elle perdait tout son intérêt dès que, par l'invention des lentilles achromatiques et par les perfectionnements de la théoric et de la technique de la dioptrique, on avait appris à corriger presqu'entièrement les défauts dus aux aberrations chromatique et sphérique. C'est pourquoi à titre historique nous nous bornerons à signaler qu'on trouve un résumé très précis et très clair de cette dernière partie de la Dioptrique de Huygens dans l'ouvrage de Robert Smith que nous avons déjà mentionné plus d'une foisGa naar voetnoot2). Toutefois Smith n'a pas suffisamment approfondi les démonstrations de Huygens pour en découvrir les points faibles. Il a accepté le Lemme 2 de la p. 559Ga naar voetnoot3) sans y apporter la correction qu'il aurait été à même de calculer parce que, comme nous l'avons vu, il connaissait la formule générale que Huygens ignoraitGa naar voetnoot4); il ne s'est pas non plus posé la question jusqu'à quelle limite il est permis de négliger, comme il le fait à l'exemple de HuygensGa naar voetnoot5), l'aberration sphérique de l'oculaire dans la série de microscopes de plus en plus grossissants déduite à l'aide de la transformation (25); série dont il admet avec Huygens l'efficacité jusqu'à l'infini si la limite dépendant de la petitesse des lentilles n'y faisait pas obstacleGa naar voetnoot6). | |||||||||||||||||||
Recherches sur la profondeur du champ du microscope.Il y a encore, concernant le microscope, un dernier sujet, touché par Huygens, qu'on ne s'attendrait peut-être pas à rencontrer dans un manuscrit du dix-septième siècle. Nous parlons de l'‘incommodité éprouvée dans les très forts | |||||||||||||||||||
[pagina CXXXVIII]
| |||||||||||||||||||
grossissements qu'une petite différence dans la distance a une si grande influence sur la netteté de l'image que, quand on voit distinctement la surface supérieure d'un cheveu étendu sous le microscope, les parties médianes à côté se montrent d'une manière confuse; incommodité qui empêche aussi d'utiliser ces grossissements extrêmes’Ga naar voetnoot1). Le passage que nous venons de citer est de 1684, mais nous avons vu que, déjà en avril 1668, Huygens avait attiré l'attention de son frère Constantyn sur cet inconvénientGa naar voetnoot2). Il reprend le même sujet vers 1690 et le projet de rédaction de la Dioptrique de l'année 1692 nous montre que l'idée lui était venue de le traiter systématiquement dans cet ouvrageGa naar voetnoot3). Malheureusement il n'a pas même donné un commencement d'exécution à cette idée; de sorte que nous ne possédons que deux Pièces peu achevées qui contiennent quelques calculs se rapportant à ce sujet. La première de ces PiècesGa naar voetnoot4) date de 1684, c'est-à-dire d'une époque à laquelle Huygens n'avait pas encore développé sa théorie générale du microscope composé, fondée sur la considération des deux aberrations. Huygens y compare deux microscopes donnant le même grossissement et possédant des oculaires à distances focales égales, tandis que la distance focale de l'objectif et les distances de l'objet et de l'image réelle à cette lentille sont doublées dans le microscope le plus longGa naar voetnoot5). Dans ces conditions il calcule l'effet d'un petit déplacement d de l'objet dans la direction de l'axe sur la position de l'image réelle formée par l'objectif. Il le trouve égal dans les deux cas si on néglige une quantité de l'ordre de d2Ga naar voetnoot6). | |||||||||||||||||||
[pagina CXXXIX]
| |||||||||||||||||||
Il en conclut qu'en doublant la distance focale de l'objectif d'un microscope (en conservant le même grossissement) ‘il n'y a rien a gagner pour avoir une distinction avec profondeur’Ga naar voetnoot7). L'autre PièceGa naar voetnoot8), de 1690, traite d'un cas aussi spécial. Cette fois c'est la comparaison des effets de deux microscopes simples, dont l'un est une boulette sphériqueGa naar voetnoot9) et l'autre une petite lentille. Et cette comparaison conduit Huygens à la conclusion suivanteGa naar voetnoot10): ‘J'ai voulu examiner ici si une petite lentille ne vaut pas mieux qu'une boulette sphérique aussi dans ceci qu'elle souffre plus facilement une plus grande dimension de l'objet dans la direction de l'axe; mais à cet égard elle surpasse à peine la boulette de quoi que ce soit’Ga naar voetnoot11). | |||||||||||||||||||
Observations microscopiques de Huygens.Nous avons reproduit dans l'Appendice XI (p. 698-732) les comptes rendus par Huygens de ses nombreuses observations microscopiques des infusoires, des bactéries, des spermatozoïdes et de quelques autres objets microscopiques. On y lira avec intérêt les notes scientifiques dans lesquelles des savants aussi compétents que M.M.W. Beijerinck et M.N.H. SwellengrebelGa naar voetnoot12) ont tâché d'identifier les organismes observés par Huygens. À ces notes et au résumé donné par Huygens lui-même, qu'on trouve aux p. 523-527 du présent TomeGa naar voetnoot13), nous n'ajouterons ici que quclques remarques générales que nous devons pour la plus grande partie à M. Swellengrebel. On a déjà vuGa naar voetnoot14) que l'intérêt de Huygens pour l'examen microscopique des infusions de poivre et d'autres substances a été éveillé par les communications qu'il avait reçues au sujet des observations de Leeuwenhoek, mais, une fois qu'il se met à l'oeuvre, il se fait connaître comme un microscopiste encore plus minutieux et plus capable que Leeuwenhoek lui-même. Cela se montre surtout | |||||||||||||||||||
[pagina CXL]
| |||||||||||||||||||
dans les figures qu'il donne avec une grande profusion. Elles sont souvent si détaillées qu'on peut deviner le genre ou l'espèce qu'il a observé. Comme M. Beijerinck l'a démontré récemmentGa naar voetnoot1) d'une façon si convaincante, Leeuwenhoek a vu et décrit des bactéries bien avant l'annéc 1683 qu'on désigne ordinairement comme l'époque de sa première découverte de ces organismes. En vérité il les a rencontrées sous ses microscopes dès le commencement de ses observations en 1675. De même, Huygens n'a pas tardé à les apercevoir. C'est surtout pendant la première série, de 1678 à 1680, de ses observations qu'il en a décrit et dessiné plusieurs espèces différentes, tandis que dans la seconde série, de 1692, son attention s'est portée plus exclusivement sur l'anatomie des infusoires et sur la manière dont ces animalcules se comportent. À propos des recherches sur ces derniers organismes nous mentionnons la description des mouvements des cils orales d'un infusoire du genre Oxytricha (p. 722) et celle de l'anatomie externe des Vorticelles (p. 716 et 727) dont il a vu probablement les formes libres (p. 718 et 729) et la division (p. 730). Il a observé de même la division (p. 703 et 704) et aussi la conjugaison (p. 711 et 713) d'autres infusoires, et il a dessiné bien exactement la forme extérieure des Rotatoires, où la présence d'une palpe dorsale ne lui a pas échappé (p. 728 et 731)Ga naar voetnoot2). Ce qu'il y a d'ailleurs de plus intéressant peut-être dans ces manuscrits, ce sont les idées et les expériences de Huygens sur l'origine des organismes de ses infusions. Il s'y montre un adversaire convaincu de la génération spontanée. ‘Il seroit estrange’ dit-il (p. 725-726) ‘que le poivre, le gingembre, et ces queues de fleurs, engendrassent tous les mesmes animaux. C'est pourquoy il est plus probable qu'ils viennent de l'air attirez par l'odeur’. Pour vérifier cette hypothèse il ferme une de ses fioles, qui contiennent les infusions, ‘d'une piece de chamois liée sur le col; pour voir s'il y naistra des animaux’ (p. 718). La première fois, en juin 1679, cette expérience n'a pas le résultat qu'il en attend. Après deux jours des organismes paraissent dans la fiole fermée ainsi que dans celle qu'il avait laissée ouverte, quoique en moindre quantité; une semaine plus tard ‘il y avoit dans la fiole fermée aussi bien que dans | |||||||||||||||||||
[pagina CXLI]
| |||||||||||||||||||
l'ouverte de ces grands animaux qui courroient tres viste et des grands a queue, outre quantitè de mediocres et une insinitè d'anguilles’ (p. 719). Il en est autrement dans des expériences faites en 1692. Une ‘eau de poivre qui avoit estè couverte et enfermée d'un cuir de chamois’ depuis plus de trois semaines contenait à peine ‘quelque chose de vivant’ et Huygens ajoute ‘cela peut avoir entrè par les pores du chamois’ (p. 730). Le jour suivant il y découvre ‘grande quantitè de tres petits a grand peine visibles. qui peut estre avoient passè a travers le chamois’Ga naar voetnoot3). De plus, Huygens a fait quelques expériences sur l'influence de la chaleur et du froid sur les organismes des infusions. Après avoir laissé geler de l'eau de poivre dans une petite fiole, il voit revenir ‘les petits animaux’ deux jours après le dégel; mais ayant mis une telle fiole dans de l'eau bouillante il ne retrouve rien de vivant après trois jours (p. 716-717). Quant à la technique suivie dans les observations microscopiques, nous avons déjà dit (p. CXIII) que Huygens se servait presqu'exclusivement du microscope simple. Il en est de même pour Leeuwenhoek, mais avec cette différence que Leeuwenhoek employait des petites lentilles taillées par lui-mêmeGa naar voetnoot4), tandis que Huygens préférait les boulettes, dont il avait étudié si assidûment, vers 1677, la | |||||||||||||||||||
[pagina CXLII]
| |||||||||||||||||||
fabrication et l'arrangement pratiqueGa naar voetnoot1). Il ne s'est pas donné moins de peine pour obtenir une bonne illumination des objets transparents qu'il observait à travers ses microscopesGa naar voetnoot2), et il est curieux de faire remarquer à ce propos que Huygens est peut-être le premier microscopiste qui se soit aperçu des avantages que l'éclairage à fond noir peut présenter quelquefoisGa naar voetnoot3). |
| ||||||||||||||||||