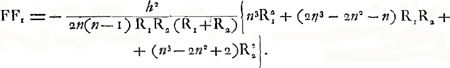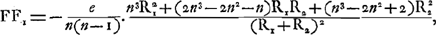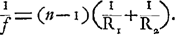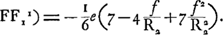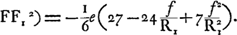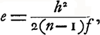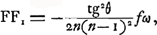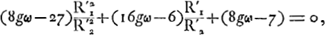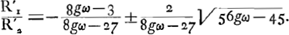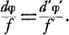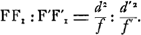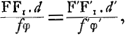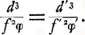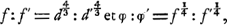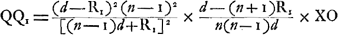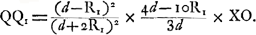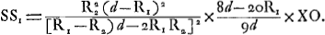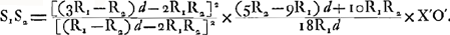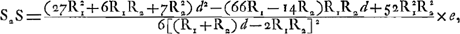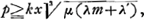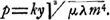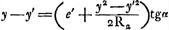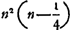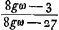Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–Deuxième partie: De l'Aberration des rayons hors du Foyer. 1666.Origine probable des recherches de Huygens sur l'aberration spherique des lentilles.La définition des foyers comme points limitesGa naar voetnoot2) devait mener nécessairement à des calculs sur ce que Molyneux appelait plus tard, ‘la profondeur du foyer’Ga naar voetnoot3), c'est-à-dire sur l'aberration sphérique longitudinale des lentilles. Aussi Huygens ne tarda pas à s'occuper de ce problème. Nous savons que déjà avant le mois de mars 1653, à l'époque de la conception de la première Partie de sa Dioptrique, il avait fait des calculs ayant pour but de comparer l'aberration sphérique d'une lentille planconvexe dans les deux positions différentes: ‘lorsque la surface convexe est opposée aux rayons incidents’ et ‘lorsque la surface plane leur est opposée’Ga naar voetnoot4). Nous ne connaissons pas ces calculs, mais il nous semble probable qu'ils ressemblaient à ceux qu'on trouve mentionnés aux pp. 283-287, qui furent exécutés d'après les formules absolument rigoureuses que Huygens apprenait plus tard à remplacer par des règles approximatives beaucoup plus simples. Or, la grande différence entre les valeurs de l'aberration dans les deux positions de la lentille planconvexeGa naar voetnoot5) devait naturellement faire surgir la question de savoir s'il ne serait pas possible de diminuer encore cette aberration en donnant une autre forme à la lentille, p.e., en choississant le rapport des deux rayons d'une lentille biconvexe de telle manière que, pour une distance focale et une ouverture données, l'aberration sphérique devint un minimum. Que c'était là, en effet, le but principal des nouvelles recherches commencées en 1665, est prouvé par l'en-tête qu'il avait donné primitivement à la Prop. IV ‘Quaenam lens sphae- | |||||||||||||
[pagina LIII]
| |||||||||||||
rica convexa melius radios parallelos colligat investigare’Ga naar voetnoot6). Et lorsque, en 1669, Huygens envoya à la Société Royale de Londres les anagrammes qui contenaient ses découvertes principalesGa naar voetnoot7), c'était encore la réponse à cette question qui constituait l'un des deux anagrammes relatifs à ses recherches sur l'aberration sphériqueGa naar voetnoot8). | |||||||||||||
Définition de l'épaisseur d'une lentille, donnée par Huygens.Un des artifices dont Huygens s'est servi afin d'obtenir des règles simples et élégantes pour le calcul approximatif de l'aberration sphérique des lentilles consiste dans l'introduction de la notion de ce que nous appellerons l'‘épaisseur mathématique’ d'une lentille, grandeur qu'il définit (p. 277) comme la différence des épaisseurs au milieu et au bord. Il suppose, comme première approximation, que l'aberration ne dépend pas de l'épaisseur réelle de la lentille, mais de cette épaisseur mathématique, de sorte que dans les calculs on peut considérer comme nulles l'épaisseur au centre d'une lentille concave et l'épaisseur au bord d'une lentille convexe. Toutefois on cherchera vainement dans l'oeuvre de Huygens une démonstration systématique de la justesse de cette supposition et, puisque c'est là un point dont la valeur des résultats de Huygens dépend en partie, on nous permettra de nous y arrêter un instant. Nous montrerons que, si ce que nous apellerons l'‘épaisseur supplémentaire’ (c'est-à-dire l'épaisseur d'une lentille concave au centre et d'une lentille convexe au bord) reste petite par rapport aux rayons de courbure et aux distances de l'objet et de l'image à la lentille, elle peut être negligée quand il s'agit d'une première approximation, et nous le ferons de manière que la démonstration soit valable aussi bien pour un faisceau de rayons correspondant à un point quelconque de l'axe que pour un faisceau de rayons parallèles à l'axe et même pour un faisceau entaché déjà d'aberration sphérique par des réfractions ou réflections préalablesGa naar voetnoot9). Soit donc h la demi-largeur d'une lentille biconvexe, c'est-à-dire le rayon du | |||||||||||||
[pagina LIV]
| |||||||||||||
cercle suivant lequel ses deux surfaces sphériques de rayons R1 et R2 se coupent, alors l'épaisseur e de la lentille, que nous supposons d'abord sans épaisseur supplémentaire, sera égale dans une première approximation à 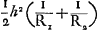 Ga naar voetnoot1). Elle sera donc de l'orde h2 et, d'après les calculs de Huygens, l'aberration sphérique longitudinale sera du même ordre. Nous pourrons donc négliger en fin de compte les termes d'un ordre plus élevé que le deuxième, ce qui n'empêche pas, comme on le verra, qu'on doive aller au commencement jusqu'au troisième ordre inclus.
Soit maintenant α l'angle sous lequel un rayon de lumière s'approche de l'axe à l'intérieur de la lentille; β celui qu'il fait avec l'axe après sa réfraction, au point P, à la surface postérieure de rayon R2; soit Q le point où il coupe l'axe, M le centre de la surface postérieure; P1 la projection du point P sur l'axe; A le point où l'axe coupe la surface postéricure; soit, de plus, PP1 = y, AQ = d, ∠PMA = ψ alors la loi des sinus exige: Ga naar voetnoot1). Elle sera donc de l'orde h2 et, d'après les calculs de Huygens, l'aberration sphérique longitudinale sera du même ordre. Nous pourrons donc négliger en fin de compte les termes d'un ordre plus élevé que le deuxième, ce qui n'empêche pas, comme on le verra, qu'on doive aller au commencement jusqu'au troisième ordre inclus.
Soit maintenant α l'angle sous lequel un rayon de lumière s'approche de l'axe à l'intérieur de la lentille; β celui qu'il fait avec l'axe après sa réfraction, au point P, à la surface postérieure de rayon R2; soit Q le point où il coupe l'axe, M le centre de la surface postérieure; P1 la projection du point P sur l'axe; A le point où l'axe coupe la surface postéricure; soit, de plus, PP1 = y, AQ = d, ∠PMA = ψ alors la loi des sinus exige: 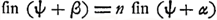 , où , où 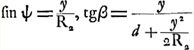 ; donc ; donc 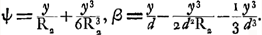 .
De ces équations on déduit comme première approximation, .
De ces équations on déduit comme première approximation, 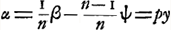 , où , où 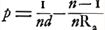 , et ensuite comme seconde approximation: , et ensuite comme seconde approximation:
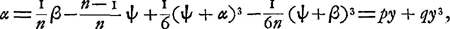 où 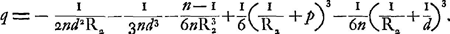 Supposons maintenant qu'on ajoute à la lentille du côté de la surface postérieure une épaisseur supplémentaire e′. Nous poursuivons alors le même rayon de lumière, de manière que l'angle α ne change pas, et R2 non plus, mais que les autres grandeurs prennent de nouvelles valeurs que nous indiquons par d′, y′, p′, q′. On aura donc 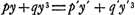 , c'est-à-dire: , c'est-à-dire:
| |||||||||||||
[pagina LV]
| |||||||||||||
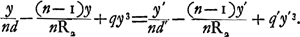 Posant alors 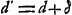 , il s'agit de calculer δ. À cet effet l'équation nous donne, en négligeant les termes d'un ordre suffisamment élevé: , il s'agit de calculer δ. À cet effet l'équation nous donne, en négligeant les termes d'un ordre suffisamment élevé:
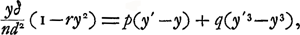 où 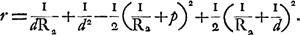 Or, on a comme première approximation 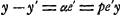 , et l'on trouve ensuiteGa naar voetnoot2): , et l'on trouve ensuiteGa naar voetnoot2):
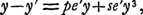 où 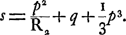 On en déduit: 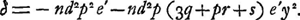 où le dernier terme peut être négligé par rapport à l'aberration (de l'ordre de y2) qui dépend de l'épaisseur mathématique; pourvu seulement que e′ reste petit par rapport a R2 et à d. On voit donc que le déplacement que les points d'intersection des rayons avec l'axe subiront par l'addition de l'épaisseur supplémentaire e′ sera représenté par l'expression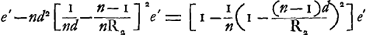 , et il est clair que ce déplacement, égal pour tous ces points, ne changera pas la valeur de l'aberration sphérique longitudinale, calculée comme première approximationGa naar voetnoot3). , et il est clair que ce déplacement, égal pour tous ces points, ne changera pas la valeur de l'aberration sphérique longitudinale, calculée comme première approximationGa naar voetnoot3).
| |||||||||||||
Déduction des règles approximatives pour l'aberration sphérique longitudinale hors du foyer.Asin de déterminer l'aberration sphérique d'une lentille pour des rayons incidents parallèles à l'axe, Huygens s'occupe en premier lieu de la distance FF1 entre | |||||||||||||
[pagina LVI]
| |||||||||||||
le foyer F, c'est-à-dire le point où les rayons les plus rapprochés de l'axe (ou leurs prolongements) atteignent cette ligne, et le point correspondant F1 pour un rayon qui a traversé la lentille à une distance h de l'axe. Si l'on désirait pour cette grandeur FF1 des formules absolument rigoureuses, cela exigerait souvent des calculs très compliqués; c'est pourquoi Huygens se contente d'exécuter ce calcul pour un exemple numérique dans chacun des deux cas d'une lentille planconvexe recevant les rayons sur sa surface plane ou sur sa surface courbeGa naar voetnoot1) et d'indiquer la marche à suivre dans les autres casGa naar voetnoot2). Mais il base ses conclusions sur des formules approximatives, qu'il déduit dans un des AppendicesGa naar voetnoot3), et qui suffisent pleinement pour les besoins de la pratique, comme il le montre en comparant dans les cas de la lentille planconvexe, les résultats numériques obtenus par ces formules avec ceux qu'on obtient par la méthode rigoureuseGa naar voetnoot4). Ces formules peuvent se résumer en une seule. Soient R1 et R2 les rayons de courbure des surfaces antérieure et postérieure d'une lentille, le rayon étant considéré comme positif pour une surface convexe, et n l'indice de réfraction. On aura alors, si la distance FF1 est appelée positive quand elle a la direction des rayons incidents, et négative dans le cas contraire,
Si l'on prend pour h le rayon de la périphérie de la lentille, on trouvera l'aberration des rayons extrêmes. C'est cette grandeur que Huygens considère en premier lieu, mais il démontre en outreGa naar voetnoot5) que, pour un rayon qui arrive en un point quelconque de la lentille, l'aberration est proportionnelle au carré | |||||||||||||
[pagina LVII]
| |||||||||||||
de la distance h. Si maintenant on introduit l'épaisseur mathématique e, dont nous avons parlé plus hautGa naar voetnoot6) et qui est égale à 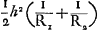 , la formule (1) prend la forme: , la formule (1) prend la forme:
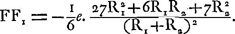 C'est cette équation que Huygens a trouvée pour différentes formes de lentillesGa naar voetnoot8). Bien entendu, comme il ne simplifie pas ses calculs par l'introduction de grandeurs négatives, il doit traiter chaque forme de lentille séparément. Ajoutons que Huygens a aussi exprimé successivement l'aberration en fonction de l'épaisseur e, de la distance focale f, et d'un des rayons de courbure R1 ou R2, dont R1 représente toujours celui de la surface exposée aux rayons incidents. En négligeant l'épaisseur de la lentille (ce qui est permis lorsqu'il s'agit de la transformation des derniers facteurs de (1) et de (2)), on peut écrire:
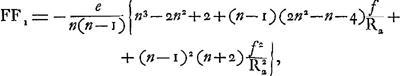 | |||||||||||||
[pagina LVIII]
| |||||||||||||
ou, pour n = 3/2,
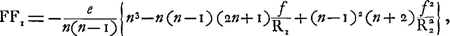 ou, pour n = 3/2,
C'est de ces formules (4) et (5), ou plutôt de celles qu'on en déduit en changeant, suivant le cas, les signes de R1, R2 et de f, de manière à n'introduire que des grandeurs positives, que Huygens a pu conclure que l'aberration d'une lentille concavo-convexe (ou ‘ménisque’ comme il l'appelle) est toujours plus grande que celle d'une lentille planconvexe de même distance focale, et qu'elle est d'autant plus grande que le plus grand des deux rayons R1 et R2 est plus petit. Il en est de même avec l'autre genre de ‘ménisque’, c'est-à-dire avec la lentille convexo-concaveGa naar voetnoot3). Notons encore qu'on a:
Nous ne répéterons pas ici toutes les conséquences que Huygens tire de ses formules. Il suffira de dire qu'il insiste sur le changement dans l'aberration produit | |||||||||||||
[pagina LIX]
| |||||||||||||
par le retournement d'une lentilleGa naar voetnoot5) et qu'il n'a pas manqué le but que probablement il s'était proposé au commencement de ses recherches, c'est-à-dire de déterminer la meilleure forme qu'on peut donner à une lentille au point de vue de l'aberration sphérique. Il trouve que, pour une telle lentille, R1 est égal à 7/12 f; ce qui donne R2 = 7/2 f. Le rapport des deux rayons de courbure doit donc être de 6 à 1; resultat qui s'applique également au cas de la lentille biconvexe et à celui de la lentille biconcaveGa naar voetnoot6). Il est presque superflu d'ajouter que Huygens obtient tous ces résultats par des considérations géométriques élémentaires; elles sont basées sur deux théorèmes qu'il énonce dans les Propositions préliminaires I et IIGa naar voetnoot7). | |||||||||||||
Compensation, dans la lunette hollandaise, de l'aberration sphérique de l'objectif par celle de l'oculaire.Une des applications les plus remarquables que Huygens ait faites des formules qui précèdent est exposée dans la Prop. IX où il énonce le théorème que l'aberration de l'objectif peut être compensée par celle de l'oculaire si l'on prend pour ce dernier une lentille concave. ‘Personne ne soupçonnait’ dit-ilGa naar voetnoot8) ‘que le défaut des lentilles convexes pût être corrigé à l'aide des lentilles concaves. Mais nous démontrerons ici que cette correction est possible et que, par conséquent, les télescopes de ce genre peuvent être rendus plus parfaits que ceux qu'on construit ordinairement’. Et encoreGa naar voetnoot9): ‘L'utilité des lunettes de ce genre, l'avantage qu'elles ont sur celles qu'on a construites ordinairement jusqu'à ce jour à l'aide de lentilles convexes et concaves sera d'abord celui-ci qu'elles rendront la vision plus nette, attendu qu'elles envoient parallèlement à l'oeil les rayons issus des différents points de l'objet, à-peu-près comme le feraient des verres de forme elliptique ou hyperbolique; mais surtout que, sans être plus longues que les télescopes ordinaires, elles pourront grossir beaucoup plus les objets, vu que leur lentille | |||||||||||||
[pagina LX]
| |||||||||||||
extérieure souffrira une ouverture plus grande que celle des télescopes ordinaires parce que l'aberration de cette lentille, due à la propriété de la figure sphérique, est corrigée par la lentille oculaire’. À ce propos nous remarquerons d'abord que le dernier facteur dans l'expression (2) est toujours positif (il ne pourrait devenir négatif que pour n < ¼Ga naar voetnoot1)) et que le signe de FF1 est donc opposé à celui de e et par suite à celui de fGa naar voetnoot2). Cela veut dire que le point F1 se trouve toujours entre la lentille et le foyer F. Considérons maintenant pour l'objectif les points F et F1, et soient F′ et F′1 les points analogues pour l'oculaire dans le cas où il recevrait des rayons parallèles à l'axe venant du côté de l'oeil; il est clair que la compensation désirée aura lieu si F coïncide avec F′ et en même temps F1 avec F′1, et que cela peut arriver avec un oculaire concave, parce que alors F1 est plus rapproché de l'objectif que F, et F′1 plus rapproché de cette lentille que F′. La condition pour la compensation se trouve le plus facilement si l'on introduit dans la formule (1) l'angle θ formé par l'axe et le rayon qui a traversé la lentille à une distance h du centre. Si l'on se contente toujours du degré d'approximation atteint dans les formules précédentes on peut poser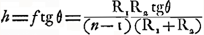 , et on aura: , et on aura:
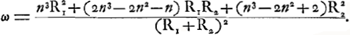 Pour obtenir la compensation, il faut évidemment que les valeurs de 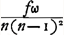 pour l'objectif et pour l'oculaire soient égales mais de signes opposés. Si donc nous supposons que les matières de l'objectif et de l'oculaire ne sont pas différentes et si nous distinguons par des accents les grandeurs qui se rapportent à l'oculaire, pour l'objectif et pour l'oculaire soient égales mais de signes opposés. Si donc nous supposons que les matières de l'objectif et de l'oculaire ne sont pas différentes et si nous distinguons par des accents les grandeurs qui se rapportent à l'oculaire,
| |||||||||||||
[pagina LXI]
| |||||||||||||
nous aurons ω' = -f/f' ω = gω, où g représente le grossissement. On en tire, en posant n = 3/2,
La grandeur ω est déterminée par le rapport des rayons de courbure de l'objectif; donc, si cette lentille est donnée et si l'on a fixé le grossissement, la formule (9), combinée avec (3), nous apprend quel oculaire il faut employer. Comme ω est toujours supérieur ou égal à 45/56, valeur minimum qu'il atteint pour R2 = 6R1, les racines de l'équation (8) sont réelles, et comme les coefficients du deuxième et du troisième termes de l'équation sont positifs pour toutes les valeurs de g dont il peut être question, les signes algébriques des racines seront déterminés par celui du coefficient du premier terme. On peut donc conclure que, pour un grossissement inférieur à 27/8ωGa naar voetnoot3), il y a une racine positive et une racine négative. On pourra alors satisfaire aux conditions du problème avec une lentille biconcave. Si, au contraire, le grossissement surpasse la valeur 27/8ω (ce qui est certainement le cas lorsqu'il est supérieur à 21/5Ga naar voetnoot4)) les racines sont négatives toutes les deux, de sorte qu'il y aura deux lentilles convexo-concaves qu'on pourra employer. Rappelons que R′1 appartient à la surface qui est censée recevoir le faisceau de rayons parallèles, c'est-à-dire, dans le cas présent, à celle qui est | |||||||||||||
[pagina LXII]
| |||||||||||||
tournée vers l'oeil et que l'une des racines de l'équation (8) est supérieure et l'autre inférieure à l'unité en valeur absolueGa naar voetnoot1); il en résulte que dans la première de ces deux solutions c'est le côté convexe et dans l'autre le côté concave de l'oculaire qui doit se trouver du côté de l'oeil. Huygens choisit la première solution parce qu'elle conduit à la courbure la moins forte de la surface concaveGa naar voetnoot2). En effet, désignons par -a1 celle des deux racines dont la valeur absolue est supérieure à l'unité et par -a2 l'autre racine. On a alors, par suite de la relation (3), dans la première solution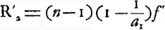 , et dans la seconde , et dans la seconde 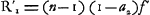 ; mais, puisque ; mais, puisque 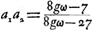 est supérieur à l'unité, on aura a2 > 1/a1. Par conséquent le rayon R′2 de la surface concave de la première solution sera plus grand que le rayon R′1 de la surface concave de la seconde solution. est supérieur à l'unité, on aura a2 > 1/a1. Par conséquent le rayon R′2 de la surface concave de la première solution sera plus grand que le rayon R′1 de la surface concave de la seconde solution.
C'est en se servant d'un calcul qui revient à l'application de la formule (9) prise avec le signe inférieur que Huygens a calculé la table numérique qu'on trouve á la p. 329. La construction de cette table est une preuve de plus de l'importance que Huygens attacha à sa découverte. Or, dans la note 4 de la p. 331 nous avons relaté les circonstances qui en ont retardé et ensuite fait abandonner la réalisation. | |||||||||||||
L'invention de février 1669 et les recher ches sur l'aberration sphérique longitudinale d'un faisceau de rayons correspondant à un point quelconque de l'axe de la lentille.On voit dans la note que nous venons de citer que la principale raison qui a conduit Huygens à renoncer à son projet de corriger l'aberration de l'objectif par celle de l'oculaire était: qu'il croyait avoir trouvé mieux. En effet, la méthode suivie n'était applicable qu'à la lunette hollandaise, et pour ses recherches astronomiques Huygens avait besoin de lunettes à oculaire convexe qui | |||||||||||||
[pagina LXIII]
| |||||||||||||
présentent un champ de vision plus étenduGa naar voetnoot3). Il valait donc mieux obtenir la compensation dans la lentille objective elle-même à laquelle la plus grande partie de l'aberration doit être attribuée; celle de l'oculaire étant même négligeable dans les circonstances ordinairesGa naar voetnoot4). Cela était possible si l'on composait l'objectif de deux lentilles différentes dont l'une était convexe et l'autre concave. C'est là l'invention de février 1669, qui supplantait dans l'esprit de Huygens celle de 1665 dont nous venons de parler. On pouvait placer la lentille concave auxiliaire derrière ou bien devant la lentille convexe, mais dans les deux cas, traités tous les deux par HuygensGa naar voetnoot5), la seconde lentille recevrait un faisceau de rayons, non plus parallèles, mais correspondant à un point donné de l'axe. Pour déterminer les rayons de courbure des lentilles de manière à obtenir la compensation nécessaire, il fallait donc calculer l'aberration sphérique d'un faisceau correspondant à un point de l'axe d'une lentille. Or, déjà en 1665 Huygens s'était occupé de ce problème, mais sans réussir dans la solution générale. Il avait indiqué la voie à suivre, mais il avait été rebuté par la complication des expressions mathématiquesGa naar voetnoot6). Il s'était contenté d'examiner quelques uns des cas qui se présentent quand il ne s'agit que d'une seule surface séparant deux milieux différentsGa naar voetnoot7). Cette solution peut suffire lorsque la lentille auxiliaire se trouve en arrière de la lentille convexe. On n'a qu'à choisir alors la surface d'entrée de la lentille auxiliaire de sorte qu'on obtienne une compensation complète dans le cas où les rayons ne sortiraient pas de la matière dont cette lentille est composée. Prenant ensuite le point de concours de ces rayons pour centre de la surface de sortieGa naar voetnoot8) on parvient à ne | |||||||||||||
[pagina LXIV]
| |||||||||||||
troubler en aucune façon la réunion parfaite des rayons dans ce point, qui devient ainsi le foyer de l'objectif composé. Ce fut de cette manière que Huygens calcula successivement les dimensions de la lentille auxiliaire pour un objectif planconvexe dont la surface convexe était tournée du côté des rayons incidentsGa naar voetnoot1); pour un objectif biconvexe, constitué de manière à donner une aberration minimumGa naar voetnoot2); pour un objectif biconvexe symétriqueGa naar voetnoot3); et enfin pour une lentille planconvexe recevant les rayons sur sa surface planeGa naar voetnoot4). Si, au contraire, la lentille auxiliaire se trouve devant la lentille convexe, il est indispensable de savoir déterminer l'aberration causée par cette dernière lentille pour un faisceau de rayons partant d'un point de l'axe. Huygens y réussit pleinement dans le cas d'une lentille planconvexe recevant le faisceau sur sa surface planeGa naar voetnoot5). Afin d'appliquer cette solution, il combine une lentille planconvexe tournant sa surface plane vers l'oculaire avec une lentille concave placée devant elle, de sorte que des rayons incidents parallèles à l'axe se réunissent en un point M de l'axe; les dimensions de la lentille concave étant choisies de manière que l'aberration qu'elle donne aux rayons parallèles à l'axe venant de l'extérieur, soit égale à l'aberration, causée par la lentille planconvexe, d'un faisceau qui partirait du point M. Il est facile de se convaincre qu'ainsi le but désiré est atteint. C'est donc de cette façon qu'il calcule au § 5 de l'Appendice VII (p. 422-424) les dimensions de la lentille auxiliaire qu'il faut placer devant une lentille planconvexe. Ayant déterminé en outre l'aberration d'une lentille biconvexe symétrique, dans le cas particulier où le point dont les rayons émanent est situé à une distance de la lentille égale à deux fois le rayon de courbure des surfaces de la lentille et où, par conséquent, les rayons du faisceau deviennent parallèles à l'axe à l'intérieur de la lentilleGa naar voetnoot6), il en profite pour déterminer au § 7 la forme d'une lentille auxiliaire qu'on peut mettre devant une lentille biconvexe symétriqueGa naar voetnoot7). Après avoir obtenu ses premiers résultats le 1 février 1669, il compose un ana- | |||||||||||||
[pagina LXV]
| |||||||||||||
gramme qui en contient le principe, et qu'il envoie à la Société Royale de Londres le 6 février suivantGa naar voetnoot8). Mais bientôt un scrupule le prend. Pour comprendre ce scrupule il faut savoir que le seul avantage que Huygens se promettait de ce système compensé était de pouvoir élargir de beaucoup l'ouverture de l'objectif sans nuire à la netteté des images, ce qui permettrait d'augmenter considérablement le grossissement sans rendre les images trop obscures. Or, pour les grandes ouvertures, auxquelles il fut ainsi conduit, la valeur des formules approchées, dont il s'était servi, devenait douteuse. Afin d'éclaircir cette question, il détermina, d'abord par un calcul rigoureux, ensuite d'après ces formules, l'aberration longitudinale de chacune des deux lentilles d'un objectif compensé dont l'ouverture était censée surpasser plus de quatre fois celle d'un simple objectif de même distance focale; les dimensions de ce dernier étant empruntées à la table que nous mentionnerons plus loin à la p. LXIX. La différence entre les valeurs obtenues par les deux méthodes devait être attribuée aux termes d'ordre plus élevé qui avaient été négligés dans le calcul des dimensions de la lentille auxiliaire. Le résultat de cette enquête ne fut pas très rassurantGa naar voetnoot10) et c'est peut-être là une des raisons pour lesquelles Huygens n'essaya pas de mettre en pratique son invention nouvelle. Mais probablement telle ne fut pas la raison principale de son abstention. Huygens savait très bien, en effet, combien il lui serait difficile de fabriquer des lentilles assez parfaitement sphériques et répondant assez exactement aux courbures calculées qu'il serait nécessaire de le faire pour réaliser son invention. Et plus tard les travaux de Newton lui donnèrent la conviction que dans les télescopes un peu longs l'aberration chromatique est de beaucoup plus nuisible que l'aberration sphérique. Cette dernière raison lui sembla décisiveGa naar voetnoot11). Elle fut la cause de ce qu'il n'a jamais admis dans sa Dioptrique ces recherches de 1669, et qu'il en a même écarté celles de 1665 sur la compensation de l'aberation de l'objectif par celle de l'oculaireGa naar voetnoot12). Toutefois, comme on le sait,
| |||||||||||||
[pagina LXVI]
| |||||||||||||
la difficulté, causée par l'aberration newtonienne, fut entièrement vaincue, beaucoup plus tard, par l'emploi des lentilles achromatiques, et la technique moderne ne recule plus devant la fabrication de lentilles à peu près parfaites ayant des dimensions données d'avance. Ainsi la question de l'élimination de l'aberration sphérique par un choix judicieux de la courbure des surfaces des lentilles s'est imposée de nouveau aux physiciens modernes, et on devra considérer Huygens, sur ce terrain aussi, comme un de leurs principaux précurseursGa naar voetnoot1). | |||||||||||||
Application des règles obtenues pour l'aberration sphérique à la détermination de l'ouverture et du grossissement admissibles dans un télescope de longueur donnée.Pendant de longues années Huygens s'est voué au perfectionnement des lunettes avec une persévérance et une patience admirables. Or, dans la construction de ses longs télescopes il s'est constamment laissé guider par des règles théoriques qu'il a cherchées d'abord, dans cette deuxième Partie de sa Dioptrique, en considérant seulement l'aberration sphérique sans compter avec l'aberration chromatique. Toutefois les résultats pratiques ne répondaient pas entièrement à ce que ses règles laissaient entrevoir, et ce ne fut que plus tard, en se servant des découvertes de Newton, qu'il réussit à établir d'autres règlesGa naar voetnoot2), basées cette fois sur la considération de l'aberration chromatique qu'il avait crue d'abord inaccessible à l'analyse mathématiqueGa naar voetnoot3). Un point essentiel dans ces théories successives est le rôle qu'y joue la clarté des images, qui se mesure par la quantité de lumière que la rétine reçoit par unité de surface. Huygens expose clairementGa naar voetnoot4) que, pour une ouverture donnée de l'objectif, la quantité totale de lumière dont on dispose est également donnée et que, par conséquent, si l'on emploie un oculaire trop grossissant la clarté de l'image deviendra nécessairement trop faible. ‘Il ne faut donc pas à la légère remplacer la lentille | |||||||||||||
[pagina LXVII]
| |||||||||||||
oculaire par une lentille plus convexe ou plus concave, mais calculer exactement quel agrandissement l'ouverture de la lentille extérieure peut supporter de manière que le télescope ne donne pas en même temps des images moins lumineuses qu'on ne doive les exiger. Et, en vérité, toute la puissance et l'effet d'un télescope quelconque dépendent à ce point de la grandeur de son ouverture qu'après avoir considéré cette dernière on peut, si elle est petite, dire avec certitude que le télescope a peu de puissance, quel que soit le nombre des autres lentilles et de quelque façon qu'elles soient placées à l'intérieur du tube. En effet, pour qu'un grossissement important soit obtenu avec une clarté suffisante il est nécessaire que beaucoup de rayons soient rassemblés, ce qui est absolument impossible si la lentille extérieure n'a pas une grande ouverture’Ga naar voetnoot5). Huygens ajoute en passantGa naar voetnoot6) que la question est différente pour les microscopes; vu que, dans ses instruments, la clarté de l'image est déterminée par l'ouverture du cône lumineux qu'un point de l'objet envoie dans l'objectif, et qu'on peut remédier à une trop grande obscurité des images en éclairant l'objet plus vivement. De même que la considération de la clarté des images, celle de leur netteté montre qu'un objectif de lunette de dimensions données ne peut supporter qu'un grossissement qui n'excède pas une certaine limiteGa naar voetnoot7). À cause de l'aberration sphérique l'image formée par l'objectif n'est pas parfaite, chaque point y étant représenté par un ‘petit cercle d'aberration’Ga naar voetnoot8). Il en est de même de l'image formée sur la rétine et pour qu'elle ne soit pas trop confuse il faut que le rayon des petits cercles n'y soit pas trop grand; or, ce rayon augmente avec le grossissement que produit l'oculaire. Les conditions auxquelles on est amené en suivant les deux ordres d'idées que nous venons d'indiquer, ne sont pas les mêmes; c'est en les combinant que Huygens arrive aux résultats qu'on trouve dans la Proposition XIGa naar voetnoot9). Comme il est difficile de dire quelle est le minimum de clarté suffisantGa naar voetnoot10) et le | |||||||||||||
[pagina LXVIII]
| |||||||||||||
défaut de netteté admissible, Huygens pose le problème sous la forme suivante: Supposons qu'on possède une lunette qui donne des résultats satisfaisants sous le rapport de la clarté et de la netteté des images, et qu'on en veuille construire une autre d'une longueur différente; quelle ouverture de l'objectif et quel grossissement devra-t-on donner à cet instrument pour qu'il ait le même degré de perfection que le premier? Dans la discussion Huygens remarque qu'à la rigueur il faut aussi tenir compte de l'aberration qui se produit dans la lentille oculaireGa naar voetnoot1). Il démontre cependant par un raisonnement sur lequel nous reviendronsGa naar voetnoot2), qu'on peut négliger cette aberration; simplification qui est due à ce que la distance focale de l'oculaire est beaucoup moindre que celle de l'objectif. Cela posé, il est facile de comparer entre elles les deux lunettes. Soient f et f′ les distances focales des objectifs, φ et φ′ celles des oculaires, g et g′ les grossissements linéaires, d et d′ les diamètres des ouvertures des objectifs. Si l'on désire que les images soient également claires, il faut que la quantité de lumière reçue par l'objectif soit proportionnelle au carré du grossissement linéaire ce qui nous donne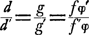 , ou: , ou:
Pour comparer les aberrations, nous supposerons avec Huygens que les deux objectifs soient de la ‘même espèce’Ga naar voetnoot3), ce qui veut dire que le rapport des rayons de courbure des surfaces antérieure et postérieure est le même pour les deux lentilles. Il en résulte d'après les formules (2) et (6) des pp. LVII et LVIII qu'on aura pour les aberrations longitudinales FF1 et F′F′1:
Considérons maintenant un rayon qui a traversé l'objectif tout près du bord et qui passe par F1 en faisant un angle θ avec l'axe. Ce rayon atteindra le ‘plan | |||||||||||||
[pagina LXIX]
| |||||||||||||
focal’ de l'objectif, c'est-à-dire le plan qui est mené par le foyer F perpendiculairement à l'axe, en un point H tel que FH = FF1.tgθ. La distance FH est alors le rayon du cercle illuminé qui se dessine sur le plan focal quand l'objectif reçoit un faisceau de rayons parallèles à l'axe. Supposons maintenant que l'oeil lui-même soit sans défauts optiques et que la rétine soit conjuguée avec le plan focal de l'objectif, qui est en même temps le plan focal de l'oculaire. Le rayon du cercle d'aberration, qui se forme sur la rétine et qui n'est autre chose que l'image du cercle dont nous venons de parler, est alors donné par l'expression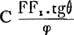 , où C est une constante déterminée par l'état de l'oeil. On peut poser tgθ = d/2f, de sorte que cette dernière expression devient , où C est une constante déterminée par l'état de l'oeil. On peut poser tgθ = d/2f, de sorte que cette dernière expression devient 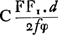
Si l'on exige maintenant que dans le cas des deux lunettes les cercles d'aberration sur la rétine aient la même grandeur il faut qu'on ait:
En combinant ce résultat avec l'équation (10), on trouve les équations:
Ce sont ces formules dont Huygens s'est servi pour calculer la table qui termine la deuxième Partie de la DioptriqueGa naar voetnoot4). Dans ce calcul il a pris pour lunette | |||||||||||||
[pagina LXX]
| |||||||||||||
‘étalon’ un instrument dont l'objectif avait 12 pieds de distance focale et une ouverture de 2 pouces, le grossissement linéaire étant de 1 à 72Ga naar voetnoot1). Il convient d'ajouter un mot sur la manière dont Huygens obtient l'équation (13)Ga naar voetnoot2); elle diffère un peu de celle que nous avons suivie. Soit Q le point de l'oculaire frappé par un rayon venant du bord de l'objectifGa naar voetnoot3) et qui a donc passé par le point F1. Après avoir traversé l'oculaire et les milieux réfringents de l'oeil, ce rayon atteindra un point de la circonférence du cercle d'aberration qui se sorme sur la rétine. D'un autre côté, comme l'oculaire est supposé libre de toute aberration sphérique, un rayon FQ atteindrait le centre de ce cercle. Huygens remarque que l'angle formé par les rayons FQ et F1Q ne change pas par leur passage par l'oculaireGa naar voetnoot4), et que le rayon du cercle d'aberration sur la rétine lui est proportionnelGa naar voetnoot5). Pour avoir le même degré de netteté dans les deux cas, il faut donc saire en sorte que les angles FQF1 et F′Q′F′1 soient égaux, condition qui nous ramène à la formule (13). Ce dernier mode de raisonnement lui sert aussi à démontrer qu'on peut négliger l'aberration propre à l'oculaireGa naar voetnoot6). À la rigueur, ce n'est pas le rayon FQ qui sortira de cette lentille dans la direction de l'axe, mais plutôt le rayon F2Q, si le point F2, situé entre F et l'oculaire, est pour ce dernier ce que F1 est pour l'objectif. On voit maintenant que l'aberration totale est mesurée par l'angle F1QF2 et non par l'angle F1QF. Or, les angles F1QF, FQF2 peuvent être censés proportionnels aux distances FF1 et FF2 et ces longueurs peuvent être calculées par la formule (7) de la p. LX appliquée à l'objectif et à l'oculaire pour une même valeur de l'angle θ. Par conséquent, si les lentilles ont des formes telles que les deux valeurs de ω ne sont pas trop différentes, les distances FF1 et FF2 seront à peu près proportionnelles | |||||||||||||
[pagina LXXI]
| |||||||||||||
aux distances focales et l'on pourra négliger l'aberration de l'oculaire qui est proportionnelle à l'angle FQF2 par rapport à celle de l'objectif qui est proportionnelle à F1QF. Ce qui précède donne encore lieu à une remarque. L'étendue de la section du faisceau de rayons, qui a traversé l'objectif, par un plan perpendiculaire à l'axe, dépendra de la position de ce plan. Si le plan passe par le foyer F, la section devient le cercle d'aberration introduit par Huygens dans le texte de la Dioptrique; mais l'Appendice IVGa naar voetnoot7) montre que Huygens lui-même a très bien compris que ce cercle ne représente pas la section la plus petite du faisceau. D'une manière très ingénieuse il a su déterminer dans cet Appendice le lieu du plus fort rétrécissement, qui se trouve dans un plan P, passant par un certain point A situé entre F et F1 de telle manière qu'on a F1A = ¼FF1. La section du faisceau par ce plan P est ce qu'on appelle souvent ‘cercle d'aberration’ dans les traités modernes, son rayon est le quart de celui du cercle d'aberration introduit par Huygens dans sa DioptriqueGa naar voetnoot8). Il est presque inutile de dire que par la considération de ce dernier cercle Huygens a exagéré l'influence de l'aberration sphérique sur la netteté des images. Si l'on veut projeter sur un écran l'image formée par la lentille objective on placera l'écran non pas en F mais au point A, et en regardant par la lunette un objet éloigné, on pourra faire coïncider avec ce point le plan qui est conjugué avec la rétine. Cependant on voit facilement que cette circonstance n'apporte aucun changement à la solution du problème traité par Huygens dans la Prop. XI, puis- | |||||||||||||
[pagina LXXII]
| |||||||||||||
que les rayons des cercles d'aberration, qui correspondent aux deux conceptions différentes, sont proportionnels entre eux. Remarquons enfin que dans le texte de la Dioptrique le problème de déterminer l'ouverture de l'objectif et la distance focale de l'oculaire pour une lunette de longueur donnée, ces grandeurs étant connues pour une lunette étalon, n'est résolu que dans le cas où les deux objectifs sont de la même espèce, mais que dans l'Appendice III, aux p. 385-386, Huygens a indiqué la solution pour le cas plus général où ils sont d'espèces différentes. | |||||||||||||
Historique des sujets traités dans cette deuxième Partie de la Dioptrique.Même si l'on se rapporte comme point de repère à l'année 1703 de la publication de la Dioptrique, comme oeuvre posthume, trente huit ans après la rédaction de la deuxième Partie de cet ouvrage, le terrain occupé aujourd'hui par la théorie de l'aberration sphérique des lentilles et par ses applications était encore presqu'entièrement en friches. Naturellement l'existence de l'aberration sphérique n'était pas inconnue aux contemporains ni même à des prédécesseursGa naar voetnoot1) de Huygens; mais ce n'est que très rarement qu'on rencontre chez eux des calculs sur la grandeur de cette aberration et même alors ils se bornent aux cas les plus simples, c'est-à-dire, à ceux d'une lentille planconvexe recevant un faisceau de rayons parallèles à l'axe sur sa surface plane ou convexe et d'une lentille biconvexe symétrique. Nous n'avons à citer à ce propos que les travaux de Newton, Picard, Molyneux et Hartsoeker. Newton ne traiteGa naar voetnoot2) que le cas le plus simple de tous, celui d'une lentille planconvexe tournant son côté plan vers les rayons, mais il le fait d'une façon magistrale. Il trouve d'abord la valeur de l'aberration longitudinale sous la forme d'une série dont le premier terme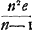 (n indice de refraction, e épaisseur de la (n indice de refraction, e épaisseur de la
| |||||||||||||
[pagina LXXIII]
| |||||||||||||
lentille) coïncide pour n = 3/2 avec la valeur approximative trouvée par HuygensGa naar voetnoot3). De cette manière, introduisant le rayon y de l'ouverture, le rayon de courbure R de la surface convexe, et la distance focale 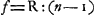 , on est conduit pour le rayon du cercle d'aberration dans le plan focal, comme première approximation, à l'expression , on est conduit pour le rayon du cercle d'aberration dans le plan focal, comme première approximation, à l'expression 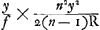 , qui peut s'écrire n2y3/2R2; donc, puisque Newton détermine le rayon du cercle minimum, qui est un quart de celui du cercle dans le plan focal, il aurait dû trouver n2y3/8R2 pour ce rayon-là, et ce n'est que par une inadvertance, signalée par les éditeurs des ‘Lectiones’, qu'il arrive à l'expression ny3/8R2Ga naar voetnoot4). , qui peut s'écrire n2y3/2R2; donc, puisque Newton détermine le rayon du cercle minimum, qui est un quart de celui du cercle dans le plan focal, il aurait dû trouver n2y3/8R2 pour ce rayon-là, et ce n'est que par une inadvertance, signalée par les éditeurs des ‘Lectiones’, qu'il arrive à l'expression ny3/8R2Ga naar voetnoot4).
Quant à Picard, dans la seconde Proposition de les ‘Fragments de Dioptrique’, (Mémoires de l'Académie Royale des sciences, depuis 1666 jusqu'à 1699. T. VII, Première Partie, Paris MDCCXXIX, p. 338-339) il a réussi à déduire, par une méthode qui ressemble beaucoup à celle de Huygens, l'expression 7/6e pour l'aberration sphérique longitudinale d'une lentille planconvexe recevant les rayons sur sa surface convexeGa naar voetnoot5). Il considère aussi l'aberration d'un rayon parallèle à l'axe, qui rencontre la lentille dans un point éloigné du bord, c'est-à-dire qu'il détermine l'influence de ce que nous avons appelé l'épaisseur supplémentaireGa naar voetnoot6); mais il le fait seulement pour le cas spécial de la lentille planconvexe, où le problème est très facile. Chez MolyneuxGa naar voetnoot7) on ne rencontre, pour chacun des trois cas prémentionnés, | |||||||||||||
[pagina LXXIV]
| |||||||||||||
que le calcul numérique d'un seul exemple. Par ce calcul il détermine la route d'un rayon se trouvant initialement à une distance donnée de l'axe, qui est la même pour les trois cas. Molyneux en tire la conclusion que la ‘profondeur du foyer’ est la plus petite dans le cas d'une lentille planconvexe recevant les rayons sur sa surface convexe et qu'il faut donc tourner cette surface vers l'objet. HartsoekerGa naar voetnoot1), enfin, arrive à la même concluson, après quoi il écrit: ‘Cependant comme il est constant par une infinité d'experiences, que les verres planconvexes, font parfaitement le même effet, sans qu'on y puisse appercevoir la moindre difference, soit que leur côté plat ou convexe soit tourné vers l'objetGa naar voetnoot2); il me semble avec beaucoup de raison qu'il seroit bien inutile de vouloir donner quelque autre figure aux verres de lunettes, que la spherique: car la difference qu'il y a entre le parfait concours des rayons qui passent au travers d'un verre planconvexe, lorsque son côté plat est tourné vers l'objet, & le parfait concours de ceux qui passent au travers de ce verre, lorsque son côté convexe est tourné vers l'objet, est si considerable, qu'il est impossible de pouvoir arriver encore par dessus cela à une difference aussi considerable, quoiqu'il y eût une figure qui ramassât les rayons paralleles à un point mathematique, pour ainsi dire’. En 1738 parut l'excellent et volumineux ouvrage de Robert Smith auquel nous avons déjà emprunté la belle formule de Cotes pour le grossissement d'un système de lentillesGa naar voetnoot3), formule qui marquait un pas en avant sur les recherches de Huygens dans cette direction. Cet ouvrageGa naar voetnoot4) est en grande partie une compilation des travaux de Huygens et de Newton, cités fréquemment par Smith et auxquels il emprunte souvent des pages entières; mais cette compilation est faite avec beaucoup d'intelligence et de bon goût, et sur le terrain, dont il s'agit à présent, nous avons à constater un progrès important, dû cette fois à Smith lui-même. Nous avons vuGa naar voetnoot5) que Huygens ne s'est pas contenté de calculer comme première approximation l'aberration ‘hors du foyer’, mais qu'il s'est efforcé de déterminer | |||||||||||||
[pagina LXXV]
| |||||||||||||
également l'aberration d'un faisceau correspondant à un point quelconque de l'axe. Nous savons que cette détermination ne lui a réussi que dans le cas d'une seule surface réfringente et dans quelques cas particuliers relatifs à une lentille entière. Huygens avait utilisé ces résultats dans son invention de 1669 d'un objectif double, compensé pour l'aberration sphérique; mais ayant perdu confiance dans la valeur de cette inventionGa naar voetnoot6) il n'en avait pas fait mention dans la Dioptrique et n'avait rien publié non plus sur les recherches dont nous venons de parler. Or, chez Robert Smith on trouve la solution complète, pour une lentille entière, du problème en questionGa naar voetnoot7). Voici comment Smith procède. Soit d la distance d'un point lumineux P à une surface sphérique concaveGa naar voetnoot8), décrite avec le rayon de courbure R1, Q l'image de P aprés la réfraction par cette surface et Q1 le point où, après cette réfraction, le prolongement du rayon extrême rencontre l'axe; de sorte que QQ1 représente l'aberration longitudinale du faisceau, partant de P, telle qu'elle résulte de cette première réfraction; soit en outre O le point où l'axe coupe la surface prémentionnée, I celui où le rayon extrême rencontre cette surface, X la projection de I sur l'axe et n l'indice de réfraction. Par une méthode qui ne diffère pas essentiellement de celle de HuygensGa naar voetnoot9) (qui lui était inconnue), Smith trouve pour QQ1 l'expression suivante
| |||||||||||||
[pagina LXXVI]
| |||||||||||||
Afin de montrer la conformité de cette formule (17) avec celle de Huygens, qu'on trouve en haut de la p. 394, il faudra commencer par changer dans la formule (17) les fignes de d et de R1 pour l'adapter au cas, traité par Huygens, d'une surface convexe sur laquelle tombe un faisceau convergent; opération qui la laisse inaltérée. Si ensuite on remplace dans la formule de Huygens ses notations par celles que nous avons employées ici, elle prend la forme:
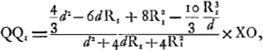 sous laquelle son identité avec celle de Smith est facile à constater. Après avoir obtenu la formule (16), Smith considère l'effet de la réfraction par la seconde surface qui termine la lentille et qu'il suppose convexe. Soient donc S et S1 les images de Q et de Q1 par rapport à cette surface, S2 le point où le rayon extrême PI (ou son prolongement) coupe l'axe après les réfractions qu'il a subies aux deux surfaces de la lentille; alors 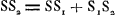 représente l'aberration longitudinale de la lentille entière. Pour la déterminer il suffit de connaître SS1 et S1S2. Or, SS1 n'est autre chose que le déplacement de l'image, correspondant au déplacement QQ1 du point Q, et, comme première approximation, on trouve donc facilement: représente l'aberration longitudinale de la lentille entière. Pour la déterminer il suffit de connaître SS1 et S1S2. Or, SS1 n'est autre chose que le déplacement de l'image, correspondant au déplacement QQ1 du point Q, et, comme première approximation, on trouve donc facilement:
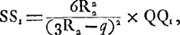 où R2 représente le rayon de courbure de la seconde surface réfringente et q la distance de Q au point O′ auquel cette sursace est coupée par l'axe, ou bien, ce qui revient au même, ayant égard à l'ordre de grandeur des lignes dont nous nous occupons, la distance QO. Si l'on substitue ensuite, afin d'introduire la distance PO = d, à q sa valeur 3dR1:(d+2R1)Ga naar voetnoot1) et à QQ1 l'expression (17), on obtient:
Quant à S1S2, cette longueur représente evidemment l'aberration longitudinale | |||||||||||||
[pagina LXXVII]
| |||||||||||||
du rayon extrême par rapport à la seconde surface, pourvu qu'on considère ce rayon comme émanant du point Q1. Soit donc I′ le point où ce rayon coupe la seconde surface, X′ la projection de ce point sur l'axe, on aura alors la valeur de S1S2 en remplaçant dans la formule (16), d par q, R1 par R2, n par n-1, XO par X′O′. Cela nous donne:
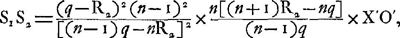 ou bien, pour n = 3/2: 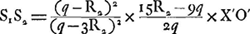 ou enfin, par l'introduction de d au lieu de q:
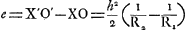 , où h = IX = I′X′. On a alors , où h = IX = I′X′. On a alors 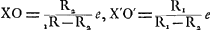 et l'addition amène, après quelques réductions, l'expression: et l'addition amène, après quelques réductions, l'expression:
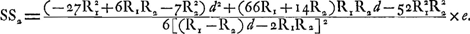 Pour adapter cette formule au cas d'une lentille biconvexe on doit changer le signe de R1. Si ensuite nous l'écrivons sous la forme:
| |||||||||||||
[pagina LXXVIII]
| |||||||||||||
Nous voulons ajouter encore que la manière dont la formule (20) est déduite par Smith permet de déterminer facilement, d'une autre façon que nous ne l'avons fait plus hautGa naar voetnoot1), les conditions dans lesquelles l'épaisseur supplémentaire est négligeable. Évidemment cette épaisseur doit rester petite par rapport aux rayons de courbure des surfaces de la lentille et aux distances de l'objet et de son image à ces surfaces, mais cette condition est-elle suffisante pour pouvoir négliger le terme qu'elle introduit dans l'expression pour l'aberration sphérique, vis-à-vis de celui provenant de l'épaisseur mathématique qui est elle-même une petite grandeur? Or, en suivant pas à pas les calculs de Smith on voit facilement que si cette première condition est satisfaite et si, de plus, l'ouverture de la lentille est suffisamment limitée pour qu'on puisse considérer comme petite l'inclinaison des rayons sur l'axe, on pourra se servir de la formule (20) dans tous les cas où il est permis de considérer comme égales les lignes IX et I′X′ que nous avons représentées toutes les deux par h. Cela exige donc que IX-I′X′ soit négligeable par rapport à h, mais si nous appelons a l'angle sous lequel, à l'intérieur de la lentille, le rayon extrême II′ s'approche de l'axe et e′ l'épaisseur au bord de lentille, on aura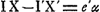 , où α = h:OQ1, puisque OQ1 représente la distance de la lentille au point Q1, où le prolongement de II′ rencontre l'axe. On en déduit: , où α = h:OQ1, puisque OQ1 représente la distance de la lentille au point Q1, où le prolongement de II′ rencontre l'axe. On en déduit:
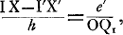 d'où il résulte (parce que l'épaisseur e′ au bord est égale à l'épaisseur supplémentaire dans le cas d'une lentille convexe et à la somme de cette épaisseur et de l'épaisseur mathématique dans le cas d'une lentille concave), que, dans les conditions formulées plus haut, l'épaisseur supplémentaire peut même surpasser considérablement l'épaisseur mathématique sans que la formule (20) soit infirmée.
Avec cette formule (20) un certain point culminant dans le développement de la théorie de l'aberration sphérique est atteint. En effet, cette formule résume les résultats de cette théorie pour autant qu'elle se rapporte à la première | |||||||||||||
[pagina LXXIX]
| |||||||||||||
approximation et au cas d'une seule lentille. Bientôt les recherches plus générales d'Euler et d'Alembert ferout dépasser ce point; mais il ne nous semble pas nécessaire de poursuivre aussi loin notre historique, puisque dans la Dioptrique de Huygens on ne trouve rien qui se rattache à ces recherches plus modernes, si on en excepte les calculs, dont nous avons déjà parléGa naar voetnoot2), sur la manière de compenser l'aberration d'une lentille par celle d'une autre. Toutefois nous ne pouvons pas passer sous silence la partie de l'oeuvre d'Euler où celui-ci critique une des conclusions auxquelles Huygens avait été conduit. Il s'agit des considérations d'Euler sur la théorie de la lunette keplérienneGa naar voetnoot3). Nous en mentionnerons le résultat principal en nous bornant au cas où l'objet se trouve à distance infinie et où les rayons redeviennent parallèles après leur passage par l'instrument. Nous supposerons de plus que les deux lentilles sont composées de la même espèce de verre. Après avoir remarqué que, dans ces circonstances, il est impossible de s'affranchir de l'aberration chromatique, Euler écrit: ‘Il importe d'autant plus de rendre insensible’ [dans l'image] ‘la confusion de la première espèce’ [celle qui est causée par l'aberration sphérique], ‘c'est-à-dire de faire en sorte que le rayon du cercle provenant de cette confusion’ [le cercle d'aberration] ‘ne surpasse pas certaine limite’Ga naar voetnoot4). Dans les notations d'Euler cette limite est désignée par ¼k-3, où il s'agit de la valeur angulaire du rayon en questionGa naar voetnoot5). | |||||||||||||
[pagina LXXX]
| |||||||||||||
D'après ses calculs la condition, pour que la limite ne soit pas dépassée, peut être exprimée par l'inégalité:
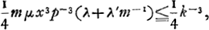 ou bien:
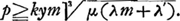 Dans le cas d'un grossissement un peu considérable, on peut négliger le terme λ′ vis-à-vis de λm, parce que λ et λ′ sont du même ordre de grandeur. La plus petite distance focale, compatible avec la condition prémentionnée, est donc donnée par:
| |||||||||||||
[pagina LXXXI]
| |||||||||||||
Après avoir obtenu ces formules, Euler continue ainsiGa naar voetnoot4): ‘De ce résultat il s'ensuit immédiatement que, si l'on désire un grossissement plus fort, la distance focale de l'objectif doit être augmentée,.. et cela non pas proportionnellement à la première puissance de m, mais presque proportionnellement à m4/3’ et un peu plus loin il ditGa naar voetnoot5): ‘Nous voyons aussi que pour obtenir un plus haut degré de clarté, il faut augmenter la longueur p, ce qui est également utile quand on désire une plus grande netteté de l'image, parce qu'il faut alors donner une plus grande valeur au nombre k’. Après avoir exposé ces résultats, Euler parle dans les termes suivants des recherches de Huygens sur le même sujetGa naar voetnoot6): ‘Se basant en partie sur une théorie assez incomplète, et en partie sur des expériences, Huygens a trouvé que la distance focale de la lentille objective doit être proportionnelle au carré du grossissement.Ga naar voetnoot7) Je suis si loin de vouloir faire objection à cette règle que je la considère même comme pratiquement utile, surtout pour le temps de Huygens. En effet, notre détermination est fondée sur la supposition qu'on puisse donner aux sursaces des lentilles une forme exactement sphérique. Si l'ouvrier peut y réussir, il n'y a aucun doute que notre formule ne soit conforme à la vérité et il semble qu'il | |||||||||||||
[pagina LXXXII]
| |||||||||||||
en soit bien ainsi maintenant grâce aux efforts des grands maîtres dans cet art. Si, au contraire, la figure des lentilles s'écarte tant soit peu de la forme sphérique, il est connu que ce défaut se fait sentir d'autant plus que la distance focale est plus grande. La seule manière d'obvier à ce défaut sera donc de donner à la distance focale une longueur plus grande que celle qui correspond à notre règle. On ne saurait affirmer qu'il en résultera précisément la proportionnalité au carré du grossissement, mais on peut dire qu'à mesure qu'on réussira mieux à former chaque lentille, le même grossissement pourra être obtenu avec une distance focale plus petite, ou plutôt que la même lentille pourra servir à produire un plus fort grossissement. Bien qu'il faille toujours faire attention à cela, je suppose ici qu'on puisse donner aux surfaces des lentilles, non seulement des formes sphériques, mais aussi les rayons de courbure prescrits’. Ces phrases ne rendent aucunement justice aux recherches de Huygens, dont évidemment Euler a pris connaissance d'une manière très superficielle. En effet, comme nous l'avons déjà ditGa naar voetnoot1), Huygens a déterminé deux fois des règles pour la longueur et l'ouverture des lunettes, d'abord en considérant seulement l'aberration sphériqueGa naar voetnoot2), et plus tard en ne faisant intervenir que l'aberration chromatiqueGa naar voetnoot3). Or, c'est la deuxième forme de ces règles à laquelle Euler fait allusion; c'est d'ailleurs la seule qu'il ait pu trouver dans l'édition de la Dioptrique publiée par de Volder et Fullenius; la première ayant été supprimée par Huygens du manuscrit de sa Dioptrique dont ces savants se sont servis. Euler aurait donc pu voir que, dans le passage qu'il avait sous les yeux, Huygens, en considérant l'aberration chromatique, avait résolu un problème entièrement différent de celui qu'il venait de traiter lui-même. Il aurait pu savoir aussi que pour l'espèce de lunettes qu'il étudiait à l'endroit cité et qui était la même que celle que Huygens avait eue en vue, ce n'est pas l'aberration sphérique, mais l'aberration chromatique, dont il importe avant tout de diminuer les effets, comme Huygens l'avait parfaitement reconnu. En vérité, le résultat d'Euler s'accorde entièrement avec les premières règles de Huygens. Pour le faire voir, nous remarquerons ce qui suit: 1o. La manière dont Huygens entend la condition que, dans le cas de deux lunettes, la vision soit également distincteGa naar voetnoot4), revient à l'égalité, pour les deux instruments, de la grandeur k introduite par Euler. | |||||||||||||
[pagina LXXXIII]
| |||||||||||||
2o. Pareillement, la condition que la clarté soit la même, s'exprime par l'égalité des valeurs de y; car, en vertu de la relation (22), cette égalité amène la proportionnalité du demi-diamètre de l'ouverture au grossissement, ce qui est précisément la condition formulée par HuygensGa naar voetnoot5). 3o. Un des points sur lesquels Huygens insiste, c'est que l'aberration sphérique de l'oculaire a beaucoup moins d'effet que celle de l'objectifGa naar voetnoot6). Cela se montre dans les formules d'Euler par les valeurs relatives des termes λm et λ′. La formule (23) correspond à la simplification que Huygens obtient en négligeant l'aberration sphérique de l'oculaire. 4o. Pour simplifier la comparaison de deux lunettes on peut supposer que λ ait la même valeur pour l'une et pour l'autre. Comme cette valeur dépend du rapport qui existe entre les deux rayons de courbure, cela revient à supposer avec HuygensGa naar voetnoot7) que les objectifs sont des lentilles ‘de la même espèce’. 5o. La formule (23) montre immédiatement que pour des valeurs données de k, y, λ et μ la distance focale p de l'objectif sera proportionnelle à m4/3. En combinant ce résultat avec la relation (22) et la formule m = p:p′, où p′ désigne la distance focale de l'oculaire, on voit que p sera proportionnel à x4/3 et p′ à x⅓ ou bien à p¼. On retrouve ainsi les deux règles énoncées par HuygensGa naar voetnoot8) dans les ‘Rejecta ex dioptricis nostris’. |
|