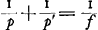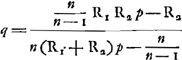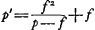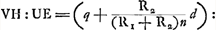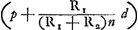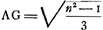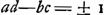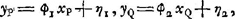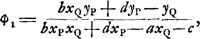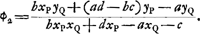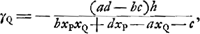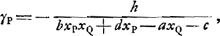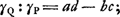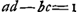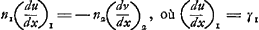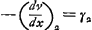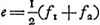Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–Première partie: Le traité de 1653 de la Réfraction et des Télescopes.Livre premier: De la réfraction due aux surfaces planes et sphériques et aux lentilles.Introduction.Les premières pages de la Dioptrique, jusqu'à la Prop. I (p. 13), peuvent être considérées comme une introduction au traité projeté ‘de la réfraction et des télescopes.’ Pour en connaître la rédaction primitive, on doit commencer | |||||||
[pagina XIV]
| |||||||
par l'Appendice I (p. 143-145) et poursuivre la lecture à la p. 9, là où les italiques finissent. Après avoir formulé la loi fondamentale de la réfraction, qu'il attribuait alors à DescartesGa naar voetnoot1), Huygens fait suivre la description de quelques méthodes pour déterminer l'indice de réfraction, qui lui ont paru être les plus commodes et d'une précision suffisante. Ainsi, pour déterminer (p. 9) l'indice de réfraction d'un liquide, Huygens fait usage d'un vase cylindrique de verre rempli du liquide. En plaçant ce cylindre de telle manière que l'axe soit perpendiculaire à la direction des rayons solaires on voit se former une ligne focale. Ensuite, après avoir mesuré la distance qui sépare cette ligne du vase, et le rayon du cylindre, on peut calculer l'indice de réfraction à l'aide de la Prop. XIII, p. 79-81 du Tome présentGa naar voetnoot2). Un autre procédé rapide (p. 11) pour déterminer l'indice du verre ou du cristal consiste dans l'emploi d'une lentille planconvexe formée de la substance en question. La Prop. IX (p. 35) permet alors de calculer l'indice au moyen du rayon de courbure de la surface convexe et de la distance focaleGa naar voetnoot3). Un troisième procédé (p. 11-13) dépend de la mesure de l'amplitude de l'arc-en-ciel produit par une petite sphère solide de la matière en question. Descartes avait appris à calculer le diamètre de l'arc-en-ciel ordinaire en partant de la valeur connue de l'indice de réfraction de l'eau de pluieGa naar voetnoot4). Huygens, charmé de l'idée ingénieuse sur laquelle reposait cette invention, avait élaboréGa naar voetnoot5) une | |||||||
[pagina XV]
| |||||||
meilleure méthode qui permettait en même temps de résoudre le problème inverse, c'est-à-dire, de calculer l'indice à l'aide de la valeur connue du diamètre de l'arc. C'est, en effet, à l'aide de la solution de ce dernier problème qu'il détermina l'indice de réfraction du verre en se ‘servant d'une petite sphère solide de cette substance, et en observant à l'aide de cette sphère que le rayon d'un arcen-ciel pour une pluie de verre si jamais une telle pluie venait à tomber, serait de 21o45′’Ga naar voetnoot6). D'ailleurs Huygens jugeait inutile d'ajouter à ces méthodes d'autresGa naar voetnoot7) plus exactes mais plus laborieuses, parce que, comme il le dit, il ne lui semblait pas ‘qu'il y eût aucune nécessité de chercher la valeur numérique de l'indice de réfraction avec une grande précision, et parce que cette valeur est un peu différente pour diverses sortes de verres ou d'eaux’Ga naar voetnoot8). | |||||||
Détermination du foyer d'une lentille et des images des points situés sur l'axe optique.Après la discussion des méthodes qui peuvent servir à mesurer la réfraction d'une substance transparente, Huygens prépare par ses trois premières propositionsGa naar voetnoot9) et par ses définitions des ‘points de concours ou de dispersion’Ga naar voetnoot10) son attaque des deux problèmes principaux qu'il s'est proposé de résoudre dans le premier livre: la détermination des foyers des lentilles et celle des lieux où se forment les images d'objets dont la position est donnée. Ce qui nous frappe avant tout dans cette partie de la Dioptrique, c'est la grande rigueur que Huygens s'est imposée. Elle se montre déjà dans sa définition des points que nous venons de nommer. Huygens a reconnu aussitôt que lorsqu'une | |||||||
[pagina XVI]
| |||||||
surface réfringente plane ou sphérique, ou bien une lentille, reçoit un rayon parallèle à l'axe ou issu d'un point donné de cette ligne, le lieu d'intersection du rayon réfracté avec l'axe tend vers une position limite déterminée, à mesure qu'on diminue l'écart entre le rayon incident et l'axe. C'est cette position limite qu'il a toujours en vue quand il parle du point de concours ou de dispersion, et, dans la démonstration détaillée et patiente de ses premiers théorèmes, on trouve toujours tous les raisonnements qui sont nécessaires pour faire ressortir cette propriété des foyers. Ce n'est que peu à peu qu'il se permet d'abréger un peu ses considérations à ce point de vue. Dans les Prop. IV-VII (p. 19-27) il s'agit de la situation des images dans le cas d'une surface réfringente plane, les rayons étant supposés former de petits angles avec la perpendiculaire à la surface. Ensuite, après avoir déterminé dans les Prop. VIII-XI (p. 33-41) les foyers pour une seule surface sphérique, Huygens considère dans la Prop. XII (p. 41-79) la situation de l'image d'un point lumineux produite par une telle surface. En traitant de ces questions il se sert d'un mode d'expression (voir la Définition de la p. 41) qui lui permet d'énoncer les théorèmes d'une manière tout-à-fait générale et d'embrasser tous les cas des points lumineux et des images, réels et virtuels. Les Prop. XIV-XVII (p. 81-93) sont consacrées à la détermination des foyers de lentilles de différentes formes. On y trouve calculées exactement les distances de ces points aux surfaces de la lentille, et Huygens n'oublie pas d'appeler l'attention sur la différence des distances des deux foyers d'une même lentille à cette lentille, lorsque les surfaces sont de courbures inégales. Il ajoute cependant que cette différence disparaît si l'on néglige l'épaisseur de la lentille, comme il va le faire dans la plupart des théorèmes qui suivent. Cela posé, il réussit, dans la Prop. XX (p. 99-109), à établir une règle générale, qui s'applique à toutes les espèces de lentilles et à toutes les situations du point lumineux. Cette règle, ainsi que celle qu'il a donnée dans la Prop. XII (p. 41) pour l'image produite par une seule surface réfringente, est présentée sous une forme très remarquable qu'on ne retrouve guère dans les traités modernes. En faisant intervenir ce qu'on appelle maintenant le premier foyer, Huygens peut dire que, dans le cas d'une seule surface réfringente, les distances du point lumineux à ce foyer, à la surface même, à son centre de courbure et à l'image forment une proportion géométrique. Pour une lentille la règle est plus simple encore; ici les | |||||||
[pagina XVII]
| |||||||
trois distances du point lumineux au premier foyer, à la lentille et à l'image sont en proportion continue. En ce qui concerne la direction dans laquelle on doit prendre la distance du point lumineux à l'image, déterminée par ces propositions, Huygens énonce une règle qui revient à dire que, dans les proportions qu'il introduit, chaque ligne doit avoir le signe algébrique qui correspond à la direction qu'elle possède à partir du point lumineux. Pour montrer la connexion qu'il y a entre les deux propositions et pour juger de leur degré de généralité, on peut les considérer comme des cas spéciaux d'un théorème qu'on déduit dans la théorie d'un système centré de surfaces réfringentes sphériques. Concevons un point lumineux quelconque situé sur l'axe du système, et soient a, b, c et d les distances de ce point au premier foyer, au premier point principal, au premier point nodal et à l'image. On aura alors: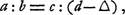 où Δ est la distance du premier point principal au second. Or, cette dernière distance s'annule dans les deux cas traités par Huygens, et on retrouve sa Prop. XII en remarquant que, dans l'hypothèse d'une seule surface réfringente, les points principaux coïncident avec le point où elle est coupée par l'axe, tandis que les points nodaux se confondent avec le centre de courbure. Quant à la règle établie dans la Prop. XX pour une lentille dont on néglige l'épaisseur, elle se déduit également du théorème général, puisque dans ce cas les points principaux et nodaux se trouvent à l'intersection de la lentille avec son axe.
Pour compléter cette partie de notre résumé du contenu du Premier Livre du Traité de la réfraction et des télescopes, nous devons parler encore des Prop. XIII, XVIII, XIX et XXI. La première (p. 79-81) traite de la détermination du foyer d'une sphère solide, ou si l'on veut, de la ligne focale d'un cylindre droit de révolution. Elle a pour but de déduire le théorème dont Huygens se sert dans sa première méthode pour la détermination de l'indice de réfractionGa naar voetnoot3). Dans la Prop. XVIII (p. 95) il suppose donnés la distance focale d'une lentille et le rayon de courbure de l'une des surfaces; il en déduit la courbure de l'autre. La | |||||||
[pagina XVIII]
| |||||||
Prop. XIX (p. 97) montre comment on peut trouver une lentille planconvexe ou une lentille à surfaces également courbées qui soit équivalente à une lentille convexe quelconque. Enfin la Prop. XXI (p. 109-111) apprend à placer en un lieu donné une surface sphérique, ou une lentille, capable de réunir en un point déterminé les rayons qui correspondent à un autre point donné. Signalons encore un résultat obtenu par Huygens dès le commencement de ses études de dioptrique. Il se rapporte au cas particulier où une surface réfringente sphérique produit une image exacte d'un point lumineuxGa naar voetnoot1). Si la surface est donnée, ainsi que l'indice de réfraction n du second milieu par rapport au premier (d'où les rayons proviennent), on peut toujours indiquer une position du point lumineux, pour laquelle les rayons après la réfraction se réunissent exactement même point. En effet, si r est le rayon de courbure, il suffit que la distance du point lumineux réel ou virtuel à la surface soit égale à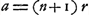 ; la distance de l'image à la surface est alors donnée par ; la distance de l'image à la surface est alors donnée par 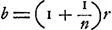 . À la condition, bien entendu, que les trois lignes r, a et b aient la même direction comptée à partir de la surface réfringente. La démonstration de ce théorème pour les quatre cas qu'on peut distinguer, la surface
pouvant être convexe ou concave, et la valeur de n supérieure ou inférieure à l'unité, se trouve aux pages 63, 69-71, 73-75, et 79Ga naar voetnoot2). . À la condition, bien entendu, que les trois lignes r, a et b aient la même direction comptée à partir de la surface réfringente. La démonstration de ce théorème pour les quatre cas qu'on peut distinguer, la surface
pouvant être convexe ou concave, et la valeur de n supérieure ou inférieure à l'unité, se trouve aux pages 63, 69-71, 73-75, et 79Ga naar voetnoot2).
Si Huygens avait publié les propositions que nous venons de mentionner à l'époque, vers 1653, où il les a obtenues, il aurait eu la priorité incontestable de la plupart d'entre elles. Il connaissait alors à fond l'oeuvre dioptrique de Kepler, | |||||||
[pagina XIX]
| |||||||
dans laquelle il n'avait trouvé que quelques résultats sur la situation des foyers dans des cas particuliersGa naar voetnoot3); il avait été devancé à son insuGa naar voetnoot4) par Cavalieri sur ce même sujet quant aux cas générauxGa naar voetnoot5); mais les propositions importantes XII (p. 41) et XX (p. 99) sur la situation des images étaient alors entièrement nouvelles, autant quant au fond que quant à la forme. | |||||||
[pagina XX]
| |||||||
Il en était déjà autrement lorsque, en septembre 1669, il envoya à la Société Royale de Londres une série d'anagrammes qui contenaient ses principales découvertes avec le but de s'en réserver la prioritéGa naar voetnoot1). De ces anagrammes le troisième se rapporte aux propositions prémentionnées. Elles y sont indiquées par la paraphrase: ‘Tertia proportionalis in lente, quarta proportionalis in superficie simplici dat punctum correspondens’. Les ‘Lectiones Opticae’Ga naar voetnoot2) de Barrow étaient alors sous presseGa naar voetnoot3). Dans cet ouvrage, écrit sous les auspices de NewtonGa naar voetnoot4), on retrouve la détermination des foyers d'une lentille sphérique quelconque d'épaisseur finie, et de même celle de l'image d'un point lumineux situé sur l'axe de la lentilleGa naar voetnoot5); c'est-à-dire les deux principales inventions du Livre I. Toutefois le procédé est bien différent, quoiqu'il soit également rigoureux chez les deux auteurs et qu'ils partent de la même définition des foyers et des images comme points limitesGa naar voetnoot6). Barrow était, en effet, un mathématicien de talent et il a composé un livre élégantGa naar voetnoot7) dont | |||||||
[pagina XXI]
| |||||||
les raisonnements peuvent être suivis plus facilement par un lecteur moderne que ceux de Huygens. Mais comme physicien il ne peut pas être considéré comme étant son égal. Tandis que Huygens a toujours en vue les propriétés des lentilles qui intéressent spécialement les observateurs, Barrow s'arrête longuement à toutes sortes de constructions qui se rapportent à des rayons faisant un angle fini avec la normale à la surface réfringenteGa naar voetnoot8) et ne donne à la considération des lentilles que quelques pages vers la fin de son livre. Il est vrai que, comme nous l'avons dit, il en détermine les foyers et qu'il énonce une règle générale qui apprend à construire l'image d'un point lumineux sur l'axe. Cette règle de Barrow, qui lui avait été communiquée par un de ses amisGa naar voetnoot9), peut être exprimée comme il suit: Soient L le point lumineux situé sur l'axe de la lentille, A1 et A2 les points d'intersection de cette ligne avec la première et la seconde surfaces, C1 et C2 les centres de courbure de ces surfaces, A1B1, A2B2, C1D1 et C2D2 des perpendiculaires à l'axe, situées dans un même plan. Tirez une ligne droite quelconque par le point L et soient α et β les points d'intersection de cette ligne avec A1B1 et C1D1. Prenez ensuite sur C1D1 un point γ tel que C1γ = C1β:n (n étant l'indice de réfraction) et joignez α et γ. La ligne ainsi obtenue coupe la droite A2B2 en un point δ et la droite C2D2 en un point ε. Si, sur la dernière ligne, on fait C2η = n.C2ε, la ligne tirée par les points η et δ déterminera sur l'axe la situation de l'image de LGa naar voetnoot10). | |||||||
[pagina XXII]
| |||||||
On comprend tout de suite cette règle en remarquant que le résultat est indépendant de l'inclinaison initiale de la ligne Lα par rapport à l'axe, et que, si cette inclinaison est infiniment petite, on n'a fait autre chose que de suivre pas à pas la marche d'un rayon lumineux issu du point L. La construction est donc exacte et parfaitement générale, s'étendant au cas d'une épaisseur finie de la lentille, mais elle a le défaut d'être bien compliquée, ce qui provient surtout de ce qu'on a fait intervenir deux fois l'indice de réfraction. Huygens, au contraire, a eu le mérite de formuler dans la Prop. XXGa naar voetnoot1) une règle, applicable, il est vrai, seulement au cas d'une lentille d'épaisseur négligeable, mais qui fait dépendre la situation de l'image de celle de certains points fixes situés sur l'axe de la lentille, sans qu'il soit nécessaire de se servir chaque fois de nouveau de l'indice de réfraction. Ainsi il a fait pour une lentille unique, de faible épaisseur, ce que Gauss et d'autres physiciens ont fait pour un système optique quelconque. C'est grâce à cette forme donnée par lui à la détermination de l'image que Huygens a pu arriver à la notion importante des lentilles équivalentesGa naar voetnoot2), notion qui a échappé à Barrow. Signalons encore la simplification considérable que Huygens a atteint, au point de vue pratique, par l'introduction du centre optique, dont il sera question bientôt, et par la manière dont il se sert de ce point dans le cas d'une épaisseur négligeable de la lentille. Or, le traité de Barrow ne contient rien relatif à ces sujets.
Une autre date importante est celle de 1703, date de la publication de la Dioptrique de Huygens, comme oeuvre posthume. À cette époque la détermination des foyers et des images des lentilles ne présentait plus aucune difficulté aux physiciens. Pour le montrer nous citerons en premier lieu le théorème suivant qu'on rencontre dans la ‘Dioptrica nova’Ga naar voetnoot3) (1692) de Molyneux: ‘As the difference | |||||||
[pagina XXIII]
| |||||||
between the distance of the object and focus is to the focus or focal length; so the distance of the object from the glass to the distance of the respective focus or distinct base from the glass’Ga naar voetnoot4); où ces dernières expressions indiquent l'image. En second lieu nous renvoyons à un article de HalleyGa naar voetnoot5) dans les ‘Phil. Transactions’ de Novembre 1693 où, sans négliger l'épaisseur de la lentille, il détermine la distance de l'image à l'une des faces par une formule algébrique unique qu'il applique à tous les cas possibles, en choisissant les signes des grandeurs suivant l'usage moderneGa naar voetnoot6). Il est donc clair qu'ici, comme souvent ailleurs, l'influence que les découvertes de Huygens auraient pu avoir sur le développement de la science a été de beaucoup amoindrie et presque anéantie par leur publication tardive; toutefois on ne doit pas oublier l'influence occulte, dont on ne saura jamais la vraie étendue, que les communications par lettres à des hommes compétents et les communications verbales, sans doutes nombreuses, à Londres et surtout à ParisGa naar voetnoot7), ont pu exercer. | |||||||
[pagina XXIV]
| |||||||
Images des points hors de l'axe optique. Centre optique. Relation entre les diamètres de l'objet et de l'image.Jusqu'à la Prop. XXII (p. 111) Huygens s'est borné à la considération des points lumineux situés sur l'axe de la lentille; dans cette proposition et les deux suivantes il s'occupe de points qui se trouvent à une petite distance de cet axe, de l'image d'un objet placé dans un plan perpendiculaire à cette ligne, et de la propriété du centre optiqueGa naar voetnoot1). La situation de ce dernier point est indiquée dans la Prop. XXIII (p. 119-123) pour les différents genres de lentilles. Du reste, dans les cas où l'épaisseur est négligée, Huygens peut considérer une ligne droite tirée par le centre optique comme le chemin suivi par un rayon qui traverse la lentille sans subir aucune réfraction. De cette manière il arrive aisément à la Prop. XXIV (p. 123) qui fait connaître la proportionnalité approximative, alors déjà bien connueGa naar voetnoot2), des dimensions de l'objet et de l'image à leurs distances à la lentille. Pour une détermination plus exacte du rapport de ces dimensions le centre optique ne pourrait servir, puisque la correction à apporter au rapport des distances à ce point, pour en déduire celui des dimensions de l'objet et de l'image, est du même ordre de grandeur que quand on prend par exemple les distances au milieu ou aux faces de la lentille, c'est-à-dire, de l'ordre du rapport de l'épaisseur aux rayons de courbure. Huygens le sait bien, et il indique le moyen d'arriver à une meilleure approximation en se servant du point V de la Fig. 97, p. 124. Il est clair qu'en construisant de même un point U, qui divise LR dans la même proportion que LD est divisée par le point V, le rapport des dimensions se trouvera égal à VH:UEGa naar voetnoot3) et, en effet, ce rapport représente le grossissement avec une approximation qui va jusqu'au carré de l'épaisseur. Or, comme nous l'avons indiqué dans la note 4 de la p. 124, la détermination précise | |||||||
[pagina XXV]
| |||||||
des sommets des triangles IVG et KUF n'aurait présenté aucune difficulté à Huygens. Si en conséquence cela lui avait paru désirable, il aurait pu donner la mesure précise du grossissement de l'objet par la lentille, et la méthode suivie aurait été celle de l'emploi des points nodaux introduits en 1845 par Moser et ListingGa naar voetnoot4). En effet, le sommet du ‘triangle formé derrière la lentille’ n'est autre que l'un de ces points et la construction du point V en donne la position approximative. | |||||||
Indice de réfraction relatif.Dans la Prop. XXV (p. 125-129), qui est publiée ici pour la première fois, Huygens énonce la règle pour la détermination de l'indice de réfraction relatif de deux milieux. Elle y est basée sur l'observation qu'une plaque plan-parallèle interposée entre deux corps transparents ne change pas la direction dans laquelle un rayon donné pénètre dans le second corps. En partant de cette observation Huygens peut démontrer facilement que l'indice relatif est égal au quotient des indices des deux corps par rapport à l'airGa naar voetnoot5). Plus tard Huygens a écarté du manuscrit de la Dioptrique cette proposition; sans doute parce qu'alors il préférait renvoyer, là où il avait besoin de la règle, c'est-à-dire à l'occasion de la construction de lentilles propres à la vision sous l'eauGa naar voetnoot6), au ‘Traité de la lumière’, où elle est déduite à l'aide des principes de la théorie ondulatoire de la lumière. | |||||||
Structure de l'oeil. Lentilles pour les myopes et les presbytes. Lentilles pour la vision sous l'eau.Vers la fin du Livre que nous venons d'analyser, Huygens s'occupe (p. 129-135) de la structure de l'oeil et de la théorie de la vision, sujets sur lesquels | |||||||
[pagina XXVI]
| |||||||
nous préférons revenir plus loin à l'occasion de quelques pièces d'une date postérieure. Enfin il conclut en donnant (p. 135-141) des règles claires et précises pour trouver les formes des lentilles ‘qui portent secours aux yeux des vieillards et des myopes’ et qui ‘permettent de voir clairement aux personnes placées sous l'eau’. Ici encore il y a occasion de comparer les solutions fournies à un même problème par Huygens et par Barrow, qui, lui aussi, a donné des règles pour la construction des verres pour les myopes et les presbytesGa naar voetnoot1). Or, Barrow a cru devoir avoir recours au cas particulier ‘de l'image exacte’, dont nous avons parlé plus hautGa naar voetnoot2). En effet, il est clair qu'une lentille, comme celle dessinée par Huygens à la p. 65 du présent Tome, peut être utile aux presbytes puisqu'elle agit de telle sorte que les rayons qui proviennent du point B semblent provenir du point A. Et de même la lentille représentée à la p. 64 peut être profitable aux myopes. À part cette restriction de Barrow, la solution de Huygens pour les presbytes ne diffère pas, en principe, d'avec la sienne. Pour Huygens, comme pour Barrow, il s'agit de faire paraître l'objet qui se trouve en un lieu donné (le point C de la fig. 101, p. 137) en un autre lieu (le point B de cette même figure) plus convenable au presbyte. Mais comme Huygens n'attache pas d'intérêt ici à avoir affaire au cas de l'image exacte et qu'il possède la notion des lentilles équivalentes, sa solution peut être bien plus simple, puisque pour lui il ne s'agit que de trouver la distance focale; après quoi une lentille de fabrication facile, planconvexe ou biconvexe à courbures égales, peut être choisie. Pour les myopes, au contraire, la solution de Huygens a pour but de projeter les objets qui se trouvent à l'infini sur un plan situé à la plus grande distance à laquelle le myope ‘voit distinctement un objet qu'on approche de lui’; ce qui ne serait pas possible si on voudrait se servir du cas de l'image exacte. | |||||||
[pagina XXVII]
| |||||||
Appendices au premier Livre. Arcs-en-ciel primaire et secondaire. Détermination des rayons de courbure d'une lentille donnée. Points de concours des rayons parallèles après deux réfractions et une réflexion aux surfaces d'une lentille. Points de confusion.La portée de l'Appendice I, qui constitue la leçon primitive du début du Livre I, a été indiquée à la p. XIV. De même pour les Appendices III, IV, V et VII il suffit de renvoyer respectivement aux notes 6, 7, 2 et 3 des p. XIV-XV. Les Appendices II, VIII et IX traitent de l'arc-en-ciel. Ici on peut de nouveau comparer le travail de Huygens à un travail analogue qu'on trouve aux p. 83-85 des ‘Lectiones Opticae’ de Barrow. À cet effet nous nous référons à la figure de la p. 149 du présent Tome où la ligne brisée PFDKO représente le chemin suivi par un rayon de soleil dans la goutte d'eau sphérique. Or, Descartes avait fait la remarque que les rayons qui produisent le phénomène de l'arc-en-ciel sont ceux pour lesquels l'angle ORP = NKO se trouve dans le voisinage de sa valeur maximum, puisqu'alors la lumière est plus concentrée dans la direction OK que dans toute autre qui en diffère sensiblement et que par suite l'angle NKO représente le demi-diamètre de l'arc-en-ciel. Il ne s'agit donc que de trouver la valeur maximum de cet angle. Descartes y avait réussi en calculant une table qui en donne les valcurs pour dix-neuf valeurs différentes du rapport de GF au rayon de la sphèreGa naar voetnoot3). Huygens dans l'Appendice II commence par démontrer qu'on a OKN = 2 DABGa naar voetnoot4); ensuite, par une belle application de la règle de Fermat pour les maxima et minima, il trouve la valeur de AGGa naar voetnoot5) pour laquelle AL devient un minimum et, par conséquent, l'angle DAB un maximum qu'on peut calculer à l'aide des valeurs des angles MAF et FAD, dont la détermination ne présente plus de difficultés. Enfin il s'occupe du problème inverseGa naar voetnoot6), celui de déterminer l'indice de réfraction, le diamètre de l'arc étant supposé connu. La genèse de la solution rapportée par Barrow est plus compliquée. Dans une | |||||||
[pagina XXVIII]
| |||||||
lettre datée du 24 nov. 1667Ga naar voetnoot1), de Sluse fit savoir à Oldenburg, le secrétaire de la Société Royale de Londres, que, si la théorie de Descartes était juste, il pourrait aisément déterminer pour un liquide quelconque le diamètre de l'arc-en-ciel qui lui appartient. À cet effet il suffirait de faire tomber des rayons parallèles sur une sphère de ce liquide, enfermée dans du verre, ce qui ne ferait pas de différence sensible, et d'observer la partie de la surface postérieure, illuminée par dedans. L'angle sous lequel cette partie est vue du centre de la sphère serait égal au semidiamètre de l'arc-en-ciel. De plus, pour un indice de réfraction donné, il savait construire cet angle, et le problème était planGa naar voetnoot2). Barrow, ayant reçu communication de cette lettre par OldenburgGa naar voetnoot3), ne manqua pas d'entreprendre la solution du problème. Or, il est clair d'abord que l'angle mentionné par de Sluse n'est autre que le double de l'angle BAD de la figure de la p. 149 dans le cas où cet angle a sa valeur maximum. Il s'agissait donc de trouver les conditions de ce cas. Alors, évidemment, l'idée ingénieuse est venue à Barrow que, pour que ce cas se présentât, il suffisait que le point D coïncidât avec le point de la caustique pour lequel FD est la tangenteGa naar voetnoot4), c'est-à-dire, avec la limite du point d'intersection avec un rayon voisin; limite que Barrow savait construire pour un rayon quelconqueGa naar voetnoot5). C'est, en effet, sur ces deux principes que la solution et la démonstration, entièrement géométriques, de Barrow sont fondées. D'ailleurs sa construction est identique avec celle de Huygens, puisque, comme celle-ci, elle revient à égaler GA à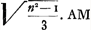 Ga naar voetnoot6). Ga naar voetnoot6).
| |||||||
[pagina XXIX]
| |||||||
Vers la même époque où Barrow élabora ses ‘Lectiones Opticae’, Huygens attaqua, en mars 1667, dans les Appendices VIII et IX (p. 163-169), le problème plus difficile de calculer le diamètre de l'arc-en-ciel secondaire. Malheureusement, quoiqu'il fût arrivé à une équation qui contient la véritable solution, il n'a pas su distinguer entre celle-ci et les solutions fausses introduites dans le cours du calculGa naar voetnoot7). Ainsi on peut dire qu'à cette occasion Huygens a échoué devant le port. Il nous reste encore à dire quelques mots sur les Appendices VI et X. Huygens y considère les rayons qui, après avoir pénétré dans une lentille, sont réfléchis à la surface postérieure, et subissent une seconde réfraction en sortant par la surface antérieure. L'Appendice VI (p. 157-159), de 1666, traite des foyers de ces rayons, c'est-à-dire, des points de concours ou de dispersion pour des rayons de cette espèce qui tombent sur la lentille dans la direction de l'axe. Huygens détermine ces foyers et fait voir comment on peut calculer les rayons de courbure des deux faces de la lentille en mesurant la distance à la lentille des deux foyers en question qu'on obtient en faisant tomber sur la lentille des rayons parallèles à l'axe arrivant alternativement de l'un et de l'autre côté. Ces deux problèmes ont été traités d'une manière analogue dans les ‘Fragments de Dioptrique’ de PicardGa naar voetnoot8) sous l'en-tête ‘Des foyers qui se font par reflexion & par refraction tout ensemble’ et il est probable que cette coïncidence n'est pas accidentelle. Dans l'Appendice X (p. 170-171), de 1690, Huygens s'occupe de deux autres points remarquables qui se présentent dans les systèmes de ces mêmes rayons et qu'il appelle les points de confusionGa naar voetnoot9). Ce sont les points où l'objet coïncide avec son image forméc après les deux réfractions et la réflexion à la surface postérieure. Après en avoir calculé la situation il montre comment on peut se servir de ces points pour trouver les rayons de courbure de la lentille. | |||||||
Livre deuxième: De la grandeur apparente des objets vus par réfraction.Définition de Huygens du grossissement d'un système de lentilles. Cas d'une seule et de deux lentilles.Le Livre deuxième du ‘Traité de la réfraction et des télescopes’ est consacré à | |||||||
[pagina XXX]
| |||||||
l'étude de l'agrandissement ou de la diminution des objets, produit par un système optique placé devant l'oeil, c'est-à-dire, à la détermination du rapport entre les grandeurs angulaires sous lesquelles un objet est vu avec et sans le système réfringent. En considérant ce rapport, qu'il trouve en comparant les dimensions que présente dans les deux cas la projection observée de l'objet sur un plan fixe, par exemple sur un plan qui coïncide avec une des surfaces réfringentes, Huygens a suivi une idée heureuse qui lui a permis d'arriver à des résultats d'une grande généralité. C'est de faire le calcul pour une position quelconque de l'oeil sans se préoccuper de la question de savoir si, dans cette position de l'oeil, l'objet ou l'image peuvent être vus distinctementGa naar voetnoot1). En effet, en se figurant l'oeil réduit à un point unique, on peut définir la grandeur angulaire comme étant l'angle entre les lignes tirées vers ce point à partir des extrémités de l'objet ou de l'image. Du reste, Huygens justifie ce procédé en faisant remarquerGa naar voetnoot2) qu'on peut toujours obtenir une vision distincte, sans que la grandeur apparente en soit changée, en plaçant tout près de l'oeil un diaphragme à ouverture très étroite, ou bien une lentille convenablement choisie. Cela posé, et en supposant toujours que l'oeil se trouve sur l'axe optique d'un système centré et que l'objet soit placé en un point de cet axe dans un plan qui lui est perpendiculaire, Huygens parvient à exprimer l'agrandissement ou la diminution par les rapports de certaines distances, comptées suivant l'axe du système. Ces considérations, dans lesquelles, bien entendu, les grandeurs apparentes sont toujours supposées infiniment petites, se rapportent à des positions de l'oeil et de l'objet, arbitrairement choisies sur l'axe; elles font savoir aussi si l'objet sera vu dans la situation droite ou renversée. Pour une lentille convexe le problème est résolu dans les Prop. II (p. 175) et III (p. 181), où l'oeil est supposé se trouver successivement entre la lentille et son foyer et au delà de la distance focale. Ensuite dans la Prop. IV (p. 185) Huygens s'occupe du cas d'une lentille concave et dans la Prop. V (p. 187-197) de l'agrandissement ou de la diminution produit par une combinaison de deux lentilles. | |||||||
[pagina XXXI]
| |||||||
Une proposition générale de Huygens, valable pour un système centré quelconque, pourvu que les indices du premier et du dernier milieu soient égaux.Tandis que pour plus de détails sur les propositions qui la précèdent au Livre deuxième, nous pouvons renvoyer au texteGa naar voetnoot3), il nous faut particulièrement appeler l'attention sur la Prop. VI (p. 199), qui doit être considérée comme un des plus beaux théorèmes de la physique théorique et qui contient le germe d'un développement ultérieur de la plus haute importance. Dans cette proposition Huygens nous apprend que la valeur de l'agrandissement ou de la diminution, pris dans le sens qu'il y attache, ne change pas si l'on échange entre elles les positions de l'oeil et de l'objet; ce qu'il a pu exprimer en disant que la grandeur angulaire sous laquelle un objet est vu à travers un système optique reste la même si l'on intervertit les positions de l'oeil et de l'objet; puisque, en effet, l'objet est vu en l'absence du système optique sous la même grandeur dans les deux cas. Huygens énonce ce théorème pour un nombre quelconque de lentilles; mais en vérité il s'applique également à chaque système centré de surfaces sphériques réfringentes dans lequel le premier et le dernier milieu ont le même indice de réfractionGa naar voetnoot4). On peut même arriver à la théorie générale d'un tel système en se basant sur la relation découverte par Huygens. C'est ce que Bosscha a fait ressortir dans un article de 1896, dans les Archives néerlandaisesGa naar voetnoot5), d'où nous avons emprunté quelques remarques dans la note 1 de la p. 198 du présent Tome. Il convient d'y ajouter encore ce qui suit. Considérons un système quelconque centré qui est traversé par des rayons lumineux dont tous les points se trouvent à une distance infiniment petite de l'axe et sont contenus dans un même plan passant par cet axe. Soit O un point fixe quelconque de l'axe, et introduisons deux axes de coordonnées, l'un OX coïnci- | |||||||
[pagina XXXII]
| |||||||
dant avec l'axe du système et dirigé dans le sens de la propagation de la lumière, l'autre OY perpendiculaire à OX. Alors chaque rayon lumineux qui entre dans le système, ou qui en sort, peut être déterminé par deux grandeurs, à savoir l'angle infiniment petit ϕ qu'il fait avec OX et la distance η de l'origine O du point d'intersection du rayon avec OY; ces deux grandeurs pouvant avoir l'une et l'autre le signe positif ou négatif, où nous prendrons pour direction positive des ϕ celle qui correspond à une rotation par un angle droit de OX vers OY. Si alors ϕ1 et η1 sont ces ‘coordonnées’ pour un rayon incident, et ϕ2 et η2 celles du rayon émergent correspondant, on démontre facilement qu'il doit y avoir deux relations de la forme:
Évidemment, si ces constantes pouvaient avoir toutes les valeurs possibles, le système aurait quatre paramètres arbitraires et pour déterminer son action dans tous les cas il serait nécessaire d'introduire quatre points cardinaux indépendants les uns des autres. Or, en réalité, un système tel que celui que nous considérons maintenant, c'est à-dire, dans lequel le premier et le dernier milieu ont le même indice, produit un effet qu'on peut déterminer au moyen de trois points cardinaux, p.e. les deux points principaux et l'un des foyers. Il en résulte qu'il doit exister une relation universelle entre les coefficients a, b, c, d. Cette relation, qui a été découverte par LagrangeGa naar voetnoot1), a la forme simple
| |||||||
[pagina XXXIII]
| |||||||
Ce qui précède, nous permet d'indiquer la portée du théorème de Huygens. En effet, son résultat est équivalent à celui qui fut obtenu par Lagrange; il donne lieu à la relation (2) et inversement peut en être déduitGa naar voetnoot2). La téorie générale du système optique peut donc aussi être obtenue par la combinaison des formules (1) avec le théorème de Huygens. Et c'est ce qui fut établi par Bosscha à la place citée plus haut. Tandis donc qu'il y a équivalence entre les règles de Lagrange et de Huygens, on est arrivé plus tard à des extensions de ces règles à des cas plus généraux. D'abord on a montré que si les indices de réfraction n1 et n2 du premier et du dernier milieu sont inégaux, il faut remplacer la relation (2) par
| |||||||
[pagina XXXIV]
| |||||||
lequel on voit un objet quand cet objet se trouve dans le dernier milieu et l'oeil dans le premier, et γ2 l'angle correspondant après invertissement de l'objet et de l'oeil, on aura:
Ensuite on peut abandonner la restriction que le système doit être symétrique autour d'un axe, et considérer au lieu de cela une distribution quelconque de matière transparente, en supposant seulement qu'en chaque élément de volume cette matière soit isotrope, et que, par conséquent, ses propriétés puissent y être caractérisées par un seul indice de réfraction n. Dans cette théorie on peut admettre aussi bien des changements continus de cet indice d'un point à un autre que des transitions brusques à des surfaces de séparation de différents milieux; dans le cas le plus général les rayons lumineux suivront des lignes courbes qui sont brisées aux points où elles traversent de telles surfaces. Soient maintenant A1 et A2 deux points quelconques, tels pourtant qu'il n'y ait qu'un seul rayon allant de A1 vers A2 ou vice versa, c'est-à-dire tels que A2 ne soit pas ‘une image’ de A1. Soit L ce rayon et plaçons en A1 et en A2 deux portions de plans infiniment petites dσ1 et dσ2 dont les normales font les angles aigus θ1 et θ2 avec la direction de L en A1 et en A2. Concevons le cône de rayons partant de A1 et atteignan tles points de la circonférence de dσ2; soit dω1 l'ouverture de ce cône à son sommet A1. Si, pareillement, un cône de rayons à ouverture dω2, issu du point A2, s'étend sur l'élément dσ1 après avoir traversé le système, et si n1 et n2 sont les indices de réfraction pour les matières qui se trouvent en A1 et en A2, on aura
Ce théorème a été énoncé il y a quelques années par StraubelGa naar voetnoot3), mais il avait | |||||||
[pagina XXXV]
| |||||||
été préparé et démontré pour des cas plus ou moins particuliers par plusieurs physiciens parmi lesquels nous pouvons citer Hamilton, Clausius et Kirchhoff. Si dans le cas d'un système symétrique autour d'un axe, on donne à dσ1 et dσ2 la forme de cercles perpendiculaires à cet axe et ayant leurs centres sur cette ligne, on en revient, en faisant pour le moment abstraction du signe, à l'équation (4)Ga naar voetnoot4) et pour le cas où n1 = n2 au théorème de Huygens. Seulement la partie du théorème qui se rapporte à la position droite ou renversée dans laquelle l'objet est vu au travers du système réfringent ne peut pas être déduite de la relation (5), c'est-à-dire du théorème de StraubelGa naar voetnoot5). On voit donc qu'il y a lieu de chercher un théorème général qui embrasse les deux parties que nous venons de distinguer dans le théorème de Huygens. Et, en effet, on peut établir pour un système transparent isotrope quelconque une formule qui contienne des éléments linéaires et qui satisfasse à cette condition; formule que nous mentionnerons ici parce qu'elle montre l'étroite connexion existant entre le résultat obtenu par Huygens et les théories modernes. Concevons, à cet effet, de nouveau deux points quelconques non-conjugués A1 et A2 et désignons encore par L le rayon lumineux qui les unit. Menons aux extrémités de ce rayon les tangentes A1T1 et A2T2, la première correspondant à la direction de A1 vers A2, et la seconde à celle de A2 vers A1. Soit ensuite V1 un plan quelconque passant par A1T1, et soit A1P1 une ligne de ce plan, perpendiculaire à A1T1; soit de même V2 un plan quelconque passant par A2T2, et enfin A2P2 une droite, située dans le plan V2, perpendiculaire à A2T2. Des points sur les lignes A1P1 et A2P2 peuvent être déterminés alors par leurs distances h1 ou h2 aux points A1 ou A2, ces distances étant prises avec le signe positif ou négatif suivant que les points se trouvent sur les lignes A1P1 ou A2P2 ou sur leurs prolongements par A1 ou A2. D'une manière analogue on peut déterminer la direction d'une ligne située dans le plan V1 ou dans le plan V2 et passant par A1 ou A2 par l'angle ε1 ou ε2, supposé infiniment petit, qu'elle fait avec A1T1 ou A2T2; cet angle étant appelé positif si la ligne dévie de A1T1 ou de A2T2 du côté de A1P1 ou de A2P2, et négatif dans le cas contraire. Cela posé, considérons un point lumineux situé sur A1P1 et déterminé par la | |||||||
[pagina XXXVI]
| |||||||
coordonnée infiniment petite h1; représentons nous ensuite le rayon lumineux qui se propage vers le point A2, et projetons sur le plan V2 la tangente en A2 de ce rayon; soit ε2 l'angle infiniment petit formé par cette projection et A2T2. Réciproquement, un rayon issu d'un point lumineux situé sur A2P2 à la distance h2 de A2, arrivera au point A1 dans une direction déterminée, et la projection de cette direction sur le plan V1 y fera un certain angle ε1 avec la tangente A1T1. On peut démontrer que les grandeurs que nous venons d'introduire satisfont à l'équation
Or, cette équation, qui pour un système centré où n1 = n2, amène immédiatement, et sans ambiguité de signe, le théorème de Huygens, suffit pour arriver à la formule (5), et il apparaît que la formule (6), plus générale, a une forme bien peu différente de celle du théorème de Huygens, dont la deuxième partie, celle dans laquelle il est question de la position droite ou renversée de l'image, revient à la règle suivante qui est évidente d'après la formule que nous venons d'indiquer: Si h1 et h2 ont le même signe algébrique, il en sera de même de ε1 et ε2. Quant à la démonstration des théorèmes généraux que nous avons cités dans ce qui précède, elle repose sur la notion de la longueur optique d'une ligne tirée dans un système de matières transparentes, cette longueur étant définie par l'expression 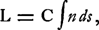 où ds est un élément de la ligne et C une constante choisie arbitrairement. On peut poser en principe que parmi toutes les lignes qui unissent deux points nonconjugués A1 et A2 donnés, le rayon lumineux est celle pour laquelle L est un | |||||||
[pagina XXXVII]
| |||||||
minimum; cela suffit pour trouver tout ce qui a été dit. Nous n'insisterons pas ici sur ce fait, mais il convient de faire remarquer que le principe, qui a été énoncé pour la première fois et pour un cas simple par FermatGa naar voetnoot2), a une signification bien différente dans les deux théories de la lumière qui se sont disputé si longtemps la victoire. Dans le système de l'émission l'indice n est proportionnel à la vitesse de la lumière v; on peut donc écrire 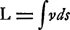 , et le principe que L devient minimum, n'est autre chose que le principe de moindre action appliqué au mouvement des corpuscules projetés par les corps lumineux. Dans cet ordre d'idées les théorèmes généraux de l'optique se rattachent à d'autres résultats qu'on déduit des principes fondamentaux de la mécanique; ils présentent alors une étroite analogie, par exemple, avec le théorème de Liouville, qui est d'une si grande utilité dans les théories moléculaires modernes.
Si, au contraire, on se place au point de vue de la théorie ondulatoire, il faut tenir compte de ce que l'indice n est inversement proportionnel à la vitesse v. On peut donc poser: , et le principe que L devient minimum, n'est autre chose que le principe de moindre action appliqué au mouvement des corpuscules projetés par les corps lumineux. Dans cet ordre d'idées les théorèmes généraux de l'optique se rattachent à d'autres résultats qu'on déduit des principes fondamentaux de la mécanique; ils présentent alors une étroite analogie, par exemple, avec le théorème de Liouville, qui est d'une si grande utilité dans les théories moléculaires modernes.
Si, au contraire, on se place au point de vue de la théorie ondulatoire, il faut tenir compte de ce que l'indice n est inversement proportionnel à la vitesse v. On peut donc poser:
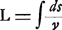 et le principe en question se confond avec celui du parcours dans un temps minimum. Or, la manière la plus simple dont on puisse arriver à ce dernier, pour les cas généraux, consiste à se représenter la propagation des ondes de la manière enseignée par Huygens. Il faut se figurer que chaque point qui est atteint par le mouvement lumineux, devient lui-même un centre de vibration secondaire; en un mot, il faut appliquer ce qu'on appelle communément le ‘principe de Huygens’. Ainsi non seulement Huygens a donné déjà en 1653, au commencement de sa carrière scientifique, le premier énoncé d'un théorème de grande valeur, mais encore dans son dernier chef-d'oeuvre, son Traité de la Lumière, il a exposé les idées qui en ont permis la généralisationGa naar voetnoot3). | |||||||
[pagina XXXVIII]
| |||||||
L'application la plus frappante que Huygens ait faite de son théorème sur l'interversion de l'oeil et de l'objet se trouve dans le troisième Livre du Traité de la réfraction et des télescopesGa naar voetnoot1), où il démontre que le grossissement d'une lunette est égal au rapport du diamètre de l'objectif à celui de l'anneau oculaire, c'est-à-dire, de l'image de l'objectif formée par les autres lentilles. En effet, pour le prouver, il suffit de s'imaginer que l'oeil qui, avant l'interversion, se trouvait au même endroit que l'anneau oculaireGa naar voetnoot2), soit transporté à la distance quasi insinie, où se trouvaient les objets qu'on regarde par la lunette, et que l'objet occupe cet anneau; alors l'image de cet objet occupera à son tour l'objectif et il est clair que le grossissement (qui n'a pas changé par l'interversion) sera égal au rapport des deux diamètres qui sont vus par l'oeil d'une distance si grande que leur distance mutuelle peut être négligée. Or, cette règle, découverte par Huygens, pour le grossissement d'une lunette quel que soit l'arrangement des lentilles, pourvu seulement qu'il existe un anneau oculaire réel, constitue un cas particulier des plus importants de la règle générale suivante pour le grossissement produit par les instruments optiques. Soient d le diamètre de l'objectif d'un télescope ou d'un microscope, d′ celui de ce qu'on appelle maintenant la pupille de sortie, c'est-à-dire, de l'image de l'ouverture de l'objectif produite par les autres lentilles du système, h la grandeur angulaire sous laquelle l'objet serait vu directement par un oeil placé au centre de l'objectif, et | |||||||
[pagina XXXIX]
| |||||||
h′ l'angle sous lequel il est vu à l'aide de l'instrument quand l'oeil se trouve au centre de la pupille de sortie; on a alors
h′:h = d:d′,
de sorte que le grossissement est donné par le rapport des diamètres d et d′. Cette dernière règle a été énoncée pour la première fois par LagrangeGa naar voetnoot3), qui y attachait beaucoup d'importance. En effet, Lagrange s'exprime à ce sujet en ces termes: ‘Comme il y a en mécanique la loi générale des vitesses virtuelles, par laquelle on peut connaître l'augmentation de force produite par une machine, sans connaître la nature ni la construction de la machine, mais par le simple rapport des vitesses simultanées du point où est appliqué la puissance et du point auquel cette puissance est transmise par la machine, de même on peut dire qu'il y a en optique une loi analogue, par laquelle, sans connaître la disposition intérieure d'un télescope ou d'un microscope, on peut juger de la force par le simple rapport du diamètre de l'ouverture de l'objectif au diamètre de l'ouverture de l'oculaire’ [c'est-à-dire à celui de la pupille de sortie]. On voit quel charme avait pour Lagrange le théorème qu'il avait découvert. Or, en ce qui concerne le télescope, ce théorème était déjà connu par Huygens et pour le microscope il se déduit très facilement du théorème de HuygensGa naar voetnoot4). | |||||||
[pagina XL]
| |||||||
Il nous reste à dire quelques mots sur la manière dont Huygens a démontré son théorème et sur l'historique de ce théorème. Dans sa démonstration Huygens se borne aux cas d'une lentille unique et de deux lentilles; puis il ajoute simplement: ‘Et lorsqu'on veut considérer trois ou plusieurs lentilles, on pourra donner une démonstration semblable à celle qui précède’. Du reste, la démonstration (p. 201-207) revient à un calcul direct du grossissement dans les deux cas en négligeant l'épaisseur des lentilles. Cette démonstration ne peut pas être considérée comme satisfaisante, ni même, à cause de cette dernière hypothèse, comme entièrement convaincanteGa naar voetnoot1). Elle n'offre aucunement la beauté et l'élégance des procédés modernes. On n'en doit pas moins admirer la sagacité avec laquelle Huygens a su trouver un tel théorème avec les moyens dont il disposait. L'historique du théorème est bientôt faite. Le 16 déc. 1653 Huygens le communiqueGa naar voetnoot2) à Kinner von Löwenthurn comme une des principales découvertes qu'il se propose de publier bientôt dans son Traité de la réfraction et des télescopes. En septembre 1669Ga naar voetnoot3), il l'inclut parmi les anagrammes, envoyés à la Société Royale de Londres, qui contenaient ses découvertes principales, dans la forme suivante: ‘Si oculus et visibile invicem loca permutent, manentibus interpositis lentibus quotcunque, eadem qua prius magnitudine, similique situ illud conspicietur’. Quand, enfin, le théorème est publié en 1703, on ne sait pas en apprécier la portée; il est oublié bientôt, ou ignoré, et ce n'est que dans les derniers | |||||||
[pagina XLI]
| |||||||
temps qu'on a appelé l'attention sur son importance capitale et sur la place qu'il mérite d'occuper parmi les théorèmes généraux de la dioptriqueGa naar voetnoot4). | |||||||
Théorèmes sur le grossissement d'une lentille unique, comme fonction des distances entre la lentille, l'objet et l'oeil.Les Prop. VII (p. 207) et VIII (p. 219) ont respectivement pour sujet la manière dont le grossissement, produit par une lentille convexe ou par une lentille concave, varie avec sa position quand l'objet et l'oeil occupent des positions données E et D. Il s'ensuit que dans le premier cas l'image peut être droite ou renversée selon les circonstances; si elle est droite lorsque la lentille se trouve à mi-distance entre l'oeil et l'objet, elle sera, pour cette position de la lentille, plus grande que pour toute autre; si elle est renversée pour cette position de la lentille, elle s'agrandira quand on déplace la lentille. Dans le cas de la lentille concave l'image est toujours droite et elle est minimum quand la lentille se trouve à mi-distance. Dans le cours du raisonnement Huygens compare le grossissement pour deux positions α et β de la lentille également éloignées du milieu de la ligne DE; il applique son théorème sur l'interversion de l'oeil et de l'image et en conclut que le grossissement doit être le même dans les deux cas; ‘en effet’, dit-il, ‘transporter la lentille de α en β équivaut à laisser la lentille elle-même à sa place, mais à faire changer de position l'oeil placé en D et l'objet placé en E’ (p. 209). Dans les Prop. IX (p. 220) et X (p. 222) Huygens considère successivement l'influence sur le grossissement du déplacement de l'objet et de celui de l'oeil. Par une application du théorème de l'interversion, le second de ces problèmes est ramené immédiatement au premier où l'on demande le changement causé par le déplacement de l'objet. Nous citons à ce dernier propos, en premier lieu le | |||||||
[pagina XLII]
| |||||||
renversement de l'image se produisant lorsque l'objet passe par le point qui est conjugué avec l'oeil, la valeur numérique du grossissement augmentant indéfiniment tant que l'objet se rapproche de ce point et diminuant après qu'il a été dépassé, et en second lieu la grandeur invariable de l'image lorsque l'oeil est situé au foyer de la lentille. | |||||||
Les trois dernières propositions du Livre deuxième.Le Livre deuxième du Traité de la réfraction et des télescopes se termine par trois propositions dont la première (p. 225-229), qui est avant tout une critique des idées de Descartes sur la théorie du télescope, fait connaître le grossissement d'une lunette dans l'hypothèse où tout l'espace entre l'objectif et l'oculaire serait rempli d'une substance du même pouvoir réfringent que celui de ces lentilles. Les deux propositions qui suivent sont d'une date inconnue mais bien postérieure à celle des autres propositions du Livre deuxièmeGa naar voetnoot1). La Prop. XII (p. 231) démontre que l'oeil placé sur l'axe d'un système centré de lentilles, qui se trouve entre lui et un objet rencontré par l'axe, apercevra toujours une partie finie de cet objet, excepté dans le cas où l'oeil serait placé justement au point qui est conjugué avec celui où se trouve l'objet. La Prop. XIII (p. 233) est d'une grande utilité dans la théorie des instruments optiques, comme nous en avons déjà donné des exemples dans la note 2 de la p. XXXVIII et dans le dernier alinéa de la note 4 qui commence à la p. XXXIXGa naar voetnoot2). Elle dit, que, dans le cas où les rayons sortant d'un point unique de l'objet sont rendus parallèles par les réfractions qu'ils ont subies dans un système centré, la grandeur de l'image est indépendante de la pofition de l'oeilGa naar voetnoot3). | |||||||
[pagina XLIII]
| |||||||
Historique des sujets traités dans le Livre deuxième.Nous avons déjà donné à la p. XL l'historique du théorème le plus important de ce Livre. En outre nous avons fait observerGa naar voetnoot4) que la conception du grossissement selon Huygens se retrouve dans la ‘Dioptrice’ de Kepler. Dans cet ouvrage de 1611 le cas d'une seule lentille, convexe ou concave, est traité d'une manière générale qui cependant n'aboutit pas à des règles précises pour la valeur du rapport de la grandeur apparente à la grandeur vraieGa naar voetnoot5). Plus tard Gregory dans son ‘Optica Promota’ de 1663Ga naar voetnoot6) et Molyneux à son instar dans la ‘Dioptrica nova’ de 1692Ga naar voetnoot7), font dépendre la détermination de cette valeur de celle du lieu et de la grandeur de l'image de l'objet formée par la lentille, appelée ‘basis distincta’ par Molyneux. Quant à Barrow, il ne consacre au problème en question qu'unc demi-page où il n'entre dans aucun détailGa naar voetnoot8). Au sujet du cas de deux lentilles considéré par Huygens dans la Prop. V (p. 187-197) nous signalons en premier lieu les cas spéciaux du télescope à oculaire concave (p. 193) ou convexe (p. 197), dont la discussion constitue très probablement la première démonstration rigoureuse du théorème d'après lequel le grossissement d'une telle lunette est égal au quotient des distances focales des deux lentilles; théorème que Molyneux, encore en 1692Ga naar voetnoot9), quand il en donnait sa démonstration, pouvait appeler ‘the great Proposition asserted by most Dioptrick Writers, but hitherto proved by none (for as much as I know)’, en ajoutant: | |||||||
[pagina XLIV]
| |||||||
‘they offer indeed Experiments and Methods of Tryal to confirm the Truth thereof, but proceed no further’Ga naar voetnoot1). Quant au problème lui-même, généralisé pour le cas de n lentilles centrées sans épaisseur, il a trouvé sa solution définitive dans un beau théorème de Cotes, publié par Robert Smith, qui avait accès à l'oeuvre posthume de Cotes mort en 1716, dans son ‘Compleat system of opticks’Ga naar voetnoot2). Pour le cas de trois lentilles
convexes on peut énoncer ce théorème comme suit: soient Ω la position de l'oeil, A, B, C, celles des trois lentilles, a, b, c, leurs distances focales, O la position de l'objet, alors le grossissement est exprimé par le quotient:
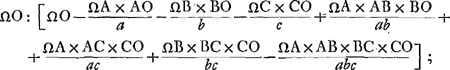 on voit combien cette solution générale est plus élégante que celle qui fut donnée par Huygens à la p. 189 pour le cas de deux lentilles, et elle amène immédiatement la Prop. VI de Huygens (p. 199) sur l'invertissement de l'oeil et de l'objet. Il nous reste encore à dire quelques mots sur l'historique de la Prop. XIII (p. 232) d'après laquelle le grossissement est indépendant de la position de l'oeil toutes les fois que les rayons partant d'un même point de l'objet sont convertis à la sortie du système optique en un faisceau de rayons parallèles. Cette proposition utile est presque évidente; ce qui n'empêche pas qu'elle semble avoir échappé longtemps | |||||||
[pagina XLV]
| |||||||
à l'attention de Huygens. En effet, lorsque dans son ‘Traité de la réfraction et des télescopes’ de 1653, il considère des dispositions de lentilles où le théorème est applicable, il démontre l'invariabilité du grossissement pour les positions différentes de l'oeil par d'autres raisonnements au lieu de citer le théorème en questionGa naar voetnoot3). Du reste, nous avons donné dans la note 9 de la p. 691 la raison qui nous fait croire que le théorème ne fut trouvé par Huygens qu'en 1690. Alors il aurait pu le retrouver dans l'Optica Promota de Gregory de 1663Ga naar voetnoot4). | |||||||
Les Appendices au Livre deuxième.Nous n'avons que peu de mots à dire sur les Appendices au Livre deuxième. Pour le premier (p. 235) nous pouvons renvoyer simplement à la note 1 de la p. 172. L'‘Appendice II’ (p. 237) donne un théorème qui a été supprimé par Huygens après avoir incorporé son contenu dans la Prop. VIIGa naar voetnoot5). L'‘Appendice III’ (p. 238) a plus d'importance. On retrouvera le théorème qu'il contient avec une autre rédaction dans la troisième Partie de la Dioptrique; mais on en verra déjà des applications importantes dans la deuxième Partie, qui traite de l'aberration sphériqueGa naar voetnoot6). Ce théorème nous apprend que si un prisme suffisamment aigu est frappé par deux rayons incidents situés dans un plan perpendiculaire à l'arête et formant l'un et l'autre un angle très petit avec la normale à la face d'entrée, l'angle formé par ces rayons sera le même avant et après leur passage par le prismeGa naar voetnoot7). L' ‘Appendice IV’ (p. 240), enfin, | |||||||
[pagina XLVI]
| |||||||
constitue une vérification numérique du théorème, déjà souvent mentionné, de l'interversion de l'oeil et de l'objet. Elle fut faite plusieurs dizaines d'années après l'invention du théorème et, comme il sembleGa naar voetnoot1), dans un moment de doute sur sa vérité, si glorieusement confirmée depuis par les méthodes modernes. | |||||||
Livre troisième: Des télescopes.Origine des premières occupations de Huygens en dioptrique pratique.Il est certain que la première impulsion concernant les recherches sur la construction des lunettes et des microscopes fut donnée à Huygens par sa découverte des lentilles sphériques aplanatiques; c'est-à-dire des lentilles qui n'imposent aucune aberration sphérique aux rayons dirigés vers ou partant d'un point déterminé. Cette découverte est faite dans les derniers jours d'octobre 1652Ga naar voetnoot2) et déjà le 4 novembre Huygens s'adresse à van Gutschoven pour lui demander toutes sortes de renseignements sur la fabrication des lentillesGa naar voetnoot3). La réponse ne venant pas assez vite au gré de son impatience, il lui écrit de nouveau le 10 décembreGa naar voetnoot4); mais sans attendre la réponse, qui n'arrive qu'en février 1653Ga naar voetnoot5), ayant reçu quelques données sur les lunettes qu'on fabriquait en AllemagneGa naar voetnoot6), il ordonne à un certain ‘Maître Paulus’ de lui tailler des verres dans les proportions qu'il lui a prescrites. ‘Si ces gens d'Allemagne connaissaient ces proportions, ou si Maître | |||||||
[pagina XLVII]
| |||||||
Paulus possédait leur science de tailler curieusement’, écrit-il, ‘je crois qu'on pourrait faire quelque chose de bien mieux’Ga naar voetnoot6). Enfin deux années plus tard, en février 1655Ga naar voetnoot7), le père Constantijn Huygens peut donner une description enthousiaste des microscopes et des télescopes construits de leurs propres mains par ses fils Christiaan et Constantijn. Or, tandis que pendant les premiers jours après sa découverte il se promet beaucoup de l'application des lentilles aplanatiques aux lunettesGa naar voetnoot8), il semble déjà avoir abandonné cet espoir dans sa lettre à van Gutschoven du 6 mars 1653, où il expose des idées très justes sur les télescopesGa naar voetnoot9), et depuis ce temps il ne mentionne plus les lentilles aplanatiques comme pouvant contribuer considérablement à l'amélioration des lunettes, ni même des microscopes. Au contraire, quand, plus tard, il essaie d'affranchir les lunettes du défaut de l'aberration sphérique, il recourt à d'autres moyens. Il se propose de compenser l'aberration de l'objectif par celle de l'oculaireGa naar voetnoot10), ou de construire un objectif formé de deux lentilles dont l'une compense l'aberration de l'autreGa naar voetnoot11). En effet, il est difficile de deviner la manière précise dont Huygens voulait utiliser les lentilles aplanatiques dans ses télescopes. Elles ne peuvent pas servir comme objectifs, puisqu'elles ne sont aplanatiques que pour un seul point situé à une distance finie comparable à leur distance focale. Et personne n'a mieux compris que Huygens ne l'a fait plus tardGa naar voetnoot12), que l'oculaire, s'il n'est pas construit expressément pour donner une grande aberration, comme dans le cas | |||||||
[pagina XLVIII]
| |||||||
de compensation mentionné plus hautGa naar voetnoot1), ne change que très peu l'aberration sphérique causée par l'objectif; mais probablement il ignorait alors cette vérité. En tout cas les manuscrits de Huygens ne donnent aucun renseignement sur l'emploi qu'il a voulu faire de ses lentilles aplanatiques. | |||||||
Portée générale du Livre troisième ‘Des télescopes’.On ne trouvera pas dans ce Livre troisième un traité complet des télescopes. Un tel traité, comme Huygens a essayé de le formuler plus tard dans la troisième Partie de la DioptriqueGa naar voetnoot2) aurait dû commencer nécessairement par une discussion des télescopes, hollandais et keplérien, à deux lentilles. Or, la copie de NiquetGa naar voetnoot3), composée vers l'année 1666, nous garantit que la Dioptrique de 1653 ne contenait sur ce sujet que ce que nous avons reproduit dans la première Partie, c'est-à-dire: dans le deuxième Livre la démonstration de la formule du grossissement, dont nous avons déjà parléGa naar voetnoot4), et dans celui dont nous nous occupons à présent, la description de la manière d'‘accommoder à un oeil quelconque une lunette composée de deux lentilles données’ (Prop. I, p. 245-247) et, si l'on veut, de la façon de redresser à l'aide d'un miroir les images renversées formées par la lunette keplérienne (Prop. V, p. 265-269). Ainsi les Prop. I-III de la troisième Partie (p. 443-460), qui traitent expressément des deux genres de télescopes à deux lentilles, ont été écrites beaucoup plus tard. Quant à une théorie générale, applicable aux télescopes et aux microscopes, Huygens ne pouvait pas en donner une, en 1653, puisque des trois bases sur lesquelles il fonda plus tard une telle théorie: la première, l'aberration sphérique, n'avait encore attiré son attention que passagèrementGa naar voetnoot5); la deuxième, l'aberration chromatique, n'avait pas encore été rendue susceptible d'un traitement mathématique par les découvertes ultérieures de Newton; enfin la troisième, l'influence de la diffraction sur la netteté des images, lui était probablement encore entièrement inconnue. | |||||||
[pagina XLIX]
| |||||||
On ne doit donc considérer ce premier traité de Huygens sur les télescopes que comme une suite de descriptions et de remarques concernant quelques combinaisons de lentilles dont l'auteur s'était servi, ou qui lui semblaient présenter certains avantages. Ce qu'on y trouve de plus remarquable, c'est, à notre avis, sa préoccupation permanente de déterminer la position la plus favorable de l'oeil de l'observateur, sa découverte de la relation qui existe entre le diamètre de l'anneau oculaire et le grossissement des lunettes, et la description de ce qu'on appelle maintenant l'oculaire de Huygens. Avant de finir nous devons encore avertir le lecteur de ce que les dates des propositions insérées dans ce troisième Livre sont quelquefois plus ou moins incertaines. Nous avons déjà fait allusion à cette incertitude dans la note 1 de la p. 252 à propos de la Prop. III qui traite de l'oculaire de Huygens. Toutefois il est sûr que toutes ces propositions existaient vers l'année 1667 dans la forme que nous leur connaissons, et que du moins quelques unes des cinq propositions que nous reproduisons ont dû faire partie du traité dont l'achèvement fut annoncé à Grégoire de Saint-Vincent le 5 janvier 1654Ga naar voetnoot6). | |||||||
Remarques sur les différentes propositions du troisième Livre. Oculaire de Huygens.La Prop. I (p. 245-247) a déjà été mentionnéeGa naar voetnoot7). Elle apprend à approprier la longueur de la lunette à la distance des objets, et à la constitution de l'oeil d'un observateur myopeGa naar voetnoot8). La Prop. II (p. 247-253) s'occupe d'un appareil employé par Scheiner pour ses observations des taches du soleilGa naar voetnoot9). Il s'agit de projeter sur un écran l'image du soleil qu'on peut obtenir en allongeant convenablement une lunette hollan- | |||||||
[pagina L]
| |||||||
daise ou keplérienne. Huygens calcule l'allongement nécessaire et discute la grandeur de l'image et sa clarté. Dans la Prop. III (p.253-259) Huygens décrit l'oculaire composé de deux lentilles convexes qui porte son nom et qu'il préfère à une lentille unique parce qu'il donne un champ plus étendu, une image moins déformée et que les défauts d'homogénéité y sont moins nuisiblesGa naar voetnoot1). Huygens indique la raison de ce dernier avantage, mais il ne justifie pas les deux autres. En effet, dans cette première Partie de la Dioptrique il ne traite pas encore systématiquement de la grandeur du champ visuel, comme il le fera plus tard dans la troisième PartieGa naar voetnoot2), et la question du calcul de la distorsion des images ne l'a jamais occupé qu'incidemmentGa naar voetnoot3). On doit donc admettre que l'expérience a eu la plus grande part dans l'invention de son oculaire; on en aperçoit la trace dans les valeurs assez différentes qu'il a recommandées sucessivement pour les rapports entre la distance mutuelle des lentilles et leurs distances focalesGa naar voetnoot4). D'ailleurs il ne se cacha pas de ce qui manquait encore à sa théorie lorsqu'il écrivit vers la fin de la Prop. IV (p. 265) ‘Et certes, il serait malaisé de donner à ce sujet’ (c'est-à-dire: les combinaisons différentes de lentilles oculaires) ‘des préceptes théoriques, parce que la considération des couleurs ne peut être réduite à des lois géométriques, et qu'il est fort difficile de calculer d'une manière satisfaisante | |||||||
[pagina LI]
| |||||||
cette courbure des lignes droites qu'on voit souvent près des bords des lentilles’. Les Propositions IV (p. 259-265) et V (p. 265-269) se rapportent au redressement des images, nécessaire dans les lunettes terrestres. Suivant la première de ces propositions une troisième lentille convexe est ajoutée aux deux lentilles d'une keplérienne; d'après la seconde un petit miroir plan est placé devant l'oculaire. Le premier de ces arrangements avait déjà été indiqué par KeplerGa naar voetnoot5). Dans le texte et dans une pièce beaucoup plus récente que nous avons ajoutée comme Appendice (p. 271), Huygens donne les distances focales des lentilles et leurs distances mutuelles. Plus tard il a toutefois déconseillé l'emploi de cet arrangement au profit d'un autre à quatre lentilles, dû à Campani, par lequel on obtient un champ de vision plus vaste avec moins de distorsion et moins de couleurs aux bords des imagesGa naar voetnoot6). Quant à l'emploi du petit miroir de la Prop. V, il a le désavantage de ‘faire voir à notre gauche, ce qui se trouve à notre droite’, mais Huygens fait suivre que ‘c'est là un faible inconvénient, pourvu qu'on en soit averti’; toutefois cet arrangement, auquel Huygens attacha longtemps une certaine importanceGa naar voetnoot7), a été délaissé aujourd'hui, du moins sous la forme que Huygens lui avait donnée. On l'a remplacé, là où il pouvait être utile, par l'emploi de systèmes de prismes à réflexion totale, amenant un redressement completGa naar voetnoot8). En parcourant ces trois dernières Propositions III, IV et V, on sera frappé du soin avec lequel Huygens indique chaque fois le lieu où l'oeil doit être placé de préférence, c'est-à-dire là où se forme une image de l'ouverture de l'objectifGa naar voetnoot9). En effet, il explique comment, lorsque la pupille de l'oeil coïncide avec ce qu'on appelle maintenant l'‘anneau oculaire’ ou la ‘pupille de sortie’, on obtiendra toujours la plus grande étendue du champ visuel et la plus grande clarté. La | |||||||
[pagina LII]
| |||||||
relation qui existe entre le grossissement et le diamètre de cette pupille de sortie, comparé à celui de l'objectif, relation sur laquelle plus tard Ramsden a fondé l'emploi de son ‘dynamètre’, n'a non plus échappé à HuygensGa naar voetnoot1). |
|


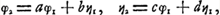
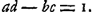
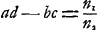 ;
;