Logo DBNL
Oeuvres complètes. Tome XIII. Dioptrique (1916)

Oeuvres complètes. Tome XIII. Dioptrique

(1916)–Christiaan Huygens–rechtenstatus Auteursrecht onbekend

Vorige Volgende

Les Compléments à la Dioptrique.

Premier Complément. Projets divers de rédaction de la Dioptrique, ou de ses parties.

Nous avons réuni dans ce premier Complément à la Dioptrique les projets de rédaction ou de révision de cet ouvrage que nous avons trouvés dans les manuscrits. Ces projets ont déjà été utilisés dans l'Aperçu de la génèse de la Dioptrique4), qui constitue le début de cet Avertissement, et dans l'historique et l'analyse de plusieurs des sujets traités5). Qu'il suffise donc ici de quelques mots pour signaler les Pièces les plus importantes qu'on trouve dans ce Complément: premièrement (p. 738-745) ‘le projet du Contenu de la Dioptrique’, de 1673, écrit peu de temps après la découverte de la théorie ondulatoire de la lumière et qui donne l'ébauche d'un ouvrage contenant en même temps la matière de la présente Dioptrique et celle du Traité de la lumière, à l'exception de l'expli-

cation de la double réfraction, qu'alors il n'avait pas encore trouvée. Ensuite nous mentionnons le ‘Commencement du traitè de ma Dioptrique en François que j'avois dessein de joindre au Traitè de la Lumiere’ (p. 754-770), de 1690, et enfin la Pièce ‘De Ordine in Dioptricis nostris servando’, de 1692, qui contient les idées de Huygens sur une révision projetée de sa Dioptrique, telles qu'il les avait formées à la même époque où il composait et rédigeait la dernière partie de sa Dioptrique, c'est-à-dire celle dans laquelle il traite de la théorie du microscope composé.

Il avait alors abandonné l'idée d'employer la langue française dans la nouvelle rédaction de sa Dioptrique. Il se proposait d'y maintenir la langue latine dans laquelle son manuscrit avait été commencé (en 1652) et poursuivi, et dont il savait d'ailleurs se servir avec facilité et élégance. Or, il est curieux d'observer de quelle manière il se préparait à cette tache. En effet, on trouvera aux dernières pages (p. 781-782) du Complément, qui nous occupe ici, toute une série de mots latins et de bouts de phrases qui constituent comme un répertoire d'expressions latines variées, concernant la science de la Dioptrique. Évidemment ces expressions devaient servir à faciliter la rédaction de l'ouvrage projeté, en y évitant une trop grande monotonie dans les locutions.

Deuxième Complément. Conformation de l'oeil et théorie de la vision.

On doit à l'admiration de Huygens pour ‘la construction de l'oeil et la maniere dont se fait la vision’ quelques pages d'une haute éloquence. On les rencontre dans une Pièce intitulée: ‘De l'oeil et de la vision’, dont la première rédaction date probablement de 16706). Cette Pièce resta inédite jusqu'en 1908, lorsqu'elle fut publiée par Straub7). Il nous serait difficile de nous abstenir d'en citer ici plusieurs passages, si nous ne pensions pas que le lecteur préférera les lire en entier aux p. 797-799 du présent Tome8).

Nous nous bornerons donc, dans ce qui suit, à indiquer les principaux sujets de l'optique physiologique ou psychologique dont Huygens s'est occupé, en y

joignant quelques remarques dont nous sommes en grande partie redevables à feu Manuel Straub, le regretté professeur d'ophthalmologie de l'Université d'Amsterdam.

Déjà la figure (p. 131) dessinée par Huygens dans la première Partie de sa Dioptrique1), qui représente une coupe méridienne de l'oeil, est remarquablement exacte quant à la forme générale et la disposition des détails. Plus tard, dans la Pièce ‘De l'oeil et de la vision’2), Huygens a pu utiliser les mesures prises, en sa présence, en février 1667, par le médecin Jean Pecquet3). Il est dommage que nous ne connaissons pas les méthodes, dans lesquelles Huygens a eu probablement sa part, qui furent employées dans cette ‘ophthalmométrie’. Les résultats obtenus prouvent qu'elles avaient été bien choisies.

Dans la première Partie de la Dioptrique et de même dans l'article ‘De l'oeil et de la vision’ on rencontre la description d'un oeil simplifié formé par deux hémisphères de différents rayons4). La surface de l'un de ces hémisphères représente la cornée, celle de l'autre la rétine5). Or il est curieux de remarquer la grande ressemblance de cet oeil simplifié, projeté par Huygens, avec l'oeil réduit bien connu de Listing6). Chez tous les deux les surfaces réfringentes de l'oeil sont remplacées par une seule surface sphérique de telle manière que le centre de cette surface (le point M de la figure 99, p. 128 du présent Tome) correspond au point K de Listing7) dans lequel il a réuni, pour obtenir la simplisication qu'il cherchait, les deux points nodaux très voisins de l'oeil réel, tandis que le point E de la figure de Huygens correspond au point F de Listing. De plus, puisqu'ils supposent tous les deux que l'intérieur de l'oeil factice est rempli d'un liquide dont l'indice de réfraction est égal à 4/3, il arrive que le rapport des distances du centre M aux deux points focaux, dont l'un se trouve en E et l'autre en avant du point B à une distance égale à ME, est le même dans les

deux constructions, qui, par conséquent, présentent une similitude géométrique complète.

Toutefois les deux inventions avaient chacune un but différent. Celle de Listing devait faciliter les calculs et les constructions des oculistes, celle de Huygens avait pour objet l'étude des dispositions qui font de l'oeil réel un instrument d'optique si merveilleux. Ainsi, par exemple, la mesure absolue du rayon MB7) n'importe pas à Huygens, tandis que chez Listing elle est choisie de manière à donner des résultats autant que possible applicables à l'oeil réel. D'autre part Listing ne s'occupe guère de la situation du diaphragme formé par la pupille, dont les avantages sont discutés par Huygens à l'aide de son oeil simplifié.

En 1691 Huygens a imaginé un oeil schématique d'une façon différente8). Il conserve à la surface antérieure de cet oeil, qui représente la cornée, sa forme sphérique, mais il donne à sa surface postérieure la forme d'une surface de révolution, dont il apprend à construire la courbe méridienne, point par point, de manière qu'elle reçoive les images des objets très éloignés, formées par les faisceaux de rayons qui après leur réfraction par la surface antérieure, passent par une petite ouverture qui représente la pupille. Ce modèle peut servir, entre autres, pour expliquer, dans l'oeil réel, la grande étendue du champ de la vision confuse9), qui excède, pour les deux yeux ensemble supposés immobiles et regardant droit devant eux, un angle de 180o10).

Huygens a trouvé chez Kepler les notions de la myopie et de la presbyopie et nous avons déjà analysé plus haut11) les règles qu'il a donné pour la construction des besicles qui doivent corriger ces défauts. Or, il est intéressant de noter que Huygens a senti le besoin d'une explication de la genèse de l'emmétropie; explication dont on commence seulement de nos jours à s'occuper plus expressé-

ment1). À ce propos on trouve à la p. 756 du présent Tome l'annotation suivante: ‘admirable dans les yeux, que les surfaces de la cornée et du cristallin sont justement de telle mesure de convexité que les rayons paralleles rompus concourent dans le fond de la choroide. peut estre que dans les petits enfans cela n'est pas encore ainsi et que les yeux s'y disposent en quelque façon, mais cela mesme n'est pas moins merveilleux’.

Quant à la manière dont l'accommodation se fait dans l'oeil, dans la première Partie de sa Dioptrique (p. 133) Huygens laisse le choix entre la supposition d'un mouvement en avant du cristallin et celle d'une augmentation de la convexité de cette lentille. Il admet aussi la possibilité que les deux causes agissent simultanément et il décrit les mécanismes qui devraient, selon lui, entrer en jeu dans l'un et dans l'autre cas. En 1667, à l'occasion des mensurations faites par Pecquet2), il observe combien le cristallin est flexible et changeant de forme sous la pression des doigts3). Il en conclut que la deuxième supposition est la plus probable et il voit dans le peu d'espace qui est laissé au cristallin pour se mouvoir en avant une autre raison pour préférer cette supposition à la première. Toutefois en 1670 il revient à la conception (fausse comme on le sait maintenant) d'un mouvement en avant du cristallin sans changement de forme4).

Parlant, vers 1653, dans la première Partie de sa Dioptrique des questions que nous appelons de nos jours psychologiques, Huygens dit (p. 135) ‘qu'elles sont trop obscures pour que des mortels, quels qu'ils soient, puissent en trouver la solution’. À cette même occasion, après avoir écarté la question d'examiner comment il se fait que la pupille en se contractant reste toujours ronde, parce que ‘l'examen de ces propriétés de l'oeil ne fait pas partie de notre plan’, il ajoute qu'il tâchera ‘encore moins de répondre à la question de favoir comment l'image des objets visibles qui se forme au fond de l'oeil parvient de là à notre cerveau et à notre esprit, comment étant renversée, elle nous fait cependant voir les objets debout, et comment il se fait, qu'en regardant avec les deux yeux, nous ne voyons pas les objets doubles’.

Toutefois, plus tard, Huygens est revenu sur les deux problèmes mentionnés en dernier lieu. À propos de celui recherchant ‘pourquoy on voit les choses droites quoyque tournees dans nostre oeil a l'envers’ il se fait connaître dans le ‘Projet du Contenu de la Dioptrique’ (de 1673) comme ‘empiriste’: ‘Ce n'est’ d'après lui ‘que l'accoustumance de juger, et..si nous avions vcu toute nostre vie toutes choses et mesme le mouvement de nos mains par un verre qui renverse les objets comme un convexe nous dirions encore que nous voions toutes choses directes et ne nous tromperions point en montrant le haut et le bas de nos mains’5). Or, on sait qu'une expérience analogue à celle indiquée par Huygens a été exécutée de nos jours par Stratton6).

Quant à l'autre problème, Huygens a développé dans l'article ‘De l'oeil et de la vision’, qui était destiné à faire partie de sa Dioptrique, avec une clarté qui ne laisse rien à désirer, la notion des points correspondants. ‘Pour ce qui est de l'action des deux yeux a la fois’ dit-il7) ‘la nature a pourvu d'une maniere bien particuliere a ce qu'ils ne fissent pas paraitre l'objet double. C'est qu'elle a fait que chaque point du fond de l'oeil a son point correspondant dans le fond de l'autre en sorte que lors qu'un point de l'objet est peint dans quelques deux de ces points correspondants, alors il ne paroit que simple comme il est’. Un peu plus loin il ajoute qu'il est à noter que ces points sont tous deux ‘du mesme costè des axes et non pas disposez semblablement a l'egard des deux nerfs optiques’ et il fait encore remarquer que ‘d'icy il est aisè de voir pourquoy un object éloignè doit paroitre double lors qu'on dispose les yeux pour regarder un autre object plus proche, et pourquoy au contraire l'object proche se doit doubler en voiant simple celuy qui est plus distant’. Comme on l'aperçoit, Huygens expose ici une théorie assez complète des points correspondants des deux rétines, telle qu'on la rencontre dans les ouvrages des physiologistes modernes8). D'ailleurs Huygens, aussi bien que les autres grands mathématiciens du dix-septième et du

dix-huitième fiècles, a laissé à Wheatstone le mérite de faire l'observation (en 1838) que les images sur les deux rétines d'objets à trois dimensions sont nécessairement inégales1); observation qui fut d'une importance si fondamentale pour la théorie de la vision binoculaire et qui le conduisit à l'invention du stéréoscope. Si Huygens s'était rendu compte de ce que l'explication qu'il donne (p. 796) du fait que, non seulement un point déterminé d'un objet, mais aussi les points qui l'environnent, sont vus simples, ne pouvait être valable qu'approximativement, il aurait fait un premier pas vers les découvertes de Wheatstone, mais on trouve qu'en réalité il n'a pas tiré cette consèquence de la théorie des points correspondants.

Nous avons réservé pour la fin une question à laquelle, vers 1673, Huygens a voulu consacrer un chapitre entier de sa Dioptrique2); dessein que, toutefois, il n'a pas exécuté. Nous parlons de l'estimation du lieu que nous assignons à l'image formée par un système optique.

Huygens a toujours émis l'opinion, qui s'écartait de celle de plusieurs de ses prédécesseurs et de ses contemporains3), que cette estimation est essentiellement un effet de la vision binoculaire. Dèjà dans la préface4) de la première Partie de sa Dioptrique on rencontre l'affirmation ‘que la vraie cause du phénomène que, en regardant d'en haut un vase rempli d'eau, le fond semble partout s'élever,..doit être cherchée en considérant les rayons de lumière qui se dirigent vers les deux yeux’.

En 1669, la question fut mise à l'ordre du jour par Barrow d'une manière qui attirait beaucoup l'attention de ses contemporains. Dans ses ‘Lectiones opticae’5), où il traite amplement de la localisation par l'observateur des images formées par les miroirs et les lentilles, il avait été arrêté par une difficulté concernant un cas particulier6) où l'expérience était en contradiction avec ses considérations théoriques, basées, comme partout dans son ouvrage, sur l'hypothèse que l'image n'est vue que d'un seul des deux yeux. Ayant tâché en vain de lever cette difficulté, sur laquelle probablement il n'avait pas manqué de consulter Newton7), il prit le parti de l'exposer au lecteur, tout en avouant qu'il n'avait pu réussir à la résoudre.

C'était sans doute la déduction par Barrow du ‘locus imaginis’, comme s'il s'agissait d'une question de vision monoculaire, que Huygens avait en vue lorsqu'il écrivait à Oldenburg, en janvier 1670, peu de temps après avoir reçu l'ouvrage de Barrow8): ‘Pour ce qui est du Locus Imaginis, j'ose dire qu'il n'a pas bien rencontrè, et la difficultè qu'il se forme luy mesme a la sin, devroit l'en avoir adverty’9). En effet, en 1673, Huygens commence le résumé du Chapitre, où il se proposait alors de traiter ‘du lieu de l'image’, par les phrases: ‘l'Erreur de plusieurs en cecy. Qu'on ne juge point la distance d'un seul oeil, les boites paintes en dedans le font voir ou on regarde par un trou. la difficultè qu'un autre aura a rencontrer vostre doit avec un oeil fermè’10). De même, lorsque, en 168311), Fullenius12) le consulte sur les difficultés qu'il avait rencontrées dans l'explication de quelques expériences ayant pour but la détermination du lieu apparent des images d'objets qu'on observe à travers une lentille, Huygens lui expose13) combien ces déterminations sont incertaines et subjectives quand on

ne se sert que d'un seul oeil et il indique quelques circonstances qui peuvent avoir de l'influence sur ces évaluations1).

Comme nous l'avons déjà dit Huygens n'a jamais réalifé son dessein de traiter expressément de la manière dont on estime le lieu où l'on voit une image. En 1692, il exprime l'opinion que, quant aux images formées par les lentilles, cette question ne vaut pas la peine de s'en occuper, mais qu'il en est autrement en ce qui concerne celles qu'on observe dans les miroirs2). Et de nouveau il se propose de résoudre dans sa Dioptrique la ‘dissiculté’ de Barrow3). Or, plus loin dans la même Pièce4) on trouve, sinon une explication détaillée des phénomènes décrits par Barrow, du moins l'exposition suivante concernant le cas du miroir, dont nous croyons utile de traduire ici la partie écrite en latin: ‘Voiez la difficultè de Barrow. Essaier avec un miroir concave. Lors qu'il pensait que le lieu et la distance de l'image peuvent être estimés d'un seul oeil il a donné contre cet écueil. Là, où il juge du lieu de l'image, ni à l'aide des deux yeux, ni à l'aide du mouvement d'un seul. car avec les deux yeux l'objet se voit double dans ce cas. Et le mouvement d'un seul ne cause pas de parallaxe, mais l'objet se déplace plus que l'oeil lui-même. Comment donc le lieu de l'image est-il perçu d'une manière quelconque? Par la seule grandeur apparente de l'objet qu'on connaît’. Cette annotation est accompagnée de quatre figures5) dont les trois premières représentent différents cas qui peuvent s'offrir quand on regarde avec les deux yeux dans un miroir concave l'image d'un point lumineux ou d'un petit objet; tandis que la quatrième figure semble avoir rapport à la vision monoculaire.

Troisième Complément. Lunettes catoptriques.

Huygens s'est intéressé vivement au télescope à miroir, inventé par Newton en 1671, dont la Société Royale de Londres lui avait fait parvenir la description par l'intermédiaire du secrétaire Oldenburg6). Il communiqua cette description à son tour à Gallois7), l'éditeur du ‘Journal des Scavans’, en faisant ressortir les avantages que le nouvel instrument avait sur la lunette dioptrique, à savoir: l'absence d'aberration chromatique et de la perte de lumière, causée par les réflexions multiples aux surfaces des lentilles comme aussi par l'absorption des rayons par la matière du verre, et surtout la valeur considérablement plus petite de l'aberration sphérique. Et il ajouta: ‘Si au lieu de miroirs spheriques, l'on en pouvoit avoir de paraboliques exactement formez & polis; ces Lunettes feroient l'effet que l'on s'est promis des verres elliptiques ou hyperboliques: & je croy bien plus facile de reüssir aux miroirs’.

Dès l'abord il voit toutefois une difficulté dans le fait qu'il sera difficile ‘de trouver une matiere pour ce miroir qui soit capable d'un poli aussi beau et uni que celuy du verre; et la maniere de donner ce poli sans gaster la figure spherique’8), et cette difficulté s'accentue de plus en plus quand il s'efforce de faire construire sous sa propre direction des miroirs de 10 à 12 pieds9). Il finit par déclarer10) à propos de cette invention de Newton qu'il a ‘pu connoistre par l'expérience’ [que] ‘le defaut de la matiere la rend presque aussi impossible d'executer que la difficultè de donner la forme repugne aux Hyperboles de Monsieur Des Cartes de sorte qu'a mon avis il en faudra demeurer à nos verres spheriques aux quels nous avons desia toute obligation et qui peuvent recevoir encore plus grande perfection tant par l'augmentation de la longueur des lunettes que par la correction de la mastiere du verre mesme’11). Ce n'est que beaucoup plus tard, en 1691, que l'idée lui est venue, sur laquelle nous reviendrons, qu'il serait possisible d'employer le verre comme matière des miroirs parce qu'il y a des

moyens de supprimer ou de diminuer l'inconvénient de la duplication des images.

Du reste, il résulte des annotations que Huygens a consacrées aux télescopes à miroir, bien qu'elles soient très brèves1), qu'il avait développé la théorie de cet instrument exactement de la même manière que celle de la lunette keplérienne. Dans ces considérations il s'agit toujours du télescope de Newton, qu'il préfère de beaucoup à ceux que Gregory et Cassegrain avaient proposés de construire2).

Or, l'instrument de Newton se compose d'un miroir concave qui sert d'objectif, et d'une lentille oculaire convexe vers laquelle les rayons sont réfléchis par un petit miroir plan; il est donc clair que les effets qu'il produit doivent être fort semblables à ceux qu'on obtient avec une lunette astronomique.

En premier lieu le grossissement est donné par le rapport entre la distance focale du miroir concave et celle de l'oculaire, règle que Newton avait déjà appliquée à son télescope3), et que Huygens démontre4) en considérant la marche de deux rayons incidents, l'un coïncidant avec l'axe et l'autre passant dans une direction quelconque par le foyer du miroir concave.

De plus, il détermine l'aberration sphérique longitudinale α pour le cas où le miroir reçoit des rayons parallèles à l'axe. Il la trouve égale à la moitié de la distance AG (voir la figure de la p. 131 du T. VII) entre le point où l'axe coupe le miroir et le plan qui passe par le bord du miroir. Il donne à cette règle une démonstration géométrique très élégante dans l'annotation de 1672, ajoutée par lui à la Pièce contenant la description du télescope de Newton5) et encore, en 1692, une seconde démonstration plus algébrique, qu'on rencontre à la p. 814 du présent Tome.

Si nous désignons par f la distance focale du grand miroir et par d le diamètre de l'ouverture, la règle que nous venons de mentionner peut s'exprimer sous la forme:

(1) α = d2/32f.

Si, au lieu du miroir, on faisait usage d'une lentille planconvexe, dont la surface sphérique est tournée vers la lumière incidente, on aurait la formule analogue6):

illustratie

ou bien, en prenant 3/2 pour l'indice de réfraction n,
(3) α′ = 7d′2 / 24f′.

La comparaison des valeurs de α et de α′ fait voir combien, au point de vue de l'aberration sphérique, le miroir concave l'emporte sur la lentille. Même pour d = 3d′ on trouve, en supposant f′ = f, que l'aberration longitudinale du miroir serait encore un peu plus petite que celle de la lentille. Toutefois Huygens fait remarquer7) qu'il n'est pas permis d'en conclure qu'on puisse admettre pour le télescope catoptrique une ouverture trois fois plus grande que pour une lunette keplérienne ayant la même distance focale, et il renvoie à ce propos à ce qu'il a démontré dans sa Dioptrique sur les ouvertures des lentilles.

Or, puisque l'annotation où l'on trouve cette remarque date de 1672, la partie de la Dioptrique, que Huygens a en vue ne peut être que la Prop. XI des ‘Rejecta’8) (p. 339). Et, en effet, les règles qu'il y donne pour la détermination des ouvertures des lunettes, en tenant compte seulement de l'aberration sphérique, peuvent servir également pour déterminer l'ouverture qui convient à un télescope à miroir9).

Cependant, dans la comparaison d'un tel télescope à une lunette keplérienne, on doit avoir égard aux facteurs numériques des formules (1) et (3). Évidemment les rayons des cercles d'aberration qui se forment dans le plan focal auront dans les deux cas respectivement les grandeurs dα/2f et d′α′/2f′; c'est-à-dire d3/64f2

et 7d′3/48f′2. Si l'on divise ces expressions par les distances focales ϕ et ϕ′ des oculaires, on trouve pour les angles d'aberration A et A′:

(4) A = d3/64f2ϕ; A′ = 7d′3/48f′2ϕ′.

Pour que la vision soit également distincte dans les deux cas, il faut que ces angles soient égaux. Cela nous donne:

(5) d3/4f2ϕ = 7d′3/3f′2ϕ′.

D'autre part l'égalité de la clarté des images exige1):

(6) dϕ/f = d′ϕ′/f′.

En combinant cette équation avec la relation précédente, on trouve:

(7) d4/4f3 = 7d′4/3f′3

ou, enfin, si les distances focales f et f′ sont supposées égales:

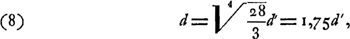illustratie

où d représente le diamètre du miroir du télescope catoptrique et d′ à le diamètre de la lunette keplérienne. Dans la même supposition l'équation (6) nous donne: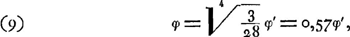

illustratie

et, par suite, si l'on désigne les grossissements par g et g′:
(10) g = 1,75g′.

Or, dans le télescope de Newton, dont la description fut envoyée le 15 jan-

vier 1672 à Huygens2), le grand miroir avait une distance focale d'environ un demi-pied3). Pour une lentille objective planconvexe qui aurait cette distance focale, on trouve d'après les règles et le Tableau des ‘Rejecta’4), fondés sur la considération de l'aberration sphérique:

 

d′ = 0,185 pouce; ϕ′ = 0,905 pouce; g′ = 6,65).

 

D'après ces données la plus grande ouverture admissible dans le télescope de Newton serait de 0,32 pouce, la plus petite distance focale de l'oculaire de 0,52 pouce et le plus fort grossissement de 11,6, tandis qu'en réalité l'ouverture du télescope de Newton était d'environ 2 pouces, la distance focale de l'oculaire d'environ 0,16 pouce, et le grossissement de 38.

Si Huygens a fait ces calculs, il a dû en conclure que le télescope de Newton devait laisser beaucoup à désirer au point de vue de la netteté des images. Mais on ne trouve aucune remarque de cette portée, ni dans l'annotation de 16726), écrite en marge de la description de ce télescope (si l'on excepte le ‘post-scriptum’ sur lequel nous reviendrons), ni dans sa Correspondance de cette époque. En effet, il paraît que dans le jugement porté par Huygens sur l'invention de Newton tel qu'on le trouve dans l'article du ‘Journal des Sçavans’ du 29 février 16727) et dans sa lettre privée à Oldenburg du 11 février de cette même année8), il ne s'est pas préoccupé beaucoup des dimensions spéciales données par Newton au télescope dont il avait reçu la description, mais qu'il s'est laissé guider par des considérations plus générales.

Ainsi, quand on lit aux endroits cités, à propos des télescopes catoptriques, ‘qu' avec la moitié ou le tiers de la longueur des Lunettes, ou peut estre encore moins, on pourra faire l'effet accoûtumé’, il faut expliquer cette assertion de la manière suivante:

On doit considérer que Huygens était convaincu de ce que la perte de lumière, causée dans la lunette keplérienne par les réflexions aux surfaces de l'objectif et par l'absorption par la matière de cette lentille, était considérablement plus grande que la perte produite par les réflexions aux miroirs de la lunette catoptrique1). Par suite l'équation (6) qui exprime l'égalité de la clarté doit être remplacée par la relation:

(6)′ dϕ/f = κd′ϕ′/f′,
où le facteur κ a une grandeur inconnue, mais qui est, en tout cas, sensiblement moindre que l'unité. L'égalité du grossissement exige:
(11) f/ρ = f′/ρ′.

En combinant ces équations avec l'équation (5), qui ne change pas, on trouve:

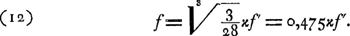illustratie

Ainsi, pour avoir p.e. f = ⅓f′, on doit supposer κ = 0.702).

 

Il nous faut dire encore quelques mots à propos du ‘post-scriptum’ ajouté plus tard à l'annotation de 16723), mentionnée plus haut. Ce ‘post-scriptum’ est conçu ainsi: ‘L'ouverture donnée par Newton à son télescope d'un demi-pied est beaucoup plus grande qu'il ne faut. Il est certain que, par suite, l'image doit paraître comme recouverte par un brouillard. Voyez la cause au Livre H, p. 71 et précédentes. L'ouverture, qu'il fait de 2 pouces, ne devait pas excéder ⅔ pouce’.

 

Les dates assez nombreuses qu'on trouve disséminées sur les pages de ce Livre H prouvent que la page citée doit avoir été écrite en 1692. A cette

époque Huygens avait pleinement reconnu l'insuffisance des règles formulées dans les ‘Rejecta’4). Il a donc dû fonder la conclusion à laquelle il arrive dans le ‘post-scriptum’ sur d'autres considérations que sur celles que nous venons d'exposer. Or, les pages qui précèdent, dans le Livre H, la p. 71 citée ont été reproduites par nous aux paragraphes 6-10 de l'Appendice IX (p. 634-643). Les calculs qu'on y trouve avaient alors donné à Huygens la conviction que le plus grand angle d'aberration sphérique admissible devait être estimé à l′40″5). Quant à la p.71 elle-même, nous ne l'avons pas reproduite parce qu'elle est biffée et que les calculs qu'elle contient sont très confus. Toutefois on y reconnaît facilement de quelle manière Huygens a cru pouvoir conclure que l'ouverture d'un télescope catoptrique de la distance focale de celui de Newton ne doit pas excéder ⅔ pouce: il a supposé que l'angle d'aberration de l'instrument devrait au plus égaler cette valeur de 1′40″.

Dans nos notations cela revient à poser, suivant l'équation (4)6):
(13) d3/64f2φ = 1′40″ = 0,000485,
ou bien, en prenant f = 6 pouces, c'est-à-dire, à peu près égale à la distance focale du grand miroir du télescope de Newton:

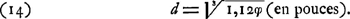illustratie

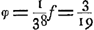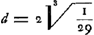Si Huygens s'était conformé au grossissement de 38, indiqué par Newton7), il aurait posé illustratie pouce et trouvé d = 0,56 pouce. Au lieu de cela Huygens a supposé qu'on se contenterait d'un grossissement de 24 et il a trouvé que même alors l'ouverture ne devrait pas surpasser illustratie pouce. En effet, la formule (14) nous donne alors d = 0,65.

C'est après avoir obtenu ce résultat, que Huygens formule la conclusion qu'on trouve dans la note 10 de la p. 132 du T. VII; conclusion qui est entièrement conforme à celle qui est empruntée plus haut au ‘post-scriptum’ en question.

D'ailleurs Huygens n'a pas longtemps persisté dans l'opinion que la limite de l'angle d'aberration admissible doit être fixée à 1′40″. Déjà huit pages plus loin que la p. 71 citée on trouve dans le Livre H un nouveau calcul, reproduit à la p. 652 du présent Tome, où cette limite est portée à 4′10″. Ensuite dans le texte de la Dioptrique (p. 565) il l'évalue à 20′, c'est-à-dire à douze fois 1′40″. Il va sans dire que cette nouvelle limite aurait conduit à des résultats numériques tout différents1) et c'est bien pour cette raison que Huygens a biffé les calculs de la p. 71.

 

Nous avons déjà dit2) que, vers 1691, Huygens s'est proposé de remplacer le miroir métallique du télescope de Newton par un miroir en verre, nonobstant la duplication des images qui semblait devoir résulter de l'emploi d'une matière transparente. Or, nous avons reproduit les recherches qui s'y rapportent aux paragraphes 2 et 3 du troisième Complément, p. 805-819 du présent Tome.

Au § 23) Huygens détermine d'abord la position relative des deux images qu'on obtient dans le cas d'un point lumineux infiniment éloigné, situé sur l'axe, en tenant compte des deux réfractions que subissent les rayons réfléchis par la surface postérieure. En désignant par b l'épaisseur du verre au milieu et en négligeant les termes de l'ordre b2/f il trouve pour la distance mutuelle des deux ‘foyers’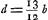 illustratie si les deux surfaces ont le même rayon de courbure (p. 805), et d = ⅓b si elles sont concentriques (p. 807). Il se propose ensuite de chercher un cas où l'on aura d = o, c'est-à-dire où les deux foyers coïncident. Il n'y réussit pas en supposant (p. 809-810) que l'épaisseur b

au milieu est si petite qu'elle peut être négligée, mais il démontre (p. 810-811) que la coïncidence se réalisera si le rayon de courbure de la surface postérieure surpasse de 13/9 b celui de la surface antérieure.

Même dans ce cas idéal, où il y aura coïncidence exacte des foyers qui correspondent à ces rayons incidents parallèles à l'axe, cette coïncidence n'existera pas nécessairement pour les deux points de convergence de rayons parallèles frappant le miroir dans une autre direction. L'image d'un objet d'une certaine étendue sera alors plus ou moins confuse vers les bords, et on pourra se faire une idée de cet effet en calculant le grossissement de chacune des deux images. Cette difficulté s'est en effet présentée à Huygens4) et il paraît même qu'elle l'a conduit en 1691 à rejeter entièrement l'emploi des miroirs en verre5). Il était alors arrivé à la conclusion que le grossissement de l'image formée par la réflexion à la surface antérieure est au grossissement de l'image due à la surface postérieure comme 1 est à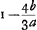 illustratie4); mais une année après il croit que le raisonnement qui l'a conduit à ce résultat est erroné, et il ajoute: ‘par conséquent une telle construction du télescope de Newton aura le meilleur succès’6).

Or, la question ne peut pas être résolue, comme Huygens a cru pouvoir le faire, en considérant exclusivement les rayons qui participent à la formation du point de l'image qui fe trouve sur l'axe. Voyons donc quelle en est la véritable solution.

À cet effet nous nous servirons de la figure 5 de la p. 812, dans laquelle A est le centre de la surface antérieure DF et N celui de la surface postérieure EG, tandis que VHK et VHGFK sont les chemins qui peuvent être suivis par un rayon VH arrivant au point H parallèlement à l'axe. Ensin Q et B sont les points où l'axe est rencontré par GH et GF prolongées. En prenant, comme plus haut, AD = a, DE = b et 3/2 pour l'indice de réfraction du verre, on aura successivement, si l'on néglige les termes de l'ordre b2/a:



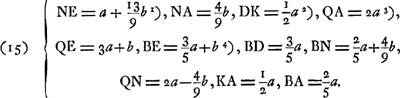illustratie

(1)(2)(3)(4) Supposons maintenant qu'un objet infiniment éloigné ait la grandeur angulaire δ. En se rappelant que pour une seule surface sphérique, soit qu'elle réfléchisse la lumière, soit qu'elle la réfracte, les dimensions linéaires d'un objet et de son image sont entre elles dans le rapport de leurs distances au centre de courbure, on trouve pour les grandeurs des images: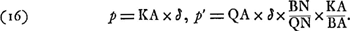

illustratie

Il en resulte:

illustratie

ou bien, après substitution des valeurs (15):

illustratie

On voit donc que la différence des grossissements, présumée par Huygens en 16915), existe bien réellement mais dans le sens inverse de ce qu'il suppose.

Notons encore, avant de passer aux recherches de 1692, qu'il a considéré aussi l'aberration chromatique, qui doit résulter des deux réfractions à la surface antérieure du verre, des rayons qui sont réfléchis par la surface postérieure6). Pour le cas où les deux surfaces sont également courbées, il calcule l'écart entre les foyers

des rayons rouges et des rayons violets, qui se trouve être seulement la 156ième partie de l'épaisseur du verre.

Au printemps de 1692 Huygens croit pouvoir constater, comme nous l'avons dit, que la difficulté provenant de la différence des grossissements des deux images, qui l'avait arrêté en 1691, n'existe pas. Toutefois il ne se dissimule pas7) qu'il sera très difficile de donner aux deux surfaces des rayons de courbure dont la différence est exactement égale à 13/9 b, ainsi que la règle qu'il a trouvée l'exige.

Sa première idée est de former le grand miroir du télescope d'une plaque de verre d'une épaisseur partout égale, mais si petite que l'écart de ⅓ b, qu'il a trouvé pour ce cas, n'ait pas d'influence nuisible8). Ensuite une autre solution de la difficulté lui semble préférable9). Au lieu de faire coïncider autant que possible les images produites par les deux surfaces on pourra, au contraire, chercher à augmenter leur distance mutuelle. Cela aura pour effet que, si l'une des deux est vue distinctement à travers l'oculaire, les détails de l'autre ne seront guère remarqués10); la netteté avec laquelle la première image se présente à l'observateur n'en souffrira que peu. Poursuivant cette idée, Huygens détermine les conditions dans lesquelles la distance mutuelle des foyers est égale à six fois9) ou bien à cinq fois11) l'épaisseur du verre, le foyer le plus éloigné du miroir appartenant dans le premier cas à la surface postérieure et dans le second à la surface antérieure.

Après avoir achevé ces calculs théoriques, Huygens s'applique à trouver les moyens pratiques de réaliser son invention12). Enfin dans une dernière annotation13) il examine l'aberration sphérique du faisceau de rayons, réfléchi par la surface postérieure.

Toutes ces recherches nous montrent quelle importance Huygens a attachée à l'idée de remplacer le miroir métallique de Newton par un miroir en verre. Pourtant on peut douter si jamais il y a eu un commencement d'exécution à ce projet. Dans des lettres du 2 et du 13 juin 16921) son frère Constantyn l'exhorte à ‘pousser’ son ‘invention ou celle de Newton des Lunettes a miroirs concaves’. Ce sont là les dernières traces de cette invention qu'on trouve dans la Correspondance.

Quatrième et dernier Complément. Critiques et remarques sur quelques ouvrages de dioptrique.

Huygens n'appartenait pas à ce genre de savants qui sont tellement absorbés par leurs propres idées et recherches qu'ils ne réussissent pas à prendre connaissance régulièrement des ouvrages des autres; type de savant qui d'ailleurs était beaucoup plus rare à l'époque où Huygens vivait qu'il ne l'est à l'état actuel, où la production scientifique a pris une extension incomparablement plus grande.

Au contraire, Huygens a toujours porté un intérêt très vif (et surtout sur le terrain de l'optique) aussi bien aux travaux de ses prédécesseurs (y compris les anciens2)) qu'à ceux de ses contemporains. Sa Correspondance et la présente Dioptrique en contiennent d'abondantes preuves; ce quatrième Complément en apporte de nouvelles.

Nous y avons réuni trois Pièces contenant des annotations, qui n'avaient pas pu trouver place dans la Correspondance, concernant des ouvrages d'Eschinardo, du père Gottignies et de Molyneux.

La première de ces Pièces3) corrige la solution d'un des problèmes qu'Eschinardo4) s'était posés dans un ‘Addendum’ à ses ‘Centuria Problematum Opticorum.’ Ce problème5) se rapporte à la construction d'une lunette hollandaise très courte6), comparable à l'un des deux tubes d'un binocle tel qu'on en

fabrique aujourd'hui; lunette, qui pourrait servir aux mêmes buts auxquels on emploie maintenant ce dernier instrument. La solution d'Eschinardo, où l'erreur qui s'y est glissée est une erreur de calcul7), n'est pas sans interêt historique, puisqu'elle montre qu'Eschinardo connaissait, en 1667, c'est-à-dire avant la publication des ‘Lectiones opticae’ de Barrow8), la solution générale du problème ayant pour objet de déterminer pour une lentille planconcave ou planconvexe9), la situation de l'image d'un point lumineux qui se trouve sur l'axe de la lentille.

La deuxième Pièce (p. 825-826) contient un passage emprunté à un manuscrit du père Gottignies10) dont Huygens a pu prendre connaissance. On y trouve en outre quelques remarques à propos de ce manuscrit. Cette Pièce, d'ailleurs, n'a pas beaucoup d'importance.

Il en est autrement de la troisième, où Huygens donne (p. 826-844) un résumé de la ‘Dioptrica nova’ de Molyneux11), rédigé peu de temps après qu'il avait reçu cet ouvrage en mars ou avril 169212). Dans ce résumé il suit le texte de Molyneux presque page par page et l'accompagne continuellement de ses remarques. En lisant ces annotations, on aperçoit, comme à vol d'oiseau, presque tout le terrain de la dioptrique, tel qu'il se présentait aux savants pendant les dernières années de la vie de Huygens.


Vorige Volgende