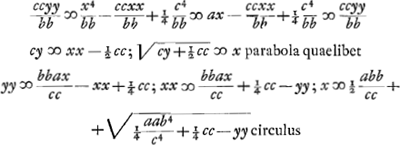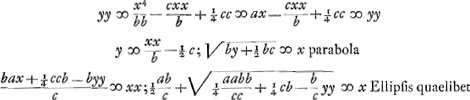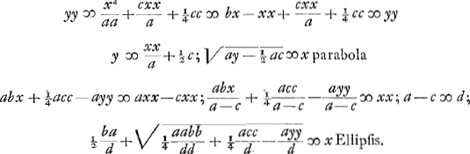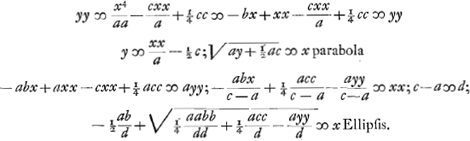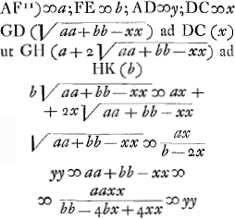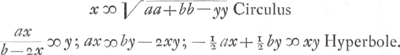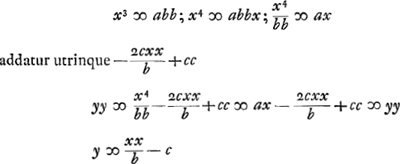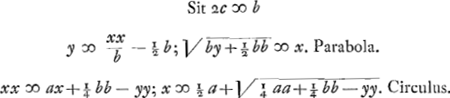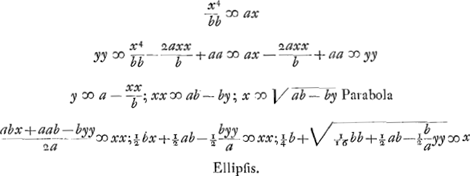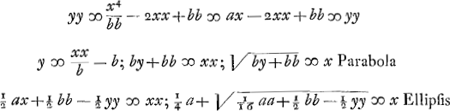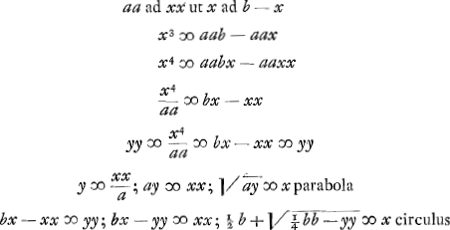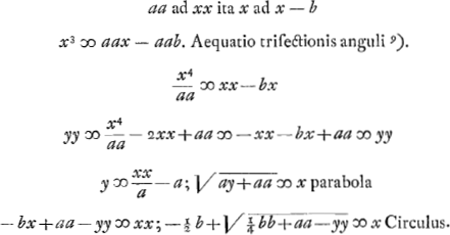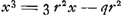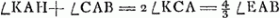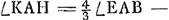
[Fig. 3.]
Ga naar voetnoot11)
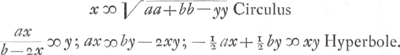
Ex his constructio oritur propositionis 13 Slusij. qua trisecat angulum per hyperbolam.
|
-
voetnoot1)
- La pièce, que nous avons divisée en quatre parties, est empruntée à quelques feuilles qui ont été détachées par Huygens du livre A des Adversaria. Le revers de la dernière feuille porte la date du 28 juillet 1659; il contient des calculs que nous mentionnerons plus bas dans la note 11 de l' Appendice IV, p. 235 du Tome présent.
En composant cette pièce, Huygens s'est appliqué surtout à retrouver par l'analyse les constructions exposées par de Sluse dans la première édition de son ‘Mesolabum seu duae mediae proportionales inter datas per circulum et ellipsim vel hyperbolam infinitis modis exhibitae. Accedit problematum quorumlibet solidorum effectio per easdem curvas, ijsdem modis & appendix de eorum solutione per circulum et parabolam. Leodij Eburorum. Typis I.F. van Milst. CIƆ IƆC LIX″. in 4o. Voir sur cette édition la note 65, p. 105 du Tome présent.
-
voetnoot2)
- Il s'agit de la construction, à l'aide du cercle et de la parabole, donnée par Descartes au Livre III de sa ‘Géométrie’ (p. 469-470 du T. VI de l'édition d'Adam et Tannery) sous le titre ‘L'inuention de deux moyenes proportionelles.’ En effet, on vérifie aisément que la construction amenée par les formules du texte est identique avec celle de Descartes. Après ce premier succès de la méthode analytique qu'il vient de découvrir, Huygens procède à en chercher de nouvelles applications.
-
voetnoot3)
- Probablement Huygens préfère cette construction à la précédente à cause de la relation entre l'axe et le paramètre de l'ellipse; ce qui permettrait d'exécuter toutes les constructions de moyennes proportionnelles à l'aide d'une seule ellipse construite d'avance, c'est-à-dire, en se servant de l'artifice mentionné dans la note 2, p. 217 du Tome présent.
-
voetnoot4)
- Voir plus loin, à la page présente, après le ‘modus 7’. Il s'agit des ‘modus 4 et modus 6’.
-
voetnoot5)
- Voici comment: Les paraboles des modes 4 et 6 sont égaux, mais leurs sommets se trouvent sur l'axe des y à des distances inégales b et ½ b de l'origine des coordonnées. Si donc on fait subir la première parabole avec le cercle qui la coupe une translation ½ b dans la direction de l'axe des y, elle couvrira la seconde parabole et le point d'intersection avec le cercle tombera nécessairement sur celui de la seconde parabole avec l'ellipse, puisque ces points doivent avoir la même distance à l'axe des y, laquelle distance est égale à la moyenne cherchée. On peut donc supprimer la parabole et déterminer ce point d'intersection à l'aide de l'ellipse et du cercle, pourvu que le centre du cercle du mode 4 soit déplacé sur une distance ½ b; ce qui amène facilement la construction du texte. Toutefois Huygens n'est pas encore satisfait, puisque la ‘Propositio Prima’ de de Sluse apprend de construire la moyenne cherchée à l'aide d'un cercle et d'une ellipse ‘infinitis modis’, c'est-à-dirè à l'aide d'une infinité d'ellipses différentes. C'est pourquoi il procéde au mode 8, ou une constante arbitraire est introduite.
-
voetnoot6)
- La ‘Propositio prima’ citée dans la note précédente, qu'on trouve à la page 3 de la première et de la seconde édition du ‘Mesolabum’. On l'obtient en effet par l'artifice même exposé dans la note précédente, en observant que la parabole du ‘modus 8’ est égale, cette fois, à celle du mode 1.
-
voetnoot7)
- Dans sa ‘Propositio septima’ (p. 27 de la première, p. 22 de la seconde édition du ‘Mesolabum’) de Sluse résolut ce problème à l'aide du cercle et d'une ellipse ‘infinitis modis’. Huygens se propose de retrouver cette solution. A cet effet il commence à chercher une solution à l'aide du cercle et de la parabole; ensuite une autre par une parabole du même paramètre et d'une ellipse de figure quelconque. Après cela il supprime la parabole et il obtient la solution désirée.
-
voetnoot8)
- Dans cette troisième partie il s'agit de la ‘Propositio undecima’ (p. 39 de la première, 31 de la seconde édition) de de Sluse, laquelle est comme il suit: ‘Datis duabis rectis P, & Q, invenire tertiam ut X, ad cujus quadratum, quadratum datae P eandem habeat rationem, quae est ipsius X, ad excessum X, supra Q.’ Ici encore le mème artifice va conduire Huygens à la solution de de Sluse.
-
voetnoot9)
- Soit r le rayon du cercle, q la corde de l'arc de l'angle donné, x celle de la troisième partie de cet arc, alors:
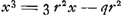 . Comparez le livre III de la ‘Geométrie’ de Descartes, à l'article: ‘La façon de diviser un angle en trois’ (T. VI, p. 470 de l'édition d'Adam et Tannery). . Comparez le livre III de la ‘Geométrie’ de Descartes, à l'article: ‘La façon de diviser un angle en trois’ (T. VI, p. 470 de l'édition d'Adam et Tannery).
-
voetnoot10)
- Dans cette partie Huygens retrouve la trisection de l'angle, telle qu'elle sut exécutée à l'aide de l'intersection d'un cercle avec une hyperbole équilatère dans la 13e proposition de de Sluse, p. 45 de la première, p. 36 de la seconde édition du ‘Mesolabum’.
-
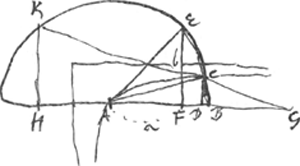
voetnoot11)
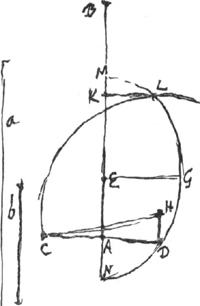
- La figure, avec omission de plusieurs lignes, est empruntée par Huygens à celle de de Sluse. On y a DG = AD; donc ∠KCA = 2∠CAB = ⅔∠EAB. De même
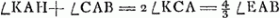 donc encore donc encore 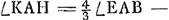 et par conséquent KH = EF = b. et par conséquent KH = EF = b.
|
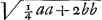 ; l. [atus] r. [ectus]
; l. [atus] r. [ectus] 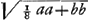 ; l. tr.
; l. tr. 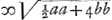 recti scilicit duplum.
recti scilicit duplum.
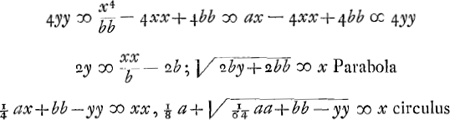
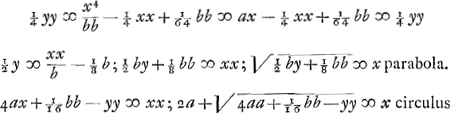
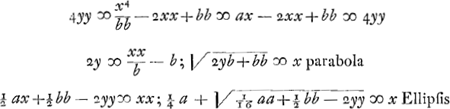
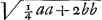 ;
; 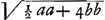 l. r.;
l. r.; 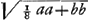 l. tr.
l. tr.