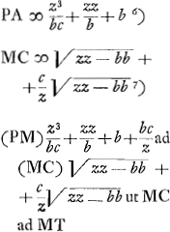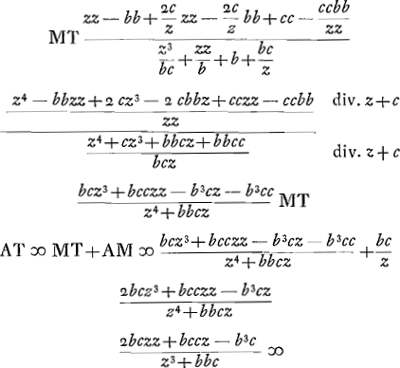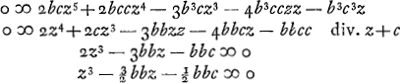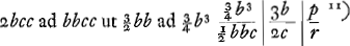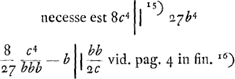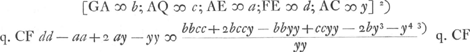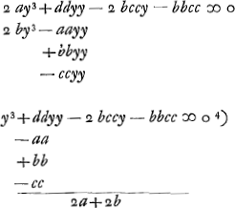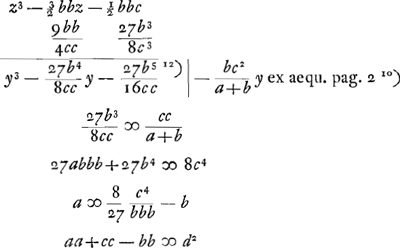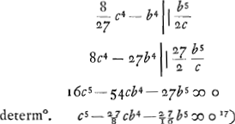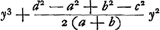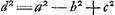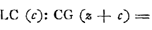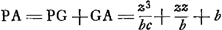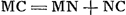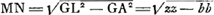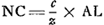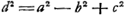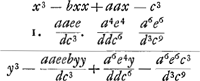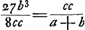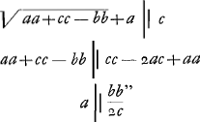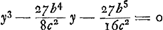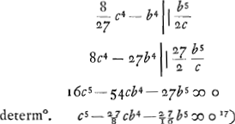
Ga naar voetnoot17)
bona est constro. cum b ad c ut 2 ad 3, non autem cum ut 20 ad 29Ga naar voetnoot18).
|
-
voetnoot1)
- Cet appendice a été emprunté aux pages 123-131 du livre A des ‘Adversaria’. Il contient la solution d'août 1659 du problème ‘In conchoide linea invenire confinia flexus contrarii.’ Voir, pour l'historique de cette solution, l'Avertissement à la page 110-111.
-
voetnoot3)
- Cette seconde valeur de CF2 découle des propriétés de la conchoïde. On la retrouve p. 83 du Tome présent. Elle est égalée à la première pour trouver l'équation cubique qui donne les intersections de la conchoïde avec un cercle ayant E pour centre.
-
voetnoot4)
- Cette équation cubique:
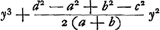 sera comparée plus loin avec celle qui détermine le point d'inflexion de la conchoïde. Remarquons tout de suite qu'on en peut faire disparaître le second terme en posant
sera comparée plus loin avec celle qui détermine le point d'inflexion de la conchoïde. Remarquons tout de suite qu'on en peut faire disparaître le second terme en posant 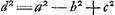 ; substituant ensuite y = kx, on peut identifier, par un choix convenable de k et de a. l'équation obtenue avec une équation cubique quelconque sans second terme. On peut donc à l'aide des intersections d'un cercle et d'une conchoïde donnée d'avance, résoudre chaque problème menant à une équation cubique; pourvu seulement que la valeur obtenue de a satisfasse à l'inégalité a2 + c2 > b2, ce qui n'est pas toujours le cas, et que de plus le cercle, qu'on obtient, coupe réellement la conchoïde donnée. Comparez la note 16 de la pièce présente et la note 10 p. 86 du Tome présent. ; substituant ensuite y = kx, on peut identifier, par un choix convenable de k et de a. l'équation obtenue avec une équation cubique quelconque sans second terme. On peut donc à l'aide des intersections d'un cercle et d'une conchoïde donnée d'avance, résoudre chaque problème menant à une équation cubique; pourvu seulement que la valeur obtenue de a satisfasse à l'inégalité a2 + c2 > b2, ce qui n'est pas toujours le cas, et que de plus le cercle, qu'on obtient, coupe réellement la conchoïde donnée. Comparez la note 16 de la pièce présente et la note 10 p. 86 du Tome présent.
-
voetnoot5)
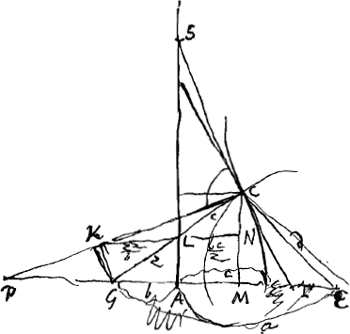
- Ces notations, que nous avons ajoutées, correspondent avec celles de la figure précédente. Dans ce qui suit Huygens va calculer la valeur de AT, laquelle, au point d'inflexion, doit être maximale, CT étant la tangente de la conchoïde au point C.
-
voetnoot6)
- La normale PC à la conchoïde est supposée avoir été construite d'après la manière qu'on trouvera décrite plus loin dans les ‘Contributions aux commentaires de van Schooten sur la Geometria Renati Dercartes’; c'est-à-dire le point K a été trouvé en tirant LK paralléle à PA et GK perpendiculaire à GC. On a donc, è cause de la similitude des triangles LNC et LGK, LN (bc/z): LC (c) = LG (z): LK (zz/b) et ensuite
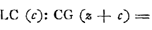 ; donc ; donc 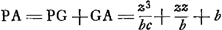 . .
-
voetnoot7)
- Puisqu'on a
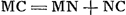 où où 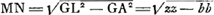 et et 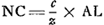 par similitude de triangles. par similitude de triangles.
-
voetnoot8)
- Il s'agit de la règle publiée dans l'ouvrage: ‘Demonstratio regulae de maximis & minimis’ (voir T. IX, p. 95, note 1) pour trouver le maximum ou le minimum d'une fraction. En effet, cette règle appliquée à la dernière expression pour AT amène immédiatement l'equation qui va suivre.
-
voetnoot9)
- En effet, cette équation en z = GL est plus simple que celle en q = GM de la pièce No. XX des ‘Travaux’ de 1652 et 1653 (p. 84 du Tome présent). Consultez encore la note 5 de la même pièce No. XX.
-
voetnoot11)
- Pour arriver à la construction désirée à l'aide de la conchoïde donnée et du cercle, il suffirait d'identifier l'équation cubique en z avec celle en y de la note 4, privée du second membre, en posant
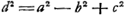 . Or, cela est impossible, puisque le rapport du troisième au quatrième terme diffère dans les deux équations. On doit donc auparavant appliquer à l'equation en z la methode enseignée par Descartes au Livre III de la ‘Geometrie’ (p. 452 du T. VI de l'édition d' Adam et Tannery) pour ‘multiplier ou diuiser les racines sans les connoistre’. De cette manière le rapport des deux derniers termes doit être changé dans la raison de ¾b3 à ½ bbc, ou de 3b à 2c; ce que Huygens achève par l'algorithme même donné par Descartes au lieu cité. . Or, cela est impossible, puisque le rapport du troisième au quatrième terme diffère dans les deux équations. On doit donc auparavant appliquer à l'equation en z la methode enseignée par Descartes au Livre III de la ‘Geometrie’ (p. 452 du T. VI de l'édition d' Adam et Tannery) pour ‘multiplier ou diuiser les racines sans les connoistre’. De cette manière le rapport des deux derniers termes doit être changé dans la raison de ¾b3 à ½ bbc, ou de 3b à 2c; ce que Huygens achève par l'algorithme même donné par Descartes au lieu cité.
Ajoutons que sur une feuille détachée, datée du ‘28 Jul. 1659’ (voir la note 1, p. 225 du Tome présent), Huygens a exposé la méthode qu'il a appliquée ici; on y lit:
‘x3 - bxx + aax - c3 ∞ 0 Aequatio data. Volo autem habere aliam similem, cujus radix ad radicem hujus habeat rationem cognitam in qua quantitas 3ij termini sit ad quantitatem 4ti termini in data ratione d ad ee.’
A cet effet, appliquant l'algorithme de Descartes, il écrit l'équation désirée: y3 - bryy/p + aarry/pp - c3r3/p3; puis il calcule r/p à l'aide de la proportion aarr/pp : c3r3/p3 = d:ee et il fait suivre:
‘Ergo loco aequationis prioris x3 - bxx + aax - c3 ponenda est alia cujus radix y ∞ rx/p hoc est aaee/dc3 x. Obtinebitur autem talis aequatio si multiplicemus hoc modo.
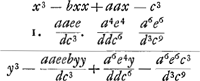 hi jam duo posteriores sunt inter se ut d ad ee ut facile apparet’.
hi jam duo posteriores sunt inter se ut d ad ee ut facile apparet’.
Après quoi il ajoute:
In constructionibus solidorum problematum magni usus.
-
voetnoot12)
- L'équation en y, obtenue par le procédé que nous venons d'indiquer, peut être identifiée maintenant à celle de la note 4. A cet effet Huygens égale les coëfficients des termes en y; l'égalisation des termes constants aurait d'ailleurs amené nécessairement la même relation
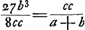 . .
-
voetnoot13)
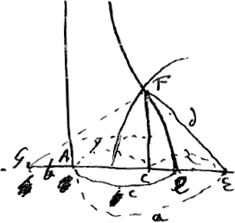
- En effet, pour trouver y, on n'a plus qu'à construire a et d d'après les formules du texte; à prendre ensuite (voir la figure 1) AE = a, à construire le cercle qui a E pour centre et d pour rayon et enfin à abaisser du point d'intersection F avec la conchoïde la perpendiculaire FC. Alors AC = y.
-
voetnoot14)
- Comparez la note 11. Il est clair qu'après cela la construction est facile à achever. On en trouve un résumé aux p. 200-201 du T. IX. Après avoir construit y = AC (fig. 1), comme nous l'avons dit dans la note 13, on n'a qu'à prendre GL (fig. 2) égal à z = 2cy/3b, ou bien GC à (z + c). Dans ce dernier cas on a encore à déterminer l'intersection de la conchoïde donnée avec un cercle ayant G pour centre et GC pour rayon. C'est la voie suivie dans le résumé mentionné qui fut envoyé le 27 août 1687 à Mr. H. Coets.
-
voetnoot15)
- Signe pour indiquer que 8c4 est plus grand que 27b4. Dans le cas contraire on obtiendra pour a = AE (fig. 1) une valeur négative; ce qui en vérité n'importe guère. Plus tard Huygens a ajouté à ce propos: ‘videndum cum centrum E circuli est ex altera parte A, qualis tunc futura sit haec aequatio. 1680’ Il s'agit de l'équation de la note 4.
-
voetnoot16)
- Voici ce qu'on trouve au lieu cité: ‘bona est constr. cum d radius potest secare conchoidem, hoc est cum d + a major quam c.
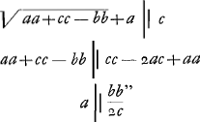
Cette condition est donc bien plus importante que la précédente, puisqu'elle décide sur la réalité du point d'intersection F (fig. 1). Au cas où a > c, la condition a + d > c est remplacée par a - d < c; mais les deux conditions peuvent être exprimées ensemble par (a - c)2 < d2, ce qui mène à la relation c5 - 27/8 cb4 - 27/16 b5 > o, ou bien, posant b = kc, 16 - 27 k4 (k + 2) > o, ce qui exige k < o, 685...
On voit dès l'abord que cette condition est suffisante et on reconnaît facilement qu'elle est de même nécessaire, en remarquant que la relation c5 - 27/8 cb4 - 27/16 b5 > 0 exprime que la seule racine positive de l'équation 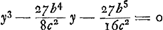 est inférieure à c; voir encore la note 4, p. 202 du T. IX, où la même relation est déduite de cette manière. est inférieure à c; voir encore la note 4, p. 202 du T. IX, où la même relation est déduite de cette manière.
-
voetnoot17)
- Lisez plutôt: c5 - 27/8 cb4 - 27/16 b5 > 0.
-
voetnoot18)
- Au premier cas k = 2/3 = 0,666... < 0,685...; au second k = 20/29 = 0,689... > 0,685...
|