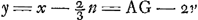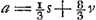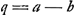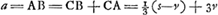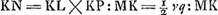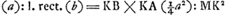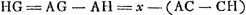Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656
(1910)–Christiaan Huygens–
[pagina 217]
| |
Appendice IGa naar voetnoot1)
| |
[pagina 218]
| |
[pagina 219]
| |
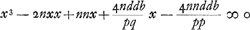 Ga naar voetnoot6). rejicitur secundus terminus ponendo x - ⅔n ∞ y 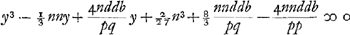 ut eliminetur terminus sub y sit 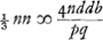 . .
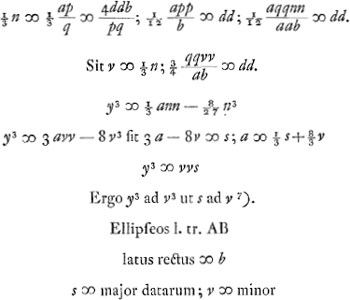 oportet inter ipsas invenire duas medias proportionales 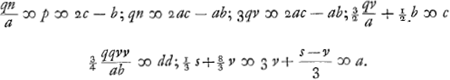 | |
[pagina 220]
| |
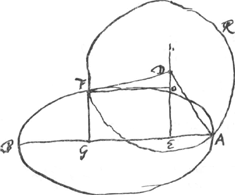
Constructio universalis data qualibet Ellipsi [Fig. 2]. 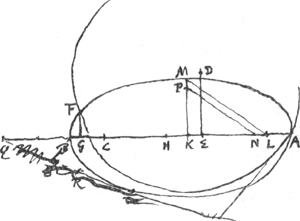 [Fig. 2.]
HQ ∞ s. HC ∞ v. CB ∞ ∞ ⅓ CQ. CA ∞ 3v ∞ 3 CHGa naar voetnoot8). AL ∞ ½ b. BK ∞ KA. Ergo KL ∞ ½ q. BA ad AC ut KL ad LE ∞ 3/2 qv/a. KP ∞ ∞ HC ∞ v. PN parall. ML. 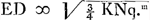 .
Ga naar voetnoot9) .
Ga naar voetnoot9)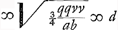 . .
D est centr. circuli AF. FG perp. BA. HG est minor duarum mediarum ∞ yGa naar voetnoot10). | |
[Seconde partie].Si ponatur b ∞ ⅓ a Erit q ∞ ⅔a. Quia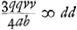 ; ; 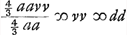 ; v ∞ d. Et quia 3/2 qv/a + ½ b ∞ c erit v + ½ b ∞ c; v + ⅙ a ∞ c. ; v ∞ d. Et quia 3/2 qv/a + ½ b ∞ c erit v + ½ b ∞ c; v + ⅙ a ∞ c.
Ergo in Ellipsi cujus latus transversum triplum est lateris recti. Sumitur AL ∞ ∞ ⅙ ABGa naar voetnoot11). LE ∞ v ∞ HC. (nam sic fit AE ∞ v + ⅙ a ∞ c). Et ED ∞ ∞ EL ∞ vGa naar voetnoot12). | |
[pagina 221]
| |
Data autem certa primum Ellipsi et dein duabus quibusvis rectis RS, RT
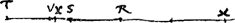 [Fig. 3].
[Fig. 3], inter quas duae mediae sint reperiendae. Oportet sumere SV ∞ ⅓ differentiae ST. Et RX ∞ 2 SR. Tum BA diameter secunda [Fig. 2] est proportionaliter in C et H sicut VX [Fig. 3] in S et R secta est. unde etiam inventâ mediâ HG [Fig. 2] oportet facere sicut HC ad HG ita RS [Fig. 3] ad RY. Eritque RY minor mediarum inter RS, RT. Et hoc ad utramque constructionem pertinetGa naar voetnoot13). |
|