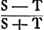Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 182]

Christiaan Huygens, fils de Constantin.
Constructions de certains problèmes célèbres.

Probl. I.

Couper une sphère donnée par un plan de manière que les segments soient entre eux dans un rapport donné¹⁾.

Archimède a résolu ce problème dans le livre 2 de son traité de la Sphère et du Cylindre²⁾. Mais il semble qu'il n'a pas exposé la construction qu'il avait promise, à moins que ne soit de lui celle qu' Eutocius inséra dans ses Commentaires, l'ayant trouvée dans un livre très vieux³⁾. Or, elle y est effectuée par l'intersection d'une parabole et d'une hyperbole comme celle dont Dionysidore est l'auteur⁴⁾, laquelle cependant diffère de la précédente. Outre celles-là Eutocius donne encore une troisième⁵⁾, tirée du livre de Dioclès sur les Miroirs ardents, laquelle demande le tracé d'une hyperbole et d'une ellipse. Quant à la nôtre, que nous décrirons ici, elle exige la trisection de l'angle; et cette façon de construire paraît pour les problèmes solides en quelque sorte la plus simple, et la plus appropriée à l'usage.

Soit donc donnée une sphère [Fig. 1] dont le centre est M, le diamètre CA. Et soit donné le rapport de la ligne S à T, d'une plus grande à une plus petite. Que l'on se figure la sphère coupée par un plan suivant le diamètre AC et soit CBAD le cercle le plus grand dans cette sphère. Et que l'on prolonge des deux côtés le diamètre CA et que chacun des deux prolongements CH et AE soit égal au demidiamètre. Et que l'on divise toute la droite HE au point Q, de façon que EQ soit à QH comme S à T. Que l'on place maintenant contre la circonférence la droite

1) Consultez, sur l'historique de ce problème, la page 102 de l'‘Avertissement’. La solution qui va suivre se retrouve dans une forme modifiée aux p. 16-18 du Tome présent sous la date du 31 janvier 1652.

2) Voir la note 3, p. 3 du Tome présent.

3) Consultez les notes 16 et 17, p. 12 du Tome présent.

4) Voir p. 37-38 du texte Latin des ‘Commentarii Eutocii’ de l'édition de Bâle, citée note 3, p. 274 du T. XI, (Heiberg, III, p. 181-188).

5) Voir p. 38-42 de l'édition de Bâle, (Heiberg, III, p. 189-209).

[p. 183]

Christiani Hugenii C.F.
Illvstrivm qvorvndam problematvm constrvctiones.

Probl. I.

Datam sphaeram plano secare, ut portiones inter se rationem habeant datam¹⁾.

Hoc Archimedes problema resolvit lib. 2. de Sphaera & Cylind.²⁾ Compositionem autem promissam non videtur explicuisse, nisi ipsius est illa quam Eutocius in vetusto quodam libro repertam commentariis suis inseruit³⁾. Ea verò paraboles & hyperboles intersectione perficitur, uti & illa cujus Dionysidorus autor est⁴⁾, quae tamen à priori differt. Praeter has tertiam quoque adfert Eutocius⁵⁾ è Dioclis de Pyriis libro, quae hyperboles & ellipsis descripcionem requirit. Nostra autem quam hic conscribemus anguli trisectionem postulat; Et haec construendi ratio in solidis problematibus quodammodo simplicissima videtur, atque ad usum maximè accommodata.

Esto igitur data sphaera [Fig. 1] cujus centrum M, diameter CA. Et data sit proportio lineae S ad T majoris ad minorem. Intelligatur secari sphaera plano secundum AC diametrum, sitque maximus in ea circulus CBAD. Et producatur utrimque diameter CA, & ponatur semidiametro aequalis utraque harum CH, AE. Et dividatur tota HE in Q, ut sit EQ ad QH sicut S ad T. Ipsi autem MQ aequalis

1) Consultez, sur l'historique de ce problème, la page 102 de l'‘Avertissement’. La solution qui va suivre se retrouve dans une forme modifiée aux p. 16-18 du Tome présent sous la date du 31 janvier 1652.

2) Voir la note 3, p. 3 du Tome présent.

3) Consultez les notes 16 et 17, p. 12 du Tome présent.

4) Voir p. 37-38 du texte Latin des ‘Commentarii Eutocii’ de l'édition de Bâle, citée note 3, p. 274 du T. XI, (Heiberg, III, p. 181-188).

5) Voir p. 38-42 de l'édition de Bâle, (Heiberg, III, p. 189-209).

[p. 184]

AR, égale à la droite MQ. Et que l'on prenne MN égale à celle qui sous-tend la troisième partie de l'arc AR. Ensin que par le point N on méne le plan KL qui soit à angles droits sur le diamètre CA. Je dis que ce plan coupe la sphère de telle maniére, que le segment dont A est le sommet est à celui dont le sommet est C dans le rapport de S à T⁶⁾.

En effet, coupons la sphère par un plan BD passant par le centre M et parallèle à KL, et joignons KM, ML; et imaginons un cône ayant comme base le cercle formé par la section KL, mais dont le sommet est en M. Comme le carré CM au carré MN, de même soit MN à NO, quant à la longueur. On aura donc, par conversion des rapports, que le carré CM, ou le carré KM, est au carré KN (car le carré KN est l'excès du carré KM sur le carré MN) comme la droite NM est à MO. Or, comme le carré KM, c'est-à-dire le carré BM, au carré KN, ainsi le cercle autour du diamètre BD est à celui décrit autour du diamétre KL. Donc aussi ce cercle la sera à celui-ci comme NM à MO. Et par conséquent le cône KML sera égal à celui dont la base est le cercle autour du diamètre BD, mais dont la hauteur est MO^*. Mais ce cône est à l'hémisphère BCD, c'est-à-dire au cône qui a comme base le même cercle autour du diamètre BD, et comme hauteur MH^*, dans le même rapport que MO à MH. Donc aussi le cône KML sera à l'hémisphère BCD comme MO à MH. Et inversement.

Mais ensuite, puisque l'hémisphère BCD est au secteur solide MKCL comme la superficie sphérique de celle-là est la superficie sphérique de celui-ci^*, c'est-à-dire comme MC à CN^†, par conversion des rapports, l'hémisphère BCD sera à la partie qui en reste après enlèvement du secteur MKCL, comme CM à MN: ou bien, après en avoir pris les doubles, comme HM à OQ. Car que OQ est le double de MN, c'est ce que nous montrerons plus tard. Mais on a démontré que l'hémisphère BCD est au cône KML comme HM à MO. Donc déjà l'hémisphère BCD sera à toute la partie comprise entre les plans BD, KL comme HM aux droites QO, OM ensemble^*, c'est-à-dire à MQ. C'est pourquoi, par conversion des rapports, l'hémisphère BCD sera au segment KCL, comme MH à HQ. Et si l'on prend les doubles des antécédents, la sphère toute

6) La construction exposée est sans doute une modification de celle qui fut communiquée le 9 aôut 1653 à Kinner à Löwenthurn, laquelle elle-même ne diffère pas essentiellement de celle inventée le 31 janvier 1652 (voir la note 1).
Consultez là-dessus la note 4, p, 16 du Tome présent. Ici encore il est facile de montrer que la corde, dont l'arc est divisé en trois parties égales, aura la longueur AC.

* 15.12. Élém.⁷⁾

7) Voir la note 10, p. 11 du Tome présent.

* 32.1. Archim. du Sphère et du Cyl.⁸⁾

8) Voir la note 7, p. 17 du Tome présent.

* 42. 1. Arch. du Sphèreet du Cyl.⁹⁾

9) Voir la note 11, p. 11 du Tome présent.

† 3. 2. Arch. du Sphère et du Cyl.¹⁰⁾

10) Voir la note 9, p. 17 du Tome présent.

* 24,5. Élém.¹¹⁾

11) Voir la note 28, p. 312 du Tome XI et de même la note 13, p. 11 et 12 du Tome présent.

[p. 185]

ponatur ad circumferentiam recta AR. Et ei quae tertiam partem subtendit arcus AR, aequalis sumatur MN. Et per N punctum ducatur planum KL quod diametro

[Fig. 1.]

CA sit ad angulos rectos. Dico hoc sphaeram sic secare, ut portio cujus A vertex est ad eam cujus vertex Crationem habeat quam S ad T⁶⁾.

Secetur enim sphaera per centrum M plano BD ipsi KL parallelo, & jungantur KM, ML; & intelligatur conus basin habens circulum factum sectione KL, verticem vero M. Et sicut quadratum CM ad quadratum MN, ita sit MN ad NO longitudine. Erit igitur per conversionem rationis ut quadratum CM sive quadr. KM ad quadratum KN (est enim quadr. KN excessus quadrati KM supra quadr. MN) ita linea NM ad MO. Sicut autem quadr. KM, hoc est, quadr. BM ad quadr. KN, ita est circulus circa diametrum BD ad eum qui circa diametrum KL. Ergo quoque ille circulus ad hunc sese habebit ut NM ad MO. Ac proinde conus KML aequalis erit cono cujus basis circulus circa diametrum BD, altitudo MO^*. Hic autem conus ad hemisphaeram BCD, hoc est, ad conum qui basin habeat eundem circulum circa BD diametrum, & altitudinem MH^*, eam habet rationem quam MO ad MH. Itaque & conus KML erit ad hemisphaeram BCD sicut MO ad MH. Et invertendo.

Porro autem quoniam hemisphaera BCD est ad sectorem solidum MKCL sicut superficies illius sphaerica ad sphaericam hujus superficiem^*, hoc est, ut MC ad CN^†. Erit per conversionem rationis hemisphaera BCD ad partem sui quae remanet dempto sectore MKCL, sicut CM ad MN: vel sumptis horum duplis ut HM ad OQ. Quod enim OQ dupla sit ipsius MN postea ostendemus. Fuit autem ostensum, quod hemisphaera BCD ad conum KML sicut HM ad MO. Ergo jam hemisphaera BCD ad totam portionem inter plana BD, KL contentam erit ut HM ad utramque simul QO, OM^*, hoc est, ad MQ. Quare & per conversionem rationis, erit hemisphaera BCD ad portionem KCL, ut MH ad HQ. Et sumptis

6) La construction exposée est sans doute une modification de celle qui fut communiquée le 9 aôut 1653 à Kinner à Löwenthurn, laquelle elle-même ne diffère pas essentiellement de celle inventée le 31 janvier 1652 (voir la note 1).
Consultez là-dessus la note 4, p, 16 du Tome présent. Ici encore il est facile de montrer que la corde, dont l'arc est divisé en trois parties égales, aura la longueur AC.

* 15.12. Elem.⁷⁾

7) Voir la note 10, p. 11 du Tome présent.

* 32. 1. Archim. de Sphaer. & Cylin.⁸⁾

8) Voir la note 7, p. 17 du Tome présent.

* 42. 1. Archim. de Sphaer. & Cyl.⁹⁾

9) Voir la note 11, p. 11 du Tome présent.

† 3. 2. Archim. de Sphaer. & Cyl.¹⁰⁾

10) Voir la note 9, p. 17 du Tome présent.

* 24. 5. Elem.¹¹⁾

11) Voir la note 28, p. 312 du Tome XI et de même la note 13, p. 11 et 12 du Tome présent.

[p. 186]

entière est au segment KCL comme EH à HQ. Et par partage, le segment KAL est au segment KCL comme EQ à QH, c'est-à-dire comme S à T. Ce qui était à faire. Quant à ce qui a été dit, que OQ est le doublé de MN, voici comment on le prouve. Puisque comme le carré CM au carré MN ainsi MN est à NO en longueur, et que QM est égal à la corde de l'arc AR dont le tiers est sous-tendu par MN, pour cette raison les deux droites QM et NO ensemble seront égales au triple de MN, ainsi que cela se démontre par le lemme suivant. Et par conséquent la portion commune ON étant enlevée, la droite QM seule sera égale au double de NM avec MO. Mais cette même droite QM est égale aux deux droites QO, OM ensemble, donc il ressort que le double de MN est égal à la droite OQ.

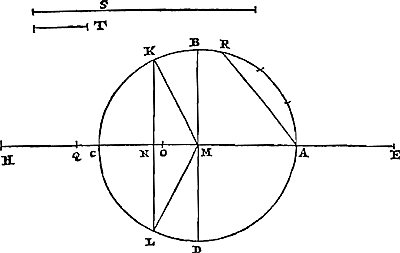
Lemme.

Lorsqu'un arc de circonférence est coupé en trois parties égales, l'ensemble des trois droites qui sont sous-tendues aux parties égales est égal à la sous-tendue de l'arc entier avec une droite qui est à la sous-tendue du tiers comme le carré de celle-ci au carré du demi-diamètre. Supposons que l'arc du secteur ABC soit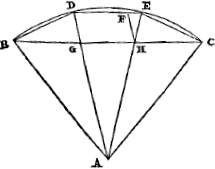

[Fig. 2.]

divisé en trois parties égales par les points D, E; et que les droites BD, DE, EC soient sous-tendues à ces parties et la droite BC à l'arc tout entier. Puis joignons DA, EA et supposons que ces droites coupent la corde BC aux points G et H. Soit ensin HF parallèle à GD.

Ainsi donc la circonférence BDE est double de la circonférence EC, mais l'angle EAC qui repose sur celle-ci est formé au centre, tandis que l'angle BCE reposant sur celle-là eft formé sur la circonférence. Pour cette raison l'angle BCE, c'est-à-dire l'angle HCE dans le triangle HCE, est égal à l'angle CAE dans le triangle CAE. Mais l'angle en E est commun à tous deux; donc les dits triangles sont semblables entr'eux; et comme AE à EC ainsi EC sera à EH. Donc le rapport de AE à EH, c'est-à-dire de DE à EF, est la deuxième puissance du rapport de AE à EC, et par conséquent le même que celui du carré AE au carré EC ou ED. Donc, en permutant, FE sera à ED comme le carré ED est au carré EA. A cause de cela il s'agit de démontrer, que les trois droites BD, DE, EC ensemble égalent la corde BC avec ce même EF; ce qui est tout à fait manifeste, car CE est égal à CH, BD égal à BG, et DE à l'ensemble des deux droites GH et FE. Donc la proposition est établie.

[p. 187]

antecedentium duplis, sphaera tota ad portionem KCL ut EH ad HQ. Et dividendo, portio KAL ad portionem KCL ut EQ ad QH, hoc est ut S ad T. Quod

[Fig. 1.]

erat faciendum. Quod autem dictum fuit OQ duplam esse ipsius MN, sic fiet manifestum. Quia enim ut quadratum CM ad quadr. MN ita est MN ad NO longitudine: Est autem QM aequalis subtensae arcus AR cujus trienti subtenditur MN. Erunt propterea duae simul QM & NO aequales triplae MN, uti sequenti lemmate demonstratur. Quamobrem ablata communi ON, erit sola QM aequalis duplae NM & ipsi MO. Sed eadem QM aequalis est duabus simul his QO, OM, ergo apparet duplam MN aequari ipsi OQ.

Lemma.

Si Circumferentiae arcus in tria aequalia secetur, tres simul rectae quae aequalibus partibus subtenduntur, aequantur subtensae arcus totius & ei quae ad subtensam trientis sese habeat, sicut hujus quadratum ad quadratum semidiametri. Arcus sectoris ABC [Fig. 2] in tria aequalia divisus sit punctis D, E. Et subtendantur partibus rectae BD, DE, EC; & toti arcui linea BC. Porro jungantur DA, EA, atque intersecent subtensam BC in punctis G & H. Sitque HF parallela GD.

Quoniam igitur circumferentia BDE dupla est circumferentiae EC, angulus autem huic insistens EAC ad centrum constitutus, qui verò illi insistit angulus BCE ad circumferentiam. Erit propterea angulus BCE, hoc est, angulus HCE in triangulo HCE aequalis angulo CAE in triangulo CAE. Sed angulus ad E utrique est communis; itaque similes inter se sunt dicti trianguli: Eritque ut AE ad EC ita EC ad EH. Ratio igitur AE ad EH hoc est DE ad EF, duplicata est rationis AE ad EC, ac proinde eadem quae quadrati AE ad quadr. EC seu quadr. ED. Erit igitur invertendo FE ad ED sicut quadr. ED ad quadr. EA. Quamobrem ostendendum est, tres simul BD, DE, EC aequari subtensae BC atque ipsi EF. quod sane manifestum est; nam CE est aequalis CH; BD aequalis BG; DE vero utrisque simul GH, & FE. Ergo constat propositum.

[p. 188]

Nous avons supposé, il est vrai, que l'arc BC est moindre que la demi-circonférence, parce que dans la construction du problème en question cela est toujours ainsi. Mais le lemme s'applique à des arcs quelconques, et pour des arcs plus grands que la demi-circonférence la démonstration est peu différente.¹²⁾

12) Cette remarque manque dans la rédaction du 31 janvier 1652 (p. 16-18 du Tome présent), où le lemme et sa démonstration se retrouvent.

Probl. II.

Trouver un cube double d'un cube donné¹³⁾.

Pour ce problème nous proposerons d'abord une construction imparfaite, utile pour les constructions mécaniques, puis nous en fournirons une exacte, qui toutefois ne s'effectue qu'en essayant à plusieurs reprises. En effet, les problèmes solides exigent toujours ou ceci ou le tracé de sections coniques.

Soit donc donné un cube dont le côté est AB; il s'agit de trouver le côté d'un cube double.

Décrivons avec le rayon BA un demi-cercle AFC. Supposons que l'arc AF soit le tiers de la demi-circonférence, CD le quart; et menons CF, AD, dont l'intersection est au point E. AE sera le côté du cube cherché; le dépassant toutefois d'une petite quantité, qui est moindre que sa 1/2000 partie, ainsi qu'on peut l'examiner facilement par les nombres. AE est, en effet, la sécante d'un angle de 37 degrés 30 minutes, et est donc plus grande que 12600 parties dont AF ou AB en a 10000. Mais elle est moindre que 12605. Donc, comme le cube sur 12600 est plus grand que le double de celui construit sur AB 10000, le cube sur AE sera plus grand que le double du cube sur AB. D'autre part, puisque AE est plus grand que 12600 parties, 1/2000 AE sera plus grand que 6 parties. Mais toute la droite AE est plus petite que 12605. Donc, enlevant de AE la deux-millième partie d'elle-même, le reste sera plus petit que 12599 parties; car il en reste autant lorsqu'on déduit 6 de 12605. Or, le cube sur 12599 est plus petit que le double du cube sur 10000. Donc aussi à plus forte raison AE diminuée de la deux-millième partie d'elle-même donne un cube plus petit que celui qui serait le double du cube de côté AB.

Puis, pour la construction exacte, CF doit être tracée comme d'abord; mais AD de telle façon, que la sous-tendue CD soit égale à la partie découpée EF. Et ceci posé, je dis que le cube AE est double de celui formé sur AB.

Prolongeons en effet CA, et soit AG égale à AE. A cause des triangles semblables EC est donc à CD, c'est-à-dire EF, comme EA à AF, c'est-à-dire comme¹⁴⁾

13) Comparez, pour ce problème, les pages 45-48 du Tome présent où on retrouvera, sous lesdates du 1^er et du 2 mars 1652, d'abord la solution exacte dans une rédaction peu différente, puis la construction approximative avec une démonstration bien plus prolixe.

14) Dans l'exemplaire que nous possédons le mot ‘isthic’ a étè changé à la plume par Huygens en ‘hoc’.

[p. 189]

Sumpsimus autem arcum BC semicircumferentiâ minorem quoniam in constructione problematis ejusmodi semper invenitur. Nam lemma ad quosvis arcus pertinet, estque in semicircumferentiâ majoribus demonstratio parum diversa¹²⁾.

12) Cette remarque manque dans la rédaction du 31 janvier 1652 (p. 16-18 du Tome présent), où le lemme et sa démonstration se retrouvent.

Probl. II.

Cubum invenire dati cubi duplum¹³⁾.

Ad hoc imperfectam primò constructionem proponemus ad mechanicen utilem; deinde accuratam subjiciemus, quae tamen non nisi saepius tentando perficiatur. Etenim solida problemata omnia vel isthic¹⁴⁾ exigunt vel sectionum conicarum descriptionem.

Sit itaque datus cubus latus AB, oporteatque invenire latus cubi dupli.

[Fig. 3.]

Radio BA semicirculus describatur AFC. Sitque arcus AF semicircumferentiae triens, CD vero quadrans; & ducantur CF, AD, quarum intersectio ad E punctum. Erit AE latus cubi quaesiti; exiguo tamen excedens, quodque minus sit 1/2000 sui parte, ut facile numeris explorari potest. Fit enim AE secans anguli p. 37. scr. 30. quae proinde major est partibus 12600 qualium AF vel AB 10000. Minor autem quam 12605. Itaque cum cubus ex 12600 sit major quam duplus ejus qui ex AB 10000, erit & cubus AE major duplo cubo ex AB. Rursus quia AE major est partibus 12600 erit 1/2000 AE major part. 6. Tota verò AE minor est quam 12605. Ergo auferendo ab AE partem bismillesimam sui ipsius reliqua minor erit partibus 12599, tot enim supersunt cum ex 12605 deducuntur 6. Atqui cubus ex 12599 minor est duplo cubo ex 10000. Ergo omnino quoque AE diminuta parte sui bismillesima cubum minorem producet quam sit duplus cubus à latere AB.

Porrò ad perfectam constructionem, CF quidem uti priùs ducenda est: AD verò sic, ut subtensa CD aequalis sit abscissae EF. Etenim his positis dico cubum AE ejus qui ex AB duplum existere.

Producatur enim CA, & sit ipsi AE aequalis AG. Propter triangulos similes igitur est EC ad CD, hoc est, EF ut EA ad AF, hoc est, ut GA ad AB. Et

13) Comparez, pour ce problème, les pages 45-48 du Tome présent où on retrouvera, sous lesdates du 1^er et du 2 mars 1652, d'abord la solution exacte dans une rédaction peu différente, puis la construction approximative avec une démonstration bien plus prolixe.

14) Dans l'exemplaire que nous possédons le mot ‘isthic’ a étè changé à la plume par Huygens en ‘hoc’.

[p. 190]

GA à AB. Et par composition, CF est à FE comme GB à BA ou AF. Puis, permutant, CF est à GB comme EF à FA. Par conséquent, comme le carré CF est au carré GB, ainsi le carré EF au carré FA. Et par composition, comme les carrés CF et GB ensemble sont au carré GB, ainsi l'ensemble des carrés EF et FA, c'est-à-dire le carré EA au carré AF. Mais les carrés CF et GB valent ensemble le rectangle GCA avec le carré AG, ce qui se démontre ainsi. Le carré GB est égal au rectangle CGA augmenté du carré AB ou AF^*. Donc, ajoutant de part et d'autre le carré FC, les carrés GB et FC pris ensemble seront égaux au rectangle CGA plus le carré AC. Or, le rectangle CGA avec le carré AC équivant au rectangle GCA avec le carré GA. Donc aussi les carrés CF et GB équivaudront ensemble au rectangle GCA avec le carré AG, comme nous l'avons dit. Donc, comme le rectangle GCA avec le carré AG au carré GB, ainsi le carré EA est au carré AF, c'est-à-dire ainsi le carré GA au carré AB. Et permutant, comme le rectangle GCA avec le carré GA au carré GA, ainsi le carré GB est au carré AB. Donc, par partage, comme le rectangle GCA est au carré GA, ainsi le carré GB diminué du carré AB, c'est-à-dire le rectangle CGA, sera au carré AB. Et permutant de nouveau, comme le rectangle GCA est au rectangle CGA, c'est-à-dire comme CA à AG, ainsi le carré GA est au carré AB. Pour cette raison, ce qu'on obtient du carré GA avec la même droite GA, c'est-à-dire le cube GA, sera égal à ce qu'on obtient du carré AB avec AC; c'est-à-dire au double du cube de AB. Ce qu'il fallait démontrer¹⁶⁾.

* 6.2. Élém.¹⁵⁾

15) Voir, sur cette proposition, la note 2, p. 46 du Tome présent.

16) On peut consulter encore sur cette démonstration la note 3, p. 46 du Tome présent.

Probl. III.

Trouver deux moyennes proportionnelles à deux droites données¹⁷⁾.

Pour ce problème Eutocius a noté plusieurs constructions des vieux géomètres dans ses commentaires sur le livre 2 d'Archimède sur la Sphère et le Cylindre¹⁸⁾; mais elles ne sont pas toutes d'invention différente, ainsi qu'il l'a lui-même justement remarqué. Car Apollonius et Philon le Byzantin²⁰⁾ paraissent avoir suivi l'invention d'Héron¹⁹⁾, bien que quelques-uns jugent que Héron est postérieur à Apollonius²¹⁾. Pappus et Sporus ont suivi la méthode de Dioclès²²⁾. On trouve au

17) Voir, sur l'historique de ce problème, les p. 103-106 de l'‘Avertissement’.

18) Voir les Commentaires d'Eutocius, aux p. 14-27 de l'édition de Bâle (Heiberg, III, p. 66-127).

20) Voir, sur ces constructions, les p. 16-17 de l'édition de Bâle (Heiberg, III, p. 72-79). L'identité essentielle des trois constructions fut déjà constatée par Eutocius.

19) Voir, sur la construction de Héron, les p. 15-16 de l'édition de Bâle (Heiberg, III, p. 70-73) et consulter encore la note 10, p. 40 du Tome présent.

21) La question de déterminer l'époque où vivait Héron a beaucoup occupé les savants jusque dans notre temps. On peut consulter à ce propos le Chap. XVIII du T. I de l'ouvrage bienconnu de Cantor ‘Vorlesungen über Geschichte der Mathematik’ qui place Héron dans le premier siècle avant J.C., c'est-à-dire après Philon de Byzance et plus d'un siècle entier après Apollonius.

22) Voir, sur ces constructions, les p. 17-20 de l'édition de Bâle (Heiberg, III, p. 78-93). Dioclès fait emploi de sa cissoïde; les autres constructions se réduisent aisément a celle de Dioclès, comme Eutocius l'a déjà remarqué.

[p. 191]

componendo CF ad FE ut GB ad BA sive AF. Et permutando CF ad GB ut EF ad FA. Quare ut CF quadratum ad quadr. GB, ita quadr. EF ad quadr. FA. Et componendo ut quadr. CF & GB ad quadr. GB, ita quadr. EF & FA simul, hoc est, quadr. EA ad quadr. AF. Quadr. autem CF & GB simul aequantur rectangulo GCA cum quadr. AG, quod sic ostenditur. Quadratum enim GB aequale

[Fig. 3.]

est rectangulo CGA & quadrato AB seu AF^*. Quare addito utrimque quadrato FC, erunt quadrata GB, FC simul aequalia rectangulo CGA & quadrato AC. Rectangulum autem CGA cum quadrato AC aequatur rectangulo GCA cum quadrato GA. Itaque & quadrata CF, GB simul aequalia sunt rectangulo GCA cum quadrato AG, sicut diximus. Sicut igitur rectangulum GCA cum quadrato AG ad quadr. GB, ita est quadr. EA ad quadr. AF, hoc est, ita quadratum GA ad quadr. AB. Et permutando, ut rectangulum GCA cum quadrato GA ad quadratum GA ita quadr. GB ad quadr. AB. Dividendo igitur, erit ut rectang. GCA ad quadr. GA, ita quadr. GB dempto quadrato AB, hoc est, rectangulum CGA ad quadr. AB. Et permutando rursus, ut rectang. GCA ad rectang. CGA, hoc est, ut CA ad AG ita quadratum GA ad quadr. AB. Quamobrem quod fit ex quadrato GA in ipsam GA, hoc est, cubus GA aequabitur ei quod fit ex quadrato AB in AC, hoc est, duplo cubo ex AB. Quod erat demonstrandum¹⁶⁾.

* 6. 2. Elem.¹⁵⁾

15) Voir, sur cette proposition, la note 2, p. 46 du Tome présent.

16) On peut consulter encore sur cette démonstration la note 3, p. 46 du Tome présent.

Probl. III.

Datis duabus rectis duas medias proportionales invenire¹⁷⁾.

Veterum Geometrarum ad hoc Problema constructiones complures retulit Eutocius ad lib. 2. Archimedis de Sphaera & Cylindro¹⁸⁾, at non omnes inventione diversas, uti rectè quoque ipse animadvertit. Heronis enim inventionem¹⁹⁾ secuti videntur Apollonius & Philo Byzantius²⁰⁾: quanquam Heronem Appolonio aetate posteriorem nonnulli existiment²¹⁾. Dioclis modum Pappus & Sporus²²⁾. Nico-

17) Voir, sur l'historique de ce problème, les p. 103-106 de l'‘Avertissement’.

18) Voir les Commentaires d'Eutocius, aux p. 14-27 de l'édition de Bâle (Heiberg, III, p. 66-127).

19) Voir, sur la construction de Héron, les p. 15-16 de l'édition de Bâle (Heiberg, III, p. 70-73) et consulter encore la note 10, p. 40 du Tome présent.

20) Voir, sur ces constructions, les p. 16-17 de l'édition de Bâle (Heiberg, III, p. 72-79). L'identité essentielle des trois constructions fut déjà constatée par Eutocius.

21) La question de déterminer l'époque où vivait Héron a beaucoup occupé les savants jusque dans notre temps. On peut consulter à ce propos le Chap. XVIII du T. I de l'ouvrage bienconnu de Cantor ‘Vorlesungen über Geschichte der Mathematik’ qui place Héron dans le premier siècle avant J.C., c'est-à-dire après Philon de Byzance et plus d'un siècle entier après Apollonius.

22) Voir, sur ces constructions, les p. 17-20 de l'édition de Bâle (Heiberg, III, p. 78-93). Dioclès fait emploi de sa cissoïde; les autres constructions se réduisent aisément a celle de Dioclès, comme Eutocius l'a déjà remarqué.

[p. 192]

même lieu²⁴⁾ la construction, plus subtile que les autres, de Nicomède²³⁾, que Fr. Viète a insérée, arrangée un peu autrement, dans son Supplément à la Géométrie²⁵⁾. La méthode de R. Descartes par l'intersection d'une parabole et d'une circonférence²⁶⁾, dont on trouve la démonstration dans les livres de Harmoniques de M. Mersenne²⁷⁾, est excellente et nouvelle. Viennent maintenant les nôtres.

Soit de deux lignes données AC la plus grande²⁸⁾, qui est divisée en deux parties égales au point E. Et soit AB la plus petite, que nous supposerons placée de telle façon, que le triangle EAB ait les côtés AE, EB égaux. Achevons le parallélogramme CABD, et prolongeons AC, AB. Puis appliquons une régle au point D et mouvons-la jusqu'à ce qu'elle ait la position GF, où elle découpe justement une portion EF égale à la droite EG; (ce que nous obtiendrons en essayant souvent, ou par le tracé d'une hyperbole, ainsi que nous le montrerons plus loin). Je dis que l'on a trouvé alors les deux moyennes BG, CF entre AC et AB.

Soit en effet EK à angles droits sur AB. Puis donc que BE est égal à EA, la droite AB sera divisée en deux parties égales en K; mais la droite BG est adjacente. Donc le rectangle AGB avec le carré sur KB sera égal au carré KG. Et ajoutant de part et d'autre le carré KE, le rectangle AGB avec les carrés BK et KE, c'est-à-dire avec le carré BE, sera égal au carré EG. De même, puisque AC est partagé en deux parties égales en E, et que la ligne CF est adjacente, le rectangle AFC avec le carré EC sera égal au carré EF. Mais le carré EF est égal au carré EG. Donc le rectangle AFC avec le carré CE sera égal au rectangle AGB avec le carré BE. Or, le carré CE ou EA est égal au carré EB. Donc aussi le rectangle restant AFC est égal au rectangle AGB. Pour cette raison, comme FA à AG ainsi BG est à CF. Mais comme FA à AG ainsi DB est à BG et ainsi aussi FC à CD.

24) Voir les p. 26-27 de l'édition du Bâle (Heiberg, III, p. 122-127).

23) Consultez, sur cette construction, la note 2, p. 13 et la p. 15 du Tome présent. Nous avons exposé ailleurs, aux p. 4-6 du Tome présent, comment l'étude de la construction de Nicomède a été pour Huygens le point de départ d'autres recherches sur les problèmes solides et surtout de ses solutions nouvelles, qui vont suivre, du problème des deux moyennes proportionnelles.

25) Voir la Prop. V, p. 242-243 de l'ouvrage cité dans la note 31, p. 10 du T. I. Pour comparer la construction de Viète avec celle de Nicomède on doit identifier respectivement les points A, B, C, D, G et H de la figure de Viète avec les points B, A, L, C, D et E de la figure de la page 15 du Tome présent. Alors on s'aperçoit que Viète commence sa construction par décrire un cercle dont le centre deviendra le point B de cette dernière figure et dont le diamètre est égal au plus grand des deux segments donnés. Dans ce cercle il inscrit une corde LA égale au plus petit segment et il prend CL = LA. Ensuite il tire la droite AD parallèle à CB et la droite BE de manière qu'on a DE = AB. Alors, d'après lui, AE est la première des deux moyennes et la seconde est la distance du point E au point d'intersection du cercle avec BE, mais puisqu' on a DE = BA on voit aisément que cette distance est égale à BD.
Ainsi la comparaison de la solution de Viète avec celle de Nicomède, qui donne AE et GK pour les deux moyennes, fait connaître une nouvelle propriété de la figure mentionnée, c'est-à dire l'égalité de BD avec GK. On a, en effet, BD : DE = CA : AE, donc BD : 2DE = ½ CA : AE, ou bien BD : AH = GH : AE; mais, puisqu' on a de même GK : AH = GH : AE, il en résulte BD = GK.

26) Voir, dans la ‘Géometrie’, l'article: ‘L'inuention de deux moyenes proportionelles,’ p. 469-470 du Tome VI de l'édition d'Adam et Tannery.

27) Voir l'ouvrage cité dans la note 5, p. 100 du T. V. Aux pages 147-148 du second volume on y trouve, en effet, une démonstration à la mode des anciens de la construction de Descartes.

28) L'analyse de la construction qui va suivre ici en premier lieu fut inventée le 9 mars 1652 (voir la première partie de la pièce N^o. XI, p. 49-50 du Tome présent). Le lendemain Huygens rédigea la construction et la démonstration en forme (voir les p. 50 et 51 de la pièce mentionnée); ensuite il les modifia ce même jour (voir la note 5 de la pièce mentionnée). C'est cette dernière rédaction qu'on retrouve ici avec de légères altérations.

[p. 193]

medea autem constructio²³⁾ prae caeteris subtilis ibidem²⁴⁾ extat, quam Fr. Viëta paulo aliter concinnatam suo Geometriae supplemento inseruit²⁵⁾. R. Cartesii egregia est & nova per paraboles & circumferentiae intersectionem²⁶⁾, cujus demonstratio legitur in libris Harmonicôn M. Mersenni²⁷⁾. Nostrae autem sequentes.

Sit datarum linearum major AC²⁸⁾, quae bifariam secetur in E. Minor autem sit AB, quae sic constituatur ut triangulus EAB habeat crura aequalia AE, EB. Et perficiatur parallelogrammum CABD. Et producantur AC, AB. Porro applicetur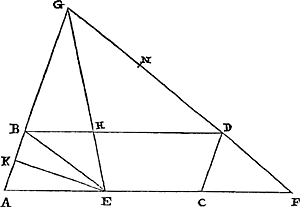

[Fig. 4.]

regula ad punctum D, & moveatur quousque positionem habeat GF, abscindens nimirum EF aequalem rectae EG; (Hoc autem vel saepius tentando assequemur, vel descriptâ hyperbole, uti postea ostendetur) Dico inter AC, AB medias duas inventas esse BG, CF.

Sit enim EK ipsi AB ad angulos rectos. Quia igitur BE aequalis EA, dividetur AB in K bifariam: adjecta autem est linea BG. Ergo rectangulum AGB cum quadrato ex KB, aequabitur quadrato KG. Et addito utriumque quadrato KE, erit rectangulum AGB unà cum quadratis BK, KE, hoc est unà cum quadrato BE, aequale quadrato EG. Similiter quia AC bifariam dividitur in E, & adjecta est linea CF, erit rectangulum AFC cum quadrato EC aequale quadrato EF. Quadratum autem EF aequale est quadrato EG. Erit igitur rectangulum AFC cum quadrato CE, aequale rectangulo AGB cum quadrato BE. Atqui quadratum CE seu EA aequale est quadrato EB. Ergo & reliquum rectangulum AFC aequale rectangulo AGB. Quare sicut FA ad AG ita BG ad CF. Ut autem FA ad AG ita est DB ad BG, & ita quoque FC ad CD. Igitur ut DB, hoc est,

23) Consultez, sur cette construction, la note 2, p. 13 et la p. 15 du Tome présent. Nous avons exposé ailleurs, aux p. 4-6 du Tome présent, comment l'étude de la construction de Nicomède a été pour Huygens le point de départ d'autres recherches sur les problèmes solides et surtout de ses solutions nouvelles, qui vont suivre, du problème des deux moyennes proportionnelles.

24) Voir les p. 26-27 de l'édition du Bâle (Heiberg, III, p. 122-127).

25) Voir la Prop. V, p. 242-243 de l'ouvrage cité dans la note 31, p. 10 du T. I. Pour comparer la construction de Viète avec celle de Nicomède on doit identifier respectivement les points A, B, C, D, G et H de la figure de Viète avec les points B, A, L, C, D et E de la figure de la page 15 du Tome présent. Alors on s'aperçoit que Viète commence sa construction par décrire un cercle dont le centre deviendra le point B de cette dernière figure et dont le diamètre est égal au plus grand des deux segments donnés. Dans ce cercle il inscrit une corde LA égale au plus petit segment et il prend CL = LA. Ensuite il tire la droite AD parallèle à CB et la droite BE de manière qu'on a DE = AB. Alors, d'après lui, AE est la première des deux moyennes et la seconde est la distance du point E au point d'intersection du cercle avec BE, mais puisqu' on a DE = BA on voit aisément que cette distance est égale à BD.
Ainsi la comparaison de la solution de Viète avec celle de Nicomède, qui donne AE et GK pour les deux moyennes, fait connaître une nouvelle propriété de la figure mentionnée, c'est-à dire l'égalité de BD avec GK. On a, en effet, BD : DE = CA : AE, donc BD : 2DE = ½ CA : AE, ou bien BD : AH = GH : AE; mais, puisqu' on a de même GK : AH = GH : AE, il en résulte BD = GK.

26) Voir, dans la ‘Géometrie’, l'article: ‘L'inuention de deux moyenes proportionelles,’ p. 469-470 du Tome VI de l'édition d'Adam et Tannery.

27) Voir l'ouvrage cité dans la note 5, p. 100 du T. V. Aux pages 147-148 du second volume on y trouve, en effet, une démonstration à la mode des anciens de la construction de Descartes.

28) L'analyse de la construction qui va suivre ici en premier lieu fut inventée le 9 mars 1652 (voir la première partie de la pièce N^o. XI, p. 49-50 du Tome présent). Le lendemain Huygens rédigea la construction et la démonstration en forme (voir les p. 50 et 51 de la pièce mentionnée); ensuite il les modifia ce même jour (voir la note 5 de la pièce mentionnée). C'est cette dernière rédaction qu'on retrouve ici avec de légères altérations.

[p. 194]

Donc comme DB, c'est-à-dire AC, à BG, ainsi BG est à FC, et FC à CD, c'est-à-dire AB. Ce qu'il fallait démontrer. Quant à ce que nous avons dit, que l'on peut également trouver par la description d'une hyperbole comment la droite FDG doit être tracée, cela sera évident par ceci: supposons que l'on ait fait en sorte que EF, EG soient égales, et que l'on prenne GN égale à DF. Le point N est ainsi sur l'hyperbole que l'on tracera par le point D avec les droites FA, AG comme asymptotes^*. Mais le même point N est aussi sur la circonférence de cercle, dont le centre est E et le rayon ED; (car ceci se comprend facilement, puisque le triangle FEG est isocèle et que NG est égal à DF). Par conséquent le point N est donné par l'intersecton de l'hyperbole et de la dite circonférence. Mais D aussi est donné, La ligne FG est donc donnée en position en la menant par les points N et D. Et la construction est évidente.

* 8. 2. Coniques²⁹⁾

29) Voir, à la p. 46 recto de l'édition de Commandin, citée dans la note 4, p. 6 du T. I, la proposition suivante: ‘Si hyperbolae recta linea occurrat in duobus punctis, producta ex utraque parte cum asymptotis conueniet: & lineae, quae ex ipsa abscissae intersectionem, & asymptotos interiiciuntur, aequales erunt.’

Autrement³⁰⁾.

Autour du diamètre AC égal à la plus grande des lignes données on décrit un cercle; on y place AB égale à la plus petite des droites données et on achève le parallélogramme AD; puis, AB étant prolongée, on mène du centre E une droite EHG, de telle manière que HD, HG soient égales entr'elles. Supposons qu'elle coupe la circonférence en L. Je dis qu' on a trouvé les deux moyennes BG et GL aux deux droites AC, AB.

Prolongeons³¹⁾, en effet, GE jusqu' à la circonférence en K, joignons AK et menons BO qui lui soit parallèle. Alors les triangles AEK, BHO sont semblables; et comme AE est égale à EK, BH et HO seront aussi égales entr'elles. Mais encore HG, HD sont égales entr'elles. Donc toute la droite OG est égale à BD, c'est-à-dire au diamètre AC ou LK; et après avoir enlevé la partie commune LO, il reste des lignes égales LG, OK. Mais le rectangle KGL est égal au rectangle AGB. Donc comme KG est à GA ainsi BG à GL. Mais comme KG à GA ainsi OG est à GB et ainsi aussi le reste OK, c'est-à-dire LG, à BA. Donc comme OG, c'est-à-dire AC, à GB ainsi BG est à GL et GL à AB. Ce qu'il fallait démontrer. Or, l'invention de cette construction a la même origine que la précédente³²⁾.

30) On retrouve la construction qui suit à la p. 52 du Tome présent.

31) La démonstration qui va suivre na diffère pas sensiblement de celle qu'on trouve, sous la date du 5 juin 1652, dans le dernier alinéa de la pièce XI. p. 49-53 du Tome présent. L'avant-dernier alinéa de cette même pièce contient une autre démonstration et fait connaître l'origine de la construction.

32) Voir la note 9, p. 52 du Tome présent.

[p. 195]

AC ad BG ita BG ad FC, & FC ad CD, hoc est, AB. Quod erat dem. Quod autem dictum est, etiam descriptâ hyperbole inveniri quomodo linea FDG ducenda sit, hinc constabit: Factum enim sit, ut EF, EG sint aequales, & sumatur GN aequalis DF. Itaque punctum N est ad hyperbolem quae describetur per D punctum circa asymptotos FA, AG^*. Sed idem punctum N est quoque ad circuli circumferentiam cujus centrum E radius ED: (Hoc enim facile intelligitur quia triangulus FEG est aequicruris, & NG aequalis DF) Itaque datum est punctum N ad intersectionem hyperboles & circumferentiae dictae. Sed & D datum est. Datur igitur positione linea FG ducenda per puncta N, D. Et compositio manifesta est.

* 8. 2. Conic.²⁹⁾

29) Voir, à la p. 46 recto de l'édition de Commandin, citée dans la note 4, p. 6 du T. I, la proposition suivante: ‘Si hyperbolae recta linea occurrat in duobus punctis, producta ex utraque parte cum asymptotis conueniet: & lineae, quae ex ipsa abscissae intersectionem, & asymptotos interiiciuntur, aequales erunt.’

Aliter³⁰⁾.

Circa diametrum AC majori datarum linearum aequalem circulus describatur & ponatur AB minori datarum aequalis, & perficiatur parallelogrammum AD: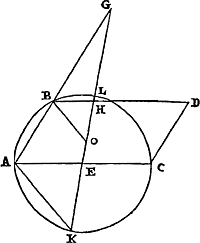

[Fig. 5.]

productâque AB, ducatur ex centro E recta EHG eâ ratione ut HD, HG sint inter se aequales. Secet autem circumferentiam in L. Dico duabus AC, AB duas medias inventas esse BG, GL.

Producatur³¹⁾ enim GE usque ad circumferentiam in K, & jungatur AK, eique parallela ducatur BO. Similes itaque sunt trianguli AEK, BHO; & quia AE aequalis EK, etiam BH, HO aequales erunt. Sed & HG, HD inter se aequales sunt. Igitur tota OG aequalis BD, hoc est, diametro AC vel LK; & ablatâ communi LO, relinquentur aequales LG, OK. Est autem rectangulum KGL aequale rectangulo AGB. Ergo ut KG ad GA ita BG ad GL. Sed ut KG ad GA ita est OG ad GB & ita reliqua OK, hoc est, LG ad BA. Ergo ut OG, hoc est, AC ad GB ita BG ad GL & GL ad AB. Quod erat demonstr. Hujus autem constructionis inventio eandem cum praecedenti originem habet³²⁾.

30) On retrouve la construction qui suit à la p. 52 du Tome présent.

31) La démonstration qui va suivre na diffère pas sensiblement de celle qu'on trouve, sous la date du 5 juin 1652, dans le dernier alinéa de la pièce XI. p. 49-53 du Tome présent. L'avant-dernier alinéa de cette même pièce contient une autre démonstration et fait connaître l'origine de la construction.

32) Voir la note 9, p. 52 du Tome présent.

[p. 196]

Autrement³³⁾.

Soient données AB et Q auxquelles il s'agisse de trouver deux moyennes proportionnelles, AB étant d'ailleurs plus grande que Q.

Prenons AF égale à la moitié de Q et, ayant prolongé AB des deux côtés, soit BR égale à cette droite même. Elevons à AB la perpendiculaire FC, et portons RC égale à RA; puis joignons BC et menons AE parallèle à cette droite. Enfin, ayant appliqué une règle au point C, mouvons la jusqu' à ce qu'elle ait la position CD, où elle fait CE égale à AD. Je dis qu'entre AB et Q les deux moyennes proportionnelles sont CE et ED.

Joignons en effet CA. Alors, comme RA et RC sont égales et que l'angle CFA est droit, RA sera à AC comme AC au double de AF, c'est-à-dire à Q, et par conséquent le carré AC sera égal au rectangle sur RA et Q. Mais le carré AC avec le carré AD et le double du rectangle DAF, c'est-à-dire le rectangle formé par DA et Q, égale le carré DC^*. Donc le carré DC équivaudra au carré DA augmenté des rectangles construits avec DA et Q et avec RA et Q, c'est-à-dire augmenté avec le rectangle sur DR et Q. Mais le carré DB est égal au rectangle RDA avec le carré AB^*. Donc, comme le carré DB au carré DC, c'est-à-dire comme le carré AB au carré AD, (car, comme DB à DC tel est AB à EC ou AD) ainsi le rectangle RDA avec le carré AB sera au rectangle sur RD, Q avec le carré AD. Et pour cette raison le rectangle RDA sera aussi au rectangle sur RD, Q comme le carré AB au carré AD^*. Mais, comme le carré AB au carré AD, ainsi AB est à ED en longueur: car, comme BA à AD, ainsi CE, c'est-à-dire la même AD, à ED. Donc le rectangle RDA est au rectangle sur RD, Q, c'est-à-dire AD est à Q, comme AB à ED. Permutant donc et invertissant, BA est à AD comme ED à Q. Mais aussi, comme BA à AD, ou CE, ainsi CE à ED. Donc, comme AB à CE ainsi CE à ED et ED à Q. Ainsi donc entre AB et Q les moyennes proportionnelles sont CE, ED. Ce qu'il fallait démontrer.

33) Comparez, aux pages 54-56 du Tome présent, la pièce N^o XII, datée du 16 et du 19 mars 1652. Elle contient dans une autre rédaction la construction et la démonstration qui vont suivre, et elle nous fait connaître l'analyse qui les a amenées.

* 12.2. Élém.³⁴⁾

34) Voir la note 15, p. 29 du Tome présent.

* 6.2. Élém.³⁵⁾

35) Voir la note 2, p. 46 du Tome présent.

* 19.5. Élém.³⁶⁾

36) Voir la note 26, p. 311 du Tome XI.

[p. 197]

Aliter³³⁾.

Sint datae AB & Q quibus duas medias proportionales invenire opus sit; AB autem quam Q major.

Dimidiae Q sumatur aequalis AF, & productâ AB utrimque, sit ipsi aequalis BR. Erigatur autem ad AB perpendicularis FC, & ipsi RA aequalis ponatur RC: & jungatur BC, & huic parallela ducatur AE. Denique applicatâ regulâ ad punctum C, moveatur ea quousque positionem habeat CD, faciens CE aequalem AD. Dico inter AB & Q duas medias esse CE, ED.

Jungatur enim CA. Igitur quia aequales sunt RA, RC & angulus CFA rectus,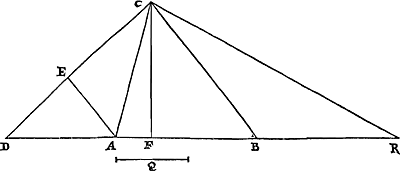

[Fig. 6.]

erit RA ad AC ut AC ad duplam AF, hoc est, Q: ac proinde quadratum AC aequale rectangulo sub RA & Q. Quadratum autem AC cum quadrato AD & duplo rectangulo DAF, hoc est, sub DA & Q contento, aequatur quadrato DC^* Igitur quadratum DC aequabitur quadrato DA unà cum rectangulis sub DA, Q, & sub RA, Q, hoc est, unà cum rectangulo sub DR & Q. Quadratum autem DB aequale rectangulo RDA & quadrato AB^*. Igitur ut quadratum DB ad quadratum DC, hoc est, ut quadr. AB ad quadr. AD, (est enim ut DB ad DC sic AB ad EC sive AD) ita erit rectangulum RDA cum quadrato AB ad rectangulum sub RD, Q, cum quadrato AD. Quamobrem & rectangulum RDA ad rectangulum sub RD, Q, sicut quadr. AB ad quadr. AD^*. Est autem ut quadratum AB ad quadr. AD, ita AB ad ED longitudine: nam ut BA ad AD sic CE, hoc est, ipsa AD ad ED. Ergo rectangulum RDA ad rectangulum sub RD, Q, hoc est, AD ad Q sicut AB ad ED. Et permutando & invertendo, BA ad AD ut ED ad Q. Atqui ut BA ad AD, hoc est, CE ita CE ad ED. Ergo ut AB ad CE ita CE ad ED, & ED ad Q. Itaque inter AB & Q mediae proportionales sunt CE, ED. Quod erat ostendendum.

33) Comparez, aux pages 54-56 du Tome présent, la pièce N^o XII, datée du 16 et du 19 mars 1652. Elle contient dans une autre rédaction la construction et la démonstration qui vont suivre, et elle nous fait connaître l'analyse qui les a amenées.

* 12.2. Elem.³⁴⁾

34) Voir la note 15, p. 29 du Tome présent.

* 6.2. Elem.³⁵⁾

35) Voir la note 2, p. 46 du Tome présent.

* 19.5. Elem.³⁶⁾

36) Voir la note 26, p. 311 du Tome XI.

[p. 198]

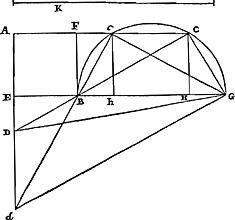
Probl. IV.

Étant donné un carré dont l'un des côtés est prolongé, appliquer dans l'angle extérieur une droite de grandeur donnée qui passe par le sommet opposé³⁷⁾.

Soit BA un carré dont le côté FA est prolongé. Soit donné aussi la ligne K Et qu'il s'agisse de mener la droite BDC de telle façon, que la partie interceptée DC soit égale à la droite donnée K.

Supposons qu' aux carrés sur K et EB soit égal le carré EG; sur BG comme diamètre décrivons le demi-cercle BCG, coupant la droite FA prolongée en C, et menons BDC. Je dis que DC est égale à cette droite K. Joignons en effet CG, GD; et soit CH à angles droits sur BG.

Puisqu' alors les triangles BED, CHG sont semblables et que les côtés BE, CH autour des angles droits sont égaux entr'eux, le côté DB sera aussi égal au côté GC, et DE à GH. Mais les carrés CD, CG, c'est-à dire les carrés DC, CH et HG, sont égaux au carré DG^*, c'est-à-dire aux carrés GE, ED. Donc, retranchant d'ici le carré ED et de là le carré HG, les deux carrés DC et CH seront égaux au carré EG, c'est-à-dire aux carrés de K et EB^*. Mais le carré EB est égal au carré CH. Donc aussi le carré restant DC sera égal au carré K, et la droite DC à K méme. Ce qu'il fallait démontrer.

Cette démonstration est différente de celle que l'on trouve chez Pappus Alex. livre 7. prop. 72³⁹⁾ Mais la construction ne diffère pas. Du reste nous avons trouvé qu'elle s'applique aussi au cas suivant.

37) Consultez, sur l'historique du problème, la p. 106 du Tome présent.

* 47.1. Élém.³⁸⁾

38) ‘In rectangulis triangulis, quadratum quod à latere rectum angulum subtendente describitur, aequale est eis, quae à lateribus rectum angulum continentibus describuntur, quadratis.’ (Clavius, p. 147).

* Par construct.

39) Voir la page 206 verso de l'ouvrage cité dans la note 3, p. 259 du T. II.

Probl. V.

Soit donné un carré dont deux côtés adjacents sont prolongés, appliquer dans l'angle intérieur une droite de grandeur donnée qui passe par le sommet opposé. Il faut cependant que la droite donnée ne soit pas moindre que le double de la diagonale du carré⁴⁰⁾.

Soit donné le carré AB [Fig. 8], et soient prolongées les côtés AF, AE. Et soit donnée la droite K, pas moindre que le double de la diagonale AB. Et qu'il faille faire passer par le sommet B une droite DC égale à K.

40) Voir, pour l'historique du problème, la p. 107 du Tome présent.

[p. 199]

Probl. IV.

Quadrato dato & uno latere producto, aptare sub angulo exteriori rectam magnitudine datam quae ad angulum oppositum pertineat³⁷⁾.

Esto quadratum BA cujus productum sit latus FA. Data verò linea K. Et oporteat ducere rectam BDC, ita ut pars intercepta DC sit datae K aequalis.

Quadratis ex K & EB sit aequale quadratum EG; & super BG diametro describatur semicirculus BCG secans rectam FA productam in C, & ducatur BDC. Dico DC aequalem esse ipsi K. Jungantur enim CG, GD; sitque CH ipsi BG ad angulos rectos.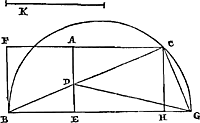

[Fig. 7.]

Quia igitur similes sunt trianguli BED, CHG, & latera BE, CH circa angulos rectos inter se aequalia, erit & latus DB aequale lateri GC, & DE ipsi GH. Sunt autem quadrata DC, CG, hoc est quadrata DC, CH, & HG aequalia quadrato DG^*, hoc est, quadratis GE, ED. Ergo dempto hinc quadrato ED, inde verò quadrato HG; erunt duo quadrata DC & CH aequalia quadrato EG, hoc est quadratis ex K & EB^*. Quadratum autem EB aequale est quadrato CH. Ergo & reliquum quadratum DC aequabitur K quadrato; & recta DC ipsi K. Quod erat ostendendum.

Demonstratio haec ab ea diversa est quae apud Pappum Alex. legitur lib. 7. prop. 72³⁹⁾. Constructio verò non differt. Caeterum eandem ad casum quoque sequentem pertinere invenimus.

37) Consultez, sur l'historique du problème, la p. 106 du Tome présent.

* 47.1. Elem.³⁸⁾

38) ‘In rectangulis triangulis, quadratum quod à latere rectum angulum subtendente describitur, aequale est eis, quae à lateribus rectum angulum continentibus describuntur, quadratis.’ (Clavius, p. 147).

* Ex construct.

39) Voir la page 206 verso de l'ouvrage cité dans la note 3, p. 259 du T. II.

Probl. V.

Dato quadrato, & duobus contiguis lateribus productis, aptare sub angulo interiori rectam magnitudine datam quae per angulum oppositum transeat. Oportet autem non minorem esse datam quam sit quadrati diameter dupla⁴⁰⁾.

Datum sit quadratum AB [Fig. 8], productaque latere AF, AE. Data vero linea K, non minor duplâ AB diametro. Et oporteat per angulum B ponere rectam DC ipsi K aequalem.

40) Voir, pour l'historique du problème, la p. 107 du Tome présent.

[p. 200]

Si K était égal au double de AB, la construction serait évidente; alors, en effet,

[Fig. 8.]

il faut mener par B la droite qui est à angles droits sur AB, et celle là résoudra le problème. Mais alors que K est plus grand que le double de AB, la construction s'exprime par les mêmes mots que dans le problème précédent; et la démonstration aussi est la même.

Or, que la circonférence BCG coupera la droite AF prolongée, cela est manifeste par ceci. Puisque K est plus grande que le double de la diagonale AB, le carré sur K sera plus grand que huit carrés EB. Donc le carré EG sera plus grand que neuf carrés sur EB; et par conséquent EG est plus grand que trois fois EB. Donc la moitié de BG, c'est-à-dire le rayon du demi-cercle décrit, est plus grand que EB ou BF; il est donc nécessaire que la droite AC soit coupée par la circonférence BCG.

Probl. VI.

Soit donné un losange dont l'un des côtés soit prolongé, appliquer dans l'angle extérieur une droite de grandeur donnée qui passe par le sommet opposé⁴¹⁾.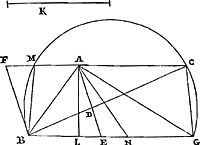

[Fig. 9.]

Soit donné le losange AB, dont le côté FA est prolongé. Soit donnée aussi la ligne K. Et qu'il s'agisse de mener la droite BDC, de telle façon que la partie interceptée DC soit égale à cette ligne K.

Menons la diagonale AB et prolongeons le côté BE; et soit le carré AG égal aux carrés de K et AB. Sur BG décrivons un arc de circonférence qui soit capable d'un angle égal à BFA. Elle coupera le côté FA prolongé, ainsi qu'il sera prouvé. Puis, vers le point d'intersection C menons BC. Je dis que la partie DC interceptée de cette ligne est égale à la droite donnée K. Mais d'abord voici comment on démontre que la circonférence décrite coupe le côté FA prolongé. Menons AN de telle façon que l'angle BAN soit égal à l'angle BFA ou BEA. Alors le triangle

41) Voir, pour l'historique du problème, les p. 107-108 du Tome présent. La rédaction du texte, qui va suivre, ne diffère que légèrement de celle de la pièce du 23 octobre 1653 (p. 247-248 du T. I), envoyée à van Schooten. Et cette dernière pièce est le résultat d'un remaniement de celle du 9 février 1652, que l'on trouve aux p. 26-31 du Tome présent et qui contient l'analyse, qui a amené la construction, dans sa forme primitive un peu différente de celle du texte. Voir, sur cette modification, la note 8, p. 28 du Tome présent.

[p. 201]

Si K aequalis fuerit duplae AB, constructio manifesta est; tunc enim per B

[Fig. 8.]

ducenda est quae sit ipsi AB ad angulos rectos, eaque propositum efficiet. Cum verò major erit K quam dupla AB, constructio iisdem verbis praecipitur atque in Problemate praecedenti: & demonstratio quoque est eadem.

Quod autem circumferentia BCG secabit productam AF hinc manifestum est. Etenim quia K major est duplâ diametro AB, erit K quadratum majus octo quadratis EB. Itaque quadratum EG majus quam quadrata novem ex EB; ac proinde EG major quam tripla EB. Dimidia igitur BG, hoc est, radius descripti semicirculi major quam EB vel BF; unde necesse est rectam AC secari à circumferentia BCG.

Probl. VI.

Rhombo dato, & uno latere producto, aptare sub angulo exteriori lineam magnitudine datam quae ad oppositum angulum pertineat⁴¹⁾.

Sit datus rhombus AB [Fig. 9], cujus productum latus FA. Data autem linea K. Et oporteat ducere rectam BDC, ita ut pars intercepta DC sit ipsi K aequalis.

Ducatur diameter AB, & latus BE producatur; & quadratis ex K & AB sit aequale quadratum AG. Et super BG circumferentiae portio describatur quae capiat angulum ipsi BFA aequalem. Secabit ea productum latus FA, ut modo ostendetur. Itaque ad intersectionis punctum C ducatur BC. Dico hujus partem interceptam DC lineae datae K aequalem esse. Quod autem circumferentia descripta latus FA productum secabit, sic primùm ostenditur. Ducatur AN ita ut sit angulus BAN angulo BFA vel BEA aequalis. Itaque triangulus BAN triangulo BEA similis est, ac proinde isosceles quoque. Quare si super BN circumferentia describatur quae capiat angulum BFA, ea continget latus FA in A puncto. Sed

41) Voir, pour l'historique du problème, les p. 107-108 du Tome présent. La rédaction du texte, qui va suivre, ne diffère que légèrement de celle de la pièce du 23 octobre 1653 (p. 247-248 du T. I), envoyée à van Schooten. Et cette dernière pièce est le résultat d'un remaniement de celle du 9 février 1652, que l'on trouve aux p. 26-31 du Tome présent et qui contient l'analyse, qui a amené la construction, dans sa forme primitive un peu différente de celle du texte. Voir, sur cette modification, la note 8, p. 28 du Tome présent.

[p. 202]

BAN est semblable au triangle BEA, et par conséquent isocèle comme celui-ci. Pour cette raison, si sur BN on décrit une circonférence capable de l'angle BFA, elle touchera le côté FA en A. Mais BG est plus grand que BN: car le carré AG est plus grand que le carré AN ou AB, puisqu'il est égal aux carrés de K et AB. Donc AG tombera en dehors du triangle isocèle BAN. Et ainsi il est établi que la circonférence décrite sur BG et capable d'un angle égal à BFA ou BAN coupe la ligne FAC. Soit M l'autre point d'intersection, joignons BM, GC, et soit AL la perpendiculaire abaissée de A sur BE.

Puis donc que le carré AG est égal aux carrés sur K et AB, et que le même carré AG est égal aux carrés AB et BG diminué du double du rectangle GBL, c'est-à-dire moins le rectangle GBN; le carré K sera égal au carré BG moins le rectangle GBN, c'est-à-dire au rectangle BGN. Mais, comme le rectangle BGN au rectangle BE, GN, ainsi BG est à BE. Donc, comme BG à BE ainsi aussi le carré K au rectangle GN, BE, c'est-à-dire au rectangle GBE moins le rectangle NBE. Mais le rectangle CBD est égal au rectangle GBE, parce que GB est à BC comme DB à BE à cause des triangles semblables GBC, DBE; ils ont en effet l'angle en B commun, et l'angle BCG est égal à l'angle BED. De même le carré AB est égal au rectangle NBE, puisque, à cause des triangles semblables, NB est à BA comme AB à BE. Donc GB sera à BE comme le carré K au rectangle CBD moins le carré AB. Mais au rectangle CBD moins le carré AB équivaut le rectangle DA, AC; cequi se prouve ainsi. En effet, puisque le quadrilatère CGBM est dans un cercle, les angles CGB et BMC ensemble sont égaux à deux angles droits. Mais de même les angles EDB, ADB. De ceux-ci EDB est égal à l'angle CGB en vertu de la similitude des triangles GBC, DBE. Donc aussi l'angle BMC sera égal à l'angle ADB. Les triangles ABM, ADB ont donc les angles M et D égaux entr'eux. Mais aussi les angles en A et le côté AB commun. Et ainsi les dits triangles sont semblables et égaux. Par conséquent AM égale AD et MB égale BD, et l'angle MBA égale ABD. Donc dans le triangle MBC l'angle B est divisé en deux parties égales par la droite BA, et par conséquent le rectangle MBC moins le carré BA est égal au rectangle MAC. Mais le rectangle CBD est égal au rectangle CBM; et le rectangle DAC égal au rectangle MAC. Donc le rectangle CBD moins le carré BA est égal au rectangle CAD, ainsi qu'il a été dit. Ainsi GB est à BE comme le carré K au rectangle DAC. Mais, comme GB à BE ainsi le rectangle GBE, c'est-à-dire le rectangle CBD, est au carré BE. Donc, comme le carré K au rectangle DAC ainsi le rectangle CBD au carré BE. Or, le rapport du rectangle CBD au carré BE est composé du rapport DB à BE, c'est-à-dire DC à CA, et du rapport CB à BE ou BF, c'est-à-dire CD à DA. Donc aussi le carré K est au rectangle DAC dans le rapport composé du rapport DC à CA et DC à DA, c'est-à-dire dans le même rapport que celui du carré DC au rectangle DAC. Pour cette raison le carré K est égal au carré DC; et DC à K en longueur. Ce qu'il fallait démontrer.

[p. 203]

BG major est quam BN: nam quadratum AG majus est quadrato AN vel AB, cum sit aequale quadratis ex K & AB. Quare AG cadet extra triangulum isoscelem BAN. Itaque manifestum est circumferentiam super BG descriptam capientemque angulum ipsi BFA vel BAN aequalem secare lineam FAC. Esto alterum intersectionis punctum M & jungantur BM, GC & cadat in BE ex A perpendicularis AL.

[Fig. 9.]

Quia igitur quadratum AG aequale est quadratis ex K & AB: atque idem quadratum AG aequale quadratis AB & BG minùs duplo rectangulo GBL, hoc est, minùs rectangulo GBN; erit K quadratum aequale quadrato BG minùs rectangulo GBN, hoc est, rectangulo BGN. Est autem ut rectangulum BGN ad rectang. BE, GN ita BG ad BE. Ergo ut BG ad BE ita quoque quadratum K ad rectangulum GN, BE, hoc est, rectangulum GBE minùs rectangulo NBE. Est autem rectangulo GBE aequale rectang. CBD, quoniam GB ad BC ut DB ad BE propter triangulos similes GBC, DBE; habent enim angulum ad B communem, & angulus BCG ipsi BED est aequalis. Item rectangulo NBE aequale est quadratum AB quia propter triangulos similes est NB ad BA ut AB ad BE. Ergo erit GB ad BE ut quadratum K ad rectangulum CBD minùs quadrato AB. Est autem rectangulo CBD minùs quadr. AB aequale rectangulum DA, AC; quod sic ostenditur. Etenim quia quadrilaterum CGBM est in circulo, sunt anguli CGB & BMC simul duobus rectis aequales. Sed & anguli EDB, ADB. Quorum EDB aequalis angulo CGB propter similitudinem triangulorum GBC, DBE. Ergo & angulus BMC aequalis erit angulo ADB. Trianguli igitur ABM, ABD angulos M & D inter se aequales habent. Verùm & angulos ad A, & latus AB commune. Itaque dicti trianguli similes sunt & aequales. Quare AM aequalis AD, & MB aequalis BD, & angulus MBA aequalis ABD. In triangulo igitur MBC angulus B in duo aequalia dividitur à recta BA, ideoque rectang. MBC minùs quadrato BA aequatur rectangulo MAC. Sed rectangulo CBM aequale est rectangulum CBD; & rectangulo MAC aequale rectang. DAC. Igitur rectang. CBD minùs quadrato BA aequale rectangulo CAD, uti dictum fuit. Est itaque GB ad BE ut quadr. K ad rectangulum DAC. Sicut autem GB ad BE ita est rectang. GBE, hoc est, rectang. CBD ad quadratum BE. Ergo ut quadratum K ad rectang. DAC ita rectang. CBD ad quadratum BE. Ratio autem rectanguli CBD ad quadr. BE composita est ex ratione DB ad BE, hoc est, DC ad CA, & ex ratione CB ad BE sive BF, hoc est, CD ad DA. Ergo & quadr. K. ad rectang. DAC eam habet rationem quae componitur ex ratione DC ad CA & DC ad DA, hoc est, eam quam quadratum DC ad rectang. DAC. Quamobrem quadr. K. quadrato DC aequale est: Et DC ipsi K longitudine. Quod erat demonstrandum.

[p. 204]

Probl. VII.

Soit donné un losange dont deux côtés adjacents sont prolongés, appliquer dans l'angle intérieur une droite de grandeur donnée qui passe par le sommet opposé. Il faut cependant que la droite donnée ne soit pas moindre que le double de la diagonale qui joint les deux autres sommets du losange⁴²⁾.

Soit donné le losange AB dont on prolonge les côtés AF, AE; soit donnée aussi la droite K égale à laquelle il faut placer une droite CD, passant par le sommet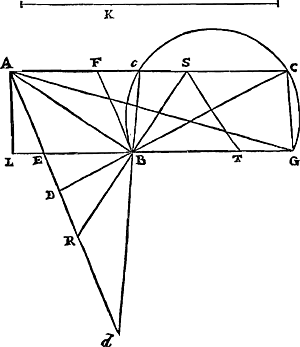

[Fig. 10.]

B. Menons la diagonale AB et à angles droits sur elle la ligne SBR, qui sera évidemment égale au double de la diagonale FE. Donc K ne doit pas être plus petite que SR. Si elle est égale, on a fait ce qui était proposé. Mais supposons que la droite donnée K soit plus grande que SR. Déjà dans la figure présente la construction sera telle qu'il fut proposé; la même que dans le Problème précédent. Mais la démonstration est un peu différente. Car d'abord on démontre autrement, que la circonférence décrite sur BG coupe AF prolongée. Soit AL perpendiculaire à EB et menons ST de façon que l'angle BST soit égal à l'angle EAF ou BFS. Alors le triangle BST est semblable au triangle BFS; (car ils ont aussi les angles en B égaux:) et par conséquent le triangle BST est de même isocèle. On voit donc que la ligne AS est égale à LB avec la moitié de BT. Pour cette raison le double de AS sera égal au double de LB avec BT toute entière. Mais le double de AS est le quadruple de AF ou EB. Donc le quadruple de EB est égal au double de LB et BT. Et si l'on prend une hauteur commune BT, le rectangle formé par le quadruple de EB et BT sera égal au double du rectangle LBT plus le carré BT. Et ajoutant de part et d'autre le carré BL, quatre fois le rectangle EBT avec le carré LB vaudra deux fois le rectangle LBT avec les carrés BT, BL, c'est-à-dire avec le carré LT. Mais puisque en vertu des triangles semblables TB est à BS comme BS à BF ou BE, le rectangle EBT sera égal au carré BS; et pris quatre fois au carré RS. Et ainsi le

42) Voir, pour l'historique du problème, les p. 109-110 du Tome présent. La construction et la démonstration qui suivent en premier lieu se trouvent sous une rédaction différente aux p. 248-250 du T. I dans la pièce du 23 octobre 1653, envoyée à van Schooten. Sons la date du 11 février 1652 on trouve, p. 32-37 du Tome présent, une rédaction plus primitive, précédée de l'analyse qui l'a produite.

[p. 205]

Probl. VII.

Rhombo dato & duobus contiguis lateribus productis, aptare sub angulo interiori rectam magnitudine datam quae per oppositum angulum transeat. Oportet autem datam non minorem esse quam duplam diametri quae reliquos duos rhombi angulos conjungit⁴²⁾.

Sit datus rhombus AB [Fig. 10] cujus producantur latera AF, AE; data autem sit recta K cui aequalem ponere oporteat CD, per angulum B transeuntem. Ducatur diameter AB, eique ad angulos rectos linea SBR, quae quidem aequalis erit duplae diametro FE. Igitur K non minor debet esse quam SR. Si vero aequalis, factum est quod proponebatur. Sed ponatur K major data esse quam SR. Erit jam in schemate hoc prout propositum est constructio eadem, quae in Problemate praecedenti. Demonstratio autem nonnihil diversa. Etenim hoc primò aliter ostenditur quod circumferentia super BG descripta secat productam AF. Sit AL ad EB perpendicularis & ducatur ST ut sit angulus BST aequalis angulo EAF vel BFS. Est itaque triangulus BST triangulo BFS similis; (nam & angulos ad B aequales habent:) ac proinde aequicruris etiam triangulus BST. Apparet igitur lineam AS aequari ipsi LB cum dimidia BT. Quare dupla AS aequabitur duplae LB & toti BT. Sed dupla AS est quadrupla AF vel EB. Ergo quadrupla EB aequalis duplae LB & BT. Sumptâque communi altitudine BT, erit rectangulum sub quadrupla EB & BT contentum, aequale duplo rectangulo LBT & quadrato BT. Et addito utrimque quadrato BL, erit rectangulum EBT quater cum quadrato LB aequale rectangulo LBT bis cum quadratis BT, BL, hoc est quadrato LT. Quia verò propter triangulos similes est TB ad BS ut BS ad BF sive BE, aequale erit rectang. EBT quadrato BS; & quater sumptum quadrato RS. Itaque quadr. SR cum quadrato LB aequale quadrato LT. Quadratum vero K (quod majus est quam RS quadr.) una cum eodem quadrato LB aequale est quadrato LG, uti ex constructione manifestum est, quia scilicet quadr. AG aequale positum fuit quadratis ex K & AB. Itaque majus est quadr. LG quam LT, & LG major quam LT, & BG

42) Voir, pour l'historique du problème, les p. 109-110 du Tome présent. La construction et la démonstration qui suivent en premier lieu se trouvent sous une rédaction différente aux p. 248-250 du T. I dans la pièce du 23 octobre 1653, envoyée à van Schooten. Sons la date du 11 février 1652 on trouve, p. 32-37 du Tome présent, une rédaction plus primitive, précédée de l'analyse qui l'a produite.

[p. 206]

carré SR avec le carré LB est égal au carré LT. Mais le carré K (qui est plus grand que le carré RS) pris avec le même carré LB est égal au carré LG, ainsi qu'il est clair par la construction, parce que, en effet, le carré AG fut posé égal aux carrés de K et AB. Donc le carré LG est plus grand que le carré LT, et LG plus grand que LT, et BG que BT. Pour cette raison la circonférence décrite sur BG, capable de l'angle EAF, coupera la droite AS; car une circonférence semblable, si elle était décrite sur BT, toucherait la même droite au point S, puisque l'angle BST est égal à cet angle EAF et que le triangle BST est isocèle.

Ensuite, que CD est égal à K se démontrera ainsi. Puisque le carré AG est égal aux carrés sur K et AB, et de même le carré AG égal aux carrés AB, BG avec le double du rectangle GBL, à cause de cela le carré K sera égal au carré BG avec le double du rectangle GBL. Mais, comme BG à BE ainsi le carré BG avec le double du rectangle GBL est au rectangle GBE avec le double du rectangle EBL; en effet, ces parties sont séparément dans le même rapport. Donc aussi le carré K est au rectangle GBE avec le double du rectangle EBL comme BG à BE. Mais au rectangle GBE équivaut le rectangle CBD, parce que CB est à BG comme EB à BD, à cause des triangles semblables CBG, EBD; car ces triangles ont les angles en B égaux et l'angle BCG égal à l'angle BED. De même le carré AB est égal au double du rectangle EBL puisque, en vertu des triangles semblables, comme SA, c'est-à-dire le double de BE, à AB ainsi AB est à BL. Donc, comme BG à BE ainsi sera le carré K au rectangle CBD avec le carré AB. Mais à ces deux-ci équivaut le rectangle CAD, parce que dans le triangle CAD l'angle A est coupé en deux parties égales par la ligne AB. Donc, comme BG à BE ainsi le carré K est au rectangle CAD. Et de là nous concluons ensuite de la même façon que dans le cas précédent, que la ligne DC est égale à cette ligne K, en répétant⁴³⁾: Mais, comme GB à BE, etc.

43) Voir la p. 202 à commencer par la ligne 9 d'en bas.

Autre solution des deux problèmes précédents⁴⁵⁾.

Soit donné le losange ADBC [Fig. 11], dont le côté DB est prolongé. Et soit donnée la ligne G. Il s'agit de mener une droite ANF, de façon que la partie interceptée NF soit égale à la droite donnée G.

45) La pièce N^o XIII, p. 57-59 du Tome présent, contient sous la date du 16 août 1652 les mêmes constructions et démonstrations dans une rédaction peu différente. On les retrouve encore dans une lettre à van Schooten du 10 déc. 1653, p. 256-257 du T. I. Consultez, sur leur origine probable, la note 1, p. 57 du Tome présent.

[p. 207]

quam BT. Quamobrem circumferentia super BG descripta capax anguli EAF secabit rectam AS; nam similis circumferentia si super BT describatur ea continget ipsam in S puncto, quoniam angulus BST ipsi EAF aequalis est triangulusque BST aequicruris.

Porro quod CD ipsi K aequalis est, sic demonstrabitur. Quia quadratum AG aequale est quadratis ex K & AB: idemque quadratum AG aequale quadratis AB,

[Fig. 10.]

BG cum duplo rectangulo GBL. Erit propterea quadratum K aequale quadrato BG cum duplo rectangulo GBL. Sicut autem BG ad BE ita est quadratum BG cum duplo rectangulo GBL ad rectangulum GBE cum duplo rectangulo EBL; singula enim ad singula eam habent rationem. Ergo & quadratum K ad rectangulum GBE cum duplo rectangulo EBL ut BG ad BE. Est autem rectangulo GBE aequale rectangulum CBD, quoniam CB ad BG ut EB ad BD, propter triangulos similes CBG, EBD; habent enim angulos ad B aequales & angulum BCG angulo BED. Item duplo rectangulo EBL aequale est quadratum AB, quia propter triangulos similes ut SA, hoc est, dupla BE ad AB ita AB ad BL. Igitur ut BG ad BE ita erit quadratum K ad rectangulum CBD cum quadrato AB. Sed hisce duobus aequale est rectangulum CAD; quoniam in triangulo CAD angulus A bifariam dividitur à linea AB. Ergo ut BG ad BE ita est quadr. K ad rectangulum CAD. Atque hinc porro eodem modo ut in casu praecedenti concludemus lineam DC ipsi K aequalem esse, repetendo ista⁴⁴⁾: Sicut autem GB ad BE, &c.

44) Voir la p. 203 à commencer par la ligne 8 d'en bas.

Vtrumque praecedentium Aliter⁴⁵⁾.

Sit datus rhombus ADBC [Fig. 11] cujus productum latus DB. Et data sit linea G. Oportet ducere rectam ANF, ut pars intercepta NF sit datae G aequalis.

45) La pièce N^o XIII, p. 57-59 du Tome présent, contient sous la date du 16 août 1652 les mêmes constructions et démonstrations dans une rédaction peu différente. On les retrouve encore dans une lettre à van Schooten du 10 déc. 1653, p. 256-257 du T. I. Consultez, sur leur origine probable, la note 1, p. 57 du Tome présent.

[p. 208]

Menons la diagonale AB, et soit le carré AH égal aux carrés de G et AB, et menons HE parallèle à cette diagonale BA. Plaçons encore AE égale à la droite G, et prolongeons la jusqu'en F. Je dis que NF est égale à cette même droite G.

Que l'on peut placer contre HE une droite AE égale à G, cela est évident par ceci. Le carré AH est plus grand que la somme des carrés AX et XH, parce que l'angle AXH est obtus. Mais le même carré AH est supposé égal aux carrés AB, ou HX, et G. Donc le carré G, ou AE, est plus grand que le carré AX. D'où il paraît que l'intersection E tombe entre les points H et X.

Prolongeons BD et plaçons une droite DR égale à BD même; soit RK parallèle à DA ou BC, et supposons que les droites FA, BA, HE prolongées la rencontrent aux points M, Q, K; enfin, joignons RA et prolongeons cette droite jusqu'en P.

Puisque DR est égale à DB, et que RQK est parallèle à DA, MA sera égale à AN et de même QA égale à AB; mais l'angle BAR est droit, parce qn'il est dans un demicercle, car les trois droites DB, DA, DR sont égales. Or, BQ et HEK sont parallèles; donc les angles en P sont droits, et aussi HP sera égale à PK. Donc le carré AH est égal au carré AE augmenté du rectangle HEK^*. Mais le même carré AH est aussi égal aux carrés sur G, ou AE, et sur AB. Donc le carré AB sera égal au rectangle KEH. Et pour cette raison KE est à AB comme AB à EH. Or, comme KE à AB, ou QA, ainsi EM est à MA: et comme AB à EH ainsi AF à FE. Donc EM est à MA comme AF à FE: Et par suite EA à AM comme EA à EF. Donc EF sera égal à AM, et par conséquent à AN. Donc aussi FN est égal à AE, c'est-à-dire, à la droite donnée G. Ce qu'il fallait démontrer.

Soit de nouveau donné le losange ADBC [Fig. 12], dont les côtés BD, BC sont prolongés, et soit donnée la ligne G. Il s'agit de mener une droite NF passant par le sommet A, et qui soit égale à cette ligne G.

Traçons la diagonale BA, et plaçons y RAL à angles droits. Si donc G est donnée moindre que RL, le problème ne saurait être construit, ainsi qu'il fut déjà dit plus haut⁴⁷⁾. Et si elle est égale, on a déjà fait ce qui était demandé. Soit donc G plus grande que RL. Dans la figure ci-jointe la construction sera telle, qu'il fut proposé, et la démonstration la même que dans le cas précédent.

* 12.2. Élém.⁴⁶⁾

46) Voir la note 15, p. 29 du Tome présent.

47) Voir l'en-tête du problème, p. 205 du Tome présent.

[p. 209]

Ducatur diameter AB, & quadratis ex G & AB sit aequale quadratum AH, & ducatur HE ipsi BA parallela. Et AE ipsi G ponatur aequalis, eademque producatur ad F. Dico NF ipsi G aequalem esse.

Quod autem ad HE poni potest AE ipsi G aequalis, hinc manifestum est. Etenim quadratum AH majus est quadratis AX & XH, quum sit angulus AXH obtusus. Sed idem quadratum AH aequale ponitur quadratis AB seu HX & G. Itaque quadratum G seu AE majus est quadrato AX. Unde apparet intersectionem E accidere inter puncta H & X.

[Fig. 11.]

Producatur BD & ponatur ipsi aequalis DR. & sit RK parallela DA vel BC, eique occurrant productae FA, BA, HE, in punctis M, Q, K: & jungatur RA, & producatur ad P.

Quoniam igitur DR aequalis est DB, & RQK parallela DA, erit & MA aequalis AN, & QA aequalis AB; angulus autem BAR rectus, quum sit in semicirculo, nam tres hae aequales sunt DB, DA, DR. Parallelae autem sunt BQ, HEK, ergo & anguli ad P recti, & erit HP aequalis PK. Est itaque quadratum AH aequale quadrato AE unà cum rectangulo HEK^*. Sed idem quadratum AH aequale est etiam quadratis ex G seu AE, & ex AB. Itaque quadr. AB aequale erit rectangulo KEH. Ac propterea KE ad AB ut AB ad EH. Verùm ut KE ad AB seu QA ita est EM ad MA: & ut AB ad EH ita AF ad FE. Igitur EM ad MA ut AF ad FE: Et proinde EA ad AM ut EA ad EF. AEqualis est igitur EF ipsi AM; quare & ipsi AN. Ideoque & F N ipsi AE, hoc est, datae G. Quod erat demonstrandum.

Sit denuo datus rhombus ADBC [Fig. 12], cujus producta latera BD, BC; & data sit linea G. Oportet ducere rectam NF transeuntem per angulum A, quaeque aequalis sit ipsi G.

Ducatur diameter BA, eique ad angulos rectos RAL. Si igitur G minor detur quam RL, problema construi nequit, uti supra quoque dictum fuit⁴⁷⁾. Si verò

* 12.2. Elem.⁴⁶⁾

46) Voir la note 15, p. 29 du Tome présent.

47) Voir l'en-tête du problème, p. 205 du Tome présent.

[p. 210]

Mais ici doit être démontré d'une autre manière que l'on peut placer contre la ligne HE une ligne AE égale à G. Soit RS égale à RB, et joignons AS. Puisque dans le triangle BAS on a mené la droite AR du sommet au milieu de la base, les carrés BR et RA pris ensemble, c'est-à-dire le carré BA avec le double du carré AR, seront la moitié des carrés BA, AS^*. Par suite le double du carré AB avec le quadruple du carré AR, c'est-à-dire avec le carré RL, sera égal aux carrés BA, AS. De sorte que, ayant retranché de part et d'autre le carré BA, le carré AS sera égal aux carrés BA et RL, et par conséquent moindre que le carré AH; car celui-ci est égal aux carrés AB et G. Donc AS est plus petite que AH. Mais elle est plus grande que AR. Donc le point S tombe entre R et H; car l'angle ARH est obtus. Par conséquent RH est plus grand que RS ou RB. Et comme, en vertu des triangles semblables, RH est à HP comme RB à BA, HP sera aussi plus grand que BA; et le carré HP plus grand que le carré AB. Mais le carré HP avec le carré PA est égal au carré AH, c'est-à-dire aux carrés BA et G. Donc, comme le carré HP est plus grand que le carré AB, le carré PA sera au contraire plus petit que le carré G. Il est donc clair que, si du point A comme centre on décrit une circonférence de rayon AE égal à G, elle coupera la ligne HE.

* d'après le livre 7. de Pappus⁴⁸⁾

48) Il s'agit de la ‘Propositio CXXII’ du ‘Liber VII’ des ‘Mathematicae Collectiones’. On y lit (p. 234 verso de l'édition de Commandin): ‘Sit triangulum ABC, & ducatur quaedam recta linea AD, quae ipsam BC bifariam secet [in D]. Dico quadrata ex BA AC quadratorum ex AD DC dupla esse’ (Hultsch, T. II, p. 856-857).

Probl. VIII.

Trouver dans une conchoide les limites de la courbure contraire⁴⁹⁾.

Nous connaissons la conchoïde qu'imagina Nicomède, par laquelle il divisa l'angle en trois parties égales⁵⁰⁾ et trouva aussi deux moyennes proportionnelles⁵¹⁾. Soit CQD [Fig. 13]⁵²⁾ cette ligne, G son pôle, et AB la règle à l'aide de

49) Voir, pour l'historique du problème, les p. 110-112 du Tome présent.

50) Voir la note 8, p. 86 du Tome présent.

51) Voir la Pièce N^o II, p 13-15 du Tome présent.

52) Dans notre figure, reproduite par phototypie d'après l'original, la lettre D est renversée et la lettre O peu différente d'une C imparfaitement imprimée.

[p. 211]

aequalis, jam factum est quod quaerebatur. Sit igitur G major quam RL. Erit in schemate adjecto, sicut propositum est, constructio & demonstratio eadem quae in casu praecedenti.

Illud autem hic aliter est ostendendum, quod ad lineam HE poni potest AE ipsi G aequalis. Sit RS aequalis RB, & jungatur AS. Quoniam igitur in triangulo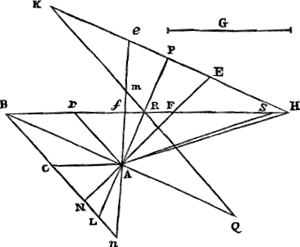

[Fig. 12.]

BAS à vertice ad mediam basin ducta est AR, erunt quadrata BR & RA simul sumpta, hoc est, quadratum BA cum duplo quadrato AR, subdupla quadratorum BA, AS^*. Itaque quadratum AB duplum cum quadruplo quadrato AR, hoc est, cum quadrato RL, aequabitur quadratis BA, AS. Quare ablato utrimque quadrato BA, erit quadratum AS aequale quadratis BA & RL, ac proinde minus quam quadr. AH; nam hoc aequale est quadratis AB & G. Est igitur AS minor quam AH. Sed major est quam AR. Ergo punctum S cadit inter R & H; angulus enim ARH obtusus est. Major itaque est RH quam RS vel RB. Et quum propter triangulos similes sit RH ad HP ut RB ad BA, erit quoque HP major quam BA; & quadratum HP majus quadrato AB. At quadratum HP cum quadrato PA aequatur quadrato AH, hoc est, quadratis BA & G. Ergo cum quadratum HP sit majus quadrato AB, erit invicem quadr. PA minus quam quadr. G. Patet igitur quod si centro A circumferentia describatur radio AE ipsi G aequali, ea lineam HE secabit.

* per 122. lib. 7. Pappi⁴⁸⁾

48) Il s'agit de la ‘Propositio CXXII’ du ‘Liber VII’ des ‘Mathematicae Collectiones’. On y lit (p. 234 verso de l'édition de Commandin): ‘Sit triangulum ABC, & ducatur quaedam recta linea AD, quae ipsam BC bifariam secet [in D]. Dico quadrata ex BA AC quadratorum ex AD DC dupla esse’ (Hultsch, T. II, p. 856-857).

Probl. VIII.

In Conchoide linea invenire confinia flexus contrarii⁴⁹⁾.

Conchoidem intelligimus quam Nicomedes excogitavit; quâ & angulum divisit trifariam⁵⁰⁾, & duas medias invenit proportionales⁵¹⁾. Esto ea CQD,

49) Voir, pour l'historique du problème, les p. 110-112 du Tome présent.

50) Voir la note 8, p. 86 du Tome présent.

51) Voir la Pièce N^o II, p 13-15 du Tome présent.

[p. 212]

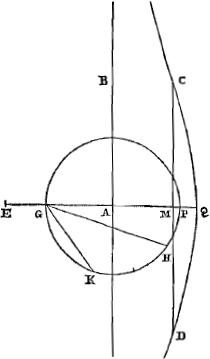
laquelle elle a été décrite, et que GQ coupe à angles droits. Telle est donc la propriété de cette ligne que, si l'on mène vers elle une droite quelconque du point G, la partie de cette droite comprise entre la conchoïde et la droite AB est égale à AQ.

Or, puisqu'il apparaît qu'une certaine partie de la conchoïde, comme CQD dans la figure présente, est concave vers le pôle G; mais que la ligne restante, prolongée de part et d'autre par manière de dire jusqu'à l'infini, est courbée en sens contraire, on demande de quelle façon on pourrait déterminer les points où commence l'inflexion contraire. Et nous avons trouvé, en effet, pour cela la construction suivante.

Soit aux deux droites AG, AQ une troisième proportionnelle AE, à prendre du côté de G. Et plaçons GF égale à GE. Soit ensuite GR à angles droits sur GQ et égale au double de GA. Et décrivons la parabole RO, dont le sommet est R, l'axe RG et dont le paramètre est égal à AG. Du centre F et avec FR comme rayon décrivons une circonférence, qui coupe la parabole en O; et menons la droite OC, parallèle à AB, qui rencontre la conchoïde aux points C, D. Ceux-ci seront les points cherchés à la limite de la courbure contraire⁵³⁾.

Cette construction-là est générale. Mais si le carré sur AQ n'est pas plus grand que le double du carré AG nous effectuerons aussi le problème par la trisection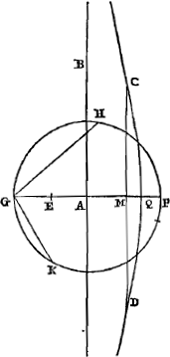

[Fig. 14.]

[Fig. 15.]

de l'arc⁵⁴⁾. Et cela de façon différente suivant que AQ sera plus grande on plus petite que AG. Car si elle est plus petite, on décrira une circonférence du centre A [Fig. 14] avec le rayon AG, et on y placera GK égale au double de GE, trouvée comme ci-devant. On prendra ensuite GM égale à la droite GH, qui sous-tend le tiers de la circonférence KHG, et par M on mènera comme avant DC parallèle à AB. Mais si AQ est plus grande que AG [Fig. 15], les autres choses seront faites de la même façon, mais il y aura cette différence, qu'il faut diviser l'arc KP, qui avec l'arc GK complète une demi-circonférence, en trois parties égales, et déterminer une des parties PH, et prendre GM égale à la sous-tendue GH.

53) Cette construction date du 25 septembre 1653, puisqu' on la retrouve avec l'analyse qui l'a amenée dans la pièce N^o XX, p. 83-85 du Tome présent.

54) Les deux constructions qui suivent se retrouvent dans la même pièce du 25 septembre 1653 aux pages 85 et 86.

[p. 213]

[Fig. 13] polus G, regula autem AB cujus ope descripta est; quam secet GQ ad angulos rectos. Haec igitur lineae proprietas est, ut ductâ ad ipsam rectâ qualibet ex G puncto, pars hujus inter conchoidem & rectam AB intercepta sit ipsi AQ aequalis.

Quum autem appareat partem quandam Conchoidis ut in schemate subjecto CQD versus polum G cavam esse, lineam verò reliquam in infinitum licet utrimque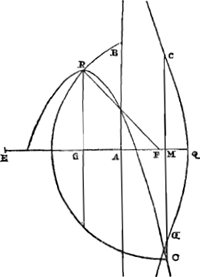

[Fig. 13.]

productam in diversum curvari; quaesitum est qua ratione puncta ea determinari possent ubi contraria flexio initium capit. Et nos quidem ad hoc sequentem invenimus constructionem.

Sit duabus AG, AQ tertia proportionalis AE, sumenda versus G. Et ponatur GF aequalis GE. Porro sit GR ipsi GQ ad angulos rectos, & aequalis duplae GA. Et describatur parabole RO, cujus vertex sit R axis RG, latus rectum ipsi AG aequale. Centro autem F radio FR circumferentia describatur, quae parabolen secet in O; & ducatur OC parallela AB occuratque conchoidi in punctis C, D. Haec erunt puncta quaesita in confinio flexionis contrariae⁵³⁾.

Ista autem Universalis est constructio. At quando quadratum ex AQ non majus est quam duplum quadrati AG, arcus trisectione propositum quoque efficiemus⁵⁴⁾. Et diversè quidem prout AQ major vel minor erit quam AG. Etenim si minor, describenda est circumferentia centro A [Fig. 14] radio AG, in eaque ponendo GK aequalis duplae GE, inventae ut priùs. Et rectae GH quae subtendit trientem circumferentiae KHG aequalis sumenda GM, & per M ducenda ut ante DC ipsi AB parallela. Cum vero AQ major est quam AG [Fig. 15], caeteris ad eundem modum compositis, haec tantum differentia erit quod arcum KP, qui unà cum arcu GK semicircumferentiam explet, in tria aequalia dividere oportet, & partium unam constituere PH, & subtensae GH aequalem sumere GM.

53) Cette construction date du 25 septembre 1653, puisqu' on la retrouve avec l'analyse qui l'a amenée dans la pièce N^o XX, p. 83-85 du Tome présent.

54) Les deux constructions qui suivent se retrouvent dans la même pièce du 25 septembre 1653 aux pages 85 et 86.

[p. 214]

Ensuite le problème est plan⁵⁵⁾ lorsque AG égale AQ. Alors en effet il faut que GM soit égal au côté du triangle équilatère inscrit dans le cercle. De même lorsque le carré AQ est double du carré AG: alors, en effet, GM est double de GA.

Mais il sera encore plan dans d'autres cas innombrables, dont on pourra aisément distinguer ceux, qui se réduiront à la trisection de l'angle.

FIN.

55) La considération des cas où le problème devient plan manque encore dans la pièce N^o XX (p. 83-86 du Tome présent); mais on la trouve déjà dans une lettre à van Schooten du 23 octobre 1653 (p. 246 du T. I). De plus on y rencontre, comme aussi dans la pièce N^o XX, mais biffée depuis, la remarque que, dans un certain sens, le problème serait toujours plan au cas où il se laisse exécuter à l'aide de la trisection de l'angle, puisqu' alors cette trisection pourrait s'accomplir à l'aide de la conchoïde même, qu'on suppose tracée. Sur cette remarque on peut consulter l'avant-dernier alinéa de la p. 7 du Tome présent, la note 10, p. 86 et la note 4, p. 232 du même Tome.

[p. 215]

Porro planum est Problema⁵⁵⁾ cum AG aequalis AQ. Tunc enim GM sit aequalis lateri trigoni ordinati in circulo inscripti. Item cum quadratum AQ duplum est quadrati AG: fit enim GM dupla ipsius GA.

Sed & aliis casibus innumeris planum erit, quorum ii quidem facilè discerni poterunt, qui ad anguli trisectionem reducuntur.

ERRATA⁵⁶⁾.

Pag. 1. lin. 2. post portioni, interpone semicirculo minori. Item tribus hisce locis, Pag. 1. lin. 7. Pag. 3. lin. 3 à fine. Pag. 4. lin. 1. post portio, lege semicirculo minor. Pag. 30. in fig. mutetur P. n B. Pag. 43. lin. penult. lege 31415926533. Pag. 44. lin. 5. pro 3144. lege 3145.

FINIS.

55) La considération des cas où le problème devient plan manque encore dans la pièce N^o XX (p. 83-86 du Tome présent); mais on la trouve déjà dans une lettre à van Schooten du 23 octobre 1653 (p. 246 du T. I). De plus on y rencontre, comme aussi dans la pièce N^o XX, mais biffée depuis, la remarque que, dans un certain sens, le problème serait toujours plan au cas où il se laisse exécuter à l'aide de la trisection de l'angle, puisqu' alors cette trisection pourrait s'accomplir à l'aide de la conchoïde même, qu'on suppose tracée. Sur cette remarque on peut consulter l'avant-dernier alinéa de la p. 7 du Tome présent, la note 10, p. 86 et la note 4, p. 232 du même Tome.

56) De ces ‘errata’ nous avons tenu compte dans le texte; voir la note 1, p. 120, qui se rapporte aux pages 121 et 123; la figure 16, p. 161 et la page 179, l. 23 et l. 27.

7) Voir la note 10, p. 11 du Tome présent.

8) Voir la note 7, p. 17 du Tome présent.

9) Voir la note 11, p. 11 du Tome présent.

10) Voir la note 9, p. 17 du Tome présent.

11) Voir la note 28, p. 312 du Tome XI et de même la note 13, p. 11 et 12 du Tome présent.

7) Voir la note 10, p. 11 du Tome présent.

8) Voir la note 7, p. 17 du Tome présent.

9) Voir la note 11, p. 11 du Tome présent.

10) Voir la note 9, p. 17 du Tome présent.

11) Voir la note 28, p. 312 du Tome XI et de même la note 13, p. 11 et 12 du Tome présent.

15) Voir, sur cette proposition, la note 2, p. 46 du Tome présent.

15) Voir, sur cette proposition, la note 2, p. 46 du Tome présent.

29) Voir, à la p. 46 recto de l'édition de Commandin, citée dans la note 4, p. 6 du T. I, la proposition suivante: ‘Si hyperbolae recta linea occurrat in duobus punctis, producta ex utraque parte cum asymptotis conueniet: & lineae, quae ex ipsa abscissae intersectionem, & asymptotos interiiciuntur, aequales erunt.’

29) Voir, à la p. 46 recto de l'édition de Commandin, citée dans la note 4, p. 6 du T. I, la proposition suivante: ‘Si hyperbolae recta linea occurrat in duobus punctis, producta ex utraque parte cum asymptotis conueniet: & lineae, quae ex ipsa abscissae intersectionem, & asymptotos interiiciuntur, aequales erunt.’

34) Voir la note 15, p. 29 du Tome présent.

35) Voir la note 2, p. 46 du Tome présent.

36) Voir la note 26, p. 311 du Tome XI.

34) Voir la note 15, p. 29 du Tome présent.

35) Voir la note 2, p. 46 du Tome présent.

36) Voir la note 26, p. 311 du Tome XI.

38) ‘In rectangulis triangulis, quadratum quod à latere rectum angulum subtendente describitur, aequale est eis, quae à lateribus rectum angulum continentibus describuntur, quadratis.’ (Clavius, p. 147).

38) ‘In rectangulis triangulis, quadratum quod à latere rectum angulum subtendente describitur, aequale est eis, quae à lateribus rectum angulum continentibus describuntur, quadratis.’ (Clavius, p. 147).

46) Voir la note 15, p. 29 du Tome présent.

46) Voir la note 15, p. 29 du Tome présent.

48) Il s'agit de la ‘Propositio CXXII’ du ‘Liber VII’ des ‘Mathematicae Collectiones’. On y lit (p. 234 verso de l'édition de Commandin): ‘Sit triangulum ABC, & ducatur quaedam recta linea AD, quae ipsam BC bifariam secet [in D]. Dico quadrata ex BA AC quadratorum ex AD DC dupla esse’ (Hultsch, T. II, p. 856-857).

48) Il s'agit de la ‘Propositio CXXII’ du ‘Liber VII’ des ‘Mathematicae Collectiones’. On y lit (p. 234 verso de l'édition de Commandin): ‘Sit triangulum ABC, & ducatur quaedam recta linea AD, quae ipsam BC bifariam secet [in D]. Dico quadrata ex BA AC quadratorum ex AD DC dupla esse’ (Hultsch, T. II, p. 856-857).