Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 120]

Christiaan Huygens, fils de Constantin.
Sur l'invention de la grandeur du cercle.

Theorème I. Proposition I.

Si dans un segment de cercle, moindre que la moitié du cercle¹⁾, on inscrit le plus grand triangle possible, et pareillement des triangles dans les segments restants, le triangle décrit en premier lieu sera moindre que le quadruple de la somme des deux décrits dans les segments restants.

Soit ABC le segment de cercle, moindre que la moitié du cercle¹⁾, dont le diamètre est BD, et le plus grand triangle inscrit ABC, c'est-à-dire ayant la même base et la même hauteur que le segment. Et soient inscrits de même dans les segment restants les plus grands triangles possibles AEB, BFC. Je dis que le triangle ABC est moindre que le quadruple de la somme des deux triangles AEB, BFC. Tirons la droite EF, qui coupe le diamètre du segment en G. Puis donc que l'arc AB est divisé en deux parties égales au point E, EA et EB seront chacune plus grande que la moitié de AB. Par suite le carré de AB sera moindre que le quadruple du carré de EB ou de EA. Mais, comme le carré de AB est au carré de EB, ainsi est la longueur de DB à celle de BG, parce que le carré de AB est égal au rectangle construit sur DB et le diamètre du cercle entier, et le carré de EB égal au rectangle construit sur le même diamètre et la droite BG. BD est donc moindre que le quadruple de BG. Mais AC est également moindre que le double de EF parce que celle-ci est égale à AB. Il paraît donc que le triangle ABC est moindre que l'octuple du triangle EBF. Mais à ce dernier triangle est égal chacun des deux AEB, BFC. Par conséquent ABC sera moindre que le quadruple de la somme de ces deux derniers triangles. Ce qu'il fallait démontrer.

1) Voir les ‘Errata’, p. 215; mais la restriction n'est pas nécessaire, le théorème et la démonstration restant valables dans le cas où le segment excède un demi-cercle.

1) Voir les ‘Errata’, p. 215; mais la restriction n'est pas nécessaire, le théorème et la démonstration restant valables dans le cas où le segment excède un demi-cercle.

[p. 121]

Christiani Hugenii, Const. f.
De circuli magnitudine inventa.

Theorema I. Propositio I.

Si Circuli portioni semicirculo minori¹⁾, triangulum maximum inscribatur, & portionibus reliquis triangula similiter inscribantur, erit triangulum primo descriptum duorum simul quae in portionibus reliquis descripta sunt minus quam quadruplam.

Esto circuli portio ABC semicirculo minor¹⁾, cujus diameter BD; maximum autem inscriptum sit triangulum ABC, hoc est, quod basin & altitudinem habeat

[Fig. 1.]

cum portione eandem. Et reliquis duabus portionibus inscribantur triangula item maxima AEB, BFC. Dico triangulum ABC minus esse quam quadruplum triangulorum AEB, BFC simul sumptorum. Jungatur enim EF, quae secet diametrum portionis in puncto G. Quoniam igitur arcus AB bifariam dividitur in E puncto, erit utraque harum EA, EB, major dimidiâ AB. Quamobrem quadratum AB minus erit quam quadruplum quadrati EB vel EA. Sicut autem quadratum AB ad quadr. EB, ita est DB ad BG longitudine; quia quadratum quidem AB aequale est rectangulo quod à DB & circuli totius diametro continetur, quadratum verò EB aequale rectangulo sub eadem diametro & recta BG. Minor igitur est BD quam quadrupla BG. Sed & AC minor est quam dupla EF, quoniam haec ipsi AB aequatur. Ergo patet triangulum ABC minus esse quam octuplum trianguli EBF. Huic autem triangulo aequantur singula AEB, BFC. Ergo utriusque simul triangulum ABC minus erit quam quadruplum. Quod erat ostendendum.

1) Voir les ‘Errata’, p. 215; mais la restriction n'est pas nécessaire, le théorème et la démonstration restant valables dans le cas où le segment excède un demi-cercle.

1) Voir les ‘Errata’, p. 215; mais la restriction n'est pas nécessaire, le théorème et la démonstration restant valables dans le cas où le segment excède un demi-cercle.

[p. 122]

Théor. II. Prop. II.

Soient donnés un segment moindre que la moitié du cercle, et sur sa base un triangle dont les côtés sont tangents au segment; soit tirée de plus une droite tangente au segment dans son sommet: cette droite coupera du triangle nommé un triangle plus grand que la moitié du plus grand triangle que l'on puisse inscrire dans le segment.

Soit ABC le segment de cercle, moindre qu'un demi-cercle, B son sommet. Et AE, CE les deux tangentes aux extrémités de la base, lesquelles se rencontrent en E; elles se rencontreront parce que le segment est moindre qu'un demi-cercle. Soit tirée de plus FG, tangente au sommet B et joignons AB, BC. Il faut donc montrer que le triangle FEG est plus grand que la moitié du triangle ABC. Il est certain que les triangles AEC, FEG, de même que AFB, BGC sont isocèles et que FG est divisée par B en deux parties égales. Or, la somme de FE et EG est plus grande que FG; donc EF est plus grande que FB, ou plus grande que FA. La droite entière AE est donc moindre que le double de FE. Par conséquent le triangle FEG sera plus grand que le quart du triangle AEC. Mais comme FA à AE, ainsi est la hauteur du triangle ABC à la hauteur du triangle AEC et la base de ces deux triangles est la même AC. Donc, comme FA est moindre que la moitié de AE, le triangle ABC sera moindre que la moitié du triangle AEC. Mais le triangle FEG était plus grand que le quart du triangle AEC. Donc le triangle FEG est plus grand que la moitié du triangle ABC. Ce qu'il fallait démontrer.

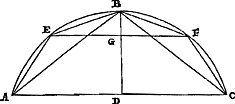
Théor. III. Prop. III.

Tout segment de cercle, moindre que la moitié du cercle¹⁾ est au plus grand triangle inscrit dans un rapport plus grand que quatre à trois.

Soit un segment de cercle [Fig. 3], moindre qu'un demi-cercle¹⁾, dans lequel est inscrit le plus grand triangle possible ABC. Je dis que ce segment est au dit triangle dans un rapport plus grand que quatre à trois. Inscrivons, en effet, dans les deux segments restants les triangles les plus grands ADB, BEC. Le triangle ABC est ainsi plus petit que le quadruple de ceux-ci ensemble^*: et pour cette raison on peut ajouter au triangle ABC un certain espace, qui, joint à lui, soit encore plus petit que le quadruple de la somme des triangles ADB, BEC. Soit donc ajouté

1) Voir les ‘Errata’, p. 215; mais la restriction n'est pas nécessaire, le théorème et la démonstration restant valables dans le cas où le segment excède un demi-cercle.

1) Voir les ‘Errata’, p. 215; mais la restriction n'est pas nécessaire, le théorème et la démonstration restant valables dans le cas où le segment excède un demi-cercle.

* d'après 1. ici.

[p. 123]

Theor. II. Prop. II.

Si fuerit circuli portio semicirculo minor, & super eadem basi triangulum, cujus latera portionem contingant; ducatur autem quae contingat portionem in vertice: Haec à triangulo dicto triangulum abscindet majus dimidio maximi trianguli intra portionem descripti.

Esto circuli portio semicirculo minor ABC, cujus vertex B. Et contingant portionem ad terminos basis rectae AE, CE, quae conveniant in E: convenient enim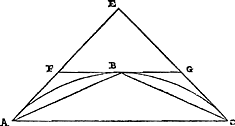

[Fig. 2.]

quia portio semicirculo minor est. Porro ducatur FG, quae contingat ipsam in vertice B; & jungantur AB, BC. Ostendendum est itaque, triangulum FEG majus esse dimidio trianguli ABC. Constat triangula AEC, FEG, item AFB, BGC aequicruria esse, dividique FG ad B bifariam. Utraque autem simul FE, EG, major est quam FG; ergo EF major quam FB, vel quam FA. Tota igitur AE minor quam dupla FE. Quare triangulum FEG majus erit quarta parte trianguli AEC. Sicut autem FA ad AE, ita est altitudo trianguli ABC ad altitudinem trianguli AEC, & basis utrique eadem AC. Ergo, quum FA sit minor quam subdupla totius AE, erit triangulum ABC minus dimidio triangulo AEC. Hujus verò quarta parte majus erat triangulum FEG. Ergo triangulum FEG majus dimidio trianguli ABC. Quod ostendendum fuit.

Theor. III. Prop. III.

Omnis circuli portio semicirculo minor¹⁾, ad maximum triangulum inscriptum majorem rationem habet quam sesquitertiam.

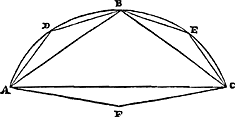
Esto Circuli portio [Fig. 3] semicirculo minor¹⁾, cui maximum sit inscriptum triangulum ABC. Dico portionem ad dictum triangulum majorem rationem habere quam quatuor ad tria. Inscribantur enim & reliquis portionibus duabus maxima triangula ADB, BEC. Itaque minus est triangulum ABC quam illorum simul quadruplum^*: ac proinde spatium aliquod adjungi potest triangulo ABC, quod una cum ipso minus etiam sit quam quadruplum dictorum simul triangulorum ADB, BEC.

1) Voir les ‘Errata’, p. 215; mais la restriction n'est pas nécessaire, le théorème et la démonstration restant valables dans le cas où le segment excède un demi-cercle.

1) Voir les ‘Errata’, p. 215; mais la restriction n'est pas nécessaire, le théorème et la démonstration restant valables dans le cas où le segment excède un demi-cercle.

* per 1. huj.

[p. 124]

pour ce motif le triangle AFC, tel que tout l'espace ABCF soit moindre que le quadruple des triangles ADB, BEC. Et figurons nous qu' ensuite des triangles maxima soient inscrits dans les segments restants; et ainsi toujours dans les segments restants, jusqu' à ce que les segments dans lesquels on a inscrit en dernier lieu soient ensemble plus petits que le triangle ACF, car cela peut se faire²⁾. Ainsi aussi les triangles inscrits en dernier lieu seront ensemble moindres que le triangle ACF. Mais puisque les deux triangles ADB, BEC sont ensemble plus grands que la quatrième partie de l'espace ABCF. Et que de nouveau les quatre triangles, qui sont inscrits dans les segments restants, sont plus grands que la quatrième partie de ceux-là. Et de même plus grands que leur quart, ceux qui sont inscrits ensuite; et ainsi continuellement, s'il y en a plusieurs qui sont décrits. En conséquence l'espace composé du quadrilatère ABCF et des autres triangles inscrits, et du tiers de ceux qui seront inscrits en dernier lieu, sera plus grand que les quatre tiers de ce quadrilatère ABCF. Car il a été démontré par Archimède³⁾ que si l'on a un nombre quelconque d'espaces, qui sont en raison quadruple, l'ensemble de tous avec le tiers du plus petit est au plus grand dans le rapport de quatre à trois. Ainsi, par partage, tous les triangles décrits dans les segments ADB, BEC, avec le tiers de ceux décrits en dernier lieu, seront plus grands que la troisième partie de l'espace ABCF. Mais le tiers susdit est moindre que le tiers du triangle ACF. Par suite, enlevant d'un côté le tiers des triangles décrits en dernier lieu; et retranchant d'autre part de l'espace ABCF le triangle AFC, tous les triangles décrits dans les segments ADB, BEC seront plus grands que le tiers du triangle ABC^*. Donc, par composition, toute la figure rectiligne inscrite dans le segment ABC est plus grande que les quatre tiers du triangle ABC, et à plus forte raison le segment lui-même. Ce qu'il fallait démontrer.

2) On peut consulter à cet égard la démonstration de la Prop. 2 du Livre 12 des ‘Elementa’ d'Euclide.

3) Voici la Prop. 23 de son ouvrage ‘Quadratura parabolae’: ‘Si magnitudines quotcunque consequenter in proportione quadrupla disponantur, hae magnitudines simul omnes cum tertia parte minimae illarum, sunt sesquitertiae magnitudini illarum maximae’; p. 154 de l'édition de Basle (Heiberg, T. II, p. 347).
Voir sur ces éditions des OEuvres d'Archimède la note 3, p. 274 du Tome XI.

* 33.5. Élem.⁴⁾

4) ‘Si fuerit maior proportio totius ad totum, quam ablati ad ablatum: Erit & reliqui ad reliquum maior proportio, quam totius ad totum’. Voir p. 526 de l'édition, citée dans la note 10, p. 97 du T. XI, des ‘Elementa’ d'Euclide, par Clavius.

[p. 125]

Esto itaque eê ratione adjectum triangulum AFC, ut totum spatium ABCF minus sit quam quadruplum triangulorum ADB, BEC. Et porro in residuis portionibus maxima triangula inscribi intelligantur; itemque in residuis semper, donec portiones quibus postremùm inscribentur simul minores sint triangulo ACF, hoc enim fieri potest²⁾. Itaque & triangula postremùm inscripta simul triangulo ACF minora erunt. Quia autem spatii ABCF quarta parte majora sunt duo

[Fig. 3.]

simul triangula ADB, BEC. Rursusque quarta horum parte majora triangula quatuor, quae portionibus reliquis inscribuntur. Et horum quartâ majora similiter, quae deinceps: atque ita continuè, si plura fuerint descripta. Erit propterea spatium ex quadrilatero ABCF & caeteris inscriptis triangulis, & triente eorum, quae postremo inscripta erunt, compositum, majus quam sesquitertium ipsius quadrilateri ABCF. Hoc enim ab Archimede demonstratum est³⁾, quod si fuerint spatia quotcunque in ratione quadrupla, ea omnia simul cum triente minimi ad maximum rationem habebunt sesquitertiam. Dividendo itaque, triangula omnia intra portiones ADB, BEC descripta cum triente postremo descriptorum majora erunt tertia parte spatii ABCF. Sed triens dictus minor est triente trianguli ACF. Igitur dempto illinc triente postremò inscriptorum; à spatio autem ABCF ablato triangulo AFC, erunt triangula omnia intra portiones ADB, BEC descripta, majora triente trianguli ABC^*. Quare componendo, tota figura rectilinea portioni ABC inscripta major quam sesquitertia trianguli ABC, multoque magis portio ipsa. Quod erat demonstrandum.

2) On peut consulter à cet égard la démonstration de la Prop. 2 du Livre 12 des ‘Elementa’ d'Euclide.

3) Voici la Prop. 23 de son ouvrage ‘Quadratura parabolae’: ‘Si magnitudines quotcunque consequenter in proportione quadrupla disponantur, hae magnitudines simul omnes cum tertia parte minimae illarum, sunt sesquitertiae magnitudini illarum maximae’; p. 154 de l'édition de Basle (Heiberg, T. II, p. 347).
Voir sur ces éditions des OEuvres d'Archimède la note 3, p. 274 du Tome XI.

* 33.5. Elem.⁴⁾

4) ‘Si fuerit maior proportio totius ad totum, quam ablati ad ablatum: Erit & reliqui ad reliquum maior proportio, quam totius ad totum’. Voir p. 526 de l'édition, citée dans la note 10, p. 97 du T. XI, des ‘Elementa’ d'Euclide, par Clavius.

[p. 126]

Théor. IV. Prop. IV.

Tout segment de cercle, plus petit que la moitié du cercle, est moindre que les deux tiers du triangle qui a la même base et dont les côtés touchent le segment.

Soit donné un segment de cercle, moindre que le demi-cercle, ABC, et supposons qu'il soit touché aux extrémités de la base par les droites AD, CD, qui se rencontrent au point D. Je dis que le segment ABC est moindre que les deux tiers du triangle ADC. Menons en effet EF, qui touche le segment au sommet B, et inscrivons le triangle maximum ABC. Comme alors le triangle EDF est plus grand que la moitié du triangle ABC^*, il est évident que l'on peut découper de celui-là une partie telle, que le reste soit pourtant encore plus grand que la moitié du dit triangle ABC. Soit donc découpé, conformément à cela, le triangle EDG. Et menons ensuite les droites HI, KL, qui touchent les segments restants AMB, BNC en leurs sommets, et inscrivons dans ces mêmes segments les triangles les plus grands. Et figurons-nous ensuite que la même chose soit faite sur les segments restants, jusqu'a ce qu'enfin les segments restants soient ensemble plus petites que le double du triangle EDG. Il y aura donc alors une certaine figure rectiligne inscrite dans le segment et une autre qui lui est circonscrite. Et puisque le triangle EGF est plus grand que la moitié du triangle ABC, et qu'à leur tour les triangles HEI, KFL sont plus grands que les moitiés des triangles AMB, BNC; et que cela a lieu pour le même motif pour les autres segments, savoir, que les triangles construits au-dessus des sommets des segments sont plus grands que les moitiés de ceux qui sont décrits dans les segments mêmes: il est clair que tous les triangles situés en dehors du segment, même sans le triangle EGD, sont ensemble plus grands que les moitiés de tous les triangles décrits dans les segments. Mais le triangle EGD est aussi plus grand que la moitié des segments restants mentionnés. Par conséquent le triangle EDF, avec les autres triangles qui sont en dehors du segment, sera plus grand que la moitié de tout le segment ABC. Donc à plus forte raison l'espace compris entre les droites AD, DC et l'arc ABC sera plus grand que la moitié du segment ABC. Et ainsi le triangle ADC est plus grand que une et demie fois le segment ABC. Ce qu'il fallait démontrer.

* d'après 2. ici.

[p. 127]

Theor. IV. Prop. IV.

Omnis circuli portio semicirculo minor, minor est duabus tertiis trianguli eandem cum ipsa basin habentis, & latera portionem contingentia.

Esto circuli portio semicirculo minor ABC, & contingant ipsam ad terminos basis rectae AD, CD, quae conveniant in puncto D. Dico Portionem ABC minorem esse duabus tertiis trianguli ADC. Ducatur enim EF quae portionem contingat in vertice B, & inscribatur ipsi triangulum maximum ABC. Quum igitur triangulum EDF majus sit dimidio trianguli ABC^*. manifestum est ab illo partem abscindi posse, ita ut reliquum tamen majus sit dimidio dicti ABC trianguli. Sit igitur hoc pacto abscissum triangulum EDG. Et ducantur porro rectae HI, KL, quae portiones reliquas AMB, BNC in verticibus suis contingant, ipsisque portionibus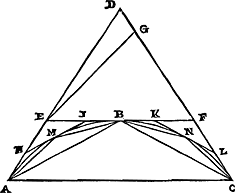

[Fig. 4.]

triangula maxima inscribantur. Idemque prorsus circa reliquas portiones fieri intelligatur, donec tandem portiones residuae simul minores sint quam duplum trianguli EDG. Erit igitur inscripta portioni figura quaedam rectilinea, atque alia circumscripta. Et quoniam triangulum EGF majus est dimidio trianguli ABC; & rursus triangula HEI, KFL, majora quam dimidiatriangulorum AMB, BNC; idque eadem semper ratione in reliquis locum habet, ut triangula super portionem verticibus constituta, eorum quae intra portiones ipsas descripta sunt, majora sint quam subdupla: apparet triangula omnia extra portionem posita etiam absque triangulo EGD majora simul esse quam dimidia triangulorum omnium intra portionem descriptorum. Atqui segmentorum in portione reliquorum triangulum quoque EGD majus est quam subduplum. Ergo triangulum EDF simul cum reliquis triangulis, quae sunt extra portionem, majus erit dimidio portionis totius ABC. Quare multo magis spatium à rectis AD, DC & arcu ABC comprehensum majus erit portionis ABC dimidio. Ac proinde triangulum ADC majus quam portionis ABC sesquialterum. Quod erat demonstrandum.

* per 2. huj.

[p. 128]

Théor. V. Prop. V.

Tout cercle est plus grand qu'un polygone à côtés égaux, qui lui est inscrit, plus le tiers de la quantité dont ce polygone en surpasse un autre polygone inscrit d'un nombre de côtés réduit à la moitié⁵⁾.

Soit un cercle à centre C; et que lui soit inscrit un polygone équilatéral, dont un des côtés soit AB. Et soit inscrit de même un autre polygone, dont AB soustend les deux côtés AD, DB. Ce dernier polygone est alors plus grand que le premier. Supposons que le tiers de l'excès soit égal à l'espace H. Je dis que le cercle est plus grand que le polygone ADB avec l'espace H. Traçons en effet à partir du centre les droites CA, CB. Comme alors le segment de cercle ADB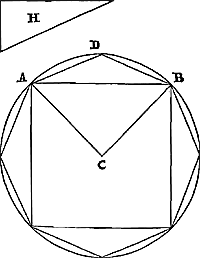

[Fig. 5.]

est plus grand que les quatre tiers du triangle ADB qui lui est inscrit^*, les segments AD, DB seront ensemble plus grands que le tiers du triangle ADB. Pour cette raison aussi le secteur CAB sera plus grand que la somme du quadrilatère CADB et du tiers du triangle ADB. Mais, comme le secteur CAB au cercle entier, ainsi le quadrilatère CDBA est au polygone ADB, et ainsi aussi le tiers du triangle ADB au tiers de l'excès du polygone ADB sur le polygone AB. Il est donc clair qu' aussi tout le cercle est plus grand que le polygone ADB augmenté du tiers de la quantité dont le polygone ADB surpasse le polygone AB, c'est-à-dire augmenté de l'espace H. Ce qu'il fallait démontrer.

5) Soit donc s_n l'aire du polygone à n côtés, inscrit dans un cercle dont le rayon est égal à l'unité; on a alors d'après le théorème présent:

π < S_2n + ⅓ (S_2n - S_n).

Introduisant ensuite, au lieu des aires des polygones leurs périmètres p, on trouve à l'aide de la relation S_2n = ½ p_n, la formule:

2π < p_2n + ⅓ (p_2n - p_n), qu'on peut comparer à la suite que nous avons déduite dans la note 7, p. 94 du Tome présent. On voit d'ailleurs qu' ici et dans le théorème suivant Huygens a atteint, pour ainsi dire d'un seul coup, une approximation qu'on ne pourrait certainement améliorer sans la rendre plus compliquée, et qui est du même ordre que celle, bien moins simple, de Snellius, que nous avons mentionnée dans la note 8, p. 95.

* d'après 3. ici.

[p. 129]

Theor. V. Prop. V.

Omnis circulus major est polygono aequalium laterum sibi inscripto & triente excessus quo id polygonum superat aliud inscriptum subduplo laterum numero⁵⁾.

Esto circulus centro C [Fig. 5]; sitque ipsi inscriptum polygonum aequalium laterum, quorum unum sit AB. Atque alterum item polygonum sit inscriptum, cujus bina latera AD, DB, subtendat AB. Hoc igitur priore polygono majus est. Sit autem excessus trienti aequale H spatium. Dico circulum majorem esse polygono ADB una cum spatio H. Ducantur enim ex centro rectae CA, CB. Quoniam igitur portio circuli ADB major est quam sesquitertia trianguli ADB sibi inscripti^*; erunt portiones AD, DB, simul majores triente trianguli ADB. Quamobrem & sector CAB major erit utrisque simul quadrilatero CADB & triente trianguli ADB. Sicut autem sector CAB ad circulum totum, ita est quadrilaterum CDBA ad polygonum ADB, & ita quoque triens trianguli ADB ad trientem excessus polygoni ADB supra polygonum AB. Ergo manifestum est circulum quoque totum majorem fore polygono ADB unà cum triente excessus quo polygonum ADB superat polygonum AB, hoc est, unà cum spatio H. Quod erat demonstrandum.

5) Soit donc s_n l'aire du polygone à n côtés, inscrit dans un cercle dont le rayon est égal à l'unité; on a alors d'après le théorème présent:

π < S_2n + ⅓ (S_2n - S_n).

Introduisant ensuite, au lieu des aires des polygones leurs périmètres p, on trouve à l'aide de la relation S_2n = ½ p_n, la formule:

2π < p_2n + ⅓ (p_2n - p_n), qu'on peut comparer à la suite que nous avons déduite dans la note 7, p. 94 du Tome présent. On voit d'ailleurs qu' ici et dans le théorème suivant Huygens a atteint, pour ainsi dire d'un seul coup, une approximation qu'on ne pourrait certainement améliorer sans la rendre plus compliquée, et qui est du même ordre que celle, bien moins simple, de Snellius, que nous avons mentionnée dans la note 8, p. 95.

* per. 3. huj.

[p. 130]

Théor. VI. Prop. VI.

Tout cercle est plus petit que les deux tiers du polygone à côtés égaux qui lui est circonscrit, plus le tiers du polygone semblable inscrit⁶⁾.

Soit donné un cercle dont le centre est A, et inscrivons-y un polygone équilatéral, dont un des côtés soit BC; et circonscrivons-y un autre semblable FEG, dont les côtés touchent le cercle aux sommets des angles du premier polygone. Je dis que le cercle est plus petit que les deux tiers du polygone FEG, augmentés du tiers du polygone BC. Menons en effet à partir du centre les droites AB, AC. Comme alors le triangle BEC repose sur la base du segment BDC et que ses côtés touchent le segment, ce segment sera moindre que les deux tiers du triangle BEC^*. Ainsi lorsqu'on ajoute au triangle ABC deux tiers du triangle BEC, c'est-à-dire, deux tiers de l'excès du quadrilatère ABEC sur le triangle ABC, l'espace formé par les deux sera plus grand que le secteur de cercle ABC. Mais il revient au même, que l'on ajoute au triangle ABC les deux tiers du dit excès, ou que l'on ajoute les deux tiers du quadrilatère ABEC, et que l'on enlève par contre les deux tiers du triangle ABC: mais par ceci on obtient les deux tiers du quadrilatère ABEC avec le tiers du triangle ABC. Il paraît donc que le secteur ABC est moindre que les deux tiers du quadrilatère ABEC augmentés du tiers du triangle ABC. Par conséquent, tout étant pris autant de fois que le secteur ABC est contenu dans le cercle, le cercle tout entier sera plus petit que les deux tiers du polygone circonscrit FEG et le tiers de l'inscrit BC. Ce qu'il fallait démontrer.

6) On a donc



,
où S_n et s_n représentent les aires des polygones circonscrit et inscrit au cercle dont le rayon est l'unité.
On en déduit aisément, en employant les relations S_n = ½ P_n et s_2n = ½ p_n,



,
où P_n et p_n désignent respectivement les périmètres des mêmes polygones.
Ensuite, afin de pouvoir comparer cette formule à la suite (1) de la note 7, p. 94, nous remplaçons P_2n par : .
De cette façon on arrive à formule ,
mentionnée dans la note 22, p. 98 et qui montre que l'approximation est du même ordre que celle qui est obtenue par le théorème précédent, dont celui-ci forme la contrepartie.

* d'après 4. ici.

[p. 131]

Theor. VI. Prop. VI.

Omnis circulus minor est duabus tertiis polygoni aequalium laterum sibi circumscripti & triente polygoni similis inscripti⁶⁾.

Esto circulus cujus centrum A, & inscribatur ipsi polygonum lateribus aequalibus, quorum unum sit BC; & aliud simile circumscribatur FEG, cujus latera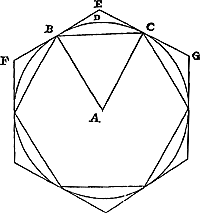

[Fig. 6.]

circulum contingant ad occursum angulorum polygoni prioris. Dico circulum minorem esse duabus tertiis polygoni FEG simul cum triente polygoni BC. Ducantur namque ex centro rectae AB, AC. Igitur quoniam super basi portionis BDC consistit triangulum BEC, cujus latera portionem contingunt, erit ipsa minor duabus tertiis trianguli BEC^*. Itaque si triangulo ABC addantur duae tertiae trianguli BEC, hoc est, duae tertiae excessus quadrilateri ABEC supra triangulum ABC, ex utrisque compositum spatium majus erit sectore circuli ABC. Idem est autem, sive triangulo ABC addantur duae tertiae excessus dicti, sive addantur duae tertiae quadrilateri ABEC, contraque auferantur duae tertiae trianguli ABC: hinc autem fiunt duae tertiae quadrilateri ABEC cum triente trianguli ABC. Ergo apparet sectorem ABC minorem esse duabus tertiis quadrilateri ABEC & triente trianguli ABC. Quare sumptis omnibus quoties sector ABC circulo continetur, totus quoque circulus minor erit duabus tertiis polygoni circumscripti FEG & triente inscripti BC. Quod erat ostendendum.

6) On a donc



,
où S_n et s_n représentent les aires des polygones circonscrit et inscrit au cercle dont le rayon est l'unité.
On en déduit aisément, en employant les relations S_n = ½ P_n et s_2n = ½ p_n,



,
où P_n et p_n désignent respectivement les périmètres des mêmes polygones.
Ensuite, afin de pouvoir comparer cette formule à la suite (1) de la note 7, p. 94, nous remplaçons P_2n par : .
De cette façon on arrive à formule ,
mentionnée dans la note 22, p. 98 et qui montre que l'approximation est du même ordre que celle qui est obtenue par le théorème précédent, dont celui-ci forme la contrepartie.

* per. 4. huj.

[p. 132]

Théor. VII. Prop. VII.

Toute circonférence de cercle est plus grande que le périmètre du polygone à côtés égaux qui lui est inscrit, plus le tiers de la quantité dont ce même périmètre surpasse le périmètre d'un autre polygone inscrit duquel le nombre des côtés est la moitié⁷⁾.

Soit donné un cercle AB, à centre O, auquel est inscrit un polygone equilatéral ACD, et un autre, d'un nombre de côtés double AECBDF. Soit encore la droite GI égale au périmètre du polygone AECBDF, tandis que GH soit égale au périmètre du polygone ACD. La différence des deux périmètres est ainsi HI, dont le tiers IK soit ajouté à GI même. Je dis que la circonférence du cercle AB est plus grande que la droite GK entière. Inscrivons, en effet, au cercle un troisième polygone équilatère ALEMC, qui ait un nombre de côtés deux fois plus grand que le polygone AECBDF. Et sur les lignes GH, HI, IK construisons des triangles dont le sommet commun soit N, et la hauteur égale au demi-diamètre du cercle AB. Alors, puisque la base GH est égale au périmètre du polygone ACD, le triangle GNH sera égal au polygone qui a deux fois autant de côtés, c'est-à-dire, au polygone AECBDF. C'est ce qui paraît, quand on a tracé du centre les droites OA et OE, dont la dernière coupe AC en P. Car le triangle AEO est égal à un triangle ayant comme base AP et comme hauteur le rayon OE. Mais, la quantième partie le triangle AEO est du polygone AECBDF, la même partie est la droite AP du périmètre ACD. Ainsi le polygone AECBDF sera égal au triangle dont la base est égale au périmètre ACD, et la hauteur au rayon EO; c'est-à-dire au triangle GNH. Pour la même raison, puisque la base GI est égale au périmètre du polygone AECBDF et que la hauteur du triangle GNI est égale au rayon du cercle, le triangle GNI sera égal au polygone ALEMC. Par suite, le triangle HNI est égal à l'excès du polygone ALEMC sur le polygone AECBDF. Mais le triangle INK est par construction le tiers du triangle HNI. Il sera donc égal au tiers du dit excès. Ainsi tout le triangle GNK sera moindre que le cercle AB^*. Mais la hauteur du triangle est égale au demi-diamètre du cercle. Il est donc évident que la droite GK est moindre que toute la circonférence du cercle. Ce qu'il fallait démontrer.

Par là il est clair que, si des quatre tiers des côtés d'un polygone inscrit au cercle on retranche le tiers des côtés d'un autre polygone inscrit, d'un nombre de côtés égal à la moitié, le reste est plus petit que la circonférence. Car il revient au même, soit qu'on ajoute au plus grand périmètre ⅓ de la quantité dont il surpasse

7) Voir la seconde formule de la note 5.

* d'après 5. ici.

[p. 133]

Theor. VII. Prop. VII.

Omnis circuli circumferentia major est perimetro polygoni aequalium laterum sibi inscripti, & triente excessus quo perimeter eadem superat perimetrum alterius polygoni inscripti subduplo laterum numero⁷⁾.

Esto circulus AB, centro O, cui inscribatur polygonum aequilaterum ACD, atque alterum duplo laterum numero AECBDF. Sitque recta GI aequalis perimetro polygoni AECBDF, GH vero aequalis perimetro polygoni ACD. Excessus igitur perimetrorum est HI; cujus triens IK adjiciatur ipsi GI. Dico totâ GK majorem esse circuli AB circumferentiam. Inscribatur enim circulo tertium polygonum aequilaterum ALEMC, quod sit duplo numero laterum polygoni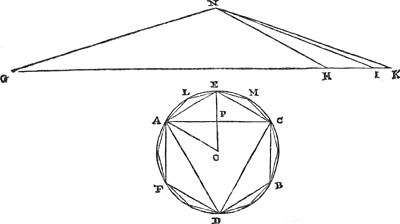

[Fig. 7.]

AECBDF. Et super lineis GH, HI, IK, triangula constituantur quorum communis vertex N, altitudo autem aequalis semidiametro circuli AB. Igitur quoniam GH basis aequalis est perimetro polygoni ACD, erit triangulum GNH aequale polygono cui bis totidem sunt latera, hoc est, polygono AECBDF. Hoc enim patet, ductis ex centro rectis OA & OE, quarum haec secet AC in P. Nam triangulum quidem AEO aequale est triangulo basin habenti AP & altitudinem radii OE. Quanta autem pars est triangulum AEO polygoni AECBDF, eadem est recta AP perimetri ACD. Itaque polygonum AECBDF aequabitur triangulo cujus basis aequalis perimetro ACD, altitudo autem radio EO: hoc est, triangulo GNH. Eâdem ratione, quoniam basis GI est aequalis polygoni AECBDF perimetro, & altitudo trianguli GNI aequalis radio circuli, erit triangulum GNI aequale polygono ALEMC. Itaque triangulum HNI aequale excessui polygoni ALEMC supra polygonum AECBDF. Trianguli autem HNI subtriplum est ex constr. triangulum INK. Ergo hoc aequale erit dicti excessus trienti. Quare totum trian

7) Voir la seconde formule de la note 5.

[p. 134]

le plus petit périmètre, soit qu'on ajoute ⅓ du plus grand périmètre et que par contre on enlève ⅓ du plus petit périmètre. Mais par là on obtient les quatre tiers du plus grand périmètre moins le tiers du plus petit. Ainsi, lorsque de seize côtés du dodécagone inscrit on déduit deux côtés de l'hexagone inscrit, c'est-à-dire le diamètre du cercle, la longueur restante sera moindre que la circonférence du cercle, ou bien, si l'on retranche le rayon de huit côtés du dodécagone, le reste sera moindre que la moitié de la circonférence. Or, ceci est utile pour une construction mécanique, parce que la différence est petite, ainsi que je le montrerai plus loin⁸⁾.

Il est clair aussi que, pour tout arc qui est moindre que la demi-circonférence, si à la corde sous-tendue on ajoute le tiers de la quantité dont la corde excède le sinus, la ligne composée est plus petite que l'arc.

8) Voir le ‘Problema II. Prop. XI’, p. 143 du Tome présent.

Théor. VIII. Prop. VIII.

Un cercle étant donné, si à l'extrémité du diamètre on mène une tangente, et que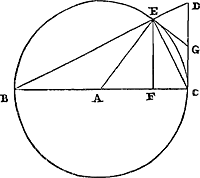

[Fig. 8.]

l'on tire aussi de l'extrémité opposée du diamètre une droite qui coupe la circonférence et rencontre la tangente menée: les deux tiers de la tangente interceptée avec le tiers de la droite qui, à partir du point d'intersection, tombe a angles droits sur le diamètre, seront ensemble plus grands que l'arc découpé adjacent⁹⁾.

Soit donné un cercle de centre A et à diamètre BC; et soit menée à partir de C une droite CD qui touche le cercle: supposons qu'il y aboutisse une droite BD, tirée à partir de l'autre extrémité du diamètre, et qu'elle coupe la circonférence en E: et soit EF perpendiculaire au diamètre BC. Je dis que les deux tiers de la tangente interceptée CD, ensemble avec le tiers de cette droite EF, sont plus grands que l'arc EC. Joignons en effet AE, EC; et menons une tangente au cercle au point E, qui rencontre la tangente CD en G. Ainsi GE sera égal à GC, et aussi à DG; car si avec G comme centre on décrit une circonférence qui passe par les points C, E, elle passera aussii par le point D, puisque l'angle CED est droit. Or nous avons montré ci-dessus, que les deux tiers du quadrilatére AEGC, ensemble avec le tiers du triangle AEC, sont plus grands que le secteur AEC^*. Et le quadrilatère AEGC est égal au triangle ayant comme base le double de CG,

9) Le but de ce théorème est surtout de préparer celui qui suit. Toutefois il est clair qu'il mène plus directement au suivant: Toute circonférence de cercle est plus petite que les deux tiers du périmètre d'un polygone à côtés égaux, qui lui est circonscrit, plus le tiers du périmètre du polygone inscrit dont le nombre des côtés est la moitié.
Mais il est probable que ce théorème, qu'on trouve exprimé par la seconde formule de la note 6 et qui est donc l'equivalent du ‘Theor. VI’, a été considéré par Huygens comme moins élégant et moins pratique que le ‘Theor. IX’, qu'il fait suivre, et dont, de plus l'approximation est un peu meilleure.

* d'après 6. ici.

[p. 135]

gulum GNK minus erit circulo AB^*. Altitudo autem trianguli aequalis est circuli semidiametro. Ergo evidens est rectam GK totâ circuli circumferentiâ minorem esse. Quod erat ostendendum.

Hinc manifestum est, si à sesquitertio laterum polygoni circulo inscripti auferatur triens laterum polygoni alterius inscripti subduplo laterum numero, reliquum circumferentiâ minus esse. Idem enim est, sive perimetro majori addatur ⅓ excessus quo ipsa superat perimetrum minorem, sive addatur ⅓ perimetri majoris contraque auferatur ⅓ perimetri minoris. Hinc autem fit sesquitertium majoris perimetri minùs triente minoris. Quare si à sexdecim inscripti dodecagoni lateribus duo latera inscripti hexagoni, hoc est, diameter circuli deducatur, reliqua circuli circumferentiâ minor erit aut si ab octo dodecagoni lateribus radius deducatur, reliqua minor erit circumferentiae semisse. Hoc autem ad constructionem mechanicam utile est, quoniam exigua est differentia, sicut postea ostendetur⁸⁾.

Manifestum etiam, in omni arcu qui semicircumferentiâ minor sit, si ad subtensam addatur triens excessus quo subtensa sinum superat, compositam arcu minorem esse.

* per. 5. huj.

8) Voir le ‘Problema II. Prop. XI’, p. 143 du Tome présent.

Theor. VIII. Prop. VIII.

Circulo dato, si ad diametri terminum contingens ducatur, ducatur autem & ab opposito diametri termino quae circumferentiam secet occurratque tangenti ductae: erunt interceptae tangentis duae tertiae cum triente ejus quae ab intersectionis puncto diametro ad angulos rectos incidet, simul arcu abscisso adjacente majores⁹⁾.

Esto circulus [Fig. 8] centro A, diametro BC; & ducatur ex C recta quae circulum contingat CD: huic autem occurrat ducta ab altero diametri termino recta BD, quae circumferentiam secet in E: sitque EF diametro BC ad angulos rectos. Dico tangentis interceptae CD duas tertias simul cum triente ipsius EF, arcu EC majores esse. Jungantur enim AE, EC; & ducatur tangens circulum in E puncto, quae tangenti CD occurrat in G. Erit igitur GE ipsi GC aequalis, itemque DG; nam si centro G circumferentia describatur quae transeat per puncta C, E, eadem transibit quoque per D punctum, quoniam angulus CED rectus est. Ostensum autem fuit suprà, duas tertias quadrilateri AEGC unà cum triente trianguli AEC simul majores esse sectore AEC^*. Estque quadrilaterum AEGC aequale triangulo basin habenti duplam CG, hoc est, CD: & altitudinem CA, triangulum verò

9) Le but de ce théorème est surtout de préparer celui qui suit. Toutefois il est clair qu'il mène plus directement au suivant: Toute circonférence de cercle est plus petite que les deux tiers du périmètre d'un polygone à côtés égaux, qui lui est circonscrit, plus le tiers du périmètre du polygone inscrit dont le nombre des côtés est la moitié.
Mais il est probable que ce théorème, qu'on trouve exprimé par la seconde formule de la note 6 et qui est donc l'equivalent du ‘Theor. VI’, a été considéré par Huygens comme moins élégant et moins pratique que le ‘Theor. IX’, qu'il fait suivre, et dont, de plus l'approximation est un peu meilleure.

* per. 6. huj.

[p. 136]

c'est-à-dire, CD, et comme hauteur CA: mais le triangle AEC est égal au triangle ayant une base égale à cette EF et la dite hauteur AC. Ainsi il est clair que les deux tiers du quadrilatère AEGC, augmentés du tiers du triangle AEC, sont égaux au triangle qui a pour base une droite composée des deux tiers de CD et du tiers de EF, et dont la hauteur est le rayon AC. C'est pourquoi aussi le triangle sera plus grand que le secteur AEC. Il résulte de là que sa base, c'est-à-dire, la droite formée des deux tiers de CD et du tiers de EF, est plus grande que l'arc CE. Ce qu'il fallait démontrer.

Théor. IX. Prop. IX.

Toute circonférence de cercle est plus petite que les deux tiers du périmètre d'un polygone à côtés égaux qui lui est inscrit plus le tiers du périmètre du polygone semblable circonscrit¹⁰⁾.

Soit donné un cercle dont le centre est A; et inscrivons-y un polygone équilatéral, dont le côté est CD: et circonscrivons-y un autre semblable, à côtés parallèles à ceux du premier, desquels un soit EF. Je dis que la circonférence de tout le cercle est plus petite que les deux tiers du contour du polygone CD plus le tiers du contour du polygone EF. Menons en effet le diamètre du cercle BG, qui divise à la fois au milieu le côté CD du polygone inscrit en H et le côté EF du circonscrit en G (car évidemment G est le point de contact du côté EF). Et prenons HL égal à HG et joignons AC, BC et prolongeons-les; et supposons que BC rencontre le côté EF en K, tandis que la droite AC prolongée atteint en E l'angle du polygone circonscrit. Puisque ainsi HL est égal à HG, BL sera le double de AH: et par conséquent comme GA à AH ainsi GB est à BL. Mais le rapport de HB à BL est plus grand que celui de GB à BH; puisque les trois lignes GB, HB, LB s'excèdent mutuellement de la même quantité. Et ainsi le rapport de GB à BL, c'est-à-dire, de GA à AH, sera plus grand que le

10) A l'aide des notations de la note 6, p. 130, le théorème s'exprime par la formule:




qu'on peut écrire:
.
Pour arriver à ce théorème, en partant de celui que nous avons énoncé dans la note précédente, il suffira de prouver qu'on a:




ou bien, en introduisant les côtés A_n et a_n des polygones circonscrits et inscrits,



c'est-à-dire, A_n + a_n > 4 A_2n, ou enfin (voir la figure 9) EG + CH > 2 KG; puisque EG = ½ A_n; CH = ½ a_n; KG = DC de la fig. 8 = A_2n.
C'est là, en effet, le but des considérations géométriques qui vont suivre, et qui auraient pu être beaucoup abrégées à l'aide de la remarque que nous ferons dans la note 11.

[p. 137]

AEC aequale triangulo basin ipsi EF aequalem habenti & altitudinem dictam AC. Itaque apparet duas tertias quadrilateri AEGC simul cum triente trianguli AEC aequari triangulo qui basin habeat compositam ex duabus tertiis CD & triente EF, altitudinum verò radii AC. Quare ejusmodi quoque triangulum majus erit sectore AEC. Unde liquet basin ipsius, hoc est, compositam ex duabus tertiis ipsius CD & triente ipsius EF, majorem esse arcu CE. Quod erat demonstrandum.

Theor. IX. Prop. IX.

Omnis circuli circumferentia minor est duabus tertiis perimetri polygoni aequalium laterum sibi inscripti & triente perimetri polygoni similis circumscripti¹⁰⁾.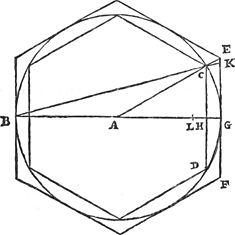

[Fig. 9.]

Esto Circulus cujus A centrum; & inscribatur ei polygonum aequilaterum, cujus latus CD: simileque aliud circumscribatur lateribus ad priora parallelis, quorum unum sit EF. Dico circuli totius circumferentiam minorem esse duabus tertiis ambitus polygoni CD & triente ambitus polygoni EF. Ducatur namque diameter circuli BG, quae simul inscripti polygoni latus CD medium dividat in H, & circumscripti latus EF in G, (constat autem G fore punctum contactus lateris EF,) Et ponatur HL aequalis ipsi HG, & jungantur AC, BC & producantur, occurratque BC lateri EF in K, producta autem AC incidet in E angulum polygoni circumscripti. Quoniam igitur HL aequalis HG, erit BL dupla ipsius AH: Ideoque ut GA ad AL, ita GB ad BL. Major autem est ratio HB ad BL, quam GB ad BH; quoniam hae tres sese aequaliter excedunt GB, HB, LB. Itaque major erit ratio GB ad BL, hoc est, GA ad AH, quam duplicata rationis GB ad BH. Sicut autem GA ad

10) A l'aide des notations de la note 6, p. 130, le théorème s'exprime par la formule:




qu'on peut écrire:
.
Pour arriver à ce théorème, en partant de celui que nous avons énoncé dans la note précédente, il suffira de prouver qu'on a:




ou bien, en introduisant les côtés A_n et a_n des polygones circonscrits et inscrits,



c'est-à-dire, A_n + a_n > 4 A_2n, ou enfin (voir la figure 9) EG + CH > 2 KG; puisque EG = ½ A_n; CH = ½ a_n; KG = DC de la fig. 8 = A_2n.
C'est là, en effet, le but des considérations géométriques qui vont suivre, et qui auraient pu être beaucoup abrégées à l'aide de la remarque que nous ferons dans la note 11.

[p. 138]

carré du rapport de GB à BH. Or, comme GA à AH, ainsi EG est à CH; et comme GB à BH, ainsi KG est à CH. Par conséquent, le rapport de EG à CH sera plus grand que le carré de celui de KG à CH. Pour cette raison le rapport de EG à KG est plus grand que celui de KG à CH. Par suite les deux lignes EG, CH sont certainement ensemble plus grandes que le double de KG¹¹⁾. Et en prenant les tiers de toutes les lignes, les tiers des deux EG et CH seront ensemble plus grands que les deux tiers de KG. Pour cette raison, si l'on ajoute de part et d'autre le tiers de CH, le tiers de EG avec les deux tiers de CH sera plus grand que les deux tiers de KG avec le tiers de CH. Mais l'arc CG est encore plus petit que ceux-ci^*. Donc, les deux tiers de CH, ensemble avec le tiers de EG, sont à plus forte raison plus grands que ce même arc CG. Si donc nous prenons toutes les grandeurs autant de fois que l'arc CG est contenu dans la circonférence entière, les deux tiers du périmètre du polygone CD, plus le tiers du périmètre du polygone EF, seront aussi plus grands que la circonférence du cercle entier. Ce qu'il fallait démontrer.

Ainsi donc, tout arc de circonférence plus petit qu'un quadrant est plus petit que les deux tiers de son sinus plus le tiers de sa tangente.

11) Ce résultat aurait pu être atteint bien plus facilement en abaissant une perpendiculaire CM sur EG. Alors CK est la bissectrice de l'angle ECM et on a par suite EK > KM, c'est-à-dire: EG - KG > KG - CH; donc EG + CH > 2 KG.

* d'après ce qui précède.

Problème I. Prop. X.

Trouver le rapport de la périphérie au diamètre, aussi proche que l'on veut du vrai.

Archimède prouva¹²⁾, par les polygones inscrit et circonscrit de 96 côtés, que le rapport de la périphérie au diamètre est moindre que le triple et un septième, mais plus grande que 3 10/71. Mais nous allons démontrer ici la même chose au moyen du dodécagone.

En effet, puisque le côté du dodécagone inscrit au cercle est plus grand que 5176⅜ des parties dont le rayon en contient 10000: la somme de douze côtés, c'est-à-dire, le périmètre du dodécagone inscrit, sera de même plus grand que 62116½: mais le périmètre de l'hexagone inscrit est le sextuple du rayon, et se compose par conséquent de 60000 parties. Ainsi donc le périmètre du dodécagone excède le périmètre de l'hexagone de plus que 2116½ parties. Le tiers de l'excès sera donc plus grand que 705½. De sorte que le périmètre du dodécagone, ensemble avec le tiers de la quantité dont il excéde le périmètre de l'hexagone, sera plus grand que la somme de 62116½ et 705½ parties, c'est-à-dire, que 62822 parties. Et par conséquent la périphérie du cercle sera à plus forte raison plus grande que cela^*. Mais le rapport de 62822 à 20000, la longueur du diamètre, est plus

12) Au lieu cité dans la note 1, p. 93 du Tome présent.

* d'après 7. ici.

[p. 139]

AH, ita est EG ad CH; & sicut GB ad BH, ita KG ad CH. Ergo major erit ratio EG ad CH, quàm duplicata ejus, quam habet KG ad CH. Quare major

[Fig. 9.]

ratio EG ad KG, quam KG ad CH. Ideoque duae simul EG, CH omnino majores duplâ KG¹¹⁾. Et sumptis omnium trientibus, erunt trientes utriusque EG & CH simul majores duabus tertiis KG. Quamobrem addito utrimque ipsius CH triente, erit triens EG cum duabus tertiis CH, major duabus tertiis KG cum triente CH. Hisce verò minor etiam est arcus CG^*. Igitur duae tertiae CH simul cum triente ipsius EG majores omnino sunt eodem arcu CG. Unde sumptis omnibus toties quoties arcus CG circumferentiâ totâ continetur, erunt quoque duae tertiae perimetri polygoni CD, cum triente perimetri polygoni EF, majores cirçuli totius circumferentiâ. Quod fuerat ostendendum.

Omnis igitur circumferentiae arcus quadrante minor, minor est sinus sui besse & tangentis triente.

11) Ce résultat aurait pu être atteint bien plus facilement en abaissant une perpendiculaire CM sur EG. Alors CK est la bissectrice de l'angle ECM et on a par suite EK > KM, c'est-à-dire: EG - KG > KG - CH; donc EG + CH > 2 KG.

* per praeced.

Problema I. Prop. X.

Peripheriae ad diametrum rationem invenire quamlibet verae propinquam.

Minorem esse peripheriae ad diametrum rationem quam triplam sesquiseptimam: majorem verò quam 3 10/71, Archimedes ostendit¹²⁾ inscripto circumscriptoque 96 laterum polygono. Idem verò hic per dodecagona demonstrabimus.

Quia enim latus inscripti circulo dodecagoni majus est partibus 5176⅜, qualium radius continet 10000: duodecim latera proinde, hoc est, perimeter inscripti dodecagoni major erit quam 62116½: perimeter autem hexagoni inscripti est radii sextupla, ideoque partium 60000. Igitur dodecagoni perimeter perimetrum hexagoni excedit ampliùs quam partibus 2116½. Quare triens excessus major erit quam 705½. Igitur dodecagoni perimeter unà cum triente excessus, quo perimetrum hexagoni superat, major erit aggregato partium 62116½ & 705½, hoc est, partibus 62822. Atque hisce proinde omninò major erit circuli peripheria^*. Est autem major ratio 62822 ad 20000, longitudinem diametri,

12) Au lieu cité dans la note 1, p. 93 du Tome présent.

* per. 7. huj.

[p. 140]

grand que celui de 3 10/71 à 1. Le rapport de la périphérie au diamètre sera donc à plus forte raison aussi plus grand.

D'autre part, puisque le côté du dodécagone inscrit est plus petit que 5176⅖ parties, huit côtés, c'est-à-dire ⅔ du périmètre, seront moindres que 41411⅕. De même, puisque le côté du dodécagone circonscrit est plus petit que 5359, quatre côtés, c'est-à-dire, le tiers du périmètre, seront moindres que 21436. Pour cette raison, ⅔ du périmètre du dodécagone inscrit plus le tiers du périmètre du circonscrit seront moindres que 62847⅕. Mais la circonférence de cercle est aussi plus petite que cette somme^*. Cette circonférence sera donc à plus forte raison au diamètre dans un rapport moindre que 62847⅕ à 20000; et bien moindre par conséquent que 62857 1/7 à 20000, ce qui est le triple et un septième. Et ainsi sont démontrées les limites du rapport de la périphérie au diamètre qu' Archimède établit. Mais nous les démontrerons dans la suite¹³⁾ en nous servant du côté du seul triangle équilatéral inscrit. Ensuite, pour trouver un rapport plus approché il faudra considérer des polygones d'un plus grand nombre de côtés, Ainsi figurons nous que nous ayons circonscrit au cercle un polygone de 60 côtés et que nous en ayons inscrit un autre. Et qu'en outre soit inscrit un polygone d'un nombre de côtés égal à la moitié, savoir celui de trente côtés.

Or, on trouve que le côté du polygone à soixante côtés inscrit est plus grand que 10467191 parties dont le rayon en contient 100000000 et le côté du polygone à trente côtés plus petit que 20905693 parties: dont la moitié 10452846½ est le sinus de l'arc égal à 1/60 de la circonférence. Mais la corde sous-tendue était 10467191. Donc la différence est 14344½, moindre que la vraie: et le tiers de la différence est 4781½, ce qui, ajouté à la sous-tendue 10467191, sait 10471972½. De sorte que l'arc de 1/60 de la circonférence est plus grand que ce nombre de parties. Mais en le comptant 60 fois on obtient 628318350. Par conséquent la circonférence entière est à plus forte raison plus grande que ce nombre de parties.

Et puis, comme le côté du polygone inscrit à 60 angles est plus petit que 10467192, les deux tiers de celui-ci seront moindres que 6978128. Mais comme le côté du polygone circonscrit de 60 angles est plus petit que 10481556, le tiers de celui-ci sera plus petit que 3493852. Ce qui ajouté à 6978128 fait 10471980. Ce nombre de parties surpasse donc certainement 1/60 de la circonférence, et le soixantuple de celles-là, c'est-à-dire, 628318800, sera plus grand que la circonférence toute entière. Mais employons encore des polygones de 10800 côtés, dont d'une part le côté de l'inscrit, qui est sous-tendu par un arc de deux minutes, a été trouvé, d'après le calcul de Ludolphe de Cologne, un arithméticien distingué, se composer de 58177640912684919 parties et pas une de plus, tandis que le côté du polygone circonscrit est de 58177643374063182 parties et pas une de moins. Et en outre le côté du polygone inscrit dont le nombre des côtés est la moitié, est de 116355276902613523 parties et pas une de moins¹⁴⁾. On déduit de

* d'après 9. ici.

13) Voir le ‘Problema IV. Propos. XX’, p. 173.

14) Les côtés des polygones de 10800 et 5400 côtés, c'est-à-dire, les cordes des arcs de 2′ et de 4′, Huygens pouvait les emprunter à une petite table des cordes de 1′ à 12′ qui les donne avec encore quatre chiffres en plus et qu'on trouve au folio 21 de l'ouvrage de Ludolphe de Cologne, mentionné en premier lieu dans la note 3, p. 93 du Tome présent.
Le côté du polygone circonscrit devait être calculé par la formule ; mais ce calcul était beaucoup simplifié par ce que la table en question contient aussi les cordes complémentaires, c'est-à-dire, les valeurs de . Ainsi, pour trouver A₁₀₈₀₀, Huygens n'avait qu' à multiplier a₁₀₈₀₀ par la fraction: 200000000000000000.../199999991538405065....

[p. 141]

quam 3 10/71 ad 1. Ergo omnino etiam peripheriae ad diametrum ratio major erit.

Rursus quoniam latus dodecagoni inscripti minus est partibus 5176⅖. Erunt octo latera, hoc est, ⅔ perimetri minora quam 41411⅕. Item quia latus dodecagoni circumscripti minus est quam 5359, erunt quatuor latera, hoc est, triens perimetri minor quam 21436. Quamobrem ⅔ perimetri dodecagoni inscripti cum triente perimetri circumscripti minores erunt quam 62847⅕. Sed istis simul minor etiam est circuli circumferentia^*. Ergo haec ad diametrum omnino minorem habebit rationem, quam 62847⅕ ad 20000; & multo minorem proinde, quam 62857 1/7 ad 20000, hoc est, quam triplam sesquiseptimam. Demonstrati itaque sunt termini Rationis peripheriae ad diametrum, quos Archimedes statuit. Eosdem verò postmodum solius inscripti trigoni aequilateri latere indagato comprobabimus¹³⁾. Porrò ut propinquior inveniatur ratio plurium laterum polygona consideranda sunt. Intelligatur igitur circumscriptum circulo polygonum aliudque inscriptum laterum 60. Et praeter haec subduplo numero laterum inscriptum, nempe trigintangulum.

Et invenitur quidem latus inscripti sexagintanguli majus partibus 10467191, qualium radius 100000000 & latus trigintanguli minus quam 20905693: cujus dimidium 10452846½ est sinus arcus aequantis 1/60 circumferentiae. Subtensa autem erat 10467191. Ergo differentia 14344½ minor verâ: & triens differentiae 4781½, qui additus ad subtensam 10467191 facit 10471972½. Quibus itaque major est arcus 1/60 circumferentiae. Ductis autem 10471972½ sexagies fiunt 628318350. Hisce igitur partibus omnino major est circumferentia tota.

Rursus quoniam latus inscripti 60 anguli minus est quam 10467192, erunt duae tertiae ipsius minores quam 6978128. Circumscripti autem 60 anguli latus cum sit minus quam 10481556, erit triens ipsius minor quam 3493852. Quibus additis ad 6978128, fiunt 10471980. Hae igitur omnino excedunt 1/60 circumferentiae, & sexagecuplum ipsarum, hoc est 628318800 majus erit circumferentiâ totâ. Quod si verò polygona adhibeamus laterum 10800, quorum inscripti quidem latus, calculo Ludolphi Coloniensis, Arithmetici nobilis, inventum est partium 58177640912684919 non unâ amplius, subtenditurque duobus scrup. primis; circumscripti autem latus 58177643374063182 non unâ minus. Praetereaque latus polygoni subduplo laterum numero inscripti, quod est 116355276902613523 non unâ minus¹⁴⁾. Hinc peripheriae longitudo invenitur major quam partium

* per. 9. huj.

13) Voir le ‘Problema IV. Propos. XX’, p. 173.

14) Les côtés des polygones de 10800 et 5400 côtés, c'est-à-dire, les cordes des arcs de 2′ et de 4′, Huygens pouvait les emprunter à une petite table des cordes de 1′ à 12′ qui les donne avec encore quatre chiffres en plus et qu'on trouve au folio 21 de l'ouvrage de Ludolphe de Cologne, mentionné en premier lieu dans la note 3, p. 93 du Tome présent.
Le côté du polygone circonscrit devait être calculé par la formule ; mais ce calcul était beaucoup simplifié par ce que la table en question contient aussi les cordes complémentaires, c'est-à-dire, les valeurs de . Ainsi, pour trouver A₁₀₈₀₀, Huygens n'avait qu' à multiplier a₁₀₈₀₀ par la fraction: 200000000000000000.../199999991538405065....

[p. 142]

là que la longueur de la périphérie est plus grande que 6283185307179584 parties et plus petite que 6283185307179589, dont le rayon en a 1000000000000000. Or, par la méthode habituelle de l'addition des côtés de ces polygones inscrit et circonscrit on trouverait seulement que la périphérie est plus grande que 62831852 parties, et plus petite que 62831855. On voit donc que nous avons trouvé un nombre de chiffres vrais plus grand que le doublé. Mais il en est de même aussi dans ce qui précède, et doit toujours arriver quel que soit le nombre de côtés des polygones dont nous faisons usage. Et par les propositions que nous donnerons dans la suite, on verra qu'on peut facilement obtenir un nombre de chiffres trois fois plus grand¹⁵⁾.

15) Soit k le nombre des chiffres fourni par la méthode d'Archimède, appliquée aux polygones de 2n côtés, alors, en posant le rayon du cercle égal à l'unité, on aura: , où a < 1;
donc, certainement:




Or, la différence des limites respectives, données par les Théorèmes VII et IX est égale à




Elle sera donc plus petite que .
On connaîtra donc, généralement parlant, le nombre 2π, à l'aide de ces limites, jusqu'en 2k chiffres au moins; mais comme a² sera souvent considérablement moins que l'unité, le nombre des chiffres connus pourra excéder facilement le nombre 2k d'une et quelquefois de deux unités, et de plus encore.
Plus loin, au ‘Problema IV’, Huygens emploie des limites dont la différence est à peu près égale à et on trouvera donc alors, en général, 3k chiffres et plus, au moyen de ces nouvelles limites.
L'assertion de Huygens est donc juste, si l'on excepte les cas très spéciaux où une légère différence excerce une influence anormale sur le nombre des chiffres connus.
Nous ne savons pas, d'ailleurs, précisément comment Huygens y est parvenu; mais il semble probable qu'en cherchant la différence des limites, il a remarqué qu'elle dépendait respectivement du carré et du cube de l'expression p_2n - p_n; ce qui, de plus, a pu lui suggérer la compàraison avec le nombre des chiffres du carré et du cube d'un nombre donné, laquelle on rencontre dans la préface à la p. 117 du Tome présent.

Problème II. Prop. XI.

Prendre une droite égale à la périphérie d'un cercle donné.

Nous avons montré ci-dessus¹⁶⁾ que huit côtés du dodécagone inscrit, diminués du rayon du cercle, sont plus petits que la demi-périphérie. Mais dans une construction, la différence ne peut pas être aperçue dans la plupart des cas. Car si l'on ajoute la quatre-millième partie du diamètre à la longueur ainsi trouvée, elle dépassera déjà la demi-périphérie. C'est ce que l'on reconnaît comme il suit. Des parties dont le rayon en a 10000, le côté du dodécagone inscrit dans le cercle en contient plus que 5176⅜. De sorte que huit côtés font plus grands que 41411, et retranchant le rayon 10000, le reste sera plus grand que 31411; si l'on ajoute à cela 5 parties, ce qui est 1/4000 du diamètre, on trouve déjà 31416; et il résulte de ce qui précède que la moitié de la circonférence est plus petite que ce nombre de parties. Or, le côté du dodécagone inscrit s'obtient facilement, puisque le rayon sous-tend un sextant de la périphérie. Et ce rapport est plus précis que si nous faisons usage du triple et un septième. Car suivant ce dernier rapport la longueur dépasse la ½¹⁷⁾ périphérie de plus de 1/1600 du diamètre.

16) Voir l'avant-dernier alinéa de la démonstration du ‘Theor. VII. Prop. VII’, p. 135.

17) Le nombre ½ a été interpolé à la plume dans l'exemplaire de Huygens, que nous possédons.

[p. 143]

6283185307179584; minor autem quam 6283185307179589, qualium radius 1000000000000000. Solitâ autem methodo ex additis inscripti circumscriptique polygoni istius lateribus, invenietur tantùm majorem esse peripheriam partibus 62831852, & minorem 62831855. Patet igitur notaram verarum ampliùs quam duplum numerum esse à nobis inventum. Hoc autem & in praecedentibus ita se habet, semperque evenire necesse est quotcunque laterum polygonis utamur. At per ea, quae postea trademus, triplum numerum notarum facilè obteneri apparebit¹⁵⁾.

15) Soit k le nombre des chiffres fourni par la méthode d'Archimède, appliquée aux polygones de 2n côtés, alors, en posant le rayon du cercle égal à l'unité, on aura: , où a < 1;
donc, certainement:




Or, la différence des limites respectives, données par les Théorèmes VII et IX est égale à




Elle sera donc plus petite que .
On connaîtra donc, généralement parlant, le nombre 2π, à l'aide de ces limites, jusqu'en 2k chiffres au moins; mais comme a² sera souvent considérablement moins que l'unité, le nombre des chiffres connus pourra excéder facilement le nombre 2k d'une et quelquefois de deux unités, et de plus encore.
Plus loin, au ‘Problema IV’, Huygens emploie des limites dont la différence est à peu près égale à et on trouvera donc alors, en général, 3k chiffres et plus, au moyen de ces nouvelles limites.
L'assertion de Huygens est donc juste, si l'on excepte les cas très spéciaux où une légère différence excerce une influence anormale sur le nombre des chiffres connus.
Nous ne savons pas, d'ailleurs, précisément comment Huygens y est parvenu; mais il semble probable qu'en cherchant la différence des limites, il a remarqué qu'elle dépendait respectivement du carré et du cube de l'expression p_2n - p_n; ce qui, de plus, a pu lui suggérer la compàraison avec le nombre des chiffres du carré et du cube d'un nombre donné, laquelle on rencontre dans la préface à la p. 117 du Tome présent.

Problema II. Prop. XI.

Rectam sumere peripheriae dati circuli aequalem.

Ostensum est superius¹⁶⁾, quod octo inscripti dodecagoni latera dempto circuli radio minora sunt peripheriâ dimidiâ. In constructione autem ut plurimum defectus animadverti nequit. Nam si quatermillesima diametri pars accedat longitudini sic inventae, jam dimidiam peripheriam excedet. Quod sic fiet manifestum. Quarum partium radius est 10000, earum latus dodecagoni inscripti circulo est amplius quam 5176⅜. Unde latera octo majora quam 41411. & dempto radio 10000, erit reliqua major quam 31411. cui si addantur partes 5, hoc est, 1/4000 diametri, fient jam 31416; quibus minorem esse circumferentiam dimidiam liquet ex praecedentibus. Latus autem dodecagoni inscripti facilè invenitur, quia radius peripheriae sextantem subtendit. Estque haec ratio accuratior quam si triplâ sesquiseptimâ utamur. Nam secundùm eam excedetur ½¹⁷⁾ peripheriae longitudo ampliùs quam 1/1600 diametri.

16) Voir l'avant-dernier alinéa de la démonstration du ‘Theor. VII. Prop. VII’, p. 135.

17) Le nombre ½ a été interpolé à la plume dans l'exemplaire de Huygens, que nous possédons.

[p. 144]

Autrement.

Soit donné un cercle dont BC est le diamètre. Divisons la demi-circonférence BC en deux parties égales au point D, et le reste en trois parties égales en E et F. Et joignons DE, DF, qui coupent le diamètre en G et H. Alors l'un des côtés du triangle GDH, ajouté à la base GH, sera un tout petit peu plus grand que le quadrant BD, et ne le dépassera même pas de 1/5000 u diamètre BC. Il faut savoir, en effet, que DG ou DH sont égaux á deux côtés du dodécagone inscrit¹⁸⁾, tandis que GH est égal au côté du dodécagone circonscrit¹⁹⁾. D'où il résulte que la somme de DG et GH est plus grande que le quadrant BD. Car, comme d'après la Prop. 8²⁰⁾ huit côtés du dodécagone inscrit dans le cercle avec quatre côtés du circonscrit sont plus grands que la périphérie toute entière, pour cette raison, en prenant la quatrième partie du tout, deux côtés de l'inscrit avec un seul côté du circonscrit seront aussi plus grands que le quart de la périphérie. Ensuite, puisque le côté du dodécagone inscrit est plus petit que 51764 parties dont BC en a 200000, deux côtés, c'est-à-dire GD, seront moindres que 103528. Mais le côté du dodécagone circonscrit est plus pecit que 53590 parties, donc aussi la droite GH. Par conséquent les droites DG et GH réunies font moins que 157118. Mais, d'après ce qui précède, on sait que le quadrant BD est plus grand que 157079. La différence est donc plus petite que 39 parties, alors que 40 ne font que 1/5000 du diamètre BC.

18) Puisque l'angle EDF égale 30^o, on a ½ DH = ½r : cos 15^o=r sin 30^o : cos 15^o=2r sin 15^o= a₁₂.

19) Soit M le centre du cercle, alors, puisque EDF est 30^o, il est évident que GH est un des côtés du dodécagone circonscrit à un cercle dont le rayon égale DM et dont D est le centre.

20) Lisez 9.

Autrement²¹⁾.

Ajoutons à trois demi-diamètres 1/10 du côté du carré inscrit; la droite ainsi composée égalera la demi-circonférence de si près, qu'elle n'est pas plus courte que 1/18000²²⁾ du diamètre. Le côté du carré est plus grand que 141421 parties dont le rayon en a 100000, d'où ce qui vient d'être dit se démontre aisément.

Ou plutôt on ajoutera à six demi-diamètres ⅕ du côté susdit du carré inscrit, pour avoir une droite égale à la périphérie totale.

21) Tout ce second ‘Aliter’ ne se trouvait pas dans le texte; Huygens l'a ajouté à la plume dans son exemplaire à une date qui nous est inconnue.

22) Lisez 1/11000. La différence est sensiblement la 1/11700^ième partie du diamètre.

[p. 145]

Aliter.

Esto datus circulus cujus BC diameter. Dividatur semicircumferentia BC bifariam in D. reliqua verò trifariam in E & F. Et jungantur DE, DF, quae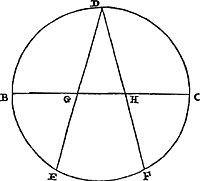

[Fig. 10.]

secent diametrum in G & H. Erit trianguli GDH latus alterum unà cum basi GH quadrante BD exiguo majus, neque enim excedet 1/5000 diametri BC. Sciendum est enim fieri DG vel DH duobus inscripti dodecagoni lateribus aequales¹⁸⁾. GH autem lateri dodecagoni circumscripti¹⁹⁾. Unde quidem junctas DG & GH majores esse constat quadrante BD. Nam quia per 8.²⁰⁾ huj. octo latera dodecagoni circulo inscripti cum quatuor lateribus circumscripti majora sunt peripheriâ totâ, ideo sumptâ omnium quartâ parte erunt quoque duo latera inscripti cum latere uno circumscripti majora peripheriae quadrante. Porro quoniam latus inscripti dodecagoni minus est quam partium 51764 qualium BC 200000: erunt latera duo, hoc est, GD, minor quam 103528. Circumscripti autem dodecagoni latus minus est partibus 53590, ipsa nimirum GH. Itaque junctae unà DG, GH efficiunt minus quam 157118. At quadrantem BD constat ex praecedentibus majorem esse quam 157079. Ergo differentia minor est quam partium 39, cum 40 demum efficiant 1/5000 diametri BC.

18) Puisque l'angle EDF égale 30^o, on a ½ DH = ½r : cos 15^o=r sin 30^o : cos 15^o=2r sin 15^o= a₁₂.

19) Soit M le centre du cercle, alors, puisque EDF est 30^o, il est évident que GH est un des côtés du dodécagone circonscrit à un cercle dont le rayon égale DM et dont D est le centre.

20) Lisez 9.

Aliter²¹⁾.

Tribus semidiametris addatur 1/10 lateris inscripti quadrati; composita semicircumferuntiae aequabitur tam propè, ut non 1/18000²²⁾ diametri brevior sit. Latus quadrati est majus quam partium 141421 qualium radius 100000, unde quod dictum est facile demonstratur.

Vel potius sex semidiametris addatur ⅕ dicti lateris quadrati inscripti ut habeatur recta aequalis peripheriae toti.

21) Tout ce second ‘Aliter’ ne se trouvait pas dans le texte; Huygens l'a ajouté à la plume dans son exemplaire à une date qui nous est inconnue.

22) Lisez 1/11000. La différence est sensiblement la 1/11700^ième partie du diamètre.

[p. 146]

Problème III. Prop. XII.

Prendre une droite égale à un arc donné quelconque.

Soit donné un arc de circonférence CD, d'abord plus petit qu'un quadrant, dont il s'agisse de trouver une droite qui lui est égale. Divisons l'arc CD en deux parties égales en E, et supposons que la droite FG soit égale à la corde sous-tendue CD. Et soit FH égale à la somme des deux cordes CE, ED, qui sous-tendent les moitiés des arcs. Et à cette FH ajoutons HI, le tiers de l'excès GH. La droite entière FI sera presque égale à l'arc CD: de manière que, en y ajoutant une petite partie, dont elle en contient 1200, elle sera plus grande, même si l'arc CD est donné égal à un quadrant. Mais dans les arcs plus petits la différence sera plus petite. Car si l'arc donné n'est pas plus grand que le sextant de la périphérie, la ligne trouvée différera moins de 1/6000 de sa grandeur de la vraie longueur de l'arc. Or, que les droites trouvées de cette façon sont plus petites que les arcs, cela résulte du thèorème 7 de cet ouvrage. Mais nous allons démontrer ce qui en est de la grandeur de la différence.

Ainsi, posant d'abord l'arc CD égal à un quadrant de la périphérie, la droite CD, ou FG, sera le côté du carré inscrit dans le cercle, et plus petit par conséquent que 141422 parties, dont le rayon du cercle en a 100000. Mais CE ou ED est le côté de l'octogone inscrit, et par suite plus grande que 76536. Mais FH est égale au double de ED. Cette droite est donc supérieure à 153072. De sorte que l'excès GH est plus grand que 11650. Et le tiers HI de cet excès est plus grand que 3883. Par conséquent la droite FI toute entière est supérieure à 156955. Mais l'arc CD, étant supposé égal à un quadrant, est plus petit que 157080. La droite FI s'écarte donc de cet arc de moins de 125 parties, dont elle en a elle-même 156955. Cela fait donc moins que 1/1200 de la droite FI elle-même.

Mais si l'arc CD est un sextant de la périphérie, la droite CD, ou FG, est le côté de l'hexagone inscrit, et se compose donc de 10000 parties, et CE ou ED est le côté du dodécagone, et est donc plus grand que 5176⅜, dont le double FH est supérieur à 10352¾. Il s'ensuit que GH est plus grande que 352¾, et HI plus grande que 117 7/12. De sorte que la droite FI toute entière est plus grande que 10470⅓. Mais l'arc CD, un sextant de la périphérie, est plus petit que 10472. Il manque donc à la ligne FI un nombre de ces mêmes parties plus petit que 1⅔. Ce qui ne fait pas 1/6000 de FI. Ensuite, si l'on donne un arc plus grand qu'un quadrant, on le divisera en 4 parties égales, ou en 6, ou en un nombre plus grand encore, suivant que nous voulons faire usage d'une dimension plus précise; mais en nombre pair: et à l'ensemble des cordes qui sous-tendent ces parties on ajoutera le tiers de la quantité dont elles surpassent la somme de celles qui sous-tendent des arcs doubles. De cette manière, en effet, on composera la longueur de l'arc entier.

[p. 147]

Problema III. Prop. XII.

Dato arcui cuicunque rectam aequalem sumere.

Esto datus circumferentiae arcus CD, primùm quadrante minor, cui rectam aequalem sumere oporteat. Dividatur arcus CD bifariam in E, sitque subtensae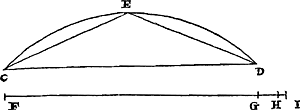

[Fig. 11.]

CD aequalis recta FG. Duabus verò CE, ED, quae subtendunt arcus dimidios, aequalis FH. Et ipsi FH jungatur HI triens excessus GH. Erit tota FI arcui CD aequalis ferè: adeò ut unâ sui particulâ, qualium 1200 continet, aucta, major futura sit, etiamsi arcus CD quadranti aequalis detur. In minoribus autem arcubus minor erit differentia. Nam si fuerit datus non major peripheriae sextante, linea inventa minus quam 1/6000 sui parte à vera arcus longitudine deficiet. Et minores quidem esse arcubus rectas eo modo inventas constat ex Theoremata 7. huj. De quantitate autem differentiae est ostendendum.

Primùm itaque ponendo arcum CD quadranti peripheriae aequalem, erit CD recta, hoc est, FG, latus quadrati circulo inscripti, & minor proinde quam partium 141422, qualium radius circuli 100000. CE autem vel ED latus inscripti octogoni, ideoque major quam 76536. Est autem duplae ED aequalis FH. Ergo haec major quam 153072. Quare excessus GH major quam 11650: Et hujus triens HI major quam 3883. Ideoque tota FI major quam 156955. Arcus autem CD cum quadranti aequalis ponitur minor est quam 157080. Itaque minus ab hoc discrepat recta FI quam partibus 125, qualium ipsa est 156955. Quae utique minus efficiunt quam 1/1200 ipsius FI.

Si verò sextans peripheriae sit arcus CD, erit recta CD, hoc est, FG, latus hexagoni inscripti, ideoque partium 10000, & CE vel ED latus dodecagoni, ac proinde major quam 5176⅜. cujus dupla FH major quam 10352¾. unde GH major quam 352¾ & HI major quam 117 7/12. Tota igitur FI major quam 10470⅓. Arcus autem CD, sextans peripheriae, minor est quam 10472. Ergo deficiunt lineae FI partium earundem pauciores quam 1⅔. Quae non aequant 1/6000 FI. Porro cum arcus quadrante major datus erit, dividendus est in partes aequales 4 vel 6 vel plures, prout accuratiori dimensione uti voluerimus; sed numero pares: Earumque partium subtensis simul sumptis adjungendus est triens excessus quo ipsae superant aggregatum earum quae arcubus duplis subtenduntur. Ita namque com-

[p. 148]

Ou bien, pour la même raison, on aura la même chose, en cherchant la longueur de l'arc restant à la demi-circonférence ou l'excès sur celle-ci, ou la longueur de celui qui reste à la circonférence entière, si l'arc donné était plus grand que les trois quarts d'une circonférence; et cette longueur serait ajoutée ou enlevée à la moitié ou à la totalité de la longueur de la circonférence, que nous avons appris à trouver ci-devant.

Théor. X. Prop. XIII.

Le côté d'un polygone équilatéral inscrit dans un cercle est moyen proportionnel entre le côté du polygone semblable circonscrit, et la moitié du côté du polygone inscrit dont le nombre des côtés est la moitié²³⁾.

Dans un cercle dont le centre est A, le rayon AB, soit BC le côté du polygone inscrit, et DE le côté, parallèle à ce BC, du polygone circonscrit semblable. Ainsi la droite AB prolongée passe par D, et AC par E. Et si l'on mène CF à angles droits sur AB, cette droite sera le demi-côté du polygone inscrit, dont le nombre des côtés est la moitié. Il s'agit donc de prouver, que BC est moyenne proportionnelle entre ED et CF, Menons AG, qui divise ED en deux parties égales; elle sera aussi le demi-diamètre du cercle et égale à AB. Et puisqu'on a DA à AB, c'est-à-dire DA à AG, comme ED est à CB, mais BC à CF, comme DA à AG, à cause des triangles semblables DAG, BCF; on a par conséquent que CB est à CF comme ED est à CB; ce qu'il fallait démontrer.

23) On a donc encore, en employant les notations de la note 7, p. 94: = p_n P_2n. Consultez, sur la connection de ce théorème avec la ‘Prop. IX’ de Snellius, la même note 7, p. 94.

Lemme²⁴⁾.

Soit la ligne BC divisée en deux parties égales en R, et en parties inégales en F, et soit FC le plus grand segment; et faisons BO égale à la somme de BC et CF,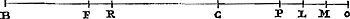

[Fig. 13.]

mais BM égale à la somme de BC et CR. Je dis que le rapport de RB à BF est plus grand que la troisième puissance de celui de OB à BM. Prenons en effet chacun des deux segments ML, LP égal à OM. Alors puisque MO est égale à RF, (car cela se comprend par la construction) PO sera le triple de FR. Mais aussi BM est le triple de BR. Donc, comme BR à BM ainsi FR est à PO. Et, en permutant, BM à PO comme BR à FR. Mais BO est plus grand que BM. Donc le rapport de BO à OP sera plus grand que celui de BR à RF et par

24) Ce ‘lemma’ doit servir à préparer le théorème qui suit, auquel Huygens attacha tant d'intérêt; voir la note 17, p. 97 du Tome présent.
En posant BR = a, RF = x, le lemme nous apprend que pour x < a on a: , ou, si l'on veut, , où ζ < 1.

[p. 149]

ponetur longitudo arcus totius. Vel hac etiam ratione eadem habebitur, si arcus reliqui ad semicircumferentiam longitudo inveniatur aut supra eandem excessus, aut reliqui ad circumferentiam totam, si dodrante major fuerit datus; eaque longitudo adjungatur vel auferatur à dimidiae vel totius circumferentiae longitudine, quam antea invenire docuimus.

Theor. X. Prop. XIII.

Latus Polygoni aequilateri circulo inscripti, proportione medium est inter latus polygoni similis circumscripti, & dimidium latus polygoni inscripti subduplo laterum numero²³⁾.

In circulo cujus centrum A, radius AB, sit latus inscripti polygoni aequilateri BC; & latus circumscripti similis polygoni DE ipsi BC parallelum. Ergo producta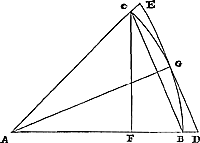

[Fig. 12.]

AB transibit per D, & AC per E. Et si ducatur CF ipsi AB ad angulos rectos, ea erit dimidium latus polygoni inscripti subduplo numero laterum. Itaque ostendendum est, BC mediam esse proportione inter ED & CF. Ducatur AG, quae dividat ED bifariam, itaque erit ipsa quoque circuli semidiameter & aequalis AB. Et quoniam est ut ED ad CB, sic DA ad AB, hoc est, DA ad AG; sicut autem DA ad AG, ita BC ad CF, propter triangulos similes DAG, BCF. Erit proinde ut ED ad CB, ita quoque CB ad CF, Quod erat demonstrandum.

23) On a donc encore, en employant les notations de la note 7, p. 94: = p_n P_2n. Consultez, sur la connection de ce théorème avec la ‘Prop. IX’ de Snellius, la même note 7, p. 94.

Lemma²⁴⁾.

Esto linea BC [Fig. 13] divisa aequaliter in R; & inaequaliter in F, sitque segmentum majus FC; & fiat BO aequalis utrique simul BC, CF; BM verò utrique BC, CR. Dico majorem esse rationem RB ad BF, quam triplicatam ejus, quam habet OB ad BM. Sumatur enim ipsi OM aequalis utraque harum ML, LP. Quoniam igitur MO ipsi RF aequales est, (nam hoc ex constructione intelligitur) erit PO tripla ipsius FR. Sed & BM tripla est BR. Ergo ut BR ad BM, ita FR ad PO. Et permutando ut BR ad FR, sic BM ad PO. Major autem est BO quam BM. Ergo major erit ratio BO ad OP, quam BR ad RF: & per conversionem rationis

24) Ce ‘lemma’ doit servir à préparer le théorème qui suit, auquel Huygens attacha tant d'intérêt; voir la note 17, p. 97 du Tome présent.
En posant BR = a, RF = x, le lemme nous apprend que pour x < a on , ou, si l'on veut, , où ζ < 1.

[p. 150]

conversion des rapports, le rapport de OB à BP sera moindre que celui de RB à BF²⁵⁾. Ensuite, puisque OM et ML sont égales, le rapport de BO à OM sera plus grand que BM à ML, et, par conversion des rapports, le rapport OB à BM sera plus petit que MB à BL. On prouvera encore de même que le rapport MB à BL est plus petit que LB à BP. De sorte qu' à plus forte raison la troisième puissance du rapport de OB à BM sera plus petit que celui qui est composé des rapports OB à BM, BM à BL, et BL à BP, c'est-à-dire que le rapport OB à BP. Mais RB à BF était plus grand que OB à BP. Donc, à plus forte raison, le rapport RB à BF sera plus grand que la troisième puissance du rapport OB à BM. Ce qu'il s'agissait d'établir.

25) Huygens, ici et plus loin, emploie un théorème de la théorie des proportions qui pour a > b, c > d permet de conclure de l'inégalité a/b > c/d à celle-ci: .

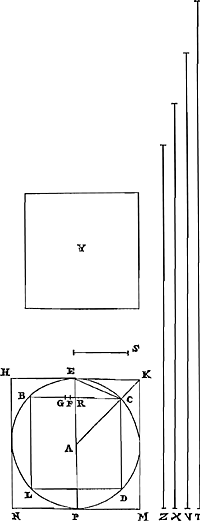
Théor. XI. Prop. XIV.

Toute circonférence de cercle est moindre que la plus petite de deux moyennes proportionnelles entre les périmètres de polygones semblables, dont l'un est régulièrement inscrit dans le cercle, l'autre circonscrit. Et le cercle est plus petit que le polygone semblable à ceux-là, dont le contour est égal à la plus grande des moyennes²⁶⁾.

Soit un cercle BD, dont le centre est A. Inscrivons-y un polygone équilatéral BCDL, et circonscrivons-en un semblable à côtés parallèles HKMN. Supposons que la droite T est égale au périmètre du polygone HKMN, et la droite Z égale au périmètre de BCDL. Et soient entre Z et T deux moyennes proportionnelles X et V, dont X est la plus petite. Je dis que la circonférence du cercle BD est moindre que la droite X. Et si l'on fait un polygone Y, dont le périmètre est égal à la droite V, mais qui est semblable au polygone BCDL ou HKMN, je dis que le cercle BD est plus petit que le polygone Y. Menons en effet le diamètre PE du cercle, qui divise en deux parties égales les côtés parallèles BC, HK des polygones inscrit et circonscrit, en R et E; E sera ainsi le point de contact du côté HK, et BC sera coupé en R à angles droits. Menons aussi du centre la droite ACK, qui divise en deux parties égales les angles C et K des deux polygones, car il est avéré que cela se fait par la même droite, et joignons CE. Mais prenons CF égale à CE, et soit CG une troisième proportionnelle à ces deux droites CR, CF. Alors, comme CE ou CF est le côté d'un polygone inscrit, CG sera le côté du polygone semblable circonscrit^*. Et par suite les deux tiers de CF avec letiers de CG seront ensemble plus grands que l'arc EC^*. Mais soit la droite S égale aux deux tiers de CF avec le tiers de CG. Cette droite sera donc plus grande que l'arc EC.

Et puisque CR est à CF comme CF est à CG, on aura aussi que le double de CR ajouté à CF est au triple de CR, c'est-à-dire que la somme de BC et CF est à la somme de BC et CR, comme le double de CF avec CG est au triple de CF: ou, en prenant les tiers de ces grandeurs, comme ⅔ CF avec ⅓ CG est à CF, c'est-à-dire comme S est à CF. Donc aussi la troisième puissance du rapport qui existe

26) Consultez, sur la première partie de ce théorème, la p. 97 du Tome présent. La démonstration de cette partie revient à l'application de l'égalité P_2n p_n = et des inégalités 2π < ⅔ p_2n + ⅓ P_2n et , prouvées au Théorème IX et au Lemme qui précède ici, et ensuite à la démonstration de l'inégalité (2p_n - P_2n)p_2n < p_n (2p_n - p_2n) (c'est-à-dire BG. CF < RB. BF) et de l'égalité : P_n ou (c'est-à-dire BG : GC = RC : EK). A l'aide de ces formules le théorème en question se démontre ainsi: C'est ici la seule fois que Huygens emploie une relation (p. 155, l. 7) qui équivaut à la relation importante Quant à la seconde partie du théorème, elle amène l'inégalité , qui, à l'aide la relation S_2n = ½ P_2n se réduit, elle aussi, à celle-ci: ; voir encore la première page de la préface et surtout la note 1, p. 115 du Tome présent.

* d'après 13. ici.

* d'après 9. ici.

[p. 151]

minor OB ad BP, quam RB ad BF²⁵⁾. Porro quoniam aequales sunt OM, ML,

[Fig. 14.]

major erit ratio BO ad OM, quam BM ad ML: & per conversionem rationis minor OB ad BM, quam MB ad BL. Eodem modo minor adhuc ostendetur ratio MB ad BL, quam LB ad BP. Itaque omnino ratio triplicata ejus quam habet OB ad BM minor erit quam composita ex rationibus OB ad BM, BM ad BL, & BL ad BP, hoc est, quam ratio OB ad BP. Major autem erat RB ad BF, quam OB ad BP. Ergo omnino major erit ratio RB ad BF, quam triplicata rationis OB ad BM. Quod erat propositum.

25) Huygens, ici et plus loin, emploie un théorème de la théorie des proportions qui pour a > b, c > d permet de conclure de l'inégalité a/b > c/d à celle-ci: .

Theor. XI. Prop. XIV.

Omnis circuli circumferentia minor est minore duarum mediarum proportionalium inter perimetros polygonorum similium, quorum alterum ordinate circulo inscriptum sit, alterum circumscriptum. Et circulus minor est polygono istis simili cujus ambitus majori mediarum aequetur²⁶⁾.

Esto circulus BD, cujus centrum A. Et inscribatur ei polygonum aequilaterum BCDL, simileque circumscribatur lateribus parallelis HKMN. Sitque perimetro polygoni HKMN aequalis recta T, perimetro autem BCDL aequalis Z. Et inter Z & T duae sint mediae proportionales X & V, quarum X minor. Dico circumferentiam circuli BD minorem esse rectâ X. Et si fiat polygonum in quo Y, cujus perimeter aequetur rectae V, simile

26) Consultez, sur la première partie de ce théorème, la p. 97 du Tome présent. La démonstration de cette partie revient à l'application de l'égalité P_2n p_n = et des inégalités 2π < ⅔ p_2n + ⅓ P_2n et , prouvées au Théorème IX et au Lemme qui précède ici, et ensuite à la démonstration de l'inégalité (2p_n - P_2n)p_2n < p_n (2p_n - p_2n) (c'est-à-dire BG. CF < RB. BF) et de l'égalité : P_n ou (c'est-à-dire BG : GC = RC : EK). A l'aide de ces formules le théorème en question se démontre ainsi: C'est ici la seule fois que Huygens emploie une relation (p. 155, l. 7) qui équivaut à la relation importante Quant à la seconde partie du théorème, elle amène l'inégalité , qui, à l'aide la relation S_2n = ½ P_2n se réduit, elle aussi, à celle-ci: ; voir encore la première page de la préface et surtout la note 1, p. 115 du Tome présent.

[p. 152]

entre la somme des deux droites BC, CF et la somme de BC et CR est égale à la troisième puissance du rapport de S à CF. Mais le rapport RB à BF est plus que la troisième puissance de celui de la somme BC, CF à la somme BC, CR^*. Donc

[Fig. 14.]

le même rapport RB à BF est plus grand que la troisième puissance de celui de S à CF, c'est-à-dire que celui du cube de S au cube de CF. Mais, comme RB à BF, ainsi le cube de RB est au volume qui résulte du carré RB et de BF. Donc le rapport du cube RB au produit du carré RB et de BF est plus grand que celui du cube S au cube CF. Mais le rectangle formé par RB, BG, multiplié par FC est moindre que le carré RB multiplié par BF; ce que l'on démontre de la manière suivante. Puisque les droites RC, CF, CG forment une proportion, la quantité dont la plus grande dépasse la moyenne, c'est-à-dire FG, sera plus grande que celle dont la moyenne dépasse la plus petite, c'est-à-dire plus grande que FR. Mais FC est plus grand que FB. Donc, à plus forte raison, le rapport CF à FR sera plus grand que BF à FG. Et par conversion des rapports, le rapport FC à CR sera plus petit que FB à BG²⁵⁾. Et en permutant FC à FB sera plus petit que CR ou RB à BG. C'est-à-dire, (en prenant BR pour la hauteur commune) que le carré RB au rectangle RBG. D'où ce qui résulte du rectangle RBG par multiplication par FC sera moindre que ce qui résulte du carré RB par FB, ainsi que je l'ai dit. Et ainsi, comme nous avons démontré que le rapport du cube RB au carré RB multiplié par BF, est plus grand que le rapport du cube S au cube CF; à plus forte raison le rapport du cube RB au solide formé par le rectangle RBG et FC sera plus grand que celui du cube S au cube CF. Et en permutant, le rapport du cube RB au cube S sera plus grand que celui du rectangle RGB multiplié par FC au cube CF; c'est-à-dire, du rectangle RBG au carré CF. Mais le carré CF est égal au rectangle GCR, c'est-à-dire le rectangle formé par GC et RB, parce que les droites CR, CF et CG forment une proportion. Par suite le rapport du cube

* d'après le lemme qui précède.

25) Huygens, ici et plus loin, emploie un théorème de la théorie des proportions qui pour a>b, c>d permet de conclure de l'inégalité a/b>c/d à celle-ci: .

[p. 153]

autem sit polygono BCDL aut HKMN; Dico circulum BN minorem haberi polygono Y. Ducatur enim diameter circuli PE, quae dividat bifariam latera parallela BC, HK, inscripti circumscriptique polygoni in R & E; erit autem E punctum contactus lateris HK, & BC secabitur in R ad angulos rectos. Ducatur etiam ex centro recta ACK, quae utriusque polygoni angulos C & K bifariam secet, nam hoc ab eadem recta fieri constat; & jungatur CE. Ipsi autem CE ponatur aequalis CF; sitque duabus his CR, CF tertia proportionalis CG. Ergo qualis polygoni inscripti latus est CE sive CF, talis circumscripti latus erit CG^*. Ideoque duae tertiae CF cum triente CG simul majores erunt arcu EC^*. Sit autem duabus tertiis CF cum triente CG aequalis recta S. Ergo & haec major erit arcu EC.

Et quoniam se habet CR ad CF, ut CF ad CG; erit quoque dupla CR una cum CF ad triplam CR, hoc est, utraque simul BC, CF ad utramque BC, CR, ut dupla CF una cum CG ad triplam CF: vel sumptis horum trientibus, ut ⅔ CF unà cum ⅓ CG ad CF, hoc est, ut S ad CF. Quare etiam triplicata ratio ejus quam habet utraque simul BC, CF ad utramque BC, CR eadem erit triplicatae rationi S ad CF. Major autem est ratio RB ad BF quàm triplicata ejus, quam habet utraque simul BC, CF ad utramque BC, CR^*. Ergo major eadem ratio RB ad BF quam triplicata ejus quam habet S ad CF, hoc est, quam cubi S ad cubum CF. Sicut autem RB ad BF, ita est cubus RB ad id quod fit ex quadrato RB in BF. Ergo major quoque ratio cubi RB ad quadratum RB in BF, quam cubi S ad cubum CF. Quadrato autem RB in BF minus est rectangulum sub RB, BG, in FC; quod sic ostenditur. Quia enim proportionales sunt RC, CF, CG, Erit id quo major mediam excedit, hoc est, FG major quam quo media minimam, hoc est, quam FR. Major autem est FC quam FB. Ergo omnino major erit ratio CF ad FR, quam BF ad FG. Et per conversionem rationis, minor ratio FC ad CR, quam FB ad BG²⁵⁾. Et permutando minor FC ad FB, quam CR seu RB ad BG: hoc est, (sumptâ communi altitudine BR) quam quadrati RB ad rectangulum RBG. Unde quod fit ex rectangulo RBG in FC minus erit quam quod ex quadrato RB in FB, uti dictum fuit. Quum itaque major ostensa fuerit ratio cubi RB ad quadratum RB in BF, quam cubi S ad cubum CF; omnino

* per. 13. huj.

* per. 9. huj.

* per lemma praec.

25) Huygens, ici et plus loin, emploie un théorème de la théorie des proportions qui pour a>b, c>d permet de conclure de l'inégalité a/b>c/d à celle-ci: .

[p. 154]

RB au cube S sera plus grand que celui du rectangle RBG au rectangle formé par GC, RB; c'est-à-dire, que BG à GC. Mais, comme BG est à GC, ainsi RC est EK. En effet, puisque CR est à CG comme le carré sur CR au carré sur CF ou au carré sur CE, et que d'autre part le carré sur CR, est au carré sur CE comme PR au diamètre PE; pour cette raison on aura CR à CG comme PR à PE. D'où le double de CR, c'est-à-dire CB, est à CG comme le double de PR est à PE, c'est-à-dire comme PR est à PA. Et, par partage, BG est à GC comme RA à AP, ou AE, c'est-à-dire, comme RC à EK, ce que nous disions. Et ainsi le rapport du cube RB au cube S, c'est-a-dire, le rapport RB à S élevé à la troisième puissance, est plus grand que celui de RC à EK. Mais nous avons montré que S est plus grand que l'arc EC. Donc à plus forte raison la troisième puissance du rapport RB ou RC à une droite égale à l'arc EC sera plus grand que celui de RC à EK. Mais, comme RC à l'arc EC, ainsi le périmètre du polygone BCDL, c'est-à-dire, la ligne Z, est a la circonférence du cercle BD; et comme RC à EK, ainsi le périmètre du polygone BCDL est au périmètre du polygone HKMN, c'est-à-dire, ainsi Z est à T. Donc la troisième puissance du rapport de Z à la circonférence entière BD sera aussi plus grande que celui de Z à T. Mais la troisième puissance du rapport de Z à X est égale au rapport de Z à T. Et ainsi le rapport de ce Z à la dite circonférence est plus grand que celui de Z à X. Et par conséquent la circonférence est plus petite que la droite X. Ce qu'il fallait démontrer.

Mais on doit savoir que cette droite X est plus petite que les deux tiers de Z avec le tiers de T, c'est-à-dire, plus petite que les deux tiers du périmètre du polygone inscrit augmentés du tiers du circonscrit; la circonférence du cercle étant d'ailleurs plus petite que cela, d'après ce qui précède²⁷⁾. Car ⅔ Z avec ⅓ T est égal à la plus petite des moyennes proportionnelles suivant une proportion arithmétique, laquelle est plus grande que la plus petite des moyennes proportionnelles suivant une proportion géométrique. Mais nous allons encore démontrer du polygone Y qu'il est plus grand que le cercle BD. Or, comme le rapport du polygone Y au polygone sembable HKMN est le carré de celui du périmètre au périmètre, et que le périmètre du polygone Y est égal à la droite V, et le périmètre HKMN égal à T, le rapport du polygone Y au polygone HKMN sera donc le carré de celui de V à T, c'est-à-dire, égal à celui de X à T. Mais, comme le polygone HKMN est au cercle BD, ainsi le périmètre de ce polygone, c'est-à-dire, la ligne T, est à la circonférence du cercle BD; parce que le polygone est égal au triangle ayant une base égale à son périmètre et comme hauteur le rayon AE, tandis que le cercle est égal à un triangle de même hauteur et dont la base est égale à la circonférence. Il résulte donc, en combinant ces proportions, que le polygone Y sera au cercle BD comme X est à la circonférence BD²⁸⁾. Mais nous avons montré que X est plus grand que la circonférence BD. Donc le polygone Y sera aussi plus grand que le cercle BD. Ce qu'il fallait démontrer.

27) D'après la ‘Prop. IX’, p. 137, déjà citée plus haut.

28) Comparez la note 1, p. 115 du Tome présent.

[p. 155]

quoque major erit ratio cubi RB ad solidum sub rectangulo RBG in FC, quam cubi S ad cubum CF. Et permutando major ratio cubi RB ad cubum S, quam rectanguli RBG in FC ad cubum CF; hoc est, quam rectanguli RBG ad quadratum CF. Est autem quadrato CF aequale rectangulum GCR, hoc est, rectangulum sub GC, RB, quia proportionales sunt CR, CF, CG. Itaque major erit ratio cubi RB ad cubum S, quam rectanguli RBG ad rectangulum sub GC, RB, hoc est, quam BG ad GC. Sicut autem BG ad GC, ita RC ad EK. Quia enim est CR ad CG, ut quadratum CR ad quadratum CF seu quadratum CE: ut autem quadratum CR ad quadratum CE, ita est PR ad PE diametrum: Erit idcirco CR ad CG, ut PR ad PE. Unde dupla CR, hoc est, CB ad CG, ut dupla PR ad PE, hoc est, ut PR ad PA. Et dividendo, BG ad GC, ut RA ad AP, seu AE, hoc est, ut RC ad EK, quod dicebamus. Itaque major quoque ratio cubi RB ad cubum S, hoc est, ratio triplicata RB ad S, quam RC ad EK. Est autem S major ostensa arcu EC. Ergo omnino major erit ratio triplicata RB seu RC ad aequalem arcui EC, quam RC ad EK. Sicut autem RC ad arcum EC, ita est perimeter polygoni BCDL, hoc est, linea Z ad circumferentiam circuli BD; Et sicut RC ad EK, ita perimeter polygoni BCDL ad perimetrum polygoni HKMN, hoc est, ita Z ad T. Ergo major quoque triplicata ratio Z ad circumferentiam totam BD, quam Z ad T. Ratio autem triplicata Z ad X eadem est rationi Z ad T. Itaque major est ratio ipsius Z ad dictam circumferentiam, quam Z ad X. Ac proinde circumferentia minor quam recta X. Quod erat demonstrandum.

Sciendum est autem ipsam X minorem esse duabus tertiis Z & triente T: hoc est, duabus tertiis perimetri polygoni inscripti & triente circumscripti, quibus alioqui minorem esse circuli circumferentiam constat ex praecedentibus²⁷⁾. Nam ⅔ Z cum ⅓ T aequantur minori duarum mediarum secundùm Arithmeticam proportionem, quae major est minore mediarum secundum proportionem Geometricam. Jam verò & de polygono Y demonstrabimus, ipsum videlicet circulo BD majus esse. Quia enim polygonum Yhabet ad polygonum simile HKMN rationem duplicatam ejus quam perimeter ad perimetrum: perimeter autem polygoni Y aequatur rectae V, & perim. HKMN ipsi T. habebit proinde polygon. Y ad polyg. HKMN rationem duplicatam ejus quam V ad T, hoc est, eam quam X ad T. Sicut autem polygonum HKMN ad circulum BD, ita est perimeter ipsius polygoni, hoc est, linea T ad circuli BD circumferentiam; quoniam polygonum aequale est triangulo basin habenti perimetro suae aequalem & altitudinem radii AE, circulus autem aequalis ejusdem altitudinis triangulo cujus basis circumferentiae aequetur. Ex aequali igitur, erit polygonum Y ad circulum BD sicut X ad circumferentiam BD²⁸⁾. Est autem X major ostensa quam BD circumferentia. Ergo & polygonum Y majus erit circulo BD. Quod erat demonstrandum.

27) D'après la ‘Prop. IX’, p. 137, déjà citée plus haut.

28) Comparez la note 1, p. 115 du Tome présent.

[p. 156]

Par là est manifeste l'erreur d'Oronce Fine²⁹⁾ qui prétendit que le quadrant d'un cercle est égal au plus petit des deux moyennes proportionnelles entre les côtés du carré inscrit et du carré circonscrit, et que le cercle est égal au carré formé au moyen du plus grand.

29) Oronce Fine, fils du médecin François Fine, naquit en 1494 à Briançon en Dauphiné. Il mourut le 8 octobre 1555 à Paris, où il jouissait d'une grande réputation comme professeur de mathématiques; réputation qui n'est pas confirmée par les ouvrages qu'il laissait. Il s'agitici de l'ouvrage: ‘Orontii Finaei Delphinatis, Regii Mathematicarum Lutetiae Professoris, Quadratura Circuli, tandem inuenta & clarissimè demonstrata. De circuli mensura & ratione circumferentiae ad diametrum, Demonstrationes duae. De multangularum omnium & regularium figurarum descriptione, Liber hactenus desideratus. De inuenienda longitudinis locorum differentia, aliter quàm per Lunares eclipses, etiam dato quouis tempore, Liber admodùm singularis. Planisphaerium geographicum, quo tum longitudinis atque latitudinis differentiae, tum directae locorum deprehenduntur elongationes. Lutetiae Parisiorum, Apud Simonem Colinaeum. 1544.’ in Folio. Toutefois dans l'exemplaire qui nous a été prêté par la Bibliothèque de l'Université de Paris à la Sorbonne, on ne trouve (à la p. 13) que le second des deux théorèmes mentionnés par Huygens, c'est-à-dire, celui qui se rapporte à l'aire du cercle; mais il faut bien que dans d'autres exemplaires ou dans une autre édition le premier théorème a été ajouté. En effet, dans la réfutation par Nonius de l'ouvrage cité, laquelle parut en 1546 sous le titre: ‘De Erratis Orontii Finaei Regii Mathematicarum Lutetiae Professoris’. on lit à la page 28: ‘His in hunc modum constructis ait Orontius quadratum bf, aequari inprimis ipsi dato circulo ah,... praeterea quadratum cg, eidem circulo ah esse isoperimetrum,’ où les carrés bf et cg sont les moyens proportionnels entre les carrés circonscrit et inscrit du cercle ah. D'ailleurs ce n'est pas là ni la première, ni la dernière fausse quadrature dont Oronce Fine se rendit responsable. On en recontre une autre au fol. 90 de son ‘Protomathesis’ de 1532 et de nombreuses, différentes entre elles et d'avec celles signalées ici par Huygens, dans l'ouvrage posthume: ‘De rebus mathematicis, hactenus desideratis, Libri IIII. Quibus inter caetera, Circuli quadratura Centum modis, & suprà, per eundem Orontium recenter excogitatis, demonstratur. Lutetiae Parisiorum, M.D.LVI. Ex officina Michaëlis Vascosani.’

Théor. XII. Propos. XV.

Si entre le prolongement du diamètre d'un cercle et la circonférence on place une droite égale au rayon, et que cette droite prolongée coupe le cercle et rencontre la droite touchant le cercle à l'autre extrémité du diamètre: cette droite découpera de la tangente une partie plus grande que l'arc adjacent découpé³⁰⁾.

Soit décrit le cercle à centre C, dont le diamètre est AB. Prolongeons celui-ci du côté de A et plaçons entre lui et la circonférence une droite ED égale au rayon. Et supposons que cette droite prolongée coupe la circonférence en F, et rencontre en G la tangente, savoir celle qui touche le cercle à l'extrémité B du diamètre. Je dis que la tangente BG est plus grande que l'arc BF. Menons en effet par le centre la droite HL parallèle à EG, qui rencontre la circonférence aux points H et M, et la tangente BG en L. Et joignons DH, qui coupe le diamètre en K. Alors les triangles EDK, CHK sont semblables, parce qu'ils ont les angles en K égaux, et l'angle E égal à l'angle C. Mais le côté ED est encore égal au côté HC, et ces côtés sont sous-tendus par des angles égaux. Par conséquent le côté DK est aussi égal au côté KH. Pour cette raison CA coupe DH en deux parties égales, et de même l'arc DAH. L'arc DH, ou l'arc FM qui lui est égal, est donc le double de l'arc AH. Mais l'arc MB est égal à l'arc AH. Donc l'arc FB sera le

30) Le théoréme, identique avec la ‘Prop. XXIX’ de Snellius, ne diffère pas essentiellement du ‘Theor. IX. Prop. IX’, p. 137 du Tome présent, auquel la démonstration le ramène. Il s'exprime donc par les deux premières formules de la note 10, p. 136.

[p. 157]

Ex his manifestus est Orontii Finei²⁹⁾ error, qui circumferentiae quadrantem aequalem minori duarum proportione mediarum inter inscripti & circumscripti quadrati latera prodidit, circulum vero aequalem quadrato quod fieret à majori.

29) Oronce Fine, fils du médecin François Fine, naquit en 1494 à Briançon en Dauphiné. Il mourut le 8 octobre 1555 à Paris, où il jouissait d'une grande réputation comme professeur de mathématiques; réputation qui n'est pas confirmée par les ouvrages qu'il laissait. Il s'agitici de l'ouvrage: ‘Orontii Finaei Delphinatis, Regii Mathematicarum Lutetiae Professoris, Quadratura Circuli, tandem inuenta & clarissimè demonstrata. De circuli mensura & ratione circumferentiae ad diametrum, Demonstrationes duae. De multangularum omnium & regularium figurarum descriptione, Liber hactenus desideratus. De inuenienda longitudinis locorum differentia, aliter quàm per Lunares eclipses, etiam dato quouis tempore, Liber admodùm singularis. Planisphaerium geographicum, quo tum longitudinis atque latitudinis differentiae, tum directae locorum deprehenduntur elongationes. Lutetiae Parisiorum, Apud Simonem Colinaeum. 1544.’ in Folio. Toutefois dans l'exemplaire qui nous a été prêté par la Bibliothèque de l'Université de Paris à la Sorbonne, on ne trouve (à la p. 13) que le second des deux théorèmes mentionnés par Huygens, c'est-à-dire, celui qui se rapporte à l'aire du cercle; mais il faut bien que dans d'autres exemplaires ou dans une autre édition le premier théorème a été ajouté. En effet, dans la réfutation par Nonius de l'ouvrage cité, laquelle parut en 1546 sous le titre: ‘De Erratis Orontii Finaei Regii Mathematicarum Lutetiae Professoris’. on lit à la page 28: ‘His in hunc modum constructis ait Orontius quadratum bf, aequari inprimis ipsi dato circulo ah,... praeterea quadratum cg, eidem circulo ah esse isoperimetrum,’ où les carrés bf et cg sont les moyens proportionnels entre les carrés circonscrit et inscrit du cercle ah. D'ailleurs ce n'est pas là ni la première, ni la dernière fausse quadrature dont Oronce Fine se rendit responsable. On en recontre une autre au fol. 90 de son ‘Protomathesis’ de 1532 et de nombreuses, différentes entre elles et d'avec celles signalées ici par Huygens, dans l'ouvrage posthume: ‘De rebus mathematicis, hactenus desideratis, Libri IIII. Quibus inter caetera, Circuli quadratura Centum modis, & suprà, per eundem Orontium recenter excogitatis, demonstratur. Lutetiae Parisiorum, M.D.LVI. Ex officina Michaëlis Vascosani.’

Theor. XII. Propos. XV.

Si inter productam circuli diametrum & circumferentiam recta aptetur radio aequalis, & producta circulum secet, occurratque tangenti circulum ad alterum diametri terminum: Intercipiet ea partem tangentis arcu adjacente abscisso majorem³⁰⁾.

Esto descriptus circulus centro C, cujus diameter AB. Haec autem producatur versus A, interque ipsam & circumferentiam ponatur ED recta radio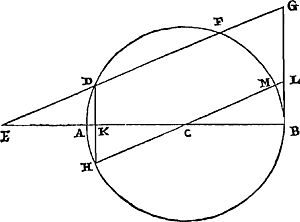

[Fig. 15.]

AC aequalis. Quae producta secet circumferentiam in F, occuratque tangenti in G, ei nimirum quae circulum contingit ad diametri terminum B. Dico tangentem BG majorem esse arcu BF. Ducatur enim per centrum recta HL parallela EG, quae circumserentiae occurrat in punctis H, M: tangenti verò BG in L. Et jungatur DH, quae diametrum secet in K. Similes itaque sunt trianguli EDK, CHK, quoniam angulos ad K aequales habent, & angulum E aequalem angulo C. Sed & latus ED aequale est lateri HC, suntque haec latera aequalibus angulis subtensa. Ergo aequale etiam latus DK lateri KH. Itaque CA secat bifariam ipsam DH, itemque arcum DAH. Arcus igitur DH sive huic aequalis FM duplus est ad arcum AH. Ipsi autem AH aequalis est arcus MB. Igitur arcus FB triplus erit

30) Le théoréme, identique avec la ‘Prop. XXIX’ de Snellius, ne diffère pas essentiellement du ‘Theor. IX. Prop. IX’, p. 137 du Tome présent, auquel la démonstration le ramène. Il s'exprime donc par les deux premières formules de la note 10, p. 136.

[p. 158]

triple de l'arc AH. Puis, comme HK est le sinus de l'arc HA et que LB est égal à la tangente de cet arc, les deux tiers de HK et le tiers de LB seront ensemble plus grands que l'arc AH^*. De sorte que si l'on prend le triple de tout, le double de HK, c'est-à-dire, HD ou GL, ensemble avec LB sera plus grand que le triple de l'arc AH, c'est-à-dire que l'arc FB. Il paraît donc que la droite GB toute entière est plus grande que l'arc FB.

Ce théorème est le second des deux sur lesquels est basée toute la Cyclométrie de Willebrord Snellius, et que lui-même voulait paraître avoir démontré, au moyen d'un raisonnement qui contient une pure pétition de principe³²⁾. Mais nous démontrerons aussi l'autre théorème, parce qu'il est surtout utile et fort digne d'être considéré.

* d'après 9. ici³¹⁾.

31) Voir le dernier alinéa du ‘Theor. IX. Prop. IX’, p, 139.

32) Il s'agit de la ‘Propositio XXIX’, p. 43 de l'ouvrage cité dans la note 6, p. 94 du Tome présent, laquelle proposition est, en effet, conforme avec le théorème du texte et nous apprend que la droite GB de la figure 15 est plus grande que l'arc BF.
Pour le montrer Snellius s'occupe du lieu géométrique d'un point P qu'on choisit sur la droite EG de la figure 15 de manière que la droite BP est égale à l'arc BF et que l'angle EPB est un angle aigu. Or, Snellius prétend que ce lieu, qui évidemment doit passer par le point B se trouvera entièrement à gauche de la tangente BG, auquel cas on aura BP < BG. Mais pour



prouver cette assertion, il se borne à montrer que dans le cas particulier, où la droite EG touche le cercle, le point P se trouve en effet à gauche de la tangente. Ainsi le lieu cherché se compose d'une courbe qui de ce point P doit s'étendre au point B et il y a donc bien une certaine probabilité, mais aucune certitude, qu'elle restera en entier à gauche de la droite BG.
Quant au cas particulier que nous venons de mentionner, Snellius le traite dans sa ‘Propositio XXVI’, p. 40 de son ouvrage. Soit alors, dans la figure ci-jointe, Q le point dans lequel D et F de la figure 15 se sont rencontrés. L'arc QTUB est donc, puisque QR = CQ, la ⅜^ième partie de la circonférence du cercle et, comme la figure le montre, elle est plus petite que six des côtés d'un polygone circonscrit à seize côtés. Snellius n'a donc qu'à prouver que BS est plus grand que ces six côtés; ce qu'il a fait en effet.

Théor. XIII. Propos. XVI.

Si au diamètre d'un cercle on ajoute dans sa direction un demi-diamètre, et qu' à partir de l'extrémité de la droite ajoutée on mène une droite qui coupe le cercle, et rencontre la droite qui touche le cercle à l'extrémité opposée du diamètre: cette droite interceptera sur la tangente une partie plus petite que l'arc adjacent découpé³³⁾.

Soit un cercle [Fig. 16], dont le diamètre est AB; prolongeons celui-ci et supposons que AC est égal au demi-diamètre. Menons la droite CL, qui coupe la cir-

33) Le théorème est, en effet, identique avec la ‘Proposition XXVIII’, p. 42, du ‘Cyclometricus’ de Snellius.
Pour juger de son efficacité, en comparaison avec les théorèmes de Huygens, il nous faut supposer, en employant les notations de la note 10, p. 136, qu'on a EG (Fig. 16) = ½ a_2n.
Posant alors α = arc EB = 2π : 4n, on trouve facilement: .
On a donc, d'après le théorème:


Comme on le voit, cette limite est du même ordre que celle, bien plus simple, indiquée par les ‘Theor. V et VII’, pp. 129 et 133 du Tome présent.
Quant à la démonstration que Snellius prétendait avoir donnée, elle souffre du même défaut que celle de sa ‘Propositio XXIX’ (voir la note précédente). Cette fois encore il s'agit d'un lieu géométrique, c'est-à-dire, de celui décrit par un point P choisi sur la droite CL (Fig. 16) de manière qu'on ait BP = arc EB et que l'angle CPB soit un angle aigu. Dans le cas particulier où CL touche le cercle il est clair qu'on aura EL = EB = BL; donc BP = arc EB sera plus grand que BL et le point P devra se trouver à droite de la tangente LB. De là Snellius se hasarde à conclure que toute la courbe, qui constitue le lieu géométrique cherché et qui doit nécessairement passer par le point B, sera située à droite de la tangente BL; auquel cas on doit avoir, en effet, arc. BE = BP > BL.
Or, pour faire voir combien cette conclusion est fallacieuse, il suffit de remarquer que si l'on place le point C un peu plus près du point A, une partie de la courbe se trouvera, dans le voisinage du point B, à gauche de BL; comme cela résulte aisément de la considération de la note 37, qui suit.

[p. 159]

ad arcum AH. Porrò quoniam HK sinus est arcus HA, ejusdemque tangenti aequatur LB, Erunt duae tertiae HK & triens LB simul majores arcu AH^*. Quare sumptis omnium triplis erit dupla HK, hoc est, HD sive GL unà cum LB major arcu AH triplo, hoc est, arcu FB. Apparet igitur totam GB arcu FB majorem esse.

Hoc Theorema alterum est ex iis quibus Cyclometria Willebrordi Snellii tota innititur, quaeque demonstrasse ipse videri voluit, argumentatione usus quae meram quaesiti petitionem continet³²⁾. Sed & alterum subjungemus, quod utile est imprimus & contemplatione dignissimum.

* per. 9. huj.³¹⁾

31) Voir le dernier alinéa du ‘Theor. IX. Prop. IX’, p, 139.

32) Il s'agit de la ‘Propositio XXIX’, p. 43 de l'ouvrage cité dans la note 6, p. 94 du Tome présent, laquelle proposition est, en effet, conforme avec le théorème du texte et nous apprend que la droite GB de la figure 15 est plus grande que l'arc BF.
Pour le montrer Snellius s'occupe du lieu géométrique d'un point P qu'on choisit sur la droite EG de la figure 15 de manière que la droite BP est égale à l'arc BF et que l'angle EPB est un angle aigu. Or, Snellius prétend que ce lieu, qui évidemment doit passer par le point B se trouvera entièrement à gauche de la tangente BG, auquel cas on aura BP < BG. Mais pour



prouver cette assertion, il se borne à montrer que dans le cas particulier, où la droite EG touche le cercle, le point P se trouve en effet à gauche de la tangente. Ainsi le lieu cherché se compose d'une courbe qui de ce point P doit s'étendre au point B et il y a donc bien une certaine probabilité, mais aucune certitude, qu'elle restera en entier à gauche de la droite BG.
Quant au cas particulier que nous venons de mentionner, Snellius le traite dans sa ‘Propositio XXVI’, p. 40 de son ouvrage. Soit alors, dans la figure ci-jointe, Q le point dans lequel D et F de la figure 15 se sont rencontrés. L'arc QTUB est donc, puisque QR = CQ, la ⅜^ième partie de la circonférence du cercle et, comme la figure le montre, elle est plus petite que six des côtés d'un polygone circonscrit à seize côtés. Snellius n'a donc qu'à prouver que BS est plus grand que ces six côtés; ce qu'il a fait en effet.

Theor. XIII. Propos. XVI.

Si diametro circuli semidiameter in directum adjiciatur, & ab adjectae termino recta ducatur quae circulum secet, occuratque tangenti circulum ad terminum diametri oppositum: Intercipiet ea partem tangentis arcu adjacente abscisso minorem³³⁾.

33) Le théorème est, en effet, identique avec la ‘Proposition XXVIII’, p. 42, du ‘Cyclometricus’ de Snellius.
Pour juger de son efficacité, en comparaison avec les théorèmes de Huygens, il nous faut supposer, en employant les notations de la note 10, p. 136, qu'on a EG (Fig. 16) = ½ a_2n.
Posant alors α = arc EB = 2π : 4n, on trouve facilement: .
On a donc, d'après le théorème:

Comme on le voit, cette limite est du même ordre que celle, bien plus simple, indiquée par les ‘Theor. V et VII’, pp. 129 et 133 du Tome présent.
Quant à la démonstration que Snellius prétendait avoir donnée, elle souffre du même défaut que celle de sa ‘Propositio XXIX’ (voir la note précédente). Cette fois encore il s'agit d'un lieu géométrique, c'est-à-dire, de celui décrit par un point P choisi sur la droite CL (Fig. 16) de manière qu'on ait BP = arc EB et que l'angle CPB soit un angle aigu. Dans le cas particulier où CL touche le cercle il est clair qu'on aura EL = EB = BL; donc BP = arc EB sera plus grand que BL et le point P devra se trouver à droite de la tangente LB. De là Snellius se hasarde à conclure que toute la courbe, qui constitue le lieu géométrique cherché et qui doit nécessairement passer par le point B, sera située à droite de la tangente BL; auquel cas on doit avoir, en effet, arc. BE = BP > BL.
Or, pour faire voir combien cette conclusion est fallacieuse, il suffit de remarquer que si l'on place le point C un peu plus près du point A, une partie de la courbe se trouvera, dans le voisinage du point B, à gauche de BL; comme cela résulte aisément de la considération de la note 37, qui suit.

[p. 160]

conférence pour la seconde fois en E; et supposons qu'elle rencontre en L la tangente qui touche le cercle à l'extrémité du diamètre B. Je dis que la longueur interceptée BL est plus petite que l'arc BE. Joignons en effet AE, EB; puis, ayant porté AH égal à AE, menons HE et prolongeons cette droite, qui rencontre la tangente en K. Enfin menons EG à angles droits sur le diamètre AB, et ED perpendiculaire à la tangente BL. Puisque le triangle HAE est ainsi isoscèle, les angles H et HEA seront égaux entr'eux. Mais comme l'angle AEB est droit, les deux angles HEA et KEB seront aussi égaux ensemble à un angle droit. Mais les deux angles H et HKB valent aussi un angle droit, parce que dans le triangle HKB l'angle B est droit. Donc enlevant de part et d'autre deux quantités égales, ici l'angle H, là l'angle HEA, il reste que les angles KEB, HKB sont égaux entr'eux. Le triangle KBE est donc isoscèle, et ses côtés EB, BK sont égaux. Mais BD est égal à EG. Donc DK est la différence, dont BE dépasse EG. Ensuite, puisque AG est à AE comme AE à AB, les deux droites AG et AB vaudront ensemble plus que le double de AE^*. Ainsi AE, c'est-à-dire, AH, est moindre que la moitié de la somme des deux droites AG, AB, c'est-à-dire, moindre que CA, augmenté de la moitié de AG. Par suite, si l'on retranche de part et d'autre CA, CH sera plus petit que la moitié de AG. Mais CA est plus grand que la moitié de AG. Donc, si l'on ajoute AC à AG, la ligne CG toute entière sera plus grande que le triple de CH. Mais, comme HG à GE, ainsi ED est à DK, et comme GE à GC, ainsi LD est à DE; on aura donc par la règle de la proportion dérangée³⁵⁾ que LD est à DK, comme HG est à GC. Et par conversion des rapports et par partage, DK est à KL comme GC est à CH. Donc aussi DK est plus grand que le triple de KL. Mais DK était l'excès de EB sur EG. Donc KL est plus petit que le tiers du dit excès. Or, KB est égal à cette corde EB. Donc KB avec KL, c'est-à-dire toute la droite LB est à plus forte raison moindre que l'arc BE^*. Ce qu'il fallait démontrer.

Mais, en considération du théorème précédent, il est clair qu'il n'est pas possible de prendre sur le prolongement du diamètre BA un autre point, qui soit moins distant du cercle que le point C et qui peut servir à la même propriété, savoir qu' en traçant CL on obtienne une tangente interceptée BL toujours plus petite que l'arc découpé BE³⁷⁾.

* 25.5. Élem.³⁴⁾

34) Si quatuor magnitudines proportionales fuerint: maxima & minima reliquis duabus maiores erunt.’ (Clavius, p. 518).

35) Voir la note 22, p. 304 du Tome XI.

* d'après 7. ici³⁶⁾.

36) Voir le dernier alinéa de la démonstration du ‘Theor. VII’, p. 135 du Tome présent.

37) Soit, en effet, dans la figure 15, E un point choisi sur le prolongement de AB de manière que AE soit un peu plus petit que le rayon du cercle. Alors on peut tirer une droite ED égale à ce rayon, qui sera l'équivalent de la droite CL de la figure 16. Ainsi LB de cette dernière figure sera alors identique avec GB de la figure 15; mais on sait que, dans cette figure 15, GB est plus grand que l'arc FB; donc il en sera de même avec LB de la figure 16, c'est-à-dire, cette droite pourra surpasser l'arc EB, aussitôt que le point C est choisi sur AB à droite de sa position actuelle.

[p. 161]

Esto circulus, cujus diameter AB; quae producatur, & sit AC semidiametro aequalis. Et ducatur recta CL, quae circumferentiam secundò secet in E; occurratque tangenti in L, ei nimirum quae circulum contingit in termino diametri B. Dico interceptam BL aren BE minorem esse. Jungantur enim AE, EB, positâque AH ipsi AE aequali ducatur HE & producatur, occurratque tangenti in K. Denique sit

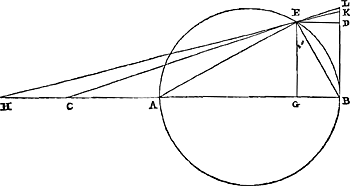[Fig. 16.]

EG diametro AB ad angulos rectos, ED verò tangenti BL. Quoniam igitur isosceles est triangulus HAE, erunt anguli inter se aequales H & HEA. Quia autem angulus AEB rectus est, etiam recto aequales erunt duo simul HEA, KEB. Verùm duo quoque isti H & HKB uni recto aequantur, quoniam in triangulo HKB rectus est angulus B. Ergo demptis utrimque aequalibus, hinc nimirum angulo H, inde angulo HEA, relinquentur inter se aequales anguli KEB, HKB. Triangulus igitur isosceles est KBE, ejusque latera aequalia EB, BK. Est autem BD aequalis EG. Ergo DK differentia est quâ BE excedit EG. Porrò quoniam est AG ad AE, ut AE ad AB, erunt duae simul AG, AB majores duplâ AE^*. Ideoque AE, hoc est, AH minor quam dimidia utriusque simul AG, AB; hoc est, minor quam CA cum dimidia AG. Quare ablatâ utrimque CA, erit CH minor dimidiâ AG. CA verò dimidiâ AG major est. Ergo si addatur AC ad AG, erit tota CG major quam tripla ipsius CH. Quia autem ut HG ad GE, ita est ED ad DK; ut autem GE ad GC, ita LD ad DE: Erit ex aequo in proportione turbata³⁵⁾ ut HG ad GC, ita LD ad DK. Et per conversionem rationis & dividendo, ut GC ad CH, ita DK ad KL. Ergo etiam DK major quam tripla KL. Erat autem DK excessus ipsius EB supra EG. Ergo KL minor est triente dicti excessus. KB autem aequalis est ipsi EB subtensae. Ergo KB unà cum KL, hoc est, tota LB omnino minor erit arcu BE^*. Quod erat demonstrandum.

Perpenso autem Theoremate praecedenti, liquet non posse sumi punctum aliud in producta BA diametro, quod minus à circulo distet quam punctum C, eandemque servet proprietatem, ut nimirum ductâ CL fiat tangens intercepta BL semper minor arcu abscisso BE³⁷⁾.

* 25.5. Elem.³⁴⁾

34) Si quatuor magnitudines proportionales fuerint: maxima & minima reliquis duabus maiores erunt.’ (Clavius, p. 518).

35) Voir la note 22, p. 304 du Tome XI.

* per. 7. huj.³⁶⁾

36) Voir le dernier alinéa de la démonstration du ‘Theor. VII’, p. 135 du Tome présent.

37) Soit, en effet, dans la figure 15, E un point choisi sur le prolongement de AB de manière que AE soit un peu plus petit que le rayon du cercle. Alors on peut tirer une droite ED égale à ce rayon, qui sera l'équivalent de la droite CL de la figure 16. Ainsi LB de cette dernière figure sera alors identique avec GB de la figure 15; mais on sait que, dans cette figure 15, GB est plus grand que l'arc FB; donc il en sera de même avec LB de la figure 16, c'est-à-dire, cette droite pourra surpasser l'arc EB, aussitôt que le point C est choisi sur AB à droite de sa position actuelle.

[p. 162]

Puis l'usage de ce théorème est multiple, tant pour trouver les angles de triangles dont les côtés sont donnés, et sela sans le secours de tables, que pour trouver les côtés quand les angles sont donnés, ou encore pour déterminer la corde d'un arc de périphérie quelconque. Toutes ces questions ont été traitées assidûment et à fond par Snellius dans sa Cyclométrie³⁸⁾.

38) Voir dans l'‘Appendicula, et Cyclometrices usus’ les problèmes V (‘Datis trianguli rectanguli lateribus ejus angulos invenire’) et VI (‘Datis trianguli rectanguli angulis oppositorum laterum rationem invenire’), p. 95-102 de l'ouvrage, cité dans la note 6, p. 94 du Tome présent; et de même aux p. 76-83 de cet ouvrage la ‘Propositio XXXVIII: Datae cuicunque peripheriae inscriptam verae tam propinquam in numeris exhibere, quam erit ratio diametri ad suam peripheriam data’.

Théorème XIV. Propos. XVII³⁹⁾.

Le centre de gravité d'un segment de cercle divise le diamètre de ce segment, de telle manière que la partie au sommet est plus grande que l'autre, et plus petite que une et demie fois cette autre.

Soit un segment de cercle ABC (mais supposons-le plus petit qu'un demi-cercle, parce que les autres ne satisfont pas à la proposition), et soit BD le diamètre du segment, qui est partagé en deux parties égales en E. Nous avons ainsi à démontrer d'abord que le centre de gravité du segment AB se trouve à partir du sommet B au-delà du point E; car nous avons montré ailleurs⁴⁰⁾ qu'il est situé sur le diamètre. Menons par E une droite parallèle à la base, qui rencontre de part et d'autre le cercle aux points F et G. Par ces points menons KI, HL, perpendiculaires à la base AC; ces droites forment, avec celle qui touche le segment au sommet, le rectangle KL. Puisque le segment est moindre qu'un demi-cercle, il est certain que la moitié FL du dit rectangle est contenue dans la figure AFGC, qui contient en outre les espaces AFI et LGC, mais que l'autre moitié KG du rectangle KL embrasse le segment FBG, ensemble avec les espaces FBK, BGH. Comme ces espaces sont tout entiers au-dessus de la droite FG, leur centre de gravité commun sera situé aussi au-dessus de cette même droite. Mais le point E sur cette droite est le centre de gravité de tout le rectangle KL. Donc le centre de gravité de l'espace restant BFILG sera sous la droite FG. Mais aussi le centre de gravité commun des espaces AFI, LGC est au-dessous de la même droite FG. Par conséquent, le centre de gravité de la grandeur formée par ces espaces et le dit espace BFILGB, c'est-à-dire, du segment ABC lui-même, doit nécessairement être trouvé au-dessous de la ligne FG, et par suite au-dessous du point E.

39) Consultez, sur la partie de l'ouvrage présent qui commence avec cette proposition, les p. 97 et 98 de ‘l'Avertissement’.

40) Voir le ‘Theorema IV’ des ‘Theoremata de quadratura hyperboles, ellipsis et circuli, ex dato portionum gravitatis centro’, p. 295 du Tome XI.

[p. 163]

Porrò usus hujus Theorematis multiplex est, cum in inveniendis triangulorum angulis quorum cognita sint latera, idque citra tabularum opem, tum ut latera ex angulis datis inveniantur, vel cuilibet peripheriae arcui subtensa assignetur. Quae omnia à Snellio in Cyclometricis diligenter pertractata sunt³⁸⁾.

38) Voir dans l'‘Appendicula, et Cyclometrices usus’ les problèmes V (‘Datis trianguli rectanguli lateribus ejus angulos invenire’) et VI (‘Datis trianguli rectanguli angulis oppositorum laterum rationem invenire’), p. 95-102 de l'ouvrage, cité dans la note 6, p. 94 du Tome présent; et de même aux p. 76-83 de cet ouvrage la ‘Propositio XXXVIII: Datae cuicunque peripheriae inscriptam verae tam propinquam in numeris exhibere, quam erit ratio diametri ad suam peripheriam data’.

Theorema XIV. Propos. XVII³⁹⁾.

Portionis circuli centrum gravitatis diametrum portionis ita dividit, ut pars quae ad verticem reliquâ major sit, minor autem quam ejusdem sesquialtera.

Esto circuli portio ABC, (ponatur autem semicirculo minor, quoniam caeterae ad propositum non faciunt) & diameter portionis sit BD, quae bifariam secetur in E. Itaque ostendendum est primò centrum gravitatis portionis AB distare à vertice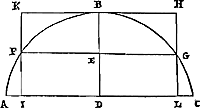

[Fig. 17.]

B ultra punctum E; nam, quod in diametro situm sit, alibi ostendimus⁴⁰⁾. Ducatur per E recta basi parallela, quae utrimque circumferentiae occurrat in punctis F & G. Per quae ducantur KI, HL basi AC ad angulos rectos, atque hae cum ea, quae portionem in vertice contingit, constituant rectangulum KL. Quoniam igitur portio semicirculo minor est, constat rectanguli dicti dimidium FL contineri intra segmentum AFGC, atque insuper spatia quaedam AFI, LGC. Alterum verò rectanguli KL semissem KG complecti segmentum FBG unà cum spatiis FBK, BGH. Quae spatia quum sint tota supra rectam FG, etiam centrum commune gravitatis eorum supra eandem situm erit. Est autem E punctum in ipsa FG centrum grav. totius rectanguli KL. Igitur spatii reliqui BFILGB centrum grav. erit infra rectam FG. Sed & spatiorum AFI, LGC commune gravitatis centrum est infra eandem FG. Ergo magnitudinis ex spatiis hisce & dicto spatio BFILGB compositae, quae est portio ipsa ABC, centrum gravitatis infra lineam FG reperiri necesse est, ideoque infra E punctum.

39) Consultez, sur la partie de l'ouvrage présent qui commence avec cette proposition, les p. 97 et 98 de ‘l'Avertissement’.

40) Voir le ‘Theorema IV’ des ‘Theoremata de quadratura hyperboles, ellipsis et circuli, ex dato portionum gravitatis centro’, p. 295 du Tome XI.

[p. 164]

Supposons maintenant que le même diamètre soit divisé en S [Fig. 18], de telle manière que BS soit une et demie fois le reste SD. Je dis que le centre de gravité du segment ABC est moins distant du sommet que le point S. Soit, en effet, BDP le diamètre du cercle entier, et menons par S une droite parallèle à la base, qui rencontre la circonférence en F et G. Et imaginons une parabole dont le sommet est B, l'axe BD, et le paramètre égal à SP. Et qu'elle rencontre la base du segment en H et K. Puisqu' alors le carré sur FS est égal au rectangle BSP, c'est-à-dire, à celui formé par BS et le paramètre de la parabole, celle-ci passera par le point F et de même par G. Mais les parties BF, BG de la ligne parabolique tomberont à l'intérieur de la circonférence, et les autres FH, GK lui seront extérieures. Car cela se démontre en menant une ordonnée NL entre B et S, qui rencontre la circonférence en N, et la parabole en M. Or, puisque le carré sur NL est égal au rectangle BLP, tandis que le carré sur ML l'est au rectangle formé par les lignes BL, SP; et que le rectangle BLP est plus grand que celui formé par BL, SP: le carré sur NL sera plus grand que le carré sur ML, et la ligne NL plus grande que la ligne ML. Et la même chose arrive quel que soit le point entre B et S ou l'on applique l'ordonnée. Par conséquent, il est nécessaire que la partie BF de la circonférence soit toute entière à l'extérieur de la parabole, et pour la même raison la partie BG. D'autre part, puisque le rectangle BDP est égal au carré sur DA, et que le rectangle formé par BD, SP est égal au carré sur DH; HD sera plus grand que AD quant aux carrés, donc aussi en longueur. La même chose arrivera quel que soit l'endroit entre S et D où l'on place l'ordonnée. Par suite les parties FA et GC de la circonférence tombent à l'intérieur de la parabole. On obtient ainsi certains espaces FNBM et BQG, ainsi que d'autres HFA, GCK. Comme les derniers de ces espaces sont tout entiers au-dessous de la ligne FG, leur centre de gravité commun est aussi au-dessous de cette droite. Mais le centre de gravité du segment parabolique HBK est dans cette droite FG, savoir au point S^*. Donc le centre de gravité de la partie restante AFMBQGC sera audessus de la droite FG. Mais il est clair que le centre de gravité des espaces FMBN, BQG est également situé au-dessus d'elle puisque ces espaces sont tout entiers au-dessus de cette droite FG. Donc on trouvera aussi au-dessus de la ligne FG le centre de gravité de l'espace formé par ces deux et AFMBQGC, c'est-à-dire du segment de cercle ABC; et comme ce centre est sur le diamètre BD, il sera moins distant du sommet B que le point S. Ce qu'il fallait démontrer.

* 8. livre 2. Archim. de Aequipond.⁴¹⁾

41) Voici cette Proposition telle qu'on la trouve p. 138 de l'édition de Bâle, mentionnée dans la note 3, p. 274 du T. XI: ‘Cuiuscunque portionis à recta linea & rectanguli coni sectione comprehensae, centrum grauitatis dividit diametrum portionis, ita ut pars eius ad verticem terminata, sit ad partem eam sequialtera, quae ad basim portionis terminatur’. (Heiberg, T. II, p. 213).

[p. 165]

Idem verò diameter BD secetur nunc in S [Fig. 18], ita ut BS sit sesquialtera reliquae SD. Dico centrum grav. portionis ABC minus distare à vertice B quam punctum S. Sit enim BDP totius circuli diameter. & ducatur per S recta basi parallela quae circumferentiae occurrat in F & G. Et parabole intelligatur cujus vertex B, axis BD, rectum verò latus aequale SP. Et occurrat basi portionis in H & K. Quoniam igitur quadratum FS aequale est rectangulo BSP, hoc est, ei quod sub BS & latere recto parabolae continetur, transibit ea per F punctum, itemque per G. Partes autem lineae parabolicae BF, BG intra circumferentiam cadent, sed reliquae FH, GK erunt exteriores. Hoc enim ostenditur ductâ inter B & S ordinatim applicatâ NL, quae circumferentiae occurrat in N, parabolae autem in M. Nam quia quadratum NL aequale est rectangulo BLP, quadratum verò ML rectangulo contento

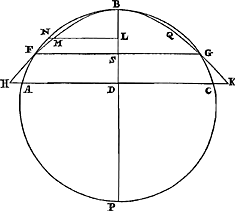[Fig. 18.]

lineis BL, SP: rectangulum autem BLP majus eo quod sub BL, SP continetur: erit quadratum NL majus quadrato ML, & NL linea major quam ML. Idem autem continget ubicunque inter B & S aliqua ordinatim applicabitur. Igitur partem circumferentiae BF totam extra parabolam ferri necesse est, eâdemque ratione partem BG. Rursus quia rectangulum BDP aequale est quadrato DA; rectangulum verò sub BD, SP contentum quadrato DH; erit HD major quam AD potentiâ, ideoque & longitudine. Idemque eveniet ubicunque inter S, D, ordinatim aliqua applicabitur. Quare partes circumferentiae FA, itemque GC intra parabolam cadent. Fiunt igitur spatia quaedam FNBM, & BQG, itemque alia HFA, GCK. Quorum haec cum tota sint infra lineam FG, etiam centrum commune gravitatis eorum infra eandem erit. At parabolicae portionis HBK centrum grav. est in ipsa FG, nimirum S punctum^*. Ergo partis reliquae AFMBQGC centrum grav. erit supra rectam FG. Sed supra hanc situm quoque apparet centrum grav. spatiorum FMBN, BQG, quum tota sint supra ipsam FG. Ergo & spatii ex hisce duobus & AFMBQGC compositi, hoc est, portionis circuli ABC centrum grav. supra lineam FG reperietur: quumque sit in BD diametro, minus aberit à vertice B quam punctum S. Quod erat ostendendum.

* 8. lib. 2. Archim. de AEquipond.⁴¹⁾

41) Voici cette Proposition telle qu'on la trouve p. 138 de l'édition de Bâle, mentionnée dans la note 3, p. 274 du T. XI: ‘Cuiuscunque portionis à recta linea & rectanguli coni sectione comprehensae, centrum grauitatis dividit diametrum portionis, ita ut pars eius ad verticem terminata, sit ad partem eam sequialtera, quae ad basim portionis terminatur’. (Heiberg, T. II, p. 213).

[p. 166]

Théor. XV. Propos. XVIII.

Un segment de cercle plus petit qu'un demi-cercle est au triangle maximum inscrit dans un rapport plus grand que quatre à trois; mais plus petit que celui de trois et un tiers fois le diamètre du segment restant au diamètre du cercle augmenté du triple de la droite qui, à partir du centre du cercle, atteint la base du segment⁴²⁾.

Soit un segment de cercle plus petit qu'un demi-cercle, dans lequel est inscrit le triangle maximum ABC. Soit BD le diamètre du segment, et BF le diamètre du cercle dont le segment est découpé, E son centre. Je dois montrer d'abord que le rapport du segment ABC au triangle inscrit est plus grand que quatre à trois. Soit G le centre de gravité du segment ABC, et coupons DF en H, de telle manière que HD soit le double du reste HF.

Alors, parce que FB est le double de EB, et que DB est plus petit que le double de GB⁴³⁾, le rapport de FB à BD sera plus grand que celui de EB à BG. Et par conversion des rapports le rapport de BF à FD sera moindre que celui de BE à EG⁴⁴⁾. Et en permutant, BF à BE (lequel rapport est de deux à un) est moindre que FD à EG. Donc FD est plus grand que le double de EG. Mais les deux tiers de cette FD font HD. Donc HD est plus grand que les quatre tiers de EG. Mais, comme HD est à EG, ainsi le segment ABC est au triangle inscrit; car c'est ce que nous avons démontré antérieurement dans les Théorèmes sur la quadrature de l'Hyperbole, de l'Ellipse et du Cercle⁴⁵⁾. Donc le rapport de la portion au triangle inscrit ABC est plus grand que de quatre à trois.

Mais nous allons démontrer maintenant que le segment est au triangle ABC dans un rapport moindre que celui de trois et un tiers fois DF au diamètre du cercle BF augmenté du triple de ED. Coupons le diamètre du segment en R, de telle façon que BR soit une fois et demie le reste RD. Le point R tombe donc entre G et D^*, car nous avons supposé que G est le centre de gravité du segment ABC. Et puisque le rapport du segment au triangle inscrit est le même que celui de HD à EG, comme nous venons de le dire, mais que le rapport de HD à EG est plus petit que celui de HD à ER, pour cette raison le rapport du segment au

42) La première partie de cette proposition n'est qu'une répétition du ‘Theor. III. Prop. III’, p. 123 du Tome présent; mais la seconde partie amène pour la limite supérieure une approximation plus forte, que celle fournie par le ‘Theor. IV. Prop. IV’, p. 127; ce qui résulte de la circonstance que le rapport dans lequel le point R, dont on fait usage dans la démonstration, divise BD, est égal á la limite du rapport BG/GD pour des arcs de plus en plus petits.

43) Voir la première partie du théorème précédent.

44) Voir la note 25, p. 151.

45) Voir le ‘Theorema VII’ de la p. 305 du Tome XI.

* d'après ce qui précède⁴⁶⁾.

46) Voir la seconde partie du théorème précédent.

[p. 167]

Theor. XV. Propos. XVIII.

Circuli portio semicirculo minor ad inscriptum triangulum maximum majorem rationem habet quam sesquitertiam, minorem verò quam diameter portionis reliquae tripla sesquitertia ad circuli diametrum cum tripla ea, quae à centro circuli pertingit ad portionis basin⁴²⁾.

Sit portio semicirculo minor, cui inscriptum triangulum maximum ABC. Diameter autem portionis sit BD; & diameter circuli à quo portio resecta est, BF, centrum E. Ostendendum est primò, portionis ABC ad triangulam inscriptum majorem esse rationem quam sesquitertiam. Esto portionis ABC centrum grav. punctum G, & secetur DF in H, ut sit HD dupla reliquae HF.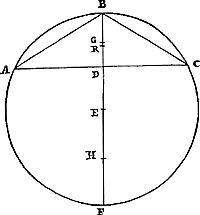

[Fig. 19.]

Quoniam igitur FB est dupla EB; DB autem minor quam dupla GB⁴³⁾. Erit major ratio FB ad BD, quam EB ad BG. Et per conversionem rationis, minor BF ad FD, quam BE ad EG⁴⁴⁾. Et permutando minor BF ad BE, (quae proportio dupla est) quam FD ad EG. Igitur FD major est quam dupla EG. Ipsius autem FD duas tertias continet HD. Ergo HD major est quam sesquitertia EG. Sicut autem HD ad EG, ita est portio ABC ad inscriptum sibi triangulum: hoc enim antehac demonstravimus in Theorematis de Hyperbolis Ellipsis & Circuli quadratura⁴⁵⁾. Itaque major est ratio portionis ad inscriptum triangulum ABC quam sesquitertia.

Quod autem ad triangulum ABC portio minorem habeat rationem quam tripla sesquitertia ipsius DF ad diametrum circuli BF unà cum tripla ED, id nunc ostendemus. Secetur diameter portionis in R, ut BR sit sesquialtera reliquae RD. Ergo cadit R punctum inter G & D^* quoniam positum fuit G centrum gravitatis in portione ABC. Quumque portionis ad inscriptum triangulum eadem sit ratio, quae HD ad EG, ut modò dictum fuit; minor autem sit ratio HD ad EG, quam HD ad ER: Erit propterea minor quoque portionis ad inscriptum triangulum

42) La première partie de cette proposition n'est qu'une répétition du ‘Theor. III. Prop. III’, p. 123 du Tome présent; mais la seconde partie amène pour la limite supérieure une approximation plus forte, que celle fournie par le ‘Theor. IV. Prop. IV’, p. 127; ce qui résulte de la circonstance que le rapport dans lequel le point R, dont on fait usage dans la démonstration, divise BD, est égal á la limite du rapport BG/GD pour des arcs de plus en plus petits.

43) Voir la première partie du théorème précédent.

44) Voir la note 25, p. 151.

45) Voir le ‘Theorema VII’ de la p. 305 du Tome XI.

* per praced.⁴⁶⁾.

46) Voir la seconde partie du théorème précédent.

[p. 168]

triangle inscrit sera aussi plus petit que celui de HD à ER, ou de HD prise cinq

[Fig. 19.]

fois au quintuple de ER. Or, HD (puisqu'il est égal aux deux tiers de DF) pris cinq fois sera égal aux dix tiers, c'est-à-dire à trois et un tiers fois DF. Mais ER, qui se compose de ED et des deux cinquièmes de DB, si on le prend cinq fois, sera égal au double de BD avec le quintuple de ED, c'est-à-dire, au double de toute la droite EB et en plus le triple de ED. Il paraît donc que le rapport du segment ABC au triangle inscrit est moindre que celui de trois et un tiers fois DF au double de EB, c'est-à-dire au diamètre BF, augmenté du triple de ED. Ce qu'il fallait démontrer.

Théor. XVI. Propos. XIX.

Un arc quelconque, plus petit qu' une demi-circonférence, est plus grand que sa corde augmentée du tiers de la différence dont la corde dépasse le sinus. Mais un tel arc est plus petit que la corde prise avec la droite qui est au dit tiers comme le quadruple de la corde joint au sinus est au double de la corde avec le triple du sinus⁴⁷⁾.

Soit un cercle dont le centre est D, le diamètre FB. Et soit un arc BA plus petit que la demi-circonférence, auquel nous menons la corde BA et le sinus AM; ce dernier est donc à angles droits sur le diamètre FB. Ensuite, soit une droite GH égale á cette AM, et GI égale à la corde AB. L'excès est donc HI, dont nous ajoutons le tiers IK à GI. Il faut montrer d'abord que l'arc AB est plus grand que toute la droite GK. Or, cela est manifeste d'après le théorème 7⁴⁸⁾. Mais si l'on ajoute à GI la droite IO qui est à IK, le tiers de HI, dans le même rapport que le quadruple de GI avec GH au double de GI avec le triple de GH; je dis que toute la droite GO est plus grande que l'arc AB. Formons, en effet, sur les lignes GH, HI, IO des triangles dont le sommet commun est L, et dont la hauteur soit égale au rayon DB. Et joignons DA, et menons le diamètre CE du cercle qui divise la droite AB en deux parties égales en N, et l'arc AB en E. Et joignons AE, EB.

47) La première partie est identique avec le ‘Theor. V. Prop. V’, p. 129 du Tome présent. D'après la seconde partie on a, en employant toujours les notations de la note 10, p. 136,




c'est-à-dire:
; expression dont les trois premiers termes correspondent avec la suite (1) de la note 7, p. 94 Tome présent.

48) Voir le dernier alinéa de la démonstration du ‘Theor. VII’, p. 135 du Tome présent.

[p. 169]

ratio quam HD ad ER, sive quam HD quinquies sumpta ad quintuplam ER. Atqui HD, (com sit aequalis duabus tertiis DF) quinquies sumpta aequabitur decem tertiis, hoc est, triplae sesquitertiae DF. ER verò quae continet ED & duas quintas ipsius DB, si quinquies sumatur, aequabitur duplae BD & quintuplae ED; hoc est, duplae totius EB atque insuper triplae ED. Igitur apparet portionem ABC ad inscriptum triangulum minorem habere rationem quam triplam sesquitertiam DF ad duplam EB, hoc est, diametrum BF, unà cum tripla ED. Quod erat demonstrandum.

Theor. XVI. Propos. XIX.

Arcus quilibet semicircumferentiâ minor, major est suà subtensâ simul & triente differentiae quâ subtensa sinum excedit. Idem verò minor quam subtensa simul cum ea quae ad dictum trientem sese habeat, ut quadrupla subtensa juncta sinui ad subtensam duplam cum sinu triplo⁴⁷⁾.

Soit un cercle dont le centre est D, le diamètre FB. Et soit un arc BA plus petit que la demi-circonférence, auquel nous menons la corde BA et le sinus AM; ce dernier est donc à angles droits sur le diamètre FB. Ensuite, soit une droite GH égale á cette AM, et GI égale à la corde AB. L'excès est donc HI, dont nous ajoutons le tiers IK à GI. Il faut montrer d'abord que l'arc AB est plus grand que toute la droite GK. Or, cela est manifeste d'après le théorème 7⁴⁸⁾.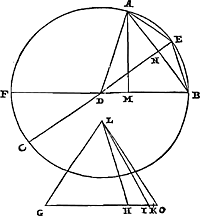

[Fig. 20.]

Esto circulus cujus D centrum, diameter FB. Et sit arcus BA semicircumferentiâ minor, cui subtensa ducatur BA, sinus autem AM: quae nimirum diametro FB sit ad angulos rectos. Porro ipsi AM sit aequalis recta GH, & GI aequalis subtensae AB. Excessus igitur est HI; cujus triens IK ipsi GI adjiciatur. Ostendendum est primò, arcum AB totâ GK majorem esse. Hoc autem ex Theoremate 7. est manifestum⁴⁸⁾. At cum ipsi GI additur IO quae ad IK trientem ipsius HI rationem habeat, quam quadrupla GI unà cum GH ad duplam GI cum tripla GH. Dico totam GO arcu AB majorem esse. Constituantur enim super lineis GH, HI, IO, triangula quorum communis vertex sit L, altitudo autem aequalis radio

47) La première partie est identique avec le ‘Theor. V. Prop. V’, p. 129 du Tome présent. D'après la seconde partie on a, en employant toujours les notations de la note 10, p. 136,




c'est-à-dire: ; expression dont les trois premiers termes correspondent avec la suite (1) de la note 7, p. 94 Tome présent.

48) Voir le dernier alinéa de la démonstration du ‘Theor. VII’, p. 135 du Tome présent.

48) Voir le dernier alinéa de la démonstration du ‘Theor. VII’, p. 135 du Tome présent.

[p. 170]

Puisque OI est à IK comme le quadruple de GI avec GH est au double de GI avec le triple de GH, en prenant les triples des conséquents, OI sera à IH (qui est notamment le triple de IK) comme le quadruple de GI avec GH est au sextuple de GI avec le nonuple de GH. Et, par composition, OH est à HI comme le décuple des deux droites IG, GH est au sextuple de IG avec le nonuple de GH; ou bien, prenant les tiers, comme les dix tiers de la somme des deux droites GI, GH est au double de GI avec le triple de GH. Mais le rapport de la ligne GI à GH, c'est-à-dire, de BA à AM, est le même que celui de BD à DN, à cause des triangles semblables BAM, BDN. Donc aussi OH est à HI, comme 10/3 de la somme des deux droites BD, DN est au double de BD avec le triple de DN, c'est-à-dire, comme 10/3 NC est au diamètre EC avec le triple de DN. Mais plus petit que ce rapport est le rapport du segment AEB au triangle AEB^*. Donc le rapport du dit segment au dit triangle est aussi moindre que celui de OH à HI, c'est-à-dire, que celui du triangle OHL au triangle IHL. Mais le triangle IHL est égal au triangle AEB. C'est ce que l'on démontre de la manière suivante. Le triangle GHL est égal au triangle DAB, parce que leurs bases et leurs hauteurs sont réciproquement égales. Et pour une raison semblable, puisque GI est égal à la droite AB, le triangle GIL sera égal

[Fig. 20.]

à la somme des deux triangles DAE, DBE, c'est-à-dire au quadrilatère DAEB. Par conséquent il faut que le triangle HIL soit égal au triangle AEB, ce que nous disions. Le segment AEB sera donc au triangle AEB qui lui est inscrit dans un rapport moindre que le triangle OHL au même triangle AEB. Pour cette raison le triangle OHL sera plus grand que le segment AEB. Et dès lors le triangle OGL tout entier plus grand que le secteur DAEB. Mais la hauteur du triangle GLO est égale au rayon DB. Donc la base GO sera plus grande que l'arc AB. Ce qu'il fallait démontrer.

Or, il résulte évidemment de cela que de la circonférence toute entière on peut dire que, si l'on inscrit dans le cercle deux polygones équilatér aux dont l'un a un nombre deux fois plus grand de côtés que l'autre, et que si l'on ajoute le tiers de la différence des périmètres au périmètre du polygone le plus grand, la droite ainsi composée sera plus petite que la circonférence du cercle. Mais si au même plus grand périmètre on ajoute une ligne qui est au dit tiers de la différence comme le quadruple du plus grand périmètre augmenté du plus petit périmètre est au double du plus grand avec le triple du plus petit, la droite ainsi composée dépassera la circonférence du cercle⁴⁹⁾.

* d'après ce qui précède.

49) Voir la seconde formule de la note 47.

[p. 171]

DB. Et jungatur DA, ducaturque diameter circuli CE quae rectam AB bifariam dividat in N, arcum verò AB in E. Et jungantur AE, EB.

Quoniam igitur OI est ad IK ut quadrupla GI unà cum GH ad duplam GI cum tripla GH; sumptis consequentium triplis erit OI ad IH (haec enim tripla est IK,) ut quadrupla GI unà cum GH ad sexcuplam GI cum noncupla GH. Et componendo, OH ad HI, ut decupla utriusque IG, GH ad sexcuplam IG cum noncupla GH: vel sumptis horum trientibus ut decem tertiae duarum simul GI, GH ad duplam GI cum tripla GH. Est autem eadem ratio linearum GI ad GH, hoc est, BA ad AM, quae BD ad DN, propter similes triangulos BAM, BDN. Ergo etiam OH ad HI, ut 10/3 utriusque simul BD, DN ad duplam BD cum tripla DN; hoc est, ut 10/3 NC ad diametrum EC cum tripla DN. Hac autem ratione minor est ratio portionis AEB ad AEB triangulum^*. Ergo dictae portionis ad dictum triang. minor quoque ratio quam OH ad HI, hoc est, quam trianguli OHL ad triangulum IHL. Triangulum autem IHL aequale est triangulo AEB. Quod sic ostenditur. Triangulum enim GHL aequale est triangulo DAB, quoniam bases & altitudines reciprocè aequales habent. Similique ratione quoniam GI aequalis est rectae AB, erit triangulum GIL aequale duobus simul triangulis DAE, DBE, hoc est, quadrilatero DAEB. Itaque triangulum HIL triangulo AEB aequari necesse est, quod dicebamus. Habebit itaque portio AEB ad triangulum sibi inscriptum AEB minorem quoque rationem quam triangulum OHL ad idem triangulum AEB. Quamobrem triangulum OHL portione AEB majus erit. Et totum proinde triangulum OGL majus sectore DAEB. Altitudo autem trianguli GLO aequalis est radio DB. Ergo basis GO major erit arcu AB. Quod erat ostendendum.

Ex his autem manifestum est de tota quoque circumferentia pronunciari posse, quod, Si circulo inscribantur polygona duo aequilatera, quorum alterum alterius sit duplo laterum numero, & differentiae perimetrorum triens perimetro polygoni majoris adjungatur, composita ex his circuli circumferentiâ minor erit. Eidem verò majori perimetro si linea addatur quae ad dictum differentiae trientem sese habeat, sicut quadrupla perimetri majoris juncta perimetro minori, ad duplam majoris cum tripla minoris, composita circumferentiam circuli excedet⁴⁹⁾.

* per praeced.

49) Voir la seconde formule de la note 47.

[p. 172]

Problème IV. Propos. XX.

Trouver le rapport de la circonférence au diamètre; et au moyen des cordes données inscrites dans un cercle donné trouver la longueur des arcs auxquels elles sont sous-tendues.

Soit un cercle de centre D, dont le diamètre est CB, et soit l'arc BA un sextant de la circonférence, dont nous menons la corde AB, ainsi que le sinus AM. Si nous supposons donc que le demi-diamètre DB est de 100000 parties, la corde BA en contiendra le même nombre. Mais AM se composera de 86603 parties, et pas une de moins (ce qui veut dire que si l'on enlevait une partie ou une unité des 86603 on aurait moins que le dû)⁵⁰⁾, puisqu' elle est la moitié du côté du triangle équilateral inscrit dans le cercle.

De là l'excès de AB sur AM devient 13397, moindre que le vrai. Le tiers en est 4465 ⅔, ce qui ajouté à AB 100000, donne 104465 ⅔ parties, ce qui est moins que l'arc AB. Et ceci est une première limite inférieure; dans la suite nous en trouverons une autre, plus rapprochée que celle-là de la vraie valeur. Mais d'abord nous devons chercher aussi une limite supérieure, conformément au theorème précédent.

Il y a donc trois nombres auxquels il s'agit de trouver une quatrième proportionnelle. Le premier est égal au double des parties de AB et au triple de AM; il sera donc 459807, moindre que le vrai, (car on doit aussi prendre soin que ce nombre soit moindre ici; et de même avec les autres de la manière que nous l'indiquerons); le second est égal au quadruple de AB et au simple AM, soit 486603, plus grand que le vrai. Et le troisième est le tiers de l'excès de AB sur AM, 4466, plus grand que le vrai. La quatrième proportionelle sera donc 4727, plus grande que le vrai, ce qui, ajouté à AB ou 100000 donne 104727, plus grand que le nombre de parties que contient l'arc AB, sextant de la périphérie^*. Nous avons donc déjà trouvé la longueur de l'arc AB d'après une limite inférieure et une supérieure, dont cependant la dernière est de beaucoup la plus rapprochée de la vraie valeur, car le nombre 104719 est le plus voisin du vrai.

Mais au moyen de ces deux là nous obtiendrons une autre limite inférieure plus exacte que la première, en faisant usage du précepte suivant, qui résulte d'un examen plus précis du centre de gravité⁵¹⁾.

50) La phrase entre parenthèses à été ajoutée par Huygens en marge de l'exemplaire que nous possédons.

* d'après ce qui précède.

51) Les manuscrits et les lettres ne donnent aucun renseignement décisif sur la manière dont la règle qui va suivre a été obtenue. Nous savons seulement par la Lettre N^o. 185 du 1^er avril 1654 (p. 279 du T. I) que sa démonstration dépendait, comme celle de la seconde partie du Théorème XVI, de l'emploi d'une parabole.
Il était donc à supposer que la règle en question s'obtiendrait suivant la voie indiquée par les Théorèmes XIV et XV, en remplaçant toutefois la parabole HBK de la figure 18 par une autre dont le centre de gravité se trouverait nécessairement au dessus de celui du segmentde cercle.



Or, la parabole qui, mieux qu' aucune autre, peut servir à ce but est celle ATC tracée dans la figure ci-jointe, où DS = ⅖ TD. Elle permet de conclure qu'on a DG < DS, où G et S représentent les centres de gravité du segment de cercle et de la parabole.
En effet, il est clair d'abord qu'une parabole passant par les points A et C est plus efficace que toute autre, qui passe par les mêmes points K et L et dont la partie au dessous de KL se trouverait entièrement à l'intérieur du segment de cercle (ce qui est nécessaire pour la démonstration); puisque pour ces dernières paraboles TD, donc aussi la distance du centre de gravité à la base AC, sera plus grande que pour la première.
Ensuite on voit aisément qu'on ne peut pas prendre les points K et L, avec avantage, ni plus bas, ni plus haut que dans la figure. En les prenant plus bas la distance du centre de gravité de la parabole à la base s'agrandit avec TD. En les prenant plus haut il est vrai que cette distance s'amoindrit; mais alors le centre de gravité de la parabole se trouve au dessous de la droite KL et on n'est plus sûr qu'il est encore au dessus du centre de gravité G du segment de cercle.
Il s'agit donc de calculer la limite inférieure pour la longueur de l'arc, et ensuite pour 2π, à laquelle on est conduit en employant la parabole de la figure. Nous avons trouvé ainsi la formule:



pour la déduction de laquelle nous renvoyons à un article de notre collaborateur M.F. Schuh à paraître dans les Archives Néerlandaises sous le titre: ‘Sur quelques formules aproximatives de la circonférence du cercle et sur la Cyclométrie de Huygens.’
Or, en comparant cette limite avec celle qui suit de la règle de Huygens (voir la note 52), on s'aperçoit qu'elle est moins rapprochée; mais puisqu' elle est la meilleure de cette forme qu'on peut obtenir par le procédé que nous avons décrit, il faut que Huygens ait suivi une autre voie; si, du moins, il n'y pas question d'une faute de calcul.
Nous aurons d'ailleurs l'occasion de revenir sur ces approximations à propos d'une pièce de 1668 composée par Huygens pendant sa polémique avec Gregory sur la quadrature du cercle. Dans cette pièce, qu'on trouve aux pages 61-64 des ‘Adversaria olim D’, Huygens arrive par une méthode différente à une formule, qui conduit à l'inégalité:



c'est-à-dire, qui donne une limite inférieure plus rapprochée que les autres; puisqu' on a:

[p. 173]

Problema IV. Propos. XX.

Circumferentiae ad diametrum rationem investigare; & ex datis inscriptis in dato circulo invenire longitudinem arcuum quibus illae subtenduntur.

Esto circulus centro D, cujus diameter CB, & sit arcus BA sextans circumferentiae, cui subtensa ducatur AB, itemque sinus AM. Positâ igitur DB semidiametro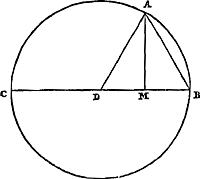

[Fig. 21.]

partium 100000, totidem quoque erit subtensa BA. AM verò partium 86603 non unâ minùs, (hoc est, si una pars sive unitas auferatur ab 86603 fiet minor debito)⁵⁰⁾, quippe semissis lateris trianguli aequilateri circulo inscripti.

Hinc excessus AB supra AM fit 13397 vero minor. Cujus triens 4465⅔ additus ipsi AB 100000, fiunt partes 104465⅔ minores arcu AB. Et hic primus est minor terminus, quo postea alium vero propiorem inveniemus. Priùs autem major quoque terminus secundùm Theorema praecedens inquirendus est.

Tres nimirum sunt numeri quibus quartum proportionalem invenire oportet. Primus est partium duplae AB & triplae AM qui erit 459807, vero minor, (nam hoc quoque observandum ut minor sit, idemque in caeteris prout dicetur) secundus quadruplae AB & simplae AM qui 486603 vero maj. Et tertius triens excessus AB supra AM, 4466 vero major. Itaque quartus proportionalis erit 4727 vero maj. quo addito ad AB 100000 fit 104727, major numero partium, quas continet arcus AB, peripheriae sextans^*. Jam igitur invenimus longitudinem arcus AB secundùm minorem majoremque terminum, quorum hic quidem longè propior vero est, cum vero proximus sit 104719.

Sed ex utroque istorum alius minor terminus habebitur priore accuratior si utamur praecepto sequenti, quod à diligentiori centrorum gravitatis inspectione dependet⁵¹⁾.

50) La phrase entre parenthèses à été ajoutée par Huygens en marge de l'exemplaire que nous possédons.

* per praeced.

51) Les manuscrits et les lettres ne donnent aucun renseignement décisif sur la manière dont la règle qui va suivre a été obtenue. Nous savons seulement par la Lettre N^o. 185 du 1^er avril 1654 (p. 279 du T. I) que sa démonstration dépendait, comme celle de la seconde partie du Théorème XVI, de l'emploi d'une parabole.
Il était donc à supposer que la règle en question s'obtiendrait suivant la voie indiquée par les Théorèmes XIV et XV, en remplaçant toutefois la parabole HBK de la figure 18 par une autre dont le centre de gravité se trouverait nécessairement au dessus de celui du segmentde cercle.



Or, la parabole qui, mieux qu' aucune autre, peut servir à ce but est celle ATC tracée dans la figure ci-jointe, où DS = ⅖ TD. Elle permet de conclure qu'on a DG < DS, où G et S représentent les centres de gravité du segment de cercle et de la parabole.
En effet, il est clair d'abord qu'une parabole passant par les points A et C est plus efficace que toute autre, qui passe par les mêmes points K et L et dont la partie au dessous de KL se trouverait entièrement à l'intérieur du segment de cercle (ce qui est nécessaire pour la démonstration); puisque pour ces dernières paraboles TD, donc aussi la distance du centre de gravité à la base AC, sera plus grande que pour la première.
Ensuite on voit aisément qu'on ne peut pas prendre les points K et L, avec avantage, ni plus bas, ni plus haut que dans la figure. En les prenant plus bas la distance du centre de gravité de la parabole à la base s'agrandit avec TD. En les prenant plus haut il est vrai que cette distance s'amoindrit; mais alors le centre de gravité de la parabole se trouve au dessous de la droite KL et on n'est plus sûr qu'il est encore au dessus du centre de gravité G du segment de cercle.
Il s'agit donc de calculer la limite inférieure pour la longueur de l'arc, et ensuite pour 2π, à laquelle on est conduit en employant la parabole de la figure. Nous avons trouvé ainsi la formule:



pour la déduction de laquelle nous renvoyons à un article de notre collaborateur M.F. Schuh à paraître dans les Archives Néerlandaises sous le titre: ‘Sur quelques formules aproximatives de la circonférence du cercle et sur la Cyclométrie de Huygens.’
Or, en comparant cette limite avec celle qui suit de la règle de Huygens (voir la note 52), on s'aperçoit qu'elle est moins rapprochée; mais puisqu' elle est la meilleure de cette forme qu'on peut obtenir par le procédé que nous avons décrit, il faut que Huygens ait suivi une autre voie; si, du moins, il n'y pas question d'une faute de calcul.
Nous aurons d'ailleurs l'occasion de revenir sur ces approximations à propos d'une pièce de 1668 composée par Huygens pendant sa polémique avec Gregory sur la quadrature du cercle. Dans cette pièce, qu'on trouve aux pages 61-64 des ‘Adversaria olim D’, Huygens arrive par une méthode différente à une formule, qui conduit à l'inégalité:



c'est-à-dire, qui donne une limite inférieure plus rapprochée que les autres; puisqu' on a:

[p. 174]

Ajoutez les quatre tiers de la différence des limites trouvées au double de la corde et au triple du sinus, et que dans le même rapport dans lequel se trouve la droite ainsi composée à trois et un tiers, ou 10/3 fois la somme du sinus et de la corde, se trouve aussi l'excès de la corde sur le sinus à une certaine autre droite; celle-ci ajoutée au sinus constituera une droite plus petite que l'arc⁵²⁾.

52) On trouve pour la différence des limites indiquées dans le Théorème XVI l'expression:



La règle en question conduit donc à l'inégalité: d'où l'on peut déduire: Pour pouvoir comparer cette limite inférieure avec la suite (1) de la note 7, p. 94 du Tome présent, nous écrivons successivement:


Ajoutons que la limite, mentionnée dans la note précédente, comme empruntée à la pièce. de 1668, amène l'inégalité:
Des deux inégalités les trois premiers termes s'accordent avec ceux de la suite en question; mais le quatrième terme de la seconde se rapproche de beaucoup plus du quatrième terme de la suite, tout en y restant inférieur comme il fallait.

[p. 175]

Inventorum terminorum differentia sesquitertia jungatur duplae subtensae & sinui triplo, & quam rationem habet ex his composita ad triplam sesquitertiam seu 10/3 utriusque simul, sinus, subtensaeque, eandem habeat subtensae supra sinum excessus ad aliam quandam; Haec ad sinum addita rectam constituet arcu minorem⁵²⁾.

52) On trouve pour la différence des limites indiquées dans le Théorème XVI l'expression:



La règle en question conduit donc à l'inégalité: d'où l'on peut déduire: Pour pouvoir comparer cette limite inférieure avec la suite (1) de la note 7, p. 94 du Tome présent, nous écrivons successivement:

Ajoutons que la limite, mentionnée dans la note précédente, comme empruntée à la pièce. de 1668, amène l'inégalité:
Des deux inégalités les trois premiers termes s'accordent avec ceux de la suite en question; mais le quatrième terme de la seconde se rapproche de beaucoup plus du quatrième terme de la suite, tout en y restant inférieur comme il fallait.

[p. 176]

La limité inférieure était 104465⅔ la supérieure 104727; leur différence est 261⅓. Nous devons de nouveau trouver une quatrième proportionnelle à trois

[Fig. 21.]

nombres. Le premier est le double des parties de AB augmenté du triple de AM et des quatre tiers de la différence des limites; on trouve 460158, plus grand que le vrai. Le second est les 10/3 des deux AB et AM ensemble, 622008, plus petit que le vrai. Enfin le troisième est l'excès de AB sur AM, 13397, plus petit que le vrai. La quatrième proportionnelle à ces nombres est 18109, plus petite que le vrai. Si donc nous ajoutons ceci au nombre de parties de AM, 86602½, moindre que le vrai, il vient 104711½, moindre que l'arc AB. Ainsi donc le sextuple de ces parties, 628269, sera plus petit que la circonférence toute entière. Mais parce que 104727 de ces parties ont été trouvées plus grandes que l'arc AB, leur sextuple 628362 sera plus grand que la circonférence. De sorte que le rapport de la circonférence au diamètre est plus petit que celui de 628362, et plus grand que celui de 628269 à 200000. Ou bien plus petit que 314181 et plus grand que 314135 à 100000. D'où résulte que ce rapport est certainement plus petit que 31/7 et plus grand que 3 10/71. Et par là aussi est réfutée l'erreur de Longomontanus⁵³⁾, qui écrivit que la périphérie est plus grande que 314182⁵⁴⁾ parties, dont le rayon contient 100000.

Supposons maintenant que l'arc AB soit ⅛ de la circonférence; alors AM, moitié du côté du carré inscrit dans le cercle, sera de 7071068 parties, dont le rayon DB en contient 10000000, et pas une de moins. Tandis que AB, côté de l'octogone, est de 7653668 parties et pas une de plus. Au moyen de ces données on trouvera, de la même façon que ci-devant, comme première limite inférieure de la longueur de l'arc AB 7847868. Puis comme limite supérieure 7854066. Et de ces deux là de nouveau une limite inférieure plus précise 7853885. D'où il résulte que le rapport de la périphérie au diamètre est moindre que 31416⅓ et plus grand que 31415 sur 10000.

Et comme la limite supérieure 7854066 s'écarte moins de la vraie longueur de l'arc que 85 parties (l'arc AB, en effet, d'après ce que nous avons prouvé plus haut⁵⁵⁾, est plus grand que 7853981), et que 85 parties font moins que deux secondes, c'est-à-dire que 2/1296000 de la circonférence, car toute la circonférence a plus de 60000000 de ces parties; il est donc clair que, si d'un triangle rectangle nous cherchons les angles au moyen des côtés donnés, de la manière dont nous avons cherché cette limite supérieure un peu avant, jamais nous ne nous trompe-

53) Voir, sur Longomontanus et son ouvrage de 1644 sur la quadrature du cercle, les notes 4 et 5, p. 176 du T. I. Déjà en 1612 il publia l'ouvrage qui suit: ‘Cyclometria ex Lunulis reciprocè demonstrata, unde tam Areae, quàm Perimetri circuli exacta dimensio, & in numeros diductio seqvuta est, hactenus ab omnibus Mathematicis unicè desiderata. Ad Christianum Qvartum Daniae & Septemtrionis Regem. Inventore Christiano S. Longomontano Regio Mathematum Professore. Hafniae Typis Henrici Waldkirchij. Anno CIƆ IƆCXII.’
La fausse quadrature qu' il y développe amène à la page 55 la valeur numérique π = 3,14185959069768...; elle est différente de celle de l'ouvrage de 1644, laquelle le conduit à la page 24 au nombre 3, 141859604427...

54) Dans l'exemplaire que nous possédons, ce dernier chiffre a été changé à la plume, probablement par Huygens lui-même. On y lit 314185.

55) Il s'agit du dernier alinéa du ‘Problema I. Prop. X’, p. 143 du Tome présent, d'aprés lequel la circonférence contient plus de 62831852 des parties mentionnées dans le texte; dont le huitième excède 7853981.

[p. 177]

Minor terminus erat 104465⅔. Major 104727. differentia horum est 261⅓. Estque rursus tribus numeris inveniendus quartus proportionalis. Primus est partium duplae AB & triplae AM & sesquitertiae terminorum differentiae, 460158 vero major. Secundus 10/3 utriusque simul AB, AM, 622008 vero minor. Tertius denique excessus AB supra AM, 13397 vero min. Quibus quartus proportionalis est 18109 vero min. Hic igitur additus numero partium AM 86602½ vero min. fiunt 104711½ minores arcu AB. Quare sexcuplum earum, 628269 minus erit circumferentiâ totâ. At quoniam 104727 majores inventae sunt arcu AB, earum sexcuplum 628362 circumferentiâ majus erit. Itaque circumferentiae ad diametrum ratio minor est quam 628362, major autem quam 628269 ad 200000. Sive minor quam 314181, major autem quam 314135 ad 100000. Unde constat minorem utique esse quam triplam sesquiseptimam, & majorem quam 3 10/71. Quin etiam Longomontani⁵³⁾ error per haec refutatur, qui scripsit peripheriam majorem esse partibus 314182⁵⁴⁾ qualium rad. 100000.

Esto nunc arcus AB ⅛ circumferentiae, & erit AM, semissis lateris quadrati circulo inscripti, partium 7071068, non unâ minùs, qualium radius DB 10000000. AB verò latus octanguli partium 7653668 non unâ majus. Quibus datis ad similitudinem praecedentium invenietur primus minor terminus longitudinis arcus AB 7847868. Deinde major terminus 7854066. Et ex utroque rursus terminus minor accuratior 7853885. Unde constat peripheriae ad diametrum rationem minorem haberi quam 31416⅓, majorem autem quam 31415 ad 10000.

Et quum terminus major 7854066 à vera arcus AB longitudine minus distet quam partibus 85; (Est enim arcus AB, per ea quae supra ostendimus⁵⁵⁾, major quam 7853981) partes autem 85 efficiant minus quam duos scrupulos secundos, hoc est, quam 2/1296000 circumferentiae, nam tota earundem plures habet quam 60000000: Hinc manifestum est, si trianguli rectanguli angulos quaeramus ex datis lateribus, eo modo quo majorem istum terminum paulò antè, nunquam duobus

53) Voir, sur Longomontanus et son ouvrage de 1644 sur la quadrature du cercle, les notes 4 et 5, p. 176 du T. I. Déjà en 1612 il publia l'ouvrage qui suit: ‘Cyclometria ex Lunulis reciprocè demonstrata, unde tam Areae, quàm Perimetri circuli exacta dimensio, & in numeros diductio seqvuta est, hactenus ab omnibus Mathematicis unicè desiderata. Ad Christianum Qvartum Daniae & Septemtrionis Regem. Inventore Christiano S. Longomontano Regio Mathematum Professore. Hafniae Typis Henrici Waldkirchij. Anno CIƆ IƆCXII.’
La fausse quadrature qu' il y développe amène à la page 55 la valeur numérique π = 3,14185959069768...; elle est différente de celle de l'ouvrage de 1644, laquelle le conduit à la page 24 au nombre 3, 141859604427...

54) Dans l'exemplaire que nous possédons, ce dernier chiffre a été changé à la plume, probablement par Huygens lui-même. On y lit 314185.

55) Il s'agit du dernier alinéa du ‘Problema I. Prop. X’, p. 143 du Tome présent, d'aprés lequel la circonférence contient plus de 62831852 des parties mentionnées dans le texte; dont le huitième excède 7853981.

[p. 178]

rons de plus de deux secondes; même si les côtés autour de l'angle droit sont égaux entre eux, comme ils l'étaient ici dans le triangle DAM.

Mais si le rapport du côté DM à MA est tel que l'angle ADM ne dépasse pas ¼ d'un angle droit, l'erreur ne sera pas même d'une tierce. En effet, posant l'arc AB égal à 1/16 de la circonférence, AM sera la moitié du côté de l'octogone équilatéral inscrit dans le cercle, et égal à 382683433 parties et pas une de moins; tandis que AB sera le côté du polygone de seize côtés, et contiendra donc 390180644 parties et pas une de plus, le rayon DB contenant 1000000000 de ces parties. On trouve par là une première limite inférieure de la longueur de l'arc AB de 392679714 parties. Et la limite supérieure est 392699148. Et de là de nouveau une limite inférieure 392699010. Or, il résulte de ce que nous avons démontré plus haut⁵⁶⁾ que l'arc AB, 1/16 de la circonférence, est plus grand que 392699081 parties, lesquelles la limite supérieure dépasse de 67 parties. Mais celles-ci font moins qu'une tierce, c'est-à-dire que 1/77760000 de toute la circonférence, puisque celle-ci est plus grande que 6000000000.

Puis, des nouvelles limites que nous venons de trouver le rapport de la circonférence au diamètre sortira plus petit que 3141593⅕, mais plus grand que 3141592 à 1000000.

Et si nous prenons un arc AB égal à 1/60 de la circonférence, soit à 6 parties dont elle en contient toute entière 360, AM sera la moitié du côté du polygone (inscrit)⁵⁷⁾ à 30 angles, formé de 10452846326766 parties dont le rayon en a 100000000000000, et pas une de moins. Et AB est le côté du polygone (inscrit)⁵⁷⁾ de 60 angles, 10467191248588 et pas une de plus. Au moyen de ces données on trouvera l'arc AB d'après la première limite inférieure 10471972889195. D'après la supérieure 10471975512584. Et de là l'autre limite inférieure 10471975511302. D'où il résulte que le rapport de la périphérie au diamètre est moindre que 31415926538, mais plus grand que 31415926533 à 10000000000.

S'il fallait chercher ces limites par l'addition des côtés des polygones inscrit et circonscrit, il faudrait aller presque jusqu à quatre cent mille côtés⁵⁸⁾. Car au moyen du polygone à 60 angles inscrit et circonscrit on prouve seulement que le rapport de la périphérie au diamètre est moindre que 3145 à 1000 et plus grand que 3140. Ainsi donc le nombre de chiffres vrais fourni par notre calcul paraît être trois fois plus grand et même plus. Mais si quelqu' un en fait l'expérience, il verra que la même chose arrive toujours avec les polygones suivants: nous n'en ignorons pas la raison, mais elle demanderait une explication trop longue⁵⁹⁾.

D'ailleurs je crois qu'il est suffisamment clair comment, étant données d'autres inscrites quelconques, on peut trouver par les méthodes exposées la longueur des arcs auxquels elles sont sous-tendues. Car, si elles sont plus grandes que le côté du carré inscrit, on devra chercher la longueur de l'arc restant à la demicirconférence, dont la corde est alors aussi donnée. Mais on doit aussi savoir trouver les cordes des moitiés des arcs, lorsque la corde de l'arc entier est donnée.

56) Voir toujours le lieu cité dans la note précédente.

57) Les mots entre parenthèses furent ajoutés en marge par Huygens dans l'exemplaire que nous possédons.

57) Les mots entre parenthèses furent ajoutés en marge par Huygens dans l'exemplaire que nous possédons.

58) En appliquant les relations approchées de la note 7, p. 94 du Tome présent, on trouve que des polygones de 240000 côtés suffiraient à déduire ces limites à l'aide de la méthode Archimédienne.

59) Voir, à ce propos, la note 15, p. 142 du Tome présent.

[p. 179]

scrupulis secundis aberraturos; etiamsi aequalia inter se fuerint latera circa angulum rectum, veluti hic erant in triangulo DAM.

Si verò ea sit ratio lateris DM ad MA, ut angulus ADM non excedat ¼ recti; non unius tertii scrupuli error erit. Posito enim arcu AB 1/16 circumferentiae, erit AM semissis lateris octanguli aequilateri circulo inscripti partium 382683433, non unâ minùs. AB verò latus sexdecanguli 390180644 non unâ ampliùs, qualium radius DB 1000000000. Unde primus minor terminus longitudinis arcus AB invenitur partium 392679714. Terminus autem major 392699148. Et ex his minor rursus 392699010. Constat autem ex supra demonstratis⁵⁶⁾ arcum AB 1/16 peripheriae, majorem esse quam 392699081, quas terminus major superat partibus 67. Hae autem minus efficiunt uno scrupulo tertio, hoc est, 1/77760000 totius circumferentiae, quoniam ea major est utique quam 6000000000.

Porrò ex novissimis terminis inventis orietur ratio circumferentiae ad diametrum minor quam 3141593⅕, major autem quam 3141592 ad 1000000.

Quod si 1/60 circumferentiae ponatur arcus AB, seu partium 6 qualium tota 360; Erit AM semissis lateris trigintanguli (inscripti)⁵⁷⁾ partium 10452846326766, non unâ minùs, qualium radius 100000000000000. Et AB latus sexagintanguli (inscripti)⁵⁷⁾ 10467191248588 non unâ amplius. Invenieturque ex his arcus AB secundùm primum minorem terminum 10471972889195. Secundùm majorem 10471975512584. Et ex his minor alter terminus 10471975511302. Unde efficitur peripheriae ad diametrum ratio minor quam 31415926538, major autem quam 31415926533 ad 10000000000.

Quos terminos si ex additis inscriptorum & circumscriptorum polygonorum lateribus inquirendum esset ferè ad laterum quadringenta millia deveniendum⁵⁸⁾. Nam ex sexagintangulo inscripto circumscriptoque hoc tantùm probatur, minorem esse rationem peripheriae ad diametrum quam 3145 ad 1000, majorem autem quam 3140. Adeo ut triplum & ampliùs verarum notarum numerum nostro ratiocinio productum appareat. Idem verò in ulterioribus polygonis si quis experiatur semper evenire cernet: non ignota nobis ratione, sed quae longiori explicatione indigeret⁵⁹⁾.

Porrò autem quomodo, datis quibuscunque aliis inscriptis arcuum quibus subtenduntur longitudo per haec inveniri queat satis puto manifestum. Si enim quadrati inscripti latere majores sunt, longitudo arcus ad semicircumferentiam

56) Voir toujours le lieu cité dans la note précédente.

57) Les mots entre parenthèses furent ajoutés en marge par Huygens dans l'exemplaire que nous possédons.

57) Les mots entre parenthèses furent ajoutés en marge par Huygens dans l'exemplaire que nous possédons.

58) En appliquant les relations approchées de la note 7, p. 94 du Tome présent, on trouve que des polygones de 240000 côtés suffiraient à déduire ces limites à l'aide de la méthode Archimédienne.

59) Voir, à ce propos, la note 15, p. 142 du Tome présent.

[p. 180]

Et de cette manière, si nous voulons faire usage des bisections, nous pourrons connaître sans difficulté pour toute corde la longueur de son arc, aussi rapprochée que nous voulons. Ceci est utile pour l'examen des tables des sinus. Et de même pour leur composition; car connaissant la corde d'un certain arc, on peut déterminer aussi avec une précision suffisante celle de l'arc qui est un peu plus grand ou un peu plus petit.

[p. 181]

reliqui inquirenda est, cujus tum quoque subtensa datur. Sciendum autem & dimidiorum arcuum subtensas inveniri cum totius arcus subtensa data est. Atque hâc ratione si bisectionibus uti placebit, poterimus ad omnem subtensam, arcus ipsius longitudinem quamlibet verae propinquam non difficulter cognoscere. Utile hoc ad sinuum tabulas examinandas. Imo ad componendas quoque: quia cognitâ arcus alicujus subtensâ, etiam ejus qui paulò major minorve sit satis accuratè definiri potest.

4) ‘Si fuerit maior proportio totius ad totum, quam ablati ad ablatum: Erit & reliqui ad reliquum maior proportio, quam totius ad totum’. Voir p. 526 de l'édition, citée dans la note 10, p. 97 du T. XI, des ‘Elementa’ d'Euclide, par Clavius.

4) ‘Si fuerit maior proportio totius ad totum, quam ablati ad ablatum: Erit & reliqui ad reliquum maior proportio, quam totius ad totum’. Voir p. 526 de l'édition, citée dans la note 10, p. 97 du T. XI, des ‘Elementa’ d'Euclide, par Clavius.

31) Voir le dernier alinéa du ‘Theor. IX. Prop. IX’, p, 139.

31) Voir le dernier alinéa du ‘Theor. IX. Prop. IX’, p, 139.

34) Si quatuor magnitudines proportionales fuerint: maxima & minima reliquis duabus maiores erunt.’ (Clavius, p. 518).

36) Voir le dernier alinéa de la démonstration du ‘Theor. VII’, p. 135 du Tome présent.

34) Si quatuor magnitudines proportionales fuerint: maxima & minima reliquis duabus maiores erunt.’ (Clavius, p. 518).

36) Voir le dernier alinéa de la démonstration du ‘Theor. VII’, p. 135 du Tome présent.

41) Voici cette Proposition telle qu'on la trouve p. 138 de l'édition de Bâle, mentionnée dans la note 3, p. 274 du T. XI: ‘Cuiuscunque portionis à recta linea & rectanguli coni sectione comprehensae, centrum grauitatis dividit diametrum portionis, ita ut pars eius ad verticem terminata, sit ad partem eam sequialtera, quae ad basim portionis terminatur’. (Heiberg, T. II, p. 213).

41) Voici cette Proposition telle qu'on la trouve p. 138 de l'édition de Bâle, mentionnée dans la note 3, p. 274 du T. XI: ‘Cuiuscunque portionis à recta linea & rectanguli coni sectione comprehensae, centrum grauitatis dividit diametrum portionis, ita ut pars eius ad verticem terminata, sit ad partem eam sequialtera, quae ad basim portionis terminatur’. (Heiberg, T. II, p. 213).

46) Voir la seconde partie du théorème précédent.

46) Voir la seconde partie du théorème précédent.