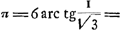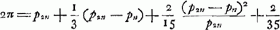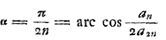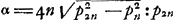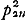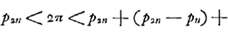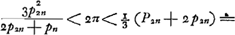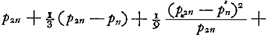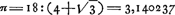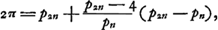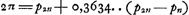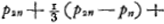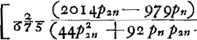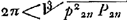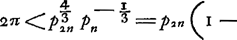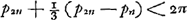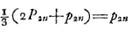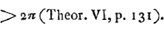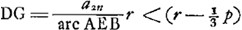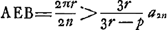|
| |
| |
| |
De circuli magnitudine inventa
Accedunt
Problematum quorundam illustrium constructiones
1654.
| |
| |
| |
Avertissement.
On sait qu' Archimède réussit à enfermer le rapport de la circonférence du cercle à son diamètre entre les limites 3 10/71 et 3 10/70 en calculant les périmètres p96 et P96 des polygones inscrit et circonscrit de 96 côtésGa naar voetnoot1). Pendant plus de dix huit siècles sa méthode restait la seule connue. Sans se laisser rebuter par les calculs énormes qu'elle exigeait, Ludolf van CeulenGa naar voetnoot2) l'employa au commencement du dix-septième siècle à déterminer le nombre π jusqu' au 36me chiffreGa naar voetnoot3); résultat qui ne fut surpassé qu' un siècle plus tard par A. SharpGa naar voetnoot4) au moyen d'un développement en série.
| |
| |
C'était Willebrord SnelliusGa naar voetnoot5) qui, le premier, dans son ‘Cyclometricus’Ga naar voetnoot6), publié en 1621, sut resserrer les limitesGa naar voetnoot7), indiquées par Archimède, sans aug- | |
| |
menter le nombre des côtés des polygones employés; mais les deux théorèmesGa naar voetnoot8) qu' il donne à ce propos, quoique vrais, n'avaient pas été prouvés rigoureusement par lui, comme Huygens l'a remarqué et que nous le montrerons à propos des démonstrations rigoureuses par lesquelles Huygens a remplacé les raisonnements de SnelliusGa naar voetnoot9).
| |
| |
Telle était la situation lorsque, en janvier ou février 1654, Huygens commença à s'occuper de la mesure du cercleGa naar voetnoot10). En très peu de temps il arriva à des résultats qui lui donnaient beaucoup de satisfactionGa naar voetnoot11). Au commencement de mars il en communiqua quelques uns à van Schooten et à LipstorpGa naar voetnoot12); d'où il paraît que déjà alors Huygens était en possession des deux derniers théorèmesGa naar voetnoot13) que, dans son ouvrage, il a déduits des propriétés du centre de gravité et qui, puisque leur approximation est d'un ordre plus élevé, permettent de tripler au lieu de doubler, comme le font les théorèmes de Snellius, le nombre des chiffres, déduisibles de deux polygones donnés de n et de 2n côtés, c'est-à-dire, en comparant ce nombre à celui fourni par la méthode Archimédienne. Il nous semble même qu'il y a là une indication que l'idée première, qui a amené toutes ces recherches de cyclométrie, était qu'on pourrait obtenir une mesure plus rapprochée du cercle en utilisant les propriétés du centre de gravité, desquelles Huygens s'était déjà occupé dans ses ‘Theoremata de quadratura hyperboles, ellipsis et circuli’Ga naar voetnoot14). En outre, on trouve indiquée dans les lettres mentionnées à Lipstorp
| |
| |
et à van Schooten la construction approchée de la circonférence du cercle, laquelle constitue le premier ‘Aliter’ du ‘Problema II. Prop. XI’Ga naar voetnoot15).
Un peu plus tard il a trouvé le théorème que la circonférence du cercle est moins que la moindre des deux proportionnelles entre les périmètres des polygones inscrit et circonscrit du même nombre de côtés à laquelle Oronce Fine avait prétendu qu'elle était égale dans le cas du carréGa naar voetnoot16). Il préfère ce théorème à tous les autresGa naar voetnoot17), probablement à cause de sa simplicité et de la difficulté qu' il a eue à le trouver, bien que ce théorème se prête bien moins que les autres au calcul et que l'approximation qu'il fournit est d'un ordre inférieur à celui des théorèmes plus compliqués dont nous avons parléGa naar voetnoot18). Il le mentionne à Kinner a Löwenthurn dans une lettre du 23 mars 1654Ga naar voetnoot19) en le cachant sous l'énigme ‘Minor minore incognita,’ qu' il lui prie de vouloir communiquer à Marcus Marci, pour savoir, si celui-ci, qui était en train de préparer un ouvrage de CyclométrieGa naar voetnoot19), avait trouvé le même théorèmeGa naar voetnoot20).
Vers la fin de mars le manuscrit est achevé et remis à van Schooten pour en avoir son avis. Mais voilà que Huygens commence à douter si ce qu' il appelle la seconde partie de son ouvrage, c'est-à-dire celle qui débute par le ‘Theor. XIV. Propos. XVII’ et contient la considération des centres de gravité, devrait bien être publiée. L'usage qu'il y a fait de la construction d'une parabole dans la démonstration du Théorème XIV lui déplaît, cependant il ne pourrait éviter
| |
| |
de le répéter s'il voulait donner la démonstration du Théorème cursivé de la ‘Prop. XX.’ Il incline à supprimer toute cette partie, sauf à mentionner dans la préface les ‘Prop XIX et XX’Ga naar voetnoot21) pour s'en réserver la priorité.
Cette seconde partie est en effet moins élégante et moins exclusivement géométrique que la première; mais de l'autre côté les théorèmes auxquels Huygens y est arrivé par la considération des centres de gravité constituent un progrès bien plus marqué dans la mesure approchée du cercle, que ne le font ceux de la première partie lesquels mènent à des approximations du même ordreGa naar voetnoot22) que celles qu'on obtient par les théorèmes de Snellius, qui, il est vrai, ne savait pas les démontrer. D'ailleurs ni les théorèmes de Snellius, ni ceux de Huygens, n'ont jamais servi à déterminer de nouveaux chiffres, inconnus jusqu' alors, du rapport de la circonférence au diamètre. Cela était réservé à des calculateurs plus infatigables que Huygens ou Snellius, à l'aide de procédés plus modernes. Toutefois on ne regrettera pas que Huygens, suivant en cela le conseil de van Schooten, a renoncé à son dessein d'omettre cette seconde partie.
Dans la même lettre, très importante, du 1er avril 1654Ga naar voetnoot23) on trouve mentionnée pour la première fois l'intention de Huygens, à laquelle il a donné suite, de joindre à son traité de cyclométrie les ‘Illustrium quorundam problematum constructiones.’
Deux fois encore, Huygens, qui était dans la crainte d'être devancé par Marci, a dû rappeler à van Schooten, qu'il attendait son avis. Enfin, le 19 avrilGa naar voetnoot24), celui-ci renvoya les manuscrits avec ses excuses, beaucoup de louanges, des annotations que nous ne connaissons pas, et le conseil, déjà mentionné, de n'en pas supprimer la seconde partie, dont les démonstrations lui semblaient suffisamment élégantes.
| |
| |
Enfin le 1er juillet 1654 Huygens put expédier à van Schooten et à quelques autres savantsGa naar voetnoot25) les premiers exemplaires du livre imprimé.
Plus tard Huygens est revenu à deux reprises au sujet de la mesure approchée du cercle. La première fois, en 1659, à l'occasion de ses recherches sur la cycloïde. Ayant découvert que le centre de gravité d'un arc cycloïdal, symmétrique par rapport à l'axe, se trouve à deux tiers de la flèche, comptée depuis la corde, l'idée lui vient que par la comparaison de la situation de ce centre de gravité avec celle du centre de gravité d'un arc de cercle, il pourra arriver à une limite pour la mesure du cercle, de même que, précédemment, dans l'ouvrage que nous traitons, il avait atteint le même but en comparant la situation des centres de gravité d'un segment de cercle et d'un segment paraboliqueGa naar voetnoot26). Et, en effet, il trouve de cette manière une limite inférieure identique, au fond, avec celle de SnelliusGa naar voetnoot27).
| |
| |
Une seconde fois, en 1668, il est ramené au même sujet par sa polémique avec Gregory, au cours de laquelle il trouve, entre autres, une nouvelle approximation semblable à celles de la note 13 et une construction approchée pour la mesure d'un arc de cercleGa naar voetnoot28), laquelle il a déduite de la seconde partie du ‘Theor. XVI. Prop. XIX’. Mais nous traiterons ces nouvelles recherches avec plus de détail à leur propre place.
Si, pour l'ouvrage ‘De circuli magnitudine inventa’, aucun manuscrit contenant des travaux préliminaires ne nous est connu, il en est tout autrement pour les ‘Illustrium quorundam problematum constructiones.’ En effet, lorsque le premier avril 1654, Huygens communiqua, comme nous l'avons vu, à van Schooten son intention de joindre au premier ouvrage les solutions de quelques problèmes qui n'avaient cessé d'occuper les géomètres anciens et modernes, il était déjà en possession de plusieurs de ces solutions, qu'il avait mises par écrit dans le manuscritGa naar voetnoot29) qui nous a fourni le texte des ‘Travaux mathématiques divers de 1652 et 1653’Ga naar voetnoot30). Il n'avait qu'à choisir et à perfectionner ceux qu'il voulait admettre dans la publication projetée, ce qui, à son avis, ne manquerait pas d'augmenter le nombre des mathématiciens qui désireraient la posséderGa naar voetnoot31). Et si, dans cette publication, il ne donne des problèmes que les constructions avec des démonstrations rédigées à la mode des anciens, sans ajouter les analyses qui y ont conduit, le même manuscrit supplée en grande partie à cette lacune et ne laisse aucun doute sur les méthodes suivies.
| |
| |
En effet, ces méthodes de traiter les problèmes solides, c'est-à-dire ceux qui mènent à des équations cubiques ou biquadratiques, ont déjà été discutées dans l'‘Avertissement’ des ‘Travaux mathématiques divers de 1652 et 1653’Ga naar voetnoot32). Il y en a deux; en voici la première qui a servi pour les problèmes I et VIII des ‘Illustrium quorundam problematum constructiones’:
Après avoir obtenu, par l'analyse, l'équation cubique qui résoud le problème, Huygens en fait disparaître le second terme, suivant en cela la règle donnée par Descartes dans sa ‘Géométrie’; ensuite il applique à l'équation réduite la solution par la trisection de l'angle, ou, si elle fait défaut, celle qui emploie les intersections de la parabole et du cercle, solutions qu'on trouve exposées toutes les deux dans ce même ouvrage de Descartes; enfin Huygens cherche à simplifier la construction obtenue de manière à économiser autant que possible sur les lignes à tirerGa naar voetnoot33).
La seconde plus spéciale qui a conduit aux constructions des problèmes III-VII est plus originaleGa naar voetnoot34). Huygens se pose un problème très général exigeant par exemple l'égalité de deux segments dont l'un se trouve sur une droite mobile. La solution de ce problème amène une équation biquadratique. Alors Huygens spécialise les données du problème de manière à simplifier systématiquement l'équation obtenue jusqu' à ce qu'elle se réduit à une équation quadratique, comme dans les problèmes IV-VII, ou à une équation cubique binomiale, comme dans le cas des trois solutions du problème III. Dans ce dernier cas Huygens est en possession d'une solution du problème des deux moyennes proportionnelles, pourvu qu'on considère accomplie l'égalisation des deux segments. Comme nous l'avons montré dans l'‘Avertissement’ que nous venons de mentionner, cette seconde méthode fut inspirée à Huygens à l'occasion de ses recherches sur l'origine possible de la solution de Nicomède de ce même problème.
Voici d'ailleurs, pour chacun des problèmes des ‘Illustrium quorundam problematum constructiones’ en particulier, l'historique des recherches de Huygens.
| |
| |
| |
Probl. IGa naar voetnoot35).
Couper une sphère donnée par un plan de manière que les segments soient entre eux dans un rapport donné.
C'est le premier des problèmes solides entamés par Huygens. L'antiquité en avait légué trois solutions complètes rapportées par EutociusGa naar voetnoot36); l'une due problablement à Archimède, les autres à Dionysidore et à Dioclès. Elles s'accomplissent à l'aide des intersections d'une hyperbole avec une parabole ou avec une ellipse. Archimède dans son ouvrage ‘De sphaera et cylindro’ avait traité le problème mais sans en achever la solutionGa naar voetnoot37).
Le 13 janvier 1652 Huygens en élabore une solution nouvelle par la première des méthodes que nous venons d'esquisserGa naar voetnoot38). Il y emploie les intersections d'une parabole et d'un cercle, considérant une telle construction plus simple que celles où l'on fait usage d'autres coniques; mais il préfère à toutes les autres les constructions par la trisection de l'angle. Il en trouve une de cette façon au 31 janvier 1652Ga naar voetnoot39) et la simplifie encore à deux reprisesGa naar voetnoot40).
| |
Probl. IIGa naar voetnoot41).
Trouver un cube double d'un cube donné.
Le problème est un cas particulier du ‘Probl. III’. Des rédactions antérieures des deux solutions dont l'une est rigoureuse et l'autre approximative, se trouvent aux p. 45-48 du Tome présent, sous les dates du 1er et du 2 mars 1652. Les raisonnements qui ont conduit à ses solutions nous sont inconnus. La solution rigoureuse a passé sans modification importante dans le texte de l'ouvrage présent; mais la démonstration de la solution approximative a été notablement abrégée.
| |
| |
| |
Probl. IIIGa naar voetnoot42).
Trouver deux moyennes proportionnelles à deux droites données.
De ce problème célèbre l'antiquité connaissait plusieurs solutions, recueillies par Eutocius dans ses ‘Commentaires’ sur le deuxième livre de l'ouvrage ‘De sphaera et cylindro’ d'ArchimèdeGa naar voetnoot43). Descartes y avait ajouté une nouvelle à l'aide du cercle et de la paraboleGa naar voetnoot44).
Parmi elles celle de Nicomède avait grandement intrigué Huygens et l'avait conduit, comme nous l'avons dit, à la seconde de ses méthodes de résolution des problèmes solides.
L'ayant inventée le 30 janvier 1652, il ne tarde pas à appliquer cette méthode au même problème général, qui avait amené la construction de Nicomède, pour obtenir, cette fois, de nouvelles solutions des ‘Probl. IV-VII’Ga naar voetnoot45), qui sont des cas particuliers de ce problème. Ensuite il se met à chercher à son aide de nouvelles solutions, analogues à celle de Nicomède, du problème des deux moyennes. Les pièces No. XI et XIIGa naar voetnoot46) des ‘Travaux mathématiques divers de 1652 et 1653’ nous font connaître les résultats de ces recherches. Des solutions obtenues celle de la pièce No. XI, trouvée le 9 mars 1652 et remaniée le 10 mars 1652, donnait naissance à la première constructionGa naar voetnoot47) qu'on trouve dans l'ouvrage présent. Un nouveau remaniement conduisit le 5 juin à la seconde constructionGa naar voetnoot48) et on reconnaît la troisièmeGa naar voetnoot49) dans celle, datée du 16 mars, de la pièce No. XIIGa naar voetnoot50) des ‘Travaux’ mentionnés.
Après la publication des ‘Illustrium quorundam problematum constructiones’ le problème n'a pas cessé d'intéresser Huygens. Il y est revenu à plusieurs reprises.
| |
| |
La première fois en 1657 à l'occasion de sa correspondance avec de Sluse. Le 11 juillet de cette année, dans sa première lettre à HuygensGa naar voetnoot51), de Sluse lui envoya du problème en question deux solutions, que nous ne connaissons pas. D'après la réponse de HuygensGa naar voetnoot52) l'une d'elles lui était entièrement nouvelle; l'autre avait beaucoup de rapport avec la dernière de celles qu'il avait publiées. Ensuite dans sa lettre du 31 juilletGa naar voetnoot53) de Sluse assura Huygens qu'il savait résoudre le problème des deux moyennes d'un nombre indéfini de modes divers. Alors Huygens lui demandaGa naar voetnoot54) s'il savait accomplir la construction à l'aide des intersections d'un cercle et d'une ellipse ou par la trisection d'un angle; lui même, il se rappelait d'avoir cherché vainement une telle construction. Aussitôt de Sluse réponditGa naar voetnoot55) qu'il le savait et de plusieurs manières. Cela décida Huygens à se remettre à l'ouvrage.
Le 3 septembre il pouvait annoncer qu'il avait trouvé une solution de cette manière; mais elle lui semblait trop compliquéeGa naar voetnoot56). Enfin le 8 septembre il trouvait mieux. Il élabora cette nouvelle solution dans une pièce que nous reproduisons comme ‘Appendice I’Ga naar voetnoot57) aux ‘Illustrium quorundam problematum constructiones’. Le 28 septembre il la mentionna à van SchootenGa naar voetnoot58) et la communiqua à de Sluse dans sa lettre du 12 octobre 1657Ga naar voetnoot59). Celui-ci lui réponditGa naar voetnoot60) qu'il en possédait une autre plus concise et aussi universelle qu'il envoya à Huygens le 7 juin 1658Ga naar voetnoot61). On la retrouve dans son ‘Mesolabum’ comme ‘Propositio quarta’Ga naar voetnoot62).
Cependant Huygens avait découvert une nouvelle méthode pour résoudre les problèmes solides. Il l'applique au problème des deux moyennes dans une pièce que nous donnons comme ‘Appendice II’Ga naar voetnoot63). Il y retrouve les constructions de Ménechme, rapportées par Eutocius’Ga naar voetnoot64).
| |
| |
Ce fut en juillet 1659 que Huygens reçut enfin un exemplaire du ‘Mesolabum’Ga naar voetnoot65), si longtemps attendu. Il y trouvait plusieurs solutions du problème des deux moyennes proportionnelles et de quelques autres problèmes solides; avec leurs démonstrations à la mode des anciens; mais sans l'analyse qui les avait amenées et que de Sluse se réservait de publier plus tard, ce qu'il fit en 1668 à l'occasion de la seconde édition du ‘Mesolabum’ dans la ‘Pars altera de analysi’.
Huygens était beaucoup intrigué par ses solutions, puisqu' il reconnut qu'il ne pouvait pas les déduire à l'aide des méthodes qu'il possédait. Il se mit donc à la recherche de nouveaux artifices par lesquels il réussit en effet à retrouver quelques unes des plus belles constructions de de Sluse. C'est là l'origine de la pièce, que nous publions comme ‘Appendice III’Ga naar voetnoot66).
En 1664, le même sujet revient pour un momentGa naar voetnoot67) dans la correspondance avec de Sluse, sans provoquer, du côté de Huygens, de nouveaux efforts. Il en est de même en 1668 lors de la publication de la seconde édition du ‘Mesolabum’, où la méthode de de Sluse fut révélée et se montrait étre très différente de celles
| |
| |
de Huygens, comme celui-ci l'avoua dans la lettre par laquelle il accusa la réception d'un exemplaire de cette éditionGa naar voetnoot68).
Ce ne fut qu'en 1680 que Huygens s'occupa de nouveau des mêmes questions dans une communication, faite à l'Académie des sciences, intitulée: ‘Methode pour construire les Equations cubiques et quarréquarrés en les resolvant en deux lieux’, dont nous ne connaissons que le débutGa naar voetnoot69).
Enfin en 1682 il composa un petit mémoire inédit: ‘Constructio problematum solidorum per resolutionem aequationis in duos Locos’Ga naar voetnoot70). Nous publierons ces pièces en leur propre lieu.
| |
Probl. IVGa naar voetnoot71).
Etant donné un carré dont l'un des côtés est prolongé, appliquer dans l'angle extérieur une droite de grandeur donnée, qui passe par le sommet opposé.
C'est de tous les problèmes des ‘Illustrium quorundam problematum constructiones’, celui dont Huygens s'est occupé le premier, savoir dans la pièce No. IV des ‘Travaux mathématiques divers de 1650’Ga naar voetnoot72). Pappus en avait donné une construction et démonstration; Descartes le traita dans sa ‘Géométrie’ et van Schooten dans ses commentaires sur cette ‘Géometrie’. Dans la pièce mentionnée Huygens arrive à une construction nouvelle; mais il préfère celle de Pappus dont il donne une démonstration différenteGa naar voetnoot73). Une autre démonstration se trouve dans une lettre à van Schooten du 23 octobre 1653Ga naar voetnoot74). C'est cette dernière qui a passé avec une modification légère dans le texte du ‘Probl. IV’ de l'ouvrage présent.
| |
| |
| |
Probl. VGa naar voetnoot75).
Soit donné un carré dont deux côtés adjacents sont prolongés, appliquer dans l'angle intérieur une droite de grandeur donnée, qui passe par le sommet opposé. Il faut cependant que la droite donnée ne soit pas moindre que le double de la diagonale du carré.
Nonobstant la ressemblance entre ce problème et celui qui précède, Huygens ne s'est occupé de celui-ci que quelques années plus tard. La première rédaction, que nous connaissons de sa construction et démonstration, est celle de la pièce No. IV des ‘Travaux mathématiques divers de 1652 et 1653’Ga naar voetnoot76). Elle n'a subi que des modifications peu importantes dans la lettre à van Schooten du 23 octobre 1653Ga naar voetnoot77) et dans le texte de l'ouvrage présent. Probablement la construction, vu sa grande ressemblance avec celle de Pappus du problème précédent, n'a pas été trouvée par l'analyse.
| |
Probl. VIGa naar voetnoot78).
Soit donné un losange dont l'un des côtés soit prolongé, appliquer dans l'angle extérieur une droite de grandeur donnée, qui passe par le sommet opposé.
Le problème fut mentionné par Pappus, comme pouvant se résoudre par la règle et le compas, dans l'aperçu de l'ouvrage ‘De inclinationibus’ d'ApolloniusGa naar voetnoot79). Il n'en donne la solution que pour le cas particulier du ‘Probl. IV’ précédent, où le losange est un carré.
Ghetaldi, dans son ‘Apollonius Redivivus, Seu Restituta Apollonii Pergaei Inclinationum Geometria’Ga naar voetnoot80) de 1607, traita le cas général, dont il trouva une solution assez élégante, en réduisant le problème à un autre mentionné également
| |
| |
par PappusGa naar voetnoot81) et résolu par Ghetaldi dans le même ouvrage. Il répéta cette solution dans l'ouvrage posthume ‘De Resolutione et Compositione Mathematica Libri Quinque’Ga naar voetnoot82), qui parut en 1640.
En 1650 Huygens, après s'être occupé du cas spécial du carré, prit en main le problème général. Guidé par une analyse semblable à celle qui lui avait réussi dans le cas spécial il trouva facilement une solution directeGa naar voetnoot83), qu'il parvint ensuite à simplifierGa naar voetnoot84).
Il reprit le même problème en 1652Ga naar voetnoot85) en le considérant cette fois comme cas particulier du problème de mener par un point une droite dont deux droites, données en position, découpent un segment de longueur donnée. Ce dernier problème amène en général une équation biquadratique, mais par le choix des données Huygens en fait disparaître les termes qui contiennent la troisième et la première puissance de l'inconnue. De cette manière il retrouve facilement le problème qui nous occupe et la nouvelle solution, à laquelle il arrive, se montre être plus simple et plus élégante que celle de l'année 1650. La démonstration, qu' il y ajoute, laisse à désirer; mais vers la fin il indique les moyens de l'améliorerGa naar voetnoot86).
Le 19 octobre 1653Ga naar voetnoot87) il procède à une rédaction nouvelle, modifiant encore légèrement la construction et donnant à la démonstration la forme sous laquelle on la rencontre, sans altérations sensibles, dans la lettre à van Schooten du 23 octobre 1653Ga naar voetnoot88) et dans le texte de l'ouvrage présentGa naar voetnoot89).
En attendant il avait élaboré en août 1652Ga naar voetnoot90) une autre solution qui provient probablement d'un remaniement de la solution de 1650. Il la communiqua à van Schooten dans une lettre du 10 décembre 1653Ga naar voetnoot91) et la publia dans l'ouvrage présent sous la suscription ‘Utrumque praecedentium Aliter’Ga naar voetnoot92).
| |
| |
| |
Probl. VIIGa naar voetnoot93).
Soit donné un losange dont deux côtés adjacents sont prolongés, appliquer dans l'angle intérieur une droite de grandeur donnée qui passe par le sommet opposé. Il faut cependant que la droite donnée ne soit pas moindre que le double de la diagonale qui joint les deux autres sommets du losange.
Aux lieux cités plus haut Ghetaldi avait donné une solution de ce problème, comme du précédentGa naar voetnoot94). Huygens s'en occupa pour la première fois le 11 février 1652Ga naar voetnoot95), deux jours après qu'il avait trouvé sa nouvelle solution du problème précédent. Il y appliqua une analyse analogue mais un peu simplifiée et ajouta une démonstration qu'il répéta le 19 octobre 1652Ga naar voetnoot96) dans une forme plus achevée, sous laquelle on la retrouve avec des modifications légères dans sa lettre à van Schooten du 23 octobre 1653Ga naar voetnoot97) et dans le texte de l'ouvrage présentGa naar voetnoot98). Cependant, à l'aide d'une analyse différente, il était arrivé le 17 février 1652 à une autre constructionGa naar voetnoot99), qu'il a considérée comme inférieure et qu'il n'a pas publiée. Une troisième construction, analogue à celle d'août 1652 du problème VI et qu'il avait élaborée le même jour,Ga naar voetnoot100) se retrouve sans modifications sensibles dans la lettre à van Schooten du 10 décembre 1653Ga naar voetnoot101) et dans le
texte de l'ouvrage présent après l'en-téte ‘Utrumque praecedentium Aliter’ et en second lieuGa naar voetnoot102).
Jusqu' à quel point Huygens a-t-il saisi la liaison intime qui existe entre les problèmes VI et VII, de manière que l'ensemble des racines de l'équation, amenée par l'analyse qui a pour but de résoudre l'un des problèmes, représente également les solutions de l'autre problème?
En 1650 il ne s'occupe que du premier problème, le seul mentionné expressé- | |
| |
ment par PappusGa naar voetnoot103). De l'équation quadratique, à laquelle l'analyse l'a conduit, il néglige la racine qui aurait pu amener la solution du second problèmeGa naar voetnoot104). Il agit de même en février 1652 avec les équations biquadratiques réductiblesGa naar voetnoot105) des pièces VI et VII des ‘Travaux mathématiques divers de 1652 et 1653’. Des quatre racines il n'en prend en considération que les deux qui se rapportent au problème qu'il s'est posé au début de la pièce.
Huygens a donc toujours traité les problèmes VI et VII (et de même les problèmes IV et V) comme des problèmes différents, nécessitant pour leur solution des analyses différentes. Toutefois l'expérience l'a convaincu de plus en plus de leur étroite analogie. Ainsi dans les ‘Illustrium quorundam problematum constructiones’ il renvoieGa naar voetnoot106) pour les constructions et les démonstrations des problèmes V et VII à celles des problèmes IV et VI, lesquelleson peut appliquer mot pour mot aux figures nouvelles. Ce n'est que la démonstration de la possibilité de la construction sous les conditions indiquées dans l'énoncé du problème, qui diffère; puisque, en effet, elle est bien plus simple dans ces derniers problèmes, qui, pour admettre des solutions réelles, n'exigent aucune limitation dans les donnéesGa naar voetnoot107).
| |
Probl. VIIIGa naar voetnoot108).
Trouver dans une conchoïde les limites de la courbure contraire.
En septembre 1653 Huygens élaboraGa naar voetnoot109), en se servant de la première des méthodes décrites à la p. 101 du présent ‘Avertissement’, une solution universelle de ce problème, dans laquelle il employa les intersections d'un cercle et d'une parabole, et une autre solution, applicable entre certaines limites des données, à l'aide de la trisection de l'angle. Il mentionna ces solutions dans sa lettre à van Schooten du 23 octobre 1653Ga naar voetnoot110). On les retrouve dans le texte de l'ouvrage présent.
En 1659 une autre solution, due à van Heuraet, fut publiée par van Schooten
| |
| |
dans les commentaires qui accompagnent sa seconde édition de la ‘Geometria’ de DescartesGa naar voetnoot111).
Huygens la jugea supérieure à la sienneGa naar voetnoot112) en ce que la détermination du point d'inflexion s'y accomplit, sans l'intervention d'une conique, à l'aide d'un cercle et de la conchoïde elle-même qu'on suppose tracée d'avance. Or, comme nous l'avons remarqué ailleursGa naar voetnoot113), Huygens préféra de beaucoup les constructions de cette façon aux autres. Il était même incliné à considérer les problèmes qui pouvaient être résolu de cette manière comme des problèmes plansGa naar voetnoot114).
Toutefois la solution de van Heuraet laissa beaucoup à désirer au point de vue de la simplicité géométrique. Elle exigeait la construction de segments dont la longueur est déterminée par des formes algébriques assez compliquées. Huygens chercha à la simplifier et y réussit en août 1659. A l'aide de ses annotations nous avons pu reconstituer cette solution, qu'on trouvera dans l'‘Appendice IV’Ga naar voetnoot115) de l'ouvrage présent. En la comparant avec celle de van Heuraet on s'aperçoit que l'artifice principal qui consiste dans la comparaison terme pour terme des deux équations cubiques après la multiplication des racines de l'une d'elles par un facteur indéterminéGa naar voetnoot116), fut déjà employé par van Heuraet; mais que d'ailleurs la solution de ce dernier est bien plus longue et moins élégante que celle de Huygens.
En 1680 Huygens s'occupe de nouveau du même problèmeGa naar voetnoot117). Enfin en 1687 il consulte ses anciennes annotationsGa naar voetnoot118) pour communiquer sa construction au sieur H. CoetsGa naar voetnoot119) et il reprend même pour un moment le fil de ses recherches. Cette fois il s'agit de la ‘determinatio’ de sa solution, c'est-à-dire, des limites entre lesquelles elle est applicable. Déjà en 1659 Huygens s'était aperçu
| |
| |
que sa construction n'était pas toujours exécutable et il avait même indiqué la limite de sa validitéGa naar voetnoot120); mais il n'avait pas encore recherché si celle de van Heuraet est sujette au même inconvénient. A cet effet il examine maintenant deux cas extrèmes et s'assure que dans ces cas elle est réalisable. Sans s'arrêter au cas général, difficile à traiter, il en conclut que la construction de van Heuraet ‘pour le point de la courbure de la conchoide peut servir toujours’Ga naar voetnoot121).
|
-
voetnoot1)
- Voir la ‘Dimensio circuli’, p. 257-271 du T. I de l'édition de Heiberg, citée dans la note 2, p. 50 de notre T. XI.
-
voetnoot2)
- Voir, sur Ludolf van Ceulen, la note 2, p. 275 du T. I.
-
voetnoot3)
- Dans son ouvrage de 1596 ‘Van den circkel’ (voir la note 2, p. 275, T. I) il trouve le nombre π jusqu'en 20 chiffres à l'aide des polygones inscrit et circonscrit de 15.231 côtés. Il ajoute toutefois un 21me chiffre qu' il ne peut pas avoir calculé avec ces polygones. On rencontre le même nombre jusqu' en 33 chiffres à la page 163 de l'ouvrage posthume: ‘De Arithmetische en Geometrische fondamenten, van Mr. Ludolf van Ceulen, Met het ghebruyck van dien In veele verscheydene constighe questien, soo Geometrice door linien, als Arithmetice door irrationale ghetallen, oock door den regel Coss, ende de tafelen sinuum ghesolveert. Tot Leyden, By Joost van Colster, ende Jacob Marcus. Ann. CIƆ IƆ CXV.’ Enfin tous les 36 chiffres qu'il a calculés, furent incisés sur sa pierre sépulcrale, disparue depuis, qui se trouvait dans l'église de Saint-Pierre
à Leyde. Il les calcula probablement à l'aide des polygones de 262 côtés, puisque dans le ‘Cyclometricus’ de Snellius (voir la note 6), où les 36 chiffres de van Ceulen sont mentionnês à la p. 55, on rencontre à la p. 54 le passage suivant: ‘Diligentissimus logista, Ludolphus noster, initio facto à latere quadrati eandem inscriptarum inventionem sexagies continuavit.’ Or, le nombre 36 des chiffres est en accord parfait avec l'emploi de ces polygones.
-
voetnoot4)
- Voir l'ouvrage de Sherwin ‘Mathematical Tables, Contriv'd after a most comprehensive Method: Containing, Dr. Wallis's Account of Logarithms, Dr. Halley's and Mr. Sharp's Ways of constructing them; with Dr. Newton's contraction of Briggs's Logarithms, viz. A Table of Logarithms of the Numbers from 1 to 10100, with the means to find readily the Logarithm of any Number, and the Number of any Logarithm, to seven places of Figures: and Tables of natural and logarithmic Sines, Tangents, Secants, and Versed-sines, to every minute of the Quadrant: with the Explication and Use prefix'd. London: Printed for William Mount and Thomas Page, at the Postern on Tower Hill, M, DCC, V.’ Aux pages 56-59 le nombre π est donné jusqu' en 73 chiffres (dont le dernier est d'une unité trop petit) à l'aide du développement en série
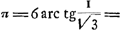 . .
-
voetnoot5)
- Voir, sur Snellius, la note 8, p. 523 du T. I.
-
voetnoot6)
- Willebrordi Snellii R.F. Cyclometricus, De circuli dimensione secundum Logistarum abacos, & ad Mechanicem accuratissima; atque omnium parabilissima. Eiusdemque usus in quarumlibet adscriptarum inventione longe elegantissimus, & quidem ex ratione diametri ad suam peripheriam data. Lugduni Batavorum, Ex Officinâ Elzeviriana, Anno CIƆ IƆ CXXI.
-
voetnoot7)
- Pour comparer entre elles les approximations diverses de la circonférence du cercle on peut se servir avec avantage de la suite:
| (1) |
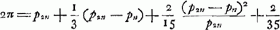 |
où pn désigne le périmètre du polygone régulier à n côtés, inscrit dans un cercle dont le rayon; est égal à l'unité.
On obtient cette suite en partant de la relation évidente:
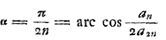
où α représente la moitié de l'arc soustendu par le côté a2n du polygone inscrit à 2n côtés. Ensuite on n'a qu'à développer l'arc sin par la série bien connue, à remplacer n par sa valeur, qui se déduit de la formule p2n = 4n sin 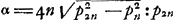 et les facteurs p2n + pn par 2p2n - (p2n - pn). et les facteurs p2n + pn par 2p2n - (p2n - pn).
Au cas où les approximations en question ont été exprimées à l'aide des périmètres P des polygones circonscrits ou des aires s et S des polygones inscrits ou circonscrits, nous les réduisons préalablement par les formules P2n = 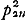 : pn, s2n = ½ pn, Sn = ½Pn; dont la première est identique avec le ‘Theor. X, Prop. XIII’ de Huygens (p. 149 du Tome présent) et équivalente à la relation sn Sn, déduite par Snellius dans la Prop. IX, p. 14 de l'ouvrage cité dans la note précédente. : pn, s2n = ½ pn, Sn = ½Pn; dont la première est identique avec le ‘Theor. X, Prop. XIII’ de Huygens (p. 149 du Tome présent) et équivalente à la relation sn Sn, déduite par Snellius dans la Prop. IX, p. 14 de l'ouvrage cité dans la note précédente.
De cette manière les limites Archimédiennes s'écrivent:
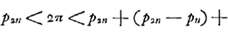 .
Ajoutons qu'on peut évaluer les différences avec la formule exacte à l'aide des relations approchées p2n - pn = π3 : 4n2 = 7,75 : n2 et (p2n - pn): p2n = 1,234: n2. .
Ajoutons qu'on peut évaluer les différences avec la formule exacte à l'aide des relations approchées p2n - pn = π3 : 4n2 = 7,75 : n2 et (p2n - pn): p2n = 1,234: n2.
-
voetnoot8)
- Voici les limites indiquées dans les Prop. XXVIII (p. 42, limite inférieure) et XXIX (p. 43-44, limite supérieure) de l'ouvrage de Snellius:
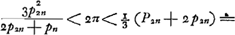 ,
c'est-à-dire (comparez les notes 30 et 33, pp. 156 et 159): ,
c'est-à-dire (comparez les notes 30 et 33, pp. 156 et 159):
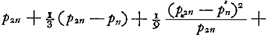
Par la comparaison avec la suite (1) de la note 7, on trouve donc pour la différence de la valeur exacte de 2π d'avec la limite inférieure à peu près 1/45 (p2n - pn)2: p2n et pour celle d'avec la limite supérieure à peu près neuf fois cette valeur.
Une rectification de l'arc de cercle, exposée par le Cardinal de Cuse (1401-1464) dans son ouvrage ‘De mathematica perfectione’ coïncide avec la limite inférieure de Snellius, comme on le voit aisément en comparant la note 33, p. 159 du Tome présent, avec la proposition suivante, qu'on trouve à la p. 106 recto de l'édition des OEuvres de de Cuse de 1514 par J. Faber Stapulensis: ‘Illa est habitudo trium semidiametrorum ad tres semidiametros minus sagittae cordae quadrantis & minoris: quae est cuiuslibet arcus ad suam chordam.’ C'est en appliquant cette proposition à l'angle de 60o que de Cuse a obtenu la valeur 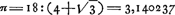 ... qu'il donne (p. 107 recto) comme exacte. De plus, dans les commentaires d'Omnisanctus, qui accompagnent dans l'édition citée le texte de de Cuse, on retrouve p. 111 recto la construction même de Snellius décrite au ‘Theorema XIII’, p. 159 du Tome présent. ... qu'il donne (p. 107 recto) comme exacte. De plus, dans les commentaires d'Omnisanctus, qui accompagnent dans l'édition citée le texte de de Cuse, on retrouve p. 111 recto la construction même de Snellius décrite au ‘Theorema XIII’, p. 159 du Tome présent.
Une autre approximation remarquable, mais bien inférieure à celles de Snellius, fut indiquée par Lansbergen dans ses ‘Cyclometriae novae libri duo, Middelburgi, 1616.’ Elle revient à poser:
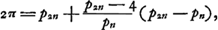
c'est-à-dire, pour un polygone d'un grand nombre de côtés à peu près 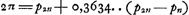 . Elle est donc presque onze fois plus approchée que celle 2π > p2n d'Archimède. . Elle est donc presque onze fois plus approchée que celle 2π > p2n d'Archimède.
Van Lansbergen l'employa à calculer 30 chiffres du nombre π à l'aide du polygone de 246 côtés (p. 34); mais ce résultat était flatté quant aux deux derniers chiffres; comme on peut s'en assurer en se servant des relations approchées de la note 7. Appliquée à un polygone donné, sa méthode ne permet en général de pousser l'approximation qu'un seul chiffre plus loin que la méthode Archimédienne; tandis que celle de Snellius double, au moins, le nombre des chiffres connus et lui permit ainsi de vérifier 35 des 36 chiffres de Ludolf van Ceulen à l'aide des polygones de 229 et 230 côtés. Mais nous nous réservons de revenir sur cette question du nombre des chiffres plus loin dans la note 15, p. 142 du Tome présent.
D'ailleurs ces approximations de de Cuse et de van Lansbergen ne permettent pas d'enfermer le rapport cherché dans des limites bien définies comme Snellius l'a fait.
-
voetnoot9)
- Voir les notes 32 et 33 p. 158 et 159 du Tome présent.
-
voetnoot11)
- Voir la Lettre No. 176, déjà citée: ‘Ego sane eidem rei à paucis diebus intentus sum, atque ea quae inveni Theoremata placent mihi prae omnibus alijs quae scripsi hactenus.’ Et comparez encore les pp. 277, 281 et 288 du T. I.
-
voetnoot12)
- Voir les Lettres No. 181 et No. 183, pp. 274-277 du T. I.
-
voetnoot13)
- Voir, pour le premier les dernières lignes du ‘Theor. XVI. Propos. XIX’, p. 171 du Tome présent, et pour le second les lignes cursivées, p. 175 de ce même Tome. Ces théorèmes conduisent aux inégalités suivantes (comparez les notes 47 et 52, pp. 168 et 175):
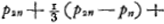
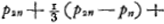
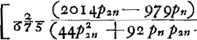 dont les trois premiers termes coïncident avec ceux de la suite (1) de la note 7, tandis que chez les limites de Snellius de la note 8 la coïncidence cesse dès le second terme.
dont les trois premiers termes coïncident avec ceux de la suite (1) de la note 7, tandis que chez les limites de Snellius de la note 8 la coïncidence cesse dès le second terme.
Et que ces théorèmes étaient connus de Huygens lorsqu'il écrivit les lettres en question, cela s'ensuit des résultats numériques qu'il assure avoir obtenu à l'aide des polygones de 30 et de 60 côtés. A l'exception du nombre 31415926537, où il faut remplacer le 7 par un 8, ces résultats sont identiques avec ceux du ‘Problema IV. Propos. XX’ (p. 179 du Tome présent) et n'auraient pu être calculés sans l'emploi des théorèmes mentionnés.
-
voetnoot14)
- Voir l'ouvrage de 1651, reproduit aux p. 288-313 du Tome XI, et consultez encore la Lettre à van Schooten du 1 avril 1654 (p. 279 du T. I), où la connection qui existe entre ces deux derniers théorèmes et les ‘Theoremata’ est mentionnée expressément.
-
voetnoot16)
- Voir le premier alinéa de la p. 157 du Tome présent.
-
voetnoot17)
- Voir la ‘Praefatio’ à la p. 115 du Tome présent et consulter au Tome I les lettres à Kinner à Löwenthurn (pp. 279 et 290), à Grégoire de Saint-Vincent p. 281 et à Golius p. 289.
-
voetnoot18)
- On a d'après le théorème en question, qu'on trouve p. 151 du Tome présent:
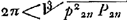 ; c'est-à-dire, en appliquant une des formules de la note 7: ; c'est-à-dire, en appliquant une des formules de la note 7:
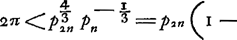 C'est donc le troisième terme qui diffère de celui de la suite de la note 7 et l'approximation est de l'ordre de celles de Snellius.
C'est donc le troisième terme qui diffère de celui de la suite de la note 7 et l'approximation est de l'ordre de celles de Snellius.
-
voetnoot19)
- Voir la p. 279 du T. I. Huygens avait été averti des intentions de Marci par le même Kinner dans ses lettres du 29 novembre 1653 (p. 252 du T. I) et du 28 février 1654 (p. 269 du T. I); d'après cette dernière lettre l'ouvrage serait publié vers Pâques de l'année 1654. Il parut en effet dans cette année 1654 sous le titre: ‘Labyrinthus in quo via ad circuli quadraturam pluribus modis exhibetur. Pragae, 1654.’
-
voetnoot19)
- Voir la p. 279 du T. I. Huygens avait été averti des intentions de Marci par le même Kinner dans ses lettres du 29 novembre 1653 (p. 252 du T. I) et du 28 février 1654 (p. 269 du T. I); d'après cette dernière lettre l'ouvrage serait publié vers Pâques de l'année 1654. Il parut en effet dans cette année 1654 sous le titre: ‘Labyrinthus in quo via ad circuli quadraturam pluribus modis exhibetur. Pragae, 1654.’
-
voetnoot20)
- Voir la réponse de Kinner à la page 284 du T. I. Marcus Marci n'a pas pu pénétrer le mystère, ce qui n'est guère étonnant vu qu'il n'avait pas trouvé le théorème.
-
voetnoot21)
- Voir les pages 169-175 du Tome présent et consulter sur les deux théorèmes en question la note 13.
-
voetnoot22)
- En outre de la limite supérieure de Snellius (voir la note 8), qui résulte du ‘Theor. IX’, p. 137, et de celle déjà mentionnée dans la note 18, on rencontre encore dans la première partie les deux limites suivantes, qui, traitées de la manière décrite dans la note 7, s'écrivent:
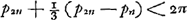
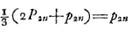
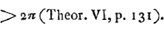 L'écart de la suite de la note 7 y commence avec le troisième terme.
L'écart de la suite de la note 7 y commence avec le troisième terme.
-
voetnoot24)
- Voir les p. 285-286 du Tome I, et consulter sur les rappels du 9 et du 17 avril 1654 les pp. 282 et 285 du même Tome.
-
voetnoot25)
- Voici la liste des personnes auxquelles Huygens fit parvenir un exemplaire: Golius (voir T. I, p. 287, note 4 et p. 289), Van Schooten (T. I, p. 287), le Ducq (p. 287, note 4), Kraen (même note), van der Wal, P. de Chanut, C. de Briene, F. Blondel, Stevin, la bibliothèque (de Leiden?) (toujours la même note), Kinner a Löwenthurn (même note et p. 288, note 3, p. 290 et p. 315, T. I), Grégoire de Saint-Vincent (même note, p. 288 et 290-291, T. I), de Sarasa (même note et p. 288, T. I), Tacquet et van Gutschoven (même note et p. 290, note 4), de Bie (p. 290, note 4); ensuite à J.J. Stöckar, 13 octobre 1654, (T. I, p. 298), la Princesse Palatine Élisabeth, décembre 1654, (T. I, p. 316-317), A. Colvius, mars 1655, (T. I, p. 322), Mylon, février 1656, (T. I, p. 376), De Carcavy et de Fermat, septembre 1656 (T. I, p. 494), Moray et Hobbes, 20 décembre 1662 (T. IV, p. 280), Pr. de Montbéliard, 15 janvier 1670 (d'après une annotation p. 254 du livre D des ‘Adversaria’). De quelques endroits de la ‘Correspondance’ on doit conclure qu'on ne pouvait trouver l'ouvrage chez les libraires à Paris (T. I, p. 400, T. VI, p. 235), ni à Londres (T. VI, p. 373).
-
voetnoot26)
- Comparez le dernier alinéa de la p. 97 du Tome présent.
-
voetnoot27)
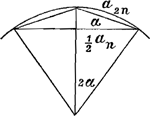
- Le calcul en question s'appuie sur ce que le centre de gravité G d'un arc de cercle AEB doit
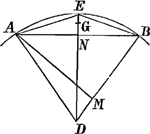
être plus près de la corde AB que le centre de gravité d'un arc cycloïdal symmétrique ayant la même flèche NE; ce qui est d'ailleurs une conséquence presqu'évidente du fait que la courbure de l'arc cycloïdal augmente régulièrement avec la distance du sommet. On a donc GN < ⅔ NE.
Posant ensuite DE = r, AB = a2n, AM = ½an, NE = p, on a
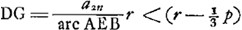 ; donc: arc ; donc: arc 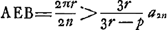 . .
Mais de la proportion DN : DB = AM : AB, c'est-à-dire:
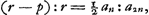
,
on déduit successivement:
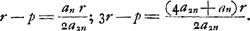
On trouve donc, en posant r = 1:
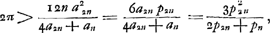
conforme à la limite inférieure de la note 8.
-
voetnoot28)
- Voir la note 51 au dernier alinéa de la p. 174 du Tome présent et la page 275 du T. VI.
-
voetnoot29)
- Le manuscrit No. 12, mentionné dans la note 1, T. XI, p. 7.
-
voetnoot33)
- Comparez le second alinéa de la p. 4, et pour le ‘Probl. VIII’ les p. 83-86 du Tome présent.
-
voetnoot34)
- Comparez les p. 4-6 du Tome présent à commencer par le troisiéme alinéa de la p. 4.
-
voetnoot36)
- Voir les notes 15 et 17, p. 12 du Tome présent.
-
voetnoot40)
- Voir les notes 3 et 4, p. 16 et la note 6, p. 184 du Tome présent.
-
voetnoot43)
- Voir les p. 14-27 de l'édition de Bâle, citée p. 137 du T. I, note 1, ou les p. 66-127 du T. III de l'édition de Heiberg, citée p. 50 du T. XI, note 2.
-
voetnoot44)
- Dans sa ‘Géométrie’, voir les p. 469-470 du T. VI des ‘OEuvres de Descartes’ publiées par Charles Adam et Paul Tannery.
-
voetnoot45)
- Voir les p. 199-211 du Tome présent et consulter les pièces VI et VII, p. 26-37 de ce même Tome.
-
voetnoot48)
- Voir la p. 195 et comparer la dernière partie de la pièce No. XI des ‘Travaux’, p. 52-53.
-
voetnoot54)
- Dans sa lettre du 13 août 1657; voir la p. 45 du T. II.
-
voetnoot55)
- Voir sa lettre du 14 août 1657 (V. S.?), p. 47 du T. II.
-
voetnoot60)
- Dans sa lettre du 19 octobre; voir la p. 71 du T. II.
-
voetnoot62)
- Voir les pages 14-16 de la seconde édition, citée p. 478 du T. II.
-
voetnoot64)
- Voir au lieu cité dans la note 43 les p. 20-21 de l'édition de Bâle; Heiberg, T. III, p. 92-99.
-
voetnoot65)
- Cette première édition, citée p. 311, note 3, T. II, est extrêmement rare. Le Paige, l'éditeur de la Correspondance de de Sluse, n'en connaissait que deux exemplaires dont l'un se trouvait dans une bibliothèque particulière et l'autre dans la Bibliothèque nationale de Paris. Par la bien veillance de l'un des bibliothécaires de cette dernière, M.M. Vienne, nous sommes en état de fournir les renseignements suivants sur cette édition. Le texte en est identique avec les 43 premières pages de la seconde édition en excluant le dernier alinea ‘Ostensum est’, etc. Elle contient donc le ‘Mesolabum’ proprement dit, intitulé: ‘Mesolabum seu duae mediae proportionales inter datas per circulum et ellipsim vel hyperbolam infinitis modis exhibitae’ avec la dédicace au Prince Léopold et l'introduction au lecteur, qui le précèdent, et ensuite encore le chapitre ‘De problematum solidorum constructione per easdem lineas iisdem infinitis modis’, à l'exception du ‘Lemma ultimum’, de la ‘Propositio ultima’ et de l'alinéa cité de la page 43 qui leur sert d'introduction. La ‘Pars altera de analysi’ et les ‘Miscellanea’ de la seconde édition, manquent complètement dans la première.
Quant à l'insertion dans la seconde édition de la ‘Propositio ultima’; elle est due à la correspondance avec Huygens. En effet, l'idée de Johan de Witt (voir la lettre No. 663, p. 477 du T. II) que les constructions de problèmes solides gagneraient en élégance si l'on pouvait les exécuter à l'aide des intersections de cercles avec une conique donnée, tracée d'avance, cette idée n'était pas venue à de Sluse lors de la première édition du ‘Mesolabum’. Toutefois comme il le remarque dans la lettre citée No. 663, du 9 septembre 1659, des constructions de cette façon pouvaient être déduites aisément de celles qu'il avait publiées. C'est ce qu'il a fait pour le problème des deux moyennes dans cette ‘Propositio ultima’, en employant un artifice semblable à celui dont Huygens s'est servi dans la seconde partie de l'‘Appendice I’, p. 221 du Tome présent.
-
voetnoot68)
- Voir la Lettre No. 641, p. 442-443 du T. II. Elle n'est pas de juillet 1659, comme nous l'avions supposé, mais de septembre ou octobre 1668, puisqu' elle se rapporte évidemment non à la première, mais à la seconde édition du Mesolabum, laquelle contient l'analyse des solutions, publiées dans la première, et traite dans les ‘Miscellanea’ le problème de la détermination du point d'inflexion de la conchoïde.
-
voetnoot69)
- On le trouve p. 227-228 du Manuscrit No. 9 (olim E).
-
voetnoot70)
- Il occupe les pages 7-15 du Manuscrit No. 11.
-
voetnoot73)
- Voir, pour plus de détails, les notes 2-6, p. 226-227 du T. XI.
-
voetnoot78)
- Voir les pp. 201-203 et 207-209 du Tome présent.
-
voetnoot80)
- Voir les p. 17-19 de l'ouvrage cité en premier lieu dans la note 5, p. 126 du T. VIII. La solution se retrouve encore dans le résumé de l'‘Apollonius Redivivus’ donné par Hérigone. Voir les p. 912-914 du Tome I du ‘Cursus mathematicus’, ouvrage cité dans la note 4, p. 202 du T. I et qui parut en 1634.
-
voetnoot81)
- Le problème cité dans la note 2, p. 255 du T. XI. Consultez encore sur ce problème la note 3 de la même page.
-
voetnoot82)
- Voir les p. 330-333 de l'ouvrage cité en dernier lieu dans la note 5, p. 127 du T. VIII.
-
voetnoot84)
- Voir la ‘Constructio brevior’ p. 241-242 du T. XI.
-
voetnoot85)
- Voir la pièce No. VI des ‘Travaux mathématiques divers de 1652 et 1653’, p. 26-31 du Tome présent.
-
voetnoot90)
- Voir la pièce No. XIII des ‘Travaux, etc.’, p. 57-58 du Tome présent.
-
voetnoot93)
- Voir les pp. 205-207 et 209-211, qui suivent.
-
voetnoot94)
- Voir les p. 19-22 de l'‘Appolonius Redivivus’; les p. 913-914 du ‘Cursus mathematicus’ d'Hérigone et les p. 333-336 de l'ouvrage: ‘De Resolutione et Compositione Mathematica’.
-
voetnoot100)
- Voir la pièce No. XIII, p. 58-59 du Tome présent.
-
voetnoot105)
- Elles se trouvent aux pages 27 et 33 du Tome présent.
-
voetnoot107)
- Comparez les énoncés des problèmes en question.
-
voetnoot112)
- Voir sa lettre à de Sluse, p. 443 du T. II; mais consultez sur cette lettre la note 68. Voir encore la lettre à Coets du 27 août 1687, p. 200 du Tome IX.
-
voetnoot114)
- Van Schooten évidemment était du même avis puisqu'au lieu cité plus haut il s'exprime comme il suit à propos de la solution de van Heuraet: ‘sic ut ad constructionem ejus non nisi regula atque circino utamur, haud secus ac si Problema foret Planum’ (p. 259).
-
voetnoot116)
- Voir, aux pp. 232 et 234, qui suivent, les notes 4 et 11 de l'Appendice mentionné.
-
voetnoot117)
- Voir la note 15 de l'Appendice IV, p. 236, qui suit.
-
voetnoot118)
- Celles que nous avons utilisées dans l'Appendice IV.
-
voetnoot120)
- Voir, dans le volume présent, la note 16 de l'Appendice IV. C'est donc à tort que dans le dernier alinéa de la note 4, p. 202 du T. IX, il a été supposé que cette question des limites de la validité de la construction ne s'est pas présentée à l'esprit de Huygens avant 1687. Une inspection plus minutieuse des annotations de 1659, très difficiles à déchiffrer, nous a mieux renseigné.
-
voetnoot121)
- Consultez encore le dernier alinéa de la note 4, p. 202 du T. IX.
|