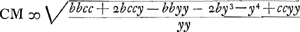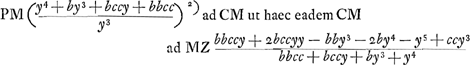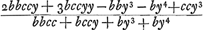Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 83]

XX.¹⁾
1653.

25. Sept. 1653.

In Conchoide Nicomedis invenire flectionis punctum.

Est Conchoides QCN. polus G, Asymptotus AB. Et ponatur inventum jam esse flexus punctum quod sit C. et ducatur tangens CZ.

[Fig. 1.]

Igitur quoniam pars conchoidis CQ est cava versus G, necesse est tangentes omnes ad puncta inter C et Q, secare rectam GZ inter Q et Z item quia pars conchoidis reliqua CN convexa est versus G, omnes quoque tangentes ad puncta partis CN quantumlibet productae, rectam GZ secare necesse est inter A et Z. Igitur tangens CZ est ejusmodi, quae abscindat AZ aut GZ omnium maximam quae a tangente abscindi possunt. Sit GA, b. AQ, c. AM, y. Ergo CM erit ex proprietate Conchoides

Cum CP tangenti CZ est perp. est

²⁾

1) La pièce est empruntée aux pages 243-243b du manuscrit N^o. 12. La construction qu'elle amène se retrouve avec des modifications de rédaction et des additions dans les ‘Illustrium quorundam problematum constructiones’ de 1654 comme ‘Probl. VIII’, et de même dans une lettre à Van Schooten du 23 octobre 1653, reproduite avec sa minute aux pages 243-246 du T. I.

2) Huygens ajoute en marge à ce propos ‘Vide infra ubi tangens conchoidis à Schotenio inventa est’. Consultez la page 18 du T. XI, où la valeur de AP, trouvée par van Schooten, est indiquée.

[p. 84]

adde MA	y sub eodem denomin.
AZ

Potest numerator et denominator dividi per b + y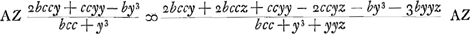

Scriptis nempe scribendis secundum regulam de maximis et min. ponendo AM ∞ y + z.³⁾

6bccy³z + 3ccy⁴z - 3by⁵z ∞ 2bbc⁴z + 2bccy³z + 2bc⁴yz + 2ccy⁴z - 3bbccyyz - 3by⁵z

y⁴ + 4by³ + 3bbyy - 2bccy - 2bbcc ∞ o div. per b + y

y³ + 3byy - 2bcc ∞ o. Auferatur secund. term. pon.^do q ∞ y + b⁴⁾ sive GM; hoc est q - b ∞ y fit

q³ - 3bbq + 2b³ - 2bcc ∞ o

q³ ∞ 3bbq + 2bcc - 2b³

sumptaque b pro unit.

q³ ∞ 3bq + 2cc/b - 2b. q est GM.

Si b ∞ c erit q³ ∞ 3b²q. qq ∞ 3bb. Planum.

Item si cc ∞ 2bb erit q ∞ 2b.

3) Il s'agit de la méthode exposée au debut de la seconde partie du N^o. XIV, p. 65-66 du Tome présent.

4) Comparez au Livre III de la ‘Géométrie’ de Descartes l'article: ‘Comment ou peut oster le second terme d'vne Equation’, p. 449-450 du T. VI de l'édition d'Adam et Tannery.

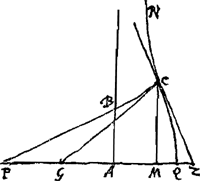
Constructio.⁵⁾

Sicut GA ad AQ [Fig. 2 et 3] ita sit AQ ad AE et ponatur ipsi GE aequalis GF. Porro sit GR parall. AB et aequalis duplac AG, et describatur parabola ver-

5) L'équation cubique en q une fois trouvée, Huygens, pour arriver à la construction qui va suivre, n'avait qu'à se servir de la règle donnée par Descartes au Livre III de sa ‘Géométrie’ (p. 464-467 de l'édition d'Adam et Tannery) pour construire à l'aide d'un cercle et d'une parabole les racines des équations cubiques et biquadratiques; en s'appliquant toutefois à réduire autant que possible le nombre des lignes à tirer. A cet effet Huygens fait correspondre les points G et R de ses figures avec les points D et A de celle de Descartes. Ensuite il construit le point E, correspondant au point E de Descartes qui est, chez Descartes, le centre du cercle qui va couper la parabole ayant R pour sommet et pour paramètre l'unité b = GA; mais avant de tirer le cercle Huygens transporte son centre au point F situé symmétriquement à l'autre côté de l'axe RG. De cette façon la droite OM, qui détermine la racine GM de l'équation cubique, peut servir en même temps à découper sur la conchoïde le point d'inflexion cherché. Remarquons encore que Huygens ne semble pas avoir tâché d'interpréter la présence, dans le cas de la Fig. 3 d'un second et d'un troisième point d'intersection du cercle et de la parabole dont l'un est situé entre R et O et l'autre à gauche de la droite RG. Évidemment le second point d'intersection correspond aux points d'inflexion de de la seconde branche de la conchoïde et le troisième à des points d'inflexion imaginaires.

[p. 85]

tice R, latere recto aequali GA quae sit RO. Centro vero F radio FR circumferentia describatur parabolam secans in O et ducatur OC parallela AB, donec Conchoidi occurrat in C. Eritque C punctum inflexionis quaesitum.

Estque notatum dignum quod (si) ad punctum C tangens (ducatur ZCL, illa simul quoque secabit conchoidem in puncto C).⁶⁾

Haec est Constructio universalis. At quando AQ minor est quam AG per trisectionem anguli semper absolvi potest. Item cum AQ major quidem est quam AG sed qu. AQ non majus duplo qu.^o AG.⁷⁾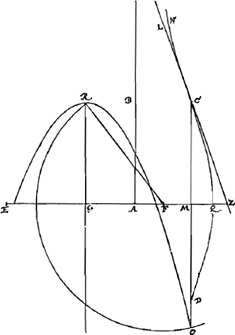

[Fig. 2.]

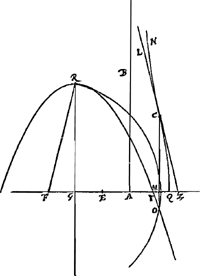[Fig. 3]

6) Les mots entre parenthèses ont été biffés depuis et remplacés par ‘duci nequit’, ce qui témoigne d'une autre conception de la notion de tangente.

7) Les constructions qui vont suivre sont des applications directes des règles données par Descartes au Livre III de sa Géométrie (p. 472-474 de l'édition d'Adam et Tannery) et ces règles mêmes conduisent à la distinction des deux cas.

[p. 86]

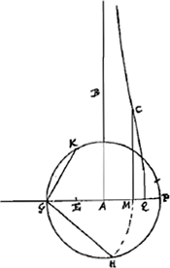
Si igitur AQ minor fuerit quam AG haec erit Constructio quae sequit. Centro A, radio AG (Fig. 4) circulus describatur KPG. inque eo accommodetur GK

[Fig. 4.]

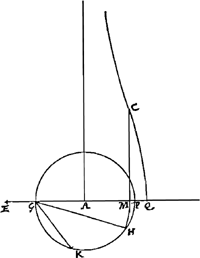[Fig. 5.]

aequalis duplae GE inventae ut prius, et rectae GH quae subtendit ⅓ arcus KPG aequalis sumatur GM, et ducatur MC parallela AB. Haec Conchoidem secabit in flexus puncto.

Cum vero AQ major est quam AG, at qu. AQ non majus duplo quadrato AG, caeteris ad eundem modum compositis, haec tantum differentia erit, quod arcum KP in tres partes aequales secare oportet, quarum una sit PH, et subtensae GH aequalem sumere GM.

(Potest autem haec angulorum trisectio fieri ope Conchoidis ipsius quae proposita est, methodo Nicomedis quam videri est apud Pappum lib. 4 prop. 32.⁸⁾ nam quod ille per Hijperbolem illic efficit,⁹⁾ idem apparet et per Conchoidem fieri posse).¹⁰⁾

8) Voir les pages 62 recto et verso de l'ouvrage cité dans la note 3, p. 259 de notre T. II.



(Hultsch, T. I, p. 274-277). Il s'agit de la construction bien connue par laquelle on obtient la trisection de l'angle ABC en tirant la droite BDE de manière qu'on ait DE = 2 BA.

9) Dans la proposition précédente sur laquelle ou peut consulter la note 9, p. 228 du T. XI.

10) Cette remarque, que nous avons mise entre parenthèses, a été biffée depuis. Elle se retrouve dans la lettre à van Schooten du 23 octobre 1653 (p. 246 du T. I); mais elle manque dans les ‘Illustrium quorundam problematum constructiones’ de 1654. Dans l'intervalle Huygens doit donc s'être aperçu que le problème de la trisection d'un angle donné à l'aide d'une conchoïde, donnée d'avance, est d'une autre nature que celui d'obtenir cette trisection par une conchoïde dont le choix est adapté à l'angle donné. Le premier problème est exécutable, du moins sous de certaines conditions, comme cela ressort indirectement d'une pièce de 1659 que nous donnerons comme Appendice IV aux ‘Illustrium quorundam problematum constructiones’ (voir la note 4 de cet Appendice) mais nous n'avons aucune preuve que Huygens s'est occupé de ce problème.