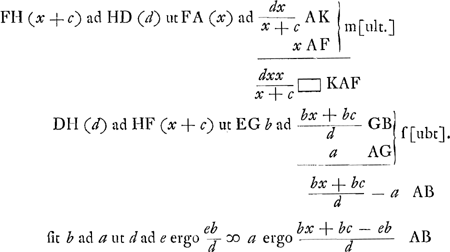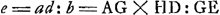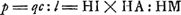Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656
(1910)–Christiaan Huygens–
[pagina 72]
| |
XVI.Ga naar voetnoot1)
| |
[pagina 73]
| |
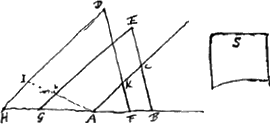
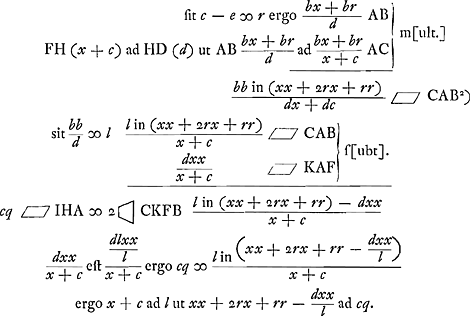 Id quod hic fecimus semper agendum est ut aequatio sit ejusmodi quae in proportionem resolvi possit, idque sine solidorum mentione. Proportio autem semel ordinata retinenda est, aut si nonnunquam ad aequalitatem redigatur, rursus repetenda, donec ad simplissimos terminos deveniatur, ex quibus x innotescat. Verùm quia demonstrationis inveniendae gratia hujusmodi analysis instituta est, oportet ut operatio omnis quae aequationem praecessit argumentationis formam accipiat. Etenim postquam repetendo analyseos vestigia demonstratum erit quod x + c ad l ut xx + 2rx + rr - dxx/l ad cq, oportebit ex ista quae aequationem praecessit argumentatione ostendere quod x + c ad l ut xx + 2rx + rr - dxx/l ad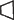 CKFB 2 CKFB 2
Itaque resolutione continua opus est hujusmodi: Factum ponatur, et sint constructa quae superius diximus. Porro autem ut b ad a 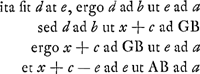 | |
[pagina 74]
| |
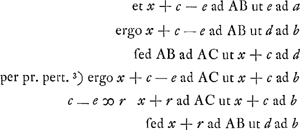 ergo ratio comp.a ex x + r ad AC et x + r ad AB, hoc est Q. x + rGa naar voetnoot4) ad ▭ CAB eadem est compositae ex x + c ad b et d ad b. Sit autem ut d ad b ita b ad l ergo Q x + r ad ▭ CAB ut x + c ad l. (nam ratio composita ex x + c ad b et b ad l eadem est quae x + c ad l.)
Itaque x + c ad l ut Q. x + r ad ▱ CAB αGa naar voetnoot5). Fiat jam ut l ad d ita xx ad dxx/l designandum dx/l.Ga naar voetnoot6) Reductio ▱ KAF; est autem d ad x + c ut ▱ KAF ad xx. per perturb.Ga naar voetnoot3) ergo x + c ad l ut dxx/l ad ▱ KAF α.Ga naar voetnoot7) ergo x + c ad l ut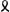 ad ▱ CAB - ▱KAF seu ▱ IHA(qc) ad ▱ CAB - ▱KAF seu ▱ IHA(qc)
AEquatio superius exhibita.Ga naar voetnoot8) 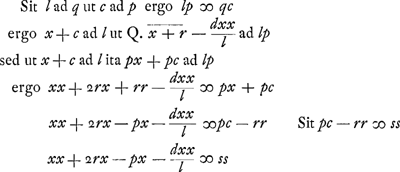 | |
[pagina 75]
| |
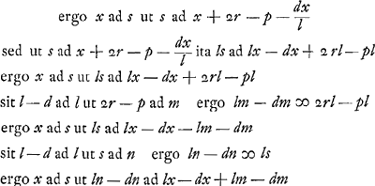 ergo x ad s ut n ad x + m et xx + mx ∞ sn quod componitur secundum 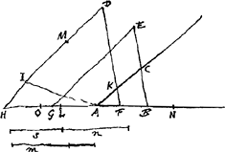 [Fig. 2.]
regulam aequationum quadraticarumGa naar voetnoot9) 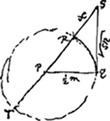 [Fig. 3.]
e. HLGa naar voetnoot10) l. HMGa naar voetnoot10) dx/l. ANGa naar voetnoot11) p. HOGa naar voetnoot12) r. LAGa naar voetnoot13) Hinc demonstratio facile conscribetur per regressum, cujus hoc sit initium;Ga naar voetnoot14) Rect. TSR [Fig. 3] aequale est quadrato SQ, hoc est ▭osn,  |
|