Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656
(1910)–Christiaan Huygens–
[pagina 69]
| |
XV.Ga naar voetnoot1)
| |
[pagina 70]
| |
q. CN (ee) ad q. NB (bb - ee) ut q. CD (yy) ad q. 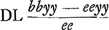
item 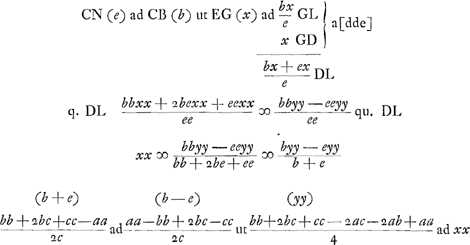 denominator primi et secundi termini quia idem est aufertur; deinde primus et tertius terminus dividi possunt per b + c - a. Et fit b + c + a ad 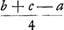 ut aa - bb + 2bc - cc ad xx.Ga naar voetnoot3)
Quia vero GD, x, ducta in ut aa - bb + 2bc - cc ad xx.Ga naar voetnoot3)
Quia vero GD, x, ducta in 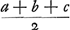 dimidium summae laterum, producit aream trianguli ABC, apparet eandem quoque provenire si xx ducatur in quadratum ex dimidium summae laterum, producit aream trianguli ABC, apparet eandem quoque provenire si xx ducatur in quadratum ex 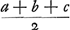 , et ex producto radix extrahatur. Sed xx est illud quod oritur ex producto terminorum tertij et secundi, ultimo positorum, diviso per primum qui est a + b + c. Ergo quoniam hoc multiplicari rursus deberet per qu. ex , et ex producto radix extrahatur. Sed xx est illud quod oritur ex producto terminorum tertij et secundi, ultimo positorum, diviso per primum qui est a + b + c. Ergo quoniam hoc multiplicari rursus deberet per qu. ex 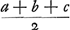 apparet tantum opus esse ut secundus terminus in tertium ducatur et hoc productum rursus in apparet tantum opus esse ut secundus terminus in tertium ducatur et hoc productum rursus in 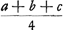 , atque ex ultimo producto radix eliciatur: Atque hanc fore aream trianguli quaesitam. , atque ex ultimo producto radix eliciatur: Atque hanc fore aream trianguli quaesitam.
Oportet igitur multiplicare aa - bb + 2bc - cc per 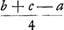 et horum pro- et horum pro- | |
[pagina 71]
| |
ductum per 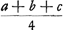 . Hoc autem idem est ac si haec tria multiplicentur, nempe . Hoc autem idem est ac si haec tria multiplicentur, nempe 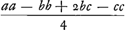 et et 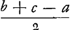 et et 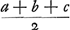 . Sed . Sed 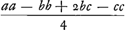 oritur ex multiplicatione oritur ex multiplicatione 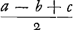 in in 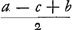 . Itaque haec quatuor multiplicanda sunt, videlicet, . Itaque haec quatuor multiplicanda sunt, videlicet, 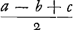 et et 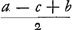 et et 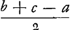 et et 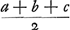 , et producti radix erit area trianguli ABC. Tres autem priores termini inveniuntur si ex dimidio summae laterum singula latera auferantur, estque quartus terminus ipsa medietas summae laterum. , et producti radix erit area trianguli ABC. Tres autem priores termini inveniuntur si ex dimidio summae laterum singula latera auferantur, estque quartus terminus ipsa medietas summae laterum.
Igitur hinc regula manifesta fit quae ad aream trianguli inveniendam praecipit, ut ex dimidia summa laterum singula latera auferantur; et haec tria residua in se mutuo ducantur et in dimidium summae laterum, atque ut ex producto radix eliciatur. |
|


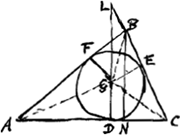
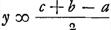 .
Sit nunc GD ∞ x et ducatur BN perpend. ad AC et producantur CB, DG donec occurrant sibi mutuo in L. Per 13. lib. 1.
.
Sit nunc GD ∞ x et ducatur BN perpend. ad AC et producantur CB, DG donec occurrant sibi mutuo in L. Per 13. lib. 1.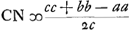 . haec vocetur e: et propter ∆la similia erit
. haec vocetur e: et propter ∆la similia erit