Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656
(1910)–Christiaan Huygens–
[pagina 60]
| |
[Première Partie.]Ostenditur quae ratio sit regulae Fermattij, cujus exempla inferius à Schotenio asscripta sunt,Ga naar voetnoot2) dein alia docetur brevior.Ga naar voetnoot3) Esto data positione recta ED et puncta A, B: oporteatque invenire in ED punctum 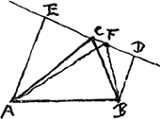 [Fig. 1.]
C, unde ductis CA, CB, quadrata earum simul sumpta sint minima quae esse possint.Ga naar voetnoot4) Sit AE ∞ a, BD ∞ b (hae autem perpendiculares intelliguntur ad ED quae sit c). Secundum Fermattij regulam ponitur primum EC si velimus ∞ x unde summa quadratorum AC, CB invenitur aa + 2xx - 2cx + cc + bb. Deinde pro eâdem EC ponitur x+y, indeque inventâ rursus summâ quadr.orum AC, CB aa + 2xx + 2yy + | |
[pagina 61]
| |
+ 4xy - 2cy - 2cx + cc + bb, horum aequatio instituitur ubi aequalibus ablatis utrimque fit 2yy + 4xy ∞ 2cy. Tum per y dividitur fitque 2y + 4x ∞ 2c. Denique termini in quibus y reperitur rejiciuntur ut hic 2y, et restat 4x ∞ 2c et x ∞ ½c. Horum ratio ut intelligatur oportet quantitatem y ab initio alicujus magnitudinis lineam denotare ut CF; Illud enim revera quaeritur, nimirum EC existente ∞ x quanta debeat esse CF, ut ductis FA, FB, harum duarum quadrata aequentur quadratis CA et CB. Semper quippe ubi maximum vel minimum quaeritur, utrimque casus aequalitatis existit. Itaque quum in aequatione inveniatur - 4x + 2c ∞ 2y vel c - 2x ∞ y hoc significat, si x, EC, pro determinatae magnitudinis linea sumatur tum CF, y, fore c - 2x, vel si certa statuatur CF, y differentia nempe duarum EC, EF, tum EC, x fore ½c - ½y. Patet autem, quanto minor statuetur y, tanto minus differre x ab ½c quare si aequalis nihilo sit y, erit x aequalis ½c. Hincque manifestum est, quod si EC ponatur ∞ ½ ED et ducantur CA, CB harum quadrata minima erunt quae esse possunt, tunc enim casus aequalitatis nullus esse poterit, et ponendo CF quamlibet exiguam si major sit quam nihil, erunt quadrata FA, FB majora quam CA, CB.Ga naar voetnoot5) Illud autem quod modo dictum est considerans, quod nempe ubi de maximis vel minimis inquiritur, semper utrimque aequalitatis casus existit, alium quoque modum ad ea determinanda inveni. Animadverti enim, quod si problema de maximo vel minimo determinando propositum, sic resolvatur quasi non maximum vel minimum sed dato aequale quaeramus, tum semper aequatio invenietur in qua radix quaesita habebit duos valores, quorum uterque proposito satisfaciet, qui quidem diversi erunt; at quanto minus inter se differunt, tanto propius ad casum determinationis accedunt, ita ut ubi alter alteri aequalis existit ibi sit determinatio minimi vel maximi. Ubi igitur quaerendo dato aequale, ut dixi, ad aequationum perveneris, et volueris ex ea maximum vel minimum reperire, ita ipsam expendes tanquam duos valores habentem, sibi mutuo aequales. itaque scibis singulos ejus terminos cum singulis terminis alius aequationis comparari posse quae oritur ex multiplicatione radicis quaesitae, multatae quantitate sibi aequali, in seipsam. quod productum si non tot habet dimensiones quot aequatio proposita, rursus ducendum erit in aliam quantitatem quae deficientes alteri dimensiones contineat, suppleatque; secundum ea quae docet Cartesius lib. 2. Geom. ubi tangentes invenire docet.Ga naar voetnoot6) Hoc pacto si punctum C quaesiverimus in exemplo praecedente, | |
[pagina 62]
| |
oportet inventam summam quadratorum AC, CB, aequare certo spatio dd, quasi propositum habeamus invenire punctum unde ductis CA, CB, quadrata earum spatio alicui dd aequalia habeantur. Itaque scribe aa + 2xx - 2cx + cc + bb ∞ dd, vel xx- cx + ½aa + ½cc - ½dd + ½bb ∞ o. Postea aliam aequationem finge ponendo x ∞ e, et x - e ∞ o, quod ductum in seipsum faciet xx - 2ex + ee ∞ o. Si itaque praecedens aequatio minimi determinationem continet, debet habere x duos valores aequales, ideoque singulos ejus aequationis terminos singulis terminis posterioris aequare licet. Primus utrimque est plane idem, itaque secundus comparetur faciendo - cx ∞ - 2ex unde invenitur e ½c hoc est x ∞ ½c. Quod inveniendum erat. Caeterum comparando terminos postremos ½bb + ½aa + ½cc - ½dd ∞ ee, invenietur quantitas dd ∞ aa + cc - 2ee + bb hoc est, dd ∞ aa + bb + ½cc; nam - 2ee est - ½cc, quoniam inventum fuit ½c ∞ e. Et hoc quidem determinationem exhibet in casu quo datum foret problema ut dato aequale quaeratur, deberet enim
dd non minus dari quam aa + bb + ½cc; sed cum maximum vel minimum quaeritur sufficit invenisse quocunque modo quantitatem x; et quoniam dd tunc tantum imaginarium est, oportet invenire x aequalem quantitati cognitae quae non admixtum habeat d, quod semper fieri potest.Ga naar voetnoot7) Rationem autem comparationis
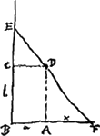 [Fig. 2.]
aequationum mox ostendam, ubi exemplum cubicae aequationis explicavero. Sint lineae angulum rectum continentes BE, BF et datum intra angulum punctum D, oporteatque ducere EDF rectam omnium brevissimam.Ga naar voetnoot8) Ductis perpendicularibus DC, DA datae sunt BC ∞ b et BA ∞ a. Sit autem AF ∞ x ergo quoniam AF ad AD ut DC ad CE erit haec ∞ ab/x et tota BE ∞ ∞ b + ab/x; cujus quadratum 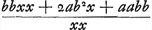 addatur ad quadratum BF aa + 2ax + xx summa est addatur ad quadratum BF aa + 2ax + xx summa est
| |
[pagina 63]
| |
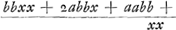 qu. EF, qu. EF,
imaginari enim oportet lineam EF datae d aequalem inveniendam esse. itaque erit 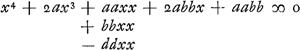 Formetur porro alià aequatio quarum haec comparetur. Sit x ∞ e vel x-e ∞ o quod in se ductum dat xx - 2ex + ee ∞ 0 caeterum quoniam duae hic dimensiones desunt per aliam quantitatem multiplicetur quae secundum Cartesium erit xx + fx + hh 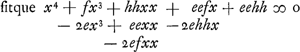 Comparetur terminus secundus hujus aequationis cum secundo praecedentis ergo f - 2e ∞ 2a et f ∞ 2a + 2e. Porro ultimus cum ultimo ergo eehh ∞ aabb et hh ∞ aabb/ee. nunc denique penultimus cum penultimo aequationis prioris: nam tertius cum tertio comparandus hic non est, quoniam habet quantitatem imaginariam d. Ergo eef - 2ehh ∞ 2abb. vel ponendo pro f et hh, ea quibus aequalia inventa sunt erit 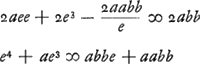 quod utrimque dividitur per e + a et fit e3 ∞ abb vel x3 ∞ abb nam x erat ∞ e. Debet itaque AF esse una e medijs proportionalibus inter BA et BC, ut fiat FDE omnium brevissima quae per punctum D ducuntur inter lineas BF, BE. ad comparationes aequationum quod attinet, apparet equidem quam eae rationem habeant in aequationibus quae quadratum non excedunt, ut in priori horum | |
[pagina 64]
| |
exemplorum. Nam in quacunque aequatione quadrata, si sciam radicem habere duos valores aequales, possum singulos eorum invenire per ejusmodi comparationem; sic posito 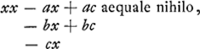 fi constet x valere duas quantitates aequales comparo a + b + c cum 2e nempe secundum terminum cum secundo meae aequationis quam formavi xx - 2ex + ee. fitque e ∞ ½a + ½b + ½c itaque valor uterque radicis x est ½a + ½b + ½c. Quod si invenire velim ex qua multiplicatione proposita aequatio sit orta, comparo porro ultimos terminos ee ∞ ac + bc, seu quoniam e erat inventum ∞ ½a + ½b + ½c, fiet 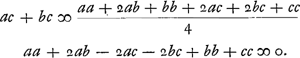 quare ejus radix a + b - c ∞ 0; a + b ∞ c unde e quae erat ∞ ½a + ½b + ½c erit, nunc ∞ a + b vel ∞ c nam haec sunt aequalia. itaque orta est aequatio proposita ex multiplicatione x - a - b ∞ 0 per x - c ∞ 0, suntque valores duo aequales radicis x, c et a + b. Omnes aequationes quadratae productae sunt hoc modo ex multiplicatione radicis in se ipsam multatae quantitatibus sibi aequalibus, ideoque non mirum, quod ubi duae istae quantitates aequales sunt, secundus terminus aequetur - 2ex hoc est - 2xx nam idem est ac si x - x multiplicatum sit in x - x. quod vero x - e ponitur ∞ 0 adscita litera e ∞ x, hoc fit ut terminorum ordo cum distinctione habeatur. Porro in cubicis et quadratoquadraticis alijsque aequationibus, talem formare oportet aequationem, ut totidem dimensiones et consequenter tot valores diversos habeat x quot sunt in illa aequatione cui comparari eam necesse est. Ut in exemplo horum posteriori, primum quidem formo aequationem quadratam xx - 2ex + ee, quae duos valores habet eosque aequales; at quoniam hanc quadratoquadraticae conferre nequeo, ducenda est porro in aliam aequationem quadratam, cujus quidem radicis valores ijdem supponuntur cum duobus valoribus radicis aequationis primariae quos habebat praeter duos aequales. nam non aliter termini singuli unius aequationis aequari possunt singulis terminis alterius nisi radix illius omnes eosdem habeat valores aequationis hujus. quod autem ibi multiplicavi per xx + fx + hh, sciendum est hanc esse quadratam aequationem in qua x habet duos valores licet falsi sint, nempe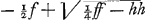 et et
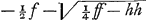 . Hi itaque valores x aequales supponuntur duobus istis quos habebat x in primaria aequatione praeter duos inter se aequales. quare ducto xx - fx + hh ∞ 0 . Hi itaque valores x aequales supponuntur duobus istis quos habebat x in primaria aequatione praeter duos inter se aequales. quare ducto xx - fx + hh ∞ 0
| |
[pagina 65]
| |
in xx - 2ex + e2 ∞ o recte aequatio inde producta cum priori secundum singulos terminos confertur, eo quod singuli quatuor valores radicis in una singulis in altera aequales supponantur; ex isto autem supposito, omnia consequenter inveniuntur quae requiruntur ut quod suppositum est verum esse possit, itaque primum invenitur f ∞ 2a + 2e et hh ∞ aabb/ee deinde e3 seu x3 ∞ abb. Nihil autem interest quae signa + et - sint in xx + fx + hh quae quantitas ducta est in xx - 2ex + ee supplendi dimensiones gratia. quia postmodum quantitates f et hh rursus eliminantur.
Potuisset etiam loco aequationis xx + fx + hh ∞ 0 aliae sumi ut xx - fx - hx + fh ∞ 0, orta ex x - f ∞ 0 per x - h ∞ 0; item xx. fx. fh, et quaelibet praeter has, dummodo praeter x duas alias literas habeant, ductaque in xx - 2ex + ee, omnes dimensiones forment quae sunt in aequatione prima. Sed omnium commodissime sumitur xx. fx. hh, quod Cartesius praescribitGa naar voetnoot9). Sciendum autem est, nihil esse aliud, tangentem quaerere secundum ipsius methodumGa naar voetnoot10) quam ex certo puncto ducere lineam rectam brevissimam earum quae possunt, lineae curvae occurrentem. Et licet aliquando hoc sit solidum,Ga naar voetnoot11) et tangentem tamen ad datum in curva punctum ducere planum sit, utrumque ea ratione simul construere discimus et discernitur simul quodnam è duobus solidum quodve planum sit. Illud modo observandum est, quae quantitas duos diversos valores habere possit, cum problema ita resolvitur ut non brevissimam, sed certae lineae aequalem ducere quaeramus. | |
[Seconde Partie.]Ga naar voetnoot12)Methodus autem Fermatij in solidis problematibus plerisque et praecipue ad tan- | |
[pagina 66]
| |
gentes inveniendas facilior est atque expeditior, si sic ea utamur ut jam dicetur.Ga naar voetnoot13) Postquam quaestionem sic resolventes quasi dato aequale quaeratur ad aequationem pervenimus, oportet ut illud suppositum datum unam aequationis partem faciat, quod plerumque spontè contingit. Deinde oportet ponere x + y vel x - y ∞ x; sed commodius x + y ∞ x ponetur. et in omnibus quantitatibus aequatîonis ubi habetur x, scribendum est x + y, ita ut quaecunque quantitates per x multiplicatae vel divisae sint multiplicentur per x + y vel dividantur. atque idem observandum in omnibus potestatibus x, ut scilicet pro xx et x3 et x4 &c. substituantur quadrata, cubi, quadratoquadrata ab x + y. Neque tamen integras potestates ab x + y scribere est opus, sed partes omnes earum omitti possunt in quibus plura quam unum y continentur.Ga naar voetnoot14) Ita ex quadratoquadr.o ab x + y, nihil aliud sumendum quam x4 + 4 x3y. ex cubo nihil nisi x3 + 3xxy; ex quadrato xx + 2xy. sed et x4, x3, et xx, ex hisce omitti sic possunt, ut pro scriptis habeantur, et deletis contra terminos omnes aequationis primae. Nam quae scimus deletum iri ea scribi non est necesse. 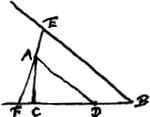 [Fig. 3.]
Esto datus angulus EBF, et intra ipsum A punctum. Oporteatque ducere EAF brevissimam quae per punctum A Intra datum angulum duci possit.Ga naar voetnoot15)
Sit AD parallel. EB, et AC perpend. ad BF. Et lineae datae vocentur a ∞ BD; b ∞ DA; c ∞ DC et ponatur quoque EF ∞ d quasi data esset. sitque DF ∞ x, quaesita. BF (x + a ad FE (d) ut DF (x) ad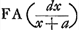 12.2. Eucl.Ga naar voetnoot16) q.AD(bb) + q.DF(xx) - q.FA
12.2. Eucl.Ga naar voetnoot16) q.AD(bb) + q.DF(xx) - q.FA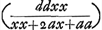 ∞ 2 ▭ FDC(2cx) ∞ 2 ▭ FDC(2cx)
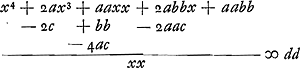 | |
[pagina 67]
| |
Sit jam x + y ∞ x et subrogetur ubique ejus quantitas, in quantum opus erit, fit aequatio comparanda cum priori. 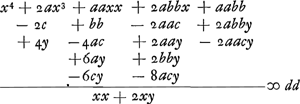 adaequanturGa naar voetnoot17) Post alternas per denominatores multiplicationes aequaliumque ablationem fit 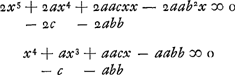 Quando c esset ∞ o hoc est angulus EBF rectus, aequatio dividi posset per x + a, fieritque x3 - abb ∞ o sicut antea quoque inventum est.Ga naar voetnoot18) Quando autem a ∞ b; dividi potest per x - a, ideoque tum x ∞ a et tum planum est problema. | |
[Troisième Partie.]Problematis hujus constructio superius allataGa naar voetnoot19) hic demonstranda est, erat autem hujusmodi.
Juncta AB [Fig. 4.] dividatur bisariam in L; positâque regula ad punctum | |
[pagina 68]
| |
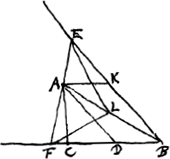 [Fig. 4.]
A, ea tam diu moveatur donec positionem habeat FE, faciens LE, LF inter se aequales, fietque EF omnium brevissima quae per punctum A intra angulum EBF duci possunt. Idem quoque factum fuit supra per intersectionem hyperboles et circuli,Ga naar voetnoot20) sed utrimque eadem est ratio. Ducantur AD, AK parallelae EB, BF, et AC perpendicularis in FB. et nomina linearum serventur quae posita fuere.Ga naar voetnoot21) Ergo existentibus FL, LE inter se aequalibus ostendendum est 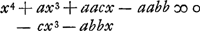 Quia in triangulo AEB ducta est EL ad mediam bafin AB erunt quadrata AE et EB dupla simul quadratorum AL et LE, similiterque in triangulo AFB erunt quadrata AF, FB simul dupla quadratorum AL, LF. Ergo si qu.LF aequale qu.o LE, erunt qu.a AF, FB simul aequalia qu.is AE, EB.
p. 12.2. Elem.Ga naar voetnoot16) 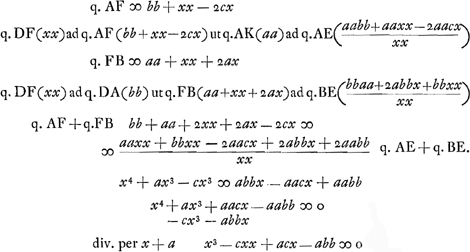 |
|

