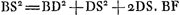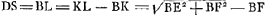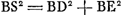Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 57]

XIII.¹⁾
[1652].

[Première partie.]²⁾

16 Aug. 1652.

Rhombo dato, et uno latere producto, aptare sub angulo exteriori lineam magnitudine datam quae ad oppositum angulum pertineat.

[Fig. 1.]

Sit datus rhombus ADBC, cujus productum latus DB. Et data sit linea G. Oportet ducere rectam ANF, ut pars intercepta NF sit datae G aequalis.

Ducatur diameter AB, et quadratis ex G et AB sit aequale quadratum AH, et ducatur HE ipsi BA parallela. et AE ipsi G ponatur aequalis, eademque producatur ad F. Dico NF datae lineae G aequalem esse. Quod autem ad HE poni potest AE aequalis G hinc manifestum est. Etenim quadratum AH majus est

1) La pièce que nous avons divisée en deux parties, est empruntée aux pages 213-215 du manuscrit N^o. 12. Elle a été reproduite sous une rédaction légèrement modifiée dans les ‘Illustrium quorundam problematum constructiones’ de 1654 à la suite des ‘Probl. VI et VII’ et sous l'en-tête ‘Utrumque praecedentium Aliter’; et de même dans une lettre à van Schooten du 10 déc. 1653 (p. 256-257 du T. I). L'analyse nous manque, mais il nous semble probable que la construction présente a résulté d'un remaniement de celle trouvée en 1650; voir la page 241 du Tome XI. En effet, la droite HE est identique avec la droite LM de la figure de la page citée. On le vérifie en prolongeant LM jusqu'à ce qu'elle coupe AD en un point S et en calculant , où . Alors on trouvera ; donc BS est égal à la droite AH de la figure présente.

2) Voir, pour d'autres solutions du même problème, la pièce N^o. VIII des ‘Travaux’ de 1650 (p. 239 du Tome XI), la pièce N^o. VI de 1652 (p. 26 du Tome présent) et la note 10 de cette pièce N^o. VI.

[p. 58]

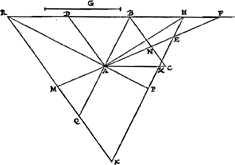
quadratis AX et XH quum sit angulus AXH obtusus. sed idem qu. AH. aequale ponitur qu.^is AB seu HX et G. itaque qu. G seu AE majus est quadr.^o AX. unde apparet intersectionem E accidere inter puncta H et X. Producatur BD et ponatur ipsi aequalis DR. et sit RK parallela DA vel BC, eique occurrant productae FA, BA, HE, in punctis M, Q, K. Et jungatur RA, et producatur ad P.

Quoniam igitur DR aequalis est DB et RQK parallela DA, erit et MA aequalis AN, et QA aequalis AB, angulus autem BAR rectus quum sit in semic.^lo quare et anguli ad P, nam BQ, HEK parallelae sunt: et erit HP aequalis PK.

Est itaque qu. AH aequale qu.^o AE una cum rectangulo HEK. sed idem qu. AH aequale est qu.^is ex AE et AB: itaque qu. AB aequale est ei quod sub KE, EH. quare KE ad AB ut AB ad EH; verum ut KE ad AB seu QA ita est EM ad MA, et ut AB ad EH ita est AF ad FE, igitur EM ad MA ut AF ad FE, et EA ad AM ut EA ad EF. Itaque aequalis est EF ipsi AM, quare et ipsi AN. ideoque et FN ipsi AE hoc est datae G. quod erat demonstrandum.

[Seconde partie.]³⁾

Rhombo dato et duobus contiguis lateribus productis, aptare sub angulo interiori rectam magnitudine datum quae ad oppositum angulum pertineat.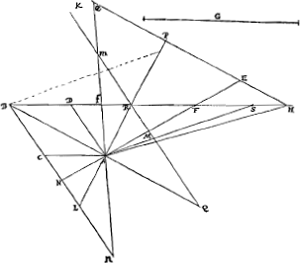

[Fig. 2.]

Oportet autem datam lineam non minorem esse eâ quae ad dictum oppositum angulum pertinens diametro rhombi ad angulos rectos constituta est, et à productis lateribus intercipitur.

Esto datus rhombus ADBC, et ductâ diametro AB secet eam ad angulos rectos linea RL occurrens utrinque productis lateribus BD, BC. Data autem sit, ipsâ RL non minor, G recta, cui aequalem ponere oporteat FAN.

In schemate adjecto sicuti propositum est, eadem constructio est et demonstratio, quae in casu praecedenti.⁴⁾

3) Voir, pour d'autres solutions du problème, la pièce N^o. VII (p. 32) du 11 février 1652; la note 16 de cette pièce N^o. VII, et la pièce N^o. IX (p. 42) du 17 février 1652.

4) Voir la première partie de la pièce présente.

[p. 59]

Illud autem hic aliter ostendendum est, quod ad lineam HE poni potest AE ipsi G aequalis. sit RS aequalis RB et jungatur AS. Quoniam igitur in triangulo BAS à vertice ad mediam basin ducta est AR, erunt quadrata BR et RA, simul sumpta, hoc est qu. BA cum duplo qu.^o AR, subdupla quadratorum BA, AS. itaque qu. AB bis sumptum cum quadruplo qu.ⁱ AR, hoc est cum qu.^o RL, aequatur qu.^is BA, AS. quare ablato utrimque qu.^o BA, erit qu. AS aequ. quadratis BA et RL, ac proinde minus quam quadr. AH. Est igitur AS minor quam AH; sed major est quam AR: itaque punctum S cadit inter R et H. ergo RH major quam RS vel RB. et quum propter triangulos similes, sit RH ad HP ut RB ad BA, erit quoque HP major quam BA, et quadr. HP majus quadr.^o AB. at qu. HP cum qu.^o PA aequatur qu.^is BA et G; ergo quum qu. HP sit majus quam qu. AB, erit invicem PA qu. minus quam qu. G. patet itaque quod si centro A circumferentia describatur semidiametro AE aequali G, ea lineam HE in duobus punctis secabit.⁵⁾

5) C'est-à-dire aux points E et e de la figure; lesquels amènent les solutions FN et fn.