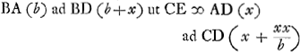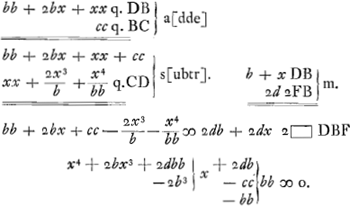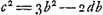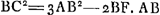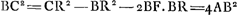Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 54]

XII.¹⁾
1652.

16 Mart. 1652.

Datis positione lineis AD, AE angulum comprehendentibus, et puncto extra angulum, C. Ducere CED rectam, et facere AD ipsi CE aequalem.

Fig. 1.

Factum jam sit, et ducatur CB parallela EA. et sit CF ipsi DB ad angulos rectos.

Vocetur AB b; BC c; BF d; DA x.

1) La pièce occupe les pages 210 et 211 du manuscrit N^o. 12. Elle contient une troisième solution du problème des deux moyennes proportionnelles avec l'analyse qui l'a amenée. Cette solution a été reproduite, avec de légères modifications, dans les ‘Ill. quor. prob. constr.’ de 1654, comme la troisième et dernière solution du ‘Probl. III. Datis duabus rectis duas medias invenire.’

[p. 55]

Si dbb - ½ccb - ½b³ quod id est quod in quantitate cognita ductum est in 2b, aequale esset - 2b³ + 2dbb, quod in x ductum est; tota aequatio dividi posset per x + 2b et fieret x³ + 2dbb - 2b³ ∞ o et 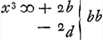adaequantur igitur dbb - ½ccb - ½b³ ∞ - 2b³ + 2dbb fit cc ∞ 3bb - 2db. Si ergo haec aequalia à principio ponantur, erit 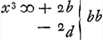unde erit DA una mediarum duarum inter AB et duplam AF. Nam dupla AF est 2b - 2d. Datis itaque duabus lineis poterimus duas medias proportionales invenire eo modo qui subjungitur.

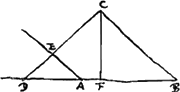
Duas medias proportionales invenire.

Sint datae AB et Q quibus duas medias invenire opus sit. Dimidiae Q ponatur aequalis AF, et sit BR aequalis AB. Et ex F erigatur perpendicularis FC, et ipsi RA aequalis ponatur RC, et jungatur BC,²⁾ eique parallela ducatur AE. Et applicatâ regula ad punctum C, moveatur ea quousque positionem habeat CD, faciens AD aequalem CE.

Dico inter AB et Q duas medias inventas esse CE, ED.³⁾

Jungatur enim CA. Igitur quia aequales sunt RA, RC et angulus CFA rectus, erit RA ad AC ut AC ad duplam AF, hoc est Q. ac proinde quadratum CA aequale contento RA, Q. quadratum autem CA cum qu.^o AD et duplo ▭^o DAF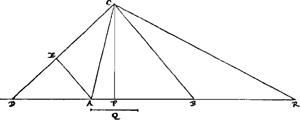

[Fig. 3.]

hoc est rectang.^o DA, Q aequatur qu.^o DC (12. 2. El.)⁴⁾ Igitur qu. DC aequabitur qu.^o DA una cum rectangulis DA, Q; AR, Q; hoc est una cum contento DR, Q. Quadratum vero DA aequale est qu.^o EC; igitur ab aequalibus aequalia auferendo erit contentum DR, Q aequale differentiae qu.^orum

2) L'analyse qui précède, exige qu'on ait ; c'est-à-dire . Or d'après la construction indiquée on a, en effet,.

3) Ici, comme dans la pièce précédente (voir la note 4, p. 50), la seconde moyenne proportionnelle ne s'est pas présentée pendant le traitement analytique du problème; mais elle a été cherchée et découverte après coup.

4) Voir la note 15, p. 29 du Tome présent.

[p. 56]

DC, CE. Quia autem DB et DC lineae similiter dividuntur in punctis A et E, est quadr. DB ad qu. AB ut qu. DC ad qu. CE; et dividendo et convertendo igitur qu. AB ad differentiam qu.^orum DB, AB ut qu. EC ad differentiam qu.^orum DC, CE; et permutando. Est autem differ.^a qu.^orum DB, BA aequalis rectangulo RDA, nam hoc duobus ▭^is DAB et qu.^o AD aequale est: Et dictum est differentiam qu.^orum DC, CE aequari contento DR, Q. Itaque quadr. AB est ad EC qu. ut ▭ RDA ad contentum RD, Q, hoc est ut AD ad Q. Ut autem qu. AB ad qu. EC ita est AB ad ED longitudine: nam BA est ad AD, hoc est, CE, ut CE ad ED. Igitur ut AB ad ED ita est AD ad Q. Et permutando, ut AB ad AD ita ED ad Q. Atqui ut AB ad AD hoc est CE, ita diximus esse CE ad ED. Ergo ut AB ad CE ita CE ad ED et ED ad Q. Quod erat ostendendum.

19 Mart. 1652.⁵⁾

5) La date se rapporte, d'après une légère différence dans l'écriture, à la démonstration géométrique à commencer par le mot ‘Jungatur.’