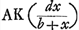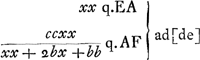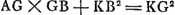Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656
(1910)–Christiaan Huygens–
[pagina 49]
| |
XI.Ga naar voetnoot1)
| |
[pagina 50]
| |
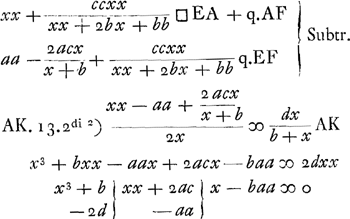 Si ponatur b ∞ 2d et a ∞ 2c erit x3 ∞ baa hoc est, erit AB et AD inter, una duarum mediarum proportionalium AE. Hinc inventae sunt constructiones duae sequentes.
10 mart. 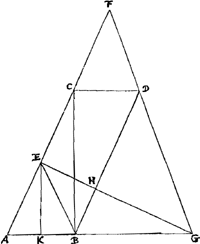 [Fig. 2.]
Duas medias proportionales invenire inter datas lineas.
Sint datae duae AB et AC, quae sic disponantur ut angulus CBA sit rectus. Compleatur parallelogrammum ABDC, et producatur AB. Et divisâ AC per medium in E, ducatur EHG ita ut abscissae HD sit aequalis HG. Hoc autem vel sepius tentando assequi possumus, vel ope Hyperboles sicut infra docebimusGa naar voetnoot3) Sed factum jam ponatur, et ducatur GDF occurrens productae AC in F. Dico duarum CA, AB medias esse proportionales BG et FC.Ga naar voetnoot4) Jungatur enim EB et sit EKGa naar voetnoot5) ipsi AB ad angulos rectos. Quia igitur BE aequalis EA, erit quoque BK aequalis | |
[pagina 51]
| |
KA. Quum itaque AB in aequalia dividatur ad K, et adjecta sit ipsi linea BG, erit rectang. AGB cum quadrato ex KB aequale quo ex KG;Ga naar voetnoot6) et addendo utrinque quadr. KE, erit rectang. AGB una cum quadratis BK, KE, hoc est una cum quadrato BE, aequale quadratis GK et KE, hoc est quadrato EG. Similiter quia AC in aequalia dividitur in E et adjecta est linea CF, erit rectang. AFC cum qu.o EC aequale qu.o EF. Quadratum autem EF aequale est qu.o EG; (quia et DH ipsi HG aequalis, et similia sunt triangula DHG et FEG)Ga naar voetnoot7) Erit ergo rectangulum AFC cum qu.o CE aequale rectangulo AGB cum quadrato BE. Atqui quadr. BE aequale est EC quadrato; et reliquum igitur rectangulum AFC rectangulo AGB aequale erit. Quare sicut FA ad AG ita BG ad CF. ut autem FA ad AG ita est DB ad BG, et ita quoque FC ad CD. Igitur ut DB hoc est AC ad BG ita BG ad FC et FC ad CD hoc est AB. Itaque inter AC ut AB duae inventae sunt mediae BG, FC. quod erat faciendum. | |
[pagina 52]
| |
Aliter.Ga naar voetnoot8)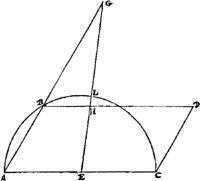 [Fig. 3.]
Super majori datarum AC [Fig. 3.] semicirculusGa naar voetnoot9) describatur, et ponatur AB minori datarum aequalis, et compleatur parallelogrammum AD; productâque AB, ducatur ex centro E recta EHG, eâ ratione ut ipsi HG sit aequalis HD; secet autem circumferentiam in L. Dico duabus AC, AB medias proportionales inventas esse BG, GL. Cujus quidem demonstratio ex praecedenti manifesta est. Namque in priori figuraGa naar voetnoot10) si aequales EF, EG, erunt propter triangula similia etiam HD, HG aequales; et contra. Ex quo manifestum est utroque modo lineam BG eandem reperiri. Porro FC differentiam fuisse constat linearum EF, EC, hoc est duarum EG, EC: atque ea hìc est LG. Subjicitur autem et alia demonstratio.Ga naar voetnoot11) Quod autem dictum est in priori constructione, lineam FDGGa naar voetnoot12) ope hyperboles duci posse, ut EF, EG sint aequales, hinc constabit. Si namque sumatur GN ipsi FD aequalis, manifestum est punctum N fore ad hyperbolen quae discribitur per D punctum, circa asymptotos AF, AG. Verum idem punctum N est quoque ad circuli circumferentiam quae describitur centro E, radio ED. Itaque datum est positione punctum N. Et D datum est: Ergo et linea FG quae per utrumque ducitur positione datur. Et Compositio manifesta est.
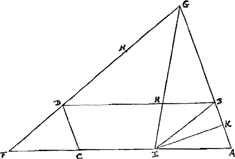
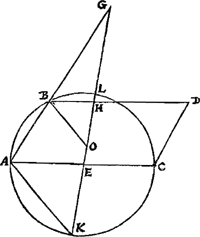
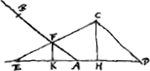
Perficiatur circulus ALCK [Fig.4], et producatur GE usque ad circumf.m in K. | |
[pagina 53]
| |
 [Fig, 4.]
Et jungatur AK, eique parallela ducatur BO. Itaque similes sunt trianguli AEK, BHO; et quia AE aequalis EK, etiam BH, HO aequales erunt. Sed et HG, HD inter se aequales sunt; igitur tota OG aequalis BD, hoc est diametri AC vel LK. Et ablatâ communi LO, relinquuntur aequales inter se GL, OK. Est autem rectangulum KGL aequale rectang.o AGB, ideoque ut KG ad GA ita est BG ad GL. Sed ut KG ad GA ita propter triang.os similes est quoque OG ad GB, et ita reliqua OK hoc est LG ad BA. Ergo ut OG hoc est AC ad GB ita BG ad GL et LG ad AB. Quod erat demonstrandum.
5 Jun. 1652.Ga naar voetnoot13) |
|


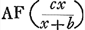 ; ergo
; ergo 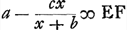 vel
vel 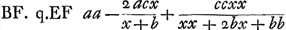 .
ED (b + x) ad DH (d) ut EA (x) ad
.
ED (b + x) ad DH (d) ut EA (x) ad