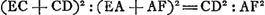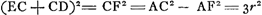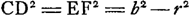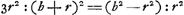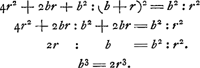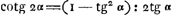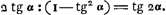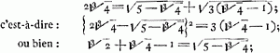Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 45]

X.¹⁾
1652.

Kal. Mart 1652.

Cubum invenire dati cubi duplum.

Sit datus cubus cujus latus AB. Radio AB semicirculus describatur AFDC, et positâ AF aequali ipsi AB jungatur FC. deinde secundum A punctum regula moveatur



inter F et C donec inveniatur FE abscissa aequalis subtensae DC. quod quidem ponatur factum esse, et regulam habere positionem AED, ut sit FE ipsi DC aequalis. Dico cubum ex AE duplum esse cubi ex AB.

Producatur enim CA et sit AG ipsi AE aequalis. Propter triangulos similes igitur est EC ad CD hoc est EF, ut EA ad AF. Et componendo CF ad FE ut utraque simul EA, AF, hoc est, GB ad AF, et permutando CF ad GB ut FE ad AF. Quare ut CF quadratum ad quadr. GB ita quadr. EF ad qu. FA. Et componendo ut quadrata ex CF et ex GB ad qu. ex GB, ita quadrata EF et FA, hoc est, quadratum EA ad qu. AF. Quadrata autem ex CF et GB simul aequalia sunt rectangulo GCA et qu.^o ex AG: Quadratum enim GB aequale est rectangulo

1) La pièce a été empruntée aux pages 203-206 du manuscrit N^o. 12. Elle contient une solution exacte du problème de la duplication du cube; supposant qu'il soit possible de construire la figure du texte, où AF = AB, de telle manière qu'on ait EF = DC. En outre elle donne une solution approximative du même problème. Ces solutions ont été reproduites, sous une autre rédaction, dans les ‘Illustrium quorundam problematum constructiones’ de 1654, comme ‘Problema II’.

[p. 46]

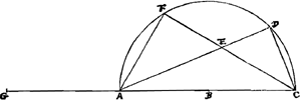
CGA et quadr.^o AB seu AF (10.2.).²⁾ quare addito utrinque qu^o FC, erunt quadrata GB, FC simul aequalia rectangulo CGA una cum quadratis AF, FC, hoc est unà cum quadrato AC. Estque rectangulum CGA cum qu.^o AC aequale rectang.^o GCA cum qu.^o GA. Itaque et quadrata GB, FC simul aequalia rectangulo GCA cum qu.^o GA, sicut diximus.

Ut igitur rectang. GCA cum qua. AG ad qu. GB ita est qu. EA ad qu. AF, hoc est, ita qua. GA ad qu. AB. Et permutando, ut rectang. GCA cum qu.^o AG ad qu. AG ita qu. GB ad qu. AB. Et dividendo, ut rectang. GCA ad qu. AG ita qu. GB dempto qu.^o AB hoc est rectang. CGA ad qu. AB. Et permutando rursus ut ▭ GCA ad ▭ CGA, hoc est ut AC ad AG ita qu. AG ad qu. AB. Quare cubus ex AG seu AE duplus erit cubi AB. Quod erat dem.³⁾

Lineam verò AD ita ducere ut sit DC subtensa aequalis abscissae EF, atque adeo cubum duplicare vel cuicunque solido dato aliud simile duplum constituere, eâ poterimus ratione quam deinceps trademus;⁴⁾ quâ quidem problema quod naturâ solidum est per plana solutum videri posset, ni demonstratio contrarium evinceret.

Etenim positâ sicut ante AF aequali AB, Hoc est posito arcu AF triente periphaeriae AFDC: Si porro arcus CD statuatur ejusdem peripheriae quadrans, junganturque FC, DA dico cubum ex AE majorem quidem fore cubo duplo ex AB. at si pars bismillesima ex AE recidatur, residui cubum minorem fore duplo cubi AB.

Manifestum enim est AE secantem esse anguli partium 37½ qualium peripheria

2) Lisez (6.2. Elem.), comme on le trouve dans les ‘Ill. quor. probl. constr.’, au lieu cité dans la note précédente. C'est la ressemblance du début des deux propositions 10.2 et 6.2 qui a causé l'erreur. Voici d'ailleurs cette dernière proposition: ‘Si recta linea bifariam secetur, & illi recta quaedam linea in rectum adiiciatur: Rectangulum comprehensum sub tota cum adiecta, & adiecta, vna cum quadrato ex dimidia, aequale est quadrato à linea quae tum ex dimidia, tum ex adiecta componitur, tanquam ab vna, descripto.’ (Clavius, p. 178.)

3) A cause de la forme que Huygens a cru devoir donner à cette démonstration, elle semble plus compliquée qu'elle ne l'est réellement. De la similitude des triangles DEC et FEA Huygens déduit la proportion: ; mais puisqu'on a par construction DC = EF et AF = AB, on trouve, en posant AB = r, AE = b, ; . La proportion peut dont s'écrire:



d'où l'on déduit successivement en appliquant, à l'exemple de Huygens, les propriétés bien connues des proportions:

4) Voir la construction approximative, qui va suivre.

[p. 47]

AFDC 180 continet. nam AF arcus est partium 60, et CD partium 45; itaque FD, 75. at angulus FAD subduplus est ejus qui ad centrum, itaque FAD angulus est partium 37½. ubi dicebamus.⁵⁾ AF autem aequalis est ipsi AB radio; qui statuatur partium 100000. ad demonstrationem vero hisce duobus theorematibus opus habebimus quorum posterius est Pellij.⁶⁾

Theor. 1. Si cujuslibet arcus, qui minor sit 45 partibus, tangentis quadratum auferatur à quadrato radij; residuum dividatur per tangentis ejusdem duplum, orietur tangens complimenti arcus illius dupli.⁷⁾ Vel sic. Duplum tangentis est ad summam tangentis et radij, sicut eorundem differentia ad tangentem complementi arcus prioris dupli.

Theor. 2. Si tangens cujuslibet arcus minoris 45 partium, ducatur in duplum quadratum radij. Productum dividatur per differentiam quadratorum radij et tangentis, orietur tangens arcus dupli⁸⁾

Esto itaque arcus alicujus ignoti tangens 26800; invenietur per theor. secundum arcus dupli tangens 57747 &c. Sed haec major est tangente 30 gr. nam tangens 30 gr. est ad radium potentia ut 1 ad 3, et longitudine ut 57735 ad 100000. Itaque arcus duplus ignoti arcus major est quam 30 gr. ac proinde arcus cujus tangens 26800, major quam 15 gr.

Esto denuò alterius alicujus arcus tangens 76700, Erit per Theor. nostrum, tangens complimenti arcus istius dupli 26839. Haec autem tangens major est quam 26800. Ergo dictum complimentum apparet majus esse quam 15 gr. Atque ideo arcus iste cujus dupli complementum erat, id est, arcus cujus tangens ponebatur 76700, minor erat quam 37½ gr. nam bis 37½ hoc est 75 gr. una cum gr. 15 quadrantem circuli explent. Itaque 76700 minor est tangente 37½ gr. hoc est minor linea FE, nam haec tangens est 37½ gr. Quadratum igitur ex AF quae est 100000 una cum qu.^o ex 76700 simul minora sunt qu.^o ex AE. Illis autem duobus simul quadratis adhuc minus est quadr. ex 126000; itaque

5) Huygens a biffé toute la partie de la pièce qui suit; ce qu'il fit probablement lorsqu'il prépara en 1654 la publication des ‘Illustrium quorundam problematum constructiones’. Ajoutant alors en marge le mot ‘Puerilia’, il remplaça toute cette partie par la seule phrase: Ergo AE ex tab. sin. 126047. Unde propositum facile comprobatur.’ Comparez les ‘Ill. quor. probl. constr.’ au ‘Problema II.’
Toutefois, nonobstant l'annotation de Huygens, nous n'avons pas supprimé cette partie du texte parce qu'il nous semblait curieux de montrer jusqu'à quel point Huygens, à cette époque, croyait devoir se conformer à la manière de démontrer des anciens, même dans une matière qui s'y prêtait fort peu; déguisant ainsi entièrement la marche qu'il avait suivie pour arriver à ses résultats.

6) Voir, sur Pell, la note 2, p. 14 du T. I. Il s'agit ici du théorème principal de l'ouvrage cité dans la note 5, p. 176 du T. I. On le rencontre la première fois à la page 13 de cet ouvrage.

7) En notation moderne; .

8)

[p. 48]

126000 omnino minus erit quam AE. atqui cubus ex 126000 qui est 2000376000000 major est duplo cubo ex AF seu ex 100000. Igitur multo magis cubus ex AE major erit duplo cubo ex AF seu ex AB. quod erat primum.

Nunc autem ostendemus, lineam AE diminutam parte sui bismillesima, producere cubum minorem duplo cubo ex AB.

Sit tangens alicujus arcus 26790. Invenietur per Theorema 2^dum tangens arcus dupli 57722 &c. Haec autem minor est tangente gr. 30, quam suprà diximus esse 57735. Ergo arcus cujus tangens ponebatur 26790 minor est quam 15 gr.

Rursus alterius alicujus arcus sit tangens 76737; Ergo per theorema 1^mum erit tangens complimenti arcus istius dupli 26789 &c. Haec verò tangens minor est quam 26790. Ergo cum 26790 ostensa fuerit minor tangente gr. 15, erit omninò 26789 minor quoque tangente gr. 15. Itaque cujus arcus tangens erat 76737, ejus arcus dupli complimentum minus est quam 15 gr. Ideoque dictus arcus duplus major est quam 75 gr. et ipse arcus cujus tangens 76737, major quam 37½ gr. Est autem FE tangens 37½ gr. Ergo FE minor quam 76737. Quadratum igitur ex AF et ex 76737, simul majora erunt quadrato ex AE.

Dictis autem quadratis duobus majus est quadratum quod fit ex 126050; Itaque 126050 omnino majus erit quam AE. Cubus autem ex 125990 minor est duplo cubo AB. Major igitur est ratio 126050 ad 125990 quam ipsius AE ad latus cubi qui duplus sit cubi ex AB. Sed ratione 126050 ad 125990 seu 12605 ad 12599 adhuc major est ratio 2000 ad 1999. Itaque ratio AE ad dicti cubi dupli latus multo minor est ratione 2000 ad 1999. Si igitur AE divisa sit in partes aequas bismille; unâ earum demptâ, reliqui cubus minor erit duplo cubo ex. AB. quod erat ostendendum.

2 mart. 1652.

Subtensa arcus aequalis arcubus AF et DC, est latus cubi subdupli ejus qui ex AC.⁹⁾

9) La remarque a été ajoutée plus tard. Il s'agit naturellement de la solution exacte. Appliquant la formule bien connue:
qu'on déduit du théorème de Ptolemée, on trouve, d'après les calculs de la note 3, qu'elle exige:




ce qu'on vérifie aisément en élevant au carré.
La remarque est donc juste.