Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 38]

VIII.¹⁾
1652.

14 Febr. 1652.

Pappus in principio libri 7.ⁱ ubi de Inclinationibus, problema universale refert.²⁾ Duabus lineis positione datis inter ipsas ponere rectam lineam magnitudine datam, quae ad datum punctum pertineat. Quod quidem problema solidum est nisi cum ductis ex puncto dato parallelis ad datas lineas positione, quadratum vel rhombus constituitur. Quos casus jam exposuimus,³⁾ et quomodo optimè construantur docuimus. Cum verò solidum est, unam quidem problematis partem resolvit Pappus prop.^e 31 libri 4.ⁱ⁴⁾ ubi angulum trifariam secare docet.⁵⁾ aliorum tamen inventa proponens.⁶⁾ Quamquam autem parallelogrammum rectan-

1) Dans cette pièce, empruntée aux pages 197-199 du manuscrit N^o. 12, Huygens reprend (voir les pièces N^o. II et N^o. VI, pp. 13 et 26) le problème solide de mener par un point donné B [Fig. 1] une droite sur laquelle les côtés d'un angle donné CNA découpent un segment RD de longueur donnée. Cette fois il traite le cas où le point donné se trouve à l'intérieur de l'angle donné et le résoud à l'aide d'une hyperbole, coupée par un cercle. Ensuite il s'occupe de la ‘determinatio’ du problème, c'est-à-dire, de la détermination des conditions sous lesquelles la solution est possible; ce qui amène un autre problème solide: celui de trouver la longueur minimale du segment découpé RD.

2) Voir la note 2, p. 239 du Tome XI. Dans l'édition de Hultsch on trouve le passage en question au T. II, p. 670-671.

3) Voir les pièces N^o. IV (p. 19), VI (p. 26) et VII (p. 32).

4) Consultez la note 9, p. 228 du Tome XI. Chez Hultsch on trouve la proposition indiquée au T. I, p. 272-275.

5) Voir la ‘Prop. 32’ où Pappus applique la construction de la proposition 31 mentionnée à la trisection de l'angle (p. 62 recto et verso de l'édition de Commandin; Hultsch T. I, p. 274-277).

6) Allusion aux phrases suivantes qui précédent chez Pappus les ‘Prop. 31 et 32’: ‘antiqui Geometrae problema jam dictum in angulo,’ [la trisection de l'angle] ‘quod natura solidum est, per plana inquirentes invenire non potuerunt. nondum enim ipsis cognitae erant coni sectiones, & ob eam causam hesitarunt. Postea nero angulum tripartito diuiserunt ex conicis, ad inuentionem infrascripta inclinatione’ [la prop. 31] ‘utentes’. (Commandin, p. 61 recto; Hultsch, T. I, p. 273).

[p. 39]

gulam constituat, eâdem tamen ratione ope hijperboles componitur, etiamsi rectangulam non sit.⁷⁾ Nunc autem eum casum pertractabimus cum punctum intra angulum datum est, nam et is ope hijperboles expediri potest. Sed et aliam pro rhombo constructionem hinc deducemus.⁸⁾

Esto angulus N et intra ipsum detur punctum B, oporteatque ducere RBD datae lineae aequalem. Factum jam sit, et ducantur BA, BF parallelae ipsis NF, NA, et posita FE ipsi FN aequali, sit quoque EH parallela NA. Producatur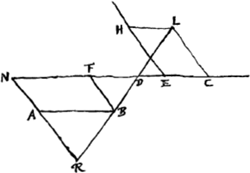

[Fig. 1.]

autem RD et ut ipsi RD aequalis BL et ducantur LH, LC ipsis quoque NF, NA parallelae.

Similia igitur constat fieri ∆^la LDC, RBA. Sed latus LD aequale est lateri RB, quoniam tota BL toti DR aequalis: Itaque et LC aequalis ipsi AR, et CD aequalis ipsi AB seu NF, hoc est, ipsi FE. et ablata communi DE, erit EC aequalis DF. Ut autem DF ad FB ita est BA ad AR. Ergo quum ipsi FD sit aequalis EC et ipsi AR aequ. LC hoc est HE erit quoque ut EC ad FB ita BA ad HE. quare contentum EC, HE aequale contento FB, BA. Est itaque punctum L ad hijperbolen sed et ad circuli circumferentiam, nam datum est B punctum, et data BL aequalis ipsi RD. datum igitur est positione punctum L; dataque propterea etiam linea LB quare et DBR positione data erit, nam cum illa coincidit.

Componetur autem hoc modo. Ductâ EH ut in resolutione dictum est, jungatur BE [Fig. 2], eaque producatur et sit ipsi EB aequalis EG. Dein per punctum G, circa asymptotos EH, EK describatur hijperbole LG. Centro autem B et semidiametro BL quae aequalis sit lineae datae, describatur circumferentia LO. quae si hijperbolen non attingit, problema construi non poterit, quod data linea sit aequo brevior.

Si vero contingat circumferentia LO hijperbolen LG, erit linea data omnium quae problema efficere possunt brevissima sin denique circumferentia hijperbolen

7) En effet, le raisonnement de Pappus, reproduit dans la note 9, p. 228 du Tome XI, reste valable quand on remplace, dans la figure 1 de la page 226, les rectangles ABCD et AK par des parallélogrammes. Seulement l'hyperbole décrite par le point K ne sera plus équilatère.

8) Voir pour la solution en question la pièce N^o. IX, qui suit.

[p. 40]

secet, ut hìc in punctis L et O, ducantur inde rectae LBR, OBQ, dico partes earum interceptas DR, SQ problema efficere, hoc est aequales esse ipsi BL, seu lineae datae.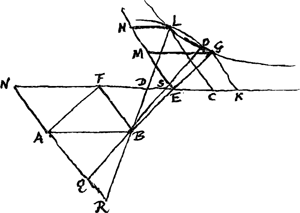

[Fig. 2.]

Ducantur enim HL, LC ipsis EK, EH parallelae, sicut et GM, GK. Quia igitur EG ipsi EB hoc est ipsi FA aequalis est, manifestum quoque aequale esse et simile parallelogr. MGKE parallelogr. NFBA. Propter hijperbolen verò est contentum LC, CE aequale contento EK, KG hoc est contento EF, FB, quare erit ut LC ad FB hoc est ut CD ad DF ita FE ad EC. linea igitur FC in eandem proportionem divisa est puncto D et puncto E, ideoque erit CD ipsi FE aequalis hoc est ipsi AB sunt autem CD et AB latera similiter posita similium triangulorum CDL, ABR; ergo et DL ipsi BR aequalis erit, et tota BL aequalis DR. sed BL aequalis est lineae datae. Itaque factum est quod proponebatur. Eâdem ratione potest ostendi QS ipsi BO seu BL aequalis.

Determinatio autem problematis solida est, nam solâ quidem regulâ et circino inveniri nequit omnium brevissima per punctum B ducta intra angulum N. Qui si rectus est, adeo ut parallelogr. NB sit rectangulum, tum eodem modo brevissima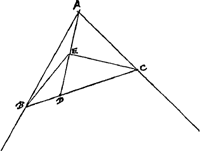

[Fig. 3.]

per punctum B ducetur, quo duae mediae proportionales inveniuntur inter lineas FN, NA.⁹⁾ Sicut Hero vel Nicomedes.¹⁰⁾ Sed Heronis quidem inventum etiam ad angulos non rectos hic extendi potest. Etenim dato intra angulum BAC [Fig. 3] puncto D, si oporteat brevissimam ducere omnium quae per idem punctum intra eundem angulum duci possunt; jungatur DA. et in duo aequalia dividatur puncto E. Tum applicetur regula puncto D, eaque moveatur donec reperiantur EB, EC aequales, quod circino sepius

9) Voir la pièce N^o. XIV aux pages 62-63, où Huygens démontre que la droite EF de la figure de la page 62 citée sera minimale, quand on a AF³ = BA × BC².

10) Consultez pour la construction de Nicomède, la ‘Compositio Nicomedis,’ p. 15 de la pièce N^o. II. En effet, la droite KE de la figure 2 de cette p. 15, n'est autre, pour le point H, que la droite cherchée de longueur minimale. Dans la construction de Héron, où il s'agit de même de trouver les deux moyennes proportionnelles entre les côtés GL et LA (voir toujours la figure de la p. 15) d'un rectangle donné, la droite LH est divisée en deux parties égales par le point I et la droite EK est supposée construite de manière qu'on ait IK = IE; alors, comme dans la construction de Nicomède, on aura GL: AE = AE : GK = GK : LA, et la droite KE sera donc identique à la droite cherchée. (On trouve cette construction de Héron p. 6 recto et verso de l'édition de Commandin des ‘Collectiones mathematicae’ de Pappus; Hultsch, T. I, p. 62-65).

[p. 41]

tentando facile assequemur, et jungatur BC, Eritque haec omnium brevissima:¹¹⁾ atque hac quidem ratione determinari problema potest.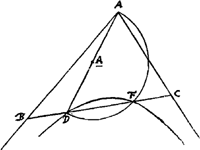

[Fig. 4.]

Aliter quoque ijsdem positis omnium brevissima ducetur, hoc modo.

Per D punctum, circa asymptotos AB, AC describatur hijperbole DF. et super AD semicirculus, qui ubi hijperbolen secabit in F, inde ducatur FD et producatur utrimque, atque haec propositum efficiet, eritque BDC omnium brevissima, quae per D duci possunt.¹²⁾

Aliter quoque, non descriptâ hijperbolâ, sed semicirculo tantum, moveatur regula secundum punctum D, donec inveniantur BD, FC inter se aequales.

Problema hoc de minima inferius resolutum vide, et calculo demonstratum.¹³⁾

11) Voir, pour la démonstration, la troisième partie de la pièce N^o. XIV, p. 67.

12) Pour déduire cette nouvelle construction de celle de la figure 3, abaissons dans cette dernière figure sur BC les perpendiculaires EE₁ et AA₁. Alors on aura BE₁ = E₁C, DE₁ = E₁A₁ et par suite BD = A₁C; donc le point A₁, correspondant au point F de la figure 4, se trouvera à la fois sur le cercle décrit sur AD comme diamètre et sur l'hyperbole passant par D et ayant BA et AC pour asymptotes.
D'ailleurs les méthodes modernes conduisent aisément à ce même résultat. En tournant le segment BC autour du point D (Fig. 4) d'un angle infinitésimal ε et en égalant à zéro l'accroissement (DC cotg C - BD cotg B) ε, on trouve; BD : DC = tg B : tg C = AC/cos B : AB/cos C = AC cos C : AB cos B = CF : FB, où F est le pied de la perpendiculaire abaissée de A sur BC; ainsi le segment BC doit être divisé par les points D et F dans un même rapport, d'où il suit: BD = FC.

13) Voir la seconde et la troisième partie de la pièce N^o. XIV, p. 65-68. La phrase a été ajoutée plus tard.