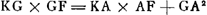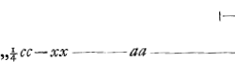Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656
(1910)–Christiaan Huygens–
[pagina 32]
| |
VII.Ga naar voetnoot1)
| |
[pagina 33]
| |
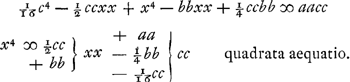 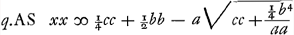 substrahe ex quadrato SF ∞ ¼ cc restat substrahe ex quadrato SF ∞ ¼ cc restat 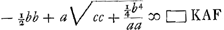 .
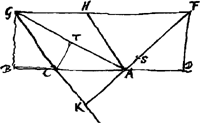
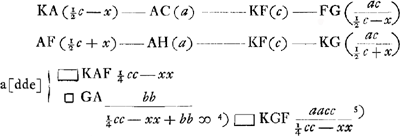
Sit ducta FD, faciens angulum AFD aequalem angulo ACKGa naar voetnoot6) et consequenter ∆los similes CAK, FAD. ergo ▭ CAD ∞ ▭ KAF. applicando itaque ▭ KAF ad CA ∞ a fit .
Sit ducta FD, faciens angulum AFD aequalem angulo ACKGa naar voetnoot6) et consequenter ∆los similes CAK, FAD. ergo ▭ CAD ∞ ▭ KAF. applicando itaque ▭ KAF ad CA ∞ a fit 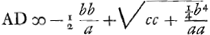 . Sit GB perp. in AC et . Sit GB perp. in AC et
| |
[pagina 34]
| |
CT in GA. Ergo similia triangula CAT, GAB sed CA est a, AT ½b, AG b, ergo AB ½ bb/a. ergo cum AD sit 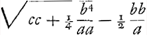 , additâ AB ∞ ½ bb/a, erit , additâ AB ∞ ½ bb/a, erit 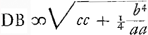 , hoc est DB qu. ∞ ┚ KF datae una cum qu.o AB. , hoc est DB qu. ∞ ┚ KF datae una cum qu.o AB.
Unde talis invenitur problematis constructio. Oportet demissâ perpendiculari GB facere BD quae possit quadr. lineae datae una cum qu. ex AB. tum super AD, describere circumferentiae partem quae capiat angulum aequalem angulo CGH. Ea enim secabit rectam GH productam in F, unde ducta FAK aequabitur datae lineae. Sed et in alio puncto secabit eandem GF inter H et F, cujus ope intersectionis problema itidem absolvetur.Ga naar voetnoot7) | |
Theorema.Ga naar voetnoot8) [1.]Sit rhombus GCHA et ducatur KHFGa naar voetnoot9) occurrens productis rhombi lateribus utrinque. et ducatur FD quae faciat angulum AFD aequalem CGH, et sit GB perpendicularis super AC. dico quadrata ex KF et AB aequari qu.o ex BD. Sit enim AL super GK ad angulos rectos ducta et FE super BD. et ponatur AP 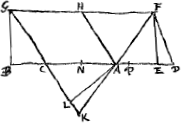 [Fig. 2.]
quidem aequalis ED; AN vero ipsi CB. Quia igitur similes sunt trianguli GBC, ACL, et latus GC aequale AC lateri, erit quoque CL aequale CB hoc est AN. Rursus quoniam similia sunt ∆la CAK, FAD, habent enim angulum ad A aequalem et est angulo ACK ex constr. aequalis angulus AFD, erit et angulus AKC aequ. ang.o ADF. anguli autem ALK, FED sunt recti, itaque similia quoque triangula sunt ALK, FED. sed FE est aequ. AL ergo et AK aequ. FD et LK aequalis ED hoc est AP. itaque tota NP etiam aequalis CK. Propter similia verò triangula, est AD ad DF ut AK ad KC. sed AK aequalis est FD et KC aequalis NP. Itaque AD ad DF ut DF ad NP, ideoque contentum sub AD, NP aequale qu.o FD et auferendo utrinque ▭ DA, AP vel AD, DE erit ▭ NAD aequale qu.o FD - ▭ ADE. Et sumptis omnium duplis, duplum ▭ NAD ∞ duplum qu. DF - 2 ▭ ADE et addito communi quo AD, erit duplum | |
[pagina 35]
| |
▭ NAD hoc est duplum ▭ BC, AD + qu. AD ∞ 2 qu. FD + qu. AD - 2 ▭ ADE; sed haec aequalia sunt qu.is ex AF et FD (nam qu.a ex FD et DA - 2 ▭ ADE aequantur qu.o AFGa naar voetnoot10)). Itaque 2 ▭ BC, AD + qu. AD ∞ quis ex AF et FD, hoc est quis ex AF et AK, nam AK ipsi FD aequalis ostensa est. Additis itaque aequalibus ad aequalia, hoc est addendo illic 2 ▭ CAD hinc vero 2 ▭ KAF (sunt autem haec aequalia, quoniam propter ∆a sim. est CA ad AK ut FA ad AD) erunt etiam summae aequales. Sed addendo ad 2 ▭ BC, AD + qu. AD, duplam ▭ CAD fit 2 ▭ BAD + qu. AD. at qu.is ex FA et AK addendo duplum ▭ KAF fit qu. KF; ergo qu. KF aequale 2 ▭ BAD + qu. AD. addito que utrinque qu. BA, erit qu. KF + qu. BA aequale quo. BD. quod erat ostendendum. Potest autem rursus angulus FDA rectus vel obtusus esse, prout fuerit angulus FKC. ijsque casibus non multum diversa demonstratione idem ostendetur facilius quidem multò si angulus FDA rectus fuerit. | |
Theorema. 2.Ga naar voetnoot11)Sit rursus rhombus GCAH, cujus ducatur diameter HC, et in productum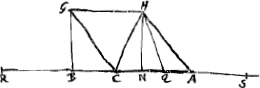 [Fig. 3.]
latus AC cadat perpendicularis GB, porro sit HQ posita aequalis HC, et ponatur BS quae possit quadratum ex BA una cum quadruplo qu.i ex CH. Dico AS ipsi CQ aequalem esse.
Sit enim HN ipsi CQ ad ang. rectos. quia igitur CHQ est triangulum isosceles erit CQ bifariam divisa in N. Ponatur BR ipsi BN aequalis, eritque jam utraque harum aequalis ipsi GH hoc est CA. Quia verò sunt similia triangula CGH, CHQ, nam angulis GCH, GHC aequales sunt singuli HCQ, HQC; erit QC ad CH ut CH ad CG, et qu. CH aequale ▭ sub GC, CQ hoc est ▭ sub BN, CQ, hoc est duplo ▭o BNQ, hoc est ▭o RNQ, seu RNC. Est autem qu. BA hoc est qu. RC una cum duplo ▭o RCQ + qu. CQ aequale quadrato RQ. Sed duplum ▭ RCQ + qu. CQ aequatur quadruplo ▭o RNC, nam ▭ RCQ aequatur duplo ▭ RCN, et qum. CQ quatuor qu.is CN. Itaque addito ad qu. BA quadruplo ▭ RNC hoc est 4 qu.is CH erunt ea simul aequalia qu.o RQ; sed ijsdem aequale positum est qu. BS, ergo BS q. ipsi RQ | |
[pagina 36]
| |
qu.o aequale: et BS ipsi RQ. Quare ablata communi BQ erit QS aequalis RB hoc est ipsi CA; et rursus communi ablata QA, erit AS aequalis CQ; quod erat demonstrandum. | |
Problema.Ga naar voetnoot12)Rhombo dato et duobus lateribus contiguis productis, aptare sub eorum angulo interiori magnitudine datam rectam lineam quae ad oppositum angulum pertineat. debet autem data linea non minor esse duplâ diametro, quae alios duos rhombi angulos jungit. Esto Rhombus GHAC [Fig. 4]Ga naar voetnoot13), et producta ejus latera GH, GC; data autem 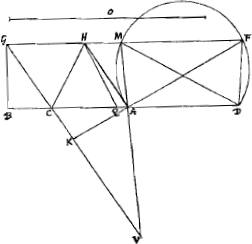 [Fig. 4.]
sit linea o, quae major sit dupla diametro HC, nam si aequalis est duplae HC constructio problematis manifesta est. Sit itaque major et oporteat ducere KAF ipsi o aequalem. Sit GB ipsi AC ad angulos rectos et qu.is ex BA, et ex o sit aequale ex BD quadratum.Ga naar voetnoot14) Dein super AD describatur circumferentiae pars capax anguli CGH, quae ubi rectam GH productam secabit, inde ducantur FAK, MAV dico harum utramque aequale esse ipsi o. Quod autem dicta circumferentia secabit rectam GH productam sic prius ostenditur. Sit HQ ipsi HC aequalis. Quia igitur qu. ex BD aequale est qu.is ex o et BA; quorum qu. o majus est 4 quis ex CH, erit ideo AD major quam CQ. hoc enim in praec. Theor. ostensum fuit. Sed et triangulum CHQ ex eodem theoremate constat similem esse triang. CGH, et isoscelem. Itaque si super CQ circumferentiae pars descripta intelligatur, capax anguli CGH, ea transibit per H, atque ibidem continget rectam GH, similis autem erit circumferentiae quae super AD descripta fuit, nam illa quoque capit angulum aequalem ipsi CGH. Ergo quum sit AD major quam CQ, manifestum est circumferentiam AMFD secare debere rectam GHF. | |
[pagina 37]
| |
Porro autem ductis MD, FD, constat quidem angulos AFD, AMD singulos aequari angulo CGH. Quapropter erunt qu.a ex KF et AB simul aequalia qu.o BD;Ga naar voetnoot15) sed huic etiam aequalia sunt ex constr.e qu.a ex o et ex AB. Ergo quae eidem aequalia etiam aequalia inter se. Et ablato communi quadrato ex AB erit qu. KF aequale qu.o ex o et KF ipsi o. Eadem ratione et qu. MV quadrato ex o aequale erit. Quod demonstrandum erat.Ga naar voetnoot16) |
|