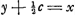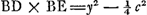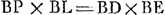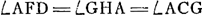Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656
(1910)–Christiaan Huygens–
[pagina 26]
| |
VI.Ga naar voetnoot1)
| |
[pagina 27]
| |
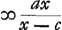 unde additis qu.is BC, CE, ablatoque hinc qu.o BE, relinquoque diviso per duplam CE orietur segmentum basis CR unde additis qu.is BC, CE, ablatoque hinc qu.o BE, relinquoque diviso per duplam CE orietur segmentum basis CR
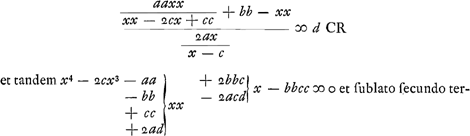 mino, ponendo nimirum y + ½c ∞ x erit post institutam operationem 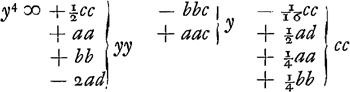 apparet hinc quod si bb ∞ aa evanescat affectio sub y, quodque propterea sit futura aequatio quadrata, cum autem a ∞ b tum AB rhombus est, et mutatis ubique b in a erit hujusmodi aequatio 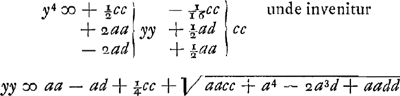 sive 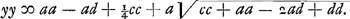 Dividatur DE bifarium in H ergo BH est y.Ga naar voetnoot4) Et ducatur EL quae faciat angulum BEL aequalem angulo BPA. erunt jam anguli ELP et EDP duobus rectis aequales,Ga naar voetnoot5) et puncta ideo D, P, L, E, in circuloGa naar voetnoot6) et rectang. LBP aequ. | |
[pagina 28]
| |
▭o EBD. Subtrahe jam qu. DH ∞ ¼cc ex qu.o 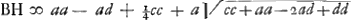 erit reliquum □ BD + 2 ▭ BDH, quae simul aegualia ▭o EBD ergo ▭ EBD seu erit reliquum □ BD + 2 ▭ BDH, quae simul aegualia ▭o EBD ergo ▭ EBD seu 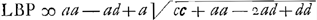 . aufer qu. BP ∞ aa fit . aufer qu. BP ∞ aa fit 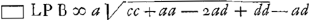 . divide per BP ∞ a fit . divide per BP ∞ a fit 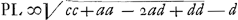 sit AQ parall. RB ergo PQ ∞ d,Ga naar voetnoot7) adde PQ erit sit AQ parall. RB ergo PQ ∞ d,Ga naar voetnoot7) adde PQ erit 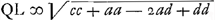 . hoc est QLq. ∞ □ DE data una cum qu. BQ nam hoc est a - d.
Nota aliquam differentiam hic inveniri cum tam exigua datur DE vel tam . hoc est QLq. ∞ □ DE data una cum qu. BQ nam hoc est a - d.
Nota aliquam differentiam hic inveniri cum tam exigua datur DE vel tam
 [Fig. 2.]
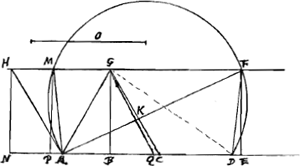
acutus angulus APB ut L cadat inter B et P. Compositio erit hujusmodi, Sit datus rhombus HGCA [Fig. 2] et linea o. Cadat GB perpendicularis in AC. Et sumatur BD quae possit duo simul quadrata, ex o et ex AB.Ga naar voetnoot8) Tum super AD describatur circumferentiae pars quae sit capax anguli GHA. et ad intersectionem F ducatur AF, dico KF ipsi o aequalem esse.Ga naar voetnoot9) JunganturGa naar voetnoot10) enim AM, FD et ducantur HN, MP, FE parallelae GB. | |
[pagina 29]
| |
Quod verò circumferentia secabit rectam HF sic fiet manifestum. Sit BQ ∞ BA et jungatur GQ, itemque GA. Itaque trianguli GAQ duo anguli A et Q inter se aequales sunt et singuli angulo A vel G trianguli HAG, quare similia erunt ∆a HAG, GAQ et angulus AGQ aequ. angulo AHG. Si itaque super AQ describeretur circumferentia similis circumf.ae AMFDGa naar voetnoot11) ea per G transiret et tangeret rectam HF; sed quoniam qu. ex BD aequale est quadratis ex AB seu BQ et ex o, erit BD major BQ, et AD major AQ, ergo necessario circumferentia AMFD secabit rectam HF. Porro quia ang. FDA aequ. angulo AKC (nam uterque addito FKC aequatur 2 rectisGa naar voetnoot12)) distantque tantum inter se lineae HF, AE quantum HA, GC, erit ideo FD ∞ AK. Sed et MA ∞ FD ergo MA quoque ∞ AK, et ∆ AMH idem cum ∆ AKCGa naar voetnoot13) utraque vero similia ∆lo ADF. Ergo ut HM ad MA, hoc est ut NP ad FD ita FD ad DA. Quare contentum sub NP, AD aequ. qu. DF; et addito utrinque ▭o PAD seu ADE, erit ▭ NAD aeq. qu. FD et ▭o ADE. Et sumptis omnium duplis erit duplum ▭ NAD aequ. duplo qu. FD et duplo ▭ ADE. Et addito communi qu. AD erit geminum ▭ NAD + qu. AD hoc est geminum ▭ sub BC, AD + q. AD (nam BC ∞ ADGa naar voetnoot14)) aequale duplo qu. FD + q. AD + 2 ▭ ADE. Sed haec simul aequantur qu. AF + qu FD, (nam duplum ▭ ADE + qu. AD + qu. DF aequantur qu. AFGa naar voetnoot15)) Ergo duplum ▭ sub BC, AD+q. AD aequale qu.o AF + q. FD, hoc est, qu.o AF + q. AK, nam diximus FD AK esse aequales inter se. ▭ verò sub CB, AD una cum ▭ BAD aequatur ▭o CAD, et dupla duplo; ergo si à qu. AD + duplo ▭ sub BC, AD, auferatur duplum ▭ CAD, relinquetur qu. AD cum defectu dupli ▭ BAD. Duplo autem ▭o CAD aequale est duplum ▭ KAF, quia puncta KCDF sunt in circuli ejusdem circumserentia. et erat qu. AF + qu. AK aequale qu. AD + | |
[pagina 30]
| |
+ 2 ▭ sub BC, AD. Ergo ablato duplo ▭ KAF à qu. AF + q. AK hoc est ablato ▭ AKFGa naar voetnoot16) + q. AK à qu. AF, restabit qu. KF aequale qu. AD minus 2 ▭ BAD, seu minus 2 ▭ ABD et 2 q. AB; quare addito utrimque quadrato AB, erit qu. KF + qu. AB aequale qu. AD minus 2 ▭ ABD minus qu. AB: hoc est quo BD. Sed eidem qu.o BD esset aequale ex constr. qu. ex o + q. AB. Ergo haec duo quoque aequalia qu.is duobus KF et AB; et ablato communi AB q. erit qu. ex o aequ. q. KF. quod erat demonstrandum. Potest autem angulus FDA vel rectus vel acutus fieri in quibus casibus vel facilior vel non multum à praecedenti differens dem.o obtinebit. Alter casus cum angulus rhombi C obtusus est, eandem habet compositionem.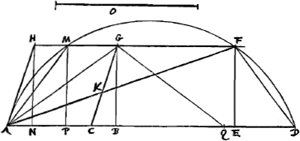 [Fig. 3.]
Et demonstrationem quoque parum diversam, quae erit hujusmodi, mutatis tantum signis affectionis ubi opus erit. Primum quidem sicut modo ostenditur id quod sub NP, AD [Fig. 3] continetur aequari quadrato DF.Ga naar voetnoot17) unde detrahendo utrumque à rectang. PAD vel ADE, erit ▭ NAD ∞ ▭ ADE - q. FD; et sumptis omnium duplis, duplum ▭ NAD ∞ 2 ▭ ADE - duplo q.o FD. et utrumque abstrahendo à qu.o AD, erit qu. AD - duplo ▭ NAD ∞ qu. AD + duplo q.o FD - 2 ▭ ADE; sed haec simul aequantur qu.is ex AF et FD, (nam qu.a. simul AD, DF - 2 ▭ ADE aequalia sunt qu.o AF per. 13. 2i Elem.Ga naar voetnoot18) Ergo qu. AD minus duplo ▭ NAD aequale est qu.is AF et FD, hoc est, qu.is AF et AK, nam FD ∞ AK ostensa est.Ga naar voetnoot19) detrahendo igitur aequalia ab aequalibus, hoc est illinc auferendo 2 ▭ CAD, hinc vero duplum ▭ KADGa naar voetnoot20) (haec enim aequalia inter se, quoniam puncta D, C, K, F in ejusdem circuli circumserentia) erunt etiam residua aequalia. Sed à quo. AD - 2 ▭ NAD seu - 2 ▭ CB, AD, si aufe- | |
[pagina 31]
| |
ratur insuper 2 ▭ CAD, relinquetur qu. AD - 2 ▭ BAD. At à qu.is FA, et AK auferendo 2 ▭ KAF, relinquetur qu. KF. Itaque qu. KF aequale qu.o AD - 2 ▭ BAD, hoc est qu.o AD - 2 ▭ ABD - 2 q. AB. quare addendo utrinque qu. AB erit qu. KF + qu. AB ∞ qu. AD - 2 ▭ ABD - qu. AB; Sed hoc residuum est aeq. qu.o BD. ergo qu. KF + qu. AB ∞ qu. BD, hoc est qu.o ex o et qu. AB. Itaque auferendo commune qu. AB, erit qu. KF. aequ. q.o ex o. quod erat ostend.
Haec autem proponentur melius eo modo quo problematis partem alteram trademus,Ga naar voetnoot21) Primum videlicet tale theorema demonstrando. Si sit rhombus HACG et ex angulo A ducatur AKF ad productum latus HF, et FD faciens angulum AFD aequalem angulo H, et GB perpendicularis ipsi AD. dico quadrata ex KF et ex AB quadrato BD aequalia esse. Hoc primum demonstrare oportuit, dein Resolutionem Compositionemque et demonstrationem problematis subjicere quae breves erunt. et schema habebunt minus implicitum. quod et Pappus in prop.e 72. lib. 7, rectè observavit.Ga naar voetnoot22) |
|


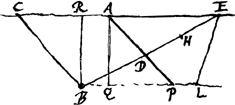
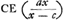 ergo ∆i CBE latus BC ∞ b, latus BE ∞ x, et CE ∞
ergo ∆i CBE latus BC ∞ b, latus BE ∞ x, et CE ∞