Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656
(1910)–Christiaan Huygens–
[pagina 21]
| |||||||||||||
V.Ga naar voetnoot1)
|
| acc ∞ abdGa naar voetnoot2) | cb ad ca ut cc ad ad | Dicendum. Ratio b ad a componitur ex ratione b ad c et c ad a. Ratio autem quadr.i cc ad rectang. ad componitur ex ration. c ad d et c ad a. Ergo ablata utrinque ratione c ad a, erit ratio b ad c eadem quae c ad d. |
| b ad c ut c ad d |
Sit a ad b ut cd ad bn, oportet ostend. a ad c ut d ad n.
| abn ∞ bcdGa naar voetnoot3) | ac ad bc ut cd ad bn | Ratio a ad b compon. ex rat. a ad c et c ad b. Ratio vero ▭i cd ad ▭ bn comp. ex ration. d ad n et c ad b. Ablata igitur communi rati.e c ad b, erit eadem ratio a ad c quae d ad n. |
| a ad c ut d ad n |
vel sic. Ratio a ad b comp. ex rat. a ad d et d ad b. Ratio autem ▭ cd ad ▭ bn comp. ex rat.s c ad n et d ad b. Ergo ablata communi rat.e d ad b, Erit eadem ratio a ad d quae c ad n et permutando.
Sit ab/c ∞ d + ef/g oportet ostendere c ad g ut ab ad dg + ef.
Dem. c est ad a ut b ad d + ef/g quae vocetur h, ergo ▭ ab ∞ ▭ ch. Est autem ▭ ch ad ▭a dg + ef hoc est ad ▭ hg ut c ad g. Ergo et ▭ ab ad ▭ hg hoc est ad ▭a dg + ef ut c ad g.
Esto ar ad bc ut c ad q. Oportet ostendere, ar ad cc ut b ad q.
| bcc/ar ∞ q. | Dicendum. ar ad bc ut c ad q. Verum bc ad cc ut b ad c. Ergo ex aequali in proportione perturbata erit ar ad cc ut b ad q. per 23. lib. 5. Elem.Ga naar voetnoot4) |
Esto no ad pq ut r ad s. Ostendendum sit, n ad p ut rq ad so. Hoc est, sit ratio composita ex ratione n ad p et ex o ad q eadem quae r ad s, et oporteat ostendere rationem n ad p eandem esse cum ea quae componitur ex ratione r ad s et ex q ad o. Dicendum; quia ratio composita ex n ad p et o ad q eadem est quae r ad s, addita utrimque ratione q ad o, erit composita ex rationibus n ad p, o ad q, et q ad o, hoc est ratio n ad p eadem quae composita ex rat. r ad s et q ad o.
Hyp. n est ad r ut c ad p. Itemque q ad r ut c ad s. Ostendendum quod n ad q ut s ad p.
Quia n ad r ut c ad p, erit ▭ np aequal. ▭o rc. Sed eidem ▭o rc aequale est ▭ qs, quia q ad r ut c ad s. Ergo ▭ np aequale ▭ qs, Ideoque n ad q ut s ad p.
Aliter. Ratio n ad q componitur ex ratione n ad r et r ad q. quarum r ad q eadem cum ratione s ad c, altera vero n ad r eadam quae c ad p. Ergo n ad q rationem habet compositam ex ratione s ad c et c ad p, hoc est rationem s ad p.
Aliter optimè. Quia n ad r ut c ad p erit invertendo r ad n ut p ad c, verum q est ad r ut c ad s. Ergo ex aequo in proportione perturbataGa naar voetnoot4) erit q ad n ut p ad s.
Hijp. e ad b ut c ad n. Item a ad b ut c ad l. Et e ad l ut a ad p. Ostendendum quod n ∞ p.
Quia e ad b ut c ad n, erit invertendo b ad e ut n ad c. Sed a est ad b ut c at l, ergo ex aequo in proportione perturbataGa naar voetnoot4) erit a ad e ut n ad l. Sed et a ad e ut p ad l quia erat e ad l ut a ad p. Igitur n ad l ut p ad l quare n ∞ p.
2. Nov. v.
1652.
Hypoth. a - ax/e ad cx/e ut a ad b Ostendendum c + b ad b ut e ad x.
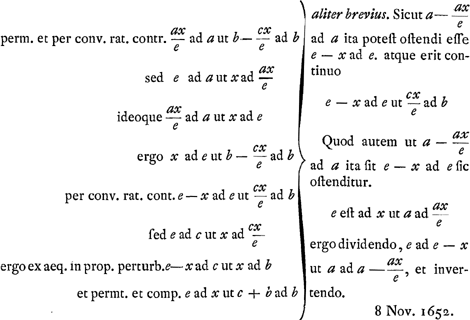
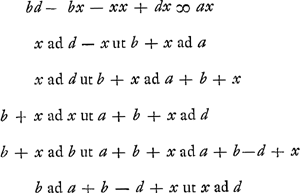 |
Quoniam ductis in sese medijs et extremis non ultra quadratum seu planum ascenditur, potest resolutio ad finem perduciGa naar voetnoot5) per solas proportiones, ut hic factum apparet. |
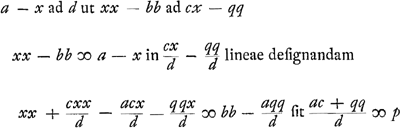
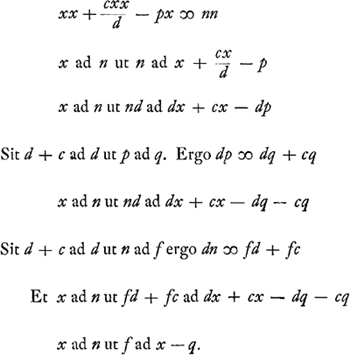
- voetnoot1)
- Le but de Huygens, en composant cette pièce curieuse, empruntée aux pages 279-281 du manuscrit No. 12, doit avoir été de se faciliter la rédaction des démonstrations géométriques à la mode des anciens, dont il accompagna ses théorèmes et constructions, trouvées sans doute, pour la plupart, par l'analyse. La pièce rappelle l'ouvrage posthume de Van Schooten ‘Tractatus de Concinnandis Demonstrationibus Geometricis ex Calculo Algebraïco’ de 1661 (voir la note 1, p. 41 du T. III) dans lequel, pour montrer que la méthode synthétique de démontrer est contenue implicitement dans l'Analyse, il apprend à déduire systématiquement de cette dernière les compositions et démonstrations purement géométriques et synthétiques. Ajoutons qu' on trouve une application des algorithmes de la pièce présente dans la pièce No. XVI, p. 72 du Tome présent.
- voetnoot2)
- Les facteurs a des deux termes de cette égalité ont été biffés. Huygens ajouta encore ici en marge: ‘vel bd ad ad ut cc ad ad; ergo bd ∞ cc; ergo b ad c ut c ad d.’
- voetnoot3)
- Les facteurs b ont été biffés.
- voetnoot4)
- Voir la note 22, p. 304 du Tome XI.
- voetnoot4)
- Voir la note 22, p. 304 du Tome XI.
- voetnoot4)
- Voir la note 22, p. 304 du Tome XI.
- voetnoot5)
- Huygens n'achève pas complètement la construction, puisqu' ici, et aussi dans le paragraphe qui suit, il s'arrête après avoir réduit le problème à celui de construire la ligne x, déterminée par une proportion b: (x ± p) = x : d. Si c'était son but, comme nous le supposons, de montrer que les problèmes plans peuvent être résolus sans sortir des proportionnalités, c'est-à-dire sans résoudre explicitement une équation quadratique, il aurait pu introduire la longueur q, définie par la proportion b : q = q : d, réduire la proportion donnée a la forme: x : q = q : x ± p et citer enfin la ‘Prop. XII. Data media trium proportionalium & differentia extremarum, invenire extremas’, qu'on trouve dans l'ouvrage de Viète: ‘Effectionum geometricarum Canonica recensio.’ (Voir la p. 233 de l'ouvrage cité dans la note 31, p. 10 du T. I). Il nous semble, en effet, que pour expliquer la portée de la dernière partie de la pièce présente, on doit sous-entendre quelque chose de cette nature.
Comparez encore à cet effet la pièce No. XVI, déjà citée dans la note 1 où, par une série de proportions, analogues à celles du texte, la construction d'un problème plan est réduite à celle de la ligne x, donnée par la proportion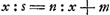 . Alors Huygens fait suivre une construction bien connue par laquelle il résoud l'équation
. Alors Huygens fait suivre une construction bien connue par laquelle il résoud l'équation 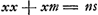 ; mais dans la démonstration qu'il ajoute, cette construction amène immédiatement la proportion
; mais dans la démonstration qu'il ajoute, cette construction amène immédiatement la proportion 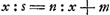 , d'où il s'ensuit qu'on peut fonder ces sortes de démonstrations sur les seules proportions.
, d'où il s'ensuit qu'on peut fonder ces sortes de démonstrations sur les seules proportions.

