Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 19]

IV.¹⁾
[1652].²⁾

Dato quadrato AB cujus duo latera AF, AE producta sint et data linea K, ponere huic aequalem lineam inter productas AC, AD quae transeat per punctum B. Oportet autem K non minorem esse dupla diagonali quadrati quod datur.³⁾

[Fig 1.]

Factum sit, et sit ex hijpot. aptata DBC aequalis ipsi K. Ducatur ipsi DC, CG ad angulos rectos occurrens productae EB in G, et jungatur DG.

Similia autem sunt ∆.^a EBD, HCG, et latus EB aequale CH, ergo et DB aequale CG, et ED ipsi HG. Quadrata autem DC, CG aequalia sunt qu.^o DG, quoniam angulus ad C rectus. Sed eidem quadrato DG aequantur qu.^a duo GE, ED, ergo qu. DC una cum qu. CG, hoc est qu.^a DC, DB, aequalia quadratis DE, EG, quare auferendo utrinque qu. DE, erit qu. DC una cum qu.^o EB, aequale qu.^o EG. Datur autem quadr. DC aequale qu.^o ex K, et datum quoque est qu. EB. Itaque et summa utriusque dabitur. Datum igitur quoque qu. EG quare et ipsa EG data erit. unde et BG data. Angulus autem BCG rectus est, ideoque punctum C erit ad circuli circumferentiam cujus diameter BG. Sed idem punctum est etiam ad lineam rectam AC. quae positione data est, et circulus quoque positione datus

1) La pièce se trouve à la page 187 du manuscrit N^o. 12.

2) Le lieu que la pièce occupe dans le manuscrit, immédiatement après la pièce N^o. III, ne laisse aucun doute sur cette date.

3) On retrouve le même problème avec la même construction et démonstration, mais sous des rédactions différentes, dans une lettre à van Schooten du 23 octobre 1653 (voir les pages 250 et 251 du T I) et dans les ‘Illustrium quorundam problematum constructiones’ de 1654 au ‘Probl. V’. Comparez encore les pages 226-228 du Tome XI où un problème analogue est traité. Les pièces N^o. VI, VII, IX et XIII, qui suivent, traitent les problèmes plus généraux qu'on obtient en remplaçant le carré AFBE par un losange. Sur l'origine de ces problèmes on peut consulter la note 2 de la page 239 du Tome XI. Pappus lui-même s'est borné à résoudre celui qu'on trouve à la page 226 du Tome cité. Ghetaldi les a traités tous dans l'ouvrage cité en premier lieu dans la note 5 de la page 126 du T. VIII.

[p. 20]

quoniam diameter BG positione data est. Ergo et punctum C positione datum erit, dictae videlicet circumferentiae et rectae AC intersectio.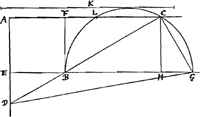

[Fig. 2.]

Componetur vero hoc modo. Quadratis ex K et ex AE sit aequale quadratum ex EG. et super BG diametro scribatur semicirculus BCG, secans rectam AF productam in L et C; et ducatur CBD vel ex L quoque. dico CD aequalem esse dictae K lineae.

Et demonstratio ex Resolutione manifesta est. Quod autem semicirculus rectam AC secabit hinc manifestum fiet. Etenim quia K major ponitur dupla diagonali qu.ⁱ AB, erit ejus qu. majus octo quadratis ex EB, itaque qu. ex EG majus novem qu.^is ex EB. Quare EG major tripla EB et consequenter dimidia BG sive radius descripti semicirc. major quam EB vel BF. Unde necessario circumf. secat AC.