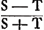Oeuvres complètes. Tome XII. Travaux de mathématiques pures 1652-1656

[p. 13]

II.¹⁾
1652.

30 Jan. 1652.

Angulo positione dato et puncto extra ipsum lineam intra angulum accommodare datae longitudinis quae pertineat ad datum punctum. Et quomodo Nicomedes duas medias prop. invenerit ope Conchoidis.²⁾

[Fig. 1.]

Sit datus angulus DAE, punctum B.

Sit BC parallela AD et productae EA occurrat in C. Sitque BR perp. in EC.

Sit AC ∞ a; CB ∞ b; DE ∞ c; CR ∞ d nam et haec data. AE ∞ x.

Fit EB detracto autem quadrato EB à summa quadratorum EC, CB, reliquoque diviso per duplam CE, habebitur segmentum basis CR.

1) La pièce est empruntée aux pages 182 et 183 du manuscrit N^o. 12. Huygens y traite le problème de mener par un point donné une droite de telle manière que deux droites données par position en découpent un segment de longueur donnée. Il arrive à une équation biquadratique et montre ensuite comment, par la considération d'un cas particulier, on peut obtenir la construction de Nicomède, â l'aide de la conchoïde, des deux moyennes proportionelles entre deux longueurs données.

2) On trouve cette construction de Nicomède avec sa démonstration par Pappus à deux reprises et sous des rédactions presque identiques au ‘Liber III, Prop. 5’ et au ‘Liber IV, Prop. 24’ des ‘Mathematicae Collectiones’ de Pappus; voir dans l'édition de Hultsch (citée dans la note 17, p. 215 du Tome XI), T. I, pp. 58-63; 246-251 (pp. 5 verso - 6 recto; 56 verso - 57 recto de l'ouvrage cité dans la note 3, p. 259 de notre T. II). On la retrouve encore dans les Commentaires d'Eutocius sur le ‘Liber II’ de l'ouvrage d'Archimède. ‘De sphaera et cylindro’; voir les p. 26-27 de l'édition de Bâle (Heiberg, T. III, p. 122-127).

[p. 14]

Hic animadvertit Nicomedes,³⁾ si bb + aa esset ∞ cc + 2ad tunc tertium terminum evanescere: tunc autem . Sed ad hoc obtinendum oportet ut AB ponatur aequalis datae DE ∞ c; tunc enim in ∆^o CBA erit segmentum basis . Ablato sic tertio termino, ductoque 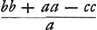in x³, loco 2d, manet ipsi haec aequatio.

Hic vidit⁴⁾ 2accx + aacc dividi posse per x + ½ a fierique tunc 2ac² si igitur id quod in x³ ductum est aequale esset ½ a, tunc etiam

3) Bien entendu Huygens suppose que Nicomède soit arrivé par cette voie à sa construction. En effet, on n'en trouve rien aux lieux cités dans la note précédente, où Nicomède égale AB à DE par construction sans le motiver d'aucune façon.

4) D'après la supposition de Huygens.

[p. 15]

[Fig. 2.]

sed d erat quod nunc erit sive ¾a. ergo d ∞ ¾a.

Ponendo igitur AB ∞ DE et CR ∞ ¾ CA habet hanc aequationem.

Est autem secunda duarum mediarum proportionalium inter c et 2a, vel etiam inter 2c et ½ a. atque hoc posterius delegit Nicomedes in sua constructione.

Compositio nicomedis.

AC⁵⁾ dupla AL, AR dimidia AL. RB perpend. LA. AB ∞ GF vel FL. Junctae CB parallela AD. BDE linea ope Conchoidis ducta ita ut intercepta DE sit ∞ AB, vel GF.

Continue prop.^les sunt HA, AE, KG, GH.⁶⁾

5) Voir la figure 2, qui correspond exactement avec celles de Pappus et d'Eutocius aux lieux cités dans la note 2.

6) En effet, posant HA = 2c, GH = ½ a (donc AB = c, AR = ¼ a, CR = ¾ a) on a d'après l'analyse qui précède: AE = x (voir aussi la fig. 1) = ; ensuite . Il est curieux de remarquer le rôle de la racine éliminée x = - ½a. Elle correspond à une solution parasitaire qu'on obtient en tirant la droite BL. Ainsi le point L appartient à la seconde branche de la conchoïde.

[p. 16]

III.¹⁾
1652.

Ult. Jan. 1652.

Sphaeram in data ratione plano secare,²⁾ per trisectionem anguli³⁾.

Esto sphaera cujus centrum M, diameter CA. et data sit proportio S majoris ad T minorem.

[Fig. 1].

Secetur sphaera plano secundum AC diametrum eaque sectio sit circulus ABCD. Porro dividatur AC in E, ut sit sicut S ad T ita EA ad EC, et sit ER perpendicularis ipsi AC. Sumatur autem arcui CR aequalis arcus AF, et ei quae subtendit tertiam partem arcus RF ponatur aequalis MN, quam manifestum est minorem fore quam ME. Denique per N punctum ducatur planum quod diametro AC sit ad angulos rectos. Dico hoc sphaeram sic secare ut portio KAL eam habet rationem ad KCL portionem quam S ad T.⁴⁾

Ducatur enim BMD parallela KL, et jungantur CD, CL et KM, ML. Ipsi vero EM sit aequalis EQ, et duplae EN aequalis MO, et jungantur OB, OD.

1) La pièce se trouve aux pages 184-186 du manuscrit N^o. 12.

2) Le problème est identique avec celui de la pièce N^o. I.

3) On retrouvera la construction et la démonstration qui vont suivre, dans les ‘Illustrium quorundam problematum constructiones’ de 1654 au ‘Problema I’; mais sous une rédaction assez différente et même avec des modifications dans la construction.

4) Une construction modifiée fut communiquée à Kinner à Löwenthurm dans une lettre du 9 aôut 1653 (p. 239 du T. I). Celui-ci en loua l'élégance et la simplicité dans ses lettres du 28 aôut 1653 et du 28 février 1654; voir les pp. 241 et 270 du T. I. Pour se convaincre de l'identité essentielle des deux constructions il suffit de calculer la corde de l'arc qui est divisé en trois parties égales. On trouvera dans les deux cas: . AC.

[p. 17]

Quia autem EN est excessus ipsius EM supra NM, manifestum est, id quo dupla EM hoc est quo QM excedit duplam NM aequari duplae EN hoc est ipsi OM. Itaque dupla NM addita ad OM aequatur ipsi QM, ac proinde erit dupla NM aequalis OQ. Ergo duae simul OQ et NM aequales triplae NM. Sed eadem OQ, NM simul aequales sunt duabus QM, ON. Itaque et tripla NM aequalis duabus QM, ON.

Est autem NM aequalis ei quae subtensa est tertiae parti arcus RF. at verò QM, cum sit dupla EM, aequatur ei quae totum RF arcum subtendit. Itaque tres simul quae tertias partes subtendunt arcus RF aequantur subtensae totius arcus et ipsi NO. Sicut igitur quadratum radij MK ad qu. ejus quae tertiam partem subtendit arcus RF, hoc est, ad qu. MN ita est ipsa NM ad NO longitudine. hoc enim postea ostendetur.⁵⁾ Quare et per conversionem rationis ut qu. KM ad qu. KN ita NM ad MO. Ut autem qu. KM hoc est qu. BM ad qu. KN ita est circulus circa diametrum BD ad circulum cujus KL diameter. Ergo quoque ille circulus ad hunc erit ut NM ad MO, ac proinde aequalis conus BOD cono KML, quia eorum bases et altitudines reciprocantur⁶⁾. Conus autem BOD est ad semisphaeram BCD, hoc est, ad conum basin habentem circulum circa diametrum BD et altitudine duplam MC,⁷⁾ ut MO ad duplam MC, quoniam eadem basi insistunt. Itaque et conus KML erit ad semisphaeram BCD ut MO ad duplam MC. Porro autem est semisphaera eadem ad sectorem solidum MKCL ut superficies sphaerica illius ad hujus superficiem⁸⁾ id est ut MC ad NC⁹⁾, quare et per conversionem

5) Voir, plus loin dans cette mème pièce, le théorème que nous avons cursivé. En effet, il est clair que est égal â la ligne du theorème ‘ad quam subtensa tertiae partis eam habet rationem quam quadratum semidiametri ad quadratum ipsius tertiae arcus parti subtensae.’

6) Huygens ajoute en marge ‘15. 12. Elem.’ Consultez la note 10 de la pièce N^o. I, p. 11 du Tome présent.

7) Huygens ajoute ‘32. l. 1. Archim. de Sphaer. et Cylind.’ Quaelibet sphaera quadrupla est eius coni, qui quidem conus habuerit basim aequalem circulo in sphaera maximo altitudinem uero aequalem semidiametro sphaerae.’ (p. 32 de l'édition de Bâle; Heiberg, T. I, p. 141, où elle porte le numéro 34).

8) Huygens ajoute ‘42. 1. Arch. de Sphaer. et Cylin.’ Voir la note 11, p. 11 du Tome présent.

9) Huygens ajoute ‘3. 2. Arch. de Sph. et Cylind.’ ‘Datam sphaeram sic secare plana superficie, ut portionum superficies inter se similem cuicumque proportioni datae retineant proportionem’ (p. 45 de l'édition de Bâle, Heiberg, T. I, p. 207). On n'y trouve pas expressément la proposition en question; mais elle se déduit facilement de celle citée dans la note 12 de la pièce N^o. I, p. 11 du Tome présent, et le même raisonnement, dont on a besoin alors, est suivi dans le texte de la Prop. 3, Libr. 2 mentionnée.

[p. 18]

rationis et invertendo, erit pars semisphaerae, quae remanet dempto sectore KMLC, ad ipsam semisphaeram, ut NM ad MC, sive ut dupla NM quae est OQ ad duplam MC. Verum ostensum fuit esse conum KML ad eandem semisphaeram, ut OM ad duplam MC. Itaque tota pars solida KLDB erit ad semisphaeram BCD ut tota QM ad duplam MC¹⁰⁾ sive ut EM ad MC. Quare invertendo rursus et per conversionem rationis erit semisphaera dicta ad portionem KLC ut MC ad CE: Et proinde sphaera tota ad KLC portionem ut AC ad CE. Et dividendo, portio KAL ad portionem KCL ut AE ad EC, hoc est ut S ad T. Quod erat ostendendum.

Circumferentiae arcu qui dimidia circumferentia minor sit in tria aequa secto; tres simul rectae quae aequalibus partibus subtenduntur, aequales sunt ei quae toti arcui subtenditur una cum ea linea ad quam subtensa tertiae partis eam habet rationem quam quadratum semidiametri ad quadratum ipsius tertiae arcus parti subtensae.

[Fig. 2.]

Arcus Sectoris ABC in tria aequa divisus sit punctis D et E, subtendanturque partibus rectae BD, DE, EC, et toti arcui linea BC.

Dico tres simul BD, DE, EC aequari subtensae BC una cum ea ad quam DE eam habeat rationem quam quadratum AE ad ED quadratum.

Ductis enim AD, AE, quae ipsam BC secant in G et H, ducatur HF parallela AD. Constat ergo similes esse triangulos ACE, CEH; quare ut AE ad EC ita erit EC ad EH. Itaque proportio AE ad EH duplicata est ejus quae AE ad EC, ac proinde eadem quae quadrati AE ad qu. EC vel qu. ED. Sicut autem AE ad EH ita est DE ad EF, ergo quoque ut qu. AE ad qu. ED ita DE ad EF. DF autem aequalis GH. Itaque cum BD sit aequalis ipsi BG, et CE ipsi CH, et DE duabus GH et FE; apparet tres simul BD, DE, EC aequari toti BC simul et FE, ad quam DE ostensa est eam habere rationem quam AE qu.ad qu. ED.

10) Huygens ajoute ‘24. 5. Elem.’ Voir sur cette proposition la note 28 de la page 312 du T. XI et la note 13, p. 11 du Tome présent. C'est encore ici la seconde partie de la proposition qu'on doit appliquer.