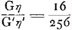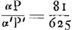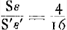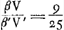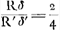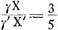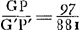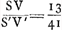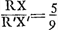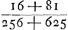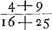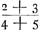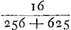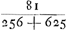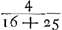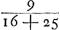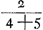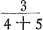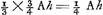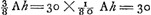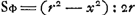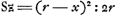Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651
(1908)–Christiaan Huygens–
[pagina 314]
| |
Examen de la cyclométrie
| |
[pagina 315]
| |
EΞ᾽Ε′ΤΑΣΙΣ cyclometriae
| |
[pagina 316]
| |
persuader, qu'il y aurait une seule discussion valable pour toutes laquelle, détruisant la première quadrature, entraînerait les autres à sa suite. Car si nous avons montré qu'il y a erreur dans celle qui est la moins obscure, je ne vois pas pour quelle raison un meilleur succès se laisserait espérer pour les trois suivantes, qui se trouvent enveloppées des plus grandes ténèbres et que l'Auteur lui-même semble mettre au-dessous de cette seule première. Les principes que j'ai dit être communs à toutes les quadratures sont les nouvelles inventions concernant les Proportionalités Géométriques ou les Proportions des proportionGa naar voetnoot4), et sur les solides produits par deux figures planesGa naar voetnoot5). Lesquelles certes je ne combattrai point, car j'estime permis aussi bien de considérer dans la géométrie des corps solides quelconques, que d'employer toute autre chose que nous croyons pouvoir être seulement de quelque utilité dans la recherche de la vérité. Cependant je ne puis laisser de dire au moins ceci, que le très-savant auteur n'a pas appliqué avec assez de bonheur quelques inventions en matière de Proportionalités aux Quadratures et que, dans mon opinion, c'est là la cause de son erreur. C'est ce que j'avais observé tout premièrement dans la proposition 39 du livre 10 de l'Opus Geometricum.Ga naar voetnoot6) Car en prenant les nombres choisis au hasard 2, 3, 4, 5, puis leurs carrés 4, 9, 16, 25 et les carrés des carrés 16, 81, 256, 625, je voyais qu'à ces douze nombres s'applique la même démonstration que celle écrite dans la proposition 39 au sujet d'autant de parallélipipèdes. Et comme pourtant la conclusion n'admettait aucune interprétation plausibleGa naar voetnoot7) je ne doutais pas que son argumentation aussi bien que la mienne que j'avais formulée dans les mêmes termesGa naar voetnoot8) contenait quel- | |
[pagina 317]
| |
nem quae quadraturam primariam infirmatura esset, reliquarum agmen ducentem. Si enim erratum in ea ostenderimus quae minus obscuritatis habet, non video quâ ratione melior successus expectandus sit in tribus sequentibus, quae maximâ caligine involuuntur, quasque Auctor ipse vel uni illi posthabere videtur. Principia quae communia esse omnibus quadraturis dixi, ea sunt nova inventa de Proportionalitatibus Geometricis sive de Proportionum proportionibusGa naar voetnoot4), & de Ductibus plani in planumGa naar voetnoot5). Quae quidem prorsus non impugnabo, nam & solida corpora quaecunque in Geometria considerare licere existimo, & alia omnia adhibere posse, quae modò ullo auxilio fore credimus ad investigationem veri. Unum tamen praetermittere nequeo quin dicam, Clar. Virum non satis feliciter quaedam inventa in materia Proportionalitatum ad Quadraturam applicasse, atque hinc, meâ opinione, ipsi extitisse erroris causam. Primùm omnium id in propos. 39. lib. 10. Oper. Geom.Ga naar voetnoot6) observaveram. Positis enim numeris fortuitò assumptis, 2, 3, 4, 5; deinde horum quadratis 4, 9, 16, 25; & quadratorum quadratis, 16, 81, 256, 625; videbam duodecim hisce eandem demonstrationem convenire, quae in dicta prop. 39. scripta est de totidem parallelepipedis. Et quum tamen conclusio nullam idoneam admitteret interpretationemGa naar voetnoot7), non dubitabam quin aequè ipsius ac mea argumentatio, quam iisdem verbis formaveramGa naar voetnoot8), aliquid absurdicontineret. Poste- | |
[pagina 318]
| |
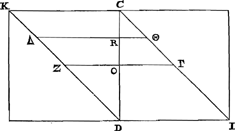
que chose d'absurde. Mais la partie postérieure de la démonstrationGa naar voetnoot9) était juste, et par cela même prouvait qu'on avait failli dans la première. Craignant toutefois que de cette manière surgirait entre nous une dispute intriquée et prolixe, j'eus recours à d'autres inventions et rencontrai enfin ce que je résolus de mettre par écrit ici en peu de mots.Ga naar voetnoot10) Aucune des propositions du très-savant Auteur ne sera l'objet de controverse, mais au contraire en ayant prouvé plusieurs et appliqué à mon usage, je ramènerai la question à ceci que, à moins qu'il ne déclare impossible de conduire sa quadrature à bonne fin et de trouver par elle réellement une figure rectiligne égale au cercle, je lui montrerai de quelle manière cela pourrait ensuite être obtenu très facilement. Après cela en suivant ses propres pas je démontrerai que, par la voie dans laquelle il nous a précedé jusqu'ici, on ne peut parvenir nullement à ce qu'il désire, mais qu'il faut s'arrêter à des conclusions tout à fait absurdes. Mais venons au fait. Soit F [Fig. 1] le centre d'un cercle dont CD est le diamètre. Et après avoir divisé au point G le rayon FC en deux parties égales, tirons les deux perpendicaires FE, GH. Je dis que, lorsque est donné le rapport du segment CHG au segment GHEF, celui du cercle à l'hexagone régulierGa naar voetnoot11) qui lui est inscrit sera également donné. Car menons les droites FH, HC, il est manifeste alors que le triangle FHC sera équilatère, de même que l'arc CE est triple de l'arc HE. Si donc le rapport du segment CHG au segment GHEF est donné, par composition sera donné aussi le rapport du quadrant FEC au segment GHEF. Mais le rapport du secteur FHE au quadrant FHE est également donné, donc est donné aussi le rapport du segment GHEF au secteur FHE, d'où sera donné aussi le rapport du segment GHEF au triangle FHG, par conséquent le rapport du secteur FHE au triangle FHG sera donné. Mais ce dernièr rapport est le même que celui du secteur FHC au triangle FCH (parce que ces deux derniers sont respectivement le double des précédents) et le même rapport est celui du cercle à son hexagone régulier inscrit. Ainsi il paraît que ce dernier rapport est également donné, ce qu'il fallait démontrer. Soient maintenant les droites AB, CD, EFGa naar voetnoot12) toutes égales au diamètre CD du cercle et que sur chacune d'elles soient construits deux carrés. Ensuite soient décrits des sommets A et B les demi-paraboles AVG, BTH dont les bases soient les côtés des carrés BG, AH. Dans les deux carrés suivants soient tirées les diagonales CI, DK. Mais dans les deux derniers carrés soient de nouveau décrits des demi-paraboles EΣL, FΠM, dont les sommets soient E et F, mais les axes les côtés EΨ, FΩ des carrés et es bases ΨL, ΩM. Ensuite après avoir divisé en deux parties égales aux points N, O, P les droites premièrement données et les moitiés | |
[pagina 319]
| |
rior autem demonstrationis parsGa naar voetnoot9) rectè se habebat, ideoque arguebat peccatum in priori. Sed veritus ne intricata & prolixa hinc nobis disputatio oriretur, ad alias inventiones me converti, & tandem ea sese obtulerunt, quae paucis hic perscribere constituiGa naar voetnoot10). Nulla per haec propositionum Cl. Viri in controversiam vocabitur; sed contrà multis earum probatis, atque in usum meum conversis, eò rem deducam, ut si quidem non impossibile dicet quadraturam suam ad exitum perducere, & per eam reapse invenire rectilineum circulo aequale, ostendam qui id facillimè imposterum assequatur. Deinde vestigia ipsius insistens demonstrabo, quibus hactenus
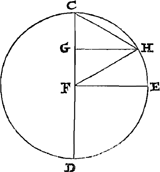 [Fig. 1.].
nobis praecessit, iis nequaquam ad optatum finem perveniri posse, sed esse subsistendum ad conclusiones perquam absurdas. Atque ut ad rem veniamus. Esto circulus cujus centrum F, [Fig. 1] diameter CD. Et diviso radio FC bifariam in G, ducantur ipsi ad angulos rectos FE, GH. Dico, datâ ratione segmenti CHG ad GHEF segmentum, dari quoque rationem circuli ad inscriptum sibi hexagonum regulareGa naar voetnoot11). Jungantur enim FH, HC, & manifestum est triangulum FHC fore aequilaterum; item quadrantis arcum CE triplum fore arcus HE. Si ergo data sit ratio segmenti CHG ad GHEF segmentum, componendo quoque, data erit ratio quadrantis FEC ad segmentum GHEF. Sed data quoque est ratio sectoris FHE ad quadrantem FEC, ergo datur quoque ratio segmenti GHEF ad sectorem FHE; ac proinde dabitur quoque ratio segmenti GHEF ad triangulum FHG; quare & ratio sectoris FHE ad triangulum FHG data erit. Sed huic rationi eadem est ratio sectoris FHC ad triangulum FCH, (quoniam haec utriusque praecedentium dupla sunt;) eademque est circuli ratio ad hexagonum regulare sibi inscriptum. Ergo & hanc datam esse apparet: quod erat demonstrandum. Sunto nunc lineae AB, CD, EFGa naar voetnoot12), singulae aequales diametro circuli CD: & super unaquaque harum construantur bina quadrata. Deinde verticibus A & B describantur semiparabolae AVG, BTH, quarum bases sint quadratorum latera BG, AH. In duobus sequentibus quadratis ducantur diagonii CI, DK. Sed in postremis rursus semiparabolae describantur EΣL, FΠM, quarum vertices E & F, axes verò sint quadratorum latera EΨ, FΩ, & bases ΨL, ΩM. Porrò divisis bifariam singulis lineis quae ab initio positae fuerunt, in N, O, P, & medietatibus rursus bifariam | |
[pagina 320]
| |
de même aux points Q, R, S, soient tirées par les points de division les droites parallèles aux côtés des carrés TV, XY; ZΓ, ΔΘ; ΠΣ, ΛΞ. Le très-savant Auteur fait donc voir dans la démonstration de la proposition 52 [Fig. 1.]
du livre 10 de l'Opus GeometricumGa naar voetnoot13), et cela est très vrai, que dans le cercle précédent [Fig. 1] le segment CHG a avec le segment GHEF le même rapport qu'a ici le solide, qui est produit par les figures planes AYQ [Fig. 2] et AHXQ au solide produit par QYVN et QXTN, car de même que lui, dans sa figure, il fait égales les droites hi, klGa naar voetnoot14), ainsi nous, nous avons pris égales dans le cercle CG, GF et égales à celles-ci AQ, QN. EtGa naar voetnoot15) afin que la méthode même de démontrer soit également connue, voici comment elle procède. Dans la proposition 51 du livre 10 on fait voirGa naar voetnoot16) que le solide produit par la demi-parabole ABG avec la demi-parabole ABH est egal au demicylindre, qui a pour base le demi-cercle CED [Fig. 1] et la hauteur CD. Ensuite dans le Corollaire de la même proposition il est exposé que la même chose convient aussi bien aux parties qu' aux solides entiers. C'est-à-dire le solide produit par les figures planes QYVN et QXTN est aussi égal à la partie du dit demi-cylindre qui a pour base le segment GHEF. De même le solide produit par AYQ et AHXQ est égal à la partie du même demi-cylindre qui repose sur le segment CHGGa naar voetnoot17). Ce dont le dernier est clair aussi par ceci qu' autrement la somme de ces deux solides, savoir le solide produit par AVN avec AHTN ne serait pas égal à la moitié du demi-cylindre indiqué et que par conséquent serait faux ce qui est concédé, savoir que le solide produit par la demi-parabole ABG avec la demi-parabole ABH est égal à l'entier demi-cylindre. Il paraît donc, puisque les deux parties nommées du demi-cylindre ont le même | |
[pagina 321]
| |
in Q, R, S, ducantur per divisionum puncta, quadratorum lateribus parallelae, TV, YX; ZΓ, ΔΘ, ΠΣ, ΛΞ. Ostendit itaque Cl. V. in demonstr. prop. 52. lib. 10. Oper. Geom.Ga naar voetnoot13) & verissimum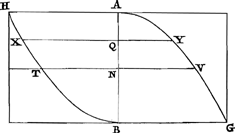 [Fig. 2.]
 [Fig. 3.]
 [Fig. 4.]
est, in circulo superiori [Fig. 1] segmentum CHG ad segmentum GHEF, eandem habere rationem quam habet hîc solidum quod fit ex ductu plani AYQ [Fig. 2] in planum AHXQ, ad solidum ortum ex ductu plani QYVN in planum QXTN; sicut enim in planum ille in suo schemate sumit aequale lineas hi, klGa naar voetnoot14), ita nobis aequales sunt sumptae in circulo, CG, GF, & hisce pares AQ, QN. AtqueGa naar voetnoot15) ut ipsa demonstrandi methodus quoque noscatur, ea hujusmodi est. In prop. 51. lib. 10. ostenditurGa naar voetnoot16) solidum quod fit ex ductu semiparabolae ABG in semipar. ABH, aequari semicylindro, basin habenti semicirculum CED [Fig. 1] & altitudinem CD. Deinde in Corollario ejusdem prop. idem quoque singulis partibus quod totis solidis conuenire docetur. Nimirum id solidum quod fit ex ductu plani QYVN in planum QXTN, aequatur quoque parti dicti semicylindri quae insistit segmento GHEF; Itemque solidum ex ductu plani AYQ in pl. AHXQ, aequatur ejusdem semicylindri parti quae insistit segmento CHGGa naar voetnoot17). Quorum hoc vel ex eò constat, quod alioqui duo ista solida simul sumpta, hoc est, solidum ex ductu plani AVN in pl. AHTN, aequale non esset dimidio ejus quem diximus, semicylindri; & consequenter falsum quoque esset quod in confesso est, nimirum solidum ex ductu semiparab. ABG in semiparab. ABH aequari toti semicylindro. Apparet igitur, quoniam dictae semi- | |
[pagina 322]
| |
rapport que celui des bases sur lesquelles elles reposent, qu'il est certain ce que nous disions, savoir que le segment de cercle CHG est à GHEF comme le solide produit par AYQ avec AHXQ nu solide produit par QYVN avec QXTN.  [Fig. 2.]
 [Fig. 3.]
 [Fig. 4.]
J'ai voulu écrire ceci si spécieusement afin qu'à quelque lecteur, qui ignorerait peut-être la nature de la démonstration qu' emploie le savant auteur, il ne puisse rester de scrupule de ce que là où lui, dans la proposition 52 du livre 10, considère deux segments de cercle, tels à peu près que GHEF, moi pour l'un d'eux j'ai pris le segment CHG: et de ce que dans la droite AB je prenne depuis l'origine A même deux parties égales AQ, QN. Ceci ne peut pas retenir le savant auteur lui-même, ni ici, ni dans ce qui suit puisque, quand dans cette proposition 52 et dans 44 du livre 10Ga naar voetnoot18) il prescrit de prendre dans la droite ab les deux hi, klGa naar voetnoot19) égales entre elles, il sait que cela n'admet aucune restriction; comme aussi dans la figure correspondante appartenantà la proposition 39 du livre 10, partout dans la ligne ab, il prend ik divisée en deux parties égales im, mk. La même chose arrive dans la proposition suivante 40.Ga naar voetnoot20) Je retourne maintenant à ce que je m' étais proposé, et il est donc démontré à présent que, lorsque est donné le rapport du solide produit par AYQ [Fig. 2] avec AHXQ, au solide produit par QYVN avec QXTN par cela même est donné aussi le rapport du segment CHG au segment GHEF, et que par consé- | |
[pagina 323]
| |
cylindri partes eandem inter se rationem habent quam bases quibus insistunt, certum esse quod diximus, segmentum circuli CHG ad GHEF, esse ut solidum ex ductu plani AYQ in pl. AHXQ ad solidum ex ductu plani QYVN in pl. QXTN.  [Fig. 2.]
 [Fig. 3.]
 [Fig. 4.]
Haec ita enucleatè scribere volui, ne cui ignaro fortasse naturae demonstrationum quibus Cl. V. utitur, scrupulus restare posset, quod ubi ille in d. prop. 52, lib. 10, duo circuli segmenta considerat, quale ferè est GHEF, ego pro altero eorum sumpserim segmentum CHG: Quodque in linea AB abipsotermino A aequales partes capiam AQ, QN. Ipsum autem Cl. Virum haec remorari non possunt, neque hîc, neque in sequentibus; quia cùm in d. prop. 52. & 44, lib. 10.Ga naar voetnoot18) praecipit in linea ab aequales inter se sumi hi, klGa naar voetnoot19), scit hoc nullam limitationem admittere; sicut & in schemate communi prop. 39, lib. 10, ubivis in linea ab sumitur ik, quae dividitur in duas aequales im, mk. Idem contingit in prop. sequenti 40Ga naar voetnoot20). Revertor autem ad propositum & constat nunc quidem, si detur Ratio solidi quod fitex ductu plani AYQ [Fig. 2] in pl. AHXQ, ad solidum ex ductu plani QYVN in pl. QXTN, eo ipso dari quoque rationem segmenti CHG [Fig. 1] ad segmentum GHEF, ac proinde continuò tunc | |
[pagina 324]
| |
quent on peut immédiatement trouver le rapport du cercle à son hexagone inscrit. Nommons, pour abréger, le solide que nous disions être produit par AYQ avec AHXQ, le solide HY. Et de même celui produit par QYVN avec QXTN le solide XV. Et nommons de même ce qui est produit par CΘR avec CKΔR le solide KΘ, et appliquons la même locution aux solides ΔΓ, MΞ, ΛΣ, desquels on comprend maintenant assez ce qu'ils doivent désigner. Cela posé, il faut savoir que pour le savant auteur tout espoir et toute base de la Quadrature à effectuer sont fondées en ceci qu'il estime facile de trouver le rapport du solide HY au solide XV (lequel rapport j'ai déjà dit être la seule chose qui reste à désirer) dès que l'on connaît les deux rapports suivants savoir celui du solide MΞ au solide ΛΣ, et celui du solide KΘ au solide ∆Γ.Ga naar voetnoot21) Car alors on pourra argumenter comme il suit. Connu est le rapport du solide MΞ au solide ΛΣ, de même celui du solide KΘ au solide ∆Γ; donc est connu aussi combien de fois le premier rapport contient le dernier, or, autant de fois que celui-là contient celui-ci, autant de fois ce dernier, c'est-à-dire le rapport du solide KΘ au solide ΔΓ contient le rapport du solide HY à XV, donc aussi ce dernier rapport sera connu. Comment on doit comprendre ces déductions paraîtra mieux plus loin, où nous répéterons la même argumentation. Entretemps je suis certain que rien de ce que j'ai dit ne sera nié par le savant auteur; qu'il considère seulement que dans la droite AB on a pris les parties AQ, QN etc. égales entre elles, et à celles-ci les parties CR, RO, ES, SP. Si donc je lui aurai indiqué quel est le rapport du solide MΞ au solide ΛΣ, et aussi quel est le rapport du solide KΘ au solide ΔΓ, et que même alors il ne puisse dire quel est le rapport du solide HY au solide XV, il devra avouer qu'il a tenté en vain la Quadrature tant du Cercle que de l'Hyperbole. Du Cercle, parce qu'il verra alors que la Proposition 44 du livre 10 de l'Opus GeometricumGa naar voetnoot21) n'aboutit nullement, laquelle sera vaine et sans valeur tant que, par les rapports connus du solide MΞ au solide ΛΣ et du solide KΘ au solide ΔΓ, n'est pas connu le rapport du solide HY au solide XV. De l'Hyperbole, parce que la proposition 146Ga naar voetnoot22) du même livre 10, sur laquelle repose cette quadrature, est la même que la proposition citée 44, et se trouve appliquée à l'Hyperbole dans les mêmes termes. Si, au contraire, lorsque ces deux rapports sont donnés, il aurait pu trouver ensuite celui du solide HY au solide XV, alors il peut croire avoir réellement carré le Cercle. Car ainsi sera connu le rapport du segment CHG [Fig. 1] dans le cercle au segment GHEF et ce qui reste à faire est facilement accompli. Je dirai maintenant quels sont ces rapports. Quant au premier, savoir celui du solide MΞ au solide ΛΣ, je dis qu'il est le même que celui des nombres 53 à 203, tandis que l'autre, le rapport du solide KΘ au solide ΔΓ est celui de 5 à 11 et de ces deux rapports je donnerai plus loin la démonstration. Mais d'abord je montrerai ce que j'ai promis au commencement, savoir que lorsque ces deux rapports sont connus, on ne peut pourtant pas, au moins par ce | |
[pagina 325]
| |
inveniri posse quam rationem circulus habeat ad inscriptum hexagonum regulare. Vocemus autem brevitatis gratia, id quod fieri diximus ex ductu plani AYQ in planum AHXQ, solidum HY. Item quod fit ex ductu plani QYVN in planum QXTN, solidum XV. Similiter quod oritur ex ductu plani CΘR [Fig. 3] in planum CKΔR, vocemus solidum KΘ; eâdemque brevitate dicamus solida ΔΓ, MΞ [Fig. 4], ΛΣ, quibus quae denotentur jam satis intelligatur. His sic constitutis, sciendum est, omnem spem & fundamentum perficiendae Quadraturae Cl. Viro in eo positum esse, quod existimet rationem solidi HY ad solidum XV (quam unicam tantum desiderari jam admonui) facilè inveniri posse, si cognitae sint duae rationes hae, nimirum ratio solidi MΞ ad sol. ΛΣ, & ratio solidi KΘ ad sol. ΔΓ.Ga naar voetnoot21) Sic enim tunc argumentabitur; Nota est ratio solidi MΞ ad sol. ΛΣ, item ratio solidi KΘ ad sol. ΔΓ, ergo notum quoque quoties illa ratio hanc contineat; Quoties autem illa hanc continet toties haec ipsa, scilicet ratio solidi KΘ ad sol. ΔΓ, continet rationem solidi HY ad XV; ergo & haec ratio nota erit. Quomodo haec intelligenda sint paulò inferiùs melius patebit, ubi eandem argumentationem repetemus. Interea certò scio nihil horum quae dixi mihi à Cl. V. negatum iri, modò consideret in linea AB, sumptas esse aequales inter se partes AQ, QN, & hisce pares CR, RO; ES, SP. Si igitur indicavero ipsi quae sit ratio solidi MΞ ad sol. ΛΣ, item quae sit ratio solidi KΘ ad sol. ΔΓ, & ne tum quidem dicere possit quam rationem habeat solidum HY ad sol. XV, fateatur sanè se frustra utramque Quadraturam tentasse, tam Circuli quam Hyperboles. Circuli; quoniam tunc videbit nequaquam procedere Propositionem 44. lib. 10. Oper. Geom.Ga naar voetnoot21) quae vana & inanis erit, nisi ex notis rationibus solidi MΞ ad sol. ΛΣ, & solidi KΘ ad sol. ΔΓ, innotescat ratio solidi HY ad sol. XV. Hyperboles verò; quoniam prop. 146Ga naar voetnoot22) ejusd. lib. 10. cui haec quadratura innititur, eadem est cum dicta prop. 44 & iisdem verbis Hyperbolae applicatur. Sin verò datis istis duabus rationibus invenire posthac potuerit rationem solidi HY ad sol. XV, tum se credat Circulum reverâ quadravisse. Nota enim sic erit ratio segmenti CHG [Fig. 1] in circulo ad segmentum GHEF, & reliqua facile perficientur. Dicam autem nunc ipsas Rationes. Et primam quidem, hoc est rationem solidi MΞ ad sol. ΛΣ, aio esse eandem quae numeri 53 ad 203. Alteram verò, rationem solidi KΘ ad sol. ΔΓ, eam quae 5 ad 11. atque horum utrumque infrà sum demonstraturus. Priùs autem quod ab initio promisi etiam ostendam, hisce Rationibus cognitis, tamen rationem sol. HY ad sol. XV, per ea quidem quae nos adhuc | |
[pagina 326]
| |
que le savant auteur nous a enseigné jusqu'ici, trouver le rapport du solide HY au solide XV. En effet, s'il veut trouver, au moyen des rapports donnés du solide MΞ au solide ΛΣ et du solide KΘ au solide ΔΓ, le troisième rapport du solide HY au solide XV, il raisonnera de la manière suivante, comme on peut le voir par la démonstration de la proposition 44 citée ci-dessus, avec laquelle manifestement ce cas est identique. Il dira donc, connus sont le premier et le second rapport (car ils sont de 53 à 203, et de 5 à 11) donc est connu aussi combien de fois le premier rapport contient le second. Mais autant de fois que le premier contient le second, autant de fois le second contient le troisième (c'est ce qu'il prétend dans la proposition 40 du livre 10 de l'Opus Geometricum.Ga naar voetnoot23) Donc est connu aussi combien de fois le second contient le troisième, et comme le second est connu, le troisième le sera également, c'est-à-dire celui du solide HY au solide XV. Par conséquent, il lui incombera maintenant de désinir combien de fois le premier rapport contient le second, c'est-à-dire combien de foit le rapport de 53 à 203 contient le rapport 5 à 11. Mais d'abord comment va-t-il expliquer ici le terme contenir? De telle manière qu'il signifie la même chose qu' ailleurs contenir par multiplication?Ga naar voetnoot24) et que le rapport 53 à 203 soit dit de multiplier le rapport 5 à 11 soit deux fois (c'est-à-dire que le premier est le carré du dernier, car ainsi il semble comprendre le terme continere dans la proposition 40, tantôt citée, du livre 10) ou trois fois, ou quatre fois ou même plus. Mais ceci ne peut pas avoir lieu parce que le rapport 53 à 203 n'est du rapport 5 à 11 ni le carré, ni la troisième puissance ou quelque puissance plus élevée, vu que ce n'est que 53 à 256½⅗ qui soit le carré du rapport 5 à 11. Va-t-il donc appliquer au terme Continere le même sens qu'il a dans la proposition 125 du livre 8 de l'Opus Geometricum?Ga naar voetnoot25) Je puis à peine le soupçonner, mais même s'il le voulût, il en résultera également une absurdité. Car selon cette interprétation autant de fois que le rapport 53 à 203 contient le rapport 5 à 11, autant de fois cette dernière même contiendra le rapport 5075 à 6413Ga naar voetnoot26) car ceci paraîtra lorsqu'on examine entre eux ces rapports d'après la règle de la dite proposition 125. Le rapport du solide HY [Fig. 2] au solide XV, ou ce qui est la même chose, le rapport du segment de cercle CHG [Fig. 1], proposé d'abord, au segment GHEF serait donc de même de 5075 à 6413. Par conséquent des parties, telles que le segment CHG en contient 5075, le segment GHEF en contiendrait 6413, et par conséquent le quadrant FCE 11488; et le secteur FHE (qui est le tiers du quadrant) 3829⅓; et le triangle GHF 2583⅔. Mais, comme le secteur FHE est au triangle | |
[pagina 327]
| |
docuit V. Cl. inveniri non posse. Etenim inventurus ex datis rationibus, sol. MΞ ad sol. ΛΣ, & solidi KΘ ad sol ΔΓ, rationem tertiam solidi HY ad sol. XV, in hunc modum ratiocinabitur, ut videre est ex demonstratione prop. 44. suprà citatae, cui hunc casum convenire liquido constat. Dicet enim, Notae sunt prima & secunda ratio, (istae enim sunt 53 ad 203, & 5 ad 11,) ergo notum quoque quoties prima secundam contineat. Sed quoties prima continet secundam, toties secunda continet tertiam, (hoc asserit prop. 40. lib. 10. oper. Geom.)Ga naar voetnoot23) Ergo notum quoque quoties secunda tertiam contineat. Quare cum nota sit secunda, etiam tertia nota erit, ea nimirum quam habet solidum HY ad sol. XV. Consequenter hoc nunc definiendum ei incumbet, Quoties Ratio harum prima secundam contineat; hoc est, quoties ratio 53 ad 203, contineat rationem 5 ad 11. Sed enim quo sensu verba continere hîc explicaturus est? Num eo, ut idem significet quod alibi continere per multiplicationem?Ga naar voetnoot24) utque ratio 53 ad 203 rationem 5 ad 11. multiplicare dicatur vel bis (hoc est ut illa hujus sit duplicata, ita enim continere intelligendum videtur in propositione 40. lib. 10, modo citata) vel ter, vel quater, saepiùs etiam. Et hoc quidem esse non potest, nam ratio 53 ad 203, rationis 5 ad 11, neque duplicata est neque triplicata vel ulteriùs multiplex, quum demum ratio 53 ad 256 ½⅗ sit duplicata rationis 5 ad 11.  [Fig. 1].
An igitur verbum Continere in eum sensum trahet, quem habet in propositione 125. lib. 8. Oper. Geom?Ga naar voetnoot25) Vix quidem illud suspicari possum; sed etiamsi vellet rursus inde absurdum consequetur. Nam secundum interpretationem istam; quoties ratio 53 ad 203 continet rationem 5 ad 11, toties haec ipsa continebit rationem 5075 ad 6413Ga naar voetnoot26); hoc autem patebit horum numerorum inter se rationes examinanti secundùm regulam dictae propositionis 125. Esset igitur ratio solidi HY [Fig. 2] ad sol. XV, hoc est, ratio segmenti circuli ab initio propositi CHG [Fig. 1], ad segmentum GHEF, eadem quae 5075 ad 6413. Quare qualium partium segmentum CHG esset 5075, talium segmentum GHEF esset 6413; & proinde quadrans FCE 11488; & sector FHE (qui quadrantis tertia pars est) 3829⅓: & triangulum GHF 2583⅔. Sicut autem sector FHE ad triang. GHF, ita est sector | |
[pagina 328]
| |
GHF ainsi est le secteur FHC au triangle FCH et ainsi le cercle CD à son hexagone régulier inscrit. Donc aussi des parties telles que le cercle en contient 3829⅓ l'hexagone inscrit en contiendrait 2583⅔. Mais des parties telles que l'hexagone inscrit en contient 2583⅔ l'hexagone regulier circonscrit en contient 34448/9, parce que ce dernier est 4/3 du premier. Par conséquent des parties telles que le cercle en contient 3829⅓, l'hexagone circonscrit en contiendrait 34448/9, de sorte que celui-ci serait moindre que le cercle ce qui est absurde. Nous avons donc rendu manifeste que des deux interprétations du mot Continere aucune ne peut convenir à notre cas. Mais en dehors de celles-là il n' en a donné aucune autre dans son ouvrage; il n'a donc pas enseigné la manière de déterminer combien de fois le rapport du solide MΞ au solide AΣ contienne le rapport du solide KΘGa naar voetnoot27) au solide ΔΓ et par conséquent ne pourrait pas non plus déterminer combien de fois ce rapport contient le rapport du solide HY au solide XV. D'où il paraît que ce rapport, même alors que les deux premiers sont donnés, ne peut être connu au moyen de ce que le très-savant auteur a trouvé, et que par conséquent il a espéré en vain de pouvoir effectuer de cette manière la quadrature du cercle. Il ne me reste maintenant que de rendre manifeste ce que j'ai posé dans ce qui précède, en disant que je démontrerais que le solide MΞ [Fig. 4] est au solide ΔΣ comme 53 à 203, et de même que le solide KΘ [Fig. 3] aurait au solide ΔΓ le même rapport que 5 à 11. Mais comme pour démontrer le premier il est nécessaire que nous fachions quelle est le Rapport de l'onglet Parabolique à son Cylindre de même base et de même hauteur; à cet effet faisant connaître ce rapport, nous allons augmenter le Traité que le très-savant Auteur donne sur cet Onglet, dans la Partie 5 du livre 9,Ga naar voetnoot28) d'un Théorème excellent, lequel je m'étonne que l'Auteur n'a pas trouvé lui-même parce qu'il se déduit facilement des choses qu'il avait déjà démontrées, ainsi qu'il paraîtra bientôt. Répétant donc pour autant qu'il sera nécessaire ici sa figure de la proposition 99Ga naar voetnoot29) du livre 9, soit un Cylindre Parabolique ayant pour bases opposées les paraboles ABD, VCE, duquel soit découpé l'Onglet ABCD ayant la même base et la même hauteur. Je dis que le rapport du Cylindre à l'Onglet est de 2½ ou comme 5 à 2. Après avoir copié de la même figure ce qui reste, FB est le diamètre de la parabole ABD et AB, BD sont des droites. Ayant tirée ensuite sur la surface du cylindre la droite BC et ayant prise sa quatrième partie CQ, le plan PQN découpe l'onglet PQCN et on joindra encore CA, CD. Enfin au cylindre entier est ajoutée encore | |
[pagina 329]
| |
FHC ad triangul. FCH, & ita circulus CD ad inscriptum sibi hexagonum regulare. Ergo quoque qualium partium circulus CD esset 3829⅓ talium hexagonum inscriptum foret 2583⅔. Qualium autem hexagonum inscriptum est 2583⅔, talium hexagonum regulare circumscriptum est 34448/9; quoniam hoc inscripti est sesquitertium: Ergo qualium partium circulus CD esset 3829⅓, talium hexagonum circumscriptum esset 34448/9, atque ita esset ipso circulo minus, quod est absurdum. Manifestum igitur fecimus, ex duabus interpretationibus verbi Continere, neutram casui nostro accommodari posse. Aliam autem praeter illas nullam in suo opere attulit; non docuit igitur modum determinandi, quoties [ratio sol. MΞ ad sol. ΛΣ contineat rationem sol.]Ga naar voetnoot27) KΘ ad solid. ΔΓ, ac proinde nec determinari poterit quoties haec ratio contineat rationem solidi HY ad solid. XV. Quare liquet, hanc rationem, ne duabus quidem prioribus istis datis, per inventa Clariss. Viri cognosci posse: ideoque frustra ipsum sperasse hoc modo perficere Circuli quadraturam. Restat nunc tantùm ut manifesta faciam quae in praecedentibus posita fuere, dixi enim me demonstraturum, quòd solidum MΞ[Fig. 4] esset ad solid. ΔΣ, ut 53 ad 203: item quòd solidum KΘ [Fig. 3] rationem haberet ad solidum ΔΓ, quam 5 ad 11. Quoniam autem ad horum primi demonstrationem necessarium est, ut notum habeamus, quae sit Ratio ungulae Parabolicae ad Cylindrum suum, qui basi insistit eidem, & eandem habet altitudinem; id circò hanc Rationem declarantes, Tractatum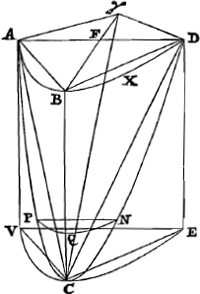 [Fig. 5.]
Clariss. Viri, quem de eadem Ungula, Parte 5. lib. 9.Ga naar voetnoot28) proposuit, uno egregrio Theoremate auctiorem reddemus, quod miror ipsum non invenisse, quum ex iis quae jam ostenderat facili negotio deducatur, ut jam statim apparebit. Repetitâ enim quatenus hîc necesse erit figurâ ipsius, quae est in propositione 99.Ga naar voetnoot29) lib. 9. Esto Cylindrus Parabolicus, bases oppositas habens parabolas ABD, VCE; à quo sit abscissa Ungula ABCD, eâdem basi & altitudine. Dico Cylindrum ad hanc Ungulam habere rationem duplam sesquialteram, sive quam 5 ad 2. Transcriptis enim reliquis ex figura eâdem, est FB diameter parabolae ABD: & lineae rectae AB, BD. Ducta porro BC recta in superficie cylindri, sumptâque ejus quartâ parte CQ, abscinditur plano PQN ungula PQCN & junguntur CA, CD. | |
[pagina 330]
| |
la pyramide ADγC égale à la partie BXDEC, découpée du cylindre par le plan BDEC. Et jusqu' ici il nous suffira d'avoir répété la construction du très-savant auteur. Or, il a démontré ces deux propriétés suivantes, comme on peut le voir dans la dite proposition 99 du livre 9, savoir que l'onglet ABCD est à l'onglet PQCN comme 32 à 1,Ga naar voetnoot30) et de même que cet onglet PQCN est à la pyramide entière AγDBC laquelle est composée des deux pyramides ADBC et ADγC, comme 1 à 30.Ga naar voetnoot31) Donc, par la règle de la proportion dérangée, l'onglet ABCD est à la pyramide comme 32 à 30 ou comme 16 à 15. De plus, comme le segment BDX est la huitième partieGa naar voetnoot32) de la parabole ABD, le segment solide BXDEC ou la pyramide ADγC qui lui est égale, sera la huitième partie du cylindre parabolique entier AVCEDB; mais l'autre pyramide ADBC est égale à deux huitièmes ou au quart du même cylindre parabolique, (car elle est le tiers de son prisme lequel est égal aux trois quarts de ce cylindre comme il paraît par la quadrature de la parabole); donc la pyramide entière AγDBC est égale aux trois huitièmes du cylindre parabolique AVCEDB. Le cylindre parabolique AVCEDB sera donc à la pyramide AγDBC comme 8 à 3, c'est-à-dire comme 40 à 15; mais on a montré que la même pyramide AγDBC est à l'onglet ABCD comme 15 à 16. Donc, par la règle citée, le cylindre parabolique AVCEDB est à l'onglet ABCD comme 40 à 16, c'est-à-dire comme 5 à 2, ce qu'il fallait démontrer. Les propriétés que j'ai dit ici avoir été démontrées par le très-savant auteur sont très vraies et par conséquent il n'y a pas de quoi faire douter de la verité de ce Théorème, dont je pourrais apporter encore une autre démonstration tout à fait différente,Ga naar voetnoot33) si je n'avais hâte d'arriver à ce qui suit. | |
[pagina 331]
| |
Denique toti cylindro adjuncta est pyramis ADγC aequalis parti BXDEC, quae à cylindro abscissa est plano BDEC. Et hactenùs quidem sufficiet nobis constructionem Cl. V. repetiisse. Demonstravit autem haec duo quae sequuntur, sicut
 [Fig. 5.]
videre est in dicta prop. 99. lib. 9. Nimirum quod ungula ABCD est ad ungulam PQCN, sicut 32 ad 1Ga naar voetnoot30). Item quòd haec ungula PQCN est ad pyramidem totam AγDBC, (quae composita est ex duabus pyramidibus ADBC & ADγC) ut 1 ad 30Ga naar voetnoot31). Erit igitur ex aequo ungula ABCD ad pyramidem AγDBC ut 32 ad 30, hoc est, ut 16 ad 15. Porrò cum parabolae ABD octava pars sit segmentum BDXGa naar voetnoot32), erit quoque segmentum solidum BXDEC vel huic aequalis pyramis ADγC, octava pars cylindri totius parabolici AVCEDB: sed pyramis altera ADBC aequatur duabus octavis sive uni quartae ejusdem parabolici cylindri; (est enim ipsa tertia pars sui prismatis quod aequale est tribus quartis cylindri istius, ut ex quadratura parabolae constat) ergo tota pyramis AγDBC tribus octavis aequatur cylindri parab. AVCEDB. Cylindrus igitur parabolicus AVCEDB erit ad pyramidem AγDBC, ut 8 ad 3, hoc est, ut 40 ad 15; sed ostensum est eandem pyramidem AγDBC esse ad ungulam ABCD ut 15 ad 16. Igitur ex aequo erit cylindrus parabolicus AVCEDB ad ungulam ABCD ut 40 ad 16, hoc est, ut 5 ad 2; quod fuit demonstrandum. Quae hîc dixi à Cl. Viro ostensa suisse, verissima sunt, ac proinde non est quòd de veritate hujus Theorematis dubitemus: Cujus aliam quoque demonstr.Ga naar voetnoot33) adferre possem, longè ab ista diversam, nisi ad sequentia properarem. | |
[pagina 332]
| |
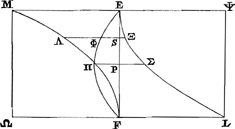
Reprenant dont la dernière partie de la figure que j'ai décrite plus hautGa naar voetnoot34), proposons nous de démontrer que le solide MΞ [Fig. 4], c'est-à-dire celui produit par EΞS avec EMΛS est au solide
 [Fig. 4.]
ΛΣ, produit par SΞΣP avec SΛΠP, comme 53 à 203. Soit décrite sur EF la parabole EΠF ayant l'axe PΠ, qu' on sait être le quart de EF ou de ME. Cette parabole EΠF sera donc la même que celle que le très savant auteur dans les propositions 41Ga naar voetnoot35) et 42 du livre 10 désigne par les lettres ARB. Car il dit dans la dite proposition 42, et cela est très vrai, que le solide produit par EΣLF avec FΠME égale le solide produit par la parabole EΠF avec soi-même, comme aussi ce qu'il ajoute dans le Corollaire 1, savoir que le solide produit par SΞΣP avec SAΠP égale le solide produit par SΦΠP avec soi-même,Ga naar voetnoot36) d'où pareillement le solide produit par EΞS avec EMΛS égale le solide produit par EΦS avec soi-même. Il faut donc montrer que le solide produit par EΦS est au solide produit par SΦΠP, l'une et l'autre avec elles-mêmes, comme 53 à 203. Soit l'onglet AEFΠ [Fig. 6], dont la base parabolique EΠF soit prise de la figure précédente [Fig. 4] et divisée de la même manière par les droites ΠP, ΦS. Mais soit la hauteur de l'onglet AΠ le double du diamètre ΠP de la base. Ce sera donc le même onglet qu'il considère, dans la dite proposition 42 du livre 10 et dans son corollaire 2, comme produit par la parabole EΠF avec soi-même. En effet, il a appliqué la même considération que celle du Scholium de la proposition 19 du livre 9.Ga naar voetnoot37) Car autrement d'un tel produit il faudrait dire plutôt que se produisent deux onglets ayant chacun la hauteur égale au diamètre ΠP. Si maintenant on mène un plan par AΠP et un autre DΦS parallèle à ce dernier et passant par la droite ΦS, alors la partie de l'onglet compris entre ces deux plans sera égale au solide produit par SΦΠP avec soi-même et la partie EDSΦ de l'onglet égale au solide produit par EΦS avec soi-même. Par conséquent il faut maintenant seulement démontrer que la partie EDSΦ est à la partie ΦAP comme 53 à 203. Soit ΦN parallèle à EP et NC parallèle à ΠA. Donc, puisque d'après la propriété de la Parabole PN est ¾ ΠP, PC sera aussi égal à ¾ AP. Mais SD est aussi égale à ¾ AP, parceque elle lui est parallèleGa naar margenoot*) et que EAF est une para- | |
[pagina 333]
| |
Repetitâ igitur parte ultimâ schematis, quod suprà descripsimusGa naar voetnoot34), sit ostendendum, quòd solidum MΞ [Fig. 4], id est, quod oritur ex ductu plani EΞS in planum EMΛS ad solidum ΛΣ, id est, quod oritur ex ductu plani SΞΣP in planum SΛΠP, eam habet rationem quam 53 ad 203. Describatur super EF parabola EΠF, axem habens PΠ, quam constat esse quartam partem ipsius EF sive ME. Erit igitur parabola EΠF eadem quam V. Cl. in prop. 41.Ga naar voetnoot35) & 42. lib. 10. notat literis ARB. Ait autem in dicta prop. 42. & verissimum est, solidum quod producitur ex ductu plani EΣLF in planum FΠME aequari solido quod fit ex parabola EΠF ducta in se ipsam: sicut illud quoque quod subjungit in Coroll. 1 nimirum quod solidum
 [Fig. 6.]
ex plano SΞΣP in planum SΛΠP, aequatur solido ex ductu plani SΦΠP in se ipsumGa naar voetnoot36); unde similiter solidum ex plano EΞS in planum EMΛS aequabitur solido ex plano EΦS in se ipsum ducto. Oportet itaque ostendere solidum ortum ex plano EΦS ad solidum ex plano SΦΠP, utroque in se ipsum ducto, esse ut 53 ad 203. Esto ungula parabolica AEFΠ [Fig. 6], cujus basis parabola EΠF repetita sit ex figura praecedenti [Fig. 4], eodemque modo ut istic divisa lineis ΠP, ΦS. Sit autem altitudo ungulae AΠ dupla diametri basis ΠP. Erit igitur haec ea ungula, quam intelligit in prop. dicta 42. lib. 10. ejusdemque coroll. 2. fieri ex ductu parabolae EΠF in se ipsam. Eâdem nimirum consideratione usus quae est in Scholio propos. 19. lib. 9.Ga naar voetnoot37) Nam alioqui ex ejusmodi ductu potius dicendum esset geminas ungulas produci, singulas altitudine aequales diametro ΠP. Ducto deinde plano per AΠP, & alio huic parallelo DΦS secundum lineam ΦS, erit jam pars ungulae hisce duobus planis terminata, aequalis solido quod fit ex ductu plani SΦΠP in se ipsum; & pars ungulae EDSΦ, aequalis ei solido quod fit ex ductu plani EΦS in se ipsum. Quare nunc demonstrandum erit duntaxat, partem EDSΦ esse ad partem ΦAP ut 53 ad 203. Sit ΦN parallela EP, & NC parallela ΠA. Ergo quoniam ex proprietate Paraboles, PN est ¾ ΠP, erit quoque PC ¾ AP. Verùm & SD aequatur ¾ AP, quum sit huic parallelaGa naar margenoot*), sitque parabola | |
[pagina 334]
| |
bole. Donc si l'on joint CD, cette droite sera parallèle et égale à PS et NΦ. Menons suivant DC le plan DBC parallèle à la base EΠF, la demi-parabole BDC sera égale et semblable à la demi-parabole ΠΦN, et ΦBN sera un demicylindre parabolique, mais DACB la moitié d'un onglet. Mais celui-ci est égal, comme nous l'avons demontré précédemment, aux deux cinquièmes du demicylindre ayant DBC pour base et la hauteur BA. Donc, puisque le demi-cylindre ΦBN a une hauteur triple de BA, le demi-onglet DACB sera au demi-cylindre ΦBN comme 2 à 15, c'est-à-dire comme 8 à 60.  [Fig. 6.]
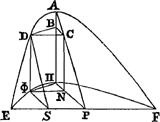
Après avoir ensuite tiré la droite ΦΠ, on sait que la demi-parabole ΠΦN est au triangle ΠΦN comme 4 à 3; mais le triangle ΠΦN est au rectangle ΦP comme 1 à 6 (car la base ΠN est le tiers de NP) c'est-à-dire comme 3 à 18. On aura donc, par la règle de la proportion dérangée, que la demi-parabole ΠΦN est au rectangle ΦP comme 4 à 18. Donc aussi le demi-cylindre ΦBN est au parallélipipède de la même hauteur sur la base ΦP comme 4 à 18. Mais la moitié de ce parallélipipède est le prisme DNS; donc le demi-cylindre ΦBN est au prisme DNS comme 4 à 9 c'est-à-dire comme 60 à 135. Donc des parties, desquelles le demi-onglet DCAB en contenait 8 le demi-cylindre parabolique ΦBN en contenait 60 (comme il a été montré ci-dessus) et le prisme DNS en contiendra 135. Et par suite le solide AΠSD, qui est composé de ces trois, en aura 203. Mais le demi-onglet ADCB est au demi-onglet EAPΠ comme 1 à 32, ainsi que le très-savant auteur l'a démontré dans la proposition 95 du livre 9.Ga naar voetnoot39) Donc des parties dont le demi-onglet ADBC en contient 8, le demi-onglet EAPΠ en contiendra 256, puisque comme 1 est à 32, ainsi 8 à 256. Mais nous avons dit que la partie AΠSD en contient 203. Donc le demi-onglet EAPΠ est à la partie AΠSD comme 256 à 203 et par division la partie restante EDSΦ à la partie AΠSD comme 53 à 203, ce qu'il fallait démontrer. Nous avons donc montré qu' aussi le solide que nous avons dit plus haut produit par EΞS [Fig. 4] avec EMΛS a le même rapport au solide produit par SΞΣP avec SΛΠP que 53 à 203.Ga naar voetnoot40) Abordons enfin l'autre théorème que nous avons promis de démontrer et, reproduisant la deuxième des trois figures décrites plus haut [Fig. 3], proposons nous de prouver que le solide produit par CΘR avec CKΔR est au solide produit par RΘΓO avec RΔZO comme 5 à 11. Sur le côté CD du triangle CDI soit élevé perpendiculairement le triangle CKD [Fig. 7], puis menée la droite KI. La pyramide CDIK sera maintenant le solideque l'on dit être produit par le triangle CDI avec le triangle CDK. Mais cette | |
[pagina 335]
| |
EAF: Itaque junctâ CD, ea parallela & aequalis erit lineis PS, NΦ. Ducatur secundùm DC planum DBC parallelum basi EΠF, fietque semiparabola BDC aequalis & similis semiparabolae ΠΦN; & erit ΦBN dimidius cylindrus parabolicus; DACB verò dimidiata ungula. Haec autem aequatur sicut antea ostendimus, duabus quintis cylindri dimidiati, basin habentis DBC & altitudinem BA. Ergo quum semicylindrus ΦBN habeat altitudinem BΠ triplam ipsius BA, erit ungula dimid. DACB ad semicyl. ΦBN, ut 2 ad 15, hoc est, ut 8 ad 60. Junctá porrò ΦΠ, constat semiparabolam ΠΦN ad triangulum ΠΦN esse ut 4 ad 3; sed triangulus ΠΦN est ad rectangulum ΦP ut 1 ad 6, (est enim basis ΠV tertia pars ipsius NP) hoc est, ut 3 ad 18. Ergo ex aequo erit semiparab. ΠΦN ad rectang. ΦP ut 4 ad 18. Itaque & semicylindrus ΦBN est ad parallelepipedum ejusdem altitudinis super basi ΦP, ut 4 ad 18. Dicti autem parallepipedi dimidium est prisma DNS; ergo semicylindrus ΦBN est ad prisma DNS, ut 4 ad 9, hoc est, ut 60 ad 135. Qualium igitur partium dimidiata ungula DACB erat 8, talium semicylindrus parab. ΦBN erat 60, (ut suprà ostensum est) taliumque prisma DNS erit 135. Ac proinde solidum AΠSD, quod ex istis tribus componitur, erit 203. Est autem ungula dimidiata ADCB ad dimidiatam ungulam EAPΠ, ut 1 ad 32, sicut Cl. Vir demonstravit in prop. 95. lib. 9.Ga naar voetnoot39) Ergo qualium partium ungula dimid. ADCB est 8, talium erit dimid. ungula EAPΠ 256, quoniam ut 1 ad 32, ita est 8 ad 256. Diximus autem partem sol. AΠSD esse talium 203. Igitur dim. ungula EAPΠ est ad partem AΠSD ut 256 ad 203; & dividendo pars reliqua EDSΦ ad partem AΠSD, ut 53 ad 203; quod erat demonst. Ostendimus igitur illud quoque solidum, quod suprà diximis fieri ex ductu plani EΞS [Fig. 4] in planum EMΛS, eam habere rationem ad solidum ortum ex ductu plani SΞΣP in planum SΛΠP, quam 53 ad 203.Ga naar voetnoot40)  [Fig. 3.]
Tandem ad alterum eorum quae demonstrare promisimus accedamus, repetitâque parte mediâ schematis triplicis quod suprà descriptum fuit [Fig. 3], ostendendum sit; solidum ortum ex ductu plani CΘR in planum CKΔR, ad solidum ex ductu plani RΘΓO in planum RΔZO eam habere rationem, quam 5 ad 11. Supra latus CD trianguli CDI, erigatur ad perpendiculum triangulum CKD [Fig. 7], & jungatur KI. Erit jam pyramis CDIK illud solidum quod intelligitur fieri ex ductu trianguli CDI in triangulum | |
[pagina 336]
| |
pyramide étant coupée selon OΓ par le plan AZOΓ, lequel soit perpendiculaire à la base CDI, la section sera un carré, c'est-à-dire un rectangle aux côtés ΓO, OZ, et cette section divisera la pyramide en deux parties égales. Mais lorsqu'elle est coupée par le plan EΔRΘ, parallèle au précédent, selon la droite RΘ, il en résultera un rectangle ER construit sur les droites ΘR et RΔ. Il faut donc prouver que le solide KCREΔ est au solide ΔAOΘΔ comme 5 à 11. Qu'il soit mené selon EΔ le plan ΔEB parallèle à la base CDI, ce plan découpera la pyramide BEΔK sembable à la pyramide entière CIDK, et qui sera par conséquent à cette dernière comme les cubes des côtés homologues BΔ et CD. Mais BΔ, parce qu'elle est égale à CR, sera le quart du côté CD. Donc des parties dont la pyramide BEΔK en contient une, la pyramide CIDK en contiendra 64; et sa moitié, c'est-à-dire le solide KAOC32. Mais, des parties dont la pyramide BEΔK en contient une, le prisme BER en contient 9, parce qu'ils ont la base commune BEΔ et que la hauteur du prisme est triple de celle de la pyramide BK. Donc le solide KCREΔ, qui consiste de ces deux ensemble, sera de 10 parties telles que le solide KAOC en contient 32. Il paraît donc que le second est au premier comme 16 à 5, et par conséquent, par division et conversion, que le solide KCREΔ est au solide ΔAOΘΔ comme 5 à 11; ce qu'il fallait montrer.
FIN. | |
[pagina 337]
| |
CDK. Etenim sectâ pyramide plano AZOΓ secundum OΓ, quod rectum sit ad basin CDI, erit sectio quadratum, id est, rectangul. quod fit ex lineis ΓO, OZ; eademque sectio dividet pyramidem bifariam. Secta item plano EΔRΘ priori parallelo, secundùm lineam RΘ, existet inde rectangulum ER, quale continetur lineis ΘR, RΔ. Oportet itaque ostendere, quòd solidum KCREΔ est ad solidum ΔAOΘΔ, ut 5 ad 11. Ducatur secundùm EΔ planum ΔEB parallelum basi CDI; abscindet illud pyramidem BEΔK similem toti pyramidi CIDK, quaeque proinde erit ad hanc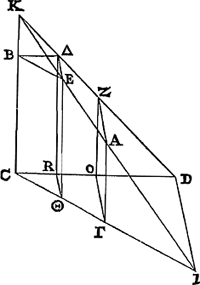 [Fig. 7.]
in triplicata ratione laterum homologorum BΔ ad CD. Sed BΔ, cum sit aequalis ipsi CR, quarta pars est lateris CD. Itaque qualium partium pyramis BEΔK est unius, talium pyramis CIDK erit 64: & dimidium hujus, hoc est, solidum KAOC erit 32. Qualium autem pyramis BEΔK est unius, talium quoque prisma BER est 9; quoniam basin habent communem BEΔ, & prismatis altitudo BC tripla est ad altitudinem pyramidis BK. Ergo solidum KCREΔ quod ex hisce duobus componitur, erit partium 10, qualium solidum KAOC est 32. Apparet igitur hoc esse ad illud ut 16 ad 5; ideoque dividendo & convertendo solidum KCREΔ esse ad solidum ΔAOΘΔ, ut 5 ad 11: quod erat ostendendum. | |
Errata.Pag. 2. lin. 10. post KN etc. deest, diametro BD parallelae. Pag. 7 lin. post hypocolGa naar voetnoot41) intersere multòque major quam AD ad DHGa naar voetnoot42).
FINIS. |
|