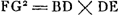Logo DBNL
Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651 (1908)

Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651

(1908)–Christiaan Huygens–rechtenstatus Auteursrecht onbekend

Vorige Volgende

Christiaan Huygens, fils de Constantin.
Théorèmes sur la quadrature
De l'hyperbole, de l'ellipse et du cercle, déduite de la position donnée du centre de gravité des segments.

Théorème I.

A un segment d'hyperbole, ou à un segment d'ellipse ou de cercle n'excédant pas la moitié de l'ellipse ou la moitié du cercle, on peut circonscrire une figure, composée de parallélogrammes d'égales largeurs, excédant le segment d'une quantité moindre qu'une aire quelconque donnée.

 

Soit donnè le segment ABC [Fig. 1], dont le diamètre soit BD. Sur la base AC soit construit le parallélogramme AE, ayant deux côtés parallèles et égaux au diamètre BD, d'où il arrivera que le côté restant touche le segment à son sommet. Ayant divisé continuellement ce parallélogramme en deux parties égales, il restera enfin une partie moindre que l'aire donnée. Soit cette partie le parallélogramme BF et soit la base AC divisée aux points G, H, K etc. en parties égales à DF, et que de ces points on mène à la circonférence les droites GL, HM, KN etc. [parallèles au diamètre]1) et que l'on achève les parallélogrammes DO, GP, HQ, KR, etc. Je dis que la figure composée de tous ces parallélogrammes (laquelle dans la suite sera nommée circonscrite par ordonnées) excédera le segment ABC d'une quantité moindre que l'aire donnée.

En effet, joignons AN, NM, ML, LB, BS etc., il résultera de cette manière aussi une figure rectiligne inscrite dans le segment, et l'excès de la figure circonstrite, qui consiste en parallélogrammes, sur la figure inscrite sera plus grand que celui sur le segment ABC. Mais l'excès de la circonscrite sur l'inscrite consiste en triangles, desquels ceux qui sont situés d'un côté du diamètre comme ARN, NQM, MPL, LOB égalent la moitié du parallélogramme OD ou BF, parce que de

Christiani Hvgenii, Const. f.
Theoremata de quadratura
Hyperboles, ellipsis et circuli, ex dato portionum gravitatis centro.

Theorema I.

Portioni hyperboles, vel ellipsis vel circuli portioni, dimidiâ ellipsi dimidiove circulo non majori circumscribi potest figura ex parallelogrammis aequalem latitudinem habentibus, quae portionem excedat spatio quod minus sit quovis dato.

 

Data sit portio ABC, [Fig. 1] cujus diameter BD. Super basin AC constituatur parallegrammum AE, latera duo habens diametro BD parallela & aequalia, quo fiet ut latus reliquum portionem in vertice contingat. Hoc parallelogrammo

illustratie
[Fig. 1].


continuè in duo aequalia secto, relinquetur tandem pars quae minor erit dato spatio; sit ea parallelogrammum BF, & dividatur basis AC in partes aequales ipsi DF, punctis G, H, K &c. atque inde ducantur ad sectionem rectae GL, HM, KN &c [diametro BD parallelae]1) & perficiantur parallelogramma DO, GP, HQ, KR &c. Dico figuram ex omnibus istis parallelogrammis compositam (quae imposterum ordinatè circumscripta vocabitur) superare portionem ABC minori quàm datum sit spatio.

Jungantur enim AN, NM, ML, LB, BS, &c. eritque hac ratione inscripta quoque portioni figura quaedam rectilinea; majorque erit excessus figurae circumscriptae quae ex parallelogrammis composita est, super inscriptam, quàm supra portionem ABC. Excessus autem circumscriptae super inscriptam ex triangulis constat, quorum quae sunt ab una diametri parte, ut ARN, NQM, MPL, LOB,

chacun d'eux la base est égale à la base DF et la somme de leurs hauteurs égale à la hauteur du parallélogramme BF. De même les triangles qui se trouvent de l'autre côté du diamètre égalent la moitié du parallélogramme BF. Donc la somme de tous les triangles, c'est-à-dire le dit excès, est égal au parallélogramme BF et par conséquent moindre que l'aire donnée. Mais moindre encore que cet excès était l'excès de la figure circonscrite sur le segment ABC. Donc ce dernier excès est beaucoup moindre que l'aire donnée. Et il paraît qu'on peut exécuter ce qui était proposé.

Théorème II.

Etant donné un segment d'hyperbole, ou un segment d'ellipse ou de cercle n'excédant pas la moitié de l'ellipse ou du cercle, et étant donné un triangle qui ait une base égale à la base du segment, on peut circonscrire à l'un et à l'autre une figure composée de parallélogrammes tous de même largeur de manière que la somme des deux aires par lesquels les figures circonscrites excèdent le segment et le triangle soit moindre qu'une aire quelconque donnée.

 

Soit ABC [Fig. 2] le segment et DEF le triangle, ayant AC et DF pour bases égales, et soit BG le diamètre du segment et EH dans le triangle une droite tirée du sommet vers le milieu de la base. Supposons encore les deux BG, EH, soit perpendiculaires, soit également inclinées sur les bases, et que l'aire donnée soit divisée en deux parties ayant le même rapport que BG à EH; soient K et L ces parties. Qu'il soit maintenant circonscrit par ordonnées, de même qu' auparavant, une figure au segment ABC, laquelle excède ce segment d'une quantité moindre que l'aire K. Et qu'il soit circonscrit au triangle DEF une figure qui consiste en autant de parallélogrammes qu'il y a dans la figure circonscrite au segment ABC.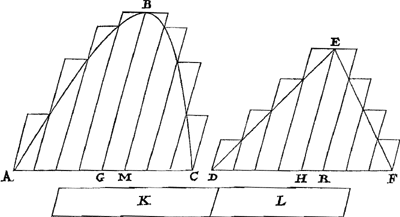



illustratie
[Fig. 2].


Puis donc que les bases du segment et du triangle sont égales il est clair que tous les parallélogrammes ont la même largeur. Donc, parce que le parallélo-

aequantur dimidio parallelogrammi OD vel BF, quia singulorum bases basi DF aequales sunt, & omnium simul altitudo, parallelogrammi BF altitudini. Eâdem ratione triangula quae sunt ab altera diametri parte, aequantur dimidio parallelogrammi BF: Ergo omnia simul triangula sive dictus excessus aequalis est parallelogrammo BF, eòque minor spatio dato. Sed eodem excessu adhuc minor erat excessus figurae circumscriptae supra portionem ABC: igitur his excessus dato spatio multo minor est. Et apparet fieri posse quod proponebatur.

Theorema II.

Data portione hyperboles, vel ellipsis vel circuli portione, dimidiâ ellipsi dimidiove circulo non majore, & dato triangulo qui basin habeat basi portionis aequalem; potest utrique figura[e] circumscribi ex parallelogrammis quorum sit omnium eadem latitudo, ita ut uterque simul excessus quo figurae circumscriptae portionem & triangulum superant, sit minor spatio quovis dato.

 

Data sit portio ABC [Fig. 2] & triangulus DEF, basibus AC, DF aequalibus; & portionis diameter sit BG, in triangulo verò ducta à vertice in mediam basin linea EH. Sint autem utraeque BG, EH vel ad bases rectae vel aequaliter inclinatae; & quam rationem habet BG ad EH, in eandem dividatur spatium datum, sintque partes K & L. Circumscribatur iam sicut antea portioni ABC figura ordinatè, quae portionem superet excessu minore quam sit spatium K. Et triangulo DEF circumscribatur figura quae totidem parallegrammis constet, quot sunt in figura portioni ABC circumscripta.



illustratie
[Fig. 2].


Quoniam igitur bases portionis & trianguli aequales sunt, apparet quidem omnium parallelogrammorum eandem fore latitudinem. Hinc quum parallogram-

gramme BM est à ER comme BG à EH, c'est-à-dire comme K à L et que BM est moindre que K*), ER sera aussi moindre que L**). Mais tous les triangles dont se compose l'excès de la figure circonscrite sur le triangle DEF sont ensemble égaux au parallélogramme ER, donc cet excès est moindre que l'aire L. Mais l'excès par lequel la figure circonscrite dépasse le segment ABC est moindre que l'aire K. Donc la somme des deux excès sera moindre que l'espace donné KL. Et il paraît possible d'exécuter ce qui était proposé.

Théorème III.

Si à un segment d'hyperbole ou à un segment d'ellipse ou de cercle n'excédant pas la moitié de l'ellipse ou du cercle, on circonscrit une figure par ordonnées, le centre le gravité de cette figure sera situé sur le diamètre du segment.

 

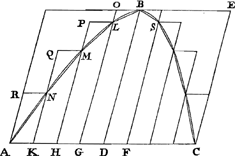
Soit ABC [Fig. 3] un quelconque de ces segments, BD son diamètre et soit circonscrit comme ci-dessus une figure par ordonnées. Il faut démontrer que le centre de gravité de cette figure tombe dans le diamètre BD. Soient menées les droites HK, NR, PS qui joignent les côtés superieurs des parallélogrammes, qui de part et d'autre sont à égales distances du diamètre.

Puis donc que FH, LK sont parallèles au diamètre BD, et DF et DL égales, il faut que la droite HK, qui joint les deux droites FH, LK soit coupée en deux parties égales par le diamètre BD, d'où cette même HK sera parallèle à la base AC*), et EHKQ une ligne droite. Donc EC est un parallélogramme dont les deux côtés opposés étant divisés en deux parties égales par le diamètre BD, ce dernier contiendra le centre de gravité.**)

Par la même raison HM, NO, PQ seront des parallélogrammes et les centres de gravité de chacun d'eux situés sur la ligne BD. Donc aussi le centre de gravité de la figure composée de tous les dits parallélogrammes doit nécessairement se trouver sur la même droite BD. Mais cette figure est la même que celle qui fut circonscrite par ordonnées au segment. Donc il paraît que le centre de gravité

mum BM sit ad ER ut BG ad EH, id est ut K ad L, sitque BM minus quam K*), erit quoque ER minus quam L**). Verùm omnia triangula quibus constat excessus figurae circumscriptae supra triangulum DEF, aequalia sunt parallelogrammo ER, ergo minor est idem excessus spatio L. Sed & excessus quo figura circumscripta portionem ABC superat minor est spatio K. Ergo uterque simul excessus minor erit spatio KL dato. Et constat fieri posse quod proponebatur.

Theorema III.

Si portioni hyperboles, vel ellipsis vel circuli portioni, dimidiâ ellipsi dimidiove circuli non majori, circumscribatur figura ordinatè; ejus figurae centrum gravitatis erit in portionis diametro.

 

Sit portio quaelibet istarum ABC [Fig. 3], diameter ejus BD; & circumscribatur ei ut supra figura ordinatè. Ostendendum est ejus figurae centrum gravitatis fore in BD diametro. Ducantur lineae HK, NR, PS, conjungentes suprema latera parallelogrammorum quae à diametro portionis aequaliter utrinque distant.

Quoniam igitur FH, LK sunt diametro BD parallelae, suntque DF, DL aequales,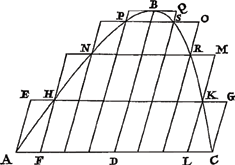

illustratie
[Fig. 3.]


oportet lineam HK, quae duas FH, LK conjungit, à diametro BD bifariam secari; quare eadem HK parallela erit basi AC*), & EHKG recta linea. Itaque EC parallelogrammum est; cujus opposita latera quum bifariam dividat diameter BD, erit in ea parallelogrammi centrum gravitatis**). Eâdem ratione parallelogramma erunt HM, NO, PQ, & singulorum centra gravitatis in linea BD. Ergo & figurae ex omnibus dictis parallelogrammis compositae centrum gravitatis in eadem BD reperiri necesse est. Ista autem figura eadem est quae portioni ordinatè fuerat circumscripta. Ergo figurae portioni ordi-

de la figure circonscrite par ordonnées au segment se trouve sur le diamètre BD du segment. Ce qu'il fallait démontrer.

Théorème IV.

D'un segment d'hyperbole, d'ellipse et de cercle le centre de gravité se trouve sur le diamètre du segment.

 

Soit ABC un segment d'hyperbole ou d'un ellipse ou d'un cercle, supposés d'abord pas plus grands que la moitié de la figure et BD son diamètre. Il faut démontrer que le centre de gravité du segment se trouve en BD.

En effet, posé, si cela peut avoir lieu, qu'il est situé hors du diamètre en E, tirons EH parallèle au diamètre BD. En divisant donc continuellement DC en deux parties égales, il restera enfin une ligne moindre que DH. Soit DF cette ligne et qu'on circonscrive par ordonnées au segment une figure à parallélogrammes dont les bases soient égales à DF et qu'on joigne BA, BC.

Le centre de gravité de la figure circonscrite au segment est donc situé sur le diamètre BD du segment. Soit K ce centre et soit tirée EK, prolongée jusqu' à rencontrer AL parallèle à BD. Puis donc que le segment est plus grand que le triangle ABC et l'aire par laquelle la figure circonscrite excède le segment moindre que le parallélogramme BF, comme il fut démontré*) plus haut, le rapport du segment ABC au dit excès sera plus grand que celui du triangle ABC au parallélogramme BF, c'est-à-dire que AD à DF, et beaucoup plus grand que AD à DH5) ou comme LK à KE. Soit donc MK à KE comme le segment ABC à l'excès par lequel il est lui-même dépassée par la figure circonscrite par ordonnées. Donc, parce que K est le centre de gravité de la figure circonscrite par ordonnées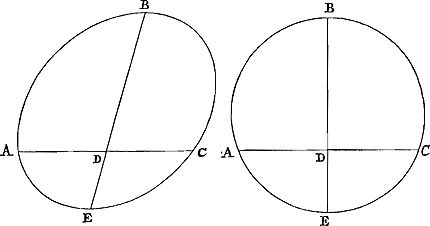

illustratie
[Fig. 5.]


au segment, et E celui du segment luimême, M sera le centre de gravité de toutes les aires qui constituent cet excès**). Ce qui ne peut pas être. Car si par M on tire une droite parallèle au diamètre BD toutes ces aires nommées seront situées du même côté. Il est donc manifeste que le centre de gravité du segment ABC est sur BD diamètre du segment.7)

natè circumscriptae centrum gravitatis constat esse in BD portionis diametro. Quod erat ostendendum.

Theorema IV.

Portionis hyperboles, ellipsis & circuli, centrum gravitatis est in portionis diametro.

 

Esto portio hyperboles, vel ellipsis vel circuli dimidiâ primùm figurâ non major, ABC [Fig. 4]; diameter ejus BD. Ostendendum est, in BD reperiri portionis ABC gtavitatis centrum.

Si enim fieri potest, sit extra diametrum in E, & ducatur EH diametro BD parallela. Dividendo itaque DC continuè bifariam, relinquetur tandem linea minor quam DH; sit ea DF, & circumscribatur portioni figura ordinatè ex parallelogrammis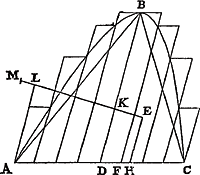

illustratie
[Fig. 4].


quorum bases aequales sint lineae DF, & jungantur BA, BC. Figurae itaque portioni circumscriptae centrum gravitatis est in BD portionis diametro. Sit hoc K, & jungatur EK, producaturque, & occurrat ei AL parallela BD. Quia autem portio major est triangulo ABC, & excessus quo figura circumscripta portionem superat, minor parallelogrammo BF, uti supra demonstratum fuit*); erit major ratio portionis ABC ad dictum excessum, quàm trianguli ABC ad BF parallelogrammum, id est quàm AD ad DF; [multòq; major quam AD ad DH,]5) vel quàm LK ad KE. Sit itaque MK ad KE sicut portio ABC ad excessum quo ipsa superatur à figura ordinatè circumscripta. Itaque cum K sit centrum grav. figurae portioni circumscriptae, & E centrum grav. ipsius portionis; erit M centrum gravitatis omnium spatiorum quae eundem excessum constituunt**). Quod esse non potest; Nam si per M linea ducatur diametro BD parallela, erunt ab una parte omnia quae diximus spatia. Manisestum est igitur, portionis ABC centrum grav. esse in BD portionis diametro7).

Soit maintenant ABC [Fig. 5] un segment d'ellipse ou de cercle plus grand que la moitié de la figure. Complétons la figure et prolongeons BD jusqu'à ce qu'elle rencontre la section [conique] en E; ED sera donc le diamètre du segment AEC et BDE le diamètre de la figure entière. Et comme sur le diamètre BDE est situé le centre de gravité de la figure entière (car ceci résultera de ce qui a été démontré auparavant, si l'on divise en deux parties égales la figure entière par un diamètre parallèle à AC) et sur cette même droite le centre de gravité du plus petit segment AEC, ce qui vient d'être montré tantôt, le centre du gravité de l'autre segment ABC sera également en BDE*), ce qu'il fallait démontrer.

Lemme.8)

Soit EB [Fig. 6] une droite à laquelle on ajoute à l'une et à l'autre extrémité les droites égales ES et BP, et encore une autre PD. Je dis que l'aire, par laquelle le recttangle EDB excède EPB, est égale au rectangle SDP. Car le rectangle EDB est égal aux deux suivants: le rectangle EDP et le rectangle sur ED, PB, dont le dernier excède le rectangle EPB de l'aire du rectangle DPB. Donc l'excès du rectangle EDB sur le rectangle EPB est égal aux deux rectangles EPD et DPB. Mais le rectangle EDP, si l'on y ajoute le rectangle DPB, c'est-à-dire le rectangle sur ES, DP, devient égal au rectangle SDP. Il est donc évident que l'excès du rectangle EDB sur EPB est ègal au rectangle SDP.

Soit9) de nouveau EB une droite [Fig. 7] de laquelle on retranche aux deux extrémités les deux égales ES, BP et de plus une autre PD. Je dis de nouveau que l'aire, par laquelle le rectangle EDB excède EPB, est égale au rectangle SDP. Car le rectangle EDB est égal aux deux suivants: le rectangle EDP et le rectangle sur ED, PB, desquels EDP est de nouveau égal aux deux suivants savoir le rectangle SDP et celui compris sous ES et DP, ou le rectangle DPB. Donc le rectangle EDB est égal à ces trois rectangles, SDP, DPB et le rectangle sur ED, PB; mais de ceux-ci les deux derniers égalent le rectangle EPB, donc le rectangle EDB est égal aux deux suivants, savoir les rectangles SDP et EPB, d'où il paraît que l'excès du rectangle EDB sur le rectangle EPB est égal au rectangle SDP.

Théorème V.

Etant donné un segment d'hyperbole, ou d'ellipse ou de cercle n'excédant pas la moitié de la figure; si sur le diamètre est construit un triangle de telle manière que

Esto nunc ABC [Fig. 5] portio ellipsis vel circuli, dimidiâ figurâ major. Absolvatur figura, & producatùr BD usque dum sectioni occurrat in E; erit igitur portionis AEC diameter ED, & BDE diameter totius figurae. Et quoniam in BDE diametro est figurae totius centrum gravitatis, (hoc enim ex praedemonstratis constabit, si in duo aequalia tota figura dividatur diametro quae ipsi AC sit parallela,) & in eadem centr. gravitatis AEC portionis minoris, sicut modò ostensum fuit; erit quoque centr. gravitatis portionis reliquae ABC in BDE*); quod erat ostendendum.

Lemma8).

Esto linea EB, cui ad utrumque terminum adjiciantur aequales duae ES, BP, & insuper alia PD. Dico id quo rectangulum EDB excedit EPB, aequari rectangulo SDP. Est enim rectangulum EDB aequale istis duobus, rectangulo EDP &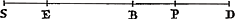

illustratie
[Fig. 6].


rectangulo sub ED, PB; quorum ultimum superat rectangulum EPB rectangulo DPB. Igitur excessus rectanguli EDB supra rectangulum EPB aequalis est duobus istis, rectangulo EDP, & DPB. Sed rectangulum EDP addito rectangulo DPB, id est rectangulo sub ES, DP, aequale fit rectangulo SDP. Manifestum est igitur, excessum rectanguli EDB supra EPB, aequari rectangulo SDP. Esto9) rursus linea EB [Fig. 7], cui ad utrumque terminum auferantur duae aequales ES, BP, & insuper alia PD. Dico iterum, id quo rectangulum EDB excedit EPB, aequari rectangulo SDP. Rectangulum enim EDB aequale est istis duobus, rectangulo EDP, & rectangulo sub ED, PB; horum autem EDP rursus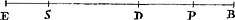

illustratie
[Fig. 7].


aequale est duobus, rectangulo nimirum SDP, & ei quod continetur sub ES, DP, sive rectangulo DPB. Igitur rectangulum EDB istis tribus aequale est rectangulis, SDP, DPB, & rectangulo sub ED, PB; horum vero duo postrema aequantur recangulo EPB; ergò rectangulum EDB aequale est duobus, rectangulo nimirum SDP & EPB, unde apparet excessum rectanguli EDB supra rectangulum EPB aequari rectangulo SDP.

Theorema V.

Datâ portione hyperboles, vel ellipsis vel circuli portione, dimidiâ figurâ non majore; si ad diametrum constituatur triangulus hujusmodi, qui verticem habeat

son sommet soit au centre de la courbe et la base égale et parallèle à la base du segment, mais telle que le carré de la droite menée du sommet au milieu de la base soit égal au rectangle construit sur les droites comprises entre la base du segment et les extrémités du diamètre de la courbe10), le centre de gravité de la figure composée du segment ensemble avec le triangle décrit sera le sommet du triangle, c'est-à-dire le centre de la courbe.

 

Soit donné ABC le segment d'hyperbole [Fig. 8] ou d'ellipse [Fig. 9]10bis) ou de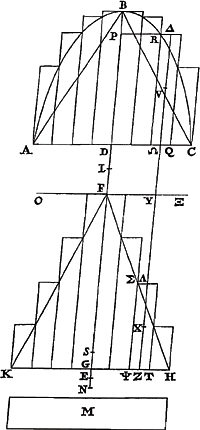

illustratie
[Fig. 9].


cercle n'excédant pas la moitié de la figure. Soit son diamètre BD, le diamètre de la courbe BE dans le milieu duquel F est le centre de la courbe. Et qu'on fasse la droite FG telle que son carré équivaut au rectangle BDE et après avoir tiré KGH égale et parallèle à la base AC et divisée au point G en deux parties égales, que l'on joigne KF, FH11). Il faut démontrer que de la figure composée du segment ABC et du triangle KFH, le centre de gravité se trouve au point F.

S'il ne se trouve pas en F, qu'il soit, si possible, d'abord du côté vers le segment ABC, en L, car il est certain qu'il se trouvera sur la droite BDG parce que dans celle-ci se trouvent les centres de gravité tant du segment que du triangle KFH. Que l'on joigne AB, BC et que le rapport de GF à FL soit aussi celui de la somme des triangles ABC, KFH à une certaine aire M.

Soient circonscrits par ordonnées au segment et au triangle KFH des figures au moyen de parallélogrammes de même largeur, de manière que la somme des deux excès par lesquels ces figures dépassent le segment ABC et le triangle KFH soit moindre que l'aire M*). Par conséquent le rapport de la somme des deux triangles ABC, KFH à la somme des deux excès ou résidus sera plus grand que celui à M c'est-à-dire que GF à FL, et partant beaucoup plus grand que GF à FL sera le rapport de la somme du segment ABC et du triangle KFH aux mêmes résidus. Soit donc NF à FL

in centro figurae, & basin portionis basi aequalem & parallelam; eam verò quae deinceps à vertice ad mediam basin pertingit tantam, ut possit ipsa rectangulum comprehensum lineis, quae inter portionis basin & terminos diametri figurae interjiciuntur.10) Erit magnitudinis, quae ex portione & praescripto triangulo componitur, centrum gravitatis punctum idem quod est trianguli vertex, centrum nimirum figurae.

 

Data sit portio hyperboles [Fig. 8], vel ellipsis [Fig. 9]10bis) vel circuli portio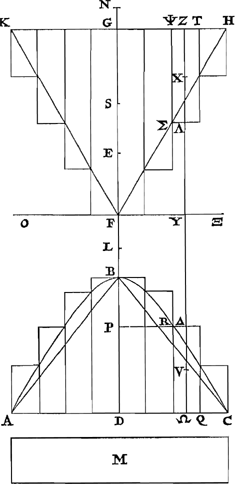

illustratie
[Fig. 8].


dimidiâ figura non major, ABC. Diameter ejus sit BD, & figurae diameter BE, in cujus medio centrum figurae F. Et sumatur FG quae possit rectangulum BDE, ductâque KGH aequali & parallelâ basi AC, quaeque ad G bifariam dividatur, jungantur KF, FH11). Demonstrandum est, quòd magnitudinis compositae ex portione ABC & triangulo KFH, centrum gravitatis est punctum F.

Si non est in F, sit si fieri potest primùm ab ea parte puncti F quae est versus ABC portionem, atque esto punctum L; constat autem futurum in recta BDG, quum in hac sint utraque centra gravitatis portionis & trianguli KFH. Jungantur AB, BC, & quam rationem habet GF ad FL, eam habeat magnitudo composita ex triangulis ABC, KFH ad spatium quoddam M; & circumscribantur portioni & triangulo KFH figurae ordinatè, ex parallelogrammis quorum omnium sit eadem latitudo, ita ut duo simul excessus quibus istae figurae superant portionem ABC & triangulum KFH, minores sint spatio M*). Igitur duorum simul triangulorum ABC, KFH ad dictos duos excessus sive residua major erit ratio quàm ad M id est quàm GF ad FL; ac proinde longè major ratio portionis ABC unà cum KFH triangulo ad eadem residua quam

comme la somme du segment ABC et du triangle KFH à la somme des deux rési dus et que le point N tombe au delà de la base KH. Maintenant que par F on tire OΞ parallèle à la base AC ou KH et que de deux parallélogrammes quelconques également distants du diamètre dans le segment et dans le triangle KFH, tels que RQ, ΣT, les centres de gravité soient V et X, par lesquels on tire la droite ZΛΔΩ coupant la droite OΞ en, ϒ et soit tiré RP parallèle à la base AC, et que de l'autre extrémité E du diamètre de la courbe on fasse ES égale à PB l'abscisse depuis le sommet.

Puis donc que CD et RP sont les ordonnées au diamètre de la courbe, le carré de CD sera à celui de RP*) comme le rectangle BDE au rectangle BPE. Mais comme CD à RP, c'est-à-dire comme HG à ΨG, ainsi HF est à ΣF et ainsi Zϒ à Λϒ, donc comme le carré de CD au carré de RP, c'est-à-dire comme le rectangle BDE à BPE, ainsi le carré de Zϒ à celui de Λϒ. D'où encore, par conversion des rapports, comme le rectangle BDE est à la différence des rectangles BDE, BPE, ainsi est le carré de Zϒ à la différence des carrés de Zϒ, Λϒ. Mais la différence des rectangles BDE, BPE est égale au rectangle SDP, ainsi qu'il a été démontré par le lemme précédent13), et la différence des carrés Zϒ, Δϒ égale à la somme du carré ZΛ et de deux rectangles ZΛϒ**), ou, ce qui revient au même, aux deux rectangles ZΛX, ZΛϒ, pris deux fois, c'est-à-dire au double du rectangle sur ZΛ, Xϒ. Donc, comme le rectangle BDE est au rectangle SDP, ainsi est le carré de Zϒ au double du rectangle sur Xϒ, ZΛ, d'où, puisque le rectangle BDE est égal au carré de FG***) et par conséquent aussi au carré de Zϒ, le rectangle SDP sera de même égal au double du rectangle sur Xϒ, ZΛ†).

Mais comme le point F divise BE au milieu et BP, ES sont égales, FP, FS seront égales aussi d'où, ajoutant de part et d'autre FD, SD sera égale à PFD16) en entier, c'est-à-dire à ΔϒΩ, mais Δ ϒΩ est double de Vϒ, puis qu'elle contient deux fois les deux ϒΔ et ΔV dans l'hyperbole [Fig. 8], mais dans l'ellipse [Fig. 9] et le cercle deux fois les deux VΩ et Ωϒ; donc SD aussi est double de Vϒ et par conséquent le rectangle SDP le double du rectangle sur ϒV, ΩΔ. Mais le même rec-

GF ad FL. Sit itaque NF ad FL, sicut portio ABC simul cum triangulo KFH

illustratie
[Fig. 8].


ad duo residua, & cadet terminus N ultra trianguli basin KH. Jam per F ducatur OΞ parallela basi AC vel KH; & duorum quorumcunque parallelogrammorum, quae in portione & in triangulo KFH aequaliter à diametro distabunt, ut sunt RQ, ΣT, sint centra gravitatis V & X; per quae ducatur recta ZΛΔΩ, secans lineam OΞ in ϒ; & ducatur RP basi AC parallela, abscissaeque ad verticem lineae PB sumatur aequalis, ex altero diametri figurae termino, ES.

Quoniam igitur ad diametrum figurae ordinatim sunt applicatae CD & RP, erit ut rectangulum BDE ad rectangulum BPE ita quadratum CD ad RP quadratum*); verùm ut CD ad RP, hoc est, ut HG ad ΨG, ita est HF ad ΣF, & ita Zϒ ad Λϒ, igitur ut CD quadratum ad quadratum RP, id est ut rectangulum BDE ad BPE, ita est quadratum Zϒ ad Λϒ quadratum. Quare & per conversionem rationis, sicut rectangulum BDE ad differentiam rectangulorum BDE, BPE, ita quadratum Zϒ, ad differentiam quadratorum Zϒ, Λϒ. Est autem differentia rectangulorum BDE BPE, aequalis rectangulo SDP, sicut lemmate praemisso demonstratum est13); differentia verò quadratorum Zϒ, Λϒ, aequalis quadrato ZΛ & duobus rectangulis ZΛϒ**), sive quod idem est, rectangulis ZΛX, ZΛϒ bis sumptis, hoc est, duplo rectangulo sub ZΛ, Xϒ. Itaque sicut est rectangulum BDE ad rectangulum SDP, ita quadratum Zϒ ad duplum rectangulum sub Xϒ, ZΛ. quare cum rectangulum BDE quadrato FG aequale sit***) ideoque & quadrato Zϒ, erit quoque rectangulum SDP aequale duplo rectangulo sub Xϒ, ZΛ†). Quia verò F punctum dividit BE per medium, suntque aequales BP, ES, etiam FP, FS aequales erunt, unde additâ utrique FD, erit SD aequalis toti PFD16) id est ΔϒΩ: sed ΔϒΩ dupla est lineae Vϒ, quia bis continet utramque ϒΔ, ΔV in hyperbole [Fig. 8], in ellipsi [Fig. 9] verò & circulo bis utramque VΩ & Ωϒ; ergo & SD dupla Vϒ, ideoque rectangulum SDP aequale duplo rectan-

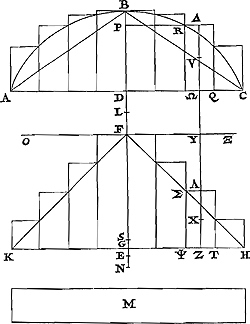
tangle SDP a été démontré être égal au double du rectangle sur Xϒ, ZΛ [Fig. 8 ou 10]; donc le rectangle sur ϒV, ΩΔ est égal au rectangle sur Xϒ, ZΛ. On a donc ϒV à ϒX comme ΛZ à ΩΔ*); mais comme ΛZ a ΩΔ ainsi est le parallélogramme ΣT à RQ, donc aussi ϒV à ϒX comme le parallélogramme ΣΤ au parallélogramme RQ. Mais les points X et V sont les centres de gravité des dits parallélogrammes, donc ϒ est le centre de gravité des deux parallélogrammes réunis**). De la même manière on peut démontrer de tous les autres parallélogrammes que de deux opposés quelconques le centre de gravité se trouve sur la droite OΞ. Donc de l'assemblage entier des deux figures circonscrites par ordonnées le centre de gravité doit se trouver nécessairement sur cette même droite OΞ. Mais de ce même assemblage le centre de gravité est aussi situé sur la droite BDG, parce que sur elle se trouvent les centres de gravité de chacune des deux figures circonscrites***), donc le centre de gravité de l'assemblage des dites figures est le point F même. Mais on a supposé que le point L fût le centre de gravité de la figure composée du segment ABC et du triangle KFH; le centre de gravité du reste de la figure se composant des deux résidus qui appartiennent encore aux deux figures se trouvera donc sur le prolongement de LF là, où cette droite se termine, de telle manière que la partie ajoutée ait à FL le même rapport que la somme du segment ABC et du triangle KFH aux deux dits résidus†). Or, N est ce point terminal, le point N est donc le centre de gravité des deux résidus. Ce qui ne peut pas être. Car, si par N on mène une droite parallèle à la base, toutes les aires, desquelles consistent l'un et l'autre résidu, se trouvent du même côté. L n'est donc pas le centre de gravité de la figure composée du segment ABC et du triangle KFH. Mais ce centre ne se trouvera non plus de l'autre côté du point F. Car si cela fût dit, une démonstration tout à fait pareille aurait pour résultat que des deux résidus qui resteront dans les figures circonscrites, après que l'on a ôté le segment ABC et le triangle KFH, le centre de gravité serait au delà du segment ABC, ce qui est également absurde. Il reste donc que le point F est le centre de gravité même, ce qu'il fallait démontrer.

gulo sub ϒV, ΩΔ. Sed idem rectangulum SDP [Fig. 8 sive 10] aequale ostensum fuit duplo rectangulo sub Xϒ, ZΛ; ergo aequale est rectangulum sub ϒV, ΩΔ, rectangulo

illustratie
[Fig. 10].


sub Xϒ, ZΛ. Est itaque ϒV ad ϒX, ut ΛZ ad ΩΔ*); verùm ut ΛZ ad ΩΔ, ita est parallelogrammum ΣT ad RQ; itaque & ϒV est ad ϒX ut parallelogrammum ΣT ad RQ parallelogr. Sunt autem puncta X & V centra gravitatis dictorum parallelogrammorum; ergo magnitudinis ex utroque parallegrammo compositae centrum gravitatis est punctum ϒ**). Eâdem ratione ostendi potest de reliquis omnibus parallelogrammis, quod duorum quorumlibet oppositorum centrum gravitatis est in linea OΞ. Ergo totius magnitudinis quae ex duabus figuris utrimque ordinatè circumscriptis componitur, centr. gravitatis in eadem OΞ reperiri necesse est. Sed ejusdem compositae magnitudinis centrum gravit. est quoque in recta BDG, quoniam in ea sunt centra gravitatis utriusque figurae circumscriptae***); igitur magnitudinis ex dictis figuris compositae centrum grav. est ipsum punctum F. Positum autem fuit L punctum centrum gravitatis ejus magnitudinis quae ex portione ABC & KFH triangulo componitur; igitur magnitudinis reliquae, compositae ex duobus residuis, quae in figuris circumscriptis remanent, erit centr. grav. in producta LF, ubi ea sic terminatur, ut pars adjecta habeat ad FL eandem rationem quam portio ABC simul cum KFH triangulo ad dicta duo residua†): is autem terminus est N; itaque N punctum est centrum gravitatis duorum residuorum. Quod fieri nequit; Nam si per N ducatur recta basi KH parallela, erunt ab una parte spatia omnia è quibus utrumque residuum constat. Non est igitur L punctum centrum gravitatis magnitudinis ex portione ABC & KFH triangulo compositae. Sed neque erit ab altera parte puncti F. Namque hoc si dicatur, planè simili demonstratione eò devenietur ut duorum residuorum quae demptâ portione ABC & KFH triangulo, in circumscriptis figuris supererunt, centrum gravitatis sit ultra portionem ABC; quod est aequè absurdum. Reliquum est igitur ut sit ipsum punctum F quod erat ostendendum.

Théorème VI.

Tout segment d'hyperbole a, au triangle inscrit de même base et de même hauteur, le rapport suivant: comme les deux tiers de la somme du diamètre de l'hyperbole et du diamètre du segment à la distance du centre de l'hyperbole au centre de gravité du segment.

 

Soit ABC [Fig. 11] le segment de l'hyperbole et le triangle inscrit comme nous avons dit; BD le diamètre du segment et BE le diamètre de l'hyperbole, dans le milieu duquel F est le centre de la courbe. Et supposons le centre de gravité du segment au point L. Je dis que le segment a le même rapport au triangle que les deux tiers de ED à FL.

Construisons, en effet, comme dans le théorème précédent, sur le diamètre le triangle KFH, c'est-à-dire de manière que le carré de FG soit égal au rectangle EDB et que la base KH soit égale et parallèle à la base AC; et soit M le centre de gravité de ce triangle, FM étant faite égale aux deux tiers de FG*).

Le triangle KFH est donc au triangle ABC comme FG à BD, mais comme FG à BD ainsi est ED à FG, parce que le carré de FG est égal au rectangle EDB et comme ED à FG, ainsi sont les deux tiers de ED aux deux tiers de FG, c'est-à-dire FM; donc le triangle KFH est au triangle ABC comme les deux tiers de ED à FM. Mais le segment d'hyperbole est au triangle KFH comme FM à FL**), parce que le segment et le triangle KFH sont équilibre au point F***) et que L et M sont leur centres de gravités respectifs; on aura donc par la règle de la proportion dérangée: le segment est au triangle, comme les deux tiers de ED à FL†); ce qu'il fallait démontrer.

Théorème VII.

Tout segment d'ellipse ou de cercle a, au triangle inscrit de même base et de même hauteur, le rapport suivant: comme les deux tiers du diamètre du seg-

Theorema VI.

Omnis hyperboles portio ad triangulum inscriptum, eandem cum ipsa basin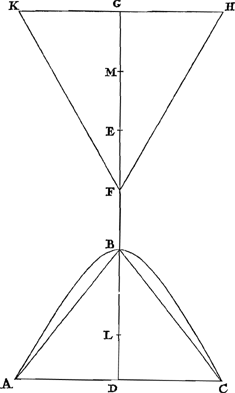

illustratie
[Fig. 11].


habentem eandemque altitudinem, hanc habet rationem; quam subsesquialtera duarum, lateris transversi & diametri portionis, ad eam quae ex centro sectionis ducitur ad portionis centrum gravitatis.

 

Esto hyperboles portio, & inscriptus ei, qualem diximus, triangulus ABC; diameter autem portionis sit BD, & latus transuersum sive diameter sectionis BE, in cujus medio centrum sectionis F. Et ponatur centrum gravitatis in portione punctum L. Dico portionem ad inscriptum triangulum ABC eam habere rationem, quam duae tertiae totius ED ad FL.

Constituatur enim ad diametrum, ut in praecedentibus, triangulus KFH; scilicet ut quadratum FG aequetur rectangulo EDB, & ut basis KH sit basi AC aequalis & parallela: ejusque trianguli sit centrum gravitatis M, sumptâ nimirum FM aequali duabus tertiis lineae FG*).

Est itaque triangulus KFH ad ABC triangulum ut FG ad BD; verùm ut FG ad BD, ita est ED ad FG, quia quadratum FG aequale est rectangulo EDB; & ut ED ad FG, ita sunt duae tertiae ED ad duas tertias FG, id est FM; ergo triangulus KFH ad triangulum ABC, ut duae tertiae ED ad FM. Est autem portio hyperboles ad triangulum KFH, ut FM ad FL**), quoniam aequilibrium portionis & trianguli KFH est in puncto F***), & centra gravitatis singulorum puncta L & M; ex aequali igitur in proportione perturbata erit portio ad triangulum ABC, ut duae tertiae lineae ED ad FL†): quod erat demonstrandum.

Theorema VII.

Omnis ellipsis vel circuli portio ad triangulum inscriptum, eandem cum ipsa basin habentem eandemque altitudinem, hanc habet rationem; quam subsesqui-

ment restant à la droite menée du centre de la courbe au centre de gravité du segment.

 

Soit ABC [Fig. 12] le segment d'ellipse ou de cercle, supposés d'abord pas plus grands que la moitié de la figure, et le triangle inscrit ayant la même base et la même hauteur que le segment; soit BD le diamètre du segment, lequel soit prolongé et passera évidemment par le centre de la courbe, qui soit F. Soit DE le diamètre du segment restant. Et supposons le point L centre de gravité du segment ABC. Je dis donc que le segment est au triangle ABC qui lui est inscrit comme les deux tiers de ED à FL. Décrivons comme précédemment le triangle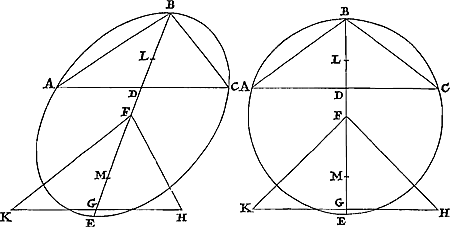

illustratie
[Fig. 12].


KFH, de manière que la base KH soit égale et parallèle à la base AC et que le carré de FG, tirée du sommet vers le milieu de la base, soit égal au rectangle BDE23); et soit le point M le centre de gravité du triangle KFH, FM étant fait égal aux deux tiers de FG*).

Le triangle KFH est donc au triangle ABC comme FG à BD; mais comme FG à BD, ainsi est ED à FG, parce que le carré de FG est égal au rectangle BDE, et comme ED à FG ainsi sont les deux tiers de ED aux deux tiers de FG, c'est-à-dire à FM. Donc le triangle KFH est au triangle ABC comme les deux tiers de ED à FM. Mais le segment ABC est au triangle KFH comme FM à FL**) puisqu'ils font d'équilibre en F***), et que leurs centres de gravité sont respectivement aux points L et M. Donc, par la règle de la proportion dérangée, le segment ABC sera au triangle ABC, comme les deux tiers de ED à FL†).

Soit maintenant le segment plus grand que la figure [Fig. 13]. Je dis qu'il aura de nouveau la même proportion au triangle inscrit que les deux tiers de ED à FL.

Car posons que H soit le centre de gravité du segment restant AEC et tirons AE,

altera diametri portionis reliquae, ad eam quae ex figurae centro ducitur ad centrum gravitatis in portione.

 

Esto ellipsis vel circuli portio primùm dimidiâ figurâ non major, & inscriptus ei triangulus ABC [Fig. 12], eandem cum portione basin habens, eandemque altitudinem; diameter autem portionis sit BD, quae producatur, & manifestum est quod transibit per centrum figurae; sit hoc F, & diameter portionis reliquae DE. Et ponatur centrum gravitatis in portione ABC punctum L. Dico igitur portionem ad inscriptum sibi triangulum ABC eam habere rationem, quam duae tertiae ED ad FL. Constituatur enim ut supra triangulus KFH, cujus nimirum basis KH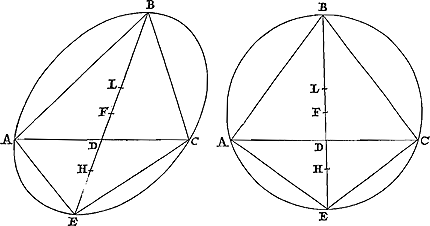

illustratie
[Fig. 13].


sit basi AC aequalis & parallela, & FG quae à vertice ad mediam basin pertingit possit rectangulum BDE23): & centrum gravitatis trianguli KFH sit M punctum, sumptâ scilicet FM aequali duabus tertiis lineae FG*).

Triangulus igitur KFH est ad triangulum ABC, ut FG ad BD; ut autem FG ad BD, sic est ED ad FG, quia quadratum FG aequale est BDE rectangulo; & ut ED ad FG, sic sunt duae tertiae ED ad duas tertias FG, id est, ad FM. Ergo triangulus KFH, ad triangulum ABC, sicut duae tertiae ED ad FM. Portio autem ABC est ad triangulum KFH, ut FM ad FL**), quoniam aequilibrium eorum est in F***), & centra gravitatis singulorum puncta L & M; Ergo ex aequali in proportione perturbata, erit portio ABC ad ABC triangulum, sicut duae tertiae ED ad FL†).

Sit nunc portio ABC [Fig. 13] dimidiâ figurâ major. Dico eam rursus ad inscriptum triangulum eam habere rationem, quam duae tertiae ED ad FL.

Ponatur enim portionis reliquae AEC centrum gravitatis H punctum, & jun-

EC. Donc, par ce que nous venons de montrer, le segment AEC sera au triangle AEC, comme les deux tiers de BD à FH; mais comme le triangle AEC est au triangle ABC, ainsi est ED à BD, ou les deux tiers de ED aux deux tiers de BD; par la règle de la proportion dérangée on aura donc: comme le segment AEC est au triangle ABC, ainsi les deux tiers de ED à FH*). Mais comme le segment ABC est au segment AEC ainsi est FH à FL**), parce que de la figure entière le centre de gravité est F, et L et H sont ceux des dits segments. Donc de nouveau par la règle de la proportion dérangée, le segment ABC sera au triangle ABC comme les deux tiers de ED à FL. Donc tout segment d'ellipse ou de cercle etc. Ce qu'il fallait démontrer.

Théorème VIII.

Dans un demi-cercle et dans un secteur de cercle quelconque l'arc a le même rapport aux deux tiers de la corde que le rayon à la droite menée du centre au centre de gravité du secteur.

 

Soit, en premier lieu, ABC le demi-cercle décrit du centre D et divisé en deux parties égales par BD, dans laquelle le centre de gravité soit E***). Je dis que l'arc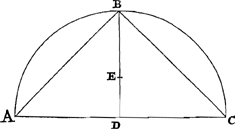

illustratie
[Fig. 14].


ABC est aux deux tiers de AC comme BD à DE. Tirons AB et BC. Donc comme le demi-cercle est au triangle ABC ainsi sont les deux tiers de BD à DE†), car BD est égal au diamètre du segment restant. Mais également comme le demi-cercle, c'est-à-dire comme le triangle, ayant la base égale à l'arc ABC et la hauteur BD, au triangle ABC, ainsi est l'arc ABC à la droite AC, donc aussi comme l'arc ABC est à AC, ainsi sont les deux tiers de BD à DE et en permutant, comme l'arc ABC est aux deux tiers de BD, ainsi est AC à DE ou bien ⅔ AC à ⅔ DE, d'où en permutant de nouveau: comme l'arc ABC à ⅔ AC, ainsi ⅔ BD à ⅔ DE ou encore BD à DE.

Soit ensuite DABC [Fig. 15] un secteur moindre que le demi-cercle, divisé en

gantur AE, EC. Igitur per ea quae jam ostendimus, erit portio AEC ad AEC triangulum, ut duae tertiae BD ad FH: verùm ut triangulus AEC ad triangulum

illustratie
[Fig. 13].


ABC, sic est ED ad BD, sive duae tertiae ED ad duas tertias BD; ex aequali igitur in proportione perturbata, erit sicut portio AEC ad triangulum ABC, ita duae tertiae ED ad FH*). Sed ut portio ABC ad AEC portionem ita est FH ad FL**)), quoniam totius figurae centrum gravitatis est F, centraque dictarum portionum L & H; Ergo iterum ex aequali in proportione perturbata, erit portio ABC ad ABC triangulum, ut duae tertiae ED ad FL. Omnis igitur Ellipsis vel circuli portio &c. Quod erat demonstrandum.

Theorema VIII.

In semicirculo & quolibet circuli sectore, habet arcus ad duas tertias rectae sibi subtensae hanc rationem, quam semidiameter ad eam, quae ex centro ducitur ad sectoris centrum gravitatis.

 

Esto primùm semicirculus ABC [Fig. 14], descriptus centro D, sectusque bifariam rectâ DB, in qua centrum gravitatis semicirculi sit E***). Dico arcum ABC esse ad duas tertias AC, sicut BD ad DE. Jungantur enim AB, BC. Igitur, ut semicirculus ad triangulum ABC, sic sunt duae tertiae BD ad DE†), est enim BD aequalis diametro portionis reliquae. Verùm etiam ut semicirculus, id est, ut triangulus habens basin aequalem arcui ABC & altitudinem BD, ad ABC triangulum, ita est arcus ABC ad AC rectam; ergo ut arcus ABC ad AC, ita sunt duae tertiae BD ad DE, & permutando, ut arcus ABC ad duas tertias BD, ita AC ad DE, sive ita ⅔ AC ad ⅔ DE, unde rursus permutando, ut arcus ABC ad ⅔ AC, ita ⅔ BD ad ⅔ DE, sive ita, BD ad DE.

Sit deinde sector DABC [Fig. 15], semicirculo minor, bifariam sectus rectâ

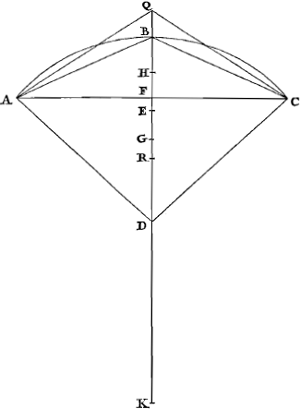
deux parties égales par la droite DB, dans laquelle le centre de gravité du secteur soit supposé se trouver en E, et soit tirée la corde AC. Je dis de nouveau que l'arc ABC est aux deux tiers de la droite AC comme BD à DE. Car si nous tirons AB,

illustratie
[Fig. 15].


BC et que le diamètre du cercle entier est KDB prolongé jusqu à Q, de sorte que QF est à BF comme le segment ACB au triangle ABC, et si l'on tire AQ, QC, le triangle AQC sera maintenant égal au segment ACB. Supposons ensuite que G soit le centre de gravité du triangle ACD, et H celui du segment ACB, et que comme DQ à QF ainsi HD à DR.

Puis donc que, comme le segment ACB ou le triangle AQC est au triangle ABC, c'est-à-dire comme QF à BF, ainsi sont les deux tiers de KF à DH*), le rectangle sur QF, DH sera égal aux deux tiers du rectangle KFB**), c'es-à-dire aux deux tiers du carré AF. Mais le même rectangle sur QF, DH est égal au rectangle QDR, puisqe comme QD à QF nous avons fait DH à DR; le rectangle QDR est donc égal au deux tiers du carré AF, donc comme QD à AF ainsi ⅔ AF à DR***); mais comme QD à AF, ainsi est aussi le rectangle sur QD, AF, auquel est égal le quadrilatère DAQC, c'est-à-dire le secteur DABC, au carré AF, d'où le secteur DABC est aussi au carré AF comme ⅔ AF à DR. Puis, comme E est le centre de gravité du secteur entier et H le centre de gravité du segment ACB, G celui du triangle ACD, il paraît que comme le triangle ACD est au segment ACB ou au triangle AQC, c'est-à-dire comme DF à FQ, ainsi HE à EG†); donc, par conversion et par composition des rapports, DQ sera à DF comme GH à HE. Mais puisque nous avons fait comme DQ à QF ainsi HD à DR, on aura aussi par conversion des rapports comme DQ à DF, ainsi HD à HR; donc HD à HR comme GH à HE, donc aussi la droite restante GD à la droite restante ER comme HD à HR††) c'est-à-dire comme DQ à DF. Mais comme DQ à DF ainsi est le

DB, in qua sectoris centrum gravitatis ponatur E punctum, & ducatur subtensa AC. Dico rursus, arcum ABC ad duas tertias rectae AC eam habere rationem, quam BD ad DE. Jungantur enim AB, BC, & totius circuli sit diameter KDB,

illustratie
[Fig. 15].


quae producatur in Q, ut fiat QF, ad BF, sicut portio ACB ad ABC triangulum, & jungantur AQ, QC; erit jam triangulus AQC portioni ACB aequalis. Ponantur deinde centra gravitatis, G trianguli ACD, & H portionis ACB; & sicut DQ ad QF, ita sit HD ad DR.

Quia igitur sicut portio ACB sive triangulus AQC ad triangulum ABC, id est, ut QF ad BF, ita ⅔ KF ad DH*), erit rectangulum sub QF, DH, aequale duabus tertiis rectanguli KFB**), c'es-à-dire aux deux tiers du carré AF. Mais le même rectangle sur QF, DH est égal au rectangle QDR, puisqe comme QD à QF nous avons fait DH à DR; le rectangle QDR est donc égal au deux tiers du carré AF, donc comme QD à AF ainsi ⅔ AF à DR***), id est, duabus tertiis quadrati AF; sed idem rectangulum sub QF, DH, aequale est rectangulo QDR, quia ut QD ad QF, ita fecimus esse DH ad DR; ergo rectangulum QDR aequale duabus tertiis quadrati AF, ideoque ut QD ad AF ita ⅔ AF ad DR***): sed ut QD ad AF, sic quoque est rectangulum sub QD, AF, cui aequale quadrilaterum DAQC, id est, sector DABC ad AF quadratum; ergo & sector DABC ad quadratum AF, ut ⅔ AF ad DR. Porrò quoniam E centrum gravitatis est totius sectoris, et H centrum grav. portionis ACB, G verò trianguli ACD, constat esse, sicut triangulus ACD a ACB portionem sive ad triangulum AQC, id est, ut DF ad FQ, ita HE ad EG†); quare convertendo & per compositionem rationis erit ut DQ ad DF, ita GH ad HE. Sed quia fecimus ut DQ ad QF, ita HD ad DR, erit quoque per conversionem rationis, ut DQ ad DF, ita HD ad HR; ergo HD ad HR ut GH ad HE; quare & reliqua GD ad reliquam ER, ut HD ad HR††), hoc est,

quadilatère DAQC, auquel est égal le secteur DABC, au triangle ACD; donc le secteur DABC est au triangle ACD comme GD à ER. Mais le triangle ACD est au carré DF comme AF à DF ou comme ⅔ AF á ⅔ DF ou DG. Donc par la règle le la proportion dérangée: comme le secteur DABC est au carré DF ainsi ⅔ AF à ER†††) et par conversion, le carré DF au secteur DABC comme ER à ⅔ AF. Mais il a été montré antérieurement que le carré AF est au secteur DABC comme DR à ⅔ AF; donc la somme des deux carrés DF et AF, ou le seul carré DA, est au secteur DABC comme la somme de ER et RD, c'est-à-dire la droite entière ED à ⅔ AF§). Mais le carré DA est aussi au secteur DABC comme la droite DA à l'arc AB, puisque, en effet, le secteur DABC est égal au rectangle ayant une base égale à l'arc AB et la hauteur DA, donc comme DA à l'arc BA ainsi ED à ⅔ AF; ou permutant: l'arc AB à ⅔ AF, ou l'arc ABC à ⅔ AC comme DA ou BD à DE.

Soit maintenant enfin le secteur DABC [Fig. 16] plus grand que le demicercle, et faisons les mêmes suppositions qu' auparavant, et soit complété le cercle BAFC, soit BDF le diamètre du cercle complet, dans lequel se trouvera aussi le centre de gravité, soit G, du secteur restant DAFC*).

Puis donc que le centre de gravité du cercle entier est D, et E et G les centres de gravité des deux secteurs, le secteur DABC sera au secteur DAFC, ou bien l'arc ABC à l'arc AFC comme GD à DE**), mais comme l'arc AFC à ⅔ AC ainsi est DF à DG ainsi qu'il a été montré tantôt, donc, pas la règle de la proportion dérangée, comme l'arc ABC à ⅔ AC ainsi sera DF ou AD à DE***). Il paraît donc que dans le demi-cercle et dans un secteur de cercle quelconque etc., ce qu'il fallait démontrer.

ut DQ ad DF. Sicut autem DQ ad DF, ita est quadrilaterum DAQC, cui aequalis sector DABC ad ACD triangulum; igitur sector DABC ad ACD triangulum ut GD ad ER: Est autem ACD triangulus ad DF quadratum, ut AF ad DF, sive ut ⅔ AF ad ⅔ DF id est DG. Igitur ex aequali in proportione perturbata, sicut sector DABC ad quadratum DF, ita ⅔ AF ad ER†††), & convertendo, quadratum DF ad sectorem DABC, ut ER ad ⅔ AF. Fuit autem ante ostensum, quadratum AF esse ad sectorem DABC, ut DR ad ⅔ AF; igitur duo simul quadrata, DF & AF, sive unum quadratum DA ad sectorem DABC ut duae simul ER & RD, id est ut tota ED ad ⅔ AF§). Est verò etiam quadratum DA ad DABC sectorem, sicut linea DA ad arcum AB, quia nimirum sector DABC aequalis est rectangulo, basin habenti aequalem arcui AB & altitudinem DA; ergo sicut DA ad arcum AB, ita ED ad ⅔ AF; & permutando, arcus AB ad ⅔ AF, sive arcus ABC ad ⅔ AC, ut DA vel BD ad DE.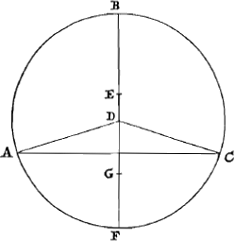



illustratie
[Fig. 16].


Esto jam denique sector DABÇ [Fig. 16] semicirculo major, & ponantur ea quae priùs, & perficiatur circulus BAFC, & totius diameter sit BDF, in qua erit quoque centrum grav. sectoris reliqui DAFC*), quod sit G.

Quia igitur circuli totius centrum gravitatis est D, & duorum sectorum centra grav. E & G, erit sicut sector DABC, ad sectorem DAFC, id est sicut arcus ABC ad arcum AFC, ita GD ad DE**): verùm ut arcus AFC ad ⅔ AC, ita est DF ad DG, sicuti modò ostensum est; ergo ex aequali in proportione perturbata, sicut arcus ABC ad ⅔ AC, ita erit DF vel BD ad DE***). Constat itaque quod in semicirculo & quolibet circuli sectore &c. quod erat demonstrandum.


Vorige Volgende