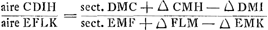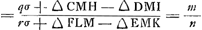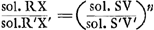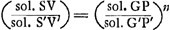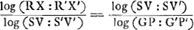Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651

[p. 271]

Theoremata de quadratura hyperboles
ellipsis et circuli
Ex dato
portionum gravitatis centro
1651.

[p. 273]

Avertissement.

Il n'est pas impossible que, dans l'ordre de la conception, les ‘Theoremata de quadratura hyperboles, ellipsis et circuli, ex dato portionum gravitatis centro’ n'aient précédé le traité ‘De iis quae liquido supernatant.’ Toutefois, tout pesé, nous supposons plutôt le contraire.¹⁾ Et puisque, en tout cas, nous ne possédons des ‘Theoremata’ aucun travail préliminaire, mais seulement l'ouvrage imprimé de 1651, nous avons cru devoir les placer ici, après les travaux de 1650.

Tout comme le traité ‘De iis, etc.’, les ‘Theoremata’ furent inspirés bien

1) Il est vrai que d'après l'‘Ad lectorem’, qui va suivre (voir la p. 283 du Tome présent) les ‘Theoremata’ étaient rédigés lorsque Huygens s'appliqua plus assidûment à l'étude de l'ouvrage de Grégoire de St. Vincent (comparez encore la Lettre N^o. 96 à Grégoire, p. 147 du T. I) et que cet ouvrage, d'après la Lettre N^o. 47^b, p. 566 du T. II, lui est parvenu pendant les vacances de Pâques de l'année 1648; mais cette Lettre elle-même prouve, comme nous le montrerons plus loin dans cet ‘Avertissement’ (p. 276), que ce premier examen de la quadrature du cercle de Grégoire n'avait été que superficiel. L'examen plus approfondi, qu'il instituait à propos des ‘Theoremata’ avait donc lieu probablement à une date postérieure, qui ne se laisse indiquer que vaguement à l'aide de la phrase ‘Mitto itaque Theoremata pauca quae non ita pridem meditatus sum’, que l'on rencontre dans la lettre à Golius du 28 décembre 1651 (p. 161 du T. I), laquelle accompagna l'envoi des ‘Theoremata’ et de l'‘Ἐξέτασις’.
En tout cas la date de la conception des ‘Theoremata’ doit être mise bien avant le 20 septembre 1651, lorsque la rédaction définitive fut renvoyée après examen par van Schooten à l'auteur (voir p. 145 du T. I).

[p. 274]

probablement par l'étude de l'oeuvre d'Archimède,²⁾ qui dans son ouvrage ‘De aequiponderantibus’ avait déterminé le centre de gravité du segment parabolique.³⁾ Ceux des segments hyperboliques et elliptiques n'y furent pas traités et Huygens se sera mis à les chercher.

Dans sa préface il nous raconte lui-même⁴⁾ qu' il parvint d'abord à montrer que chez l'hyperbole la détermination du centre de gravité dépend de la quadrature de cette courbe. Il s'ensuivait que réciproquement l'hyperbole se laisserait carrer si l'on savait construire ce centre; mais, comme Huygens nous le déclare, cette relation avec la quadrature de l'hyperbole n'était pas le but, mais seulement le résultat de ses recherches.⁵⁾

Ensuite il réussit à tracer une voie meilleure qui avait l'avantage de réussir de même avec les segments du cercle et de l'ellipse. En effet, le théorème central⁶⁾ des ‘Theoremata’ est valable pour les trois segments et la démonstration est donnée pour tous les trois à la fois. Aussi cette concordance admirable a-t-elle fortement impressionné Huygens, comme cela ressort de sa préface.

Ce n'était probablement qu' après l'achèvement du petit traité jusqu' au ‘Theorema VII’ inclus, qu'il prit connaissance de l'ouvrage de Della Faille, qu'il mentionne avec tant de louanges dans sa préface⁷⁾ et dans une lettre à Grégoire de St. Vincent du 8 novembre 1651⁸⁾; ce qui occasionna l'addition du ‘Theorema

2) Les Lettres N^o. 107 de décembre 1651 (p. 161 du T. I) à Golius et N^o. 117 de janvier 1652 (p. 170 du T. I) à de Sarasa témoignent de l'extrême admiration que le jeune Huygens avait conçue pour Archimède, qu' il estimait au-dessus de tous les autres géomètres; Apollonius venant en second lieu.

3) Voir les pages 189-217, T. II de l'édition de Heiberg, citée dans la note 2, p. 50 du Tome présent, ou bien les pages 133-139 du texte Latin de l'édition de Bâle de 1544, Grec et Latin, citée dans la note 1, p. 137 du T. I. C'est à cette dernière édition que nous emprunterons dans la suite nos citations, puisque Huygens probablement s'est servi d'elle ou l'a connue tout au moins. Voir, à ce propos, la Lettre N^o. 53, p. 98 du Tome I où l'on doit toutefois remplacer, dans la note 2, l'édition de Rivault, qui ne donne du texte grec que des fragments, par celle que nous venons de nommer.

4) Voir la page 283 du Tome présent.

5) Voir la même page de l' ‘Ad lectorem’ ou préface, citée dans la note 4.

6) Le ‘Theorema V’, p. 297 du Tome présent. Dans ce théorème Huygens apprend à construire un triangle dont le moment par rapport au diamètre de la conique, parallèle à la corde du segment, est égal à celui du segment. Dès lors la dépendance de la détermination des centres de gravité des segments hyperboliques ou elliptiques de la quadrature de l'hyperbole ou du cercle sautait aux yeux.

7) Voir la page 285 du Tome présent.

8) Voir la page 154 du T. I.

[p. 275]

VIII’ où le résultat principal⁹⁾ de Della Faille est déduit du ‘Theorema VII’, que nous venons de nommer.

Le 20 septembre 1651 le manuscrit des ‘Theoremata’ fut renvoyé à l'auteur par van Schooten, qui l'avait examiné.¹⁰⁾ Van Schooten le loua beaucoup et exhorta Huygens de ne pas tarder à le publier. Huygens répondit par la Lettre N^o. 97 d'octobre 1651¹¹⁾, dans laquelle il remercia chaleureusement van Schooten de lui avoir indiqué quelques inadvertances dans la ‘compositio’ et ‘conversio’ des rapports. Puis, dans une lettre du 25 octobre¹²⁾, il annonça à Grégoire de St. Vincent, après lui avoir donné un aperçu de ses ‘Theoremata’, sa résolution de les faire paraître simultanément avec la critique de la quadrature de Grégoire.

Le 11 novembre 1651 Huygens attendait chaque jour les figures gravées par van Sichem.¹³⁾ Enfin le 26 décembre des exemplaires de l'ouvrage imprimé, contenant les ‘Theoremata’ et l'‘Ἐξέτασις’ furent expédiés à Grégoire¹⁴⁾ et à d'autres savants.¹⁵⁾

Déjà en 1647 ou au commencement de 1648, pendant son séjour à Bréda, le jeune Huygens fut vivement intrigué par un gros volume qui se trouvait dans la

9) Toutefois Huygens a pu connaître ce résultat par la lettre de Mersenne à son père du 12 octobre 1646, où on le trouve exprimé, quoique avec quelque ambiguité; voir la page 23 du T. I. Ajoutons qu' en décembre 1646, d'après l'énumération de ses travaux qu'il transmit à Mersenne dans la lettre, citée p. 4 et 5 du Tome présent, Huygens avait trouvé le centre de gravité du segment de cercle (le théorème de Della Faille se rapporte au secteur). Peut-on en inférer qu'il était alors en possession de ses ‘Theoremata’ qui traitent les segments? Nous ne le croyons pas, puisque le segment de l'hyperbole n'est pas mentionné; de plus la phrase de la lettre à Golius, citée dans la note 1, semble exclure absolument une date si précoce.

10) Voir la page 145 du T. I.

11) T. I, p. 148.

12) T. I, p. 151.

13) Voir la lettre à van Schooten de cette date, p. 156 du T. I.

14) Voir la lettre N^o. 106, p. 159 du T. I.

15) Voici la liste des personnes, qui reçurent à cette occasion, ou plus tard, ce premier ouvrage de Huygens, pour autant qu'on peut reconstruire cette liste au moyen de la correspondance: Grégoire (T. I. p. 160); de Sarasa (p. 160, 169, 170); Della Faille (p. 160, 164, 168, 171); Golius (p. 161); van Schooten (p. 162); Pell (p. 162), Constantyn Huygens, frère (p. 162, 163); van Gutschoven (p. 162, 166); Roberval (p. 162); Seghers (p. 167, 168, 173); Cl. Richardus (p. 168, 171); Tacquet (p. 168, 171); Brereton (p. 176); Hobbes (p. 182); Cavendish (p. 182); Wallis? (p. 182); Carcavy (p. 429, 439, 446, 494); Milon (p. 429); Fermat (p. 439, 446, 494); mais les trois derniers seulement en 1656; les autres en décembre 1651 ou en 1652.

[p. 276]

possession du professeur Pell et qui devait contenir, d'après le titre, la quadrature du cercle et des sections coniques; mais le professeur Pell ne le lui voulait ‘jamais prester, ny en dire une sentence definitive encor qu'il l'ayt eu assez long temps’ et de même tous les autres mathématiciens à qui il en avait parlé ‘se trouvoyent empeschez a en venir à bout, n'osants dire absolument si’ l'auteur, Grégoire de St. Vincent, avait ‘rencontrè la quadrature ou non.’

Enfin, pendant les vacances de Pâques, Huygens réussit à avoir le livre et dans sa lettre à Mersenne du 20 avril 1648,¹⁶⁾ dont nous venons de citer quelques passages, il lui raconte le résultat de l'examen du livre et surtout de la première des quatre quadratures du cercle que Grégoire prétendait avoir données. Toutefois, dans cette lettre, il n'indique pas encore, comme il le fera dans l'‘Ἐξέτασις’¹⁷⁾, le lieu exact où le raisonnement, qui conduit à cette quadrature, est irrémédiablement en défaut.¹⁸⁾ Ensuite, la ‘Correspondance’ ne nous apprend rien sur l'‘Ἐξέτασις’ avant octobre 1651 quand l'échange des lettres avec Grégoire commence. Pour plus d'informations nous renvoyons à cette correspondance¹⁹⁾ ainsi qu' à celle avec van Schooten²⁰⁾ sur le sujet de l'‘Ἐξέτασις’.

16) La Lettre N^o. 47^b, p. 566 du T. II. On trouve la réponse de Mersenne, du 2 mai 1648, aux pages 89 et 90 du T. I.

17) Et aussi dans la Pièce N^o. 98 de date incertaine, p. 149 du T. I.

18) Dans la lettre mentionnée il cherche la faute dans la ‘Prop. 43’. Or, quoiqu'on pense des démonstrations de Grégoire qui ont mené à cette proposition, la proposition elle même est véritable où elle dit que le rapport des solides RX et R′X′, comme aussi celui des solides SV et S′V′ est construisible. Comparez l'‘Aperçu’, qui suit, de la première quadrature du cercle de Grégoire, au § 8, p. 279.

19) Comparez la note 13 de l'‘Ad Lectorem’, p. 286 du Tome présent.

20) Voir les lettres N^o. 97, d'octobre 1651 (p. 148 du T. I.); N^o. 104 du 13 novembre (p. 157 du T. I); N^o. 108, du 28 décembre 1651 (p. 162 du T. I.) et N^o. 110 du 2 janvier 1652 (p. 163 du T. I).

[p. 277]

Aperçu de la première quadrature du cercle de Grégoire de St. Vincent.

Nous croyons utile pour faciliter l'intelligence de l'‘Ἐξέτασις’, d'ajouter à cet ‘Avertissement’ un résumé de la quadrature du cercle dont l'‘Ἐξέτασις’ contient la réfutation. Nous l'avons divisé en paragraphes à cause des renvois que nous ferons dans les notes.

1. Nous commençons par la ‘Prop. 53’ (p. 1133) où Grégoire démontre que le cercle sera carrable si l'on peut satisfaire aux deux conditions suivantes:

1^o. qu'on sache construire deux arcs de cercle CD et EF,²¹⁾ dont les projections HI et KL sur un même diamètre sont égales et qui soient commensurables entre eux et avec la circonférence du cercle.

2^o. qu'on sache construire le rapport des aires CDIH et EFLK.²²⁾

2. Or, il est facile de montrer que la première condition peut être remplie. Grégoire l'a fait par sa ‘Prop. 22’ (p. 1111) et Huygens en donne un exemple bien simple dans la première figure de son ‘Ἐξέτασις’²³⁾, où CH = 60^o, HE=30^o.

3. Tout dépend donc de la seconde condition, c'est-à-dire, de la détermination du rapport des aires CDIH et EFLK, rapport que Grégoire, dans la ‘Prop. 52’ (p. 1133), remplace par celui des solides GP et G′P′²¹⁾ qu' il obtient en soumettant les paraboles AGNZ et BP′O′Y, dont les sommets se trouvent en A et B, à l'opération qu' il appelle: ‘ducere planum in planum’.

21) Voir la figure de la page suivante.

22) En effet, ces deux conditions étant remplies, soient pσ, qσ, rσ les aires du cercle entier et des secteurs DMC, FME (voir toujours la figure de la page suivante), proportionelles respectivement à la circonférence du cercle et aux arcs DC et EF; on aura alors: Or, cette dernière égalité permet de calculer et de construire la commune mesure σ du cercle et des secteurs et par suite l'aire du cercle lui-même.

23) Voir la page 319 du Tome présent.

21) Voir la figure de la page suivante.

[p. 278]

4. Disons d'abord que cette opération consiste à tourner le carré AZ, avec les lignes qui s'y trouvent, autour de la droite AB jusqu' à ce qu' il soit perpendiculaire au plan du carré BY; à compléter ensuite le rectangle qui a τα et τη pour côtés et enfin à faire mouvoir ce rectangle de sorte qu' il demeure perpendiculaire à l'axe AB et que le point τ décrive l'axe AB et les points α et η les courbes ANZ et YPB. Ainsi, pour avoir le solide GP, on doit mouvoir le rectangle αη depuis la position GO jusqu' à la position NP.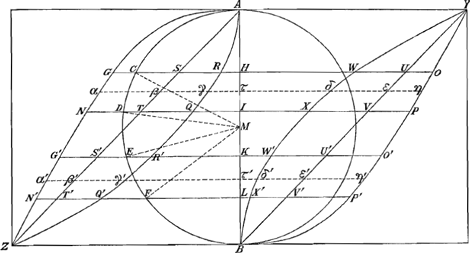

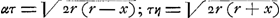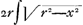5. Posant alors AM = MB = r; AY = ZB = 2r; Mτ = x; Mτ′ = x′; on a et on trouve pour le volume du solide GP: dx, d'où il suit que ce volume égale celui d'un cylindre droit ayant pour base la figure CDIH et pour hauteur AB. C'est le ‘Corollarium’ de la ‘Prop. 51’ (p. 1132) de Grégoire.²⁴⁾

6. Le problème se réduit donc à celui de construire (à l'aide de la règle et du compas) deux lignes qui représentent le rapport des solides GP et G′P′. Et Grégoire croit être arrivé à la solution de ce problème par la comparaison des solides

24) Inutile de dire que la démonstration de Grégoire est purement géométrique et entièrement à la mode des anciens.

[p. 279]

GP et G′P′ avec les solides SV, S′V′, RX et R′X′ qu' on obtient en soumettant les droites AZ et BY et les paraboles AQZ et BXY, dont les sommets se trouvent en A et en B, à l'opération ‘ducere planum in planum’.

7. Cette solution de Grégoire se trouve résumée dans sa ‘Prop. 44’ (p. 1126), où il prétend:

1^o. que le rapport des solides RX et R′X′ doit contenir autant de fois (‘toties continere’) le rapport des solides SV et S′V′, que celui-ci contient le rapport des solides GP et G′P′.

2^o. que le rapport des solides RX et R′X′ et celui des solides SV et S′V′ sont construisibles.

8. La vérité de la seconde assertion, pour laquelle il renvoie à la ‘Prop. 43’ (p. 1125), se démontre aisément puisqu' on peut trouver les cubatures des solides RX et SV.²⁵⁾ Grégoire traite ces cubatures respectivement dans la ‘Prop. 42’ (p. 1124) du ‘Lib. 10’ qui nous occupe, et dans la ‘Prop. 5’ (p. 708) du ‘Lib. 7: De ductu plani in planum’, comme le fait aussi Huygens dans l'‘Ἐξέτασις’²⁶⁾.

9. Il s'agit donc uniquement encore de vérifier la première assertion et de connaître le sens exact du mot ‘continere’.

Or, en considérant les solides en question comme des tranches infinement petites d'épaisseurs égales, HI = KL, on trouve aisément: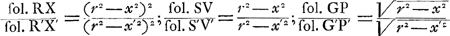

On a donc: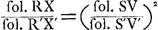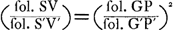

;

et on peut dire: que le rapport de RX à R′X′ contient deux fois le rapport de SV à S′V′, et que de même ce dernier rapport contient autant de fois le rapport de GP à G′P′²⁷⁾; mais il est clair 1^o. que cette assertion n'est plus valable pour des

25) Ces cubatures se réduisent respectivement aux intégrales ∫ (r²-x²)²/4 r² dx et ∫ (r²-x²) dx.

26) Voir les pages 329-337 du Tome présent.

27) Ces résultats sont démontrés par Grégoire dans les ‘Prop. 31-34’ (p. 1116-1117), c'est-à-dire, non pas pour les tranches infiniment petites, mais pour les sections rectangulaires qui les engendrent; ce qui revient au même.

[p. 280]

solides d'épaisseurs finies; 2^o. que dans ce dernier cas l'expression ‘continere’ perd sa signification primitive, si simple, et qu'une nouvelle définition devient nécessaire.²⁸⁾

10. La première assertion du § 7, qui constitue la ‘Prop. 40’ (p. 1123) de Grégoire, est donc erronée. Elle se fonde sur la ‘Prop. 39’ (p. 1121) dont la démonstration est à peu près incompréhensible²⁹⁾; mais qui a la portée suivante: que, si l'assertion en question est vraie pour les solides qui possèdent respectivement les épaisseurs Hτ = Kτ′ et τI = τ′L, elle l'est alors également pour leurs sommes qui possèdent l'épaisseur HI = KL.

C'est dans cette dernière proposition, comme Huygens le signale dans l'‘ Ἐξέτασις’,³⁰⁾ que réside l'erreur, qui rend vicieuse la quadrature de Grégoire.

28) En se plaçant au point de vue moderne le choix de la nouvelle définition ne serait pas douteux. Elle exigerait, si la proposition de Grégoire était vraie, l'existence d'une valeur n entière, fractionnaire ou irrationnelle, pour laquelle on aurait à la fois: et Ceci amènerait la relation: ;

mais il est clair que cette relation n'est pas exacte.

29) Comparez la note 8, p. 317 du Tome présent.

30) Voir la page 317 du Tome présent.