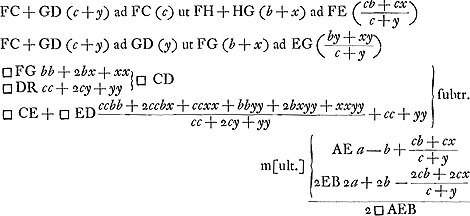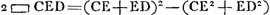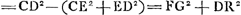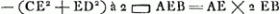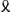Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651
(1908)–Christiaan Huygens–
[pagina 249]
| |
XI.Ga naar voetnoot1)
| |
[pagina 250]
| |
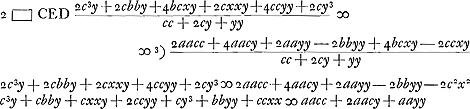 dividendo utrinque per c + y fit 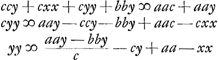
Sit c ad a + b ut a - b ad d. Erit yy ∞ dy - cy + aa - xx 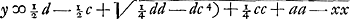 Hinc apparet punctum D esse ad circuli circumferentiam, Eritque constructio hujusmodi. | |
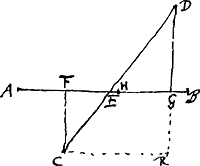
Constr.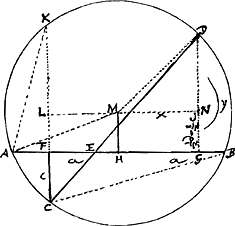 [Fig. 2.]
Tribus CF, FB, AF, inveniatur quarta proportionalis FK quae erit d sive 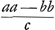 . totâque KC bifariam divisâ in L, erit LF ∞ ½ d - ½c. et posita perpendiculari HM ∞ LF, ductâque AM, erit haec . totâque KC bifariam divisâ in L, erit LF ∞ ½ d - ½c. et posita perpendiculari HM ∞ LF, ductâque AM, erit haec 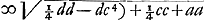 Ga naar voetnoot4). descripto igitur circulo AKDB, centro M, radio MA, si sumatur in ejus circumferentia aliquod punctum ut D unde ducta secet lineam AB, manifestum est hoc problemati satisfacere, nam quum HG vel MN sit x et MD □ ∞ ¼ dd - dcGa naar voetnoot4) + ¼ cc + aa, erit ND ∞ Ga naar voetnoot4). descripto igitur circulo AKDB, centro M, radio MA, si sumatur in ejus circumferentia aliquod punctum ut D unde ducta secet lineam AB, manifestum est hoc problemati satisfacere, nam quum HG vel MN sit x et MD □ ∞ ¼ dd - dcGa naar voetnoot4) + ¼ cc + aa, erit ND ∞
| |
[pagina 251]
| |
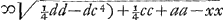 Ga naar voetnoot4) et Ga naar voetnoot4) et 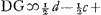 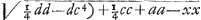 Ga naar voetnoot4) ut oportebat. Sumptâ autem x majore quam a erit y ∞ ½ d - ½ c Ga naar voetnoot4) ut oportebat. Sumptâ autem x majore quam a erit y ∞ ½ d - ½ c 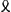 Ga naar voetnoot5) Ga naar voetnoot5)
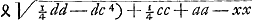 Ga naar voetnoot4). Quum autem fecerimus sicut CF ad FB ita AF ad FK, apparet triangula CFB, AFK esse similia; atque ideo angulos CBA, CKA aequales. Sunt itaque quatuor puncta K, A, C, B in eadem circumferentia circuli; L autem est medium KL,Ga naar voetnoot6) et H medium AB; igitur centrum circuli ad quem sunt puncta K, A, C, B, necessario est in intersectione perpendicularium LM, HM, quae est M. Igitur constat punctum C esse ad circuli circumferentiam quem descripsimus centro M per punctum A. Adeo ut ad constructionem hujus problematis tantum sit opus describere circulum per tria puncta A, C, B, quae data sunt. Idem autem colligitur ex prop. 35. lib. 3. Elem.Ga naar voetnoot7) [Euclid.] Ga naar voetnoot4). Quum autem fecerimus sicut CF ad FB ita AF ad FK, apparet triangula CFB, AFK esse similia; atque ideo angulos CBA, CKA aequales. Sunt itaque quatuor puncta K, A, C, B in eadem circumferentia circuli; L autem est medium KL,Ga naar voetnoot6) et H medium AB; igitur centrum circuli ad quem sunt puncta K, A, C, B, necessario est in intersectione perpendicularium LM, HM, quae est M. Igitur constat punctum C esse ad circuli circumferentiam quem descripsimus centro M per punctum A. Adeo ut ad constructionem hujus problematis tantum sit opus describere circulum per tria puncta A, C, B, quae data sunt. Idem autem colligitur ex prop. 35. lib. 3. Elem.Ga naar voetnoot7) [Euclid.]
|
|