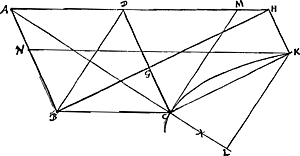
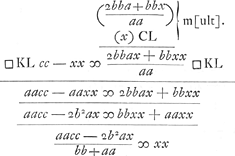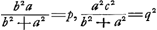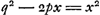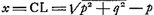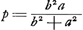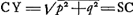Rhombo dato DB, ejusque producto latere AD: Oportet ex angulo B educere lineam BGH, cujus pars GH sit aequalis lineae E datae.Ga naar voetnoot3)
[Fig. 1.]
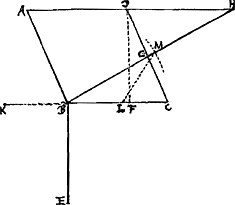
Factum jam sit, et ducantur ipsis CG, GH, parallelae HK, KC. Est igitur DC ad GC vel HK, ut HB ad GB vel ut HA ad DA, ideoque quod continetur lineis DA, DC aeq. ei quod continetur medijs HA, GC vel HK: Ergo punctum K est ad hijperbolen, quae vertice C describitur ad asymptotos AB, AH. linea
| |
autem CK aequalis est ipsi GH sive E. datum est igitur punctum K, unde et H datum erit.
Scribit autem PappusGa naar voetnoot2) hoc problema solidum non esse sed planum, lib. 7. in pr. de inclinat.; Quaerenda est igitur alia constructio. Sit AC ∞ a, DB ∞ b, linea E ∞ c, CL ∞ x, Sunt autem KL, CM, parallelae diametro DB. CM igitur vel DB potest quartam figurae partem quae sub latere transverso et recto hijperboles CK continetur per 1, lib. 2, Con.Ga naar voetnoot4) et est AC ½ lateris transversi. Igitur bb/½a sive 2bb/a est latus rectum. Ad inveniendum nunc. qu LK, fiat
ut l. trans. (2a) ad l. rect. (2bb/a) ita 2 AC + CL (2a + x) ad lineam
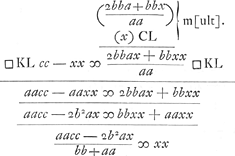
| |
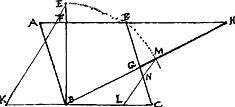
[Fig. 4.]
CN ∞CL.Ga naar voetnoot7)
Eadem est constructio si angulus C sit obtusus. nisi quod tum producere oportet BA ut ipsi occurrat BF.
Alia solutio hujus probl. est in geometria inclin. Apollonij, restituta à Marino Getaldo;Ga naar voetnoot8) sed constructio prolixior.
Aliam ego postea inveni.Ga naar voetnoot9)
|
-
voetnoot1)
- La pièce se trouve p. 155-156 du manuscrit No 12, décrit dans la note 1 de la page 7 du Tome présent.
-
voetnoot2)
- Voir, à la page 163 verso du ‘liber VII’ de l'ouvrage cité p. 259, T. II, note 3, l'aperçu de l'ouvrage ‘De inclinationibus’ d'Apollonius, où on lit: ‘Et cum hoc sit problema universale. Duabus lineis positione datis inter ipsas ponere rectam lineam magnitudine datam, quae ad datum punctum pertineat: in hac particularibus subiecta differentia habentibus, alia quidem erant plana, alia solida alia vero linearia. Ex planis autem, quae ad multa vtiliora sunt eligentes problemata haec ostenderunt .... Rhombo data, & vno latere producto aptare sub angulo exteriori magnitudine datam rectam lineam, quae ad oppositum angulum pertineat.’
-
voetnoot3)
- Le problème peut être considéré comme une généralisation du problème traité dans la pièce No. IV, p. 226. Huygens y est revenu plus d'une fois. Voir, là-dessus, la note 1 de la pièce No. IV citée.
-
voetnoot2)
- Voir, à la page 163 verso du ‘liber VII’ de l'ouvrage cité p. 259, T. II, note 3, l'aperçu de l'ouvrage ‘De inclinationibus’ d'Apollonius, où on lit: ‘Et cum hoc sit problema universale. Duabus lineis positione datis inter ipsas ponere rectam lineam magnitudine datam, quae ad datum punctum pertineat: in hac particularibus subiecta differentia habentibus, alia quidem erant plana, alia solida alia vero linearia. Ex planis autem, quae ad multa vtiliora sunt eligentes problemata haec ostenderunt.... Rhombo data, & vno latere producto aptare sub angulo exteriori magnitudine datam rectam lineam, quae ad oppositum angulum pertineat.’
-
voetnoot4)
- Voir la note 51 de la page 114 du Tome présent.
-
voetnoot5)
- Voici cette construction telle qu'elle se déduit de l'équation quadratique qui précède, et qu'on la retrouve dans la Fig. 2.
Posons 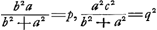 ; alors l'équation quadratique s'écrit: ; alors l'équation quadratique s'écrit: 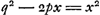 , et l'on a , et l'on a 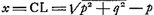 . Or, pour construire . Or, pour construire 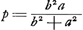 il suffit de mener CN perpendiculaire sur BC et d'abaisser la perpendiculaire NO sur AC; alors OC = p comme il est facile à vérifier. De même, pour trouver q, on n'a qu' à prendre AP égal à la ligne donnée E = c et à abaisser la perpendiculaire PQ; alors AQ = q. Prenant ensuite, sur le prolongement de NO, OY égal à AQ, on a il suffit de mener CN perpendiculaire sur BC et d'abaisser la perpendiculaire NO sur AC; alors OC = p comme il est facile à vérifier. De même, pour trouver q, on n'a qu' à prendre AP égal à la ligne donnée E = c et à abaisser la perpendiculaire PQ; alors AQ = q. Prenant ensuite, sur le prolongement de NO, OY égal à AQ, on a 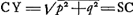 (le cercle SY ne passe par le point B que par accident), et OS = x = CL. On peut donc construire le triangle rectangle CKL, où CK = E = c, et mener enfin, comme il est indiqué dans le texte, BGH parallèle à CK. (le cercle SY ne passe par le point B que par accident), et OS = x = CL. On peut donc construire le triangle rectangle CKL, où CK = E = c, et mener enfin, comme il est indiqué dans le texte, BGH parallèle à CK.
-
voetnoot6)
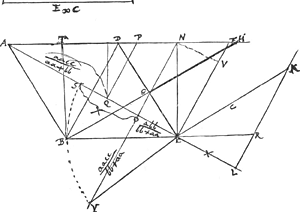
- Voici comment. On a d'après les remarques qui précèdent: CR/CL = TD/OC = c/OY = λ; donc (mettant entre crochets les lignes qui se rapportent à la Fig. 3 de la construction abrégée): (BE) = λOY, (BK) = (BF) = TD = λOC, (KL) = (KE) = λCY = λSC, (BL) = (KL) - (KB) = λSC - λOC = λOS = λCL = CR; mais alors le triangle (BLM) est égal au triangle CRK, puisqu' on a (BL) = CR, BM = CK, ∠ (BLM) = ∠ CRK; d'où il suit que l'angle (MBL) est égal aux angles KCR et HBR et que les lignes BH des deux figures se correspondent.
-
voetnoot7)
- La construction de la Fig. 4 ne diffère pas essentiellement de celle de la Fig. 3. La remarque CN ∞ CL peut servir à construire la ligne LN qui sera parallèle à la ligne BB.
-
voetnoot8)
- Voir la note 5 de la page 126 du T. VIII. On trouve en effet la construction en question aux pages 330-333 de l'ouvrage de Ghetaldi cité en dernier lieu dans la note mentionnée. Toutefois Huygens fait allusion ici à l'ouvrage cité en premier lieu dans la même note, où l'on rencontre la même construction aux pages 17-19.
-
voetnoot9)
- Voir les ‘Travaux mathématiques divers de 1652 et 1653’, où l'on trouvera sous la date du 9 févr. 1652 une autre solution du même problème. Consultez aussi la note 1 de la pièce No. IV, p. 226.
|