Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651
(1908)–Christiaan Huygens–
[pagina 229]
| |
V.Ga naar voetnoot1)
| |
[pagina 230]
| |
Jungantur AB puncta, et in AB cadat perp. CE; et sit AF vel FB ∞ a; FE ∞ b; EC ∞ c. Et ponatur jam inventum punctum D: sitque perp. DG ∞ y, et distantia FG ∞ x. 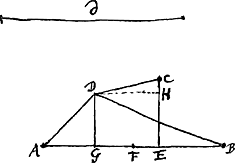 [Fig. 1.]
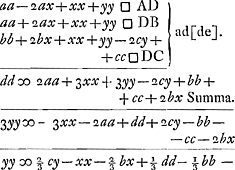 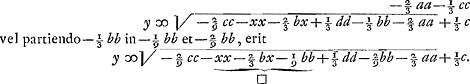 sint autem quantitates cognitae - 2/9 cc + ⅓ dd - 2/9 bb - ⅔ aa ∞ qq fietque 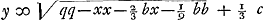 , vel si punctum D alio loco quaeratur, adeo ut perp. DG cadat ad alteram partem puncti medij F, erit , vel si punctum D alio loco quaeratur, adeo ut perp. DG cadat ad alteram partem puncti medij F, erit 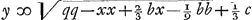 . Et si punctum D quaeratur infra lineam AB, habebitur in aequatione yy ∞ - ⅔ cy - xx &c.Ga naar voetnoot4) et erit . Et si punctum D quaeratur infra lineam AB, habebitur in aequatione yy ∞ - ⅔ cy - xx &c.Ga naar voetnoot4) et erit 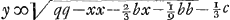 . quae omnia procedunt à primâ quadratorum supputatione. Si autem qu. x . quae omnia procedunt à primâ quadratorum supputatione. Si autem qu. x 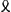 Ga naar voetnoot5) ⅓ b majus sit quam qq - ⅙ cc, erit Ga naar voetnoot5) ⅓ b majus sit quam qq - ⅙ cc, erit 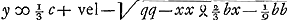 Ga naar voetnoot4). Ga naar voetnoot4).
| |
[pagina 231]
| |
Constructio.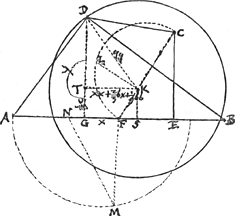 [Fig. 2.]
Jungatur FC. sitque FK ∞ ⅓ FC, estque KL qu. ∞ 2/9 bb + 2/9 cc. sit FN ∞ KL, et FM qu. ∞ ⅔ aa. fit NM q. ∞ ⅔ aa + 2/9 cc + 2/9 bb. ┚ OP [Fig. 3] sit ∞ ⅓ q. OQ, id est ⅓ dd. PR ∞ NM. et centro K describatur semidiam.o KD ∞ RO circulus; et ubicunque in eo capiatur punctum D; ductisque DA, DB, DC, erunt harum trium quadr.a aequalia qu.o OQ.  [Fig. 3.]
Determinatio haec est; quod ⅔ aa + 2/9 cc + 2/9 bb non debeat major esse quam ⅓ dd, et siquidem haec aequalia fuerint erit quaesitum punctum in K, atque ibi tantum. Animadversione dignum est, centrum K esse quoque grav. centrum trianguli quem data puncta A, B, C, constituunt.Ga naar voetnoot6) | |
[pagina 232]
| |
 [Fig. 4.]
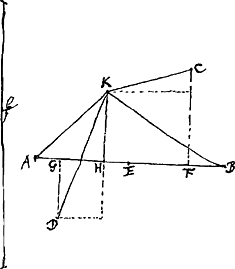
Sint jam data puncta quatuor, A, B, C, D et ponatur jam inventum quintum K. Jungantur duo puncta A et B, et ex reliquis cadant in AB perpendiculares CF, DG et KH, et sit AE vel EB ∞ a; EF ∞ b; FC ∞ c; EG ∞ d; GD ∞ e; EH ∞ x; HK ∞ y et datum quadr. ∞ ff. 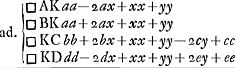 4yy - 2cy + 2ey + 4xx - 2dx + 2bx + 2aa + bb + dd + cc + ee ∞ ff yy ∞ ½ cy - ½ ey - xx + ½ dx - ½ bx - ½ aa - ¼ bb - ¼ dd - ¼ cc - ¼ ee + ¼ ff et quaedam partiendo, et addendo et detrahendo ⅛ bd fit: 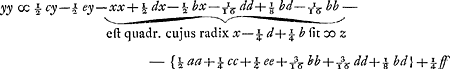 ergo fit yy ∞ ½ cy - ½ ey - zz + ¼ ff - ½ aa - ¼ cc - ¼ ee - 3/16 bb - 3/16 dd - ⅛ bd addendo jam quadr. ex ¼ c - ¼ e ad reliquas quantitates cognitas fit ¼ ff - 3/16 cc - ⅛ ce - 3/16 ee - ½ aa - 3/16 bb - 3/16 dd - ⅛ bd quod vocetur qq. Ergo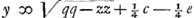 . Unde patet punctum K rursus esse ad circuli circumferentiam. Eritque constructio problematis hujusmodi. . Unde patet punctum K rursus esse ad circuli circumferentiam. Eritque constructio problematis hujusmodi.
Sit EL [Fig. 5] ∞ ¼ EF - ¼ EG sumenda versus F quoniam EF major est quam EG. sit perpd. LM ∞ ¼ FC - ¼ GD, sumenda supra lineam AB quoniam FC major est quam GD. Et inventâ lineâ q, sit ea semidiameter circuli descripti centro M; et quodcunque punctum ejus circumferentiae proposito satisfaciet, ut ex ipsa constructione manifestum esse potest. Evidens quoque est, punctum M esse illud, è quo si ducantur quatuor lineae ad data puncta A, B, C, D, omnium simul quadrata sint minima quae esse possint.Ga naar voetnoot6) | |
[pagina 233]
| |
Si puncta ita dentur ut utrumque C et D sit ad easdem partes lineae AB, tum erit LM ∞ ¼ FC + ¼ GD. 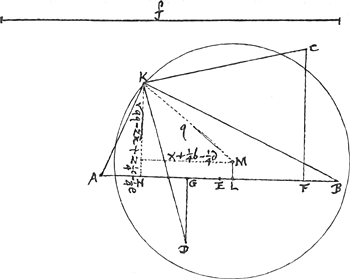 [Fig. 5.]
Item si utraque perpendicularis cadat in lineam AB ad easdem partes medij E. tum EL erit ∞ ¼ EF + ¼ EG; atque haec ex prima quadratorum supputatione manifesta sunt.
Datis autem quotcunque punctis invenietur circuli quaesiti centrum hoc pacto: duo quaevis ex datis punctis jungantur lineâ rectâ, quae bifariam dividatur, et cadant in eam ex punctis reliquis perpendiculares; tum omnes distantiae perpendicularium quae sunt ab una parte puncti medij, auferantur ab omnibus distantijs quae sunt ab altera parte ejusdem medij et residuum dividatur in tot partes aequales quot sunt data puncta, earumque partium una statuatur à puncto medio. versus eam partem ubi summa distantiarum major est; atque ad ejus partis terminum ponatur versus partem ubi summa perpendicularium major est, perpendicularis aequalis uni parti differentiae quae est inter omnes perpendiculares ab una et altera parti lineae, divisae similiter in tot partes aequales quot sunt data puncta: Eritquae hujus perpendicularis terminus centrum circuli quaesitum.Ga naar voetnoot7) Longitudo autem semidiametri pendet à quantitate spatij dati.Ga naar voetnoot8) Verùm si invento centro quilibet circulus describatur, atque à puncto quod sit in ejus circumfer.a ducantur lineae ad data puncta. atque item ex alio ejusdem | |
[pagina 234]
| |
circumfer.ae puncto ad data puncta lineae ducantur; erunt omnium harum quadrata illarum omnium quadratis aequalia. Centrum circuli quaesitum semper est centrum gravitatis datorum punctorumGa naar voetnoot9), ut hic punctum M centr. gr. punctorum A, B, C, D, quod ex constructione superiori facile deducitur. |
|

