Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651

[p. 226]

IV.¹⁾
[1650].

Problema.
Datum est quadratum BD, etque productum latus AD: oportet ex angulo B, ducere lineam BGH, ita ut pars GH sit aequalis datae lineae quae est E.²⁾

Factum jam sit, et ducantur ipsis GH, GC parallelae CK, HK. est igitur DC

Fig. 1.

ad GC vel HK sicut HB ad GB sive ut HA ad DA. quare erit ▭ quod lineis HA, HK continetur aequale ei quod continetur sub DA, DC, id est quadrato DB. est igitur punctum K ad hijperbolen, quae vertice C describitur ad asymptotos AB, AH. estque CK aequalis ipsi GH sive E. ducatur diagonalis AC, eaque producatur, et ducatur ad eam perpend. KL.

Sit AC ∞ a; E ∞ b; CL ∞ x; quia autem asymptoti continent angulum rectum, erit hijperboles ÇK latus rectum aequale transverso, unumquodque vero

1) La pièce se trouve pp. 147a-149 du manuscrit N^o. 12 décrit dans la note 1 de la page 7 du Tome présent.

2) Le problème est emprunté à Pappus, Lib. VII, probl. IIII, Prop. LXXII, p. 206, verso de l'ouvrage cité p. 259 du T. II, note 3, où l'on trouve une construction très élégante (celle reproduite ici par Huygens en second lieu) et une démonstration de cette construction. Descartes au Livre III de la Géométrie (p. 461-463 du T. VI de l'édition d'Adam et Tannery) le traite comme un exemple de l'usage de sa méthode de réduire les équations ‘solides’, puisqu' en posant CG comme inconnue on arrive à une équation biquadratique qui se réduit à deux équations quadratiques. Van Schooten, dans ses ‘Commentarii’ (p. 266-270 de l'édition de 1649 de l'ouvrage cité dans la note 1, p. 218 du T. I) explique la signification des racines rejetées pas Descartes.
Le texte qui va suivre semble en quelques endroits avoir été rédigé avec peu de soin; mais le point principal consiste dans la démonstration que le point K décrit une hyperbole équilatère, propriété connue déja par Pappus (voir la note 9), suivie de la remarque que le point C est le sommet de cette hyperbole. Dès lors il était clair que le problème est un problème plan dont la construction ne pouvait plus présenter aucune difficulté.
Plus tard, en 1652 (voir plus loin dans le Tome présent les ‘Travaux mathématiques divers de 1652 et 1653’), et ensuite en 1653 (voir ses lettres à van Schooten du 23 oct. et du 10 déc. p. 247-251 et 256-257 du T. I), Huygens est revenu sur ce problème et sur celui de la pièce N^o. VIII (p. 239), qui en est une généralisation, pour en donner des solutions et démonstrations qu'il a reproduites avec de légères modifications dans les ‘Illustrium quorundam problematum constructiones’ de 1654 aux ‘Probl. IV-VII.’ On y retrouvera, quant au problème qui nous occupe, au ‘Probl. IV’, la construction de Pappus avec une démonstration bien plus simple que celle du texte présent.

[p. 227]

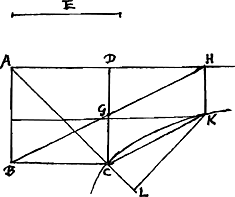
aequ. duplae AC. itaque quadr. KL aequale erit rectangulo sub CL et dupla AC³⁾, excedetque figura simili quae erit quadr. CL: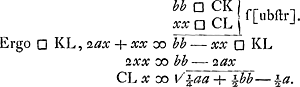

3) Il y a ici quelque confusion; mais les calculs, qui suivent, sont corrects.

Constructio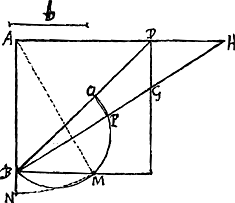

[Fig. 2.]

ex hisce inventa est hujusmodi.

Sit BM ∞ b. AN ∞ AM. descriptoque semicirculo BMO, ponatur OP ∞ BN, et ducatur BPGH, eritque GH ∞ b. quod erat faciendum.⁴⁾

Hujus demonstratio facile elicitur ex demonstratione constructionis sequentis⁵⁾, quae talis est.

Sit DR ∞ b [Fig. 3]. CS ∞ CR. BT ∞ TS. et scribatur semicirc. SMB. et jungatur BH, eritque HG aequalis b.⁶⁾.

4) La construction est bonne; mais on ne voit pas comment elle découle de ce qui précède.

5) On ne le voit pas, puisque le demi-cercle de la figure 4 ne correspond nullement avec celui de la figure 2. Évidemment le texte à été composé à l'aide de plusieurs fragments, empruntés à des travaux préliminaires, dont le raccordement laisse à désirer.

6) C'est la construction de Pappus.

[p. 228]

Demonsratio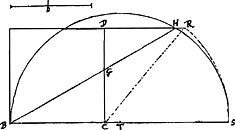

[Fig. 3.]

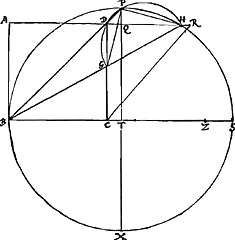[Fig. 4.]

ducantur [Fig. 4] lineae BDP, PTX⁷⁾, PH, PG. et super GH scribatur ½ circ. GDH. et sit CZ ∞ BC.

Est igitur ZS diff. duarum CR, CD. BT autem dimidia est BS, et BC dimidia BZ; ergo CT sive PQ est dimidia ZS. quum autem BS sit summa duarum CD, CR; et ZS differentia earundem; erit rectangulum ZSB⁸⁾ aequale differentiae quadratorum CR, CD, id est qu^o. DR. ideoque rectang. QPX sive quad. PH aequ. dimidio quadrato DR. Porro quum angulus PDG una cum angulo GDB semirecto aequetur duobus rectis, sitque etiam angulus PHB semirectus, quoniam PB est quadrans circuli, manifestum est etiam duos angulos PDG, PHG aequari duobus rectis: quare necesse est semicirculum GDH etiam transire per punctum P. Est igitur et angul. PGH semirectus et aequalis angulo PHG. Igitur et quadr. ex PG aequale est quadr^o. ex PH, id est dimidio quadrato DR. Ergo quadr. GH aequale quadrato DR; et linea GH aequalis DR. quod erat ostendend.

Problema hoc est apud Pappum Alex. lib. 7 prop. 72. et prima fronte omninò solidum esse videtur, quemadmodum revera esset, si quidem loco quadrati proponeretur rectangulum: ut videre est apud eund. Pappum lib. 4. propos. 31.⁹⁾ de eodem hoc Problemate vide quae scripsit Cartesius lib. 3. Geom. Demonstratio Pappi¹⁰⁾ â mea diversa est, sed prolixior videtur et difficilior.

7) PTX est l'un des diamètres du cercle BPSX, quisqu'on a < PBT = 45^o, donc arc. PS = 90^o.

8) C'est-à-dire le rectangle qui a ZS et SB pour côtés.

9) Au lieu cité Pappus démontre que l'aire du rectangle AK (voir la Fig. 1) est égale à celle du rectangle ADCB. Ainsi le point K se trouve sur une hyperbole équilatère qui passe par le point C. Après quoi Pappus remarque que, pour achever la construction, on cherchera le point d'intersection de cette hyperbole avec un cercle ayant C pour centre et la ligne donnée pour rayon. Or puisque, dans le cas du rectangle traité par Pappus au lieu cité, le point C n'est plus le sommet de l'hyperbole, le problème devient solide.

10) Voir les ‘Propositiones LXXI et LXXII’ du ‘Lib. VII’.