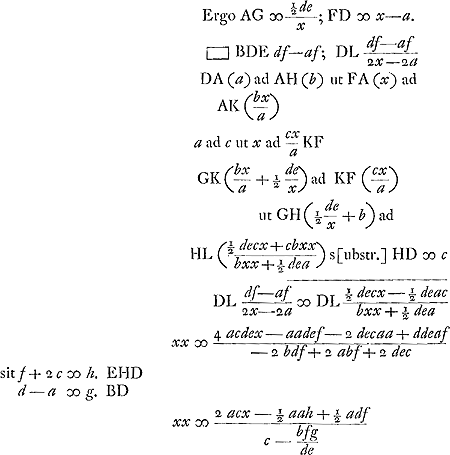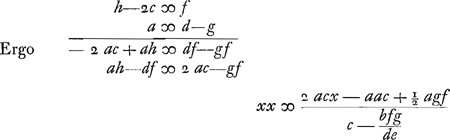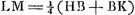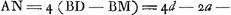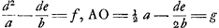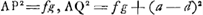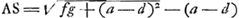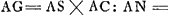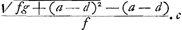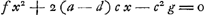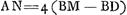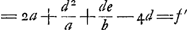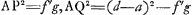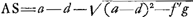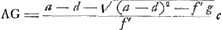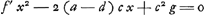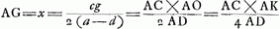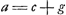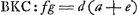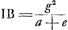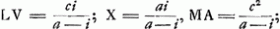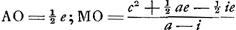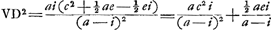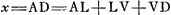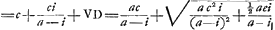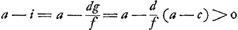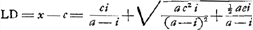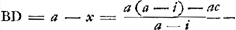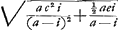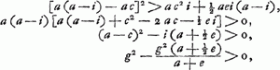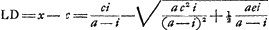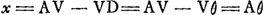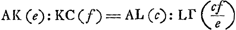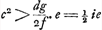Problema. 1650.
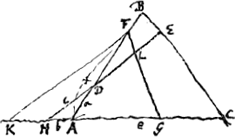
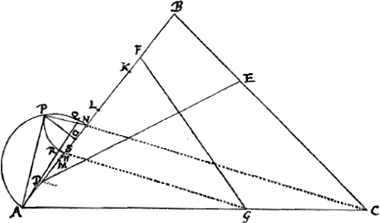
Triang. ABC, sectus utcunque lineâ DE, dividendus est aliâ lineâ, FG, ita ut utraque pars, DBE et ADEC bifariam dividatur.Ga naar voetnoot2)
Siquidem linea DE, vel ex uno angulorum ducta sit, vel uni laterum parallela, facilis erit constructio problematis. Verùm hic ponitur, ED, si versus D producatur concursuram cum producto latere CA.
Sit duarum AB, DB, tertia proportionalis HB, et trium CB, EB, DB, quarta
[Fig. 1.]
| |
prop.lis BK. sit L medium AB, et ponatur LM aequalis ¼ totius HBK:Ga naar voetnoot3) et advertatur num BM sit major vel minor vel aequalis ipsi BD. et siquidem minor est, ut hìc, sumatur quadruplum differentiae MD idque sit AN. et sit O medium AK. et inveniatur inter AO, AN, med. prop. AP. et quadrato AP addatur qu. AD, ponendo PQ ∞ AD, et jungendo AQ. Ab AQ auferatur QP, et residuo AR sit aequalis AS. jungatur jam NC, eique parallela ducatur SG. critque inventum punctum G, è quo triangulum ABC oportebit bifariam dividere, rectâ GF, quod factu facile est. et erit constructio perfecta.Ga naar voetnoot4)
Si verò BM major fuisset quam BD, debuisset quadrat. AP substrahi à qu. AD,Ga naar voetnoot5) (quum prius haec addita fuerint) et radix residui substrahi ex DA. atque à termino reliquae partis, duci linea parallela ipsi NC; eaque rursus ostendisset punctum G.Ga naar voetnoot6).
| |
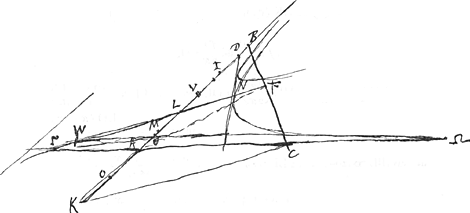
radices.Ga naar voetnoot12) sed altera inutilis VΘGa naar voetnoot13) in fig. postrema quae facit ut triang. LWΘ sit aequale ½ ∆i BLF, simulque ∆m ΘΑΩ dimido. ∆i BAC.Ga naar voetnoot14)
duo igitur veri valores erunt radicis, si cc majus ½ ie, hoc est quando ∆m LΓΑ majus dimidio triangi. BLF.Ga naar voetnoot15)
|
-
voetnoot1)
- La pièce a été empruntée, quant aux parties datées 1650 et 1656 au manuscrit mentionné dans la note 1 de la page 7 du Tome présent. Elle s'y trouve écrite sur une feuille attachée avec de la cire à une page vide. La dernière partie est extraite du livre des Adversaria D. Le lieu, où elle s'y trouve, indique la date de 1668.
-
voetnoot2)
- Ce problème, qui a occupé Huygens à trois reprises, se réduit, comme il est aisé de le voir, à celui de mener les tangentes communes à deux hyperboles, enveloppes de droites qui avec deux droites fixes déterminent des triangles dont l'aire est donnée. Et la figure 4 démontre que ce point de vue n'a pas échappé à Huygens.
Or, comme l'asymptote commune, AB, compte pour deux de ces tangentes, il en reste deux à déterminer. Le problème est donc un ‘problème plan,’ menant à une équation quadratique.
-
voetnoot4)
- Posons AB = a, BC = b, AC = c, BD = d, BE = e, et ensuite, d'après les constructions indiquées,
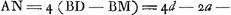 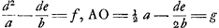 . On a alors . On a alors 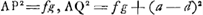 , , 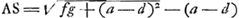 , et enfin , et enfin 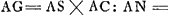 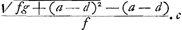 . c; d'où il s'ensuit que AG représente la racine positive de l'équation quadratique: . c; d'où il s'ensuit que AG représente la racine positive de l'équation quadratique: 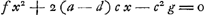 , ,
équation dont nous avons vérifié l'exactitude en suppléant à l'analyse de Huygens, qui manque, par une autre qu'il n'est pas difficile de deviner.
Or, nous montrerons dans la note 11 que le problème, dans sa conception la plus stricte, admet toujours une solution unique qui doit être identique ici avec celle indiquée par Huygens.
-
voetnoot5)
- Huygens semble négliger ici le cas où AP > AD; mais ce cas mènerait à des solutions imaginaires, qui ne peuvent pas se présenter, comme nous le montrerons dans la note 11.
-
voetnoot6)
- Posons dans ce cas:
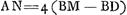 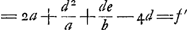 . Ou trouve alors, par les constructions indiquées, . Ou trouve alors, par les constructions indiquées, 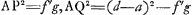 , , 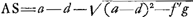 , et ensuite , et ensuite 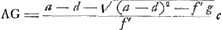 . .
Ainsi AG représente la racine la plus petite de l'équation quadratique: 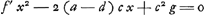 , ,
mais, puisqu'on a f′ = - f, cette équation est identique avec celle de la note 4. Et il est évident que la racine la plus petite, choisie par Huygens, correspond à la plus grande racine de l'équation qui donnerait la valeur de AF, puisque l'aire AFG est donnée. Or, cela justifie le choix de Huygens, car nous montrerons dans la note 11 que c'est cette racine qui amène la seule solution qui satisfait à toutes les exigences du problème.
-
voetnoot7)
- Lisez AK. En effet, alors f = o et l'équation quadratique de la note 4 nous donne:
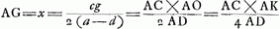 . .
-
voetnoot8)
- Voir la ‘Constructio problematis’ qui va suivre. On la trouve à la page 12 du Livre D.
-
voetnoot9)
- On remarquera que les données sont surabondantes. Outre la relation evidente
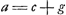 , on a encore, à cause des triangles semblables BLF et , on a encore, à cause des triangles semblables BLF et 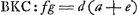 ; relation qu'on trouve mentionnée dans le manuscrit. ; relation qu'on trouve mentionnée dans le manuscrit.
-
voetnoot10)
- On a donc
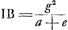 ; c'est-à-dire, à cause de la relation de la note précédente, IB = dg/f = i. ; c'est-à-dire, à cause de la relation de la note précédente, IB = dg/f = i.
-
voetnoot11)
- On a, en effet, par les constructions du texte:
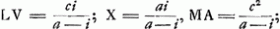 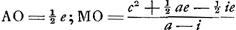 ; ; 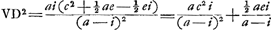 ; donc finalement; ; donc finalement; 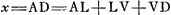 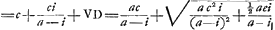 ; conforme au résultat de l'analyse, qui précède à la ‘Constructio’. ; conforme au résultat de l'analyse, qui précède à la ‘Constructio’.
Voir encore, sur la signification de l'autre racine de l'équation quadratique, ce qui va suivre dans le texte. Celle choisie par Huygens est la seule qui puisse satisfaire au problème pris dans sa conception la plus stricte, et elle y satisfait toujours.
Pour le montrer nous commençons par remarquer qu'on a toujours d < f, donc 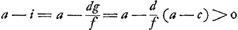 . Ensuite, laissant de côté le cas, qui ne présente aucune difficulté, que LF est parallèle à AC, nous supposons que les lettres A et L, C et F de la figure sont placées de telle manière que le point L soit plus près du côté AC que le point F. Alors AK = e est positif, et l'on voit immédiatement que les racines de l'équation quadratique seront toujours réelles. . Ensuite, laissant de côté le cas, qui ne présente aucune difficulté, que LF est parallèle à AC, nous supposons que les lettres A et L, C et F de la figure sont placées de telle manière que le point L soit plus près du côté AC que le point F. Alors AK = e est positif, et l'on voit immédiatement que les racines de l'équation quadratique seront toujours réelles.
Soit maintenant AD = x égal à la plus grande des deux racines. Alors 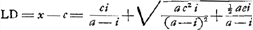 , c'est-à-dire, toujours positif. Il en est de même avec , c'est-à-dire, toujours positif. Il en est de même avec 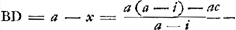 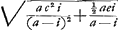 ; puisque la condition que cette valeur soit positive conduit successivement aux relations: ; puisque la condition que cette valeur soit positive conduit successivement aux relations:
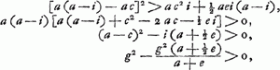
à la dernière desquelles il est évidemment satisfait.
Il en résulte que le point D tombe entre les points L et B, et que les conditions du problème seront donc toujours remplies par la solution de Huygens.
En choissisant au contraire pour la valeur de x la racine la plus petite, on aura 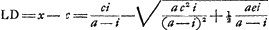 ; mais la condition que cette valeur soit positive ne sera jamais remplie, puisque cela exigerait: ; mais la condition que cette valeur soit positive ne sera jamais remplie, puisque cela exigerait:
ac2 i + ½ aei (a - i) < c2 i2;
c'est-à-dire (c2 i + ½ aei) (a - i) < 0.
-
voetnoot12)
- Puisqu' alors dans l'équation quadratique, qui précède la ‘Constructio problematis,’ le produit des deux racines est nécessairement positif.
-
voetnoot13)
- En effet, on aura, en se servant de cette autre racine,
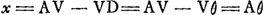 . .
-
voetnoot14)
- Inutile de dire que dans le cas où la racine Aθ deviendrait négative la solution rejetée admettrait une explication analogue; mais Huygens ne s'occupe pas de ce cas.
-
voetnoot15)
- On a
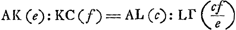 . L'inégalité ∆ LΓΑ > ½ ∆ BLF, c'est-à-dire, AL × LΓ > ½ LD × LN entraîne donc c2 f > ½ edg, ou bien . L'inégalité ∆ LΓΑ > ½ ∆ BLF, c'est-à-dire, AL × LΓ > ½ LD × LN entraîne donc c2 f > ½ edg, ou bien 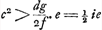 . .
|