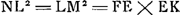Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651

[p. 204]

Appendice IV¹⁾
A l'ouvrage: De iis quae liquido supernatant.
[1650].

Pars Cylindri quae inter duo plana parallela, cylindrum oblique secantia continetur, frustum cylindri vocatur.

1) L'appendice contient une déduction, d'après les méthodes des anciens, du ‘Theorema 3,’ p. 160, du ‘Liber III’ de l'ouvrage: ‘De iis quae liquido supernatant.’ Comparez la note 2 du ‘Liber’ cité, p. 158 du Tome présent.

Pr[opositio]. 1. Frustum cylindri aequale est cylindro ejusdem cylindri parti, qui latera habeat lateribus frusti aequalia.

A cylindro AB absciiïa sint frustum DE et cylindrus FH, quorum latera DC,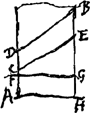

[Fig. 1.]

FA sint aequalia ideoque et HG, EB. dico frustum DE aequale esse cylindro FH. additâ enim utrinque ÇF aequalibus AF et CD erit AC aequ. FD; eademque ratione HE aequ. GB. Habet itaque cylindri portio ACEH latera lateribus portionis FDBG aequalia, verum et bases AH, EC basibus FG, DB aequales et similiter positas, itaque manifestum est ipsas portiones ACEH, FDBG inter se similes et aequales esse, quare ablata portione communi FCEG, remanet frustum DE aequale cylindro FH, q. er. dem.

Pr. 2. Si super cunei Cylindrici base circulari conus scalenus constituatur cujus vertex sit in producto cunei latere, cadet cunei convexa superficies extra conicam, eritque coni pars solida quae intra cunea comprehenditur, ipso cuneo minor.

Esto Cuneus cylindricus ABC [Fig. 2] et super ejus base circulari AFC constitu-

[p. 205]

[Fig. 2.]

tus conus ADC cujus vertex D sit in producto cunei latere AB faciens in plano BEC sectionem ellipsin BMC. dico cunei convexam superficiem cadere extra superficiem coni ADC.

Sumatur enim in cunei superficie convexa quodcunque punctum G, constructoque super baseo AFC cylindro AK, secentur simul hic et conus plano HGK, per punctum G transeunte, quodque aequidistans basi AC; fiet igitur cylindri sectio circulus HEK, coni vero, circulus minor HML qui priorem intus contingit in puncte H lateris BA. Itaque major minorem undique comprehendit, et punctum G quod est in majori circumferentia HEK erit extra minorem HML, circulus autem HML est plani per HGK sola pars quae intra conum ADC continetur. Igitur punctum G erit extra conum ADC. Eadem erit demonstratio si alia puncta in cunei convexa superficie sumantur; tota igitur est extra conum.

Atqui hinc quoque manifestum est ellipsin BMC ab ellipfi BEC quae in eodem plano et circa eandem diam. est contineri, quum sit BEC circumf. in superficie convexa cunei at BMC in superficie conica: Et patet cuneum cylindricum coni parte quam comprehendit majorem esse, duabus figuris solidis, qualis est ea quae continetur superficiebus curvis BECFA, BMCFA et planâ BMCE.

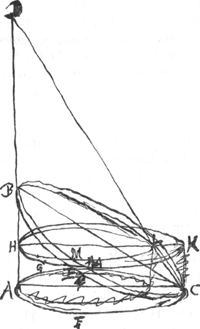
Pr. 3. Dato Cuneo Cylindrico, potest super ipsius base circulari Conus scalenus constitui verticem habens in producto cunei latere cujus pars intra cuneum comprehensa deficiat à cuneo magnitudine figura solidâ, quae minor sit quacunque datâ.²⁾

Detur curieus cylindricus ABC [Fig. 3] cujus basis circularis sit circa diametrum AC, elliptica vero circa diametrum BC. diviso AB latere bifariam in F, exstruatur super base AC cylindrus AFGC; quem constat cuneo aequalem fore; diameter vero superioris basis FG secabit quoque BC per medium in E. denuo intra cylindrum AG extruatur cylindrus AK qui ab ipso AG

2) Huygens aura recours à cette proposition dans la démonstration de la ‘Pr. 6.’

[p. 206]

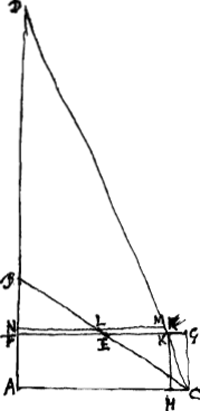Fig. 3.

deficiat solido minore quam sit magnitudo data. diametri vero basium AH, FK conveniant cum diametris AC, FG, ductaque CKD quae conveniat cum producto latere AB, intelligatur conus scalenus ADC; dico partem hujus quae intra cuneum ABC continetur ab eodem cuneo deficere solido minore quam sit data magnitudo.

Sit enim inter FE et EK media proportion. LM aptata intra lineas BC, DC ut parallela sit diametro AC, eaque producatur usque in latus AB in N, et secundum MN ducatur planum basi AC aequidistans quod conum circulo secabit, constat autem hoc magis à basi AC distare debere quam planum FG, quoniam LM major est necessario quam EK. Cum autem quadr. LM aequale sit rect. FEK et FK, LM parallelae sint, sequitur si per E punctum describatur in plano ADC hijperbole ad asymptotos DA, DC, eam contactum iri à recta ML in puncto L,³⁾ sed eadem quoque tangetur à recta BC in puncto E quoniam ibi bifariam dividitur⁴⁾, itaque secundum ea quae in primo libro⁵⁾ ostensa sunt, erit abscissor coni BDC aequalis cono NDM quare et partes coni ABC, ANMC erunt aequales, pars autem ANMC manifestò major est cylindro AK; itaque minor est excessus cylindri AG suprà partem coni ABC quam suprà cylindrum AK. at Cylindro AG aequalis est cuneus cylindri ABC, ergo minor quoque est excessus cunei ABC supra coni partem ABC quam cylindri AG supra cylindrum AK, ideoque et minor data solida magnitudine. quod erat ostend.

3) Il y quelque confusion dans cette partie de la démonstration. En effet, pour que l'hyperbole en question touchela ligne NM au point L, on doit construire cette ligne NM parallèle à la base AC de telle manière qu'on ait ; mais alors le point L se trouvera à gauche de la ligne BC. D'ailleurs la démonstration reste valide, puisqu'elle exige seulement que la ligne NM se trouve au-dessus de la ligne FK, ce qui a lieu aussi bien avec la ligne NM dont nous venons d'indiquer la construction qu'avec la ligne NM du texte.

4) On lit encore en marge: ‘9. 2 con.’ Voir à la page 46 verso des ‘Coniques’ d'Apollonius (éd. Comm., citée p. 6 du Tome I, note 4): ‘Si recta linea asymptotis occurrens ab hyperbola bifariam secetur; in uno tantum puncto sectionem contingit.’

5) Voir le ‘Lemma 2’ à la page 113 du Tome présent.

[p. 207]

Pr. 4. Cunei Cylindrici centrum gravitatis est in linea rectâ quae à contactu basium ad medium latus ducitur.⁶⁾

Esto Cuneus Cylindricus plano ABC in aequales partes et similes sectus cujus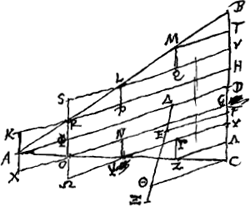

Fig. 4.

cunei basis circularis circa diametrum AC, elliptica vero circa diametrum AB; ab harum contactu A ducatur AD ad medium latus BC. dico in linea AD reperiri centrum grav. cunei ABC. Si enim non est in linea AD, sit alibi in plano ABC nimirum in E; (nam quod sit in plano ABC manifestum est quum ab hoc cuneus in partes duas oppositas aequales et similes dividatur) et ducatur EF lineae AD aequidistans. Porro secetur cuneus plano secundum AD erecto super planum ABC, (quae sectio ellipsis erit) et lineae DB, DC eousque continuè bifariam secentur, donec habeatur tandem linea minor quam DF, DH, et à sectionis punctis plana exeant HR, VL &c. plano secundum AD aequidistantia inde autem ubi haec ellipsi AB occurrunt et circulo AC, ducantur alia plana MQ, LP &c. aequidistantia plano quod cuneum secundum latus BC contingeret, quae quidem omnia rectangula efficere constat. Et erit hac ratione cuneo inscripta quaedam sigura ex frustorum cylindri segmentis constans, et quodque ipsa residuum relinquit erit aequale frustro cylindrico DX. quod ut apertum fiat compleantur frustorum segmenta quaecunque inter plana VL, YΨ medias bases AB et AC secantia continentur, ut fiant frustra integra DK, DX, segmenta verò frustorum SH, OY aequalia segmentis RD, ϕG. Certum est itaque partem solidam AKR nihil prorsus differre a parte BTM neque partem RSL à parte LQM, quum iisdem superficiebus similiter etiam sed subcontrarie positis contineantur. ideoque omnes partes triangulares AϕR, RPL, LQM, MTB aequari partibus Kϕ et SP; eâdem quoque ratione triangulares AϕO, ONΨ, ΨΓZ, ZΛC, aequantur partibus Xϕ, ΩN; atqui hasce ipsas Xϕ et ΩN manifestum est aequari dimidio frustri XD sicut et Kϕ, SP; igitur totum residuum ex partibus triangularibus constans. aequale est frusto XD. Porro autem in Figurâ cuneo inscriptâ binae quaeque partes sibi invicem respondent, ut qualis frusti cylindrici pars est MV talis et ΓΛ eadem magnitudine et figura et qualis LH talis quoque NY atque ita de caeteris, et omnes à

6) Comparez le ‘Theorema 1’ du ‘Liber III’, p. 159 du Tome présent.

[p. 208]

plano ABC dividuntur in duas partes oppositas, inter se similes et aequales, unde manifestum est omnium quoque centra gravitatis in eodem plano ABC reperiri; itaque unius partis centr. gr. erit in parallelog. MV, et partis oppositae in parallelogr. ΓΛ, verum et similiter posita erunt centra haec in dictis parallelogrammis, eoque aequaliter distabunt à lineâ AD, igitur quae utrumque centrum conjunget à linea AD bifariam dividetur sed ubi illa bifariam dividetur ibi erit compositae magnitudinis ex duabus aequalibus centrum gravitatis, ergo compos. magn.^is ex partibus solidis MV et ΓΛ centr. gr. erit in linea AD; eadem ratione mag.^is comp.^ae ex partibus LH, NY erit centr. gr. in linea AD, ut et compositae ex partibus RD, ϕG itaque totius figurae cuneo inscriptae centr. grav. est in linea AD; Sit hoc Δ et jungatur ΔE, et producatur et ducatur CΘ ipsi lineae DA aequid. quae proinde cadet extra cuneum.

Quia igitur cuneus ABC aequalis est cylindro habenti basin circ. AC et altitudinem CD⁷⁾; frustum verò DX aequ. cylindro eandem basin AC habenti et altit.^m DG, sequitur cuneum ABC esse ad frustum DX ut CD ad DG. DF autem major est quam DG; igitur CD ad DF vel Θ Δ ad Δ E minorem habet rationem quam cuneus ad frustum DX sive residuum ex partibus triangularibus constans, quare et dividendo minor erit ratio ΘE ad E Δ quam figurae cuneo inscriptae ad dictum residuum; sit itaque ΞE ad E Δ sicut inscripta figura est ad idem residuum. Ergo quum E positum fuerit c. gr. totius cunei, Δ autem sit c. gr. figurae inscriptae, erit residui c. gr. punctum Ξ, quod esse nequit nam plano quod per Ξ agetur ellipsi circa AD aequidistans in eandem partem erunt omnes partes triang.^es e quibus residuum componitur.

7) Comparez le dernier des ‘Manifesta’ du ‘Liber III,’ p. 159 du Tome présent.

Pr. 5. Portionis Cylindri centr. gr. est in linea recta quae à medio majoris lateris ducitur ad medium minoris.⁸⁾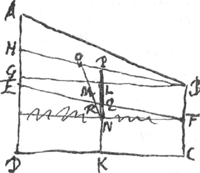

Fig. 5.

Esto portio cylindr. cujus latera AD maius et BC minus, secundum quae secta intelligatur plano ABCD, ipsa vero latera bisariam secentur et sectionum puncta jungantur linea EF, dico in hâc reperiri c. gr. Portionis propositae. Sit enim si potest extra lineam EF in M (erit autem centrum M in plano ABCD quum ab hoc portio dividatur in duas partes oppositas, similes et aequales) et dividatur portio plano secundum GB quod basi DC aequidistet in cuneum AGB et cylindrum GC; Porro ducatur linea BH ad mediam AG, sitque cylindri GC axis LK, in

8) Comparez le ‘Theorema 2’ du ‘Liber III,’ p. 160 du Tome présent.

[p. 209]

cujus medio ejusdem centr. gr. N. Jungatur NM et producatur usque dum occurrat lineae BH in O, eòdem que producatur axis KL qui ei occurat in P, lineam autem EF secet NO in R, et KP in Q.

Quia igitur M est c. gr. totius portionis, N vero cylindri GC, erit partis reliquae nimirum cunei AGB c. gr. in producta NM, sed idem quoque in linea BH reperiri ostensum est⁹, itaque necessario cunei ABC c. gr. est punctum O, eritque reciprocè MN ad MO, sicut cuneus AGB ad cylindr. GC. Porro quum AE sit aequalis dimidiae AD, id est aequalis dimidiae AG cum dimidia GD, erit ablata AH reliqua HE aequalis dimidiae GD id est BF; igitur parallelae sunt HB, EF quare erit NR ad RO, sicut NQ ad QP id est PL ad LN; ut autem PL ad LN ita est HG ad GD, (quoniam utraque utriusque est dupla), et ut HG ad GD ita est cuneus AGC ad cylindrum GC; ergo sicut cuneus AGB ad cylind. GC ita est NR ad RO; sed sic etiam esse NM ad MO ostensum suit; itaque idem erit punctum R et M, quod esse non potest, quoniam M ponebatur extra lineam EF in qua est punctum R. Apparet igitur centr. gr. portionis ABCD non posse statui extra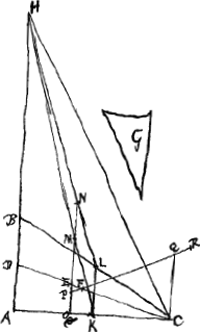

Fig. 6.

lineam EF, quamobrem id in ipsa reperiri necesse est. q. er. dem.

9 Voir la ‘Pr. 4’ qui précède,

Pr. 6. Cunei Cylindrici centr. gr. lineam rectam quae à contactu basium ad medium latus oppositum ducitur ita dividit ut pars versus contactum sit ad reliquam ut quinque ad tria¹⁰.

Esto cuneus Cylindricus ABC cujus bases circulus circa diametrum AC et ellipsis circa diam. BC, ab harum contactu C ducta sit CD ad medium latus AB, eaque dividatur in puncto E ut sit CE ad ED sicut quinque ad tria. dico punctum E esse cunei gravitatis centrum. Si enim fieri potest sit alibi in linea DC et primò magis versus contactum basium in F. et quam rationem habet CE ad EF eam habeat cuneus ABC ad magnitudinem quandam solidam G. Tum super base AC constituatur conus scalenus AHC, cujus vertex H sit in producto latere AB, ita ut pars coni intra cuneum ABC comprehensa ab eodem cuneo deficiat solido mi-

10 Comparez le ‘Theorema III’ du ‘Liber III,’ p. 160 du Tome présent.

[p. 210]

nore quam sit G.¹¹⁾ Et dividantur AC et BC bifariam in puntis K et L, quae jungantur, et ducantur KH, quae erit axis coni AHC, et LH axis abscissoris coni BHC, hi rursus dividantur in punctis M et N, ita ut HM sit tripla MK, et HN tripla NL; eritque hac ratione M c. gr. coni AHC, et N abscissoris BHC. Jungatur NM, et producatur; eâque transibit per punctum E, nam quum KL utràque AC et BC bifariam dividat, sequitur eam aequidistare lateri AB, ipsi autem LK aquidistat NM quoniam duas HK, HL, in eandem rationem dividit, itaque et NM lateri AB aequidistat ac proinde producta secabit AK in O puncto in eandem rationem ac HK; est igitur AO tripla OK, et consequenter CO ad OA vel etiam CE ad ED ut quinque ad tria in hanc autem proportionem linea DC à puncto E divisa fuerat, itaque constat NM productam transire per E punctum. Porro quum M sit totius coni centr. gr., N autem abscissoris BHC, necesse etiam est partis coni reliquae ABC centr. gr. reperiri in producta NM: sit hoc P, et jungatur PF, eaque producatur et occurrat ei CQ parallela lateri AB. Quoniam igitur cuneus cylindricus ad excessum quo ipse superat coni partem ABC, majorem habet rationem quàm ad magnitudinem G, ad quam eam habet quam CE ad EF, etiam dividendo coni pars ABC majorem habebit rationem ad dictum excessum quam CF ad FE vel quam QF ad FP; habeat itaque RF ad FP eam rationem quam pars coni ABC ad excessum quo superatur ipsa à cuneo cylindrico, ergo quum F positum fuerit centr. gr. totius cunei, P, autem c. gr. partis coni quae cuneo comprehensa est, erit c. gr. magnitudinis reliquae punctum R quod esse non potest, nam si planum per R ducatur faciens angulos rectos cum plano per ABC, tota magnitudo reliqua. qua coni pars à cuneo ipsam comprehendente superatur erit ab una eius plani parte. Non est igitur Cunei ABC c. gr. magis versus contactum. Verum neque esse ab altera parte puncti E simili ratione ostendi poterit, itaque est ipsum punctum E. q. er. dem.¹²⁾

11) Voir la ‘Pr. 3.’

12) L'Appendice finit ici sans traiter le cas du tronc de cylindre droit; mais on doit remarquer que la démonstration du ‘Theorema 4’ qui se rapporte au centre de gravité d'un tel tronc et qu'on trouve p. 161 du Tome présent, est indépendante de la méthode de Cavalieri. Ainsi le but que Huygens s'était évidemment proposé, c'est-à-dire: de remplacer les démonstrations du ‘Liber III’ qui dépendent de cette méthode, par d'autres, qui lui semblaient plus rigoureuses, a été atteint dans l'Appendice présent.
En outre du texte que nous avons reproduit ici, la même feuille contient encore le théorème que voici: ‘Si conus secetur plano basi parallelo, idemque secetur alio plano transverso quod circulum ex priori sectione factum et basin coni contingat; fiet abscissor coni medius proportione inter conum propositum et eum qui abscissus est.’ Après quoi suivent quelques phrases, biffées depuis, qui constituent le commencement de la démonstration de ce théorème, lequel d'ailleurs se déduit sacilement du ‘Lemma 2’ de la page 113.