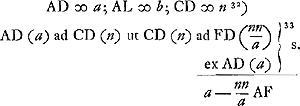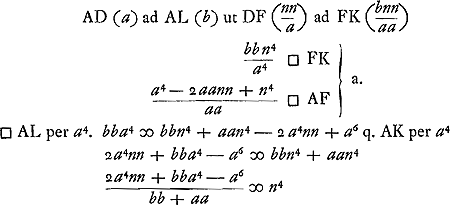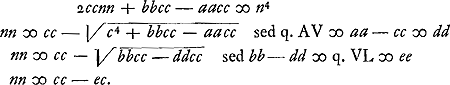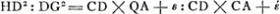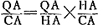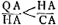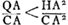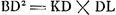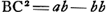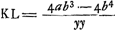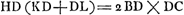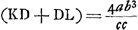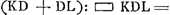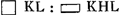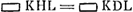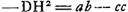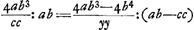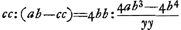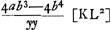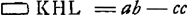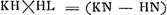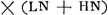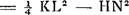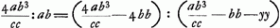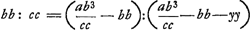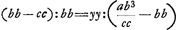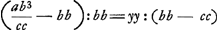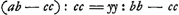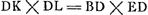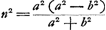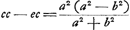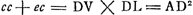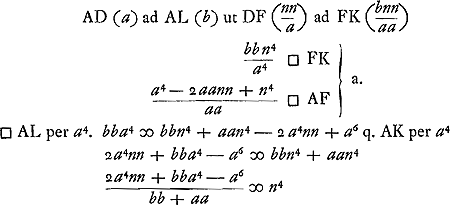
SitGa naar voetnoot34) AV perp. in DL ergo □ DV ∞ a4/aa + bb sit hoc ∞ cc ergo:
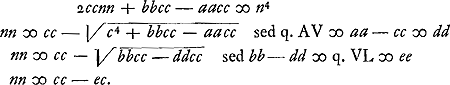
Ga naar voetnoot35)
|
-
voetnoot1)
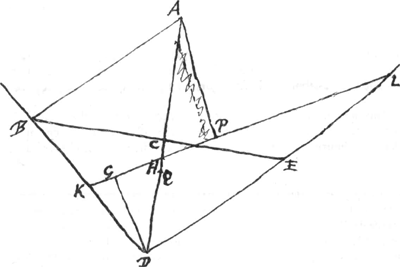
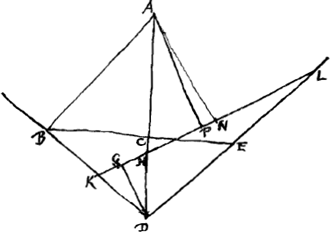
- Dans les deux premières parties de cet Appendice, que nous avons divisé en trois parties, Huygens s'occupe des conditions de stabilité de l'équilibre du cône de révolution homogène flottant dans une position verticale; le sommet en bas. Pour s'en convaincre on n'a qu' à comparer les figures et le texte avec ceux du ‘Theorema 14’ (p. 115) du ‘Lib. 1’. En effet, le point A des deux figures de la pièce présente représente le centre de gravité du cône. Il est donc identique avec le point G de la figure 17 (p. 115); de même les lignes BE et KL, DB et DE, AC et AP correspondent aux lignes NO et PQ, BN et BO, GM et GS de la même figure 17. En conséquence le triangle KDL doit toujours égaler le triangle isoscèle BDE.
La troisième partie de cet Appendice traite l'équibre du cône de révolution dans une situation inclinée.
-
voetnoot2)
- Dans cette première partie Huygens' s'efforce à démontrer la stabilité de l'équilibre sous les conditions formuleés au ‘Theorema 14’, cité dans la note précédente, par la méthode qu' il a suivie partout dans le premier livre du traité présent, c'est-à-dire en partant des ‘Theoremata 6 et 7’ (p. 103-104) du ‘Liber i’. Il doit donc démontrer qu'on a, sous ces conditions, AP > AC.
Or, il est clair que dans la figure 17 (p. 115) la ligne GN, qui correspond à la ligne AB des figures de l'Appendice présent, serait parallèle à la ligne DX, d'où il suit facilement que l'angle GNB, (l'angle ABD des figures présentes) sera, sous les conditions du ‘Theorema 14’ plus petit que l'angle DFB = DEB; c'est-à-dire plus petit qu'un angle droit; supposition qu'on retrouvera plusieurs fois dans cette pièce.
Toutefois Huygens a débuté, en composant cette première partie, par supposer dans la Fig. 1 de cet Appendice ABD = 90o; soit parce que ce cas limite de la stabilité l'intéressait particulièrement; soit parce qu'il croyait pouvoir arriver facilement à la démonstration du cas général, celle du cas particulier une fois trouvée. Ainsi, après avoir achevé cette dernière démonstration, il a commencé par y apporter les changements nécessaires pour l'accommoder au cas plus général; mais alors, comme nous l'indiquerons dans la note 16, il a fait fausse route.
Dans ces circonstances il nous semblait préférable de donner la pièce telle qu'elle avait été conçue primitivement, mettant entre crochets les mots biffés après coup et indiquant dans les notes les changements apportés par Huygens pour la rendre applicable à la supposition plus générale ABD ≦ 90o.
-
voetnoot3)
- Voir la démonstration du ‘Lemma 2’, p. 113-114, vers la fin.
-
voetnoot4)
- En tête de la pièce on lit encore: ‘τό Erat autem in hac deme. non omittendum.’
-
voetnoot7)
- Huygens ajouta plus tard: ‘invertenda est ea ratio. [▭ KDL] ad ¼ q. KDL potius. et sic deinceps.’
-
voetnoot8)
- C'est-à-dire le rectangle qui a KD et DL pour côtés.
-
voetnoot11)
- Huygens remplaça ‘aeq.’ par ‘non majus’. Voir la note 2. Mais lisez: ‘non minus.’
-
voetnoot12)
- Huygens remplaça le mot ‘rectus’ par la phrase ‘non major recto, nam si rectus est aeq. est qu. BD ▭o CDA.’
-
voetnoot13)
- Remplacé dans la seconde rédaction par ‘non minor’, ce qui est vrai dans la supposition ABD ≦ 90o,
-
voetnoot14)
- Remplacé par ‘non majorem habebit rationem quam’.
-
voetnoot15)
- Huygens intercala ici: ‘oportuit ostendere ▭ DCA non maj. q. BC;’ mais nous verrons que ce changement ne suffit pas pour sauver la démonstration appliquée à la supposition ABD ≦ 90o.
-
voetnoot16)
- Remplacé par ‘non major quam’. Mais cette conclusion n'est pas justifiée. Pour le montrer il suffit de remarquer, que si
ε et έ représentent des quantités ou positives, ou nulles, il a été démontré:
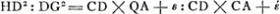 , mais évidemment on n'a pas le droit d'en conclure HD2: DG2 ≦ QA: CA. Dès ce moment la démonstration doit donc être considérée comme manquée pour ce qui concerne le cas plus général; mais elle reste rigoureuse pour le cas ABD = 90o, , mais évidemment on n'a pas le droit d'en conclure HD2: DG2 ≦ QA: CA. Dès ce moment la démonstration doit donc être considérée comme manquée pour ce qui concerne le cas plus général; mais elle reste rigoureuse pour le cas ABD = 90o,
-
voetnoot17)
- On a en effet:
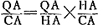 ; mais comme on l'a vu ; mais comme on l'a vu 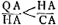 , donc aussi: , donc aussi: 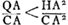 . .
-
voetnoot18)
- Remplacé par: ‘non minor’. Comparez la note 16; il s'agit de la même relation prise en sens inverse.
-
voetnoot19)
- Sur une feuille détachée on retrouve en partie l'analyse qui, évidemment, a servi de point de départ pour la partie qu'on vient de lire. Elle porte l'inscription ‘ad modum meum’ (comparez la note 29). On y lit ensuite
‘GD ∞ y’ (voir la fig. 1 du texte). De plus Huygens a représenté CD par b,
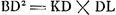 par ab, HD par c. On a alors par ab, HD par c. On a alors 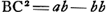 et au moyen de la proportion GD2: CD2 = 4BC2: KL2 Huygens trouve facilement□ et au moyen de la proportion GD2: CD2 = 4BC2: KL2 Huygens trouve facilement□ 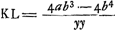 . De même, par la relation: . De même, par la relation: 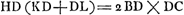 , mentionnée à la page 196 du texte, on trouve □ , mentionnée à la page 196 du texte, on trouve □ 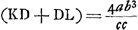 . Ensuite la proportion . Ensuite la proportion 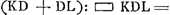 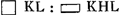 (où (où 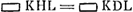 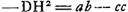 ) qu'on retrouve également dans le texte, conduit immédiatement à la relation ) qu'on retrouve également dans le texte, conduit immédiatement à la relation 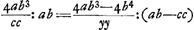 , d'où Huygens déduit , d'où Huygens déduit 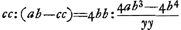 ; puis il ajoute: ‘sed est etiam yy [GD2] ad ab-bb [BC2] ut 4bb [4CD2] ad ; puis il ajoute: ‘sed est etiam yy [GD2] ad ab-bb [BC2] ut 4bb [4CD2] ad 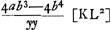 ergo cc [DH2] ad ab-cc [▭ KHL] ut yy [DG2] ad ab-bb [BC2]: proportion qu'on retrouve,
sous un autre arrangement, dans le texte même à la dernière ligne de la page 196. ergo cc [DH2] ad ab-cc [▭ KHL] ut yy [DG2] ad ab-bb [BC2]: proportion qu'on retrouve,
sous un autre arrangement, dans le texte même à la dernière ligne de la page 196.
-
voetnoot20)
- Dans cette seconde partie Huygens démontre la stabilité de l'équilibre sous les conditions du ‘Theorema 14’ (p. 115) par la méthode d'Archimède; c'est-à-dire par la considération du couple qu'on obtient en appliquant au centre de gravité A du cône une force dirigée vers le bas et au centre de gravité N de la partie immergée une force égale dirigée vers le haut. Or, comme AP est la direction de la gravité dans la position inclinée du cône, il suffira de prouver qu'on ait HN > HP, puisqu' alors le couple en question tendra à ramener l'axe DA du cône vers la situation verticale.
-
voetnoot21)
- Voir la première partie; mais il s'agit ici de la supposition la plus générale, c'est-à-dire, ABD ≦ 90o. Comparez la note 2.
-
voetnoot22)
- Par cette construction le point N coïncide avec le point R de la Fig. 17 (p. 115), c'est-à-dire, avec le centre de gravité de la partie immergée du cône.
-
voetnoot23)
- La numération est de Huygens et nous avons arrangé la pièce qui suit en accord avec elle.
-
voetnoot24)
- Puisque HD < CD comme il a été démontré dans la première partie de cet Appendice.
-
voetnoot25)
- Lisez ‘majus’, puisqu'il s'agit de démontrer ‘▭ KHL majus ▭o DHA.’ En effet, le ‘majus’ qui précède dans le texte remplace un ‘major’, qui s'y trouvait primitivement; mais ce même changement a été oublié ici.
-
voetnoot26)
- Voir, pour la démonstration, l'alinéa qui a été numéroté 2 par Huygens. Sur la feuille du manuscrit elle précédait celui numéroté 1.
-
voetnoot27)
- Voir, pour la démonstration, l'alinéa numéroté 3.
-
voetnoot28)
- Voir encore, dans la première partie de cet Appendice, à la page 196, la dernière ligne du texte.
-
voetnoot29)
- Voir, dans la première partie, p. 196, la phrase qui suit le signe 9).
-
voetnoot30)
- Sur la feuille, mentionnée dans la note 19, on trouve encore, sous l'inscription ‘ad modum Archim.’ l'analyse incomplète qui suit. Partant de la proportion □
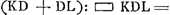 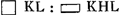 , Huygens, employant les notations de la note 19 à l'exception de l'y qui représente maintenant la ligne HN, écrit, comme il avait trouvé au paravant, 4ab3/cc pour □ (KD + DL) ab pour ▭ KDL: ensuite 4ab3/cc - 4bb pour □ KL (formule correcte qu'on déduit aisément de la proportion par laquelle l'alinéa numéroté 3 débute, puisque ▭ , Huygens, employant les notations de la note 19 à l'exception de l'y qui représente maintenant la ligne HN, écrit, comme il avait trouvé au paravant, 4ab3/cc pour □ (KD + DL) ab pour ▭ KDL: ensuite 4ab3/cc - 4bb pour □ KL (formule correcte qu'on déduit aisément de la proportion par laquelle l'alinéa numéroté 3 débute, puisque ▭ 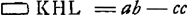 ) et enfin pour ▭ KHL ab3/cc - bb - yy; ce qui est exact, puisqu'on a: ) et enfin pour ▭ KHL ab3/cc - bb - yy; ce qui est exact, puisqu'on a:
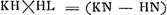 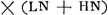 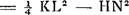 . Ainsi il obtient la
proportion . Ainsi il obtient la
proportion 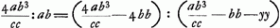 , qui amène successivement: , qui amène successivement: 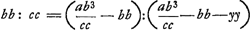 ; ; 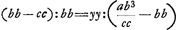 ; ; 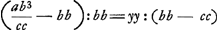 et enfin et enfin 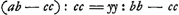 ; ou bien ; ou bien  ce qui constitue la relation par laquelle le texte finit. ce qui constitue la relation par laquelle le texte finit.
-
voetnoot31)
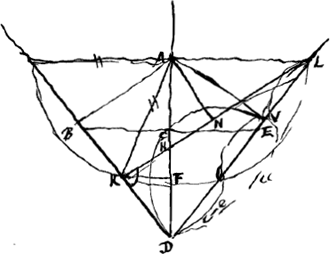
- Dans cette troisième partie, très peu achevée quant à la forme, Huygens détermine la condition sous laquelle un cône de révolution pourra flotter, le sommet en bas, dans une position inclinée, de manière que le cercle de base touche justement à la surface du liquide.
En effet, si l'on se reporte à la figure 17, p. 115, du ‘Liber 1’, on voit que dans cette figure pour une telle position la surface HI du liquide passera par le point C; mais, puisque PQ passe par le centre de gravité R du cône HIB, on a toujours BI/BQ = ¾ = BD/BG. On aura donc pour la position que nous considérons: BC/BQ = BD/BG, d'où il suit que GQ sera parallèle à DC.
Or, la ligne PQ de la figure 17 est représentée dans les figures de l'Appendice présent par KL et le point G par A. Dans la figure présente AL devra donc, pour la position considérée, être perpendiculaire sur AD. En même temps l'équilibre exige, d'après le ‘Theoreme 1’ du ‘Liber II’ (p. 122) que la ligne AN (où N représente le centre de gravité de la partie immergée) soit perpendiculaire au niveau du liquide, donc aussi à KL. D'autre part on a KN = NL, d'où il suit AK = AL et c'est cette relation qui va servir à déterminer la condition cherchée.
-
voetnoot32)
- Comme partout dans les figures de cet Appendice, le point C représente le centre de gravité de la partie immergée dans la situation verticale de l'axe du cône; A celui du cône entier. La densité du cône sera donc à celle du liquide comme n3 à a3. De plus on aura
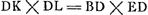 . .
-
voetnoot33)
- On a, d'après la note précédente, LD : ED = BD : KD; mais LD : ED = AD : CD et BD : : KD = CD : FD; donc aussi AD : CD = CD : FD.
-
voetnoot34)
- Ayant trouvé la relation cherchée, Huygens se propose de la simplifier et d'en déduire la construction. Ajoutons que la résolution directe de l'équation quadratique en n2 amène les racines n2 = a2 et
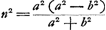 . La première de ces racines conduit à la supposition que la densité du cône est égale à celle du liquide, auquel cas en effet, LK se superposant avec AL, la condition AK = AL est satisfaite. Le cône, il est vrai, pourra flotter alors avec le cercle de base tout entier au niveau du liquide; mais ce n'est pas là la solution désirée. Celle-là est obtenue au moyen de la seconde racine. . La première de ces racines conduit à la supposition que la densité du cône est égale à celle du liquide, auquel cas en effet, LK se superposant avec AL, la condition AK = AL est satisfaite. Le cône, il est vrai, pourra flotter alors avec le cercle de base tout entier au niveau du liquide; mais ce n'est pas là la solution désirée. Celle-là est obtenue au moyen de la seconde racine.
-
voetnoot35)
- En effet, on vérifie aisément qu'on a :
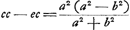 . De plus, on voit que l'autre solution . De plus, on voit que l'autre solution 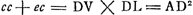 , mène à n = a. Ajoutons que la construction n'est pas achevée dans la figure. Le demi-cercle, qu'on voit tracé sur DV comme diamètre, y pourra servir, mais elle ne passera pas par le point C. , mène à n = a. Ajoutons que la construction n'est pas achevée dans la figure. Le demi-cercle, qu'on voit tracé sur DV comme diamètre, y pourra servir, mais elle ne passera pas par le point C.
|