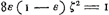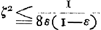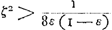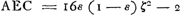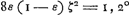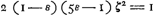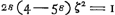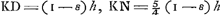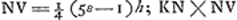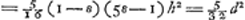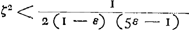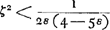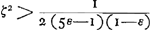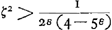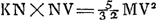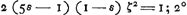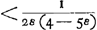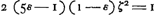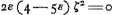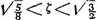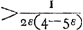Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651
(1908)–Christiaan Huygens–
[pagina 158]
| |
De iis quae liquido supernatant.
| |
Definitiones.Cylindri appellatione intelligatur Cylindrus rectus. Portiones Cylindri vocentur, quae fiunt cum Cylindrus secatur plano, neutram basium vel parallelam habente vel secante. Cuneus Cylindricus appelletur, Portio cujus bases se mutuo contingunt. | |
[pagina 159]
| |
Manisesta.His constitutis, illa quidem tanquam demonstratione non egentia pro veris habeantur; nempe quod in portione Cylindri, latera maximum et minimum sint è diametro opposita; sicut in Cuneo, angulus contactus basium et latus sive maxima altitudo. Item portionem, si plano secundum longitudinem utriusque lateris secetur, dividi in segmenta duò aequalia et similia: Et Cuneum similiter dividi si secetur plano per punctum contactus basium et secundum latus oppositum. Denique quod si Cylindrus plano per oppositos angulos secetur, futuri sint duo cunei similes et aequales, ideoque singuli aequales dimidio cijlindri cujus sunt partes. Ex quo colligitur Cuneos ex eodem cylindro inter se rationem habere quam eorundem altitudines sive latera. | |
Theorema 1.
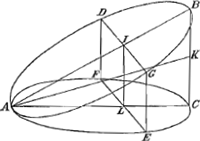
Esto Cuneus ABC, cujus bases AECF, ADBG: ab harum contactu A ducatur
| |
[pagina 160]
| |
AK, (nam quum LI sit in plano triangulari ABC, et perpendicularis ad planum AECF, ideoque parallela lateri BC, sequitur eam ita ut BC dividi à linea AK) ergo H centrum grav. rectanguli DGEF est in AK. Quum autem eodem modo demonstrari possit omnium rectangulorum quae fiunt sectionibus huic parallelis, centra gravitatis esse in eadem rectâ AK, concludimus inde totius Cunei ABC, qui quasi ex innumeris talibus rectangulis constat, in linea AK esse centrum grav. quod erat ostendendum. | |
Theorema 2.
| |
Theorema 3.
| |
[pagina 161]
| |
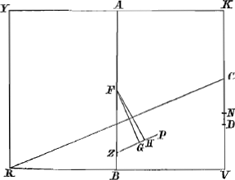
eritque sectio quidem cunei rectangulum DE, coni autem sectio parabole ENF, quoniam lateri CM facta est parallela. Sit coni AMC axis MO, cujus sumantur tres quartae MP, et erit P centrum grav. in cono, hoc enim à Commandino demonstratum est.Ga naar voetnoot5) ducatur denique PQR aequidistans ipsi BM. Quum igitur CM sit sesquialtera CB, erit quoque LN sesquialtera LI, ideoque parabole FNE aequalis rectangulo DE, ut patet ex quadratura paraboles.Ga naar voetnoot6) Haec autem aequalitas eodem modo ostendi potest, ubicunque cuneus et conus secti fuerint eodem plano, quod parallelum sit plano DGENF. Quare si AC consideretur tanquam libra horizonti parallela, apparet infinitas numero parabolas, parabolae FNE aequidistantes, quae ex libra AC supensae conum AMC quodammodo conficiunt, ex eodem puncto aequiponderare debere, quo aequiponderant infinita rectangula eidem librae superimposita, quae similiter componunt cuneum ABC. Conus autem id est omnes, quas dixi, parabolae, aequiponderant ex puncto Q, (quia perpendiculum QP transit per coni gravitatis centrum) ergo et omnia rectangula, sive cuneus ABC aequiponderat ex eodem Q puncto; unde sequitur perpendiculum QR, transire per centrum gravitatis cunei ABC. Sed et linea AK transit per ejusdem cunei centrum gravitatis: Igitur istud centrum est in intersectione R. Quum vero MP sit ¾ MO, est quoque CQ ¾ CO; CO autem dimidia est CA; ergo CQ tres octavae diametri AC. Et quia QR, CK sunt parallelae, est KR ad KA sicut CQ ad CA; igitur KR quoque tres octavae totius AK; Itaque qualium partium KR est trium, talium RA est quinque: Ergo cunei ABC centrum gravitatis R lineam AK ita dividit ut pars-versus contactum basium sit ad reliquam, sicut quinque ad tria: quod erat demonstr. | |
Theorema 4.
| |
[pagina 162]
| |
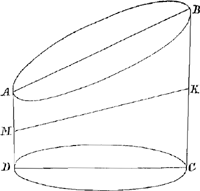
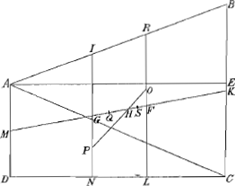 Fig. 4.
rectâ KM. Ostendendum est, centrum grav. portionis ABCD ita dividere lineam KM ut pars versùs M ad eam quae versùs K, rationem habeat quàm quintupla BC cum triplâ AD ad quintuplam AD cum triplâ BC. Secta intelligatur portio primum plano ABCD secundum latus utrumque; deinde planis AE, AC, rectis ad planum ABCD, quorum AE basi DC sit parallelum, AC verò ab angulo A ad C pertingat. Porrò sumantur KF, MG, singulae aequales ⅜ MK; et ducantur RFL, IGN parallelae lateribus portionis. Constat igitur portio ABCD ex tribus Cuneis ABE, ACE, ACD, et cunei quidem ABE centr. gr. est in lineâ RLaGa naar voetnoot7) sicut et cunei ACE, (quia videlicet CL est ⅜ CD,) quare totius partis ABC centr. gr. erit in eâdem RL, inveniatur hoc et sit punctum O. Similiter erit centr. gr. cunei ACD in recta IN, sitque hoc P. Junctis igitur O et P, erit centrum grav. totius portionis ABCD in lineâ OP. Sed idem quoque est in lineâ MKbGa naar voetnoot8), ergo erit intersectio H centrum grav. portionis ABCD. dividantur jam partes GH, HF, bifariam in Q et S. Est igitur PH ad HO ut pars ACB ad cuneum ACD, sed pars ACD, id est duo cunei ABE, ACE, sunt ad cuneum ACD ut duo latera BE et EC ad latus AD, ergo PH ad HO, ut tota BC ad AD: et sic quoque GH ad HF; et tandem QH ad HS, ut BC ad AD. Ergo sicut quintupla BC cum triplâ AD ad quintuplam AD cum triplâ BC, ita et quintupla QH cum triplâ HS ad quintuplam HS cum triplâ QH. Sed, quintupla QH cum triplâ HS est aequalis ipsi MH, et quintupla HS cum triplâ QH ipsi HK; nam quum MG et KF simul sint 6/8 sive ¾ MK, erit GF ¼ MK, ideoque QH et HS quae simul faciunt ½ GF, erunt ⅛ MK; quare quintupla QH cum quintuplâ HS erunt ⅝ MK, id est, aequales ipsi MF, unde detractâ FH, quae bis continet HS, relinquetur HM aequalis quintuplae QH cum triplâ HS. Et similiter si ex MF, (quam diximus continere quintuplam QH cum quintuplâ HS) vel ex KG auferatur HG quae bis continet ipsam QH, relinquetur HK aequalis quintuplae HS cum triplâ QH. apparet igitur partem MH ad HK habere rationem, quam quintupla BC cum triplâ AD ad quintuplam AD cum triplâ BC; quod erat demonstrandum. | |
[pagina 163]
| |
LemmaGa naar voetnoot9).
divisis enim lateribus RM et CV bifariam in punctis N et O, jungantur ea rectâ
| |
[pagina 164]
| |
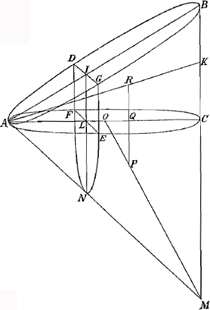
Theorema 5.Ga naar voetnoot10)
| |
[pagina 165]
| |
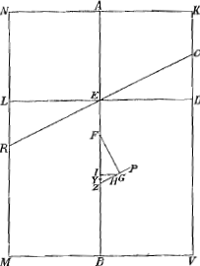
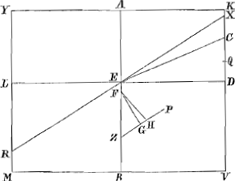
autem ponatur duplum quadr. AEB cum defectu ½ quadr. DC, majus esse quadrato AK vel ED, erit, addito utrinque integro quadrato DC, duplam rectanguli AEB unà cum ½ quadr. DC, majus quadrato EC: Ergo et rectang. sub quadruplâ EB et FZ, majus erit quadrato EC. Igitur quadrupla EB ad EC majorem habet rationem, quàm EC ad FZ; atqui ut quadrupla EB ad EC, ita rectang. sub quadruplâ EB et DC est ad rectang. sub EC et DC, propter communem altitudinem DC; ergo et rectang. sub quadruplâ EB et DC ad rectang. sub EC et DC majorem habet rationem quam EC ad FZ. sed rectang. sub EC et DC, (quia quadrupla EB est ad DC, ut EC ad HZcGa naar voetnoot13)) aequale est rectangulo sub quadrupla EB et HZ; Igitur quoque rectangulum sub quadruplâ EB et DC ad rectang. sub quadruplâ EB et HZ, sive basis DC ad HZ majorem habet rationem quam EC ad FZ, et permutando DC ad EC majorem, quàm HZ ad FZdGa naar voetnoot14). Sed propter triangula similia EDC, ZFG est sicut DÇ ad EC, ita GZ ad FZ; igitur GZ ad FZ majorem quoque habet rationem, quam HZ ad FZ: quare GZ major quàm HZ; quod erat demonstrandum. Iam si duplum rectang. AEB cum defectu dimidii quadrati DC aequale sit quadrato AK; dico tum quoque ZH, ZG aequales fore; cujus demonstratio dependet à praecedenti. nam si duplum rectang. AEB cum defectu ½ quadr. DC aequale sit quadrato AK vel ED, omnia quae modo major erant hìc erunt aequalia, quare et tandem GZ aequalis HZ. Similiter si duplum rectang. AEB cum defectu ½ quadr. DC minus sit quadrato AK, omnia quae in praecedenti demonstratione erant majora, hìc erunt minora, et tandem GZ minor HZ, ut oportebat. Quare constat propositum. Manifestum autem est etiam tum constare, quum punctum R incidit in angulum M, ita ut loco portionis, abscindatur plano RC cuneus cylindricus, de quo casu est praeterea Theor. sequens. | |
[pagina 166]
| |
Theorema 6.Ga naar voetnoot15)
| |
[pagina 167]
| |
Quòd si rectang. sub KN, DV, aequale sit octavae parti quadrati RV, dico tum quoque ZG aequalem fore ZH. Omnia enim quae modo majora fuerunt hìc erunt aequalia, quare et tandem duplum rectang. AEB cum defectu ½ quadr. DV, aequale quadrato AK. ideoque ZG aequalis ZHbGa naar voetnoot17), ut oportebat. Eâdem ratione si rectang. sub KN, DV minus sit octavâ parte quadrati RV, erit quoque ZG minor quàm ZH. Quare constat propositum. | |
Theorema 7Ga naar voetnoot18).
Sit Cylindrus KM, cujus quadratum diametri basis MV, non minus sit quam duplum quadrati lateris KV. Habeat verò ad liquidum in gravitate rationem
| |
[pagina 168]
| |
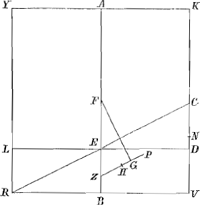
quadr. AK non minus quàm duplum quadrati AF; quum autem quadratum AF non sit minus rectangulo AEBaGa naar voetnoot19), erit duplum quadrati AF non minus quam duplum rectangi. AEB; quare et quadr. AK non minus duplo rectangulo AEB. Ergo duplum rectangulum AEB cum defectu ½ quadr. DC minus erit quadrato AK; ideoque ZG minor ZHbGa naar voetnoot20). Ergo quum FG sit perpendicularis in ZP et consequenter in liquidi superficiem RC, in eandem superficiem non erit perpendicularis FH. FH autem jungit centra gravitatis totius cylindri et partis mersae RCVM, ergo totus Cylindrus inclinabit in quam partem inclinat linea FHcGa naar voetnoot21), ascendetque versùs K, deprimetur verò versùs Y, donec bases MV et YK erunt liquidi superficiei parallelae; quod erat demonstr. | |
Theorema 8.
| |
[pagina 169]
| |
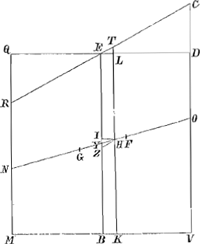
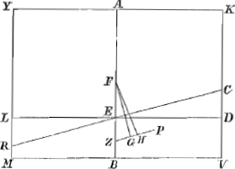
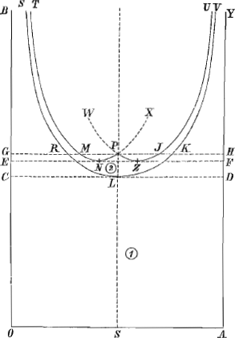
duplum quadrati lateris KV. Sectum autem sit latus KV in Q, ita ut rectangulum KQV aequetur octavae parti quadrati MV. Et habeat primò Cylindrus ad liquidum in gravitate proportionem non minorem eâ, quam QV habet ad KV; et liquido supernatans positus sit inclinatus, ita ut liquidi superficies sit RC: dico rectum restitutum iri. Abscindatur enim plano DL basi MV parallelo cijlindrus DM aequalis portioni mersae RCVM, et manifestum est diametrorum DL et RC intersectionem fore in cylindri axe AB, in E. Porrò sit F centrum gr. cylindri KM, et H portionis RCVM, per quod agatur ZHP parallela RC, et in eam cadat perpendicularis FG. denique jungatur FH. Quia igitur cylindrus ad liquidum in gravitate habet rationem majorem quam QV ad KV, habebit quoque portio demersa RCVM sive qui eidem aequalis est cylindrus DM ad cylindrum KM non minorem rationem quam QV ad KVaGa naar voetnoot23); quare latus DV non minus est quam QV. Ergo rectangulum KDV sive AEB non majus rectangulo KQV. Ergo rectang. AEB non majus quoque octavâ parte quadrati MV, et duplum rectang. AEB non majus quartâ parte quadrati MV id est, quadrato AK. Quamobrem duplum rectang. AEB cum defectu ½ quadr. DC minus erit quadrato AK, atque ideo ZG minor ZHbGa naar voetnoot24). Ergo quum FG sit perpendicularis ad ZP, atque ideo ad liquidi superficiem RC, ad eandem non erit perpendicularis FH; quare cylindrus inclinabit in quam partem inclinat FH,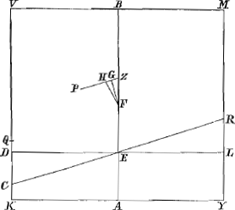 Fig. 10.
ascendetque versùs K, deprimetur verò versùs Y, donec bases ejus sint liquidi superficiei parallelae; quod erat demonstr. Habeat nunc [Fig. 10] Cylindrus ad liquidum in gravitate proportionem non majorem eâ, quam KQ habet ad KV, et liquido supernatans demersâ base positus, sit inclinatus, ita ut liquidi superficies sit CR; dico similiter rectum restitutum iri. Sit enim H centr. gravitatis portionis enatantis MVCR, per quod agatur ZHP parallela RC, caeteraque construantur ut in casu praecedenti. Quum itaque Cylindrus MK ad liquidum in gravitate non majorem habeat rationem quam KQ ad KV, habebit quoque portio demersa RCKY, sive qui ei aequalis est | |
[pagina 170]
| |
cylindrus DY, ad cylindrum KM non majorem rationem quam KQ ad KVaGa naar voetnoot23), quare latus DK non majus erit quam KQ, ideoque DV non minor quam QV. Unde eodem modo quam in casu praecedenti hic quoque demonstrari potest FH non esse perpendicularem in ZP, ideoque nec in superficiem liquidi RC. FH autem hic jungit centra gravitatis, totius cylindri et portionis enatantis MVCR, ergo totus cylindrus inclinabit ad quam partem inclinat FHbGa naar voetnoot25), descendetque versùs V ascendet verò versùs M, donec bases ejus sint liquidi superficiei parallelae, quod erat demonstr. Ex hoc Theoremate manifestum est Cylindrum cujusvis longitudinis tam magnam vel tam parvam proportionem posse habere ad liquidum in gravitate, ut ei supernatans demerfâ base et positus inclinatus, ita tamen ut neutra basium contingat liquidi superficiem, rectus restituatur, et bases fiant liquidi superficiei parallelae. | |
Theorema 9.
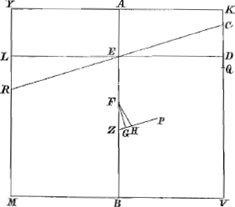
Sit Cylindrus KR, çujus quadratum à diametro basis RV vel YK ad quadratum
| |
[pagina 171]
| |
et jungatur FH. Porrò ut CV secta in D et N, ita ut VD quidem sit dimidia CV, VN verò ⅝ CV sive 5/4 DV. Rectangulum KNV non potest majus esse quàm ¼ quadrati KVaGa naar voetnoot27); rectangulum autem sub KN et DV facit ⅘ rectanguli KNV, (quia NV est 5/4 DV,) ergo rectangulum sub KN et DV non est majus quàm 4/20 sive ⅕ quadrati KV. Porrò quia quadr. RV ad quadr. KV majorem habet rationem quàm 8 ad 5 erit ⅛ quadrati RV major quam ⅕ quadrati KV: Ergo etiam ⅛ quadrati RV major rectangulo sub KN et DV, quare in lineâ ZP erit pars ZH major parte ZGbGa naar voetnoot28): Et quum FG sit perpendicularis ad ZP et ad liquidi superficiem RC, ad eandem superficiem non erit perpendicularis FH, quae jungit centra grav. totius cylindri et partis mersae RCV; quamobrem Cylindrus inclinabit in quam partem inclinat linea FH, et deprimetur versùs Y, ideoque mergetur angulus R; quod erat demonstrandum. Habeat jam Cylindrus ad liquidum in gravitate proportionem majorem subduplâ,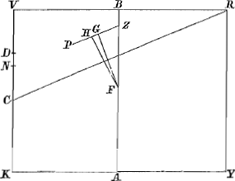 Fig. 12.
et liquido supernatans demersâ base inclinetur donec angulus R [Fig. 12] sit in liquidi superficie, quae sit CR: dico angulum R supra liquidi superficiem sublatum iri. Sit enim H centrum gravit. cunei enatantis CVR, et reliqua construantur ut supra. Demonstrari igitur potest sicut in casu praecedenti, FH non esse perpendicularem ad PZ neque ad liquidi superficiem CR. FH autem hic jungit centra gravitatis totius cylindri et partis enatantis CVR; ergo Cylindrus inclinabit quò inclinat linea FH, et deprimetur quidem versùs V, extolletur verò versùs R, ideoque angulus R supra liquidi superficiem exsurget; quod erat demonstr. | |
[pagina 172]
| |
Theorema 10.
Sit Cylindrus KM, cujus quadratum à diametro basis MV ad quadratum lateris KV minorem rationem habeat quam duplam, sive quam 8 ad 4, majorem verò
| |
[pagina 173]
| |
tionis RXVM, per quod ducatur ZHP parallela RX, atque in eam cadat perpendicularis FG, et denique jungatur FH. Quia igitur Cylindrus est ad liquidum in gravitate ut DV ad KV, sive ut cylindrus DL ad cylindrum KM, atque etiam ut pars mersa ad eundem cylindrum KMaGa naar voetnoot31), erit portio mersa RXVM aequalis cylindro DM; quare diametri RX et LD in eodem puncto E secabunt axem AB. Erit itaque ex hypothesi angulus AEX minor angulo AEC, et XD major CD. Quum autem quadratum DC per constr. sit duplum excessus quo duplum rectanguli AEB superat quadratum AK, erit duplum rectanguli AEB cum defectu ½ quadr. CD aequale quadrato AK; et quum XD sit major CD, erit duplum rectanguli AEB cum defectu ½ quadr. XD, minus quadrato AK; ergo ZG minor quam ZHbGa naar voetnoot32), et quum FG sit perpendicularis in ZP, et in liquidi superficiem RX, in eandem superficiem non erit perpendicularis FH, quae jungit centra grav. cylindri totius et portionis mersae RXVM; quare Cylindrus inclinabit quò inclinat FHcGa naar voetnoot33), idque fiet quàm diu superficies liquidi non convenit cum lineâ EC. Jam ita disponatur Cylindrus ut liquidi superficies RX [Fig. 14] cum axe AB faciat angulum majorem angulo ECD vel AEC. Sit autem constructio reliqua ut in casu praecedenti. Sicut supra ita hìc quoque diametri planorum, LD et RX in eodem puncto E secant axem AB; ergo hìc ex hijpothesi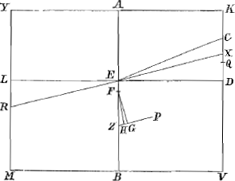 Fig. 14.
angulus AEX major angulo AEC, et XD minor CD. Quum autem quadratum CD aequale sit duplo excessui quo duplum rectang. AEB superat quadratum AK dGa naar voetnoot34), erit duplum rectanguli AEB cum defectu ½ quadr. DC aequale quadrato AK; et quum XD sit minor quam CD, erit duplum rectang. AEB cum defectu ½ quadr. XD majus quadrato AK: Ergo ZG major quàm ZHeGa naar voetnoot35); et quum FG sit perpendicularis ad ZP et ad liquidi superficiem RX, ad | |
[pagina 174]
| |
eandem superficiem non erit perpendicularis FH, quae jungit centra grav. totius Cylindri et portionis mersae RXVM: quare Cylindrus inclinabit quò inclinat FH, et deprimetur à parte K, idque donec superficies liquidi conveniat cum lineâ EC. Non consistet igitur Cylindrus nisi cùm axis AB cum liquidi superficie faciet angulum aequalem angulo AEC vel ECD; quod erat demonstr. | |
Theorema 11.
| |
2.Sit itaque Cylindrus KM cujus quadratum à basis diametro MV ad quadratum lateris KV rationem habeat mino- | |
[pagina 175]
| |
rem quam 8 ad 5, majorem verò quam 3 ad 2. Et latere KV diviso primùm bifariam in P, secundò in Q, ita ut rectangulum KQV aequale sit ⅛ quadrati MV, deinde in N, ita ut rectangulum KNV aequale sit 5/32 quadrati MV, factisque KD ⅘ KN, et KT ⅘ NV; sumatur punctum ubivis inter Q et D ut α, et aliud infra T, non autem ultra P, ut β. Habeat autem Cylindrus ad liquidum in gravitate proportionem quam αV, vel βV, vel αK, vel βK, ad latus KV; et liquido supernatans ponatur inclinatus, ita ut neutra basium liquidi superficiem contingat: dico neque rectum restitutum iri; neque inclinatum mansurum; nisi cùm axis cum superficie liquidi angulum faciet aequalem angulo inveniendo ut supra Theor. 10o.Ga naar voetnoot37).
Ut autem appareat omnes hos casus locum habere posse, et esse differentes, duo sunt ostendenda; primum, quòd punctum T cadat intra K et P: alterum, quòd puncta D et T non coincidant, quorum illud sic ostenditur. Quia rectangulum KNV est 5/32 quadrati MV, quadratum verò MV majus quam 3/2 quadrati KV ex constr. et hijpothesi: erit rectang. KNV majus quam ⅙5/4 quadrati KV. Unde sequitur latus KV ita sectum esse in N, ut segmentorum minus, KN, majus sit quàm ⅜ KV, segmentorum verò majus, NV, minus sit quam | |
[pagina 176]
| |
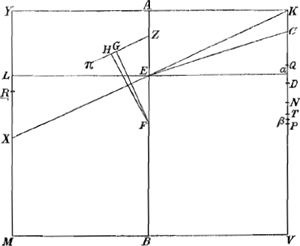
⅝ KVGa naar voetnoot38). Ergo KT, quae est ⅘ NV, minor est quam 4/8 sive ½ KV. Apparet itaque punctum T cadere intra K et P. Alterum sic ostenditur, nimirum quòd puncta D et T non coincidant. quia enim rectangulum KNV est 5/32 quadrati MV, quadratum verò MV minus quam 8/5 quadrati KV (utramque ex constr.): erit rectangulum KNV minus quam 8/32 seu ¼ quadrati KV, unde sequitur latus KV non bifariam dividi in N; segmentorum verò majus est NV, minus autem NK, ergo KD, quae est ⅘ KN, minor est ipsâ KT, quae est ⅘ NV. non igitur coincidunt puncta D et T. Primùm itaque habeat Cylindrus ad liquidum in gravitate proportionem quam αV ad KV; et facto plano αL parallelo basi YK, veniat ex centro ejus E linea EC, | |
[pagina 177]
| |
comprehendens partem Cα, cujus quadratum duplum sit excessus, quo duplum rectang. AEB superat quadr. AK.Ga naar voetnoot30) Ponatur autem cylindrus inclinatus, ita ut neutra basium contingat liquidi superficiem. Ostendendum est neque rectum restitui, neque inclinatum manere, nisi cùm axis AB faciet cum liquidi superficie angulum aequalem angulo ECα vel AEC. Abscindatur à Cylindro Cuneus KXY plano cujus maxima diameter KX transeat per E intersectionem duarum αL et AB. Porrò sit H centrum gravitatis cunei KXY, per quod agatur ZHπ parallela KX, in eamque cadat ex F centro grav. cylindri, perpendicularis FG, et jungatur FH: denique sit YR 5/4 YL. Quoniam igitur rectangulum KQV per constr. aequale est ⅛ quadrati MV, Cylindrus autem KM ad liquidum in gravitate proportionem habet quam αV ad KV, quae minor est eâ quam QV, major verò eâ quam QK habet ad KV, sequitur Cylindrum non rectum restitutum iriaGa naar voetnoot39). Sed neque eousque inclinabitur ut basis YK contingat liquidi superficiem; nam si eousque jam inclinatus ponatur et angulus K sit in liquidi superficie KX, continuò idem angulus supra liquidi superficiem extolletur. quod sic ostenditur. Quia enim cylindrus est ad liquidum in gravitate, ut αV ad KV, sive ut cylindrus αM ad KM; erit etiam portio demersa XKVM aequalis cylindro αMbGa naar voetnoot40), quare liquidi superficies KX, (id est, diameter plani quod est secundum liquidi superficiem) in eodem puncto E secabit axem AB, ubi sectus fuit à plano αL, eritque YL dimidia ipsius YX. YL autem sive Kα minor est quàm KD, (quia punctum α sumptum est inter Q et D,): ergo quoque YR, quae est 5/4 YL, minor erit quàm KN, quae est 5/4 KD. Ergo rectangulum YRM minus est rectangulo KNV; hoc aùtem aequale est 5/32 quadrati MV, ergo rectangulum YRM minus est quam 5/32 quadrati MV; rectangulum autem sub YL et RM est ⅘ rectanguli YRM, (quia YL est ⅘ YR,) ergo rectangulum sub YL et RM minus est quàm 4/32 sive ⅛ quadrati MV. Quare in lineâ Zπ erit pars ZG minor parte ZHcGa naar voetnoot41). Ergo quum FG sit perpendicularis in liquidi superficiem XK, in eandem non erit perpendicularis FH, quae jungit centra grav. cylindri et cunei enatantis XYK. Quamobrem cylindrus inclinabit quò inclinat linea FHdGa naar voetnoot42), ascendetque versùs K, isque angulus supra liquidi superficiem extolletur. Demonstratum igitur est Cylindrum neque rectum restitutum iri, neque tamen eousque inclinari posse ut alterutra basium contingat liquidi superficiem. Quòd autem angulus, quem, consistente Cylindro, axis AB faciet cum liquidi superficie, | |
[pagina 178]
| |
aequalis futurus sit angulo ECα vel AEC, demonstrari poterit sicut in Theoremate 10o h. lib. Habeat nunc [Fig. 16] Cylindrns ad liquidum in gravitate rationem quam βV habet ad KV, et, facto plano βEL parallelo MV, inveniatur angulus ECβ ut in casu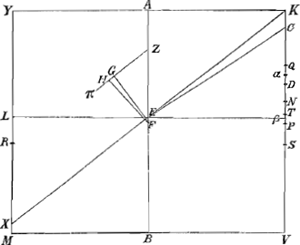 Fig. 16.
praecedenti. Dico, si Cijlindrus liquido supernatans ponatur inclinatus, ita ut neutra basium contingat liquidi superficiem, quòd neque rectus restituetur neque inclinatus manebit, nisi cùm axis AB faciet cum liquidi superficie angulum aequalem angulo AEC vel ECβ. Construantur enim reliqua ut in casu praecedenti; et praeterea sit KS aequale ipsi VN et YR 5/4 YL. Quia igitur Cylindrus ad liquidum in gravitate habet rationem quam βV ad KV, quae minor est eâ quam QV, major autem eâ quam QK habet ad KV, non poterit quidem rectus restituiaGa naar voetnoot43). Sed neque eousque poterit inclinari, ut basium alterutra contingat liquidi superficiem; nam si jam eousque ponatur inclinatus, ut angulus K sit in liquidi superficie KX, statim idem angulus supra superficiem liquidi extolletur. Primò enim facile sicùt in casu praecedenti ostenditur YL esse dimidiam ipsius YX; sed YL sive Kβ major est quam KT, (quia punctum β sumptum fuit inter T et P): ergo YR quae est 5/4 YL major erit quam KS, vel NV quae singulae sunt 5/4 KT; quare rectangulum YRM minus erit rectangulo KSV vel KNV; hoc autem aequale est 5/32 quadrati MV, ergo rectang. YRM minus est quam 5/32 quadrati MV; Rectangulum autem sub YL et RM est ⅘ rectanguli YRM, (quia YL est ⅘ YR) ergo rectang. sub YL et RM minus est quam 4/32 sive ⅛ quadrati MV. Ergo in lineâ Zπ, erit pars ZG minor parte ZHbGa naar voetnoot44), et quum FG sit perpendicularis in Zπ et in liquidi superficiem XK, in eandem non erit perpendicularis FH, quae jungit centra grav. cylindri et cunei enatantis XYK. quamobrem Cylindrus inclinabit quò inclinat linea FHcGa naar voetnoot45), et angulus K ascendet supra | |
[pagina 179]
| |
liquida superficiem. Quòd autem rùrsus angulus quem manente cylindro axis AB faciet cum liquidi superficie, aequalis futurus sit angulo ECβ vel AEC, demonstrari poterit ut in Theor. 7oGa naar voetnoot46) hujus lib. Quòd si Cylindrus sit ad liquidum in gravitate ut αK vel βK ad KV, inversa tum intelligantur duo praecedentia schemata, et eaedem quae in praecedentibus casibus erunt demonstrationes, nisi quòd tunc eae partes mersae erunt quae prius enatabant. Si igitur Cylindrus sit ad liquidum in gravitate ut αV vel βV vel αK vel βK ad latus KV, etc.; quod erat dem. | |
3.diviso latere KV, ut suprà, punctis P, N, D, T, nempe in P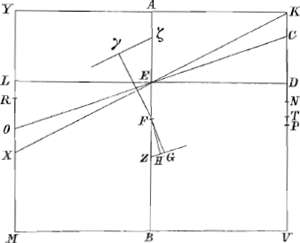 Fig. 17.
bifariam, et in N ita ut rectangulum KNV sit 5/32 quadrati MV, et KD sit ⅘ KN, KT verò ⅘ VN; Si Cylindrus ad liquidum in gravitate proportionem habeat quam DV vel TV vel DK vel TK ad latus KV, et liquido supernatans ponatur inclinatus ita ut neutra basium liquidi superficiem contingat, eousque inclinabitur donec alterutra basium eandem superficiem contingat in uno puncto.Ga naar voetnoot47)
Habeat enim primò ad liquidum in gravitate rationem quam DV ad KV, et | |
[pagina 180]
| |
ponatur inclinatus, ita ut liquidi superficies sit OC. dico eousque inclinatum iri donec basis YK liquidi superficiem contingat in puncto K. Sit enim planum DL parallelum basi KY, et planum KX abscindat cuneum KYX aequalem cylindro KL: Porrò sit F centrum gravitatis cijlindri; item H centr. gravitatis portionis OCVM, et γ cunei XYK, per quae ducantur ZHG parallela OC et ζγ parallela XK, in easque cadant perpendiculares FG et Fγ: Jungatur etiam FH, et denique sit YR aequalis KN. Quia igitur rectangulum KNV sive YRM sunt 5/32 quadrati MV, rectangulum autem sub YL et RM est 4/5 rectanguli YRM (quia RY est 5/4 LY,): sequitur rectangulum sub YL et RM aequale esse 4/32 sive ⅛ quadrati MV; quare erit in lineâ ζγ, pars ζγ, quae est inter axem AB et perpendicularem Fγ aequalis parti quae est inter eandem axem AB et centrum gravitatis cunei XYKaGa naar voetnoot48); et quià hae partes sunt aequales, erit duplum rectanguli AEB cum defectu ½ quadr. XL aequale quadrato AYbGa naar voetnoot49) vel AK nimirum quartae parti quadrati YK. Ergo duplum rectanguli AEB cum defectu ½ quadrati CD (quia CD minor est quam KD vel XL) majus erit quadrato AK. Qùare in lineâ ZG erit pars ZG major parte ZHcGa naar voetnoot50), et quum FG sit perpendicularis in ZG; ideoque in liquidi superficiem OC, in eandem superficiem non erit perpendicularis FH, quae jungit centra gravitatis cylindri et partis mersae OCVM; quamobrem Cylindrus inclinabit quò inclinat linea FH dGa naar voetnoot51), descendetque versùs K, idque donec angulus K sit in ipsâ liquidi superficie: Cum autem eò pervenerit tum manifestum est enatare debere cuneum KYX; nam quum in hujus centrum gravitatis incidat Fγ, quae simul etiam perpendicularis est in liquidi superficiem XK, (quod in principio hujus demonstrationis ostensum fuit,) cylindrus tunc ad neutram partem magis inclinabit; quod erat demonstr. Habeat jam [Fig. 18] Cylindrus ad liquidum in gravitate rationem quam TV ad KV, et liquido supernatans ponatur inclinatus ita ut superficies liquidi sit OC; dico eousque inclinatum iri donec basis YK contingat liquidi superficiem in puncto K. Sit enim planum TL parallelum basi MV, et reliqua ad eum modum construantur quo in casu praecedenti constructa fuere, fiant verò KS, YR aequales ipsi NV, Eritque pene eadem demonstratio, quae fuit modò. Nam quum rectangulum KNV sive KSV sive YRM sit 5/32 quadrati MV, rectangulum autem sub YL et RM sit ⅘ rectanguli YRM, (nam sicut KT est ⅘ NV sive KS, ita etiam YL est ⅘ YR,) erit rectangulum sub YL et RM aequale 4/32 sive ⅛ quadrati MV; unde sequitur perpendiculum Fγ incidere in ipsum centrum gravi- | |
[pagina 181]
| |
tatis cunei KYXaGa naar voetnoot52). Hinc autem primò demonstrari potest ut in casu praecedenti,
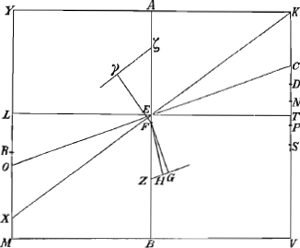 Fig. 18.
Cylindrum quidem non consistere cùm liquidi superficies est OC, sed descendere versus K, donec angulus K sit in ipsâ liquidi superficie, atque ea sit KX; secundò etiam hoc inde sequitur, quòd cylindrus consistat cùm liquidi superficies est KX; quod erat demonstrandum. Denique si Cylindrus sit ad liquidum in gravitate ut DK vel TK ad KV inversa intelligantur duo praecedentia schemata (adeo ut Fγ tum fiat ea quae jungit centra gravitatis cylindri et partis demersae) et eadem quae in praecedentibus casibus erunt quoque demonstrationes. Si igitur Cylindrus ad liquidum in gravitate habeat rationem quam DV vel TV vel DK vel TK ad KV, &c. quod erat demonstr. | |
4.Secto rursus latere KV [Fig. 19], ut supra, in punctis P, N, D, T, nempe in P bifariam, et in N ita ut rectangulum KNV aequetur 5/32 quadrati MV, et KD sit ⅘ KN, KT autem ⅘ NV, sumptóque puncto α ubivis inter D et T; Si Cylindrus ad liquidum in gravitate proportionem habeat quam αV vel αK habet ad KV, et liquido supernatans, demersâ base, ponatur inclinatus, ita ut neutra basium contingat liquidi superficiem; ulteriùs inclinabitur, quam ut alterutra basium contingat eandem superficiem in uno puncto.Ga naar voetnoot53) | |
[pagina 182]
| |
Habeat primò cylindrus ad liquidum in gravitate rationem quam αV ad KV, et ponatur inclinatus ita ut liquidi superficies sit OC; dico ulteriùs inclinatum iri
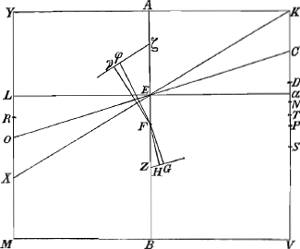 Fig. 19.
quàm ut basis YK liquidi superficiem contingat in puncto K. Fiat enim planum αEL parallelum basi KY vel MV, et planum KEX abscindat à cylindro cuneum KYX aequalem cylindro KL. Porrò sit H centrum grav. portionis OCVM, et ϕ centrum grav. cunei KYX, per quae agantur ZHG parallela OC, et ζϕγ parallela XK, in easque cadant ex F centro grav. cylindri, perpendiculares, FG ad ZG et Fγ ad ζγ: jungantur etiam FH et Fϕ; et denique fiat KS aequalis NV, et YR 5/4 YL. Quia igitur Cylindrus est ad liquidum in gravitate ut αV ad KV, sive ut cylindrus αM ad cylindrum KM, atque ita etiam portio mersa OCVM ad cylindrum KMaGa naar voetnoot54), sequitur portionem OCVM aequalem esse cylindro αM, ac proinde diametros αL, OC et KX in eodem puncto E secare axem AB. Porrò quum Kα, cui aequalis est YL, major sumpta sit quam KD, minor verò quam KT, erit YR sive 5/4 YL major quam KN sive 5/4 KD, minor autem quàm KS, quae (sicuti VN) est 5/4 KT; Ergo quum puncta N et S aequaliter distent à P, sive medio lateris KV, punctum R minus distabit à medio lateris YM, quàm N vel S distant à P: quamobrem rectangulum YRM majus erit rectangulo KNV sive 5/32 quadrati MV, et rectangulum sub YL et RM sive ⅘ rectanguli YRM, majus quam 4/32 sive ⅛ quadrati MV: Ergo in lineâ ζγ erit intercapedo ζγ major ζϕbGa naar voetnoot55); unde constat duplum rectanguli BEA cum defectu ½ quadrati XL majus esse quadrato AYcGa naar voetnoot56): ergo quum OL vel Cα minor sit quàm XL vel Kα, erit duplum rectanguli AEB cum desectu ½ quadrati Cα multò majus quadrato AY vel AK, quare in lineâ ZG erit intercapedo ZG major ZHdGa naar voetnoot57). Ergo quum FG fit perpendicularis ad ZG et ad liquidi superficiem OC, ad eandem superficiem non erit perpendicularis FH, | |
[pagina 183]
| |
quae jungit centra gravitatis totius cylindri et portionis mersae OCVM; Ideoque Cylindrus inclinabit quò inclinat linea FHeGa naar voetnoot58), descendetque à parte K donec angulus K sit in liquidi superficie atque ea sit KX. Sed neque tum consistet; nam quum jam fuerit ostensum in lineâ ζγ, intercapedinem ζγ majorem esse quam ζϕ, et Fγ sit perpendicularis in ζγ et in liquidi superficiem, quae tum erit KX, in eandem superficiem non erit perpendicularis Fϕ, quae jungit centra gravitatis totius cylindri et cunei enatantis KYX, ideoque Cylindrus inclinabit quò inclinat linea FϕfGa naar voetnoot59), mergeturque angulus K; quod erat demonstrandum. Quod si Cylindrus ad liquidum in gravitate rationem habeat quam αK ad KV, tum inversa intelligatur praecedens figura, et demonstratibur angulum K emersurum esse supra liquidi superficiem, neque differet demonstratio à praecedenti, nisi quod partes eae hìc mersae erunt quae prius enatabant. | |
Corollarium. 1.Fuit hoc Theorema de Cylindro cujus quadratum à diametro basis ad quadratum lateris minorem habet rationem quam octo ad quinque, majorem verò quam sesquialteram Fig. 20.
[3/2]; verùm si ejusmodi si Cylindrus ut quadratum à diametro basis ad quadratum lateris sit ut octo ad quinque; tum diviso latere KV ut supra in P, Q et N, incidet quidem punctum N in P, id est, in medium lateris KV,Ga naar voetnoot60) et ideo puncta D et T diversa non erunt, latusque KV ita divident ut pars versus V sit sesquialtera reliquae versùs K. Unde fiet ut Cylindrus semper inclinatus consistat, ita ut neutra basium contingat liquidi superficiem, praeterquam si ad liquidum in gravitate rationem habeat quam DV vel DK ad KV, id est, quam tria vel duo ad quinque tum enim alterutra | |
[pagina 184]
| |
basium continget liquidi superficiem in uno puncto: Vel si habeat rationem majorem quam QV vel minorem quam QK ad KV, tum enim rectus consistet.Ga naar voetnoot61) Quòd si Cylindrus talis sit [Fig.21] ut quadratum diametro basis, quadrati lateris sit sequialterumGa naar voetnoot62); tum diviso latere KV ut suprà in P, Q et N, erit KQ ¼ KVGa naar voetnoot63); NK ⅜ KVGa naar voetnoot64); et ideo DK 3/10 KVGa naar voetnoot65), punctum verò T incidet in P, id est, medium Fig. 21.
lateris KVGa naar voetnoot66). Unde fiet ut Cylindrus primò, rectus quidem consistat, si ad liquidum in gravitate rationem habuerit majorem quam QV, vel minorem quam QK ad KV id est majorem quam subsequitertiam, vel minorem quam subquadr. [¼] Secundo, inclinatus ita ut neutra bafium contingat liquidi superficiem, si rationem habuerit ad liquidum in gravitate minorem quàm QV, majorem verò quam DV ad KV; vel si minorem quam DK, majorem verò quàm QK ad KV. Tertiò, inclinatus ita ut altera basium liquidi superficiem contingat uno in puncto, si fuerit ad liquidum in gravitate ut DV vel DK ad KV, id est, ut 7 vel 3 ad 10. Quartò autem si ad liquidum in gravitate rationem habeat minorem quàm DV, majorem verò quam DK ad KV, tum ulteriùs inclinabitur quàm ut altera basium liquidi superficiem in uno puncto contingat; Praeterquam, si eam habeat rationem quam PV ad KV, id est subduplam, tum enim ita consistet ut utraque basis liquidi superficiem contingat in uno puncto.Ga naar voetnoot67) | |
[pagina 185]
| |
Theorema 12.
| |
[pagina 186]
| |
2.Latere KV diviso ut suprà in Q, et praeterea punctis N et D, ita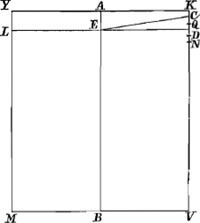 Fig. 23.
ut rectangulum quidem KNV aequetur 5/32 quadrati MV, KD autem sit ⅘ segmenti minoris NK; si habeat Cylindrus ad liquidum in gravitate proportionem majorem quam DV, minorem verò quam QV habet ad KV; vel majorem quidem quam QK, minorem verò quam DK habet ad KV, et liquido supernatans ponatur inclinatus, ita ut neutra basium contingat liquidi superficiem; dico neque rectum restitutum iri, neque mansurum inclinatum, nisi cùm axis AB faciet cum liquidi superficie angulum aequalem angulo ECαGa naar voetnoot69), seu AEC, invento ut in Theoremate 10o hujus libri.Ga naar voetnoot70).
demonstrari hoc potest eodem modo quo Conclusio 2a Theorem. 11i h. lib. verum ut appareat casus hos quandoque locum habere posse, ostendendum est, punctum D magis distare à K quam punctum Q. Quoniam itaque rectangu- | |
[pagina 187]
| |
lum KNV continet 5/32 quadrati MV, et KD est ⅘ KN, continebit rectangulum sub KD et NV 4/32 seu ⅛ quadrati MV; rectangulo autem sub KD et NV, majus est rectangulum KDV, ergo idem hoc majus quoque quàm ⅛ quadrati MV, sive rectangulo KQV; quare necessariò KD major quam KQ. Potest itaque Cylindrus ad liquidum in gravitate habere rationem majorem quàm DV, minorem verò quam QV habet ad KV: potest et consequenter habere majorem quam KQ, minorem verò quam KD habet ad KV; quae erant ostendenda. | |
3.Latere KV diviso ut in Conclusione praecedenti punctis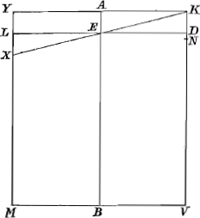 Fig. 24.
N et D, nempe ut rectangulum KNV contineat 5/32 quadrati à diametro basis MV, KD, autem sit ⅘ KN segmenti minoris; Si habeat Cylindrus ad liquidum in gravitate rationem quam DV habet ad KV, vel quam DK ad KV, et liquido supernatans ponatur inclinatus ita ut neutra basium contingat liquidi superficiem; dico eousque inclinatum iri ultrò, ut alterutra basium liquidi superficiem contingat in uno puncto.Ga naar voetnoot71)
Hoc autem demonstrari postest eodem modo, quo Concl. 3a Theorematis praecedentis 11i. | |
[pagina 188]
| |
4. Fig. 25.
Diviso rursus latere KV punctis N et D, nimirum ut rectangulum KNV contineat 5/32 quadrati MV, KD autem sit 4/5 KN segmenti minoris. Si Cylindrus ad liquidum in gravitate rationem habeat minorem quam DV, majorem verò quam DK ad KV, et liquido supernatans ponatur inclinatus, ita ut neutra basium contingat liquidi superficiem, ulteriùs inclinabitur, quàm ut altera basium contingat liquidi superficiem in uno puncto.Ga naar voetnoot72)
Dividatur enim praeterea latus KV bifariam in P, et quum manifestum sit, Cylindrum ad liquidum in gravitate habiturum proportionem majorem subduplâ [½] vel non majorem, habeat primò majorem subduplâ, nempe quam αV habet ad KV (sumpto puncto α intra D et P). Dico ulteriùs inclinatum iri Cylindrum quàm ut basis YK contingat liquidi superficiem in uno puncto. fiat enim KT aequalis ⅘ NV segmenti majoris, et KS aequalis ipsi NV. Quia igitur Cylindrus est ejusmodi, ut quadratum à diametro basis MV ad quadratum lateris KV minorem habeat rationem quàm sesquialterum, id est, quam 3 ad 2, erit rectangulum KNV sive 5/32 quadrati MV, minus quam ⅙5/4 quadrati KV; quamobrem KN minor erit quam ⅜ KV, et NV sive KS major quam ⅝ KVGa naar voetnoot73); et KT (quae est ⅘ NV sive KS) major quam 4/8 sive ½ KV. Itaque punctum α sumptum inter D et P, cadet etiam inter D et T; Unde sicut in Conclus. 4a. Theor. 11i demonstrari poterit, Cylindrum ulteriùs inclinatum iri quàm ut basis YK in uno puncto contingat liquidi superficiem; quod erat demonstrandum. Secundò, si Cylindrus ad liquidum in gravitate proportionem habeat non majo- | |
[pagina 189]
| |
rem subduplâ, ea vel subduplâ erit vel minor subduplâ; et siquidem subduplâ, tum eadem adhuc quae in casu praecedenti erit demonstratio, nam ipsum punctum P cadit inter D et T. Si verò minor subduplâ, invertenda est praecedens figura et eadem rursus erit demonstratio, nisi quòd jam pars ea demersa erit, quae priùs enatabat, et contra. | |
Experimenta.Quoniam Parallelepipeda sive trabes, et Cylindracea corpora ubique obvia sunt, vel saltem facilia paratu, non dubito quin futuri sint qui facto periculo de veritate horum Theorematum cognoscere cupient; eos autem monitos velim ne temere credant suis experimentis, ut priùs perspectum habeant solida, quibus ad ea utuntur, esse e materiâ quae per omnia gravitatis sit aequalis. Et lignum quidem, quod tantae perfectionis sit, reperiri posse, vix crediderim; metalla autem non nisi argento vivo supernatant, alioquin existimo, haec magis accommoda fore. Sed vitandis hisce difficultatibus, fabricentur corpora intus cava, et tenui tantum constantia superficie. deinde disponantur introrsus pondera, hâc lege, ut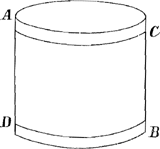 Fig. 26.
omnium simul centrum grav. idem sit, quod centrum corporis vacui, si foret solidum; atque ita pro lubitu gravia et levia habebuntur, additis vel demptis ejusmodi ponderibus. Exemplo sit Cylindrus AB, tenui constans superficie, in quo disponantur ad oppositas bases pondera paria, velut cylindri aequales è plumbo vel aliâ ponderosâ materiâ, AC, BD, et plures si res exiget; dummodo observetur ut pares sint, qui ab oppositis basibus aeque distant: et erit eadem hujus liquido supernatantis positio, quae cijlindri similis figurae et ponderis, qui totus solidus esset et è materiâ sibi ipsi in gravitate per omnia simili.
FINIS. |
|