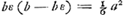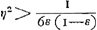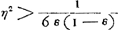Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651

[p. 120]

De iis quae supernatant liquido
Liber 2.¹⁾
De Parallelepipedis.

Certum quidem est superficiebus nullam tribui posse gravitatem, cumque nihilominus videamus Geometras²⁾ earum gravitatis centra investigare, hoc illos eò facere intelligimus, quòd determinatis hisce centris in quocunque plano, non referat in quantam altitudinem idem ducatur,³⁾ Similis autem consideratio locum habet in hujusce libri Theorematis, et sciendum, rectangula quae proponuntur,

Fig. 1.

bases esse parallelepipedorum, quorum longitudo ad arbitrium fingi possit. Ita quod demonstratum est de quadrato ABCD, subduplam habente pro-

1) Dans le livre qui suit, Huygens, après une courte introduction de portée plus générale, s'applique à donner une solution aussi complète que possible des problèmes qui se rattachent à l'équilibre d'un parallélipipède rectangle flottant dont les arêtes longitudinales restent parallèles au niveau du liquide. Il débute par discuter les conditions pour lesquelles cette supposition sera remplie.

2) Le manuscrit fait précéder au mot ‘Geometras’ les mots biffés: ‘Archimedem et aliosque.’

3) Le manuscrit ajoute encore les mots suivants, biffés depuis: quum semper hoc modo corpus efficiatur, cujus centrum gravitatis futurum sit in rectâ, quae jungit centra gravitatis oppositarum basium.’

[p. 121]

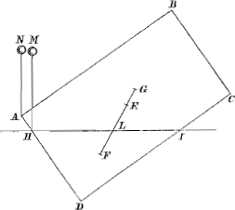
portionem ad liquidum in gravitate, illud liquido impositum ad perpendiculum, ita sponte suâ componi, ut media pars ADC demergatur; idem affirmari credatur de parallelepipedo cujuslibet longitudinis ut AE, quod quadratum basin habeat et in gravitate ad liquidum subduplam proportionem. Ubi notandum, quòd etiamsi exigua tantùm, respectu basis, fuerit altitudo seu longitudo parallelepipedi, ut FA, vel minor etiam, tamen illud consistet lateribus FA et reliquis superficiei liquidi parallelis, modò ita impositum sit; neque enim erit cur magis in hanc quàm in illam partem procumbat. Et hoc quidem Geometricè loquendo: Caeterum experienti aliud eveniet; namque hoc parallelepipedum altitudinis AF, proculdubio ad alterutram partem inclinabit, donec planum basis ABCD superficiei liquidi fiat parallelam: quamobrem qui simili parallelepipedo experimentum capere volet sequentium Theorematum, ita illud continere debebit ut planum basis ABCD semper perpendiculare maneat ad liquidi superficiem;⁴⁾ verum qui molestiam hanc effugere volet, is longitudinem parallelepipedi duplam faciat maximae in base diametri, vel tantùm ut ad hanc ratione habeat quam quinque ad tria: Et certus sit hujusmodi parallelepipedi latera, si secundum longitudinem liquido impositum fuerit, semper ejusdem superficie parallela fore. Nam non tantum de parallelepipedo verùm in universum de omni corpore cylindroïdeo, quod basium oppositarum ambitum habet in easdem partes cavum, quo praeter parallelepipe-

4) Au lieu du passage qui va suivre, jusqu'aux mots: ‘Nam non tantum’ on trouvait primitivement ce qui suit: ‘quod commodè fieri poterit duobis planis perpendicularibus, quae distent inter se spatio FA. Verùm nihil hisce opus erit si in multam longitudinem extendatur parallelepipedum ut AE, tum enim ultro jacebit, imo et erectum recidet. Sed bene hic interrogabor, quanta igitur longitudo futura sit parallelepipedi, si illud jacere velimus. et puto quidem non majori opùs esse, quàm cujus longitudinis quadratum ad quadratum maximi in base lateris rationem habeat quàm tria ad duo; idque propter Theorema 4^tum [lisez: 2^dum] ex quo manifestum est tum saltem non majorem requiri, quum ex figurâ basis et conveniente gravitate, parallelepipedum ita liquido supernatat, ut alterum laterum basis ad superficiem liquidi faciat angulos rectos. Verùm si quis metuet ut eadem longitudo sufficiat parallelepipedo, quod contrà sic liquido supernatet ut neutrum laterum basis ad superficiem liquidi perpendiculare sit, velut hoc quod modò propositum fuit, is producat eandem longitudinem donec rationem habeat ad maximum in base diametrum quàm quinque ad tria, et certus sit hujusmodi paralellepipedi longitudinem seu latus, quomodocumque liquido impositum fuerit, semper ejusdem superficiei parallelam mansura.’
A propos de ces phrases biffées Huygens avait annoté au crayon: ‘malim haec omnino explorata habere, quàm hic dubiè aliquid afferre.’

[p. 122]

dum cylindrus quoque et prisma continentur, idem affirmare licet; ejusque certissima est demonstratio, quam tamen hìc afferre visum non fuit, tum quòd caeterorum Theorematum veritas ex eâ non pendeat, tum maximè quòd asserere nolim, non minorem longititudinem omnibus praedictis corporibus sufficere.⁵⁾.

5) Nous regrettons toutesois de ne pas posséder cette démonstration et de ne pas avoir réussi à y suppléer.

Theorema 1.
Corpus solidum liquido supernatans, non quiescet, nisi cum linea, quae jungit centrum grav. totius corporis cum centro grav. partis mersae, vel enatantis, fuerit perpendicularis ad superficiem liquidi, et si non fuerit perpendicularis, corpus ad eam partem ultro inclinabit ad quam inclinat dicta linea.

Fig. 2.

Sit corpus ABCD supernatans liquido, cujus superficies HI. centrum grav. totius corporis sit E, partis verò mersae F, et enatantis G. linea autem EF vel EG (sunt enim in eâdem rectâ) non sit perpendicularis ad superficiem HI, sed inclinet ad partem C; dico corpus ABCD non quiescere sed inclinare ad eandem partem.

Si⁶⁾ enim fieri potest quiescat, et deinde ita firmari intelligatur ut tantùm circumagi possit ad axem exhibitum puncto L, ubi linea GF intersecatur a liquidi superficie ita ut circa centrum L converti possit.

6) La démonstration qui va suivre, et qui avait déjà subi plusieurs altérations, comme l'état du manuscrit le prouve, a fini par ne plus satisfaire à Huygens, puisqu'il l'a biffée après coup. Il est vrai que nous possédons du même ‘Theorema’ une autre démonstration, écrite sur une feuille détachée et que nous avons reproduite dans l'Appendice III. Mais cette démonstration nous semble plutôt antérieure à celle du texte; et même, s'il en était autrement, on en devrait conclure qu'elle a semblé à Huygens encore moins satisfaisante puisque en traçant la figure 2, que nous donnons telle qu'elle était destinée à la publication définitive du traité, (voir la page 90 de l'Avertissement), il est évidemment revenu à la rédaction du texte.
En effet, il y a tout lieu de s'étonner que Huygens, pour autant que nous connaissons ses manuscrits, n'ait pas réussi, ce qu'il a tâché certainement, de rattacher le ‘theorema’ en question aux ‘theoremata 6 et 7’ du ‘liber i’ et par ce moyen aux hypothèses fondamentales, formulées au commencement du traité.
Avec nos méthodes de raisonnement modernes cela n'aurait pas été difficile. Pour y réussir on n'a qu'à se représenter le corps flottant dans une situation voisine choisie tellement que le point I′ de la nouvelle ligne de niveau se trouve plus près de C que le point I, et H′ plus près de D que H. Alors, en prenant les moments par rapport au plan HI, on voit facilement que le nouveau centre de gravité F′ de la partie immergée DH′I′ ne se sera rapproché ni eloigné du plan HI que d'une quantité infiniment petite du second ordre. Donc, dans la situation de la figure, la différence de niveau de F′ et G sera quasi la même que celle de F et G; mais pour amener le corps flottant dans sa situation nouvelle on devra le faire tourner d'un angle égal à celui de H′I′ avec HI, et dans le même sens. Or, puisqu'il ne s'agit que de la position relative de F′ par rapport à G, on peut tourner autour de G et il est évident qu'alors la différence de niveau entre F′ et G s'amoindrira. Elle sera donc, dans la situation nouvelle, plus petite que celle entre F et G; et, d'après le ‘Theorema 6’ du ‘liber i’, le corps sera donc libre de se mouvoir dans le sens indiqué.
Et ce même raisonnement nous apprend encore que le plan tangent de la surface, qui est le lieu dans le corps du centre de gravité F de la partie immergée, sera toujours parallèle à la surface de niveau HI. Pour le voir il suffit de remarquer que la droite FF′ (où F′ est pris dans sa situation primitive, c'est-à-dire, avant la rotation autour de G) sera toujours parallèle à la ligne HI, puisque les distances de F et de F′ à HI ne diffèrent que d'une quantité infiniment petite du second ordre.
Ajoutons que cette dernière propriété dont la découverte fut attribuée à Dupin par M. Paul Appell dans son ‘Traité de mécanique rationelle’ (voir les pp. 192-195, T. 3, de l'édition de 1903, Paris, Gauthier-Villars), fut déjà formulée et démontrée en 1746 par Bouguer aux pages 259 et 270 de son ‘Traité du navire, de sa construction et de ses mouvemens. à Paris, quay des Augustins, chez Jombert.’

[p. 123]

Si quidem igitur corpus ABCD antea quiescebat, etiam nunc quiescere debebit, (certum enim est in corpore quiescente quotlibet puncta firmari posse, ut tamen illud non commoveatur;) atqui firmato puncto L quia pars mersa HDI levior est liquido suae molis, punctumque L circa quod vertitur non est ad perpendiculum supra centrum suae gravitatis F ideo inquam pars HDI ascendet à parte H nisi impediatur a parte HABCI quae liquido exstat.

Verum pars HABCI quum sustineatur in L, quod non est ad perpendiculum centro suae grav. suppositum, descendere conabitur à parte C, non obstabit igitur motui partis mersae HDI sed eandem juvabit, totumque corpus ABCD ascendet à parte A et descendet a parte C; Itaque firmato corpore circa axem L, opus est duobus ponderibus M et N, (quae manifestò erunt ad eandem partem axis L) ut ne inclinet ad partem C: unde liquet quod eodem inclinabit sublatis hisce ponderibus. Ergo etiam antequam firmaretur circa axem L, non quiescebat, sed inclinabat versus partem C. quod erat demonstrandum.

[p. 124]

Lemma 1.⁷⁾
Sit rectangulum QV, cujus axis EB, centrum Y; et ductâ per E, RC, quae jungat latus QM cum producto latere VD, sit trapezii RCVM centrum grav. H; unde ducatur HZ par all. RC lateri obliquo trapezii, et HI perpendicularis in axem EB. dico, ut tripla axis EB est ad DC, ita esse CE ad HZ, et ita quoque DC ad IZ. Item IZ, dividi bifariam à centro rectangi. Y.

Fig. 3.

Divisis enim CV et RM bifariam in O et N, ducantur RO et VN, quae erunt diametri triangulorum CRV, RVM. hae rursus dividantur in A et S, ita ut partes ad verticem reliquarum sint duplae, et ducantur AS et NO, quarum haec transibit per Y et H, centra gravitatis rectanguli QV et trapezii RCVM^a8). Item ducantur AX, SG parall. EB: eidemque parallela TK, quae transeat per H.

Quia itaque RO et VN sunt diametri triangulorum CRV, RVM, et RA dupla AO, ut et VS dupla SN. sequitur, A et S dictorum triangulorum esse centra grav. ergo SA transit per H, centr. grav. trapezii RCVM; atque ita in H dividitur, ut pars SH ad HA sit ut triang. CRV ad RVM, id est, ut basis CV ad basin RM, ergo etiam GH ad HX, ut CV ad RM; quare etiam ut CV et RM simul ad suam differentiam, id est, ut dupla EB ad duplam DC, sive ut EB ad DC, ita GH et HX simul ad suam differentiam quae est dupla HY, sive, sumpto utrinque dimidio, ita XY ad YH. Sed OY est tripla XY, ergo est tripla EB ad DC, ut OY ad HY, sive ut EC ad TE vel HZ; quod erat primum. Et quia triangula ECD, HZI sunt similia, est quoque ut EC ad HZ, sive ut tripla EB ad DC, ita CD ad IZ; quod erat alterum.

7) Avec les trois, ‘lemmata’ qui suivent, Huygens va construire, pour ainsi dire, l'échafaudage géométrique dont il aura besoin dans ses recherches sur l'équilibre des parallélipipèdes flottants.

8) Huygens annota en marge: ‘a pr. 15. lib. 2. Arch. de aequipond’; mais il s'agit du ‘lib. 1’ de l'ouvrage cité. Comparez la page 183 du Tome 2 de l'édition de Heiberg où la proposition en question est formulée comme il suit: ‘Cuiusuis trapezii duo latera inter se parallela habentis centrum grauitatis in ea linea positum est, quae media puncta parallelarum iungit, ita diuisa, ut pars eius terminum habens punctum medium minoris parallelarum ad reliquam partem eam habeat rationem, quam habet linea duplici maiori aequalis simul cum minore ad duplicem minorem simul cum majore parallelarum.’

[p. 125]

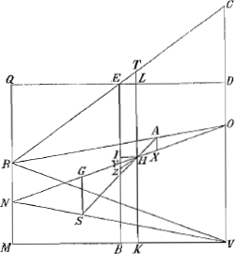
Porrò quum Y sit centr. grav. rectanguli QV, est BY dimidia BE; sed et KH dimidia est TK; ergo differentia duarum BY et HK, quae est YI, est dimidia differentiae TL duarum EB et TK. TL autem manifestò est aequalis IZ, ergo IY dimidia quoque ipsius IZ; quod erat tertium.

Lemma 2.⁹⁾
Sit Rectangulum KM, à quo abscissum sit rectangulum DM, et trapezium ejusdem magnitudinis RCVM: agatur autem per H centrum grav. dicti trapezii linea ZHP parallela ejusdem lateri obliquo RC; et demittatur perpendicularis FG ex F centro rectanguli KM in lineam ZP. dico in lineà ZP, partem ZG, interceptam ab hâc perpendiculari et AB axe rectanguli KM, majorem, aequalem aut minorem fore, parte ZH, intercepta ab eodem axe AB et H centro grav. dicti trapezii; prout sesquialterum rectanguli AEB, detracto dimidio quadrato DC, majus, aequale, vel minus erit quartâ parte quadrati basis MV vel NK id est quadrato AK.¹⁰⁾

Fig. 4.

Sit primò sesquialterum rectang.ⁱ AEB detracto dimidio quadr. DC majus quadrato AK; dico GZ majorem fore ZH.

Sit enim Y centrum rectang. DM, et ex H cadat in axem perpendicularis HI.

Quum igitur tripla EB sit ad CD, ut CD ad IZ^a11); erit rectang, sub triplâ EB et IZ aequale quadrato DC; et rectang. sub triplâ EB et dimidiâ IZ, quae est YZ^b12), aequale dimidio quadrato DC. porrò

9) Primitivement le lemme avait été compté comme un théorème; mais les mots ‘Theorema 2’ furent biffés et remplacés par ‘Lemma 2.’ C'est le lemme principal auquel Huygens aura recours constamment dans la suite. Aussi on voit aisément que le point F représente le centré de gravité du parallélipipède flottant, H celui de la partie submergée dans une situation où RC est la ligne de niveau du liquide et que le sens dans lequel alors le parallélipipède tendra à se mouvoir dépend de la situation relative des points Z, H et G.

10) En notation moderne: ZG ⪌ ZH selon qu'on alt 3/2 AE × EB - ½ DC² ⪌ AK².

11) Huygens annota en marge ‘a lemm. praec.’

12) ‘b lemm. praec.’ [Huygens].

[p. 126]

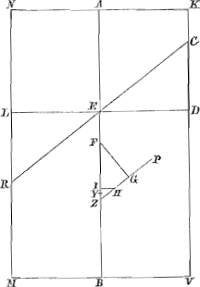
quum AB sit dupla FB, et EB dupla YB; erit AE quoque dupla FY; ergo rectang. AEB duplum rectang. sub EB et FY; quare sesquialterum rectang.ⁱ AEB erit triplum rectang.ⁱ sub EB et FY, ideoque aequale rectang. sub triplâ EB et FY; sed et ½ quadr. CD ostensum fuit aequale esse rectang. sub tripla EB et YZ; ergo rectang. sub triplâ EB et totâ FZ aequale est sesquialtero rectang. AEB una cum dimidio quadr. DC. quum autem ponatur sesquialterum rectang. AEB cum defectu dimidii quadr. DC majus quadr. AK vel ED, erit, addito utrinque quadr.^o DC, sesquialterum rectang. AEB una cum dimidio quadr.^o DC majus quadr.^o EC; Ergo et rectang. sub tripla EB et FZ, majus erit quadr.^o EC. Igitur tripla EB ad EC majorem habet rationem, quàm EC ad FZ; atqui ut tripla EB ad EC ita necessario est rectang. sub triplâ EB et DC at rectang. sub EC et DC; igitur et rectang. sub tripla EB et DC ad rectang. sub EC, DC, majorem habet rationem quam EC ad FZ. Atqui rectang. sub. EC et CD (quia tripla EB est ad CD, ut EC ad HZ^c13)) aequale est rectang. sub tripla EB et HZ: igitur quoque rectang. sub tripla EB et CD ad rectang. sub tripla EB et HZ, sive basis CD ad HZ basin majorem habet rationem, quàm EC ad FZ; et permutando CD majorem ad EC quam HZ ad FZ. sed propter similia triangula ECD, FZG, sicut CD est ad EC, ita est GZ ad ZF; igitur GZ ad ZF majorem quoque rationem habet quàm HZ ad FZ; quare GZ major HZ; quod erat ostendendum.

Jam si sesquialterum rectang. AEB, detracto dimidio quadr. DC, aequale sit quadr.^o AK; dico tum quoque ZG aequalem fore HZ. Cujus demonstratio dependet à praecedenti. nam si sesquialterum rectang. AEB detracto ½ quadr. DC aequale sit quadr. ED, omnia quae modò majora erant hìc erunt aequalia, quare et tandem GZ aequalis HZ.

Similiter si 3/2 rectang. AEB detracto ½ quadr. DC minus fuerit quadr.^o AK, omnia quae in praecedentibus erant majora, minora erunt, et tandem GZ minor HZ ut oportebat. Quare constat propositum.

Manifestum autem est etiam tum constare, quum punctum R incidit in angulum M, ita ut loco trapezii abscissum sit triangulum, quamvis de hoc casu speciatum sit Theorema sequens.

13) ‘c lemm. praec.’ [Huygens].

[p. 127]

Lemma 3.¹⁴⁾
Sit rectangulum KR, à quo abscissum triangulum RCV eductâ lineâ RC ex uno angulorum. agatur autem per H centrum gravitatis dicti trianguli linea ZHP parallela RC. et cadat ex F centro rectang.ⁱ KR, FG perpendicularis in ZP. porrò sit VD dimidia VC, et VN tres quartae VK. dico in lineâ ZP, partem ZG interceptam ab axe rectanguli, AB, et perpendiculari FG, majorem aequalem vel minorem fore parte ZH, intercepta ab eodem axe et centro grav. trianguli RCN;¹⁵⁾ prout rectang. VDN majus aequale vel minus erit octavâ parte quadrati basis RV, vel YK.

Fig. 5.

Sit primò rectang. VDN majus octavâ parte quadrati RV; dico ZG majorem fore ZH.

ducatur enim recta DL aequidistans basi RV, quam manifestum est in eodem puncto E secare axem AB ubi idem sectus est à linea RC et abscindere rectang. DR aequale triang. RCN¹⁵⁾ praeterea CD bifariam dividatur in O.

Quia igitur rectang. VDN majus est ⅛ quadrati RV, erit duplum rectanguli VDN id est rectang.^um sub VC et DN majus ¼ quadr. RV, seu quadrato BV. rectang. verò sub VC et DN aequale est excessui rectanguli sub VC et VN supra rectang. sub VC et VD, id est excessui ¾ rectang.ⁱ CVK supra ½ quadr. VC. ergo et hic excessus major est quadrato BV. sed ¾ rectang. CVK aequale est rectangulo sub KV et VO; id est rectangulis duobus, nempe rect.^o sub KD et VO, et rect.^o sub DV et VO; id est rectang.^o sub KD et VO una cum ⅜ quadr. VC. Ergo et haec duo cum defectu ½ sive 4/8 quadr. VC majora quadrato BV. Id est rectang.^um

14) Primitivement il y avait ‘Theorema 3.’ Le ‘Lemma’ contient une simplification du lemme précédent pour le cas où le point R coïncide avec le point M de la figure 4. En effet, les relations 3/2 AE × EB - ½ DC² ⪌ AK², peuvent s'écrire alors (voir la fig. 5, où VN = ¾ KV): 3/2 KD × DV - ½ DV² ⪌ ¼ RV², ou bien: (¾ KD - ¼ DV) DV ⪌ ⅛ RV², 'est-à-dire: (¾ KV - DV) DV ⪌ ⅛ RV²; (NV - DV) DV ⪌ ⅛ RV² et finalement: ND × DV ⪌ ⅛ RV².

15) Lisez RCV.

15) Lisez RCV.

[p. 128]

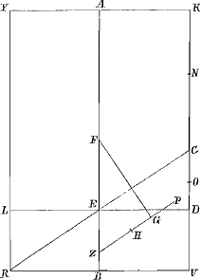
sub KD et VO sive sesquialterum rectanguli KDV cum defectu ⅛ quadr. VC sive cum defectu ½ quadrati DC majus quadrato BV; quare et ZG major erit ZH^a16), quod erat ostendendum.

Jam si rectang. VDN aequale sit octavae parti quadrati RV; dico ZG quoque aequalem fore ZH. Omnia enim quae modò majora fuere hìc erunt aequalia, quare et tandem sesquialterum rectang. KDV cum defectu ½ quadr. DC aequale quadrato BV: ideoque ZG aequalis ZH^b17), ut oportebat.

Eâdem ratione fi rectang. VDN minus sit octavâ parte quadrati RV, erit quoque ZG minor ZH. quare constat propositum.

16) ‘a lemm. 2.’ [Huygens].

17) ‘b lemm. 2.’ [Huygens].

Theorema 2.¹⁸⁾
Rectangulum cujus quadratum basis quadrati lateris non est minus quàm sesquialterum [3/2], quamcunque proportionem ad liquidum habeat in gravitate; liquido supernatans demersâ base et positum inclinatum, ita ut neutra basium contingat liquidi superficiem, non manebit inclinatum, sed rectum restituitur, id est ut axis sit ad perpendiculum.¹⁹⁾

Fig. 6.

Sit Rectangulum KM, cujus quadratum basis MV non minus sit quàm sesqùialterum quadrati lateris VK, habeat autem quamcunque ad liquidum in gravitate proportionem, eique supernatet demersâ base et positum sit inclinatum, adeo ut superficies liquidi sit RC; dico Rectangulum non ita consistere sed res-

18) Primitivement ‘Theorema 4’ (comparez les notes 9 et 14). Ce theorème et le ‘theorema 3’ qui suit, contiennent ensemble la solution complète du problème de la stabilité de l'équilibre d'un parallélipipède slottant dans la situation verticale. Cette solution est conforme à celle, publiée pour la première fois en 1746 par Bouguer dans l'ouvrage cité vers la fin de la note 6. Voir la page 265 du Chapitre IV, Livre II, Section II. Euler, de même, a donné une solution identique, p. 107 du Tome I de l'ouvrage: Scientia navalis seu tractatus de construendis ac dirigendis navibus. Auctore Leonhardo Eulero. Prof. Honorario academiae imper. scient. et directore acad. reg. scient. Borussicae. Petropoli. Typis Academiae Scientiarum CIƆ IƆCCXLIX.

19) Le théorème indique que la position ①, voir l'Avertissement à la p. 87 du Tome présent, sera stable toutes les sois qu'on aura η≦√⅔, c'est-à-dire, toutes les fois que le point représentatif (ε, η) tombera au Tableau de l'Avertissement dans l'intérieur du rectangle ORSA, ou sur la droite RS.

[p. 129]

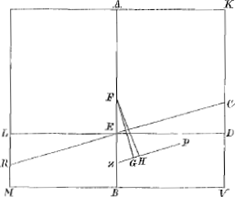
titui, ut axis AB sit ad perpendiculum. Sit enim, divisâ AB bifariam, in F centrum grav. rectanguli KM. et H centrum gravit. trapezii RCVM, per quod ducatur ZHP parallela RC, et in eam ex F cadat perpendicularis FG. denique per E ubi superficies liquidi secat axem AB ducatur LED parallela MV.

Quia igitur quadratum VM non est minus quàm sesquialterum quadrati KV sive AB, erit quoque quadratum AK non minus quàm sesquialterum quadrati AF. quum autem quadratum AF non sit minus rectangulo AEB ^a20): erit quoque sesquialterum quadrati AF non minus sesquialtero rectanguli AEB: quare et quadratum AK non minus quàm sesquialterum rectang. AEB. Ergo sesquialterum rectanguli AEB cum defectu dimidii quadrati DC minus erit quadrato AK. quare in lineâ ZP, pars ZG minor erit quam ZH ^b21). Ergo quum FG perpendicularis sit in ZP et in superficiem liquidi RC, sequitur FH ad eandem non esse perpendicularem: ergo totum rectangulum ad eam partem inclinabit ad quam inclinat linea FH^c22), ascendetque à parte K et ab alterâ descendet, donec axis AB ad superficiem liquidi perpendicularis sit; quod erat demonstr.

20) ‘a pr. 5 lib. 2. Eucl.’ [Huygens].

21) ‘b lemm. 2.’ [Huygens]. C'est-à-dire le ‘Lemma 2’ du ‘Liber’ présent. Primitivement on lisait ‘Theor. 2 h. lib.’ Consultez la note 9. Et il en est de même plusieurs fois dans la suite; mais nous ne mentionnerons plus les altérations qui ont eu pour cause le changement des ‘Theoremata 2 et 3’ en ‘Lemmata’ et qui prouvent que ce changement n'a été apporté qu'après l'achèvement du ‘liber II.’

22) ‘c Theor. 1. h. lib.’ [Huygens].

Theorema 3.
Rectanguli cujus quadratum basis quadrati lateris sit minus quam sesquialterum [3/2], latere ita secto, ut rectangulum sub segmentis aequale sit sextae parti quadrati basis; si rectangulum ad liquidum in gravitate non minorem proportionem habeat quàm segmentum majus habet ad latus, vel non majorem quàm segmentum minus habet ad idem latus; supernatet autem liquido demersâ base et ponatur inclinatum ut tamen neutra basium liquidi superficiem contingat, rectum restituetur.²³⁾.

Sit rectangulum KM, cujus quadratum basis MV quadrati lateris VK minus sit

23) Le théorème nous apprend que le parallélipipède flottant pourra conserver la position ①, indiquée p. 87 de l'Avertissement, pourvu que le point représentatif (ε, η) tombe dans l'espace BEFGCSFR du Tableau, et de même qu'il pourra conserver la position ⑤ toutes les fois que le point représentatif se trouvera dans l'une des divisions BEO ou GAC.
Pour le montrer supposons en premier lieu MV = a, KV = b, a > b. Soit alors bε l'un des segments du coté KV. Dans ce cas le théorème nous apprend que la stabilité exige que pour un rapport η donné de b à a la densité relative soit inférieure ou égale à la moindre, ou bien supérieure ou égale à la plus grande racine de l'équation quadratique: , qui se laisse écrire: . Or, c'est là précisement l'équation de la courbe EFG du Tableau.
Supposons maintenant MV = b, KV = a, a toujours > b. Alors le parallélipipède se trouve dans la position ⑤, mais si alors a ε représente le segment en question, le théorème exige que la densité relative soit inférieure ou égale à la moindre, ou bien supérieure ou égale à la plus grande racine de l'équation quadratique , qui s'écrit maintenant ; ce qui coïncide avec l'équation de l'ellipse à laquelle appartiennent les lignes OE et GA du tableau.
Ajoutons que les conditions de stabilité formulées dans les ‘Theoremata 2 et 3’ peuvent être exprimées par la seule relation:
MV² ≥ 6 ε (1 - ε) KV².

[p. 130]

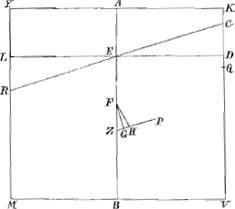Fig. 7.

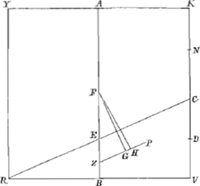
quàm sesquialterum. sectum autem sit latus KV in Q, ita ut rectang. KQV aequaetur ⅙ quadr. basis MV vel YK. habeat verò rectang. KM ad liquidum in gravitate primò rationem non minorem eâ, quam QV habet ad KV: et liquido supernatans positum sit inclinatum, ita ut liquidi superficies sit RC: dico rectum restitutum iri.

Sit enim rectang.ⁱ KM axis AB, et per E ubi is secat liquidi superficiem RC ducatur LED parallela MV. porro sit F centr. grav. rectanguli KM, et H trapezii mersi RCVM, per quod agatur ZHP parallela RC atque in eam ex F cadat perpendicularis FG. denique jungatur FH.

Quia igitur rectang. KM ad liquidum in gravitate non minorem habet rationem quàm QV ad KV, habebit quoque trapezium demersum RCVM sive quod ei aequale est rectang. DM ad rectang. KM non minorem rationem quam QV ad KV^a24); quare DV non minor erit QV. Ideoque rectang. KDV seu AEB non majus rectangulo KQV. Ergo rectang. AEB non majus quoque quàm ⅙ quadrati MV; et triplum rectang. AEB non majus quàm ½ quadr. MV; et 3/2 rectang. AEB non majus quàm ¼ quadr. MV sive quàm quadratum AK. quamobrem 3/2 rectang. AEB cum defectu ½ quadr. DC minus erit quadrato AK, atque ideo ZG minor ZH^b25) Ergo quum FG sit perpendicularis ad ZP et ad superficiem liquidi RC, sequitur FH ad eandem non esse perpendicularem. Ergo totum rectangulum

24) ‘a Theor. 4. lib. 1.’ [Huygens].

25) ‘b lemm. 2.’ [Huygens].

[p. 131]

KM ad eam partem inclinabit ad quam inclinat linea FH^c26), ascendetque à parte K et ab altera descendet, donec axis AB, ad superficiem liquidi fiat perpendicularis; quod erat primò demonstr.

Habeat nunc rectang. KM ad liquid. in gravitate proportionem non majorem eê, quam KQ habet ad KV, et liquido supernatans positum sit inclinatum ita ut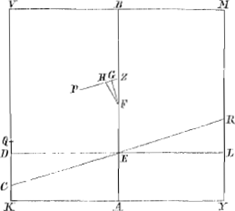

Fig. 8.

liquidi superficies sit CR: dico similiter rectum restitutum iri.

Sit enim H centrum grav. trapezii enatantis RMVC, per quod agatur ZP parallela RC, caeteraeque construantur ut in casu praecedenti.

Quum itaque rectang. MK ad liquidum in gravitate non majorem habeat rationem, quam KQ ad KV, habebit quoque trapezium demersum RCKY sive quod ei aequale est rectang. DY ad rectang. MK non majorem rationem quam KQ ad KV.^a24) quare KD non major erit KQ et DV non minor QV. Unde sicut in casu praecedenti demonstari potest FH non esse perpendicularem ad ZP, ideoque nec ad superficiem liquidi RC. FH autem hic jungit centrum gravitatis totius rectanguli cum centro grav. partis enatantis; ergo totum rectangulum inclinabit eò quò inclinat linea FH^b27); descendetque à parte V et ascendet à parte M, donec axis BA ad liquidi superficiem fiat perpendicularis; quod erat demonstrandum.

Hinc manifestum est parallelepipedum quodcunque, tam magnam vel tam parvam proportionem posse habere ad liquidum in gravitate, ut supernatans liquido demersâ basium minimâ, et positum inclinatum, ita tamen ut neutra minimarum basium liquidi superficiem contingat, rectum restituatur, et planum basium superficiei liquidi fiat parallelum.

26) ‘c Theor. 1 h. lib.’ [Huygens].

24) ‘a Theor. 4. lib. 1.’ [Huygens].

27) ‘b Theor. 1 h. lib’. [Huygens].

[p. 132]

Theorema 4.
Rectangulum, cujus quadratum basis ad quadratum lateris minorem quidem habeat rationem quàm tria ad duo, majorem veró quàm novem ad octo, quamcunque ad liquidum in gravitate proportionem habuerit, eidem supernatans demersâ base nunquam ita consistet, ut unus angulorum sit in ipsâ liquidi superficie.²⁸⁾

Fig. 9.

Sit rectangulum KR cujus quadratum basis RV ad quadratum lateris KV minorem quidem rationem habeat quam 3 ad 2, majorem vero quam 9 ad 8;

Habebit autem ad liquidum in gravitate rationem, quae vel minor erit subduplâ vel non minor: quare habeat primò minorem subduplâ, et liquido supernatans dermersâ base, ponatur ita, ut angulus R sit in liquidi superficie, quae sit RC, dico angulum R infra eandem demersum iri.

Sit enim AB axis rectanguli, et F ejusdem centr. grav. sicut et H centr. grav. demersi trianguli RCV per quod agatur ZHP parallela CR; atque in eam cadat perpendicularis FG, et jungatur FH. Porrò sit CV bifariam secta in D; et KV in N, ita ut NV sint ¾ KV.

28) Le théorème démontre que, si dans le Tableau vis à vis de la p. 87 de l'Avertissement le point représentatif tombe à l'intérieur du rectangle TUSR, alors le parallélipipède ne pourra jamais flotter de telle manière que l'un des sommets de la section verticale soit dans le niveau du liquide et qu'en même temps ce soit l'un des côtés les plus courts de cette section qui se trouve en partie au dessus et en partie au dessous du niveau du liquide.
On observera que le théorème aussi bien que sa démonstration, qui l'un et l'autre supposent RV > KV, n'excluent nullement le cas où c'est le plus long côté qui est coupé par la ligne RC qui désigne le niveau du liquide. En effet, cette dernière situation pourra se réaliser, comme l'indique le Tableau, dans les limites données, toutes les fois que le point représentatif appartiendra à l'une des lignes HO ou NA et où par conséquent le parallélipipède pourra prendre la situation intermédiaire entre les cas ③′ et ④, ou ③ et ④.
Ajoutons que le théorème doit surtout servir à préparer le ‘Theorema 5’ qui suit; à l'exemple d'ailleurs d'Archimède qui, dans les recherches sur la flottation du conoïde parabolique dont l'axe se trouve dans une situation inclinée, prépare de la même manière les Prop. VIII et IX du ‘Liber secundus’ (pp. 22 verso et 26 recto de l'ouvrage cité dans la note 4 du ‘Liber i’ p. 94 du traité présent) par les Prop. VI et VII (pp. 16 verso et 21 verso du même ouvrage).

[p. 133]

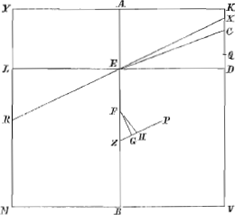
Rectang. VDN non potest majus esse quam ¼ quadrati VN^a29); quia verò VN est ¾ VK, erit quadratum VN 9/16 quadrati KV, ideoque ¼ quadrati VN erit 9/64 quadrati VK; ergo rectang. VDN non est majus quam 9/64 quadrati VK. porrò quia quadr. RV ad quadr. VK majorem habet rationem quam 9 ad 8, erit octuplum quadrati RV majus noncuplo quadrati VK; et 8/64 seu ⅛ quadrati RV major quàm 9/64 quadrati VK. Ergo ⅛ quadrati RV major quoque rectangulo VDN. quare pars ZH major erit parte ZG^b30). et quum FG perpendicularis sit in ZP, ac proinde in liquidi superficiem RC, in eandem linea FH perpendicularis non erit. quapropter totum rectangulum in eam partem inclinabit in quam inclinat linea FH^c31); ascendetque à parte K et ab alterâ parte descendet, ideoque angulus R mergetur infra liquidi superficiem; quod erat demonstr.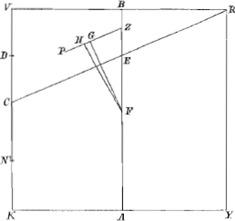

Fig. 10.

Jam habeat rectang. ad liquidum in gravitatem non minorem subduplâ rationem, et liquido supernatans demersâ base ponatur ita ut angulus R sit in liquidi superficie, quae sit RC; dico angulum R supra liquidi superficiem sublatum iri.

Sit enim H centr. grav. trianguli enatantis CVR, et reliqua construantur ut in casu praecedenti, adeo ut CV rursus bifariam secetur in D; et VK in N, ita ut VN sit ¾ VK.

Demonstrari itaque potest, sicuti in casu praecedenti, FH non esse perpendicularem in ZP, neque in superficiem liquidi CR: FH autem hic jungit centrum gravitatis totius rectanguli cum centro grav. partis enatantis CVR; Ergo totum rectangulum inclinabit in quam partem inclinat linea FH^d32); et deprimetur versùs V, extolletur verò versùs R ideoque angulus R supra liquidi superficiem exsurget; quod erat demonstrandum.

29) ‘a pr. 5. lib. 2. Eucl.’ [Huygens].

30) ‘b lemm. 3. h. lib.’ [Huygens].

31) ‘c Theor. 1. h. lib.’ [Huygens].

32) ‘d Theor. 1. h. lib.’ [Huygens].

[p. 134]

Theorema 5.
Rectangulum cujus quadratum basis quadrati lateris minus est quàm sesquialterum [3/2], majus verò quàm sesquioctavum [9/8]; si, diviso latere sicut in Theor. 3^o, ad liquidum in gravitate minorem habeat rationem, quàm segmentorum majus, majorem verò quàm segmentorum minus habet ad idem latus: liquido supernatans demersâ base et positum inclinatum ut tamen neutra basium liquidi superficiem contingat, neque rectum restituetur neque inclinatum manebit, nisi quando axis cum superficie liquidi fecerit angulum aequalem certo angulo, de quo infra dicetur.³³⁾

Fig. 11.

Esto rectang. KM, cujus quadratum basis MV ad quadratum lateris KV minorem rationem habeat quam 3 ad 2, majorem verò quàm 9 ad 8, et diviso latere KV in Q ita ut rectangulum KQV aequetur ⅙ quadrati basis MV, habeat rectangulum ad liquidum in gravitate rationem quam DV ad KV, ita ut DV minor quidem sit QV, major verò QK. et ductâ DL parallelâ VM, veniat ex E, ubi DL ab axe AB secatur, linea EC, ita ut partis compraehensae CD quadratum sit duplum excessus sesquialteri rectanguli AEB supra quadratum AK.³⁴⁾

dico rectang. KM liquido supernatans et positum inclinatum, ita tamen ut neutra basium liquidi superficiem contingat, neque rectum restitui, neque consistere nisi cùm axis AB cum liquidi superficie faciet angulum aequalem angulo ECD. sive AEC.

33) Le théorème nous apprend que le parallélipipède flottant pourra prendre la situation indiquée dans l'‘Avertissement’ par le numéro ②, toutes les fois que le point représentatif tombera dans l'espace VFWV du Tableau; c'est-à-dire toutes les fois qu'entre les limites , on aura .
La forme sous laquelle le théorème a été rédigé, surtout l'introduction de l'‘angulus, de quo infra dicetur,’ a été empruntée aux Prop. VIII et IX d'Archimède, dont il est question dans la note 28. De même les démonstrations se ressemblent par le principe.

34) C'est ici la définition de l'‘angulus, de quo... dicetur.’ On en déduit facilement pour sa valeur: cotg² , où η = KV: MV et où η représente, comme toujours, la densité du parallélipipède relative à celle du fluide.

[p. 135]

Primò enim ita disponatur rectangulum ut liquidi superficies sit RX, quâcum axis AB faciat angulum minorem angulo AEC. Sit autem F centr. grav. rectang.ⁱ KM et H trapezii RXVM, per quod ducatur ZP parall. RX; atque in hanc cadat perpendic. FG, denique jungatur FH.

Quia igitur rectang. KM est ad liquidum in gravitate, sicut linea DV ad KV, sive ut rectang. DM ad KM; erit necessariò trapezium mersum RXVM aequale rectang.^o DM^a35); quamobrem superficies liquidi RX et linea LD in eodem puncto E secant axem AB. erit itaque ex hijpothesi angulus AEX minor angulo AEC: quare XD maior CD. quum autem quadr. CD per constr. sit duplum excessus sesquialteri rectanguli AEB supra quadratum AK, erit 3/2 rectang. AEB cum defectu dimidii quadrati CD aequale quadrato AK: et, quum XD sit major CD, 3/2 rectanguli AEB cum defectu dimidii quadrati XD minus erit quadrato AK; ergo ZG minor ZH^b36), et quum FG sit perpendicularis ad ZP atque ideo ad liquidi superficiem RX, ad eandem superficiem non erit perpendicularis FH; Ergo totum rectang. inclinabit, in quam partem inclinat linea FH,^c37) idque fiet quam diu superficies liquidi non convenit cum lineâ EC.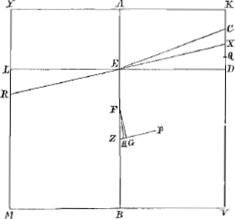

Fig. 12.

Jam ita disponatur rectangulum ut liquidi superficies RX cum axe AB saciat angulum majorem angulo AEC. sit autem H centr. grav. trapezii mersi RXVM, per quod ducatur ut supra ZP parall. RX, atque in eam cadat perpendicularis FG. et denique jungatur FH.

Sicuti suprà ita hic quoque lineae LD et RX in eodem puncto E secant axem AB: Ergo hìc ex hijpothesi angulus AEX major angulo AEC; quare XD minor CD. quum autem quadratum CD aequali sit duplo excessui 3/2 rectanguli AEB supra quadratum AK^d38), erit 3/2 rectanguli AEB cum defectu ½ quadrati CD aequale quadrato AK; et, quum XD sit minor CD, erit 3/2 rectang. AEB cum defectu ½ quadrati XD, majus quadrato AK; ergo ZG major ZH^e39), et quum FG sit perpendicularis ad ZP

35) ‘a Theor. 4. lib. 1.’ [Huygens].

36) ‘b lemm. 2. h. lib.’ [Huygens].

37) C'est-à-dire de telle manière que le point K s'élèvera et que par conséquent la ligne de niveau EX s'approchera de EC. Huygens ajoute en marge ‘c Theor. 1. h. libr.’

38) ‘d per constr.’ [Huygens].

39) ‘e lemm. 2. h. lib.’ [Huygens].

[p. 136]

ideoque et ad liquidi superficiem RX, in eandem superficiem non erit perpendicularis FH; quare totum rectangulum inclinabit in quam partem inclinat linea FH^f40), et deprimetur versùs K; quod semper fiet donec linea EC jaceat in liquidi superficie. Non consistet igitur rectangulum nisi quum axis AB cùm liquidi superficie faciet angulum angulo AEC aequalem; quod erat demonstr.

40) ‘f Theor. 1. h. lib.’ [Huygens].

Theorema 6.
Rectangulum cujus basis major latere, quadratum verò basis ad quadratum lateris minorem habet rationem quàm novem ad octo, liquido supernatans; Aliquando rectum consistet; aliquando ita ut unus angulorum contingat liquidi superficiem, idque quatuor casibus; saepe ita inclinatum ut neutra basium liquidi superficiem contingat. nonnunquam ut tres anguli demersi sint; nonnunquam denique ut demersus sit tantum unus. secundum diversam proportionem quam rectangulum ad liquidum habebit in grav.⁴¹⁾

41) Le théorème nous fait connaître que, si le point représentatif tombe dans l'intérieur du rec tangle BCUT du Tableau de l'‘Avertissement,’ c'est-à-dire quand on η > √8/9, alors les positions ①, ②, ③ et ③′, indiquées p. 87 de l'‘Avertissement’, et aussi leurs positions intermédiaires, peuvent se présenter selon que ce point se trouve dans l'une ou l'autre des divisions qui apartiennent au rectangle mentionné. Voir, pour plus de détails les ‘Conclusiones.’

Conclusio 1.

Eorum quae dicta sunt primum hìc demonstrare superfluum est, nam quod Theoremate 3^o de omnibus quae inclinare possunt rectangulis ostensum fuit, sine dubio etiam huìc convenit.⁴²⁾

42) La ‘Conclusio’ se rapporte aux divisions BEVT et GCUW du Tableau, où la position ① peut se réaliser d'après le ‘Theorema 3.’ Comparez la note 23.

2.

Sit itaque rectangulum KM [Fig. 13] cujus basis MV major latere KV, quadratum verò MV ad quadratum KV minorem habeat rationem quàm novem ad octo; et latere KV diviso in quatuor partes aequales punctis O, P, S, praetereàque in D et T ita ut rectangula KDS, KTS, singula sint aequalia octavae parti quadrati basis MV; habeat rectangulum ad liquidum in gravitate proportionem quàm DV vel DK vel TV vel TK ad latus

[p. 137]

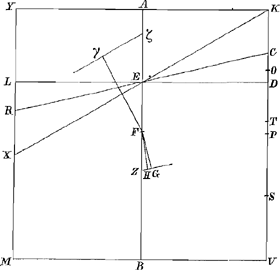Fig. 13.

KV, et liquido supernatans ponatur inclinatum, ita ut neutra basium liquidi superficiem contingat; dico eousque ultro inclinatum iri, donec unus angulorum sit in liquidi superficie.⁴³⁾

Ut autem appareat omnes hosce casus differentes esse, et omnes posse habere locum, duo sunt ostendenda; primum, quòd punctum T non cadat infrà P sive medium lateris KV; alterum, quòd puncta D et T non coincidant. Quorum illud sic ostenditur.

Quum rectangula KOS, KPS singula sint aequalia ⅛ quadrati KV, (utpote contenta sub dimidiâ KV et ejusdem quartâ parte,) rectangula verò KDS, KPS singula per constr. aequalia ⅛ quadrati MV, quadr. autem MV majus sit quadr.^o KV per hijpothesin erunt rectangula singula KDS, KTS majora rectangulis KOS, KPS, ideoque puncta D et T propiora erunt medio linea KS, quàm puncta O et P, quare punctum T erit supra punctum P.

Alterum quoque facilè demonstratur; nam si puncta D et T coincidunt, id erit

43) Dans cette ‘Conclusio’ il s'agit évidemment des cas, où l'on a , ε = DV : KV ou TV : KV), ou bien (ε = DK : KV ou TK : KV), c'est-à-dire: , ou . Dans le premier cas le point représentatif se trouve sur la courbe LMN du Tableau, dans le second sur la courbe HKL et la ‘Conclusio’ nous apprend qu'alors le parallélipipède pourra prendre l'une des positions intermédiaires entre les positions ② et ③, ou ② et ③′ indiquées dans l'Avertissement, c'est-à-dire tel que l'un des sommets de la section verticale se trouve dans le niveau du liquide. Comme le tableau nous le montre, il y a, pour une valeur donnée de , quatre de ces positions, correspondant aux ‘quatuor casibus’ dont il est question dans le ‘Theorema 6’. Mais alors on doit supposer expressément que c'est le côté le plus court de la section verticale qui est coupé par le niveau du liquide. Si l'on admet que cela arrive aussi pour le côté le plus long, on trouve deux nouvelles positions pour lesquelles le point représentatif se trouvera sur l'une des courbes HO ou NA du tableau. Comparez la note 86.
Ajoutons la remarque que la stabilité des positions en question n'est pas démontrée complètement dans ce qui suit, puisque à cet effet on devrait connaître encore la manière dont le parallélipipède se comportera quand il est poussé vers la position ③ ou ③′.

[p. 138]

in mediò lineae KS, quia rectangula KDS, KTS sunt aequalia; itaque singula aequalia erunt ¼ quadrati KS: sed quia quadratum KV ad qu. MV majorem habet rationem quam 8 ad 9, erit noncuplum quadrati KV majus octuplo quadrati MV, et 9/16 quadrati KV, id est, quadr. KS majus quàm 8/16 sive ½ quadrati MV, et ¼ quadrati KS majus quàm ⅛ qu. MV: ergo etiam singula rectangula KDS, KTS majora quàm ⅛ qu. MV; quod est absurdum, nam singula ex constr. aequalia sunt ⅛ quadr. MV. Puncta igitur D et T non coincidunt.

Habeat itaque primò rectang. ad liquidem in gravitate proportionem quàm DV ad KV, et liquido supernatans ponatur inclinatum, ita ut liquidi superficies sit RC: dico eousque inclinatum iri ultro, donec angulus K sit in liquido superficie.

Sit enim DL parallela KY, et fiat triangulum KYX aequale rectangulo KL; Porrò sit in axe AB, F centr. rectanguli KM. item H centr. grav. trapezii mersi RCVM, et γ trianguli XYK, per quae ducantur ZHG parall. RC et γζ parall. XK. in easque cadant perpendiculares FG et in alteram Fγ. Jungatur denique FH.

Quia igitur rectang. ad liquidum in gravitate est sicut DV ad KV, sive ut rectang. DM ad KM; sequitur trapezium mersum RCVM rectangulo DM aequale esse^b44), quare lineae DL, RC et KX in eodem puncto E secant axem AB. Quia autem rectangulum sub YL et excessu ¾ YM supra YL id est rectang. KDS aequale est per constr. ⅛ quadr. MV; sequitur in lineâ γζ, (quae per centr. grav. trianguli XYK parallela ducta est ipsi XK), spatium γζ interceptum à perpendiculari Fγ et axe AB, aequale esse spatio intercepto à centro gr. trianguli XYK et eodem axe AB^c45). et quoniam haec spatia sunt aequalia, sequitur 3/2 trianguli AEB cum defectu ½ quadr. LX aequari quadrato AK^d46). Igitur 3/2 rectanguli AEB cum defectu ½ qu. DC (quia DC minor est DK) majus erit quadrato AK: quamobrem in lineâ ZG, quae per H centr. gr. trapezii RCVM ducta est parallela RC, majus erit spatium ZG spatio ZH^e47). Ergo quum FG sit perpendicularis ad lineam ZG et consequenter ad liquidi superficiem RC, in eandem non erit perpendicularis linea FH. quare totum rectang. inclinabit in quam partem inclinat eadem

44) ‘b Theor. 4. lib. 1.’ [Huygens]. Primitivement il y avait ici ‘a’ dans le texte et le signe d'annotation ‘b’ s'y trouvait dans une phrase biffée. Depuis l'‘a’ du texte fut changée en ‘b’ et l'annotation ‘a’ biffée en marge. Elle était d'ailleurs identique à l'annotation ‘b’ que nous donnons.

45) ‘c lemm. 3 h. lib.’ [Huygens]. En effet les points K, D, S de la figure 13 correspondent aux points V, D, N de la figure 5 (p. 127 du Tome présent) dont il faut tourner le bas en haut. On a donc d'après le lemme cité dans cette dernière figure, au cas présent, ZH = ZG; donc HF, c'est-à-dire le Fγ de la présente figure, perpendiculaire à ZP, c'est-à-dire à γζ; où γ représente le centre de gravité du triangle XYK.

46) ‘d per conv. lemm. 2 h. lib.’ [Huygens].

47) ‘e lemm. 2. h. lib.’ [Huygens].

[p. 139]

FH^f48), et deprimetur versùs K, extolletur verò versùs Y, donec superficies liquidi sit XK; et quia tunc linea Fγ, quae jungit centr. gr. rectanguli KM cum centro grav. trianguli enatantis XYK perpendicularis erit in γζ et consequenter in superficiem liquidi, sicuti modò ostensum est, manifestum est rectang. ad neutram partem magis inclinatum iri; quod erat demonstr.

Jam habeat rectang. ad liquidum in gravitate proportionem quam TV [Fig. 14]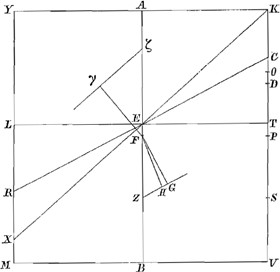



ad KV; et liquido supernatans ponatur inclinatum, ita ut superficies liquidi sit RC; dico eousque ultro inclinatum iri donec angulus K sit in liquidi superficie, eaque sit XK.

ducatur enim TL linea loco DL, et reliqua construantur ut in casu praecedenti, Eritque eadem demonstratio; nimirum quia hìc rectang. KTS aequale est ⅛ quadr. MV^g49), incidet perpendiculum Fγ in ipsum centrum grav. trianguli XYK^h50), quare cum rectangulum erit ita inclinatum ut superficies liquidi sit XK, ad neutram partem magis inclinabit.

Item si rectang. ad liquidum in gravitate sit ut DK vel TK ad KV, invertantur praecedentia schemata, (adeò ut Fγ tum fiat ea quae jungit centr. gr. rectanguli KM cum centro grav. partis mersae) et eaedem quae in duobus prioribus casibus erunt demonstrationes. Si igitur rectangulum sit ad liquidum in gravitate ut DV vel TV vel DK vel TK ad KV, etc. quod erat demonstrandum.

48) ‘f Theor. 1. h. lib.’ [Huygens].

49) ‘g p. constr.’ [Huygens].

50) ‘h lemm. 3. h. lib.’ [Huygens].

3.

Latere KV [Fig. 15] diviso ut supra bifariam in P, et PV bifariam in S; ut et punctis D et T, ita ut singula rectangula KDS, KTS, aequentur ⅛ quadrati basis MV vel YK; praetereaque in Q, ita ut rectang. KQV aequetur ⅙ quadrati MV, sicut factum fuit

[p. 140]

Theor. 3^o: sumptòque puncto ubivis inter Q et D ut α, et alio infra T, non tamen ultra P, ut β: Si rectang. ad liquidum in

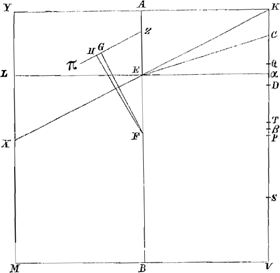Fig. 15.

gravitate proportionem habeat quam αV vel βV vel αK vel βK ad latus KV; et liquido supernatans ponatur inclinatum, ita ut neutra basium contingat liquidi superficiem, neque rectum restituetur, neque inclinatum manebit, nisi axis cum liquidi superficie fecerit angulum aequalem angulo invento ut supra Theor. 5^o.⁵¹⁾

Habeat primò rectang. ad liquidum in gravitate rationem quam α V ad KV, ductâque αL parallela YK, veniat ex E, ubi eadem αL secat axem AB, linea EC, ita ut partis interceptae Cα quadratum sit duplum excessus sesquialteri [3/2] rectanguli KαV supra quadratum AK.

dico si rectang. KM liquido imponatur inclinatum ita ut neutra basium contingat liquidi superficiem, ita ultro dispositum iri ut axis AB cum liquidi superficie faciat angulum aequalem angulo AEC vel ECα.

ducatur enim ex angulo K linea KX, quae transeat per E ubi axis secatur à

51) La ‘Conclusio 3’ nous apprend que la position ② pourra se présenter toutes les fois que le point représentatif se trouve dans les divisions EVKH, NMWG ou KLM du Tableau de l'Avertissement. Sur l'angle que l'axe du parallélipipède fera alors avec le plan horizontal, voir la note 34 (p. 134).
Ajoutons que la ‘Conclusio’ peut être formulée encore d'une autre façon de telle manière qu'elle soit valable pour toutes les valeurs de ε. En effet, la position ② pourra se présenter toutes les fois qu'on a: et simultanément: ; comme aussi .
C'est sous cette dernière forme qu'on retrouve chez Euler, p. 41 ‘Coroll. 4’ de l'ouvrage de 1749 cité dans la note 18 (p. 128), les conditions nécessaires et suffisantes pour qu'une des positions ② puisse être une position d'équilibre; toutefois Euler n'y démontre pas, comme Huygens, la stabilité d'une telle position.

[p. 141]

linea αL; sitque trianguli XYK centrum grav. H, per quod agatur linea πZ parallela XK, in eamque cadat ex F centro rectang.ⁱ KM, perpendicularis FG; denique jungatur FH.

Quoniam igitur rectang. KQV per constr. aequale est ⅙ quadr. basis MV, rectangulum verò KM ad liquidum in gravitate proportionem habet quam αV ad KV, quae minor est eâ, quam QV, major verò eâ, quam QK habet ad latus KV; sequitur rectangulum KM non rectum restitutum iri.^a52) Sed neque eousque inclinabitur ut basis YK contingat liquidi superficiem; nam si eousque jam inclinatum ponatur ut angulus K sit in liquidi superficie KX, continuò idem angulus supra liquidi superficiem extolletur. quod sic ostenditur; quia enim rectang. est ad liquidum in gravitate, sicut αV ad KV, sive ut rectang. αM ad KM, erit etiam trapezium demersum XKVM aequale rectangulo αM^b53), quare liquidi superficies KX in eodem puncto E secabit axem AB, ubi sectus fuit à lineâ αL, eritque YL dimidia ipsius YX. Rectangulum autem sub YL et excessu ¾ YM supra YL, id est rectang. KαS minus est rectangulo KDS, (quia punctum D propiùs est medio lineae KS quàm punctum α,) ergo idem illud rectang. minus quoque octavâ parte quadrati MV.

Ergo in lineâ πZ pars GZ minor HZ^c54): ergo quum FG sit perpendicularis ad πZ et consequenter ad liquidi superficiem, ad eandem superficiem non erit perpendicularis FH, quae jungit centr. gravitatis totius rectanguli cum centro grav. partis enatantis XYK: quare totum rectang. inclinabit quò inclinat linea FH^d55), et angulus K supra liquidi superficiem ascendet.

Demonstratum igitur est, rectangulum KM, neque rectum restitutum iri, neque tamen ita consistere posse ut alterutra basium contingat superficiem liquidi. Quòd autem angulus, quem, rectangulo consistente, axis AB cum liquidi superficie faciet, neque major neque minor futurus sit angulo AEC vel ECα, demonstrari facile poterit, ita ut in Theoremate 5^o hujus libri.

Habeat nunc rectangulum ad liquidum in gravitate proportionem quam βV ad KV, ductâque βL [Fig. 16] sicut in casu praecedenti ducta fuit αL inveniatur etiam simili modo angulus ECβ.

dico si rectangulum KM liquido imponatur inclinatum ut tamen neutra basium liquidi superficiem contingat, ita ultro dispositum iri, ut axis AB cum liquidi superficie faciat angulum aequalem angulo AEC vel ECβ.

52) ‘a p conv. Theor. 3. h. lib.’ [Huygens].

53) ‘b per Theor. 4. lib. 1.’ [Huygens].

54) ‘c lemm. 3. h. lib.’ [Huygens]. En effet, les points K, α, S de la présente figure, correspondent aux points V, D, N de la figure 5 (p. 127), qu'on doit considérer comme tournée le bas en haut.

55) ‘d Theor. 1. h. lib.’ [Huygens].

[p. 142]

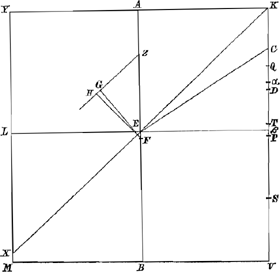Fig. 16.

Construantur enim reliqua ut in casu praecedenti, et non absimilis erit demonstratio.

Nam quia hìc rectang. ad liquidum in gravitate rationem habet quam βV ad KV, quae minor est eâ quam QV, major verò eâ quam QK habet ad KV, non poterit rectangulum rectum restitui.^a56)

Et rursus quia hic rectang. KβS minus est rectangulo KTS, id est octavâ parte quadrati MV, non poterit rectangulum eousque inclinari, ut angulus K descendat usque in liquidi superficiem KX, quia continuò idem angulus rursus ascendat, nam FH non erit perpendicularis in liquidi superfic. KX.

Ergo rectang. neque rectum consistit neque ita ut alterutra basium ullo modo contingat liquidi superficiem. quòd verò angulus, quem, consistente rectangulo KM, axis AB faciet cum liquidi superficie, aequalis futurus sit angulo AEC vel ECβ, iterum demonstrare licebit, sicut factum fuit Theoremate 5^o hujus libri.

Quòd si rectang. ad liquidum in grav. sit ut αK vel βK ad KV, inversa tum intelligantur praecedentia duo schemata, et eaedem quae in praecedentibus casibus erunt demonstrationes, nisi quod tunc eae partes mersae erunt, quae priùs enatabant.

Si igitur rectangulum sit ad liquidum in gravitate, ut αV vel βV vel αK vel βK ad latus KV etc. quod erat demonstr.

56) ‘a per conv. Theor. 3. h. lib.’ [Huygens].

4.

Latere KV [Fig. 17] ut supra diviso punctis S, T et D, nempe ut KS sit ¾ KV, et singula rectangula KDS, KTS aequalia octavae parti quadrati MV vel YK; rectangulum ad liquidum in gravitate rationem habet quam χV ad KV, quae minor sit eâ, quam

[p. 143]

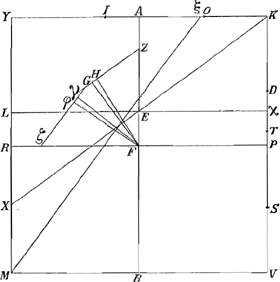Fig. 17.

DV, major verò eâ, quam DK habet ad KV; et liquido supernatans, ponatur ita ut tres anguli mersi sint, K, V et M; dico omnes tres necessariò mersos manere⁵⁷⁾

Siquidem enim angulus K emersurus est, quum sit positus infra liquidi superficiem, oportet ut prius sit in ipsâ liquidi superficie, eàque sit KX.

Sit itaque trianguli XYK centrum gravitatis H, per quod agatur GHZ parallela XK, in eamque ex F centro rectanguli KM, cadat perpendicularis FG, et denique è χ ducatur χL parallela YK. quia igitur rectang. KM est ad liquidum in gravitate, sicut χV ad KV, sive ut rectang. χM ad KM, erit etiam trapezium mersum XKVM aequale rectangulo χM^a58), ideoque supersicies liquidi KX in eodem puncto E secabit axem AB, ubi secatur à linea χL, et erit YL dimidia ipsius YX. Rectang. autem sub YL et excessu ¾ YM supra YL, id est, rectang. KχS, majus est rectangulo KDS vel KTS, (quia punctum χ propius est medio lineae KS quàm punctum D vel T,⁵⁹⁾ ergo idem rectang. majus quoque octavâ parte quadrati MV. Ergo in lineâ GZ pars GZ major erit parte HZ^b60); igitur quum FG sit perpendi-

57) La ‘Conclusio 4’ nous fait connaître que le parallélipipède pourra prendre la position ③ toutes les fois que le point représentatif (ε, η) se trouve dans l'intérieur de la région LMN du Tableau de l'Avertissement. On remarquera que l'angle que l'axe fera avec le plan horizontal n'est pas indiqué. En réalité, comme nous l'avons montré dans la note 10 de l'Avertissement, la détermination de cet angle mènerait à la résolution d'une équation biquadratique.
D'ailleurs les conditions nécessaires et sussisantes, contenues dans la ‘Conclusio 4’, pour que la position ③ soit possible peuvent être indiquées par les relations: .

58) ‘a per Theor. 4. lib. 1.’ [Huygens].

59) En effet, le point milieu de la ligne KS se trouve à égale distance de D et de T.

60) ‘b lemm. 3. h. lib.’ [Huygens].

[p. 144]

cularis ad GZ, et consequenter ad liquidi superficiem XK, in eandem superficiem non erit perpendicularis FH, quae jungit centrum grav. totius rectanguli cum centro grav. partis enatantis XYK; quare totum rectangulum inclinabit in quam partem inclinat linea FH^c61), descendetque angulus K infra liquidi superficiem. Ergo quidem angulus K non emerget.

Jam si dicatur emersurus angulus M, oportebit similiter ut sit priùs in ipsâ liquidi superficie, eàque sit Mξ.

Sit itaque φ centrum gravitatis trianguli MYξ, per quod agatur ζφγ parallela Mξ, in eàmque cadat perpendicularis Fγ. porrò jungatur Fφ, et per F ducatur RFP parallela YK; et denique sit OY ¾ YK, et IY dimidia ipsius Yξ.

Quia igitur rectang. KM, ut modò dictum fuit, est ad liquidum in gravitate, sicut rectang. χM ad KM; erit etiam trapezium demersum MξKV aequale rectangulo χM^d62), et consequenter trapezio XKVM: quare et triangulum MYξ aequale erit triangulo XYK. Ergo ut KY ad YM, ita erit ξY ad YX; et ita quoque IY ad YL sive Kχ: sed ita praeterea etiam est OY ad SK; et dividendo,⁶³⁾ ita quoque OI ad Sχ. Igitur quum KY major sit quam YM^e64), erit etiam IY major YL sive Kχ, et OI major Sχ; ergo rectangulum YIO majus rectangulo KχS; hoc autem majus est rectangulo KDS vel KTS, sive octavâ parte quadrati MV; (quia videlicet punctum χ propius est medio lineae KS quam puncta D et T,) haec autem octava pars major est octavâ parte quadrati KV, quia MV major est quam KV; Rectangulum itaque YIO multo majus est octavâ parte quadrati KV vel YM.

quare in lineâ ζγ erit pars ζγ intercepta à perpendiculari Fγ et axe PR, major parte ζφ^f65) interceptâ ab eodem axe PR et centro grav. trianguli MYξ. Ergo Fφ non erit perpendicularis ad ζγ, ideoque nec ad liquidi superficiem Mξ; quare totum rectangulum inclinabit eò quò inclinat linea Fφ^g66), descendetque angulus M infra liquidi superficiem. Igitur neque angulus M emergere poterit.

Quapropter necessariò tres anguli K, V et M demersi manebunt, quod erat demonstrandum.

61) ‘c Theor. 1. h. lib.’ [Huygens].

62) ‘d per Theor. 4. lib. 1.’ [Huygens].

63) Consultez, sur cette expression, la note 10 du ‘liber i’, p. 97 du Tome présent.

64) ‘e per constr.’ [Huygens] Comparez le début du ‘Theorema 6’.

65) ‘f lemm. 3. h. lib.’ [Huygens].

66) ‘g Theor. 1. h. lib.’ [Huygens].

[p. 145]

5.

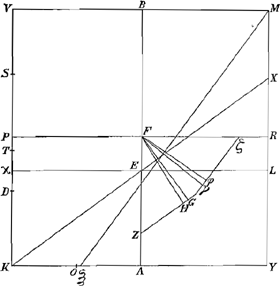Fig. 18.

Invertatur figura praecedens, habeatque rectangulum KM ad liquidum in gravitate proportionem quam χK ad KV, quae major sit eâ quàm DK, minor vero eâ, quam TK habet ad KV; liquido supernatans, ponatur ita ut tres anguli K, V et M enatent supra liquidi superficiem: dico nullum eorum demergi posse.⁶⁷⁾

Hujus eadem quae praecedentis conclusionis est demonstratio, nisi quòd triangula quae illìc enatabant hìc sint demersa.

67) La ‘Conclusio 5’ se rapporte à la position ③′ mentionnée dans l'‘Avertissement’. Elle apprend que cette position pourra se présenter toutes les fois que le point représentatif tombe à l'intérieur de la division HKL du Tableau, c'est-à-dire lorsqu'on a .

Theorema [7].⁶⁸⁾
Quadratum supernatans liquido, aliquando rectum consistet; aliquando inclinatum ita ut neutrum oppositorum laterum liquidi superficiem contingat; aliquando ut unus angulorum sit in liquidi superficie, idque duobus casibus; nonnunquam etiam ut duo anguli sint in liquidi superficie, idque uno casu; aliquando ita ut tres anguli sint demersi; aliquando denique ut tantum demergatur unus: pro diversâ proportione quam quadratum ad liquidum habebit in gravitate.⁶⁹⁾

68) Le manuscrit a ‘Theorema 6’, mais nous avons remplaçé le 6 par le 7 pour éviter un double emploi.

69) Le théorème nous montre que, si le point représentatif tombe sur la ligne BC du Tableau de l'Avertissement, comme cela a lieu nécessairement quand la section verticale est un carré, alors les positions ①, ⑤; ②, ④; ③ et ③′, dont les quatre premières sont devenues identiques deux à deux, peuvent toutes se présenter selon que le point est situé dans l'une ou l'autre des divisions dans lequelles cette ligne est partagée par les points B, E, H, L, N, G, C. Voir, pour plus de détails, les ‘Conclusiones’ et en particulier, pour une division essentielle qui n'a pas été aperçue par Huygens, la note 79.

[p. 146]

Conclusio 1.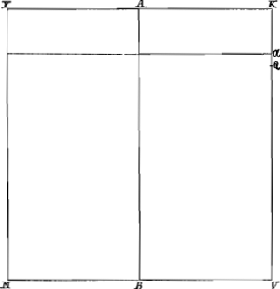

Fig. 19.

Esto quadratum KM, cujus axis AB: et latere KV diviso in Q, ita ut rectangulum KQV aequetur sextae parti quadrati KY vel MV; habeat ad liquidum in gravitate proportionem quam αV ad KV, quae major sit eâ quam QV habet ad KV, vel habeat eam quam αK ad KV, quae minor sit eâ quam QK habet ad KV: dico necessariò rectum consistere.⁷⁰⁾

Hoc enim Theoremate 3^o h. lib. demonstratum fuit de omnibus quae inclinare possunt rectangulis, quare et quadrato convenit.

70) La ‘Conclusio’ nous apprend que la position, dans laquelle les côtés du carré se trouvent respectivement dans les situations horizontales et verticales, sera stable toutes les fois que le point représentatif tombe sur l'une des lignes BE ou GC du Tableau, c'est-à-dire toutes les fois que la densité relative est plus petite que ou plus grande que

2.

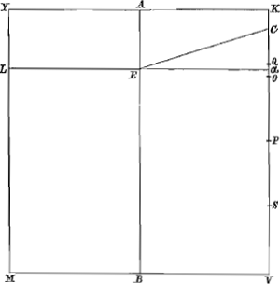Fig. 20.

Latere KV, praeterquam in Q, diviso in quatuor aequalia punctis O, P et S; si habeat quadratum ad liquidum in gravitate proportionem majorem subsesquitertiâ [¾], id est, majorem quàm OV ad KV, minorem verò quam QV ad KV; vel minorem subquadrupla [¼], id est, minorem quam OK ad KV, majorem vero quam QK ad KV, majorem vero quam QR ad KV; et liquido supernatans ponatur incli-

[p. 147]

natum, ita ut neutrum oppositorum laterum contingat liquidi superficiem; neque rectum restituetur neque inclinatum manebit, nisi cum axis AB cùm liquidi superficie faciet angulum aequalem angulo invento ut in Theor. 5^o.⁷¹⁾

Primò quia OV est ¾ lateris KV et OK ejusdem ¼, erit rectang. KOV 3/16 quadrati KV vel MV, ideoque majus quàm ⅙ ejusdem quadrati, id est, rectangulo KQV; unde patet punctum O propius esse medio lateris KV quàm punctum Q, ideoque quadratum KM ad liquidum in gravitate posse habere rationem, quae major sit eâ quam OV, minor autem eâ quam QV habet ad KV, vel quae minor sit eâ quam OK, major autem eâ quam QK habet ad KV.

Sumpto itaque puncto α ubivis inter Q et O, habeat quadratum ad liquidum in gravitate primùm rationem quam αV ad KV; et ductâ αL parallela YK, veniat ex intersectione E linea EC, ita ut spatii comprehensi Cα quadratum sit duplum excessus sesqualteri rectanguli AEB supra quadratum AK.⁷²⁾

dico quadratum KM, liquido supernatans et positum inclinatum, ita ut neutrum oppositorum laterum YK vel MV contingat liquidi superficiem, neque rectum restitutum iri, neque mansurum inclinatum, nisi cùm axis AB cum liquidi superficie faciet angulum aequalem angulo AEC vel ECα.

Primò enim quia quadratum ad liquidum in gravitate proportionem habet quam αV ad KV, quae minor est eâ quam QV, major verò eâ quam QK habet ad KV, non poterit quidem rectum restitui. ^a73)

deinde quia rectangulum KOS est ⅛ quadrati KV sive MV, erit rectang. KαS minus quàm ⅛ quadrati MV; unde sicuti in conclusione 3^a Theorematis praecedentis demonstrari poterit quadratum KM non eousque inclinari posse ut basis YK ullo modo contingat liquidi superficiem.

Ergo quadratum neque rectum restituetur, neque ita consistet ut alterutra basium contingat liquidi superficiem; quòd autem angulus, quem, consistente quadrato, axis AB faciet cum liquidi superficiem aequalis futurus sit angulo AEC vel ECα, demonstrari potest sicuti in Theorem. 5^o h. lib.

Quod si quadratum sit ad liquidum in gravitate ut αK ad KV, inversa intelligatur figura praecedens, et similis omnino erit demonstratio, nisi quod tum pars ea demersa erit quae in casu praecedenti enatabat.

71) La ‘Conclusio’ exprime que le carré prendra la position ②, identique ici avec la position ④, toutes les fois que le point représentatif tombera sur l'une des lignes EH ou NG du Tableau de l'Avertissement, c'est-à-dire, toutes les fois que la densité sera comprise entre les limites et ¼, ou bien entre les limites et ¾.

72) C'est la définition de l'angle AEC sous lequel le carré flottera. Elle nous donne: cotg² . Comparez la note 34.

73) ‘a per conv. theor. 3. h. lib.’ [Huygens].

[p. 148]

3.

Latere KV diviso, ut supra, in quatuor aequalia punctis O,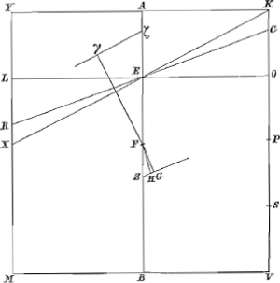

Fig. 21.

P et S; Si habeat quadratum ad liquidum in gravitate proportionem quam OV ad KV, id est, subsesquitertiam [¾]; vel quam OK ad KV, id est, subquadruplam [¼], et liquido supernatans ponatur inclinatum ita ut neutra basium oppositarum contingat liquidi superficiem; eousque ultro inclinabitur, donec unus angulorum sit in liquidi superficie.⁷⁴⁾

Primùm habeat quadratum KM ad liquidum in gravitate proportionem subsesquitertiam, id est, quam OV ad KV. dico si liquido supernatet et ponatur inclinatum ita ut liquidi superficies sit RC, ultro eousque inclinaturum, donec angulus K sit in liquidi superficie, eaque sit KX.

Constructio enim eadem sit quae in conclusione 2^a. Theor. praecedentis et eadem quoque erit demonstratio. Nimirum quia hic rectangulum sub YL et excessu ¾ YM supra YL, id est, rectang. KOS, aequale est octavae parti quadrati KV sive MV, incidet Fγ, quae perpendicularis est ad γζ, in ipsum centrum grav. trianguli XYK; quare quum superficies liquidi erit KX, quadratum KM ad neutram partem magis inclinabit, ideoque tum consistet, quod erat demonstrandum.

Si verò quadratum ad liquidum in gravitate sit ut OK ad KV, tum praecedens figura inversa intelligatur, et eadem rursus erit demonstratio, quae fuit conclusionis 2^ae. Theorematis praecedentis, nisi quod triangulum XYK quod modo enatabat, nunc demersum futurum sit.

74) La ‘Conclusio’ nous fait connaître sous quelles conditions le carré prendra une des positions intermédiaires entre les positions ③ ou ③′ et les positions ② et ④, dont les dernières sont identiques entre elles, c'-est-à-dire telle que l'un des sommets du carré se trouve dans le niveau du liquide. Le point représentatif se placera alors à l'un des points H ou N du Tableau de l'Avertissement.

[p. 149]

4.

Si quadratum ad liquidum in gravitate habeat proportionem subduplam, et liquido supernatans, ponatur inclinatum, ita ut neutrum oppositorum laterum contingat liquidi superficiem, eousque ultro inclinabitur donec duo anguli oppositi sint in liquidi superficie.⁷⁵⁾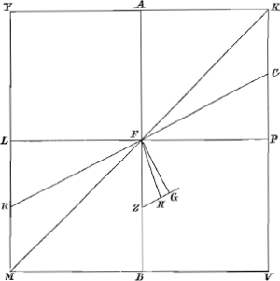

Fig. 22.

Habeat quadratum KM ad liquidum in gravitate proportionem subduplam, id est, quam PV ad KV; et liquido supernatans ponatur inclinatum, ut liquidi superficies sit RC: dico eousque ultro inclinatum iri, donec anguli oppositi K et M sint in liquidi superficie, atque ea sit KM.

ducatur enim PL parallela YK, et per H, centrum grav. trapezii RCVM, linea ZHG parallela RC, in eamque ex F centro quadrati cadat perpendicularis FG: denique jungatur FH.

Quia igitur trapezium RCVM aequale est dimidio quadrati KM^a76) id est rectangulo PM, sequitur superficiem liquidi RC transire per F centrum quadrati. Rectangulum autem AFB aequale est quadrato AF; ergo erit sesquialterum rectanguli AFB cum defectu ½ quadrati AF seu KP aequale quadrato AF sive AK. quare sesquialterum rectanguli AFB cum defectu ½ quadrati CP, majus erit quadrato AK: ideoque in linea ZG erit spatium ZG majus spatium ZH^b77) Ergo quum FG sit perpendicularis in ZG et consequenter in liquidi superficiem RC, in eandem

75) La ‘Conclusio’ se rapporte au cas spécial où la densité relative du parallélipipède est égal à ½. Elle démontre qu'alors la position dans laquelle deux sommets opposés du carré se trouvent au niveau du liquide, est une position stable. Inutile de dire que le point représentatif du Tableau de l'Avertissement se trouve alors en L.

76) ‘a Theor. 4. lib. 1.’ [Huygens].

77) ‘b lemm. 2 h. lib.’ [Huygens].

[p. 150]

non erit perpendicularis FH, quae jungit centr. grav. totius quadrati cum centro grav. partis mersae RCVM. Quamobrem totum quadratum inclinabit in quam partem inclinat linea FH ^c78), descendetque versùs K, et ascendet versùs M, idque donec anguli K et M sint in liquidi superficie, atque ea sit KM.

Et tum quidem manifestum est quadratum ampliùs inclinari non posse. nam si dicatur angulum K demersum iri, M verò emersum, simili omnino demonstratione evincetur, quadratum inclinatum iri retrorsum, donec ijdem anguli K et M sint denuo in liquidi superficie.

Si igitur quadratum subduplam proportionem habeat ad liquidum in gravitate &c. quod erat demonstr.

78) ‘c Theor. 1. h. lib.’ [Huygens].

5.

Diviso latere KV in quatuor aequalia punctis O, P et S, sumptoque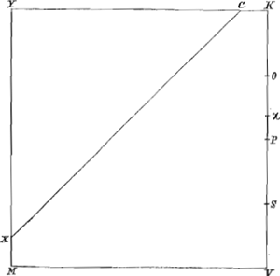

Fig. 23.

puncto χ ubivis inter O et P, habeat quadratum ad liquidum in gravitate proportionem quam χV ad KV, id est, majorem subduplâ, minorem autem subsesquitertiâ[¾]; et liquidi supernatans ponatur tribus angulis mersis K, V et M, ita ut superficies liquidi sit XC: dico nullum trium angulorum emergere posse supra liquidi superficiem.⁷⁹⁾

Hoc demonstrari poterit sicut conclusio 4^a Theorematis praecedentis. nam sicuti illìc singula rectangula KDS, KTS aequalia erunt octavae parti quadrati MV, ita hic rectangula KOS et KPS.

79) La ‘Conclusio’ indique que le carrè prendra la position ③ toutes les fois que le point représentatif est situé sur la ligne BC du Tableau de l'Avertissement entre les points L et N, c'est-à-dire toutes les fois que la densité relative du parallélipipède flottant tombe entre les limites ½ et ¾.
Or, quoique cette assertion soit correcte, il y avait lieu ici de distinguer encore entre les parties LQ et QN de la ligne LN. En effet, tant le point représentatif tombe dans la partie LQ, le carré se placera de telle manière que ses diagonales sont respectivement dans la situation horizontale et verticale. Dans le cas contraire, où le point tombe entre Q et N, les diagonales prendront une situation inclinée.
Et cette distinction n'aurait pu échapper à Huygens, si l'idée lui était venue comme plus tard à Euler (voir les pages 110-113 du Tome I de l'ouvrage cité dans la note 18, p. 126), de rechercher entre quelles limites de la densité ε, la position avec les diagonales dans la situation horizontale et verticale était une position stable. Il aurait trouvé alors pour ces limites les valeurs 9/32 et 23/32 correspondant aux points P et Q du Tableau.
Ajoutons encore qu'une solution complète du cas du carré avec discussion de la stabilité pour toutes les positions d'équilibre a été donnée en 1849 par J. Badon Ghijben aux pages 17-24 de l'article: ‘Over de Stabiliteit des evenwigts, bij drijvende ligchamen’, Tijdschrift voor de wis- en natuurkundige wetenschappen, uitgegeven door de eerste klasse van het Koninklijk-Nederlandsche Instituut. T. 3, 1850, Amsterdam.

6.

[p. 151]

Si quadratum ad liquidum in gravitate proportionem habeat majorem subquadruplâ, minorem verò subduplâ, et liquido

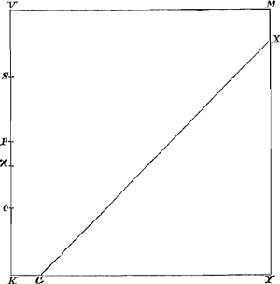Fig. 24.

supernatans ponatur ita ut unus tantùm angulus demersus sit, reliqui verò enatent supra 1iquidi superficiem, nullus eorum demergi poterit.⁸⁰⁾

Invertatur figura praecedens, habeatque quadratum ad liquidum in gravitate proportionem quam χK ad KV; et liquido supernatans demerso tantùm angulo Y, enatantibus verò K, V et M: dico nullum eorum demergi posse.

Hoc autem demonstratur sicuti conclusio 5^a Theorematis praecedentis.

80) La ‘Conclusio’ se rapporte à la position ③′ qui pourra se présenter toutes les fois que le point représentatif tombe sur la division HL de la ligne BC du Tableau. Ici il y a lieu de distinguer entre la partie PL, où le point représentatif indiquera une position du carré aux diagonales verticale et horizontale, et la partie PH à laquelle correspondent des positions dans lesquelles les diagonales sont inclinées.

[p. 152]

Theorema [8].⁸¹⁾
Rectangulum cujus basis minor est latere, liquido supernatans demersâ base et positum inclinatum, ita ut neutra basium contingat liquidi superficiem; aliquando rectum restituetur; aliquando inclinatum manebit, ita ut neutra basium contingat liquidi superficiem. Interdum eousque inclinabitur donec angulorum unus sit in liquidi superficie; ut plurimùm denique ulteriùs adhuc inclinabitur: Pro diversâ proportion quam ad liquidum habebit in gravitate.⁸²⁾

Conclusio 1.

Fig. 25.

Esto rectang. KM cujus latus KV majus sit base MV; Et latere KV diviso in Q, ita ut rectang. KQV aequetur sextae parti quadrati MV vel YK, habeat rectang. ad liquidum in gravitate proportionem majorem quam QV habet ad KV, vel minorem quam QK habet ad KV. dico, si liquido supernatans, ponatur inclinatum, ita ut neutra basium contingat liquidi superficiem, rectum restitutum iri.⁸³⁾

Hoc enim Theor.^e 3^o h. lib. demonstratum fuit de omnibus rectangulis quae inclinare possunt.

81) Le manuscrit a ‘Theorema 7.’ Le changement a été rendu nécessaire par celui indiqué dans la note 68.

82) Le théorème se rapporte à toutes les formes possibles de la section verticale rectangulaire du parallélipipède flottant, à l'exception seulement de la forme carrée. Il y est question surtout des positions ④ et ⑤, indiquées dans l'Avertissement, lesquelles n'ont pas encore été traitées expressément. Voir, pour les détails, les ‘Conclusiones’ qui suivent. A propos de la dernière ‘Conclusio’ nous indiquerons le lieu précis où les lignes de démarcation OP et QA du Tableau, desquelles l'existence est ignorée dans les recherches de Huygens, se présentent logiquement, si l'on poursuit la marche de ses recherches; voir les notes 92 et 93.

83) La ‘Conclusio’ nous apprend que la position ⑤ sera une position stable, tant que le point réprésentatif tombera dans l'une des divisions BEO ou CGA du Tableau de l'Avertissement. Comparez le dernier alinéa de la note 23.

[p. 153]

2.

Latere KV, diviso sicut supra in Q, et praeterea in S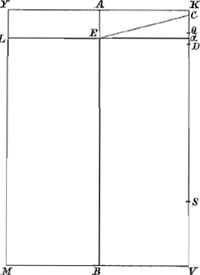

Fig. 26.

et D, ita ut KS quidem sit ¾ KV, rectang. verò KDS (sumpto puncto D magis versùs K quàm versùs S) aequale octavae parti quadrati basis MV; si habeat rectangulum ad liquidum in gravitate proportionem majorem quàm DV ad KV, minorem verò quam QV ad KV; vel majorem quidem quam QK ad KV, minorem verò quàm DK ad KV, et liquido supernatans ponatur inclinatum, ita ut neutra basium contingat liquidi superficiem, neque rectum restituetur, neque inclinatum manebit, nisi cùm axis AB cum liquidi superficie faciet angulnm aequalem angulo invento ut in Theor. 5^o h. lib.⁸⁴⁾

Quòd autem hi casus quandoque locum habere possint, sic ostenditur. Quum rectang. VQK sit ad SQK, ut VQ ad SQ, et VQ ad SQ majorem habeat rationem quam VK ad SK, id est majorem quam 4 ad 3, etiam rectang. VQK ad SQK majorem habebit rationem quam 4 ad 3 sive quàm ⅙ ad ⅛ ergo quum rectang. VQK sit ⅙ quadrati MV, erit rectang. SQK minus quàm ⅛ ejusdem quadrati MV: Ergo minus quoque rectangulo SDK; unde sequitur punctum D propiùs esse medio lineae KS quam punctum Q. Quamobrem poterit quidem rectang. ad liquidum in gravitate habere proportionem quae major sit eâ, quam DV, minor veró eâ, quam QV habet ad KV; vel quae major quidem sit eâ quam QK, minor autem eâ, quam DK habet ad KV.

84) La ‘Conclusio’ démontre que la position ④ pourra se présenter toutes les fois que le point représentatif (ε, η) se trouve à l'intérieur de l'une des divisions NGA ou EHO du Tableau de l'Avertissement. En effet, les équations et des courbes NA et HO se déduisent de la même manière des données de la ‘Conclusio’, lesquelles se rapportent au point D, que les équations des courbes LMN et HKL des données de la ‘Conclusio 2’ du ‘Theorema 6’; voir la note 43, p. 138. On doit seulement observer que les lettres a et b ont changé de rôle, puisqu'on a maintenant a = KV, b = MV, de manière que, dans les équations de la note 43, on doit remplacer η par η^-1.

[p. 154]

Sumpto itaque puncto α ubivis inter Q et D, habeat rectang. ad liquidum in gravitate primùm rationem quam αV habet ad KV; et ductâ αL parallelâ KY, veniat ex intersectione E linea EC, ita ut spatii comprehensi αC quadratum sit duplum excessus sesquialteri rectanguli AEB supra quadratum AK.⁸⁵⁾

dico rectang. KM liquido supernatans et positum inclinatum, ita ut basis YK non contingat liquidi superficiem, neque rectum restitutum iri, neque inclinatum mansurum, nisi cùm axis AB cum liquidi superficie faciet angulum aequalem angulo AEC vel ECα.

Demonstratur autem hoc eodem modo quo Conclusio 3^a Theorem. 6ⁱ. Quòd si rectang. ad liquidum in gravitate habeat proportionem quam αK habet ad KV, tum inversa intelligatur figura praecedens et rursus similis erit demonstratio.

85) C'est la définition de l'angle AEC, qui n'est autre que l'angle que l'axe du parallélipipède flottant fera dans la position ④ avec le niveau du liquide. On trouvera pour sa valeur cotg². , où . Comparez la note 34, p. 134.

3.

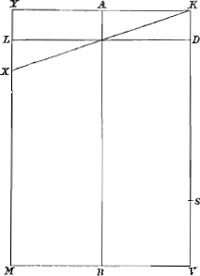Fig. 27.

Latere KV diviso sicut Concl. praecedenti in S et D, nempe ut KS sit ¾ lateris KV, rectang. verò KDS aequale ⅛ quadrati MV; habeat rectang. ad liquidum in gravitate proportionem quam DV habet ad KV, vel quam DK ad KV; et liquido supernatans ponatur inclinatum, ita ut neutra basium contingat liquidi superficiem. dico eousque inclinatum iri donec unus angulorum sit in liquidi superficie.⁸⁶⁾

Hoc autem eodem modo demonstratur quo Conclusio 2^a Theorem. 6ⁱ.

86) Dans cette ‘Conclusio’ il s'agit des cas, où le point représentatif tombera justement sur l'une des lignes de démarcation NA ou HO du Tableau de l'Avertissement. Elle nous apprend qu' alors le parallélipipède flottant prendra l'une des positions intermédiaires entre les positions ③ et ④ (pour NA), ou ③′ et ④ (pour HO), c'est-à-dire telle que l'un des sommets du rectangle se trouve dans le niveau du liquide. Consultez encore la dernière phrase de la note 43.

[p. 155]

4.

Diviso rursus latere KV in S et D; ita ut KS sint ¾ KV, rectang.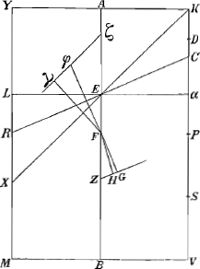

Fig. 28.

verò KDS aequale ⅛ quadrati MV; Si habeat rectang. ad liquidum in gravitate proportionem minorem quidem eâ, quam DV, majorem verò eâ, quam DK habet ad KV, et liquido supernatans ponatur inclinatum, ita ut neutra basium contingat liquidi superficiem, ulteriùs adhuc inclinabitur, quàm ut unus angulorum sit in liquidi superficie.⁸⁷⁾

Dividatur latus KV bifariam in P, et quum manifestum sit rectangulum ad liquidum in gravitate habiturum proportionem majorem vel non majorem subduplâ, habeat primò majorem subduplâ, nempe eam, quam αV habet ad KV, (sumpto puncto α intra P et D,) et liquido supernatans, positum sit inclinatum, ita ut liquidi superficies sit RC. dico ulteriùs inclinatum iri, quam ut angulus K sit in liquidi superficie. Sit enim αL parall. KY, et per intersectionem E ducatur ex angulo K linea KEX. Porrò sit H centr. gravitatis trapezii RCVM, per quod agatur recta ZHG parall. RC, in eamque ex F, centro rectanguli KM, cadat perpendicularis FG, et jungatur FH. Item sit φ centr. grav. trianguli XYK, et per ipsum agatur ζφγ parallela KX, in eamque cadat perpend. Fγ; et denique jungatur Fφ.

Quoniam igitur rectangulum KM est ad liquidum in gravitate ut αV ad KV, sive ut rectang. αM ad KM, atque ita etiam trapezium mersum RCVM ad rectang. KM^a88), sequitur idem trapezium RCVM rectangulo αM aequale esse, ac proinde

87) La ‘Conclusio’ démontre que, tant que le point représentatif tombera dans la division OHNAO du Tableau de l'Avertissement, le parallélipipède flottant ne pourra jamais rester dans la position ④, indiquée dans l'Avertissement. S'il est mis dans une telle position, l'axe AB, c'est-à-dire le grand axe de la section verticale, tendra à s'éloigner de plus en plus de la position verticale, tout au moins jusqu' à ce qu' une position ③ ou ③′ soit atteinte. La ‘Conclusio’, toutefois, ne nous apprend pas quelle sera la position d'équilibre à laquelle le parallélipipède finira par arriver, si l'on continue de le tourner dans ce même sens. Voir, à ce propos, les notes 92 et 93.

88) ‘a Theor. 4. lib. 1.’ [Huygens].

[p. 156]

lineas RC et αL in eodem puncto E secare axem AB. Porrò quum KP sit ½ KV, et PS ¼ KV: erit rectang. KPS aequale ⅛ qu. KV; latus autem KV per constr. majus est base MV, ergo ⅛ quadr. KV, sive rectang. KPS majus quoque quam ⅛ quadr. MV, sive quàm rectang. KDS: Ergo punctum P propius est medio lineae KS quàm punctum D, et quum punctum α sit inter puncta P et D, erit hoc quoque propius medio lineae KS quam punctum D. Rectangulum igitur KαS, sive rectang. sub YL et sub excessu ¾ YM supra YL, majus est rectangulo KDS, sive octavâ parte quadrati MV: Ergo in lineâ γζ pars γζ major φζ^b89), unde sequitur sesquialterum rectanguli AEB cum defectu ½ qu. LX, majus esse quadr.^o AY sive AK^c90); Ergo quum Cα sit minor quam LX sive αK, erit 3/2 rectanguli AEB cum defectu ½ quadr. Cα, multo majus quadrato AK: quare in lineâ ZG erit pars ZG major parte ZH ^e91). quum igitur FG sit perpend. ad ZG, et consequenter ad liquidi superf. RC, ad eandem superficiem perpendicularis non erit FH, quae jungit centr. grav. rectanguli KM cum centro grav. partis mersae RCVM, ideoque totum rectangulum inclinabit in quam partem inclinat linea FH, adeo ut descensurus sit angulus K; idque donec pervenerit usque in liquidi superficiem, eaque sit KX: sed tum quoque ulterius inclinabitur; nam quum jam ostensum fuerit in linea ζγ partem γζ majorem esse parte φζ, et Fγ sit perpendicularis ad ζγ, ideoque ad liquidi superficiem quae tum erit KX; in eandem superficiem non erit perpendicularis Fφ quae jungit centrum gravitatis rectanguli KM cum centro trianguli enatantis XYK; quamobrem totum rectangulum inclinabit in quam partem inclinat Fφ, et mergetur angulus K; quod erat demonstr.⁹²⁾

89) ‘b lemm. 3. h. lib.’ [Huygens].

90) ‘c per conv. lemm. 2. h. lib.’ [Huygens].

91) ‘e. lemm. 2. h. lib.’ [Huygens]. Une annotation ‘d’ manque dans le texte comme en marge.

92) En effet, la démonstration est parfaite et nous fait connaître que le parallélipipède, parvenu à la position dans laquelle le sommet K de la section normale touche au niveau du liquide, tendra à continuer sa rotation. Il passera alors à la position ③; mais il est clair qu'ensuite plusieurs cas différents peuvent se présenter. En premier lieu, il se pourra qu'une (ou plus d'une) des positions ③ par lesquelles le parallélipipède passera en poursuivant sa rotation, soit une position d'équilibre stable dans laquelle il peut s'arrêter. C'est là ce qui en effet arrivera toutes les fois que le point représentatif (ε, η) tombe à l'intérieur de la division LMZANL du Tableau de l'Avertissement.
En second lieu, il se peut que le parallélipipède en parcourant les positions ③ ne rencontre aucune position d'équilibre stable. Alors il passera aux positions ② et il est possible qu'il y trouve une position dans laquelle il pourra s'arrêter. Ce sera le cas tant que le point représentatif tombe à l'intérieur de la division LMZDFL.
En troisième et dernier lieu, il est possible que le parallélipipède ne rencontre aucune position d'équilibre stable avant d'avoir atteint la position ①. C'est ce qui arrive si le point représentatif se trouve à l'intérieur de la division TFDAT.
Pour connaître les conditions sous lesquelles ces divers cas se présenteront, on doit étudier les positions d'équilibre qui se trouvent parmi les positions ③. Or, la détermination de ces positions dépend de la résolution d'une équation du quatrième degré, c'est-à-dire, elle constitue ce qu'on appelait à l'époque de Huygens un problème solide. Pour cette raison ou pour une antre, Huygens n'a pas entamé ce problème et par suite aucun de ses résultats n'est en rapport avec la ligne de démarcation QA relative au problème mentionné. Voir encore le dernier alinéa de la page 88 de l'‘Avertissement.’

[p. 157]

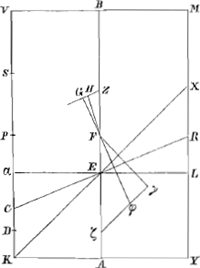Fig. 29

Quod si rectangulum ad liquidum in gravitate proportionem habeat minorem subdupla, tum inversa intelligatur praecedens figura, et eadem quoque erit demonstratio, nisi quod hìc partes eae mersae erunt quae istic enatabant, et contra; quodque hic ostenditur angulum K emergere debere suprà liquidi superficiem.⁹³⁾

Manifestum autem est, siquidem quadratum lateris KV ad quadratum basis MV non majorem habeat rationem quam novem ad octo, tum Conclusiones duas ultimas Theorematis 6.i⁹⁴⁾ hic quoque posse habere locum, si accedat debita proportio rectanguli ad liquidum in gravitate.

93) Ici des considérations analogues à celles de la note précédente, sont valables. On n'a qu'à changer ③ en ③′ et à remplacer les différentes divisions du tableau par celles qui leur sont symmétriques par rapport à l'axe de symmétrie du tableau. De même la ligne QA par PO.

94) Il s agit des ‘Conclusiones 4 et 5’ expliquées dans les notes 57 et 67 et qui se rapportent aux positions ③ et ③′ que le parallélipipède flottant pourra prendre toutes les fois que le point représentatif tombe à l'intérieur des divisions respectives LMN et HKL.