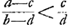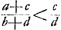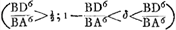|
| |
| |
| |
De iis quae liquido supernatant.
Libri 3.
Ao. 1650.Ga naar voetnoot1)
[Liber I.]
I.
Si Corpus sponte, seu gravitate suâ moveri incipiat, deorsum moveri; id est ut centrum gravitatis propius fiat plano horizonti parallelo.
| |
II.
Si Corpora plura gravitati suâ moveri incipiant, ea deorsum moveri; id est, ut centrum gravitatis ex omnibus compositae propius fiat plano horizonti parallelo.
| |
| |
| |
Si liquido corpus solidum immergatur, tantam liquidi molem supra propriam superficiem ascendere, quanta est moles corporis infra eandum superficiem depressi.
| |
Theorema 1.
Liquidum quiescit cùm supersicies ejus plana est, et horizonti parallela.Ga naar voetnoot4)
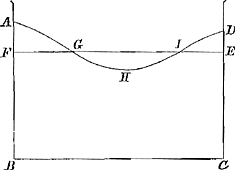
Sit vas ABCD continens liquidum cujus superficies FE plana sit et parallela horizonti; dico illud quiescere.
Si enim non quiescit, moveatur itaque, ut superficies ejus fiat AGHID.
Quia igitur spatia AGHIDCB, et FECB sunt aequalia, dempto communi spatio FGHIECB, erit spatium GHI aequale duobus FAG et EDI. Porro quia spatium GHI totum est infra planum FE, sequitur centrum gravita- | |
| |
tis liquidi quod eo continebatur fuisse infra planum FE; similiter quia spatia FAG, EDI, sunt tota supra planum FE, sequitur centrum grav. liquidi quod iis continetur esse supra idem planum. Igitur centrum gravitatis liquidi quod continebatur spatio GHI, altius factum est postquam idem liquidum ascendit in spatia FAG, EDI; liquidi autem quod continetur spatio FGHIECB centrum grav. codem manet loco. Ergo centrum gravitatis omnis liquidi altius est cum continetur spatio AGHIDCB, quam cum terminatur superficie FE. Sed quia liquidum sponte motum est, oportet ut centrum suae gravitatis eo motu descenderitaGa naar voetnoot6), igitur simul et ascendit et descendit, quod est absurdum.
| |
Theorema 2.
Corpus solidum, quod liquido suae magnitudinis aequiponderat, demissum in liquidum, ita ut totum demersum sit, contingatque tantummodo liquidi superficiem, ita ut positum est manebit.Ga naar voetnoot7)
Sit vas ADCB continens liquidum, in quod demersum sit corpus ERF, aequiponderans
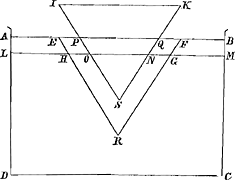
Fig. 2.
liquido suae magnitudinis, ita ut totum demersum sit, contingatque tantummodo liquidi superficiem AB secundum EF: dico ita positum quiescere.
Si enim non quiescit, ascenderit primum usque in ISK, ideoque liquidum descenderit ex spatiis AEHL, FBMG. ad replendum spatium HOSNGR, quod necessario prioribus duobus aequale est.
Quia igitur spatium LMCD utrâque corporis positione plenum est materia ejusdem gravitatis, sequitur etiam eodem loco habiturum centrum suae gravitatis; at reliqua gravitas quae priori positione continetur spatio ABML, minus altum habet centrum suae gravitatis quam positione secunda cum continetur spatio IONK, quia pars PONQ communis est, et partis IPQK centrum grav. supra planum AB, partium vero APOL, BQNM infra idem planum, Igitur centrum gravitatis universae tam liquidi quam corporis
| |
| |
impositi posteriori positione altius est quam priori, quod est contra hypoth. 2dam, quum statuatur corpus ultro motum esse. Non ascendet igitur corpus ERF; Sed neque descendet, nam si recesserit a superficie liquidi; continuò is locus quo excessit replebitur liquido, unde fiet ut semper totum spatium ABCD plenum sit materia ejusdem gravitatis, ideoque habeat centrum gravitatis eodem loco. Absurdum igitur quoque est corpus ERF amplius descendere, Ergo ut positum est manebit, quod erat demonstrandum.
| |
Theorema 3.
Corpus solidum levius liquido ita ei supernatat, ut tanta moles liquidi, quanta est partis mersae, toti corpori aequiponderet.Ga naar voetnoot8)
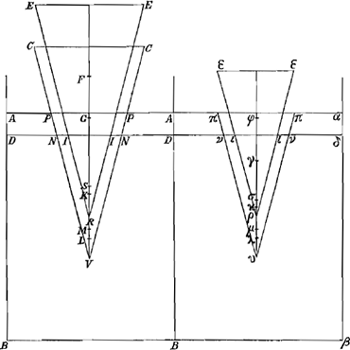
Fig. 3.
Sit vas ABBA continens liquidum, cui impositum sit corpus CVC, ita ut liquidum tantae molis, quanta est partis mersae PVP, toti corpori aequiponderet; dico corpus CVC neque emersurum magis, neque ulteriùs demersum iri.
Si enim fieri potest emergat primum, et ponatur sublatum usque in ERE. Sit G centrum gravitatis corporis CVC, et F ejusdem quum sustulit sese in ERE; sit etiam M centrum grav. omnis liquidi primâ corporis positione, nimirum liquidi APVPABB; L vero positione secundâ, nimirum liquidi DIRIDBB; constat autem M fore supra L, nam
| |
| |
utrâque positione commune quidem est liquidum DNVNDBB, at reliqua liquidi pars quae primò continebatur spatiis duobus APND, quae sunt supra planum DD, postea descendit ad replendum spatium NIRINV, quod est infra planum DD. divisa porro sit linea GM (quae interjacet centra grav. corporis, et omnis liquidi, primâ positione) in K, ita ut MK sit ad KG, sicut gravitas corporis ad gravitatem liquidi, eritque K centrum gravitatis universae primâ corporis positione. Item FL divisa sit in S, secundum proportionem eandem eritque S centrum grav. universae positione corporis secunda. Si igitur punctum S puncto K altius esse demonstratum fuerit, sequetur absurdum esse, corpus CVC sponte suâ motum fuisse, nam S deberet esse infra KaGa naar voetnoot9) Illud autem sic demonstrabitur. Sit juxta positum vas alterum ABβα, priori simile et aequale, eâdem positum altitudine; liquidi etiam contineat tantundem cujus superficies sit Aα, nempe dum ei immersum est corpus πυπ, quod figuram et magnitudinem habeat partis mersae PVP, gravitatem vero quam liquidum suae molis, id est gravitatem totius corporis CVC; et centrum gravitatis γ. Jam idem corpus è liquido extrahatur usque in ερε, in quantum sublatum ponebatur corpus CVC, ita ut ρ sit eâ altitudine quâ R; sitque φ centrum grav. corporis positi in ερε. et manifestum est distantiam γφ aequalem esse GF. praeterea quoque manifestum est priori positione corporis πυπ, centrum gravitatis omnis liquidi fuisse in
μ altitudinis M, posteriori vero esse in λ altitudinis L. denique divisa sit μγ in ϰ, ita ut μϰ sit ad ϰγ, sicut gravitas corporis πυπ ad gravitatem omnis liquidi, et λφ in σ secundum proportionem eandem, eritque ϰ centrum gravitatis universae posito corpore in πυπ, et σ sublato eodem in ερε.
Quia igitur patet ex Theorematis praecedentis demonstratione, quod corpore πυπ sublato in ερε, centrum gravitatis universae altius sit quam fuerit antea, sequitur hic centrum grav. σ altius esse quam ϰ; Est autem per constr. λσ ad σφ ut μφ ad ϰγ, igitur λϰ ad ϰφ minorem habet rationem quam μϰ ad ϰγ; igitur et dividendo λμ ad γφ minorem habet rationem, quam μϰ ad ϰγ,Ga naar voetnoot10) sive quam MK ad KG, hanc enim manifestum est esse eandem.
ergo quum λμ, LM, et γφ, GF sint aequales, habebit LM ad GF rationem minorem quam MK ad KG, et componendo LK ad KF minorem quam MK ad KGGa naar voetnoot11),
| |
| |
sive quam LS ad SF; unde sequitur punctum S esse supra K; quare absurdum est dicere corpus CVC ascendisse usque in ERE.
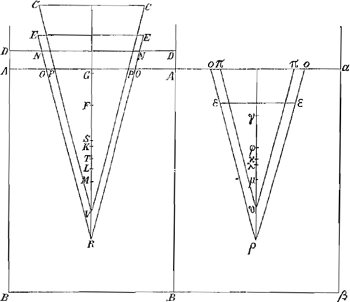
Fig. 4.
Jam corpus CVC, si fieri potest, amplius demergatur usque in ERE,Ga naar voetnoot12) ideoque liquidum ex spatio OPVPOR ascenderit in spatia DNOA. Sit rursus G centrum gravitatis corporis CVC; F verò ejusdem cum est in ERE. Sit etiam M centrum gravitatis omnis liquidi primâ positione corporis, nimirum liquidi APV PABB, T verò liquidi omnis DNRNDBB: divisaque sit GM (quae interjacet centra gravitatis corporis et liquidi,) in K, ita ut MK sit ad KG, sicut gravitas corporis ad gravitatem omnis liquidi, eritque K centrum gravitatis universae posito corpore in CVC. Item TF divisa sit secundum proportionem eandem, in S, eritque S centrum gravitatis universae posito corpore in ERE. Si itaque demonstratum fuerit punctum S puncto K altius esse, sequetur absurdum esse, corpus CVC sponte sua motum fuisse, nam S deberet esse infra KbGa naar voetnoot13). Illud autem sic demonstrabitur.
Ponatur ut suprà alterum vas ABβα, liquidi continens tantundem ac vas ABBA, cujus liquidi superficies sit Aα, dum ei immersum est corpus πυπ, quod figurâ quidem magnitudine et dispositione idem sit cum parte mersâ PVP, gravitate verò aequale liquido suae molis, ut nempe aequet gravitatem totius corporis CVC. dicti corporis πυπ centrum gravitatis ut suprà sit γ, et μ liquidi AπυπαβB. deinde idem corpus deprimatur usque in ερε, in quantum descendit corpus CVC, ita ut ρ sit eâ altitudine quâ R; atque hâc ejus positione, ipsius quidem centrum gravitatis sit φ, liquidi vero circumfluentis centrum grav. λ. Manifestum autem est, quia vas ABβα utrâque corporis positione plenum est materia ejusdem gravitatis, cen- | |
| |
trum universae gravitatis utrâque positione idem esse; unde si ϰ fuerit centrum gravitatis universae, erit tam μϰ ad ϰγ quàm λϰ ad ϰφ sicut gravitas corporis ad gravitatem omnis liquidi. Jam porrò sumatur ex M, ML aequalis ipsi μλ, eritque L infra T quod est centrum gravitatis liquidi DNRNDBB; nam quia liquidi contenti spatio AOROABB centrum grav. est ejusdem altitudinis atque centrum grav. liquidi similis AοροαβB, reliqui verò liquidi contenti spatiis DNOA, centrum grav. altius quam reliqui liquidi contenti spatio
οοεε, sequitur centrum gravitatis omnis liquidi DNRNDBB quod est T, altiùs esse centro grav. omnis liquidi circumfusi corpori ερε quod est λ, ideoque T etiam supra L, nam L positum fuit ea altitudine quâ λ. Quum igitur sit λϰ ad ϰφ, sicut μϰ ad ϰγ, erit etiam dividendo λυ ad φγ, sicut μϰ ad ϰγ, sive ut MK ad KG, eadem enim est proportio. et quia λμ ipsi LM, et φγ ipsi FG sunt aequales, erit quoque LM ad FG, ut MK ad KG, et dividendo LK ad KF, ut MK ad KG, five ut TS ad SF; quare cum T sit supra L, erit etiam S supra K. Igitur absurdum quoque est dicere corpus CVC ulterius demersum fuisse. Restat igitur ut neque magis emergere possit neque ulterius demergi, quod erat demonstrandum.Ga naar voetnoot14)
| |
| |
| |
Theorema 4.
Corpus solidum ita liquido supernatat ut pars mersa ad totum eam habeat rationem, quam corpus ad liquidum in gravitate.
Sit Corpus AB liquido supernatans cujus superficies CD; dico partem mersam
| |
| |
B ad corpus AB eam habere rationem, quam idem corpus ad liquidum in gravitate
Fig. 5.
id est, quam habet gravitas corporis ad gravitatem liquidi suae molis. Liquidum namque tantae molis quanta est partis B aequiponderat corpori AB aGa naar voetnoot15), atqui pondus liquidi magnitudinis B est ad pondus liquidi magnitudinis totius corporis, sicut pars B ad totum corpus AB, ergo quod aequiponderat corpori AB, sive gravitas corporis AB est ad gravitatem liquidi tantae molis quanta est corporis AB, ut magnitudo B ad magnitudinem totius corporis AB; quod erat ostendendum.
| |
| |
| |
Theorema 5.
Si corpus solidum liquido supernatans inclinetur ultro et alium situm acquirat, tum punctum in medio positum lineae, quae conjungit centra gravitatis, corporis totius in posteriori situ et partis mersae in priori, inferius est puncto quod item est medium lineae alterius, quae jungit centra gravitatis totius corporis in priori situ et partis mersae in posteriori.
Sit vas LXMV, et superficies liquidi eo contenti LV, supernatante ei corpore
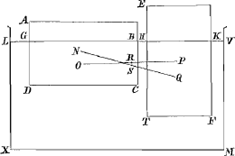
Fig. 6.
EF, quod ponatur ultro inclinari et situm acquirere diversum, ita ut jam contineatur spatio AC. dico punctum S, in medio linea NQ, quae jungit centrum gravitatis corporis in posteriori situ, cum centro partis mersae in priori, inferius esse puncto R, quod est in medio lineae OP, quae jungit centrum gravitatis corporis in priori situ cum centro gravitatis partis mersae situ posteriori.
Intelligatur enim corpus EF nondum inclinatum esse, atque idea spatium DGBC adhuc liquido plenum, quod tamen ipsum concipiatur ut distinctum à reliquo liquido. Ergo quia liquidum quod continetur spatio DGBC aequiponderat corpori ACaGa naar voetnoot16) sive EF, erit utriusque commune centrum gravitatis in R, medio lineae OP quae eorum centra gravitatis conjungit. Jam deinde intelligatur corpus in posteriori situ in AC, et excessisse e priore loco: et quia pars mersa DGBC exactè aequalis est parti THKF, ideo quantum liquidi illâ continebatur, jam continetur spatio HKTF; quod liquidum, quia aequiponderat corpori AC erit utriusque gravitatis centrum commune in S, medio lineae, quae eorum centra gravitatis conjungit. quum autem EF corpus ultro motum fuerit, debet centrum universae gravitatis, quae ex ipso et ex omni liquido componitur posteriori corporis situ inferius esse quam fuit dum corpus adhuc erat in EF. unde quum utroque situ centrum gravitatis reliqui liquidi XLGDCBHTFKVM maneat eodem loco, sequitur centrum ejus gravitatis quae cum illo universam gravitatem constituit, posteriori situ cum est in S, inferius esse debere quam priori corporis situ cum est in R. quod erat demonstrandum.
| |
| |
| |
Theorema 6.
Si Corpus solidum liquido supernatans ultrò inclinetur et alium situm acquirat; altitudo centri gravitatis totius corporis supra centrum gravitatis partis mersae, minor erit positione corporis posteriori quam priori.
Sint C et F centra gravitatis, illud totius alicujus corporis, hoc vero partis
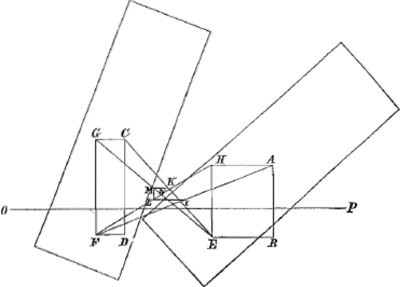
Fig. 7.
mersae corporis ejusdem. Idem verò corpus ponatur ultro inclinatum, talemque situm acquisijsse, ut jam totius centrum gravitatis sit A, partis verò mersae centrum gravitatis E. [dico altitudinem C suprà F majorem quàm est altitudo A supra E]. Ga naar voetnoot16) aganturque per puncta E et F lineae EB et FD parallelae superficiei liquidi OP. dico perpendicularem AB, quae ex centro gravitatis A cadit in BE, minorem esse perpendiculari CD, quae cadit ex centro grav. C in FD.
absolvuntur enim rectangula DG et BH, si opus est. (p[otes]t enim fieri ut perpd. CD inciderit in punctum F et AB ppd. inciderit in punctum E). junganturque AF, CE, HF et GE, quae duae sese intersecant in N puncto, divisisque CE et AF bifariam in K et I ducantur IL et KM superficiei liquidi parallelae, quibus manifestum est etiam HF et GE bifariam dividi. denique jungatur ML.
Quum igitur supra demonstratum sitGa naar voetnoot17), punctum I quod bifariam secat AF inferius esse puncto K. quod secat CE bifariam, sequitur et punctum L inferius esse puncto M: cumque GF et HE sunt parallelae, erit linea ML, quae utramque GE et FH bifariam dividit, iisdem GF et HE parallela. caditque eadem ML necessario ab eâ parte intersectionis N, quae est versus positionem corporis prio- | |
| |
rem. quia itaque GM aequalis est ME, erit GN major quàm NE; quae quum sint homologa latera similium triangulorum GNF, ENH, erit et GF major quam HE. unde et CD major quam AB; quod erat demonstrandum.
| |
Theorema 7.
Si corpus solidum liquido supernatans ultrò inclinetur et alium situm acquirat, altitudo centri gravitatis partis enatantis supra centrum gravitatis totius corporis minor erit positione corporis posteriori quam priori.
Sint A et B centra gravitatis, illud totius alicujus corporis, hoc verò partis quae enatat. Idem verò corpus ponatur ultro inclinatum talemque situm aquisijsse, ut
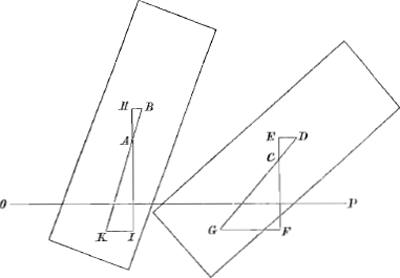
Fig. 8.
jam totius centrum grav. sit C, partis verò quae enatat centrum grav. D. dico altitudinem B suprà A majorem, quàm est altitudo D supra C. id est, ductis BH et DE parallelis superficiei liquidi OP, in easque perpendicularibus AH, CE, majorem esse HA quam CE.
Productis enim BA et DC, fiat AK ad AB, nec non CG ad CD, ut partes enatantes ad partes mersas; et manifestum est K et G fore centra gravitatis partium mersarum. similiter productis HA et EC fiant AI ad AH nec non CF ad CE, ut KA ad AB, sive ut GC ad CD, eadem enim est proportio. jungantur KI et GF et manifestum est utramque parallelam fore superficiei liquidi. Igitur propter triangula similia KAI, BAH, est IA ad AH, sicut KA ad AB; sed KA est ad AB, sicut GC ad CD, quia utroque corporis situ pars mersa ad enatantem habet eandem rationem; igitur IA est ad AH, ut GC ad CD; GC autem est ad CD, ut FC ad CE, propter similia triangula GCF, DCE; igitur IA ad AH, sicut FC ad CE, est autem IA major quam CFaGa naar voetnoot18), ergo et AH major quàm CE. quod erat demonstrandum.
| |
| |
| |
Theorema 8.Ga naar voetnoot19)
Sphaerae portio liquido supernatans demerso vertice, quamcunque ad liquidum in gravitate proportionem habuerit, consistet axe ad liquidi superficiem perpendiculari.Ga naar voetnoot20)
Sit portio sphaerae ACB, liquido supernatans, cujus superficies ED. ponendo
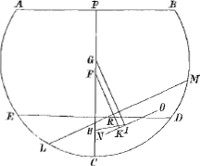
Fig. 9.
videlicet portionem ad liquidum in gravitate esse, ut pars ECD est ad totam portionem, axis autem PC sit ad perpendiculum superficiei ED. dico portionem ita positam quiescere. Si enim fieri potest moveatur, ita ut jam superficies liquidi sit LM, et pars mersa LCDM et portio secari intelligatur plano ACB per axem, recto ad superficiem liquidi: Sitque G centrum sphaerae; F centrum gravitatis portionis ACB; H verò partis prius mersae ECD. Item I partis LCDM. Sit porrò per I ducta NO parallela LM: et junctâ GI, quam manifestum est perpendicularem esse ad NO; in eandem NO perpendicularis cadat FK. jungantur rectâ lineâ centra gravitatis H et I, quam manifestum est alicubi secare debere FK, ut in R, quia centrum grav. F semper cadit inter G et H.
Quum igitur PC sit perpendicularis ad superficiem liquidi ED, sequitur FH esse prius altitudinem centri gravitatis portionis ACB supra centrum grav. partis mersae ECD. Similiter FK est altitudo centri grav. portionis ACB supra centrum grav. partis mersae LCDM, nempe quum portio mota est. quia autem partes ECD, LCDM sunt aequales, sequitur centrum sphaerae ab earum centris gravit. H et I aequaliter distare; quam ob rem GI aequalis est GH; unde et FR aequalis FH;
| |
| |
FK vero major est quàm FR; ergo et major quàm FH; quod est absurdum, quum portio ultro mota dicaturbGa naar voetnoot21). Non movebitur igitur, quod erat ostendendum.
| |
Theorema 9.
Sphaerae portio liquido supernatans demersà base quamcùnque ad liquidum in gravitate proportionem habuerit, consistet axe ad liquidi superficiem perpendicular.Ga naar voetnoot22)
Repetatur eadem figura sed invertatur, habeatque jam portio ad liquidum in
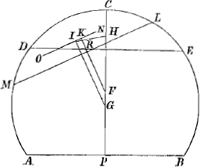
Fig. 10.
gravitate proportionem, quam pars DABE ad totam. unde si axis CP ponatur ad perpendiculum superficiei DE, erit pars mersa DABE, enatabit verò pars DCE quae theoremate praecedenti mersa erat, dico autem sic positam quiescere.
Si enim non quiescit itaque moveatur ut jam superficies liquidi sit ML et reliqua constructa sint ut supra. Igitur iterum altitudo KF major erit altitudine FH, quod est absurdumcGa naar voetnoot23), quum portio ultro motá dicatur; quiescetergo; quod erat demonstr.
| |
Lemma 1.
Sit parabole vel hijperbole EBC, in cujus axe DB, sumpta sit BD non major dimidio latere recto; ductaque sit ex D alia linea DE quae sectioni occurrat. dico DE majorem esse quam DB.Ga naar voetnoot24)
Ducatur enim ordinatim applicata EF. Quia igitur rectangulum sub BF et
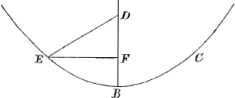
Fig. 11.
latere recto aequale vel minus est quadrato FE, DB vero non major dimidio latere recto, sequitur duplum rectanguli DBF non majus esse quadrato FE: ergo addito utrinque quadrato DF, erit duplum rectanguli DBF una cum quadrato DF non majus quadrato DE. sed duplum rectanguli DBF una cum quadrato
| |
| |
DF excedit quadratum DB, quadrato FB. Igitur quum duplum rectanguli DBF una cum quadrato DF non majus esse demonstratum fuerit quadrato DE, erit quadratum DB minus quadrato DE; quare et DB minor quam DE; quod erat ostendendum.
| |
Theorema 10.
Recta portio Conoidis parabolici, si axem habuerit minorem quam subsesquitertiumGa naar voetnoot25) lateris recti aGa naar voetnoot26), et proportionem ad liquidum in gravitate quamcunque; liquido supernatans demerso vertice, consistet axe ad liquidi superficiem perpendiculari.Ga naar voetnoot27)
Sit recta portio Conoidis parabolici ACB, cujus axis DC minor sit ¾ lateris recti et liquido supernatans posita sit recta, ita ut axis DC sit perpendicularis ad liquidi superficiem quae sit FG (ponendo videlicet portionem ad liquidum in gravitate habere eam proportionem quam pars FCG ad totam portionem,) dico eam ita positam necessario consistere.
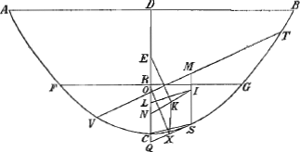
Fig. 12.
Si enim sieri potest inclinet ad partem aliquam ita ut jam liquidi superficies sit VT. Et intelligatur portio secari per axem plano ACB, recto ad liquidi superficiem. dividatur autem axis DC in E ita ut pars EC reliquae sit dupla, eritque E centr. gravitatis conoidis ACB, hoc enim a Comman- | |
| |
dino demonstratum estGa naar voetnoot28). porro secetur VT bifariam in M, et ducatur MS parallela DC, eritque ea axis partis mersae VST, aequalis axi RC partis FCGbGa naar voetnoot29), quia partes ipsae sunt aequalescGa naar voetnoot30). Item dividantur MS, RC in I et L, sicut axis DC divisus fuit in E, eruntque I et L centra gravitatis partium VST, FCG. Per I ducatur NI parallela VT, in eamque ex E cadat perpendicularis EKGa naar voetnoot31).
eidem VT ducatur parallela SQ, quae ideo continget sectionem ACB in puncto SdGa naar voetnoot32). Sit item KX parallela axi DC, et XO parallela KE: et jungantur IL et SC, quae similiter inter se parallelae erunt, eo quod LC, IS sunt aequales, utpote subsesquialteraeGa naar voetnoot33) axium aequalium RC, MS. Est igitur triangulus OXQ triangulo EKN similis et aequalis, ideoque latus OX aequale lateri EK, et latus OQ
| |
| |
lateri EN; sed et lineae CQ, LN aequales sunt, propter triangula CSQ, LIN similia et aequalia; ergo auferendo aequalia ab aequalibus, remanet OC aequalis EL. Quia autem DC minor est ¾ lateris rectis, et EC est ⅔ DC, erit EC minor quam 6/12 sive ½ lateris recti; ergo EL sive OC multo minor dimidio lateris recti: quare OX (etiamsi in circumferentia sectionis terminari dicatur) major erit quam OCeGa naar voetnoot34). Igitur et EK major quam EL. Quia autem NI transit per I centr. gr. partis VST et parallela est superficiei liquidi VT, sequitur lineam EK quae in eam perpendicularis est, esse altitudinem centri grav. portionis totius, supra centrum gravitatis partis mersae VST. EL autem similiter est altitudo centri gr. totius portionis supra centrum gr. partis mersae FCG: Igitur quia EK major EL, altitudo centri grav. totius portionis supra centr. grav. partis mersae major esset situ portionis secundo, motâ videlicet portione, quam fuerat situ primo, cum staret recta, quod est contra Theor. 6 h. lib. Quum itaque absurdum sit portionem ad ullam partem inclinatam dicere, necessario recta consistet; quod erat demonstr.
| |
Theorema 11.
Recta portio Conoides parabolici, si axem habuerit minorem quam subsesquitertium lateris recti, et ad liquidum in gravitate portionem quamcunque: liquido supernatans demersà base, consistet axe ad liquidi superficiem perpendiculari.Ga naar voetnoot35)
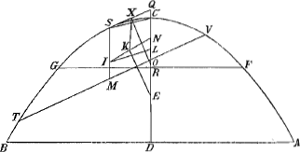
Fig. 13.
Repetatur figura praecedens sed inversa, jamque pars mersa sit BGFA, sitque portio posita situ recto, adeo ut axis CD perpendicularis sit ad liquidi superficiem GF. dico portionem BCA ita positam necessario consistere.
Si enim fieri potest inclinetur, ita ut jam superficies sit TV.
Igitur constructis reliquis ut suprà, demonstrabitur eisdem verbis EK majorem esse quam EL. unde repugnat
| |
| |
Theoremati 7. h. lib. ut portionem motam dicamus, quum prius LE fuerit altitudo centri grav. partis enatantis supra centr. gr. totius portionis, postea vero ea altitudo sit KE. Consistet igitur portio: quod erat dem.
| |
Theorema 12.
Recta portio Conoidis parabolici axem habens majorem tribus quartis lateris recti, si in gravitate ad liquidum majorem habeat rationem eâ quam habet quadratum quod fit ab excessu axis supra tres quartas lateris recti, ad quadratum axis; supernatans liquido demerso vertice consistet axe ad liquidi superficiem perpendiculari.Ga naar voetnoot36)
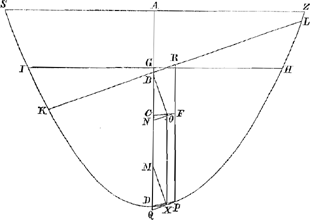
Fig. 14.
Sit haec Conoidis portio SDZ, liquido supernatans, et posita recta, ita ut liquidi superficies sit IH, ponendo videlicet portionem ad liquidum in gravitate eam habere rationem quam habet pars IDH ad totum, quae ratio major sit eâ quam habet quadratum excessus axis AD supra tres quartas lateris recti, ad quadr. AD: dico portionem ita positam necessario consistere.
Nam si fieri potest inclinet ad aliquam partem, ut jam liquidi superficies sit KL; et portio per axem secari intelligatur plano SDZ, recto ad liquidi superficiem. dividatur autem KL bifariam in R unde ducatur RP parallela AD, eritque RP axis partis KPL, eademque aequalis axi GD partis IDHaGa naar voetnoot37) quia partes ipsae IDH, KPL sunt aequalesbGa naar voetnoot38). Et sit B centrum grav. portionis totius SDZ; C centr. grav.
| |
| |
partis IDH, et F partis KDL, perque hoc ducatur FN parallela KL, et in FN cadat perpendicularis BO. Porro ducatur PQ parallela LK vel ipsi FN, ac proinde contingens sectionem in P. Item siat OX parallela axi AD, et XM parallela OB; et denique jungantur PD et FC, quae similiter inter se parallelae erunt, quoniam CD, FP sunt aequales, utpote subsesquialteraeGa naar voetnoot33) axium aequalium GD, RP.
Sunt igitur trianguli BNO, MQX similes et aequales, ideoque latus MX aequale lateri BO, et MQ aequale BN, verum et lineae DQ, CN sunt aequales propter triangulos similes et aequales CFN, DPQ; ergo auferendo aequalia ab aequalibus manent MD, BC aequales. Porro quia sicut portio ad liquidum in gravitate ita est pars mersa IDH ad totamcGa naar voetnoot39) portionem, et ita quadratum axis GD ad quadratum axis ADdGa naar voetnoot40), sequitur quadr. GD ad quadratum AD quoque majorem habere rationem quam quadratum excessus axis AD supra ¾ lateris recti habet ad quadr. AD: ergo quadratum GD majus quadrato excessus axis AD supra tres quartas lateris recti, ideoque GD major excessu axis AD suprà tres quartas lateris recti. sed GD est excessus axis AD suprà AG, ergo AG minor est tribus quartis lateris recti. quum autem centra grav. axes portionum similiter dividant, est AD ad BD ut GD ad CD, et permutando AD ad GD ut BD ad CD, et dividendoGa naar voetnoot41), et permutando AD ad BD ut AG ad BC: sed AD est 3/2 BD, ergo et AG est 3/2 BC; ergo quum AG sit minor ostensa ¾ lateris recti, erit BC minor 2/4 sive ½ lateris recti. MD autem ostensa fuit aequalis BC, ergo et MD minor dimidio latere recto: quamobrem MX (etiamsi terminari dicatur ad sectionis circumferentiam) major
erit quam MDeGa naar voetnoot42). ideoque BO, quae ipsi MX aequalis est, major quam BC, quae aequalis est ipsi MD. Hoc autem absurdum est; nam quoniam posteriori portionis positione linea BO est altitudo centri grav. totius portionis supra centrum grav. partis mersae, eaque altitudo priori positione est BC, deberet BO minor esse quam BCfGa naar voetnoot43). Non potest itaque portio ad partem ullam inclinare, sed recta consistet; quod erat demonstrandum.
| |
| |
| |
Theorema 13.
Recta portio Conoidis parabolici axem habens majorem tribus quartis lateris recti, si in gravitate ad liquidum minorem habeat rationem eâ quam habet id quo quadratum axis majus est quadrato quod fit ab excessu axis supra tres quartas lateris recti, ad quadratum axis; liquido supernatans demersâ base, consistet axe ad liquidi superficiem perpendiculari.Ga naar voetnoot44)
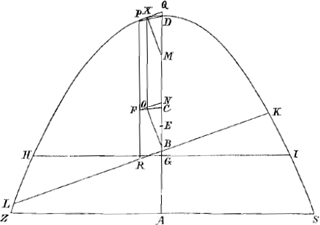
Fig. 15.
Sit haec portio SDZ, quae liquido supernatet demersâ base, et posita sit recta ita ut axis DA sit perpendicularis ad liquidi superficiem, quae sit IH, ponendo videlicet rationem partis IHZS ad totam portionem esse minorem eâ ratione de qua dictum: dico portionem ita positam consistere.
Si enim fieri potest inclinet, ut jam liquido superficies sit LK. Et construantur omnia ut in Theoremate praecedenti; praetereaque ponatur AE aequalis tribus quartis lateris recti.
Quoniam itaque AE aequalis est tribus quartis lateris recti, apparet proportionem quam portio habet ad liquidum in gravitate minorem esse eâ quam habet differentia quadratorum AD, ED ad quadratum AD. Est autem pars mersa IHZS ad totam portionem, sicut portio ad liquidum in gravitateaGa naar voetnoot45), ergo pars mersa IHZS ad portionem totam minorem habet rationem quam differentia quadratorum AD, ED ad quadratum AD. quia verò pars IDH est ad portionem
| |
| |
SDZ ut quadratum GD ad quadr. ADbGa naar voetnoot46), est etiam dividendoGa naar voetnoot41) pars IHZS ad portionem SDZ ut differentia quadratorum AD, GD ad quadratum AD; ergo quum pars IHZS ad portionem SDZ minorem habeat rationem quam differentia quadratorum AD, ED ad quadratum AD, apparet hanc differentiam quadratorum AD, ED majorem esse differentiâ quadratorum AD, GD; ergo linea GD major quam ED, et AG minor AE, id est tribus quartis lateris recti; unde rursus ut in demonstratione Theorematis praec. ostendi potest lineam BO majorem esse BC, quod est absurdum. nam quum BO sit hic altitudo centri gravitatis partis enatantis supra centrum grav. portionis totius situ portionis posteriori, eaque altitudo priori situ fuerit BC, deberet BO minor esse quam BCcGa naar voetnoot47). Non potuit itaque portio ultro inclinari, ideoque recta consistit quod erat demonstrandum.
| |
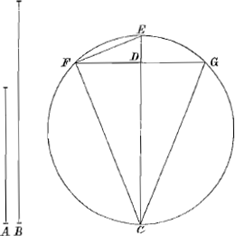
Lemma 2.Ga naar voetnoot48)
Esto Conus plano ABC sectus per axem BD. sumptoque in axe puncto G, eo vertice descripta sit hijperbole ad asymptotos BA, BC. Et intelligatur praeterea conus secari planis EF, et IL, rectis ad planum ABC, ita ut hujus quidem sectionis maxima diameter IL contingat hijperbolen in puncto K, alterius autem diameter EF eandem contingat in vertice G. dico portiones coni abcissas EBF, IBL aequalesesse.
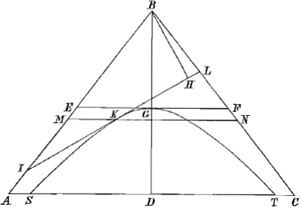
Fig. 16.
Ducatur per contactum K linea MKN parallela AC, sitque BH ad IL perpendicularis.
Manifestum est sectionem EF circulum esse, IL autem esse ellipsin; cujus maxima diameter IL quum hijperbolen contingat, bifariam ideo secatur ad contactum in KaGa naar voetnoot49); dimidiumque minoris diametri ejusdem ellipseos (quod diversum non est ab ordinatim applicata in sectione circulari MN) poterit rectan- | |
| |
gulum MKN; hoc vero rectangulum aequale est quartae parti figuraebGa naar voetnoot50), sive quadrato EGcGa naar voetnoot51), igitur tota minor diameter ellipseos aequalis est lineae EF, ellipsis itaque IL est ad circulum EF, sicut diameter IL ad diametrum
EFdGa naar voetnoot52): et quum abscissor coni IBL ad conum EBF habeat proportionem compositam ex proportione basium ellipticae ad circularem, et ex proportione altitudinum, componetur ideo dicta proportio abscissoris IBL ad conum EBF, ex proportione lineae IL ad EF et ex proportione altitudinis BH ad altitudinem BG. Verum et triangul. IBL ad triangulum EBF habet proportionem compositam ex dictis proportionibus, nimirum ex proportione basium IL ad EF, et altitudinum BH ad BG; ergo abscissor IBL est ad conum EBF, sicut triangulus IBL ad triangulum EBF. Ei autem trianguli sunt aequales (quoniam id quod continetur lateribus IB, BL, aequale est ei quod continetur lateribus EB, BF,eGa naar voetnoot53)) ergo et abscissor IBL aequalis est cono abscisso EBF, quod erat ostendendum.
| |
| |
| |
Theorema 14.
Conus isosceles si in gravitate ad liquidum non minorem habeat rationem quam duplicatam cubi axis ad cubum lateris; liquido supernatans demerso vertice consistit axe ad liquidi superficiem perpendiculari.Ga naar voetnoot54)
Esto conus ABC, axem habens BD, et ductâ DE perpendiculari ad unum è lateribus
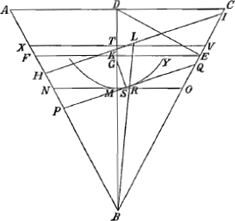
Fig. 17.
BC, fiat planum EF basi AC parallelum, eritque conus FEB ad conum ACB in duplicata proportione cubi axis BD ad cubum lateri BC; nam quia trianguli DEB, EKB sunt rectanguli, habentque communem angulum ad B, erunt similes, ideoque latera KB, BE, BD proportionalia; itaque KB ad BD est in duplicata proportione KB ad BE sive DB ad BC, et cubus lineae KB ad cubum BD, sive conus FBE ad conum ABC in duplicata proportione cubi axis DB ad cubum lateris BC.
Cono ABC igitur in liquidum demisso, positoque axe DB ad perpendiculum, demergatur conus XBV; et quoniam pars mersa est ad totum sicut conus ad liquidum in gravitate, coni autem ad liquidum in gravitate non minor ponitur proportio quam duplicata cubi axis ad cubum lateris, id est non minor eâ quam habet conus FBE ad conum ABC, manifestum est conum demersum XBV non minorem fore cono FBE. dico autem conum ABC ita positum consistere. Nam si potest inclinet ad aliquam partem, ita ut liquidi superficies jam sit HI: et intelligatur conus secari per axem plano ABC recto ad liquidi superficiem; sitque G centrum grav. coni ABC; M centr. gr. coni XBV, et R abscissoris HBI, cujus axis sit BRL. porro fiat planum NMO basi AC parallelum, et planum PRQ parallelum plano HI; et cadat in diametrum PQ perpendicularis GS.Ga naar voetnoot55)
Quum igitur puncta M et R quae sunt centra grav. portionum XBV, HBI, axes TB, et LB similiter dividant, erit conus XBV ad conum NBO, sicut abscissor
| |
| |
HBI ad abscissorem PBQ, et commutando; quare sicut conus XBV sectori HBI aequalis, ita et conus NBO aequalis abscissori PBQ. Si igitur describatur hijperbole MRY vertice M, et ad asymptotos BA, BC, eam continget linea PQaGa naar voetnoot56) et quia PQ ad contactum bifariam dividi debetbGa naar voetnoot57), sicut dividitur à puncto R, manifestum est punctum R fore punctum contactus. Porro quum BM sit ad BT ut BG ad BD (centra enim gravitatis M et G, axes BT et BD similiter dividunt) est quoque commutando sicut BT ad BD ita BM ad BG: BT autem ad BD non minorem habet rationem quam BK ad eandem BD, sive quam quadratum BK ad quadratum BE, ergo et BM ad BG non minorem habet rationem quam quadratum BK ad quadratum BE, sive quam quadratum BM ad quadratum BO: quare et dividendoGa naar voetnoot41) BM ad MG non minorem quam quadratum BM ad quadratum MO. Est autem quadr. MO aequale quartae parti figuraecGa naar voetnoot58), id est rectangulo sub BM et sub dimidio lateris recti hijperboles MRY; sed ad hoc rectangulum quadratum BM propter communem altitudinem eam habet rationem quam linea BM ad dimidium lateris recti, ergo quadratum BM est ad quadratum MO sicut linea BM ad dimidium lateris recti. Ostensum est autem lineam BM ad MG non minorem habere
rationem quam quadratum BM ad quadr. MO; ergo linea BM ad MG non minorem habet rationem quam eadem BM ad dimidium lateris recti: Itaque MG non major dimidio latere recto. Unde linea GS quae ad tangentem PQ perpendicularis est (etiamsi ad hijperboles circumferentiam terminari dicatur) major est quam GMdGa naar voetnoot59); quod est absurdum; nam quoniam linea GS posteriori coni positione est altitudo centri gravitatis totius coni suprà centrum gravitatis partis mersae HBI, eaque altitudo priori positione est GM, deberet GS minor esse quam GMeGa naar voetnoot60). Non potest itaque conus inclinare ad ullam partem, quare rectus consistet, quod erat demonstrandum.
| |
Theorema 15.
Conus isosceles si in gravitate ad liquidum non majorem proportionem habuerit eâ quam habet excessus cubi lateris supra cubum lineae, quae sit ad axem ut axis ad coni latus, ad cubum lateris; liquido supernatans demersâ base, consistit axe ad superficiem liquidi perpendiculari.Ga naar voetnoot61)
Repetatur figura praecedens, et invertatur; et habeat conus ad liquidum in
| |
| |
gravitate proportionem quam habet portio CVXA, non major CEFA, ad conum
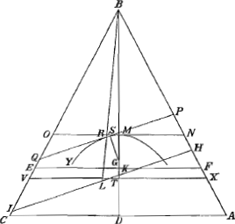
[Fig. 18.]
integrum ABC; quae proportio propterea non major erit eâ de qua dictum, nempe quam habet differentia cuborum AB, FB ad cubum AB: portio enim CVXA est ad conum ABC ut differentia cuborum AB, XB, ad cubum AB, quae minor est proportio quam differentiae cuborum AB, FB ad cubum AB. demisso itaque cono ABC in liquidum, axe ad liquidi superficiem recto, portio demersa erit CVXA, quia haec est ad conum ABC sicut idem ad liquidum in gravitate. Ostendendum est autem conum ita positum consistere.
Si potest inclinet, ut jam superficies liquidi sit IH. Constat igitur ex demonstratione Theorematis praec. lineam GS majorem esse quam GM. verum id hic quoque absurdum est; nam quia GS posteriori coni positione est altitudo centri gravitatis partis enatantis IBH suprà centrum
[Fig. 19.]
gravitatis totius coni, eaque altitudo priori positione est GM, deberet GS major esse quam GM aGa naar voetnoot62). Absurdum itaque est dicere conum inclinasse; ergo rectus consistet, quod erat demonstr.
| |
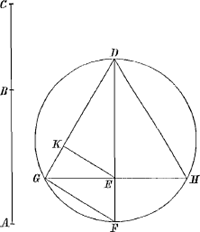
Propos. 16. Problema 1.
Datâ proportione cujusvis materiae solidae quam ad liquidum habet in gravitate, conum ex eâ facere, qui in liquidum demissus vertice demerso rectus consistat.
Data sit proportio materiae ad liquidum in gravitate, quae est lineae A ad B.
Inveniantur inter A et B duae mediae proportionales, quae sint CD, CE; et
| |
| |
fiat circulus diametro CE, ductâque FDG quae dictam diametrum CE secet in D ad angulos rectos, jungantur CF, CG, dico conum FCG esse qui quaerebatur.
Jungatur enim FE. Sunt igitur CD, CF, CE, continuè proportionales, quare CD ad CE in duplicata proportione CD ad CF; est autem ut CD ad CE sic A ad CD, igitur A ad CD quoque in duplicata proportione CD ad CF; unde et cubus A ad cubum CD in duplicata proportione cubi CD ad cubum CF. cubus autem A ad cubum CD est in triplicata proportione lineae A ad CD; quod idem est ac si dicamus cubum A esse ad cubum CD, sicut est linea A ad B, (nam A est ad B in triplicata ratione A ad CD, quum B sit quarta proportionalium in ratione eâdem;) Igitur A ad B, id est conus FCG ad liquidum in gravitate, est in duplicata proportione cubi axis CD ad cubum lateris CF. Quare si conus FCG demittatur in liquidum demerso vertice, consistet rectusaGa naar voetnoot63), qualem invenire oportebat.
Manifestum autem est, omnes ex data materia conos, quorum angulus ad verticem aequalis vel major erit angulo FCG similiter rectos consistere debere.
| |
Propositio 17. Problema 2.
Datâ proportione cujusvis materiae solidae quam ad liquidum habet in gravitate, conum ex eâ facere qui in liquidum demissus demersâ base, rectus consistat.
[Fig. 20.]
Sit data proportio quae est lineae AB ad AC. Inveniantur inter earum differentiam quae est CB et ipsam AC duae mediae proportionales DE et DF. factoque circulo ad diametrum DF, ducatur HEG quae diametrum DF secet ad angulos rectos in E, et jungantur DH, DG. dico conum HDG esse quem invenire oportebat. Jungantur enim FG, et sit EK ad latus DG perpendiculairs.
Sunt igitur FG, EK parallelae, ideoque ut DE ad DF, sive ut CB ad DE ita DK ad DG: cubus autem DK ad cubum DG est in triplicata ratione lineae DK ad DG, ergo etiam in triplicata ratione lineae CB ad DE. ratio autem triplicata CB ad DE, est ea quam CB habet ad CA, (quia CA est quarta proportionalis in ratione CB ad DE;) igitur cubus DK ad cubum DG est ut linea CB ad CA: et dividendo, differentia cuborum DK, DG ad cubum DG sicut AB ad AC, id est
| |
| |
sicut conus HDG ad liquidum in gravitate. Conus itaque HDG ad liquidum in gravitate non majorem habet proportionem sed eandem quam excessus cubi lateris suprà cubum lineae quae est ad axem ut axis ad coni latus, habet ad cubum lateris; ideoque in liquidum demissus demersa base, consistet axe ad liquidi superficiem recto aGa naar voetnoot64), ut oportebat.
Similiter vero recti consistent omnes coni ex ista materia, quorum angulus ad verticem aequalis vel major erit angulo HDG.
|
-
voetnoot1)
- Sur la feuille qui contient le titre Huygens a ajouté plus tard: ‘Omnia mutanda 1652, mart. 23’ et ensuite: ‘1679. Pleraque rejicienda si non omnia. quia speculatio parum utilitatis habet, quamquam et Archimedes ipse in his operam posuit’. Consultez à propos de ces annotations la dernière page de l'‘Avertissement’ qui précède cette pièce.
-
voetnoot2)
- Ici encore, c'est-à-dire sur la première feuille du traité, Huygens a annoté en marge: ‘Haec de corporibus solidis in liquido supernatantibus in primà adolescentia scripsi, cum nullum adhuc majoris momenti argumentum sese obtulisset, In his autem utilitas nulla, vel perquam exigua, Etsi Archimedes secundo περὶ ὀχ♉μένων libro non absimilia tractaverit. E primis Theorematis quaedam retineri possent item de Cylindris. Reliqua vulcano tradenda’. Voir l'‘Avertissement’, p. 92.
-
voetnoot3)
- Sur une feuille contenant, à ce qu'il nous semble, l'avant-projet de la première partie du traité présent (jusqu'au theorème 3 inclus), on trouve, au lieu des trois hypothèses formulées du texte, les considérations suivantes: ‘Liquidi naturam esse ut quatenus se extendere a vase continente non prohibetur, descendat, ac proinde eam figuram sumat cujus centrum grav. sit quam humillimum.
Corpore autem solido super liquidum innatante, ita utrumque se componere ut centrum gr. commune sit quam humillimum’.
Ensuite on rencontre sur la même feuille une esquisse de la figure du ‘Theorema 1’ du texte et une démonstration du ‘Theorema 3’ que nous reproduirons dans la note 14.
-
voetnoot4)
- Le théorème correspond à la ‘Propositio II’ d'Archimède: ‘Omnis humidi consistentis, atque manentis superficies sphaerica est; cuius sphaerae centrum est idem, quod centrum terrae’, que nous citons d'après l'ouvrage: ‘Archimedis de iis quae vehuntur in aqua libri duo. A'Federico Commandino Urbinate in pristinum nitorem restituti, et commentariis illustrati. Cum privilegio in annos X. Bononiae, Ex Officina Alexandri Benacii. MDLXV’. 4o. Voir la page 1 verso. On le trouve sous une autre rédaction, p. 360 du T. II de l'édition de Heiberg, mentionnée dans la note 2 de la page 50 du Tome présent; mais nous préférons ici et ailleurs de citer d'après Commandin parce que Heiberg a suivi l'édition de Tartalea et qu'il est bien plus probable que Huygens se soit servi de celle de Commandin ou d'une de celles qui en dérivent.
Ajoutons que la démonstration qui va suivre, partant d'un autre principe, diffère complètement de celle d'Archimède. On en rencontrera une autre leçon dans l'Appendice I du traité présent.
Voir encore, sur une déduction moderne du même théorème, analogue à celle de Huygens, la note 26 de l'Avertissement.
-
voetnoot6)
- La lettre a est un signe de renvoi ajouté par Huygens. En effet, on lit en marge: ‘a hypoth. 1’.
-
voetnoot7)
- Theorème correspondant à la Prop. III (p. 2 verso) de l'édition de Commandin: ‘Solidarum magnitudinum, quae aequalem molem habentes aeque graves sunt, atque humidum; in humidum demissae demergentur ita, ut ex humidi superficie nihil extet: non tamen ad huc deorsum ferentur’. (Heiberg, T. II, p. 362). Démonstration essentiellement différente.
-
voetnoot8)
- Théorème correspondant à la Prop. V, p. 4 recto de l'édition de Commandin: ‘Solidarum magnitudinum quaecunque levior humido fuerit, demissa in humidum usque eô demergetur, ut tanta moles humidi, quanta est partis demersae, eandem, quam tota magnitudo, gravitatem habeat.’ (Heiberg, T. II, p. 367). Démonstration différente.
Voir encore, sur une demonstration moderne fondée sur le même principe, la note 26 de l'Avertissement.
-
voetnoot10)
- En effet l'inégalité a/b < c/d entraîne
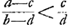 , quand on a, comme ici, c < a, d < b. Quant à l'emploi du terme ‘dividendo’, comparez p.e. l'ouvrage de Clavius ‘Euclidis Elementorum Libri XV’, eité dans la note 6 de la Lettre No. 325 (p. 477 du T. I), où l'on rencontre ce terme dans la ‘Prop. 29’ du ‘Liber V’ (p. 521 de l'édition de 1607). La proposition appliquée ici par Huygens se déduit facilement en combinant le ‘Scholium’ de cette ‘Prop. 29’ avec celui de la ‘Prop. 27’ du même livre. , quand on a, comme ici, c < a, d < b. Quant à l'emploi du terme ‘dividendo’, comparez p.e. l'ouvrage de Clavius ‘Euclidis Elementorum Libri XV’, eité dans la note 6 de la Lettre No. 325 (p. 477 du T. I), où l'on rencontre ce terme dans la ‘Prop. 29’ du ‘Liber V’ (p. 521 de l'édition de 1607). La proposition appliquée ici par Huygens se déduit facilement en combinant le ‘Scholium’ de cette ‘Prop. 29’ avec celui de la ‘Prop. 27’ du même livre.
-
voetnoot11)
- Puisque encore a/b < c/d entraîne
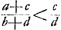 . Comparez la ‘Prop. 28’, p. 520 de l'ouvrage mentionné dans la note précédente. . Comparez la ‘Prop. 28’, p. 520 de l'ouvrage mentionné dans la note précédente.
-
voetnoot14)
- Voici une autre démonstration du même theorème, empruntée à la feuille détachée que nous avons mentionnée dans la note 3.
‘Demonstratio propositionis archimedeae de innatantibus’
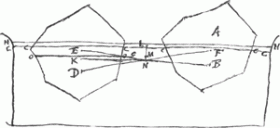
‘Priori positu’ [voir la figure de droite] ‘corpus AB, partem demersam habet B sub aquae superficie CC, et ponitur aquae moles aequalis parti B gravitatem habere corpori toti AB aequalem. Ostendendum est ita mansurum, ut nec magis nec minus demergatur. Si enim potest demergatur primo amplius, ut parti B quam abscindebat superficies aquae CC, jam infra aquam aequalis sit pars D infra superficiem OO sita, quo fiet ut aquae pars aequalis corporis portioni E, inter CC et OO interceptae, ascendat supra superficiem CC, puta ad HH.
Sit F centr. gr. totius AB corporis. B centr. gr. partis demersae sub CC D centr. gr. partis isti aequalis sub OO, sive aquae spatium D replente. Sit E centr. gr. spatii E inter CC et OO comprehensi. K vero centr. gr. corporis totius ut est in secundo positu.
Jungatur FD. Et dividatur bifariam in N. Erit in primà positione punctum N centr. gr. compositae ex corpore AB et aqua D sub OO contenta, quia cum haec aequalis sit aquae contentae spatio B sub CC posito, quae pondere aequalis ponitur corpori AB, oportet centr. gr. N dividere bifariam rectam centra connectentem FD. Sed et spatium E inter CC, OO aqua plenum est primà positione. Ergo juncta NE erit in ea centr. gr. compositae ex corpore AB et ex aqua spatii DE, quod centrum sit G.
Rursus in secunda positione quia distantia centrorum gr. K, D eadem est quae in primà positione erat centrorum F, B, apparet ducta K, B quae jungit centr. gr. totius corporis in secunda positione cum centro aquae occupantis jam spatium B sub CC, apparet inquam rectam KB transire per punctum N atque ibidem bifariam secari, adeo ut N quoque sit centr. gr. compositae ex toto corpore in secunda positione et aquae mole quae successit in spatium B sub CC. Quia autem aqua quae primà positione continebatur spatio E inter CC et OO, jam in secunda positione ascendit super CC in spatium CCHH necesse est ejùs aquae centr. gr. esse supra CC. sit in L et jungatur NL. Ergo in ea erit jam centr. gr. compositae ex corpore toto in secunda positione et ex aqua spatii B sub CC, et ex aqua supra CC elevata. quod centrum sit M. Erit autem necessario LN ad NM ut EN ad NG. Sed punctum L est altius quam E cum hoc sit infra illud supra superficiem CC. Ergo et punctum M altius quam G. Est autem M et G centr. gr. corporum quae positum mutant haec in prima, illud in secunda positione, reliquà aqua pristinum spatium obtinente.
Ergo et centrum gravitatis illud ultro altius ascendisset quod est absurdum.
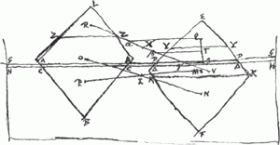
Dicatur jam corpus EF [voir la figure à côté] altius extra aquam emersurum, eoque posito intelligatur collocatum in LB. prima positione EF corpus, ABA aqua, itemque HHGG circumfusa.
Sit aqua ABA aequalis ponderis cum corporis parte YFY cujus centr. grav. M. et abscindatur KFK ∞ ABA. Ergo aqua spatii DDKK aequipond. parti corporis reliquae YEY vel ZLZ. quia aqua totius spatii DFD aequiponderans ponitur corpori toti EF. Sit P centr. gr. spatii ABA, N spatii KFK. O partis ZBZ aequalis YFY. Jam secunda positione erit LB corpus, et aqua quae erat in ABA complebit KFK. Et reliqua aqua circumfusa quae erat inter GG et HH replebit spatium ∆∆KK.
In prima pos.e centrum gr. compositae ex corpore YFY et aqua ABA erit punctum I quod bifariam secat PM. In secundo pos. erit idem I punctum centr. grav. compositae ex corpore ZBZ et aqua KFK, adeo ut quantum ad haec nihil mutaverit altitudo centri gr.
At in prima pos.e centr. gr. aquae circumfusae inter GG, HH (excepta tamen hic ea quae replet spatium AACC) centrum gr. est inter GG, HH, quod sit S. ductaque SQ ad centr. gr. partis YEY, erit inter SQ centr. gr. compositae ex dicta aqua circumfusa et partem corporis YEY, esto illud T. In secunda pos. vero dicta aqua circumfusa continetur spatio K∆∆K ideoque centr. grav. habet inter ∆∆ et KK, quod sit V, et ducatur VR ad centr. gr. partis ZLZ ipsi YEY aequalis. Eritque in recta VR centr. grav. compositae ex aqua spatii ∆∆KK et corporis ZLZ. quod centrum sit X. Ergo RX ad XV ut QT ad TS. estque ratio minoris ad majus, quia cum aqua spatii DDKK aequiponderet corpori ZLZ, erit hoc gravius aqua spatii ∆∆KK, unde RX brachium brevius quam XV. Est autem altitudo S super V minor quam DD supra KK cui aequalis altit. R supra Q. hinc jam ostenditur X altius quam T. nam ductis ab Q, T, et S horizontalibus quae occurrant rectae RV in α, β, γ. Quia RX minor quam XV, et Rα major quam Vγ. Erit utique minor ratio αX ad Xγ quam RX ad XV, hoc est quam αβ et βγ unde αX minor quam αβ. Et X proinde altior β’. Dans l'Appendice I du traité présent on rencontrera une troisième démonstration du même théorème.
-
voetnoot16)
- Au lieu de la phrase entre crochets ou trouve dans le texte un signe de renvoi correspondant à l'annotation en marge; ‘dico altitudinem &c. ut in Theor. sequ.’; mais nous avons préféré de construire la phrase d'après l'indication contenue dans cette annotation.
-
voetnoot19)
- Avec le théorème qui suit, la série des théorèmes généraux, auxquels le théorème 1 du livre II se joindra plus tard, est interrompue. Et Huygens procède à appliquer les résultats obtenus, d'abord aux théorèmes plus spéciaux, découverts par Archimède, qui se rapportent aux segments sphériques et aux conoïdes paraboliques flottants, et dont il va donner des démonstrations nouvelles; ensuite à la détermination de la stabilité des positions d'équilibre d'autres corps flottants; c'est-à-dire des cônes de révolution flottant avec l'axe dans la situation verticale.
-
voetnoot20)
- Théorème correspondant à la Prop. VIII p. 6 recto de l'édition de Commandin: ‘Si aliqua magnitudo solida leuior humido, quae figuram portionis sphaerae habeat, in humidum demittatur, ita ut basis portionis non taugat humidum: figura insidebit recta, ita ut axis portionis sit secundam perpendicularem. Et si ab aliquo inclinetur figura, ut basis portionis humidum contingat; non manebit inclinata si demittatur, sed recta restituetur’. (Heiberg, T. II, p. 371).
-
voetnoot22)
- Théorème correspondant à la Prop. IX p. 8 recto de l'édition de Commandin: ‘Quòd si figura’ [portionis sphaerae] ‘leuior in humidum demittatur, ita ut basis tota sit in humido; insidebit recta, ita ut axis ipsius secundum perpendicularem constituatur’. (Heiberg, T. II, p. 372).
-
voetnoot24)
- Inutile de faire remarquer que BD est inférieur ou égal au rayon de courbure du sommet B de la parabole ou hyperbole EBC.
-
voetnoot26)
- Huygens annota en marge: ‘a. latus rectum conoidis appello id quod est latus rectum paraboles quae fit si conoides secetur plano per axem vel axi parallelo, omnes enim sectiones hae exhibent eandem parabolen.’ [Comparez la pièce No. IX, à la page 52 du Tome présent]. ‘Ea autem quae Archimedi appellatur adjecta axi, dimidium est lateris recti’.
Ajoutons qu'on doit lire ici ‘quae usque ad axem’, au lieu de ‘adjecta axi’, puisque Archimède réserve cette dernière expression: ‘ποτεοῦσα τῷ ἄξονι’ au cas de la conoïde hyperbolique, où elle indique le demi-diamètre de l'hyperbole méridien. (Comparez T. I, p. 278 et 279 de l'édition de Heiberg). La ligne que Huygens a en vue et qui se rencontre dans le cas de la conoïde parabolique est appeléc par Archimède ‘τἀ μέχϱι τοῦ ἄξονος’ (Comp. Heiberg, T. I, p. 304) ce qui se traduit chez Commandin par ‘quae usque ad axem’, expression qu'on retrouve dans le théorème de la note 27 et dans quelques autres théorèmes cités dans les notes suivantes.
Voir d'ailleurs le ‘Commentarius’ de Commandin à la page 11 verso de l'ouvrage cité dans la note 4, où on lit: ‘Linea, quae usque ad axem apud Archimedem, est dimidia eius, juxta quam possunt, quae à sectione ducuntur; ut ex quarta propositione libri de conoidibus, & spheroidibus apparet. cur uero ita appellata sit, nos in commentariis in eam editis tradidimus’. Consultez pour ces derniers commentaires la page 30 recto des ‘Commentarii’ qu'on trouve dans l'ouvrage: ‘Archimedis Opera non nulla à Federico Commandino Urbinate nuper in Latinum conversa, et commentariis illustrata. Quorum nomina in sequenti pagina leguntur. Cum privilegio in annos X. Venetiis, apud Paulum Manutium, Aldi F. MDLVIII.’ 4o.
-
voetnoot27)
- Théorème correspondant à la Prop. II Libr. II, p. 10 recto, de l'édition de Commandin, citée dans la note 4: ‘Recta portio conoidis rectanguli, quando axem habuerit minorem, quam sesquialterum’ [3/2] ‘eius, quae usque ad axem’ [voir la note 26] ‘quamcunque proportionem habens ad humidum in gravitate; demissa in humidum, ita ut basis ipsius humidum non contingat; & posita inclinata, non manebit inclinata; sed recta restituetur. Rectam dico consistere talem portionem, quando planum quod ipsam secuit, superficiei humidi fuerit aequidistans’. (Heiberg, T. II, p. 376). On remarquera que la démonstration qui va suivre diffère de celle suppléée par Commandin.
-
voetnoot28)
- Aux pages 41 verso-45 recto de l'ouvrage suivant: Federici Commandini Urbinatis Liber de Centro Gravitatis Solidorum. Cum privilegio in annos X. Bononiae, Ex Officina Alexandri Benacii. MDLXV. 4o.
-
voetnoot29)
- ‘b pr. 25. Archim. de Conoid.’ [Huygens]. Il s'agit de la Prop. XXV, p. 41 recto de l'édition de Commandin, citée vers la fin de la note 26: ‘Si rectanguli conoidis duae portiones abscindantur; altera quidem plano super axem erecto, altera autem non erecto: et sint portionum axes aequales: ipsae quoque portiones aequales erunt’ (c'est la Prop. XXIII de l'édition de Heiberg, p. 405 du T. I.).
-
voetnoot30)
- ‘c Theor. 4, lib. 1.’ [Huygens]. Voir le ‘Theorema 4’ p. 100 du Tome présent; theorème qui équivaut à la loi d'Archimède.
-
voetnoot31)
- Dès lors il ne s'agira plus que de prouver qu'on a EK > EL,
-
voetnoot32)
- ‘d per conv. prop. 5 lib. 2 Con.’ [Huygens]. Voici cette proposition, telle qu'on la trouve à la page 45 verso de l'édition des ‘Coniques’ d'Apollonius, citée dans la pièce No. 5, note 4 (p. 6 du T. I): ‘Si parabolae, uel hyperbolae diameter lineam quandam bifariam secet; quae ad terminum diametri contingit sectionem aequidistans est lineae bifariam sectae’.
-
voetnoot35)
- Théorème correspondant à la Prop. III, Libr. II, p. 12 verso, de l'édition de Commandin: ‘Recta portio conoidis rectanguli quando axem habuerit minorem, quam sesquialterum’ [3/2] ‘eius quae usque ad axem, quamcunque proportionem habens ad humidum in grauitate; demissa in humidum, ita ut basis ipsius tota sit in humido; & posita inclinata, non manebit inclinata, sed ita restituetur, ut axis ipsius secundum perpendicularem fiat’. (Heiberg, T. II, p. 378).
-
voetnoot36)
- Théorème correspondant à la Prop. IIII Libr. II, p. 13 recto de l'édition de Commandin: ‘Recta portio conoidis rectanguli, quando fuerit humido leuior, & axem habuerit maiorem, quàm sesquialterum eius, quae usque ad axem: si in gravitate ad humidum aequalis molis non minorem proportionem habet ea, quàm quadratum, quod sit ab excessu, quo axis maior est, quàm sesquialter eius, quae usque ad axem, habet ad quadratum, quod axe, demissa in humidum, ita ut basis ipsius humidum non contingat; & posita inclinata, non manebit inclinata, sed recta restituetur’. (Heiberg, T. II, p. 379).
-
voetnoot37)
- ‘a pr. 25. Archim. de Conoid.’ [Huygens]. Voir la note 29.
-
voetnoot38)
- ‘b pr. 4. h. lib.’ [Huygens]. Comparez la note 30.
-
voetnoot40)
- ‘d Prop. 26. Archim. de Conoid.’ [Huygens]. Il s'agit de la Prop. XXVI, p. 41 verso de l'édition de Commandin: ‘Si rectanguli conoidis duae portiones abscindantur planis quomodocunque ductis: portiones eandem inter sese proportionem habebunt, quam ipsarum axium quadrata’. (C'est la Prop. XXIV de l'édition de Heiberg, p. 411 du T. I).
-
voetnoot41)
- Sur l'expression ‘dividendo’, comparez la note 10.
-
voetnoot44)
- Théorème correspondant à la Prop. V Libr II, p. 15 recto, de l'édition de Commandin: ‘Recta portio conoidis rectanguli, quando leuior humido axem habuerit maiorem, quàm sesquialterum’ [3/2] ‘eius, quae usque ad axem; si ad humidum in gravitate non maiorem proportionem habeat, quàm excessus, quo quadratum quod fit ab axe maius est quadrato, quod ab excessu, quo axis maior est, quàm sesquialter eius, quae usque ad axem, ad quadratum, quod ab axe: demissa in humidum, ita ut basis ipsius tota sit in humido; & posita inclinata non manebit inclinata, sed restituetur ita, ut axis ipsius secundum perpendicularem fiat’ (Heiberg, T. II, p. 383).
-
voetnoot46)
- ‘b pr. 26 Archim. de Conoid’. [Huygens]. Comparez la note 40.
-
voetnoot41)
- Sur l'expression ‘dividendo’, comparez la note 10.
-
voetnoot48)
- Huygens, ayant achevé de retrouver à l'aide du principe formulé dans les théorèmes 6 et 7 les conditions, données par Archimède, de la stabilité de l'équilibre d'un segment de conoïde parabolique, flottant avec son axe dans la direction verticale, laisse de côté les beaux théorèmes d'Archimède qui se rapportent à la flottation des mêmes segments dans une position inclinée. Il procède à appliquer le même principe à d'autres corps flottants et commence à cet effet par préparer, au moyen du lemme qui va suivre, la solution du cas du cône de révolution.
-
voetnoot49)
- ‘a prop. 3. lib. 2. Conic.’ Voir, à la page 44 verso des ‘Coniques’, ouvrage cité p. 6 du T. I: ‘Si hyperbolen contingat recta linea, cum utraque asymptoton conveniet, & ad tactum bifariam secabitur: quadratum uero utriusque eius portionis aequale erit quartae parti figurae, quae ad diametrum per tactum ductam constituitur’.
-
voetnoot50)
- ‘b prop. 10. lib. 2. Conic.’ Voir à la page 46 verso des ‘Coniques’ (éd. Comm.): ‘Si recta linea sectionem secans cum utraque asymptoton conveniat; rectangulum contentum rectis lineis, quae inter asymptotos & sectionem interiiciuntur, aequale est quartae parti figurae factae ad diametrum, quae aequidistantes ipsi ductae lineae bifariam dividit.’
-
voetnoot51)
- ‘c prop. 1. lib. 2. Conic.’ Voir à la page 43 verso: ‘Si hyperbolen recta linea ad verticem contingat: & ab ipso ex utraque parte diametri sumatur aequalis ei, quae potest quartam figurae partem: lineae, quae à sectionis centro ad sumptos terminos contingentis ducuntur, cum sectione non convenient’.
-
voetnoot52)
-
d prop. 7. Archim. de Conoid.’ Il s'agit de la prop. VII, p. 31 verso de l'édition de Commandin, citée vers la fin de la note 26: ‘Spatia acutianguli coni sectione contenta eam inter se se proportionem habent, quam quae fiunt ex coni acutianguli sectionum diametris rectangula.’ (C'est la prop. VI de l'édition de Heiberg, p. 315 du T. I).
-
voetnoot53)
- ‘e prop. 43. lib. 3. Conic.’ Voir à la page 94 verso des ‘Coniques’ (ed. Comm.) ‘Si hyperbolen recta linea contingat, abscindet ex asymptotis ad sectionis centrum lineas continentes rectangulum aequale ei, quod continetur lineis ab altera contingente abscissis ad uerticem sectionis, qui est ad axem’.
-
voetnoot54)
- La condition de la stabilité de l'équilibre d'un cône de révolution flottant, l'axe étant dans la situation verticale avec le sommet en bas, fut publiée pour la première fois, par Daniel Bernoulli, dans les Comment. Acad. Petrop. de l'année 1738, p. 163. Elle est identique avec celle de Huygens, d'après laquelle la stabilité de l'équilibre exige que la densité relative du cône, par rapport à celle du fluide, excède ou égale la valeur BD6: BC6.
-
voetnoot55)
- D'après le ‘Theorema 6’ il suffira donc dès lors de prouver qu'on a GS > GM. Ajoutons qu'en janvier 1652 Huygens a essayé de substituer à la démonstration qui va suivre, une autre que l'on trouvera dans l'Appendice II du traité présent.
-
voetnoot57)
- ‘b prop. 3. lib. 2. Conic.’ [Huygens]. Comparez la note 49.
-
voetnoot41)
- Sur l'expression ‘dividendo’, comparez la note 10.
-
voetnoot58)
- On retrouve en marge le signe de renvoi ‘c’; mais la citation manque. Elle pouvait être identique avec celle de la note précédente; et c'est peut-être la raison qu'elle a été supprimée.
-
voetnoot59)
- ‘d lemm. 1 h. lib.’ [Huygens]. Voir la page 106.
-
voetnoot61)
- La condition de stabilité exige donc que la densité relative δ du cône soit plus petite que, ou égale à, 1 - BD6/BA6. Comme on le voit facilement, il y a des cas
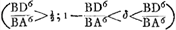 , où l'équilibre du cône flottant ne peut être stable dans aucune des deux situations qui sont compatibles avec la direction verticale de l'axe; mais Huygens se contente d'avoir donné les conditions de la stabilité pour la position verticale et ne s'occupe pas de la flottation dans des positions inclinées. , où l'équilibre du cône flottant ne peut être stable dans aucune des deux situations qui sont compatibles avec la direction verticale de l'axe; mais Huygens se contente d'avoir donné les conditions de la stabilité pour la position verticale et ne s'occupe pas de la flottation dans des positions inclinées.
|