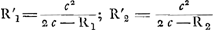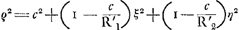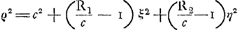Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651
(1908)–Christiaan Huygens–
[pagina 81]
| |
De iis quae liquido supernatant.
| |
[pagina 83]
| |
Avertissement.Même après tant de siècles, le mathématicien, en pleine possession des méthodes modernes, ne prendra connaissance de l'ouvrage d'Archimède sur les corps flottants sans éprouver un sentiment d'admiration profonde, mêlé d'étonnement à cause des résultats obtenus, lesquels au premier abord lui ont dû sembler dépasser les moyens de recherche et même tomber en dehors de la préoccupation des anciens. On comprend donc aisément que la lecture de cet ouvrage ait fait une vive impression sur le jeune Huygens et l'ait excité à l'émulation. Et cela d'autant plus parce que, par des études dans cette direction, il se plaçait tout de suite sur un terrain particulièrement approprié à son génie, où il remporterait dans la suite tant de succès et qui doit avoir excercé aussitôt sur lui une grande attraction, savoir la physique mathématique. Ce sont les résultats de ces études qui ont été réunis par Huygens dans le Traité qu'il intitula: ‘De iis quae liquido supernatant Libri 3.’ Les sujets à examiner n'étaient pas difficiles à trouver. En premier lieu | |
[pagina 84]
| |
Archimède s'était borné à la considération des segments sphériques et des conoïdes paraboliques; Huygens pouvait donc excercer ses forces sur d'autres figures géométriques simples. De plus il avait reconnu, en traitant l'équilibre de la chaîne, qu'un seul principe, celui d'après lequel le centre de gravité se place toujours aussi bas que possible, pouvait suffire à résoudre toutes les questions sur l'équilibre des corps sous l'influence de la gravité comme force motriceGa naar voetnoot1). Il était donc tout indiqué de rattacher les résultats obtenus par Archimède à ce principe général. C'est là en effet le but principal du livre premier. Dans les quatre premiers théorèmes Huygens déduit successivement du principe en question la situation horizontale du niveau des liquides, l'équilibre des corps flottants dont la densité est égale à celle du liquide, et enfin la loi célèbre d'Archimède appliquée au cas où la densité du corps est moindre que celle du liquide. De cette dernière déduction, plus compliquée que les autres, nous possédons même trois variantes reproduites dans le texte (p. 96-99), dans la note 14 du ‘liber i’ (p. 99-101), et dans l'Appendice I de ce traité. Viennent ensuite (p. 102-104) trois nouveaux théorèmes généraux qui se démontrent par des raisonnements aussi simples qu'ingénieux et dont les deux derniers, les ‘Theoremata 6 et 7,’ vont servir de base aux recherches qui suivent, celles sur la stabilité de divers corps flottants homogènes dont l'axe de révolution est dans la situation verticale. D'après ces théorèmes la stabilité exige que la différence de niveau du centre de gravité du corps flottant d'avec le centre de gravité de sa partie immergée (Theor. 6), ou, ce qui pour les corps homogènes revient au même, d'avec celui de la partie qui surnage (Theor. 7), soit un minimum. Pour éprouver cette stabilité il suffit donc de couper le corps flottant par un plan variable α (qui représente les positions diverses du niveau du liquide) de manière que le volume des segments découpés soit égal à celui de la partie immergée (ou surnageante); de déterminer les centres de gravité de ces segments; de mener par ces centres de gravité un plan β parallèle au plan variable α correspondant, et de vérifier si pour toutes les positions voisines la distance du | |
[pagina 85]
| |
centre de gravité du corps entier au plan β soit plus grande que pour la position initiale.Ga naar voetnoot2) C'est là la méthode suivie par Huygens pour retrouver (p. 105-113) les théorèmes d'Archimède sur la stabilité de l'équilibre d'un segment sphérique ou parabolique flottant avec l'axe de révolution dans une situation verticale et pour | |
[pagina 86]
| |
déterminer (p. 113-117) les conditions de stabilité d'un cône droit, flottant dans la même situation, soit avec le sommet en bas (Theor. 14), soit avec le sommet en haut (Theor. 15).
En abordant le second livre, qui traite l'équilibre des parallélipipèdes rectangles flottants, on éprouvera, nous le croyons, une certaine déception. Huygens, au lieu de poursuivre l'application de la méthode générale qu'il vient de développer dans le livre premier, retourne, par le ‘Theorema 1’ (p.122) du ‘Liber ii’ à celle d'Archimède, qui consiste dans la considération du couple formé par l'action de la gravité sur le corps flottant, représentée par une force appliquée au centre de gravité de ce corps, et par l'action de la pression vers le haut du liquide, représentée par une force appliquée au centre de gravité de la partie submergée. Il semble possible que cette incongruité a été introduite par la révision, sur laquelle nous reviendrons, subie par le ‘Liber i.’ Alors cette révision ne s'est pas étendue aux autres livres, peut-être parce que la méthode que Huygens venait d'introduire dans le ‘Liber i’, se montrait, dans les problèmes compliqués dont il s'occupe dans les ‘Libri ii et iii,’ moins maniable, qu'il ne l'avait prévu, et c'est probablement pour une raison semblable qu'il a laissé de côté dans le ‘Liber i’ les beaux théorèmes d'Archimède sur l'équilibre des conoïdes paraboliques flottants avec l'axe dans une situation inclinée. Toutefois, même alors il y a lieu de s'étonner que Huygens n'a pas au moins rattaché ce ‘Theorema 1’ du ‘Liber ii’ aux ‘Theoremata 6 et 7’ (p. 103-104) du ‘Liber i’ et cela d'autant plus que la démonstration qu'il en donne et qui ne repose pas sur les ‘Hypotheses’ formulées en tête du livre premier, n'a pas pu lui satisfaire entièrement.Ga naar voetnoot3) Quoiqu'il en soit, le ‘Liber ii’ nous apporte des recherches très profondes. Huygens évidemment a tâché d'obtenir une solution, aussi complète, qu'il lui était possible, du problème du parallélipipède rectangle flottant, limité seulement dans sa généralité par la supposition que la longueur du parallélipipède soit suffisante pour assurer l'horizontalité des arêtes dans le sens de cette longueur.Ga naar voetnoot4) | |
[pagina 6]
| |
Tableau représentant la solution complète du problème du parallélipipède rectangle flottant avec les arêtes longitudinales dans la situation horizontale.ε rapport de la densité du parallélipipède à celle du liquide. η rapport du côté le plus petit de la section verticale rectangulaire au plus grand côté de cette section. 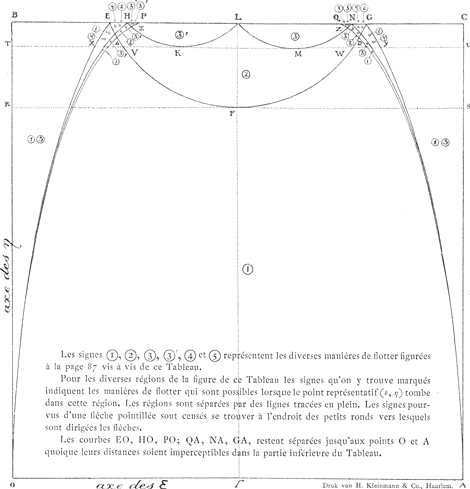 | |
Données principales.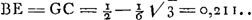 ; ; 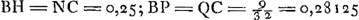
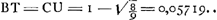 ; ; 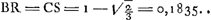
| |
Equations des courbes du Tableau.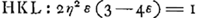 ; ; 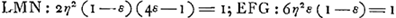 ; ;
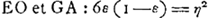 ; ; 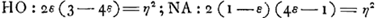 ; ;
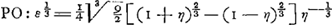 ; ; 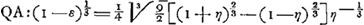 . .
| |
[pagina 87]
| |
Pour faire juger plus facilement jusqu'à quel point ce but a été atteint par le jeune Huygens; nous avons construit le tableau placé en regard de cette page, lequel contient, sous la forme d'une représentation graphique, la solution du problème en question.Ga naar voetnoot5) Pour expliquer ce tableau nous remarquerons en premier lieu que les signes ①, ②, ③ et ③′, ④ et ⑤ représentent dans leur suite naturelle les diverses manières de flotter qui sont possibles, en omettant toutefois les cas intermédiaires où l'un des sommets de la section verticale du parallélipipède se trouve dans la surface du liquide. 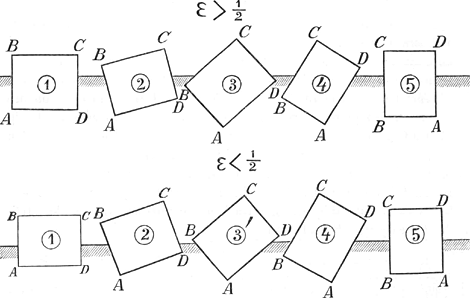 Comme le montrent les figures que nous donnons ici, cette suite est un peu différente, mais seulement pour le troisième cas, selon que l'on a ε > ½, ou ε < ½; ε représentant le rapport des densités du parallélipipède et du liquide. Soit, de plus, η = b/a le rapport du côté le plus courte b au côté le plus long a de la section verticale du parallélipipède, alors il est clair que les positions d'équilibre d'un parallélipipède flottant donné, de densité donnée, ne dépendront que des | |
[pagina 88]
| |
quantités ε et η. En considérant ces quantités comme des coordonnées rectangulaires, on peut donc représenter chaque parallélipipède par un point situé dans l'intérieur d'un carré OBCA dont les côtés sont égaux à l'unité. Ensuite on peut diviser ce carré de telle manière que la nature des positions diverses d'équilibre qu'un parallélipipède flottant peut prendre, soit indiquée par les chissres ①, ②, etc. qu'on trouve marqués dans l'intérieur ou à côté de la divisionGa naar voetnoot6) où tombe le point représentatif. C'est ce que nous avons fait dans notre tableau; là où l'on trouve deux chiffres, deux positions diverses sont possibles. Ces positions appartiennent alors d'ordinaire à des cas différents. C'est seulement dans les divisions peu étendues HΞP et QZN, marquées à côté ③ ③ et ③′ ③′, que les deux positions possibles appartiennent au même cas. Pour chacun des ‘Theoremata’ et ‘Conclusiones’ de Huygens nous indiquerons dans les notes la portée à l'aide de ce tableau explicatifGa naar voetnoot7). Il en résultera que les lignes de démarcation EFG, EO, HO, NA, GA, HKL et LMN ont été parfaitement reconnues et définies par Huygens; mais qu'il n'en est pas de même pour les lignes PO et QA. Pour trouver ces lignes Huygens aurait dû discuter les positions ③ et ③′ aussi complètement que les positions ② et ④.Ga naar voetnoot8) Il ne l'a pas fait et la raison en doit être cherchée probablement dans la plus grande difficulté de l'entreprise. Ainsi la détermination des conditions d'équilibre, qui pour ces dernières positions s'accomplit aisémentGa naar voetnoot9), dépend pour les positions ③ et ③′ de la résolution d'une équation biquadratique.Ga naar voetnoot10) | |
[pagina 89]
| |
Le troisième livre traite l'équilibre du cylindre droit flottant. La solution que Huygens donne de ce problème est plus bornée que celle du problème analogue pour le parallélipipède. En effet, désignons les positions diverses du cylindre flottant par les mêmes signes ①, ②, ③, ④, ⑤, en supposant que l'axe du cylindre soit parallèle à la ligne AB des figures de la page 87, qui ont servi pour indiquer les positions diverses du parallélipipède; alors ce ne sont que les positions ① et ② qui ont été traitées par Huygens. Pour ces positions d'ailleurs sa solution est complète.Ga naar voetnoot11) Avant de pouvoir aborder le problème du cylindre flottant Huygens avait à déterminer le centre de gravité d'un tronc de cylindre droit. Cette besogne une fois accomplie au moyen des ‘Theoremata 1-4’ (p. 159-162), les recherches pouvaient être menées par les mêmes voies que celles du ‘Liber ii.’ Souvent même les théorèmes et les démonstrations ne présentent qu'une différence d'ordre numérique. Ainsi les ‘Lemmata 1-3’ (p. 124-127) du ‘Liber ii,’ qui constituent pour ainsi dire le fondement géométrique de ce qui va suivre, correspondent au ‘Lemma’ et aux ‘Theoremata 5 et 6’ (p. 163-166) du ‘Liber iii.’ De même les ‘Theoremata 2, 3, 4, 5, 6’ (p. 128-136) du ‘Liber ii’ correspondent respectivement aux ‘Theoremata 7, 8, 9, 10, 11’ (p. 167-184) du ‘Liber iii.’ Plus loin le parallélisme cesse d'être aussi complet, à cause d'une certaine différence dans la nature des résultats.Ga naar voetnoot12) | |
[pagina 90]
| |
Notons enfin que vers la conclusion du ‘Liber iii,’ p. 189, se trouve discutée la manière dont les résultats obtenus dans les recherches sur les corps flottants, pourraient être vérifiés expérimentalement.
Le manuscrit du traité ‘de iis quae liquido supernatant,’ tel que nous le possédons, est écrit sur des feuilles de grand format, de quatre, ou quelquefois, de deux pages. Ces pages sont numérotées régulièrement de 1-16 pour le ‘Liber i’; de 23-48 pour le ‘Liber ii’; de 49-75 pour le ‘Liber iii’. Elles contiennent un grand nombre de figures; mais ces figures ont été tracées une séconde fois, sur de petits carrés de papier,Ga naar voetnoot13) avec plus de soin, mais sans modifications importantes; évidemment pour préparer la publication du traité. Dans l'automne de 1650 le traité avec les figures fut en voyé à van Schooten afin de le soumettre à son jugement. Il comptait alors quatre livres.Ga naar voetnoot14) Dans ses lettres du 27 septembre 1650 (No. 85, p. 130 du T, I) et du 21 novembre 1650 (No. 89, p. 135 du T. I) van Schooten le loua beaucoup et le renvoya avec la dernière lettre dans laquelle il présenta quelques remarques de peu d'importance et auxquelles Huygens n'a pas donné suite. Ensuite les deux premiers livres furent revisés et condensés dans un seul livre, le ‘Liber i’ de notre texteGa naar voetnoot15). Enfin tout était prêt pour la publication, qui | |
[pagina 91]
| |
toutefois n'eut pas lieu. Probablement elle fut remise d'abord pour faire précéder l'‘Εξέτασις’Ga naar voetnoot16) qui avait plus d'actualité; puis les travaux sur la dioptrique ont beaucoup occupé Huygens.Ga naar voetnoot17) En attendant Huygens ne perdait point de vue entièrement le traité qu'il avait composé. Il en donne un résumé à Gregorius à St. Vincentio dans une lettre du 25 octobre 1651 (notre No. 100, p. 151 et 152 du Tome I)Ga naar voetnoot18) mentionnant avec une certaine prédilection le ‘Theorema 7’, p. 167 du ‘Liber iii’, c'est-à-dire, le premier des deux théorèmes sur la stabilité d'un cylindre flottant avec l'axe dans la situation verticale. De même il en écrit le 29 décembre 1652 à G.A. Kinner de Löwenthurm (voir le No 146 à la page 212 du T. I), le 27 juillet 1657 à de Sluze (voir le No. 397 à la page 41 du T. II) et enfin le 19 novembre 1667 (voir le No. 1610 à la page 162 du T. VI) à Leopold de Medicis. Le 25 janvier 1652 il se remit à l'oeuvre et commença à s'occuper de nouveau des conditions d'équilibre d'un cône droit flottant traitées déjà d'une autre façon dans le ‘Theorema 14’, p. 115, du ‘Liber i.’ Nous avons reproduit ces travaux inachevés dans l'Appendice II du présent traité. | |
[pagina 92]
| |
Le 23 Mars de cette même année Huygens annota sur la page du titre: ‘Omnia mutanda’ et de même en 1679. ‘Pleraque rejicienda si non omnia. quia speculatio parum utilitatis habet, quamquam et Archimedes ipse in his operam posuit.’ Et encore, à la même ou à une autre occasion, sur la première page du ‘Liber i’: ‘Haec de corporibus solidis in liquido supernatantibus in primà adolescentia scripsi, cum nullum adhuc majoris momenti argumentum sese obtulisset, In his autem utilitas nulla, vel perquam exigua, Etsi Archimedes secundo περὶ ὀχ♉μένων libro non absimilia tractaverit. E primis Theorematis quaedam retineri possentGa naar voetnoot19) item de Cylindris.Ga naar voetnoot20) Reliqua vulcano tradenda.’ Mais nous croyons que l'on nous saura gré de n'avoir pas donné suite à cette dernière recommandation et qu'on ne souscrira pas au jugement si sévère, porté par Huygens sur son propre travail. A ce propos nous remarquerons seulement qu'au nom illustre d'Archimède, mentionné par Huygens, on pourrait joindre aujourd'hui les noms de plusieurs autres savants qui, depuis, se sont occupés du même sujet et qui ont été devancés par Huygens sur des points importants dans le traité que nous publions; à commencer par Daniel BernoulliGa naar voetnoot21), BouguerGa naar voetnoot22) et EulerGa naar voetnoot23) et à finir par M. Guyou qui a donné en 1879Ga naar voetnoot24) une théorie nouvelle, appelée par M. AppellGa naar voetnoot25) ‘la première théorie rigoureuse de la stabilité des corps flottants’; théorie qui repose sur le même principe que celle de Huygens.Ga naar voetnoot26) |
|