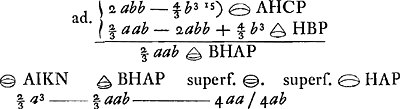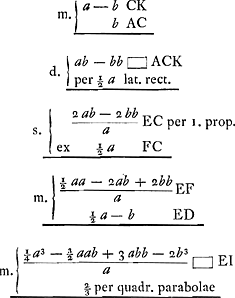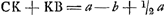|
| |
| |
| |
Prop. 1.
Si in parabola ABC ducatur utcunque parallela FE, axi BD, dico rectangulum sub segmentis AE, EC aequale esse rectangulo sub FE et latere recto parabolaeGa naar voetnoot2)
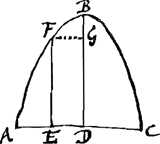
Cum enim rectangulum sub latere recto et BD aequale sit quadrato AD, si utrinque auferatur rectangulum sub latere recto et BG sive quadratum FG sive ED, remanebunt, hinc, rectangulum sub lat. recto et FE, inde, rectangulum AEC, aequalia.
Hinc manifestum est BD esse ad FE ut rectangulum ADC ad rect. AEC.
| |
Prop. 2.
Si sit semicirculus ABC cui sit inscripta parabola ABC, et utcunque ducta FE perp. est ut BD ad GE longitudine sic BD ad FE potentia.
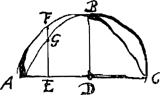
BD namque est ad GE, ut rectangulum ADG.Ga naar voetnoot3) sive quadratum BD ad rectangulum AEC sive quadratum FE.
| |
| |
| |
Prop. 3.
Si convertatur semicirculus ABC et semiquadratum AHIC dico sphaeram factam a semicirculo in conversione, esse ad cylindrum ex conversione semiquadrati AHIC, ut 2 ad 3.Ga naar voetnoot4)
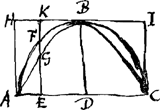
Cum enim ut prius utcunque ductâ perp. KE, quae etiam inscriptam parabolam secat, sit ut BD vel KE ad GE longitudine, sic KE ad FE potentiâ, vel circulus ex conversione KE ad circulum ex conversione FE, erit ideo totus cylindrus ex conversione AHIC ad sphaeram ex conversione semicirculi ABC, ut rectangulum AHIC ad parabolam AGBCGa naar voetnoot5), id est ut 3 ad 2 ut patet ex quadratura parabolae.Ga naar voetnoot6)
| |
Prop. 4.
Superficies sphaerae quadrupla est maximi in eâ circuli.Ga naar voetnoot7)
Quia enim dimidia sphaera ABC est ad cylindrum AEFC Ga naar voetnoot8) ut 2 ad 3 constat
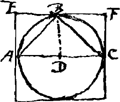
eam quoque duplam esse coni inscripti ABC. Porro cum constet sphaeram aequalem esse cono altitudinis DB et qui basin habeat superficiei ejusdem sphaerae aequalem Ga naar voetnoot9), sequitur quoque conum altitudinis DB qui aequalis sit quartae parti sphaerae, basin habere quartae parti superficiei sphaerae aequalem: Atqui talis est conus ABC, ergo basis ejus maximus in sphaera circulus AC aequalis est quartae parti superficiei sphaerae: quod erat demonstrandum.
| |
| |
| |
Prop. 5
Si parabolam secet parallela axi linea FS et simul sphaeram NAHIK, erit ut rectangulum CG ad partem parabolae abcissam AEC, ita cylindrus RF ad portionem sphaerae PAH.
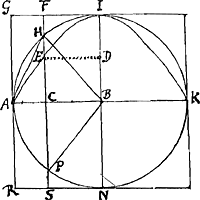
Hoc manifestum satis est ex prop. 2.Ga naar voetnoot10)
| |
Prop. 6.
Datae portioni sphaerae conum vel cylindrum aequalem invenire.
Sit data portio HAP: AK ∞ a, AC ∞ b. Quia autem constat ex praecedenti prop. partem abscissam ex parabola, AEC, esse ad rectang. CG ut portio sphaerae HAP ad cylindrum RF quaeram primo valorem partis AEC.
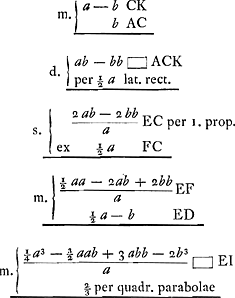
| |
| |
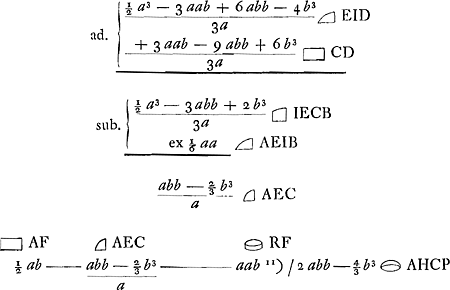
Ga naar voetnoot11
apparet hinc portionem sphaerae AHCP aequalem esse cylindro cujus basis circulus descriptus radio AC, altitudo vero AB - ⅓ AC nam 4 bb basin m. per ½ a - ⅓ b altitudinem fit 2 abb - 4/3 b3 ut ante.
Si autem conum velimus reperire portioni huic aequalem, cujus basis sit eadem quae basis portionis id est circulus HP: dividatur 2 abb - 4/3 b3 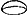 AHCP per triplum circuli Ga naar voetnoot12) 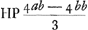 fit altitudo coni quaesita 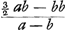 . Id est ut CK ad CKB Ga naar voetnoot13) sic AC ad quaesitam altitudinem. Haec est propos... Archim. Ga naar voetnoot14)
| |
Prop. 7.
Datae sphaerae portionis superficiei circulum aequalem invenire.
Data sphaerae portio sit AHCP.
| |
| |
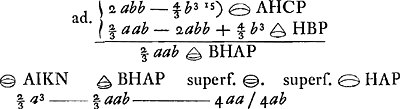
Ga naar voetnoot15)
Hinc liquet superficiem datae partis AHCP aequalem esse circule cujus radius AH. Quae est prop... Archimedis.Ga naar voetnoot16)
|
-
voetnoot1)
- C'est ici la pièce indiquée dans la lettre No. 23b (p. 557 du T. II) à Mersenne du 23 déc. 1646 comme comprenant ‘Une autre démonstration de ce qui est contenu au livre d'Archimède, de sphaera et cylindro.’ Voir l'Avertissement à la p. 5 du volume présent.
-
voetnoot2)
- Sur une des pages précédentes du ‘boeckje’ on rencontre une démonstration ‘par lettres,’ c'est-à-dire algébrique, de la même proposition.
-
voetnoot4)
- C'est la première partie du ‘Corollarium’ de la Prop. XXXIV du premier Livre de l'ouvrage ‘De Sphaero et Cylindro’ d'Archimède. Voir la p. 147 du T. I de l'édition de Heiberg mentionnée dans la note 2 de la pièce No. IX (p. 50).
-
voetnoot5)
- Ici encore on croit reconnaître l'influence de Cavalieri. Voir la note 8 de la pièce No. XI (p. 60).
-
voetnoot6)
- Comparez la pièce No. XI (p. 56) où Huygens déduit la quadrature de la parabole par une voie nouvelle.
-
voetnoot7)
- C'est la Prop. XXXIII de l'ouvrage mentionné d'Archimède. Voir Heiberg, T. I, p. 137.
-
voetnoot8)
- Il s'agit du cylindre dont la base est le cercle décrit sur AC comme diamètre et dont BD est la hauteur.
-
voetnoot9)
- Comparez chez Archimède la démonstration de la Prop. XXXIV (Heiberg I, p. 141).
-
voetnoot10)
- C'est-à-dire en appliquant la méthode de démonstration de la proposition 3.
-
voetnoot11
- Toutes les expressions algébriques qui suivent, pour autant qu'elles représentent des volumes ou des aires, ne sont que proportionelles à ces volumes et à ces aires, desquelles on trouve les valeurs véritables en multipliant les expressions en question par ¼ π.
-
voetnoot14)
- Voir en effet la Prop. II du Livre II ‘De Sphaera et Cylindro,’ p. 195, T. l de l'édition de Heiberg.
-
voetnoot16)
- Voir la Prop. XLII du Livre I de l'ouvrage cité d'Archimède, p. 177, T. I, de l'édition de Heiberg.
|
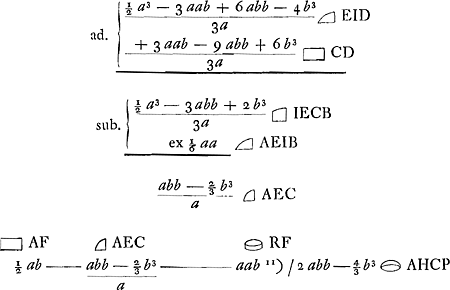
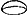 AHCP per triplum circuliGa naar voetnoot12)
AHCP per triplum circuliGa naar voetnoot12) 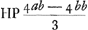 fit altitudo coni quaesita
fit altitudo coni quaesita 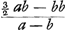 . Id est ut CK ad CKBGa naar voetnoot13) sic AC ad quaesitam altitudinem. Haec est propos... Archim.Ga naar voetnoot14)
. Id est ut CK ad CKBGa naar voetnoot13) sic AC ad quaesitam altitudinem. Haec est propos... Archim.Ga naar voetnoot14)