Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651

[p. 61]

XII.¹⁾
[1646].
De Tactionibus.²⁾

Probl. 1.
Linea AB et punctum D sunt datae: Oportet circulum describere qui tangat lineam et transeat per punctum.

Ex puncto D ducatur DA perpend. AB, dividatur DA bisariam in E, describaturque parabola EC, cujus latus rectum sit quadruplum ED et vertex sit E, axis



EP: dico quodcunque punctum in hac sumptum esse centrum quaesiti circuli.

Sumatur punctum C in dicta parabola ex quo, radio CD describatur circulus DB dico hunc tangere lineam AB; Demonstrandum ergo est CB perpend. super AB aequalem esse CD. Fiat itaque GD aequalis DC et erit GC contingens in C³⁾, unde si demittatur perpend. CF erit FE aequalis GE, et GD aequalis AF, quia AE est aequalis ED; itaque cum FA sit aequalis DG, erit etiam BC aequalis CD quod erat demonstrandum.

1) Cette pièce traite les coniques considérées comme lieux géométriques du centre d'un cercle passant par un point donné et touchant à une droite ou à un cercle donné,

2) Ce titre, sans doute, fait allusion à celui d'un des ouvrages perdus d'Apollonius, décrits par Pappus dans l'Introduction au Livre septième des ‘Mathematicae collectiones,’ (voir, à la page 159 recto, l'ouvrage cité dans la note 3 de la Lettre N^o. 538, p. 259 du T. II). Toutefois chez Apollonius il s'agissait de la construction des cercles déterminés par trois conditions d'attouchement et ici il s'agit des lieux géométriques des centres des cercles satisfaisant à deux de ces conditions.

3) Voir le § 8 de la Pièce N^o. IV (p. 33).

[p. 62]

Probl. 2.
Data sunt linea AB et circulus HDI, oportet circulum describere qui utrumque contingat.

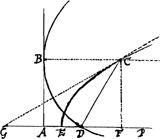
Vertice E in media AD, axi EH, quartâ parte lateris recti EH parabola describatur



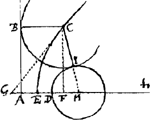
EC; et ubivis in ea punctum sumatur, ut C dico id esse centrum quaesiti circuli. Oportet igitur demonstrare perpendicularem CB super BA aequalem esse CI. Ponatur GH aequalis HC et erit GC contingens parabolam in C, unde demissa perp. CF erit et FE aequalis EG, additisque hinc ED illi AE erit AF sive BC aequalis GD, haec vero aequalis est CI, quod erat dem.

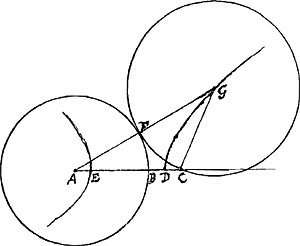
Secet autem nunc data linea AB datum circulum HDI. Dividatur AD bisariam in E; hinc axi EF, ¼ lateris recti EH, parabola describatur EcC; dico omnia puncta hujus parabolae esse centra quaesiti circuli.

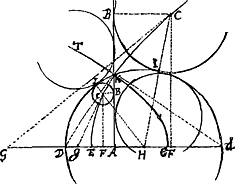
Primum autem probabo lineam AB et circulum datum et parabolam sic descriptam in eodem puncto ut hic in K sese secare.

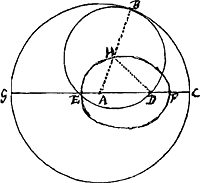
DE est ½ DA, DH est ½ Dd, itaque et EH est ½ Ad, et rectangulum sub DA, Ad duplum rectanguli sub DA, EH. Quia autem EH est ¼ lateris recti, duplum rectanguli sub DA, EH est aequale quadrato AK, ergo ut K sit et in parabola et in circulo, debet esse rectangulum DAd (hoc enim et quadrato AK aequale est) duplum rectanguli sub DA, EH, atqui sic esse demonstratum est, ergo etc.

Sumatur nunc in parabola punctum ubicunque ut C, describaturque circulus CBI, dico illum et lineam et circulum tangere, sive BC aequalem esse CI.

Ponatur enim HG aequalis HC et quia tunc ducta GC parabolam contingit in C, demissâ perpendiculari CF, erit GE aequalis EF, et si ab aequalibus aequalia detrahantur manebit DG aequalis AF sive BC; GD autem etiam aequalis est CI, quia antea HG, HC erant aequales, Ergo et BC aequalis est CI; quod erat demonstrandum. Sic quoque demonstrari potest de parabola eKT, quae non minus huic rei inservit quam EKC.

Notandum est duas hasce parabolas in K invicem ad angulos rectos secare, quia

[p. 63]

nimirum contingentes earum DK, aK sese in eodem puncto K ad angulos rectos secant; contingunt autem quia DE, EA sunt aequales.

Probl. 3.
Sit datus circulus ABF et punctum C; oportet describere circulum qui circulum datum contingat et per datum punctum transeat.

Ducatur AC, et dividatur BC bifariam in D; describatur porro hyperbola foco



C, vertice D, axi ED, qui aequalis sit AB; dico quodcunque sumatur in ea punctum, esse centrum quaesiti circuli.

Sumatur in ea punctum G ducaturque circulus per punctum C datum, probandum est illum contingere quoque circulum ABF: sive ducta GA, GF aequalem GC. Excessus AG supra GC aequalis est axi hijperbolae ED, per 51, 3^tii Apol.⁴⁾ AB sive AF aequalis est axi ED ex constructione; ergo si ab AG auferatur AF, remanet FG aequalis GC quod erat demonstrandum.

Si datum punctum D sit intra circulum datum ACB, ducatur recta per punctum



D et centrum dati circuli quae sit CG, et focis, circuli dati centro A, punctoque dato D, diametro maximâ EF, aequali radio circuli dati AC, describatur ellipsis EHF. dico quodvis punctum in ipsius circumferentia sumptum esse centrum quaesiti circuli; ut si sumatur punctum H et semidiametro HD describatur circulus HBD, dico hunc tangere quoque circulum datum ACB, sive ducta e centro AB, HB, HD aequales esse. Ex constructione EF aequalis est AC; sed AH una cum HD quoque aequalis est EF, per 52 tertij Apoll.⁴⁾ ergo et AH cum HD aequalis est AC vel AB, et detracta communi AH, manet BH aequalis HD, quod erat demonstrandum.

4) Voir p. 98 recto de l'édition de Commandin, citée dans la Pièce N^o. 5, note 4 (p. 6 du T. I).

4) Voir p. 98 recto de l'édition de Commandin, citée dans la Pièce N^o. 5, note 4 (p. 6 du T. I).