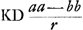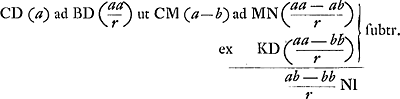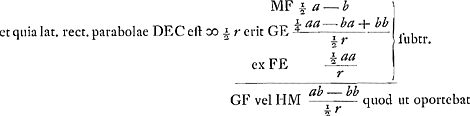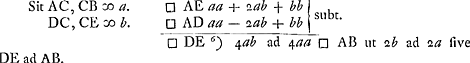Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651

[p. 56]

XI.¹⁾
[1646].
Quadratura Parabolae.

Communis notio.

Quod minus est quavis quantitate non est quantitas, sed ipsum nihil.

1) La pièce contient une suite de théorèmes qui mènent à la quadrature de la parabole et à la cubature de divers solides de révolution engendrés par elle.

Theorema. 1.
Si Parabolae ABC inscribatur supra dimidium basis ipsius similis parabola DEC, id est cujus latus rectum sit dimidium lateris recti BO parabolae ABC, et ex puncto I ubivis sumpto ducatur parallela axi BD IM, secans parabolam DEC in H, et basim in M; Dico HM duplum esse NI.

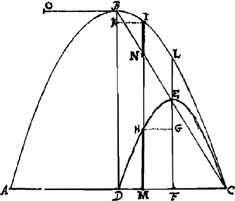
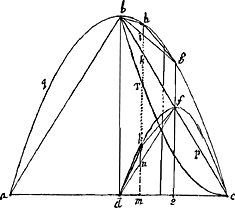
Sit enim DC ∞ a, DM ∞ b, lat. rectum B O ∞ r. BK autem est bb/r ergo

[p. 57]

est duplum NI.

Vide demonstrationem hujus in pagina ad sinistram.²⁾

2) Cette annotation a été ajoutée plus tard, à une date inconnue. Elle se rapporte à la démonstration plus géometrique qui suit et qu'on trouve à la page précédente du ‘boeckje’.

‘Demonstratio.



Quia parabolae ABC, DEC sunt similes; utcunque ex angulo C ducatur CR, semper à parabola DEC bifariam dividetur, ut hic in H. Linea autem LC tangit parabolam in C ergo KI aequalis IH, ut patet ex pr. 49.2^di Con. Apoll. si ergo dematur IN ex IH et addatur lineae KI, quae ante aequalis erat IH, excedet KN, NH duplo lineae IN : HM vero addita NH fit NM aequalis ipsi KN, ergo necessario HM fuit dupla IN. quod demonstrandum erat.’

Theorema 2.
In omni parabola si à vertice B ducatur recta ad extremum basis C; tota parabola octupla est partis abscissae BHGCFK.

Quia enim gf est dimidia fe ex praecedenti theor. erit triangulum def duplum trianguli fgb:et rursus quia hk dimidia est lm, et ik dimidia nm, et per id ih dimidia ln; erit triangulum dlf duplum trianguli bhg: Cum autem sic in infinitum procedi possit, semper reliquis segmentis inscribendo triangula, certum est totam portionem dlfe duplam esse portionis bhgfk, et quia haec dimidia est totius bhgcfk³⁾,

3) Puisque ge est le bisecteur des cordes parallèles à bc; ce qui permet de démontrer l'égalité des aires paraboliques fghb et gfc par des raisonnements analogues à ceux qui précèdent.

[p. 58]

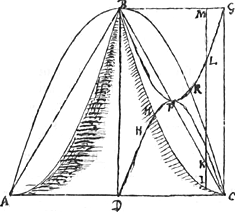
hanc totam aequalem esse dimidio parabolae dfc. parabola vero dfc (quia similis est parab. abc, et quia similes figurae sunt in duplicata ratione ut earum latera homologa) quarta pars est parabolae abc, ergo bhgcfk octava pars totius parabolae abc: et bhgcfk una cum aqb quarta pars parabolae; et triangulum abc tres quartae totius parabolae, et ideo tota parabola sesquitertia trianguli abc ut demonstravit Archimedes.⁴⁾

4) Voir la Prop. XXIV de la ‘Quadratura parabolae’ d'Archimède, p. 349 du T. II de l'édition de Heiberg citée dans la note 2 de la pièce IX.

Corollarium 1. Theorematis 2.^di

hk utrunque ducatur aequalis semper kr.⁵⁾.

5) Ici brc représente une parabole dont le sommet se trouve à c et dont l'axe est parallèle à bd.

2.

hl aequalis rm.

Theor. 3.
Sit centrum A, et linea AB, bifariam divisa in C, et CD aequalis CE: Dico quod si vertatur AB circa centrum A; spatium quod percurret linea AB, ad spatium quod percurret linea DE, proportionem habiturum, quam linea AB ad DE.

⁶⁾

Circuli autem proportionem habent quam quadrata.

6) Au lieu de □ DE lisez: l'aire comprise entre les carrés construits sur AD et sur AE.

Corollar. Theor. 3.^tii

Id quod circumeundo fit corpus à rectangulo EG ad cylindrum cujus basis circulus BB, ut ED ad AB.

Theor. 4.
Si parabola ADC vertatui circa axem AB donec in eundem locum redierit solidum corpus quod eo circuitu faciet, eam

[p. 59]

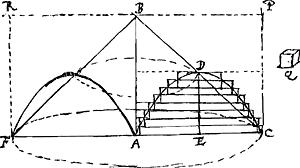
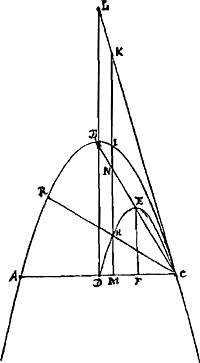
proportionem habebit ad cylindrum FRPC qui basim et altitudinem duplam habet, quam parabola ADC ad rectangulum AP; quamobrem etiam aequalem erit cono FBC.

Si negetur aequale esse, cono FBC sive tertiae parti cylindri FP, corpus factum ex circumvolutione parabolae ADC sit differentia cubus Q; et sit primo minus cono: Inscribantur ergo et conscribantur parabolae parallelogramma aequalis altitudinis, ut inscripta à conscriptis ablata, rectangula quaedam relinquant, quae una cum parabola circumversa, omnia simul nimus solidum efficiant quam cubus Q. Quia itaque ex praecedenti 3^o. theor. patet singulas bases parallelog.^um circumversas spatia circularia describere quae sunt ad FC circulum, ut bases eorum ad radium AC; sequitur quoque omnia simul solida circularia quae dicta parallelogramma essicient circumcurrendo, proportionem habitura ad cylindrum FP, quam ipsa parallelogramma omnia ad Parallelogrammum AP. ergo figura constans ex parallelogrammis circumscriptis (quia major est ipsa parabola, sive tertia parte rectanguli AP) circumversa efficiet solidum quod majus erit tertiâ parte cylindri FP, sive majus cono FBC, cui aequale erat solidum ex parabola una cum cubo Q; Sed quia parvula relicta rectangula, omnia simul circumversa minus solidum efficiunt quam est cubus Q, sequitur si horum solida subtrahantur à solido ex conscriptis parall.^s, remansura solida ex inscriptis parall.^s quae simul majora erunt ipso solido parabolae, quo tamen continentur, quod est absurdum: ergo solidum quod efficit circumvoluta parabola non est minus cono FBC.

Sit jam parabolae solidum majus cono FBC, ergo detracto cubo Q aequale erit cono. Sed omnia simul solida ex parvulis rectangulis minora sunt cubo Q, parte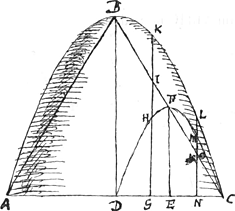



vero horum (id est quae intra parabolam continetur) à parabola detractâ, relinquuntur solida ex inscriptis parall.^is, quae minora simul sunt cono, et parabolae solidum detracto cubo Q aequale debebat esse cono, quod est absurdum.

Theor. 5.⁷⁾ Conoides parabolicum sesquialterum est coni, qui eandem basin et altitudinem habet.

Sit conoides ABC, conus basis et altitudinis ejusdem ABC; dico conoides sesquialterum esse coni.

7) Ce théorème est mentionné par Huygens dans sa lettre N^o. 11 (p. 18 du T. I) du 3 septembre 1646 à son frère Constantyn, après quoi il ajoute: ‘Cecij a este demonstre d'Archimede mais d'une autre demonstration que la miene’. On retrouve en effet le théorème en question dans la proposition XXI (Heiberg, T. I, p. 387) de l'ouvrage ‘De Conoidibus et Sphaeroidibus’.

[p. 60]

Quia enim per prop. 1. GH est dupla KI, MN dupla OL et sic de caeteris, erit solidum in circumvolutione sactum circa axem BD à parabola DFC duplum solidi à parte BKLCIB⁸⁾. Solidum autem à parabola per antecedentem aequale est cono ABC, ergo conus, ejusdem partis BKLCIB circumversae duplus erit. Ergo totum conoides ad inscriptum ut 3 ad 2, id est sesquialterum coni.

8) C'est bien l'influence qui se fait sentir ici, de la méthode de Cavalieri, dont van Schooten était l'un des promoteurs. Voir, à ce propos, les Lettres N^o 85, N^o 85a, N^o. 86 et N^o 87 (p. 130, 561, 132 et 133 du T. I).

Theor. 6.⁹⁾
Corpus quod fit circumvolutione partis BHCD dimidium est coni eandum basin et altitudinem habentis.

Quia IK dimidia est LM per 1.^mam pr. et sic de ceteris omnibus, solidum quod fit circumversione totius partis BFKCHB etiam dimidium solidi a parabola BFG, hoc vero aequale est cono ABC; ergo et praedictae partis solidum dimidium coni ABC, et solidum à parte BHCDB etiam dimidium coni, quia simul conum componunt.

9) Ce théorème, comme le précédent, est mentionné dans la lettre du 3 sept. 1646; mais avec la remarque: ‘ce que je ne pense pas qu'il avoit esté demontré cijdevant.’

Corollarium 1.

Item corpus ex circumvolutione figurae BKCHB aequale est cono ABC.

Corollarium 2.

Conoides convexum ABRC ad concavum ABHC ut 3 ad 1.